TEORIA GIER

8 czerwca 2021

Gra



to dowolna sytuacja konfliktowa,



gracz natomiast to dowolny jej uczestnik



każda strona wybiera pewną strategię
postępowania, po czym zależnie od strategii
własnej oraz innych uczestników każdy gracz
otrzymuje wypłatę w jednostkach
użyteczności (pieniądze, wzrost szansy na
przekazanie

własnych genów

czy też

cokolwiek innego, z czystą satysfakcją
włącznie)



wynikowi gry zwykle przyporządkowuje się
pewną wartość liczbową.



istota tej gry nie polega na

próbie odgadnięcia intencji

gracza, lecz na skrywaniu

własnych zamiarów.



Podstawowym założeniem teorii gier

jest racjonalne działanie wszystkich

podmiotów decyzyjnych (graczy).

8 czerwca 2021

8 czerwca 2021

Aby dana sytuacja mogła być nazwana grą, musi
spełniać następujące warunki:



istnieje skończona liczba uczestników,



każdy uczestnik posiada skończoną

liczbę sposobów działania (strategii),



uczestnik, który chce posłużyć się teorią

gier, musi znać wszystkie dostępne

pozostałym graczom strategie, lecz nie

może wiedzieć, która z nich będzie

obrana,



wygrana każdego uczestnika zależy

zarówno od działania pozostałych graczy,

jak i od jego własnego działania,



wszystkie możliwe wyniki są mierzalne.

8 czerwca 2021

Teoria gier



to dział matematyki zajmujący się
badaniem optymalnego
zachowania w przypadku konfliktu
interesów

8 czerwca 2021

8 czerwca 2021

Badania w zakresie teorii gier i jej
zastosowań wielokrotnie zostały uznane
przez Komitet Nagrody Nobla



1978 Herbert Simon

– za wkład w rozwój ewolucyjnej teorii

gier, w szczególności za koncepcję
ograniczonej racjonalności.

– Komitet nagrody określił te rezultaty

jako przełomowe badania nad
procesem podejmowania decyzji
wewnątrz organizacji gospodarczych
oraz teorię ich podejmowania.

8 czerwca 2021



1994 John Nash, Reinhard

Selten i John Harsanyi

– za rozwój teorii gier i jej

zastosowania w ekonomii.



1996 William Vickrey i James

Mirrlees

– za stworzenie modeli przetargów i

badanie konfliktów z niesymetryczną

informacją uczestników.

8 czerwca 2021



2005 Thomas C. Schelling i Robert J. Aumann

–

za zastosowanie teorii gier w naukach społecznych

i mikroekonomii (dot. zachowania jednostek i

rozwiązywania konfliktów) . Ich teoria pozwoliła

zastosować teorię gier – lub teorię decyzji

interaktywnej – do poszukiwania odpowiedzi na

pytanie, dlaczego niektóre grupy, organizacje i

kraje odnoszą sukcesy we współpracy, natomiast

inne popadają w konflikty.

–

Thomas Schelling stosował teorię gier do analizy

negocjacji międzynarodowych w okresie "zimnej

wojny". Analizował takie zagadnienia, jak: polityka

wzajemnych ustępstw, gróźb, zastraszania.

–

Aumann użył teorii gier by zanalizować Talmud.

Między innymi rozwiązał starą tajemnicę "podziału

spadku zmarłego męża pomiędzy jego trzy żony".

Rozwiązaniem było podanie zmniejszenia wartości

spadku (porównanego do jego pierwotnej wartości).

8 czerwca 2021



2007 Leonid Hurwicz, Eric S. Maskin,

Roger B. Myerson

– za prace nad teorią wdrażającą systemy

matematyczne w procesy gospodarcze, która przy

zastosowaniu równań matematycznych i

algorytmów pozwala ocenić prawidłowość

funkcjonowania rynków.

– Teoria ta pomogła określić ekonomistom skuteczne

mechanizmy rynkowe, schematy regulacji i

procedury wyborów i dziś odgrywa główną rolę w

wielu dziedzinach ekonomii oraz w naukach

politycznych.

8 czerwca 2021

Zalety teorii gier:



pozwala ustrukturyzować proces decyzyjny i

wyznaczyć racjonalne rozwiązanie.



możliwość wyznaczenia dobrego rozwiązania

zależy jednak od tego, jak dobrą informacją

dysponuje dany podmiot.



bada jakie strategie powinni wybrać gracze

żeby osiągnąć najlepsze wyniki.

8 czerwca 2021

Gry ze względu na wartość dzielą
się na:



gry o sumie stałej (zysk jednego
gracza jest równoważny stracie
drugiego) i na gry o sumie
zmiennej



gry sprawiedliwe (gdy wartość
oczekiwana wypłaty każdego z
graczy jest taka sama) oraz gry
niesprawiedliwe

8 czerwca 2021

Gra w kasynie



uznając za wypłatę sumę pieniężną,

jest grą o sumie zerowej (wygrana

gracza to strata kasyna, i na odwrót;

nie rozpatrujemy tu zadowolenia z

samego faktu gry), jednakże nie jest

ona grą sprawiedliwą (z przyczyn

oczywistych prawdopodobieństwa

wygranej są dla gracza

niekorzystne, a wartość oczekiwana

wygranej pieniężnej ujemna).

8 czerwca 2021

Gry

W zależności od liczby tych

przeciwników i ich interesów
rozróżniamy różne rodzaje gier, na
przykład:



gry dwuosobowe,



gry wieloosobowe,



gry koalicyjne.

8 czerwca 2021

Macierz wypłat



jest tablicą, która przedstawia kwoty
otrzymane przez gracza wymienionego po
lewej stronie tej tablicy po wszystkich
możliwych partiach gry. Wypłat dokonuje gracz
wymieniony u góry tablicy macierz ta składa
się z tylu kolumn, ile jest wszystkich
możliwych sposobów działania gracza
zamieszczonego u góry tablicy, i z tylu wierszy,
ile jest wszystkich możliwych sposobów
działania gracza zamieszczonego po lewej
stronie tablicy).

8 czerwca 2021

Przykład normalnej formy macierzy

wypłat dla gry dwuosobowej i dwóch

możliwych strategii

Gracz 2 wybiera

lewą kolumnę

Gracz 2 wybiera

prawą kolumnę

Gracz 1 wybiera

górny wiersz

4

,

3

-1

,

-1

Gracz 1 wybiera

dolny wiersz

0

,

0

3

,

4

8 czerwca 2021

Historycznym przykładem gry
niekooperacyjnej jest dylemat
więźnia.

Problem decyzji

aresztowanego A

D z i a ł a n i a A

D z i a ł a n i a B
Nie przyznawać się wsypać
kompana

Nie przyznawać

się

1 rok

10 lat

Wsypać kompana

0 lat

5 lat

Problem decyzji

aresztowanego B

D z i a ł a n i a B

D z i a ł a n i a A
Nie przyznawać się wsypać
kompana

Nie przyznawać

się

1 rok

10 lat

Wsypać kompana

0 lat

5 lat

Gra dwuosobowa

aresztowanych

D z i a ł a n i a A

D z i a ł a n i a B
Nie przyznawać się wsypać
kompana

Nie przyznawać

się

1 rok

1 rok

10 lat

0 lat

Wsypać kompana

0 lat

10 lat

5 lat

5 lat

8 czerwca 2021

Gra dwuosobowa o sumie zero



Grami dwuosobowymi o sumie
zero są takie sytuacje, gdy w grze
biorą udział tylko dwie strony, a
przegrane jednej ze stron są
wygranymi drugiej.

8 czerwca 2021

Macierz wypłat

 

m

mn

n

m

m

ij

d

d

a

a

a

a

a

a

a

....

....

...

...

...

....

....

s

...

s

s

1

1

2

1

12

11

n

2

1























8 czerwca 2021

Przykład



Dwie konkurencyjne firmy Alfa i Beta są dealerami

dobrze znanej marki odbiorników telewizyjnych. Roczne

zyski tych dwóch firm wynoszą odpowiednio 4 i 8 mln zł.



Alfa chce rozszerzyć swoją działalność i otworzyć zakład

montażu odbiorników zakładając, że przyniesie to jej

roczny zysk równy 10 mln zł. Oczekuje przy tym, że

firma Beta będzie kontynuować swoją działalność bez

podejmowania montażu odbiorników u siebie. Jednakże

szef firmy Beta usłyszał o planach firmy Alfa i obliczył, że

jeśli plany firmy Alfa będą urzeczywistnione, to zyski

firmy Beta spadną do 2 mln zł.



Natomiast jeśli Beta uruchomi zakład montażu, a Alfa

nie zrobi tego, to zysk firmy Beta wzrośnie do 11 mln zł,

a zysk firmy Alfa spadnie do 1 mln zł.



Gdyby obydwie firmy uruchomiły zakłady montażu, to

wtedy obie zarobiłyby po 6 mln zł na rok.



Jaką strategię powinna wybrać firma Alfa, a jaką Beta,

aby zyski ich były możliwie jak największe?

8 czerwca 2021

Macierz

Strategie firmy Beta

Kontynuowanie

sprzedaży

Uruchomienie

zakładu

montażu

odbiorników

telewizyjnych

Strategie

firmy Alfa

Kontynuowani

e sprzedaży

0

-3

Uruchomienie

zakładu

montażu

odbiorników

telewizyjnych

6

2

8 czerwca 2021

Gra jest rozwiązana, gdy
wyznaczymy:



wartość gry,



strategię, którą ma zastosować gracz
umieszczony w macierzy wypłat po lewej
stronie, aby zapewnić sobie średnią wygraną
na partię co najmniej równą wartości gry,



strategię, którą ma zastosować gracz
umieszczony w górnej części macierzy
wypłat, aby średnia przegrana na partię nie
była większa niż wartość gry.

8 czerwca 2021

dr inż. Iwona Staniec

Strategie firmy Beta

Kontynuowanie

sprzedaży

Uruchomienie

zakładu

montażu

odbiorników

telewizyjnych

Najmniejsze

wartości w

wierszach

Min a

ij

Strategie firmy
Alfa

Kontynuowanie

sprzedaży

0

-3

-3

Uruchomienie

zakładu montażu

odbiorników

telewizyjnych

6

2

2

Max (Min a

ij

)

Największe

wartości w

kolumnach

Max a

ij

6

2

Min (Max a

ij

)

8 czerwca 2021

strategia zdominowana



występuje, kiedy gracz posiada

strategię dającą mu wyższą wypłatę bez

względu na to, jak zagra konkurent.

Strategia dominująca



to najlepsza możliwa reakcja na
dowolną strategię zastosowaną
przez konkurenta.



Jej logika nieuchronnie prowadzi
do pogorszenia wyniku, gdy gra
ma charakter niekooperacyjny.

8 czerwca 2021

8 czerwca 2021

Punkt siodłowy



gra posiada punkt siodłowy, jeżeli każdy z graczy

podczas całej gry stosuje tylko jeden sposób

działania.



Punktem siodłowym jest punkt w macierzy wypłat

znajdujący się na przecięciu tych dwóch

sposobów działania, natomiast wypłata w tym

punkcie stanowi wartość gry



V = V

A

=Max (Min a

ij

) = V

B

=Min (Max a

ij

)



Wartość gry jest średnią kwotą przypadającą na

partię, którą wygrałby w długim okresie jeden z

graczy, gdyby obaj stosowali swe najlepsze strategie.

8 czerwca 2021

dr inż. Iwona Staniec

KRYTERIA WYBORU
DECYZJI W WARUNKACH
NIEPEWNOŚCI



Kryteria nieprobabilistyczne



Kryteria probabilistyczne

8 czerwca 2021

dr inż. Iwona Staniec

Kryteria nieprobabilistyczne

MaxiMin

Pesymista (asekurant) określa dla
każdej swojej decyzji najgorszy
możliwy wynik (minimalna
wypłatę) , a następnie
wybiera taką decyzję , dla
której określona minimalna
(gwarantowana) wypłata jest
największa.

p

i

w

k

d

},

max{

:

p

i

p

k

k

w

w

d



}

{

min

ij

j

p

i

a

w 

8 czerwca 2021

dr inż. Iwona Staniec

Kryteria nieprobabilistyczne

MaxiMax

Optymista (ryzykant) określa dla

każdej swojej decyzji najwyższy
możliwy wynik (maksymalną
wypłatę) , a następnie wybiera
taka decyzję , dla której tak
określona maksymalna (ale nie
gwarantowana) wypłata jest
największa.

o

i

w

k

d

},

{

max

:

o

i

i

o

k

k

w

w

d



}

{

max

ij

j

o

i

a

w 

8 czerwca 2021

dr inż. Iwona Staniec

Kryteria nieprobabilistyczne
kryterium Hurwicza

Reguła

Hurwicza

przyporządkowuje

każdej decyzji indeks , który
jest ważoną przeciętną minimalnej
i maksymalnej

wypłaty

wynikającej

z decyzji. Wybierana jest strategia,
której odpowiada maksymalna wartość

Oznaczmy przez - skłonność do bycia

pesymistą przy wyborze strategii

i

d

)

(

i

d

h

)

(

h



]

1

,

0

[



i



8 czerwca 2021

dr inż. Iwona Staniec

Kryteria nieprobabilistyczne
kryterium Hurwicza

Dla każdej decyzji wyznaczamy

hipotetyczną wygraną
postaci:

Należy wybrać taką decyzję, dla

której hipotetyczna wygrana
jest największa

o

i

p

i

i

w

w

d

h

)

1

(

)

(











i

d

)

(

i

d

h

)}

(

{

max

)

(

:

i

i

k

k

d

h

d

h

d



)

(

i

d

h

8 czerwca 2021

dr inż. Iwona Staniec

Macierz"żalu"

Macierz wypłat transformujemy do

postaci macierzy "żalu" .

W tym celu: określamy maksymalną

wypłatę dla każdego "stanu natury"

w dalszym postępowaniu obliczamy wartości

elementów według wzoru:

Elementy macierzy "żalu" wyrażają stratę

z powodu podjęcia decyzji nieoptymalnej
z punktu widzenia zaistniałego stanu natury.

 

ij

a

 

ij

r

}

{

max

ij

i

j

a

a 

ij

r

ij

j

ij

a

a

r





8 czerwca 2021

dr inż. Iwona Staniec

Kryteria nieprobabilistyczne

Minimax "żalu"

Do macierzy "żalu" stosujemy

postępowanie według reguły
MinMax, tzn. wskazujemy decyzję,
dla której największa strata ("żal")
z powodu źle podjętej decyzji
będzie możliwie najmniejsza, czyli

},

{

min

:

i

i

k

k

r

r

d



}

{

max

ij

j

j

r

r 

8 czerwca 2021

dr inż. Iwona Staniec

Kryteria probabilistyczne

Maksymalna oczekiwana

wygrana

Wybieramy taką decyzję, dla której

wartość oczekiwanej wygranej
(zysku) będzie największa, tj.

)

(

j

s

P

}

{

max

:

a

i

i

a

k

k

E

E

d







j

ij

j

a

i

a

s

P

E

)

(

8 czerwca 2021

dr inż. Iwona Staniec

Kryteria probabilistyczne
Minimalny oczekiwany "żal"
(strata)



Wybieramy taką decyzję, dla
której wartość oczekiwanej straty
("żalu") będzie najmniejsza, tj.

}

{

min

:

r

i

i

r

k

k

E

E

d







j

ij

j

r

i

r

s

P

E

)

(

8 czerwca 2021

dr inż. Iwona Staniec

W zarządzaniu działalnością gospodarczą wynik decyzji

jest zwykle rozpatrywany z punktu widzenia

rentowności danego przedsięwzięcia, a poszczególne

stany natury są wyrażane w postaci efektów

finansowych wynikających z różnych wyników podjętej

decyzji. W takiej sytuacji wartość oczekiwana ma

wymiar finansowy i stąd nazywamy ją

oczekiwanym efektem finansowym.

Parametr ten często oznacza się angielskim skrótem EMV

(Expected Monetary Value) i oblicza się dla każdej

strategii według równania:

gdzie:
- efekt finansowy j-tego stanu natury (wartości

dodatnie dla zysku, wartości ujemne dla strat),

- prawdopodobieństwo uzyskania j-tego efektu

finansowego.

j

n

j

j

P

V

EMV







1

j

V

j

P

8 czerwca 2021

dr inż. Iwona Staniec

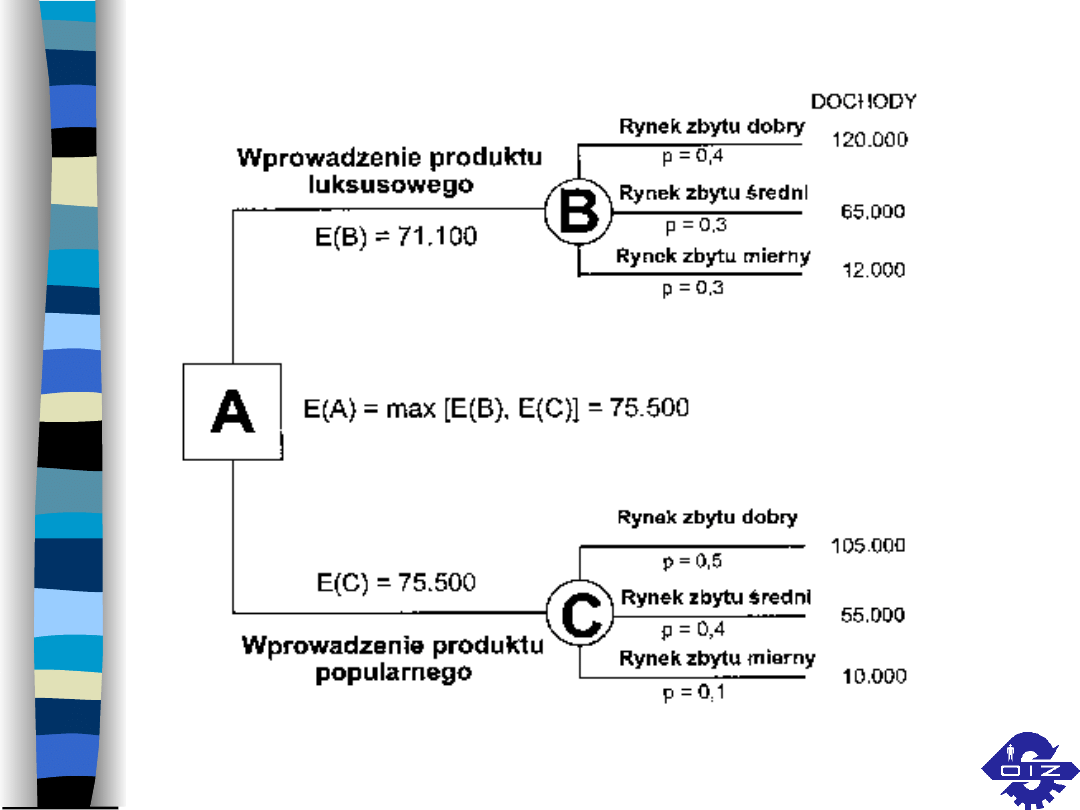
Przykład

Przedsiębiorstwo ma możliwość uruchomienia produkcji i

sprzedaży produktu luksusowego lub produktu popularnego.

Dla każdej opcji decyzyjnej określono - na podstawie prognoz

i analiz danych statystycznych - prawdopodobieństwa

uzyskania sprzedaży dobrej, średniej i miernej oraz efekty

finansowe tych wyników.

Dla produktu luksusowego prawdopodobieństwo wystąpienia

dobrej sprzedaży (z której dochody wyniosą 120000 zł)

wynosi 0,4, sprzedaży średniej (o dochodzie 65 000 zł) - 0,3

oraz sprzedaży miernej (dochód 12 000 zł) - 0,3.

Analogicznie dla produktu popularnego - prawdopodobieństwo

dobrej sprzedaży wynosi 0,5 (dochód 105 000 zł), sprzedaży

średniej - 0,4 (dochód 55 000 zł) i sprzedaży miernej - 0,1

(dochód tylko 20000 zł).

Oceń, która z opcji decyzyjnych dotycząca wyboru nowej

produkcji jest bardziej opłacalna dla przedsiębiorstwa.

8 czerwca 2021

dr inż. Iwona Staniec

Rozwiązanie

Obliczamy wartość oczekiwaną dochodu dla produktu

luksusowego (PL):

EMV(PL) = 0,4*120000 + 0,3*65000 + 0,3*12000 =

71100 zł.

Tak więc wartość oczekiwana dla PL wynosi 71 100 zł.
Podobnie liczymy dla produktu popularnego (PP):
EMV(PP) = 0,5*105000 + 0,4*55000 + 0,1*10000 =

75500 zł.

Z porównania wartości EMV(PL) i EMV(PP) wynika, że

korzystniejszą opcją decyzyjną jest wprowadzenie na

rynek produktu popularnego.

8 czerwca 2021

dr inż. Iwona Staniec



STRATEGIA CZYSTA gracz
wybiera jedna konkretną strategię



STRATEGIA MIESZANA gracz
wybiera z określonym
prawdopodobieństwem jedną z
kilku strategii

8 czerwca 2021

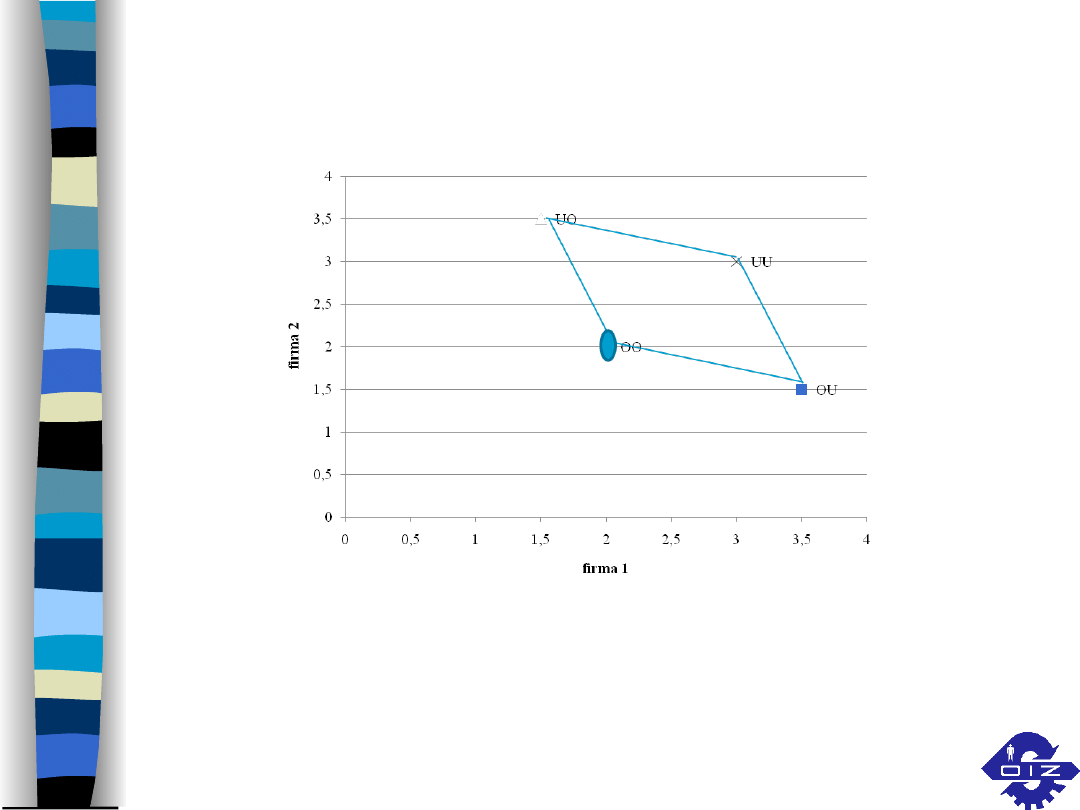
Gra 3 o sumie nie zerowej

F
I
R 1
M
A

F I R M A 2

oszustwo uczciwoś

ć

oszustwo 2

2

3,5

1,5

uczciwoś
ć

1,5
3,5

3
3

8 czerwca 2021

8 czerwca 2021

Pretooptymalny



Wynik gry jest nieooptymalny w
sensie Pareto jeżeli gra ma inny
możliwy wynik dający oby graczom
co najwyżej nie gorsze wygrane



Kryterium Pareto jest podstawową
zasada racjonalności grupowej
(wchodzi w konflikt z zasadą
racjonalności indywidualnej)

8 czerwca 2021