#5 Pobieranie prób i
rozkład z próby

STATYSTYKA - ĆWICZENIA

Prowadzący: Rafał Styła
([e-mail])

Zadania statystyki

Większość zadań, jakimi zajmuje się

statystyka, polega w praktyce na

wykorzystywaniu statystyk z próby jako

estymatorów parametrów w populacji, w

szczególności zaś na określeniu wielkości

błędu, którymi estymatory te są

obciążone.

Zadania statystyki



Statystyka próby



Metody statystyczne służące do formułowania
twierdzeń na temat parametrów populacji na
podstawie statystyk próby



Wnioskowanie statystyczne



Pod postacią indukcyjną „od szczegółu do
ogółu”

Metody pobierania prób



Wymagania



Próba pobrana losowo z populacji



Próba losowa



Losowy



Pojęcie jednakowego prawdopodobieństwa znalezienia się
każdego elementu populacji w próbie



Metody - Przybliżenie teorii losowości:



Losowanie z kapelusza, tablice liczb losowych



http://www.randomizer.org/form.htm



Systematyczny dobór próby (np.. Co piąty wynik?)

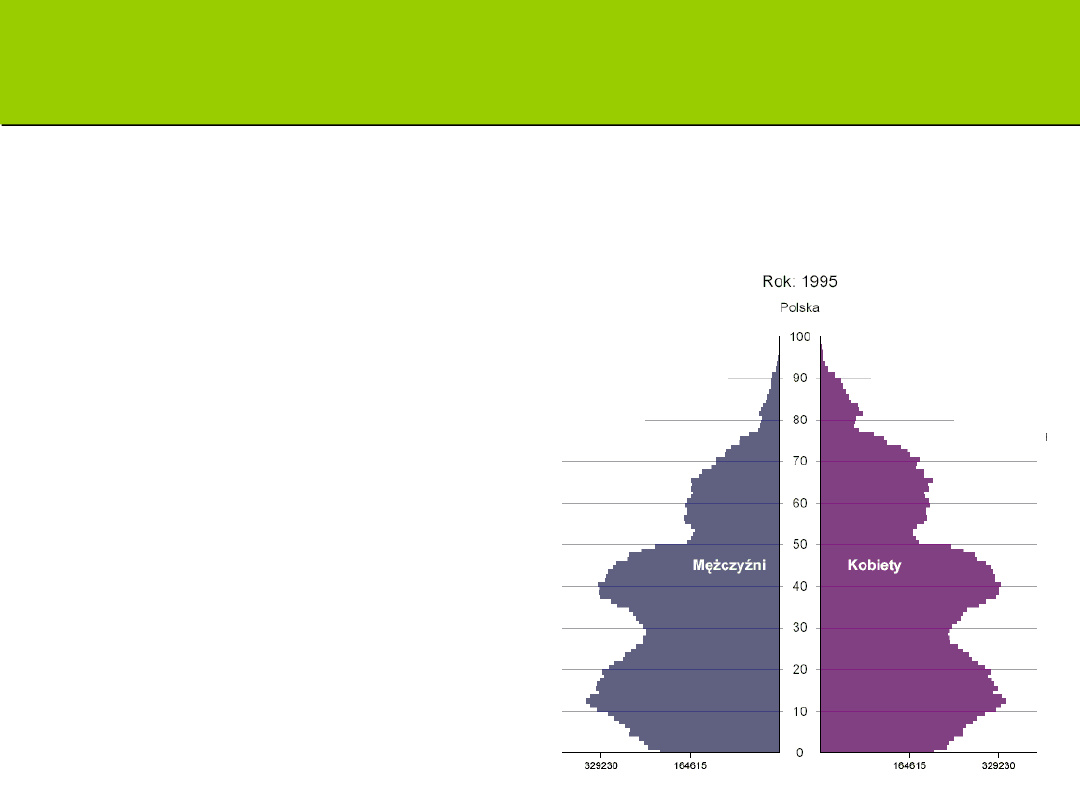
Metody pobierania prób



Losowa próba warstwowa



Proporcjonalna próba warstwowa

Gdy nie spełniony warunek losowości



Trudności zdefiniowania populacji



Badanie a posteriori



Porównywanie próby z populacją pod względem danych
wymiarów

Błąd próby



Błąd próby



Różnica miedzy wartością w populacji, czyli parametrem, a
konkretną wartością z próby



μ-x

śr

=e

i



Np: μ=4,56 x

śr

=4,61 e

i

=0,05



Odpowiedź na pytanie: jakim błędem obarczony jest
estymator parametru?



Wielokrotny pomiar i podanie średniego błędu oraz wariancji
i odchylenia standardowego

Błąd standardowy



Błąd standardowy



Odchylenie standardowe rozkładu z próby odnoszące się do
danej statystyki (np. średniej).



Np. błąd standardowy średniej pobieranej z danej populacji



S

xśr



„Wyciągam kilka prób z danej populacji, a następnie ustalam
rozkład średnich z tych prób”



Większość układa się w rozkład normalny, błąd standardowy
mówi o wielkości rozrzutu, czyli odchyleniu standardowym



Gdy kształt rozkładu błędu jest znany, wówczas z danym
stopniem ufności, możemy ustalić czy dana wylosowana
próba należy, czy też nie należy do danej populacji

Rozkład z próby średnich w populacji skończonej

Rozkład z próby średnich

w populacji skończonej

1







p

p

x

N

N

N

N

śr





Liczba elementów w populacji

Liczebność próby

Odchylenie

standardowe w
populacji

Zadanie 1 Oblicz błąd standardowy



Populacja studentów uniwersytetu wynosi 1000 osób



Odchylenie standardowe testu zdolności akademickich
wynosi w tej populacji 80.



Oblicz błąd standardowy średnich wyników testu zdolności
akademickich dla próby 100 studentów bez zwracania

Rozkład z próby średnich w populacji
nieskończenie wielkiej

Rozkład z próby średnich w

populacji nieskończonej

Liczebność próby

Odchylenie standardowe w

populacji

N

śr

x







Błąd standardowy średniej



Im większa jest zmienność w populacji tym większy jest
błąd standardowy



Im większe jest N, tym mniejszy jest błąd



Błąd standardowy dla N, równa się odchyleniu
standardowemu w populacji

N

śr

x







Zadanie 2 Oblicz błąd standardowy



Populacja studentów uniwersytetu wynosi 1000 osób



Odchylenie standardowe testu zdolności akademickich
wynosi w tej populacji 80.



Oblicz błąd standardowy średnich wyników testu zdolności
akademickich dla próby 100 studentów ze zwracaniem

Rozkład z próby średnich w populacji
nieskończenie wielkiej

Błąd standardowy średniej

Liczebność próby

Odchylenie standardowe w

próbie

N

S

S

śr

x



Rozkład populacji a rozkład średnich



Teoretyczny rozkład z próby średnich pobranych z populacji
normalnej jest rozkładem normalnym.



Jeśli wiemy, że rozkład w populacji jest normalny, wiemy też,
że rozkład z próby średnich jest normalny



CENTRALNE TWIERDZENIE GRANICZNE



Rozkład średnich z prób zbliża się coraz bardziej do postaci
normalnej w miarę jak rośnie liczebność kolejnych prób, mimo
odchyleń od normalności rozkładów w populacji

Znajomość odchylenia standardowego rozkładu średnich ma tylko znaczenie

praktyczne, gdy znamy kształt rozkładu. Dlatego tak ważne jest centralne
twierdzenie graniczne.

Zadanie 3



Posługując się procedurą dla dużej próby, określ 95
procentowy przedział ufności dla średniej 105 przy N=100 i
s=10.

Zadanie 3



Posługując się procedurą dla dużej próby, określ 95
procentowy przedział ufności dla średniej 105 przy N=100 i
s=10.



Błąd standardowy średniej=10/10=1



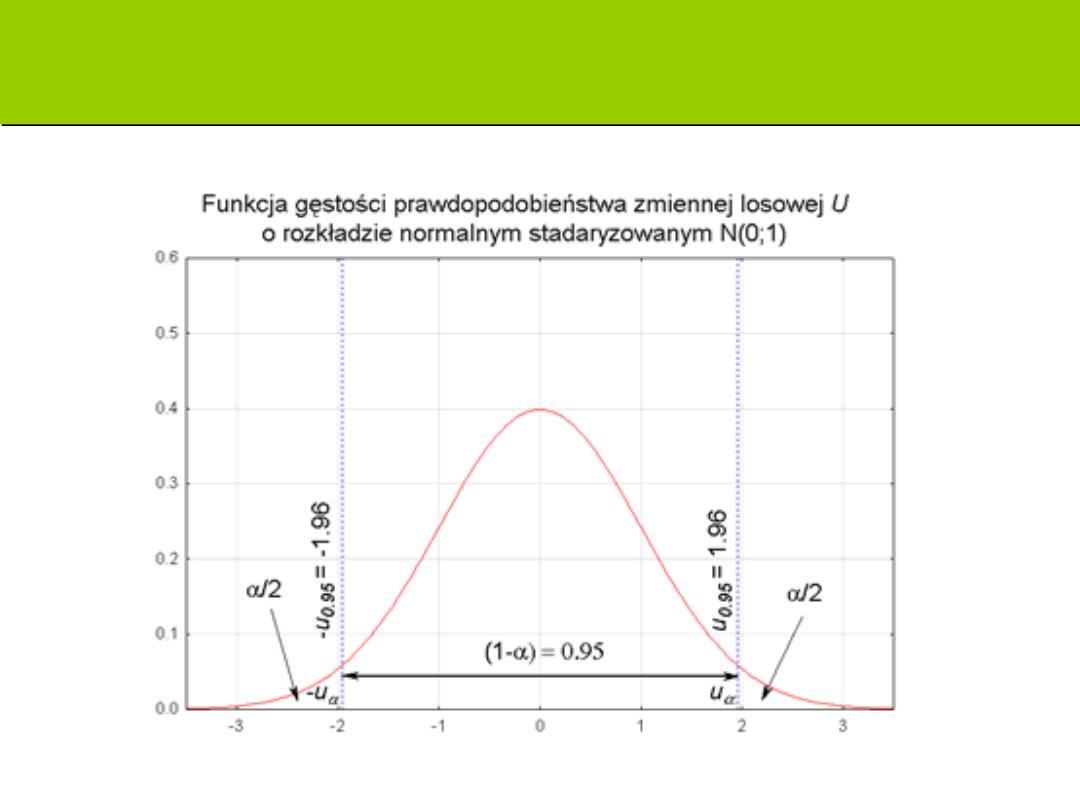
W jednostkowej krzywej normalnej granice z=+- 1,96
obejmują 95%,



Połowa szerokości przedział ufności 1,96*1=+-1,96



Odpowiedź: przedział ufności to 105 – 1,96 do
1,96+105= <103,04 – 106,96)

N

S

S

śr

x



Zadanie 4



Posługując się procedurą dla dużej próby, określ 99
procentowy przedział ufności dla średniej 150 przy N=100 i
s=20.

Praca domowa



Z Ferguson, Takane



S.179-180 Zadania 1-4; 12, 14

Dziękuję za uwagę.