#3 Wariancja, odchylenie
standardowe, skośność i
kurtoza
STATYSTYKA - ĆWICZENIA
Prowadzący: Rafał Styła
(rstyla@psych.uw.edu.pl)
#3 Wariancja, odchylenie
standardowe, skośność i
kurtoza
STATYSTYKA - ĆWICZENIA
Prowadzący: Rafał Styła
(rstyla@psych.uw.edu.pl)
Miary rozproszenia – rozstęp, wariancja,
odchylenie standardowe
Populacja - parametry
Rozstęp – odcinek wartości
wyników populacji, dla
których prawdopodobieństwa
są różne od zera
Wariancja
Odchylenie standardowe
Próba - estymatory
Rozstęp R=x
max
-x
min
Szerokość przedziału, w
którym znalazły się wyniki w
danej próbie
Wariancja
Odchylenie standardowe
1
)
(
2
n
x
x
S
śr
1
)
(
2
2
n
x
x
S
śr
p
N
x
2
2
)
(
p
N
x
2
2
)
(
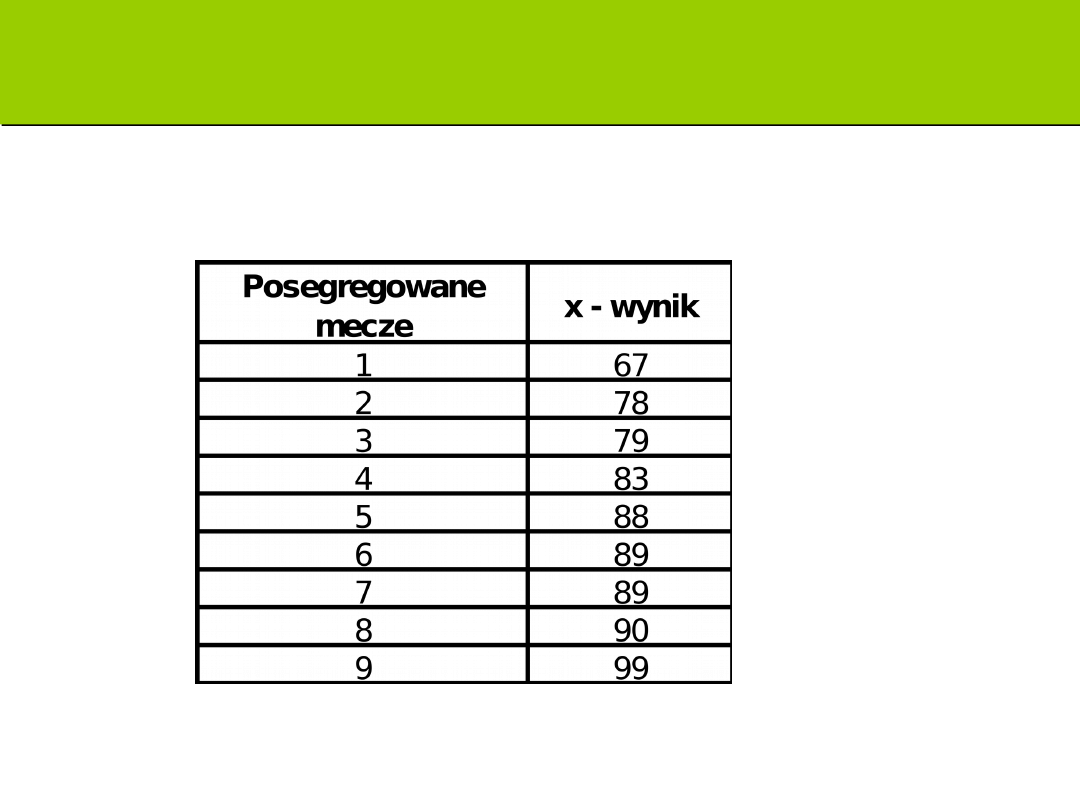
Zadanie A: ilość punktów koszykarzy Warszawa
Polonia
Oblicz rozstęp
Zadanie A: ilość punktów koszykarzy Warszawa
Polonia
Oblicz rozstęp
R=x
max
-x
min
=99-67=32
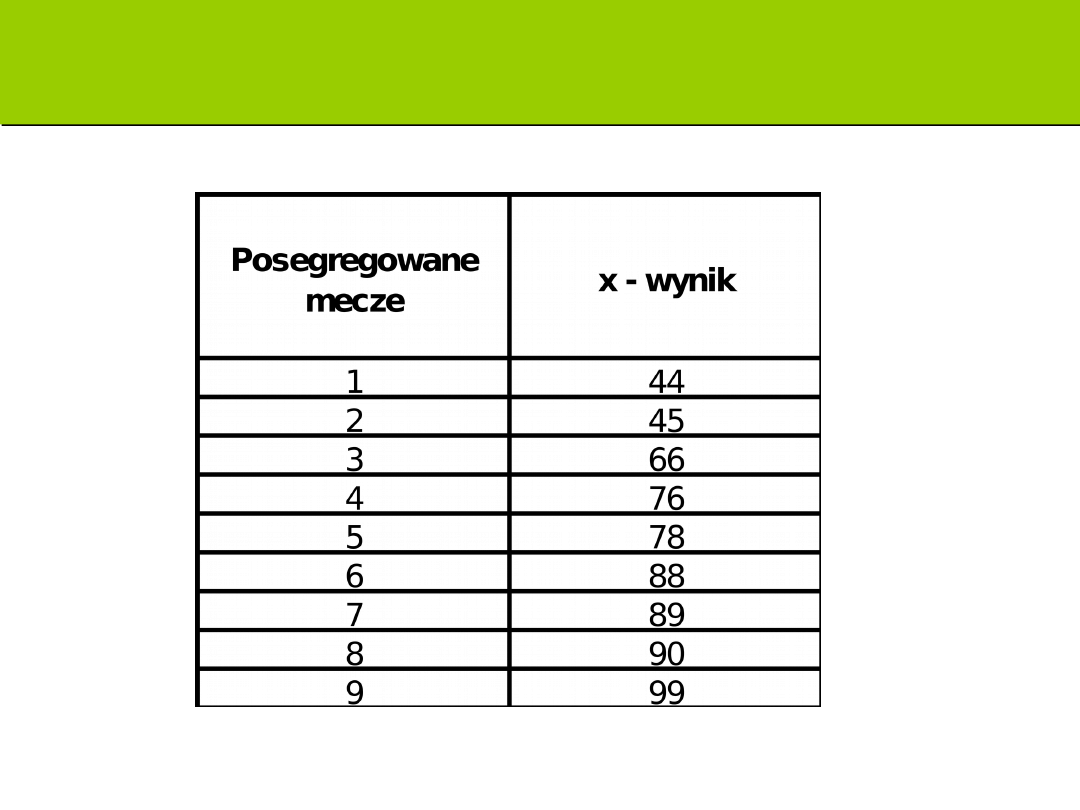
Zadanie B: ilość punktów koszykarzy Warszawa
Polonia
Oblicz rozstęp
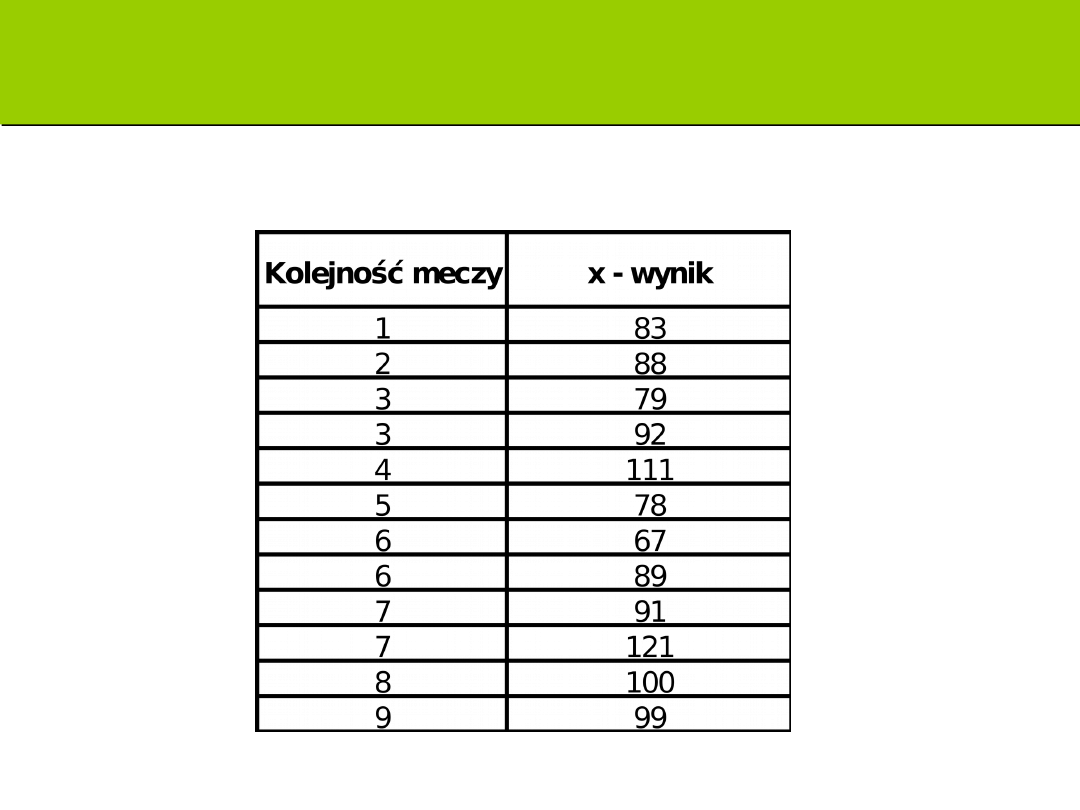
Zadanie C ilość punktów koszykarzy Warszawa
Polonia
Oblicz rozstęp
Miary rozproszenia
Populacja
Wariancja
Odchylenie standardowe
Próba
Wariancja
Odchylenie standardowe
1
)
(
2
n
x
x
S
śr
1
)
(
2
2
n
x
x
S
śr
p
N
x
2
2
)
(
p
N
x
2
2
)
(
Miary rozproszenia
Próba
Wariancja
Odchylenie standardowe
Wzór ten można również zapisać
jako
1
)
(
2
n
x
x
S
śr
1
)
(
2
2
n
x
x
S
śr
Stopnie swobody
1
2
2
n
nx
x
S
śr
Próba
N – liczba pomiarów
N-1 – liczba odchyleń od
średniej, które mogą się
zmieniać
Podzielenie kwadratów
odchyleń daje obciążony
estymator wariancji w
populacji
Podzielenie przez stopnie
swobody daje nieobciążony
estymator wariancji w
populacji
Przykłady
10 10 10 10 10
6 8 10 12 14
2 6 10 14 18
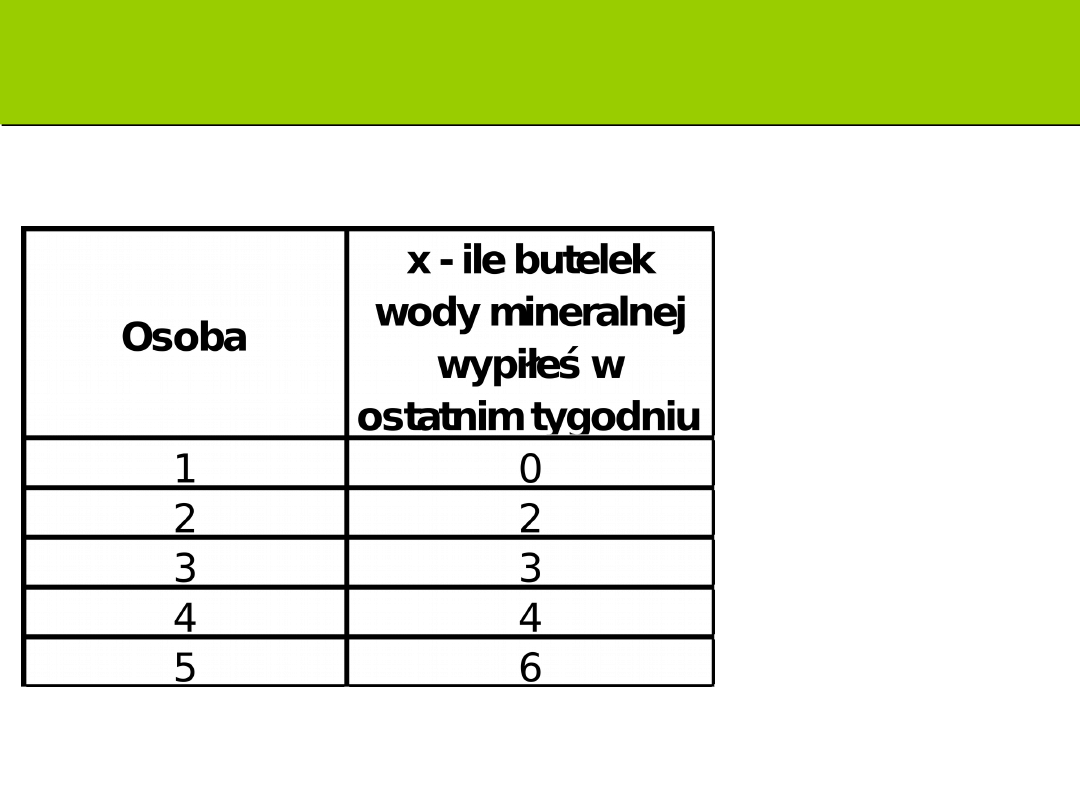
Zadanie A: ilość wypitej wody
Wariancja i odchylenie standardowe
Zadanie A: ilość wypitej wody
Wariancja i odchylenie standardowe
Xśr=(0+2+3+4+6)/5=15/5=3
S
2
= [(0-3)
2
+(2-3)
2
+(3-3)
2
+(4-
3)
2
+(6-3)
2
]/5-1
=[9+1+0+1+9]/4=20/4=5
1
)
(
2
2
n
x
x
S
śr
23
,
2
5
2
S
S
Zadanie A: ilość wypitej wody mineralnej
Wariancja i odchylenie standardowe
Xśr=(0+2+3+4+6)/5=15/3=3
Albo
S
2
=[(4+9+16+36)-5*9]/5-
1=(65-45)/4=5
23
,
2
5
2
S
S
1
2
2
2
n
nx
x
S
śr
Zadanie B: ilość wypitej wody mineralnej
Wariancja i odchylenie standardowe
Zadanie C: ilość wypitej wody mineralnej
Wariancja i odchylenie standardowe
Wariancja – wzór, gdy wyniki w postaci
przedziałów klas
Próba
Wariancja – wzór, gdy wyniki w postaci przedziałów klas
Odchylenie standardowe
1
)
(
2
przedzialu
srodek
i
2
n
f
x
x
S
i
śr
1
)
(
2
przedzialu
srodek
i
n
f
x
x
S
i
śr
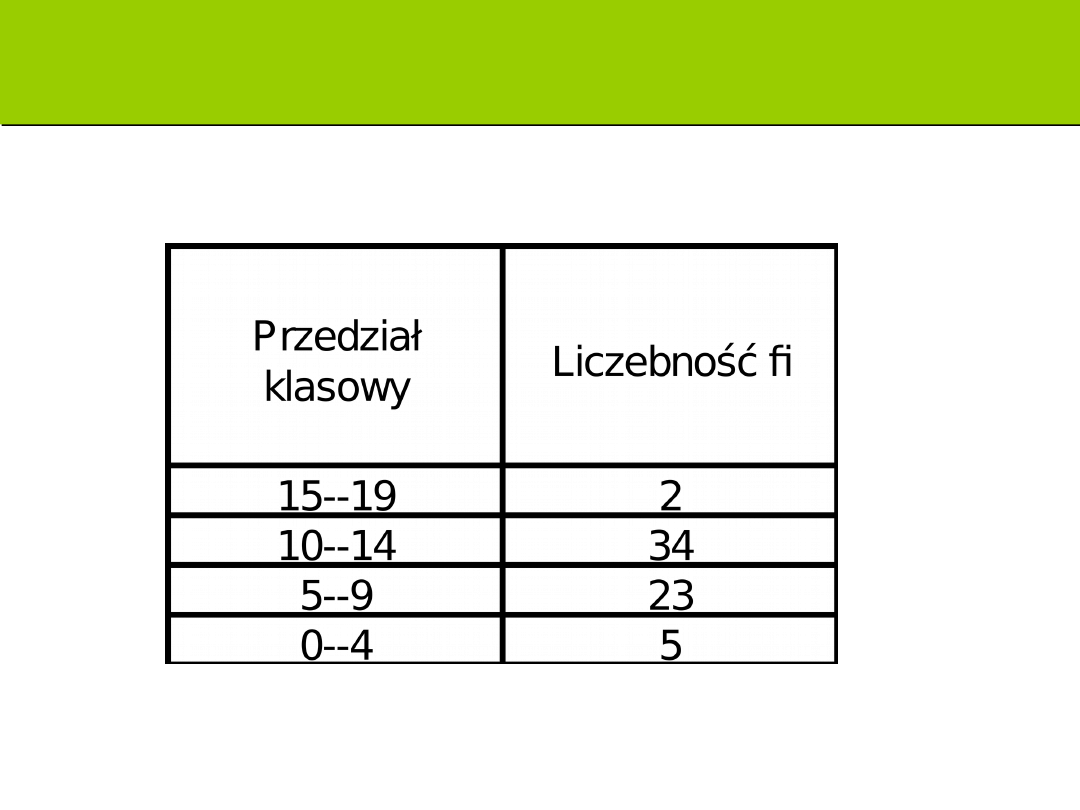
Wariancja i odchylenie standardowe
Ilość punktów z testu wiedzy
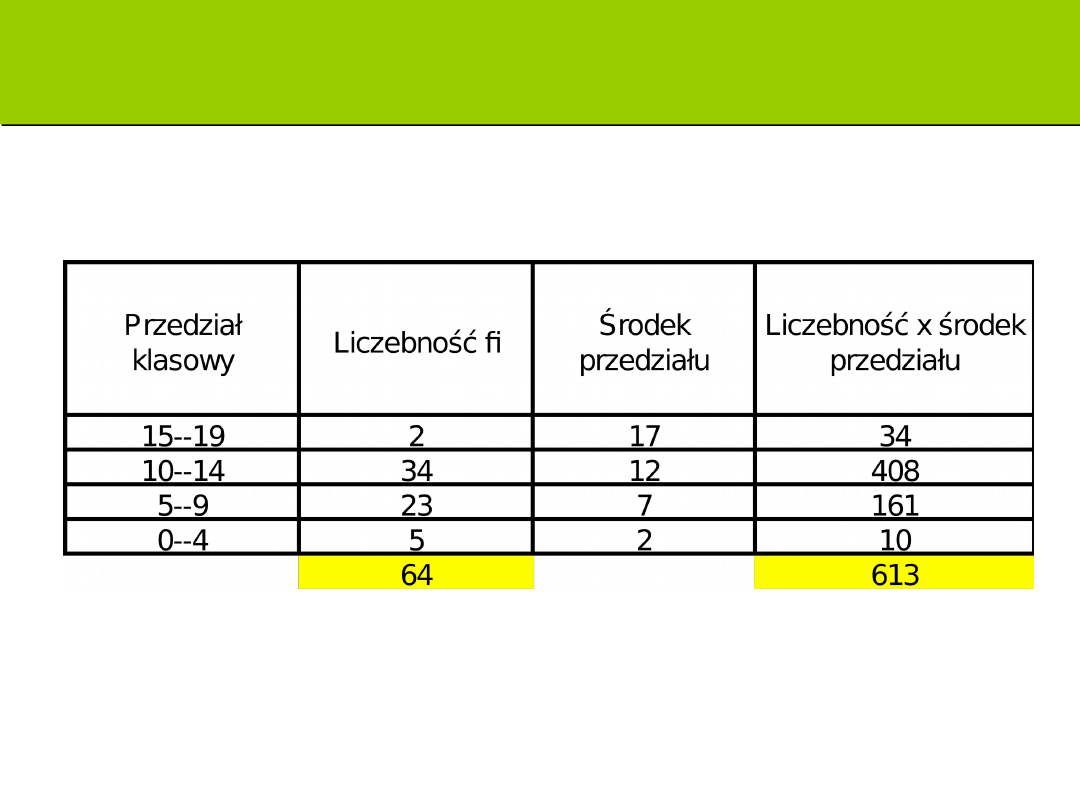
Zadanie: oblicz średnią arytmetyczną
Rozwiązanie
Średnia= 613/64=9,6
S2= {[(17-9,6)2*2]+[(12-
9,6)2*34]+[(7-9,6)2*23]+[(2-
9,6)2*5]}/64-1= 749,6/63=11,9
S=3,4
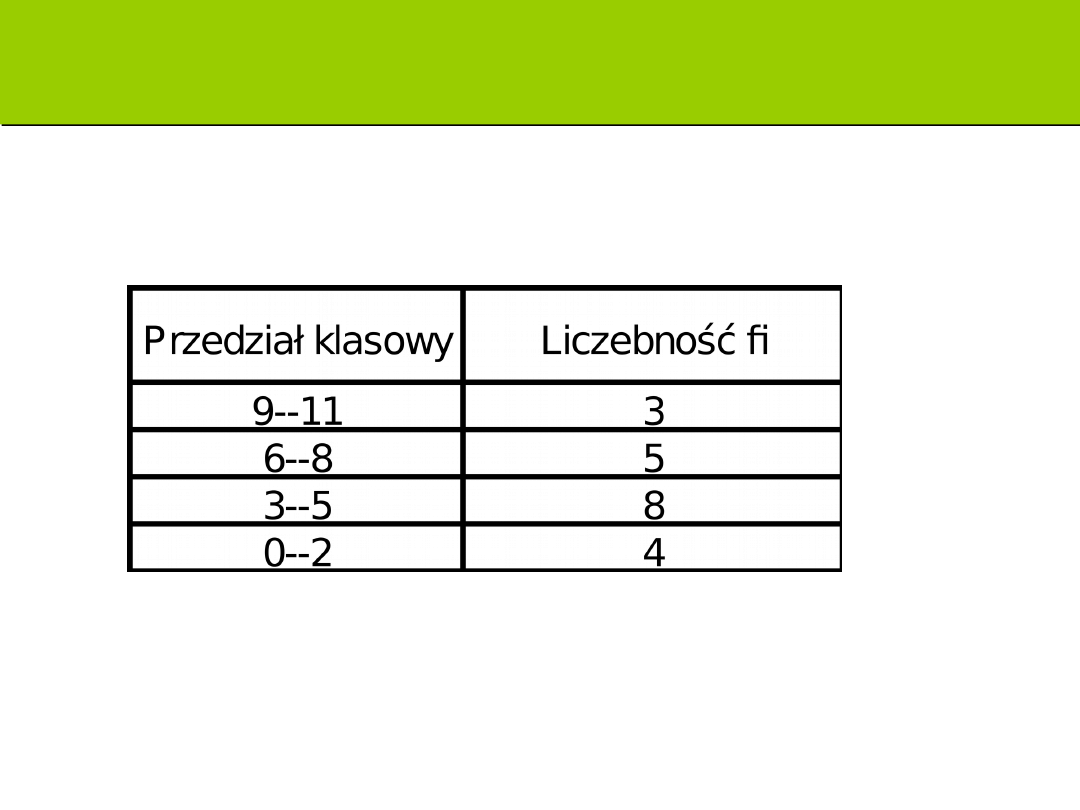
Zadanie: oblicz odchylenie standardowe
Wiek dzieci świetlicy szkoły numer 319
Właściwości odchylenia standardowego
Jeżeli do wszystkich pomiarów z próby dodamy pewną
wartość stałą, to odchylenie standardowe pozostanie nie
zmienione.
Jeżeli wszystkie pomiary z próby zostaną pomnożone przez
pewną wartość stałą, to odchylenie standardowe również
zostanie pomnożone przez wartość bezwzględną tej stałej.
Momenty średniej
Pojęcia wzięte z mechaniki
służą do wyliczenia skośności i kurtozy
2
2
2
1
)
(
S
n
n
n
x
x
m
śr
0
)
(
1
n
x
x
m
śr
n
x
x
m
śr
3
3
)
(
n
x
x
m
śr
4
4
)
(
n
x
x
m
r
śr
r
)
(
Skośność
Skośność – czy rozkład wyników jest
symetryczny, czy też jest przegięty
w którąś ze stron
Gdy g
1
=0 – rozkład symetryczny
Gdy g
1
<0 – rozkład skośny ujemnie
Gdy g
1
>0 – rozkład skośny dodatnio
2
2
3
1
m
m
m
g
Zadanie A: oblicz skośność
A 6 8 10 12 14
B 6 8 10 11 15
Zadanie A: oblicz skośność
Xśr=10
Odejmujemy wyniki od średnie
A -4 -2 0 +2 +4
B -4 -2 0 +1 +5
Aby obliczyć m2 podnosimy do kwadratu
i sumujemy
A +16 +4 0 +4 +16 = 40/5=8
B +16 +4 0 +1 +25 =46/5=9,2
Aby obliczyć m3 podnosimy do sześcianu
A -64 -8 0 +8 +64 =0/5=0
B -64 -8 0 +1 +125 = 54/5=10,8
G
1A
=0/22,6=0
G
1B
=10,8/27,9=0,387
2
2
3
1
m
m
m
g
n
x
x
m
r
śr
r
)
(
Zadanie B: oblicz skośność
A 1 3 4 5 7
B 1 2 4 5 7
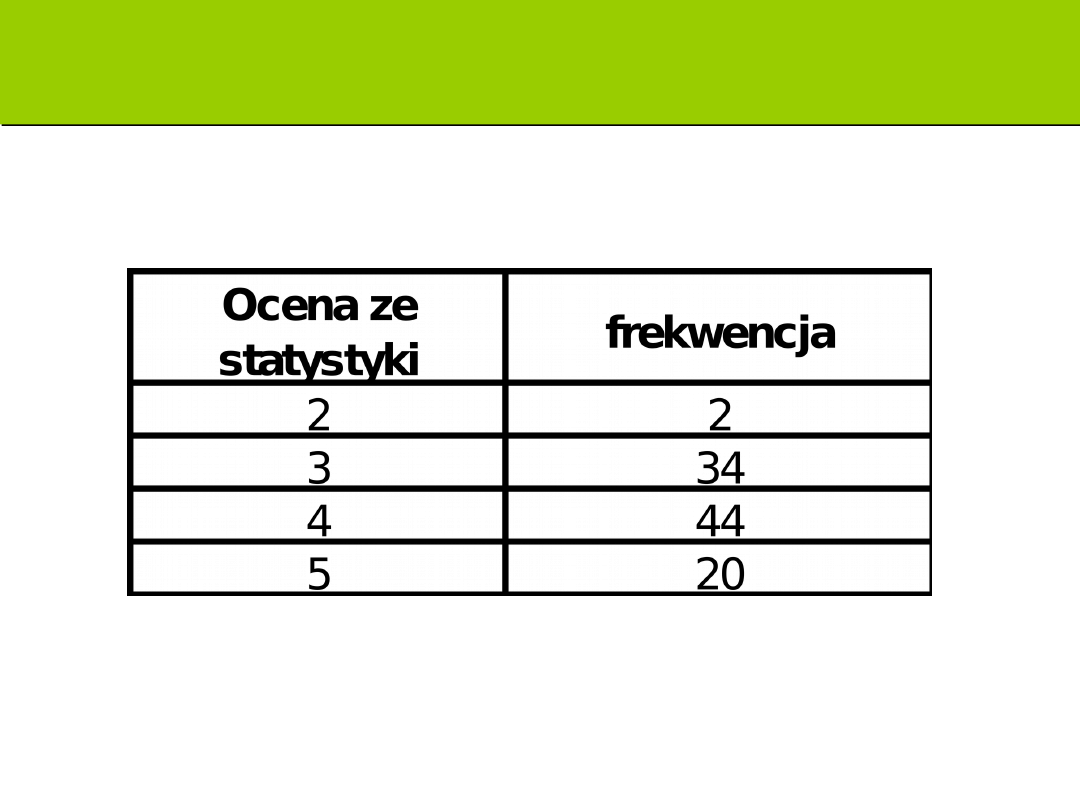
Zadanie C: oblicz skośność
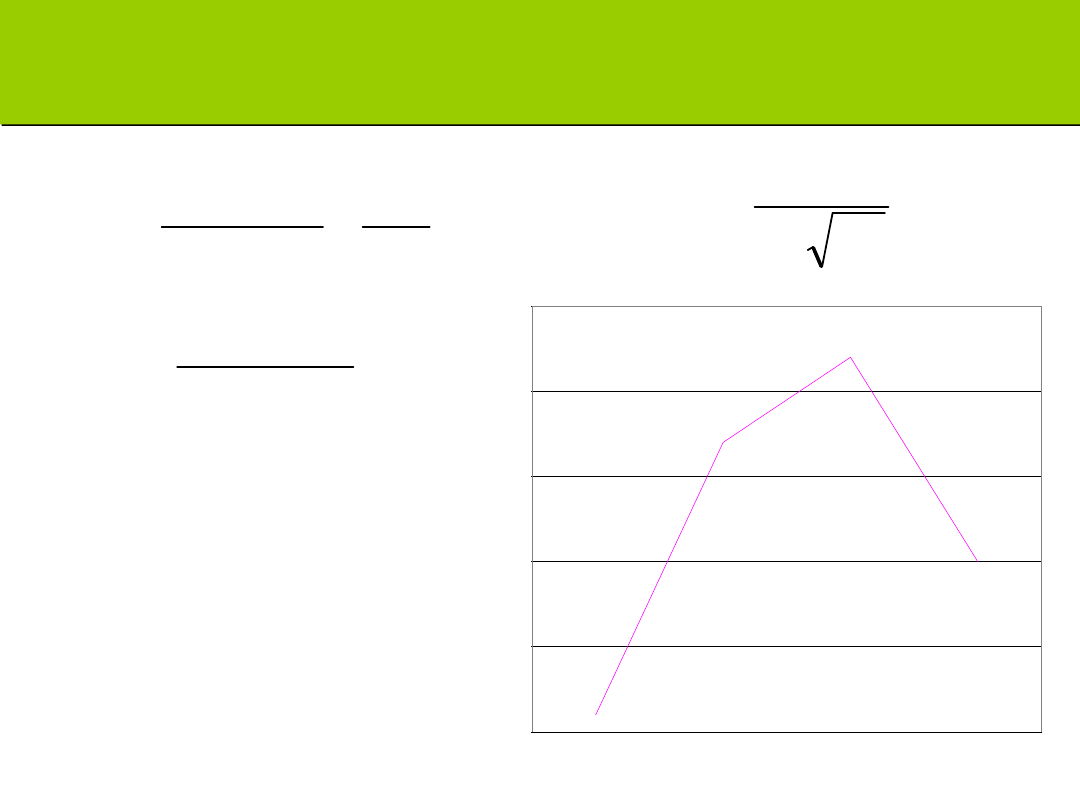
Zadanie C: oblicz skośność
Średnia arytmetyczna z rozkładów
liczebności=Σx
i
*f
i
/n
X
śr
=(4+68+176+100)/100
=3,48
m
2
=(2*2,19+34*0,23+44*0,27+2
0*2,31)/100=4,38+7,82+11,88+4
6,2=70,28/100=0,7
M
3
=(2*-3,24+34* -0,11
+44*0,14+20*3,51)/100=-6,48-
3,74+6,16+
70,2=66,14/100=0,66
0
10
20
30
40
50
2
3
4
5
2
2
3
1
m
m
m
g
2
2
2
1
)
(
S
n
n
n
x
x
m
śr
n
x
x
m
śr
3
3
)
(
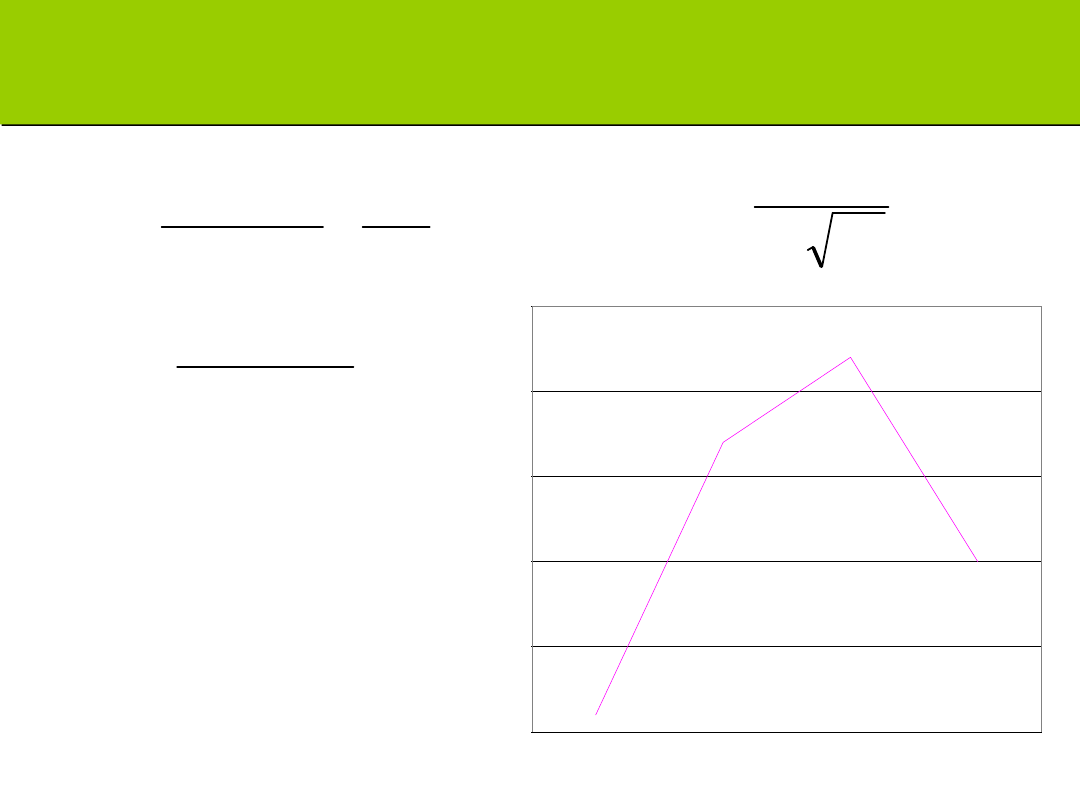
Zadanie C: oblicz skośność
m
2
=0,7
m
3
=0,66
g
1
=0,66/07*0,83=0,66/0,58=
1,13
0
10
20
30
40
50
2
3
4
5
2
2
3
1
m
m
m
g
2
2
2
1
)
(
S
n
n
n
x
x
m
śr
n
x
x
m
śr
3
3
)
(
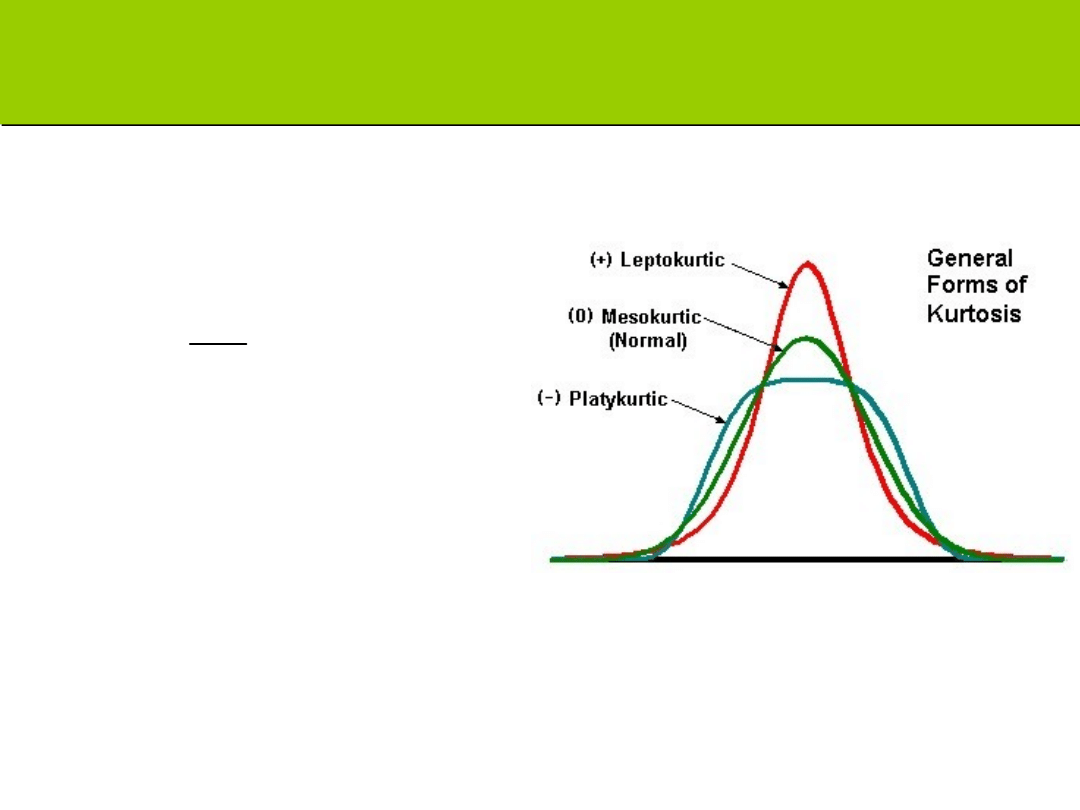
Kurtoza
Kurtoza – czy rozkład wyników jest
spłaszczony, czy spiczasty, czy
normalny
Gdy g
2
=0 – rozkład normalny
Gdy g
2
<0 – rozkład platykurtyczny
(rozpłaszczony)
Gdy g
2
>0 – rozkład leptokurtyczny
(spiczasty)
3
2
2
4
2
m
m
g
Zadanie A: oblicz kurtozę
A 6 8 10 12 14
B 5,64 9 10 11 14,36
Zadanie A: oblicz kurtozę
Xśr=10
Odejmujemy wyniki od średniej
A -4 -2 0 +2 +4
B -4,36 -1 0 +1 +4,36
Aby obliczyć m2 podnosimy do kwadratu i
sumujemy
A +16 +4 0 +4 +16 = 40/5=8
B +19 +1 0 +1 +19 =40/5=8
Aby obliczyć m4 podnosimy do potęgi
czwartej
A 256 16 0 16 256 =544/5=108,8
B 361,36 1 0 1 361,36 =
724,72/5=144,94
g
2A
=(108,8/64)-
3=1,7-3=-1,3
g
2B
=(144,94/64)-
3=2,26-3=-0,73
3
2
2
4
2
m
m
g
Zadanie B: oblicz skośność
A 1 3 4 5 7
B 1 2 4 6 7
Praca domowa – rozstęp, wariancja, odchylenie
standardowe
Z Ferguson, Takane
S.98-99
Zadania 1, 2, 3
Wzory do zapamiętania
n
x
f
x
k
i
i
1
n
x
n
x
x
x
x
x
n
i
i
n
1
3
2
1
...
2
1
n
me
i
i
c
di
h
f
f
n
x
me
i
1
2
1
)
(
2
n
x
x
S
śr
1
)
(
2
2
n
x
x
S
śr
1
)
(
2
przedzialu
srodek
i
2
n
f
x
x
S
i
śr
1
)
(
2
przedzialu
srodek
i
n
f
x
x
S
i
śr
2
2
3
1
m
m
m
g
n
x
x
m
r
śr
r
)
(
3
2
2
4
2
m
m
g
Dziękuję za uwagę.