Twierdzenie 

Pitagorasa

Twierdzenie 

Pitagorasa

Opracowanie Jadwiga 
Niedziółka

 

 

Zapewne pamiętasz, jak nazywają się boki 
trójkąta prostokątnego:

przyprostokątna

przyprostokąt
na

przeciwprostokątna

 

 

Starożytni 
matematycy odkryli 
następującą własność 
trójkątów 
prostokątnych:

 

 

c

2

b

2

a

2

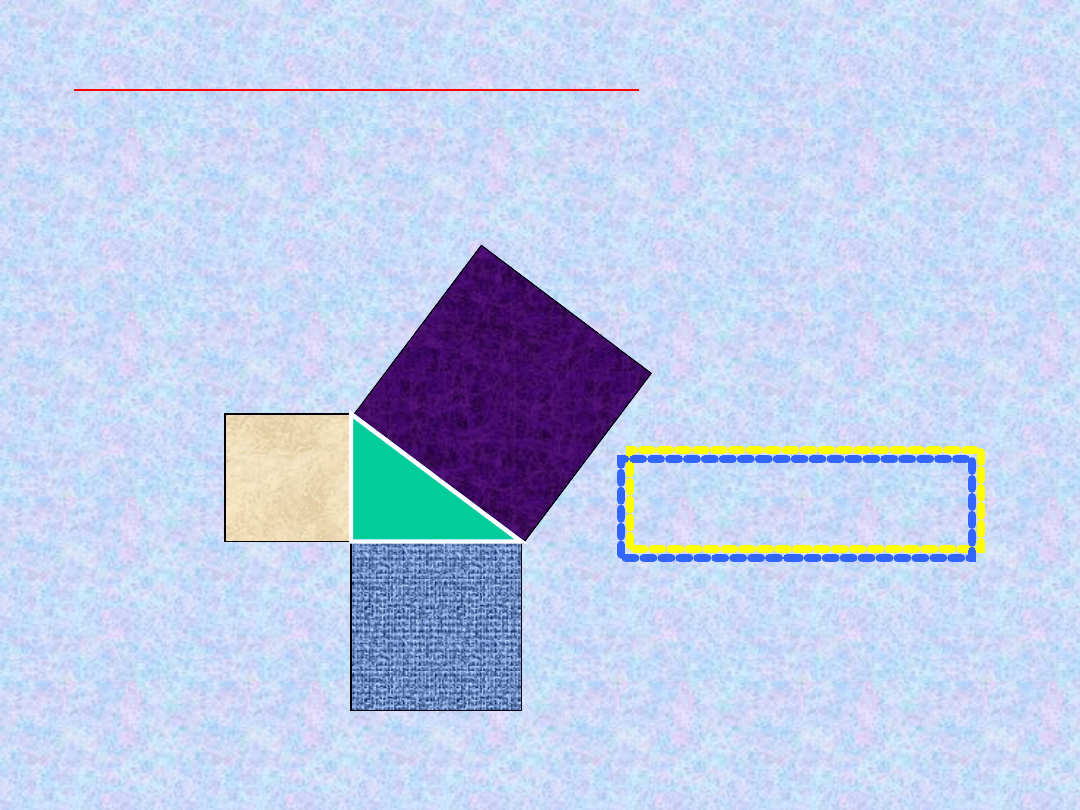
W trójkącie prostokątnym suma pól kwadratów 
zbudowanych na przyprostokątnych jest równa polu 
kwadratu zbudowanego na przeciwprostokątnej.

a

a

2

2

 + b

 + b

2

2

 = c

 = c

2

2

TWIERDZENIE PITAGORASA:

 

 

c

c

2

2

a

a

2

2

b

b

2

2

c

c

2

2

 = a

 = a

2

2

 + b

 + b

2

2

a

a

a

a

c

c

b

b

b

b

b

b

b

b

a

a

a

a

Dowód:

 

 

Twierdzenie Pitagorasa możemy też 
sformułować w następujący sposób:

Założenie:

 

Jeżeli trójkąt jest prostokątny

Teza:

 

to suma kwadratów długości 

przyprostokątnych jest równa kwadratowi 
długości przeciwprostokątnej.

 

2

2

2

c

b

a





a, b – długości 

przyprostokątnych

c – długość przeciwprostokątnej

a

b

c

 

 

Twierdzenie Pitagorasa 
wbrew swojej nazwie było 
znane już dawno przed 
urodzeniem tego 
mędrca.Znali je zarówno 
Babilończycy jak i Egipcjanie.

 

 

Słów kilka o 
Pitagorasie

•żył w latach 572p.n.e. –497 p.n.e.
•pochodził z Samos
•założył Związek Pitagorejski-bractwo religijno-
polityczne

•uważał wraz ze swoimi uczniami, że świat 
można opisać za pomocą liczb

•pitagorejczycy odkryli jakie  długości powinny 
mieć dwie  struny, aby razem pięknie brzmiały  

•po udowodnieniu twierdzenia Pitagoras złożył 
bogom hekatombę, czyli ofiarę ze stu wołów

•żył w latach 572p.n.e. –497 p.n.e.
•pochodził z Samos
•założył Związek Pitagorejski-bractwo religijno-
polityczne

•uważał wraz ze swoimi uczniami, że świat 
można opisać za pomocą liczb

•pitagorejczycy odkryli jakie  długości powinny 
mieć dwie  struny, aby razem pięknie brzmiały  

•po udowodnieniu twierdzenia Pitagoras złożył 
bogom hekatombę, czyli ofiarę ze stu wołów

 

 

Ciekawostka

Mówimy, że trzy liczby naturalne a, b, c 
tworzą trójkę pitagorejską, jeśli 
spełniają równość : 

                  

Archeolodzy znaleźli listę takich trójek 
już tysiąc lat przed Pitagorasem!

A oto przykłady trójek pitagorejskich:

                3,4,5               6,8,10      
5,12,13

Mówimy, że trzy liczby naturalne a, b, c 
tworzą

 

trójkę pitagorejską

, 

jeśli 

spełniają

 

równość :

 

                  

Archeolodzy znaleźli listę takich trójek 
już tysiąc lat przed Pitagorasem!

A oto przykłady trójek pitagorejskich:

                3,4,5               6,8,10      
5,12,13

2

2

2

c

b

a





 

 

Ciekawostka

3

4

5

Trójkąt o bokach 3,4,5nazywa się

 

trójkątem egipskim

 

 

Znając długości dwóch boków 
trójkąta możesz obliczyć długość 
trzeciego boku

 

Przykład:

2cm

3cm

x

Oblicz długość 
przeciwprostokątnej.

 

 

Twierdzenie odwrotne do twierdzenia 
Pitagorasa:

 

Założenie: Jeżeli suma kwadratów 
długości dwóch krótszych boków trójkąta 
jest równa kwadratowi długości 
najdłuższego boku

Teza: to 

trójkąt jest prostokątny.

 

 

Twierdzenie odwrotne do 
twierdzenia Pitagorasa 
służy do sprawdzania, czy 
trójkąt jest prostokątny.

 

 

ZADANIE

Który z trójkątów o podanych 
długościach boków jest 
prostokątny?

5

,

2

,

3

4

,

3

,

2

5

,

3

,

2

5

2

,

5

,

4

a
)
b
)
c
)
d)

 

 

W starożytności Babilończycy 
wyznaczali w terenie kąt prosty 
używając sznura z zaznaczonymi w 
równych odstępach dwunastoma 
węzłami. Pomyśl,  jak to można 
zrobić.