Multicast Flows

Lecture Outline

• Introduction
• Integer Programming Formulations
• Cost Problem
• Network Design Problem
• Maximum Delay Problem
• Throughput Problem
• Multicast Packing Problem
• Concluding Remarks

Lecture Outline

• Introduction

• Integer Programming Formulations
• Cost Problem
• Network Design Problem
• Maximum Delay Problem
• Throughput Problem
• Multicast Packing Problem
• Concluding Remarks

Introduction (1)

• In traditional networks two basic techniques

are used for routing:

– Unicast (one-to-one)
– Broadcast (one-to-all)

• Both routing methods are not sufficient when

information is to be delivered to a relatively large

group of users, geographically separated and

with similar interest on content

• This situation has triggered development

multicast routing defined as one-to-many

transmission

Introduction (2)

Example application of multicasting:
• IP TV
• Video on Demand (VoD)
• Radio Streaming
• Content Delivery Networks (CDN)
• Distance learning
• Software updates
• Monitoring
• Result distribution (computing systems)

Introduction (3)

• Multicast modeling can use two classical network

problems:

– Steiner tree problem. Given a set V of points

(network nodes), interconnect them by a subgraph

of shortest length (sum of the lengths of all edges)

– Minimum Spanning Tree (MST) problem is a

subgraph of the orginal graph (network) which is a

tree (no loops) and connects all the vertices

together

• The difference between both problems is that, in the

Steiner tree problem, extra intermediate vertices

(Steiner vertices) and edges may be added to the

graph in order to reduce the length of the spanning

tree

Introduction (4)

Multicasting can be divided into two categories:
• Traditional IP multicast is a method to send

packets to a group of interested receivers in a

single transmission. The multicasting is in layer 3

and IP routers are responsible to create the

delivery tree. End hosts (receivers) are leafs of

the tree

• Overlay multicast (P2P multicast, application-

layer multicast) is realized in layer 7. End hosts

can also upload the stream to other peers

Traditional IP multicast (1)

• Protocol-Independent Multicast (PIM) is a

family of IP multicast protocols that provide one-to-

many and many-to-many distribution of data over

an IP network. PIM is protocol-independent, since it

does not include its own topology discovery

mechanism, but instead uses routing information

supplied by other traditional routing protocols (e.g.,

BGP)

• Internet Group Management Protocol (IGMP) is

a protocol used to manage the membership of IP

multicast groups. IGMP is used by hosts and

adjacent multicast routers to establish multicast

group memberships

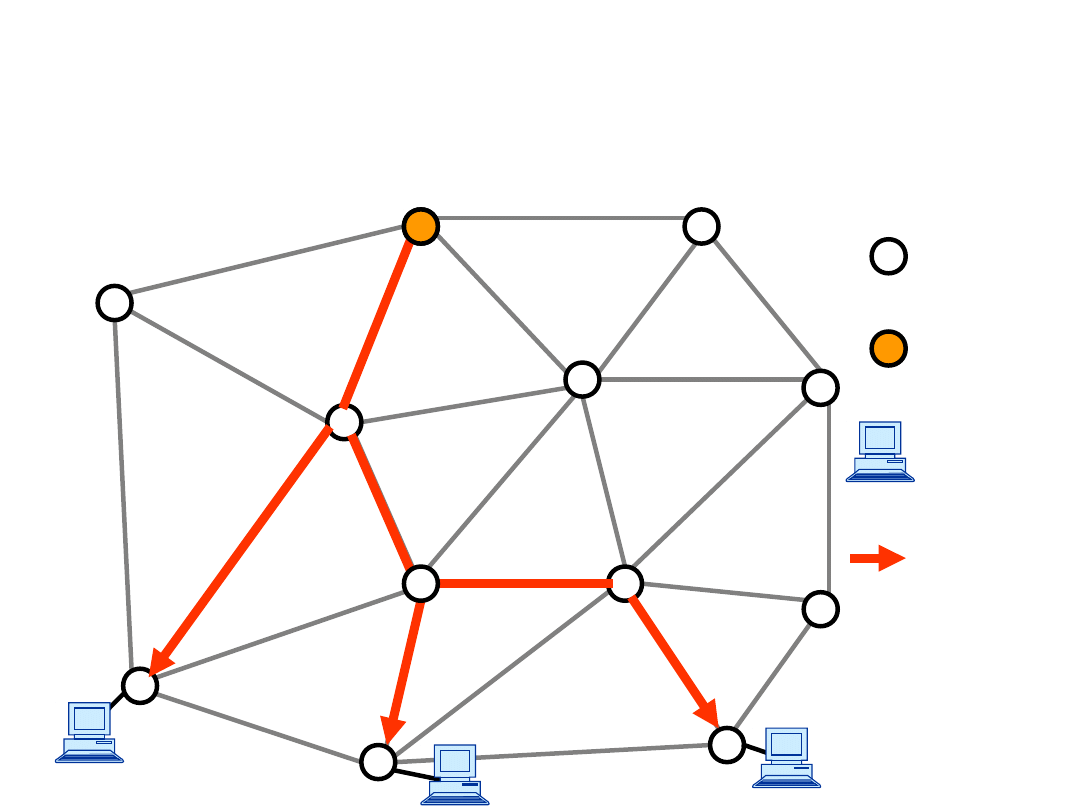
Traditional IP multicast (2)

2

1

3

4

11

8

7

6

9

Root
node

IP Router

Multicast
tree

12

5

10

1

End host
(receiver
)

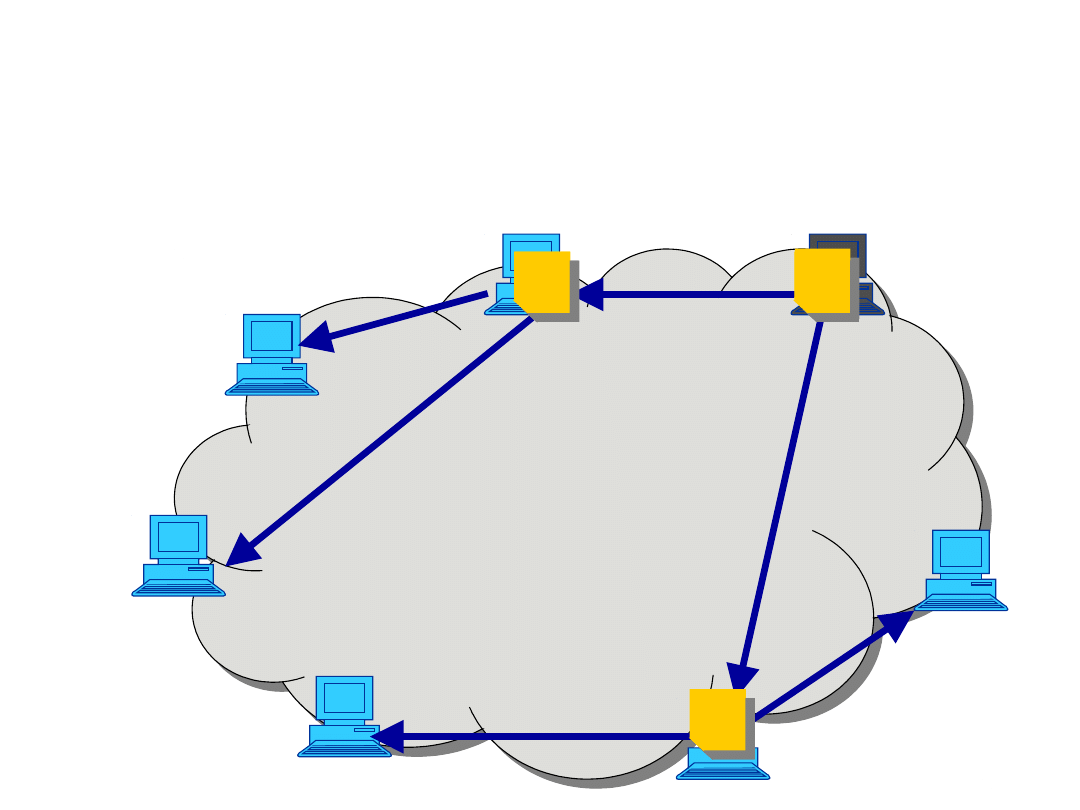
P2P Multicast

1

2

3

4

5

6

7

Lecture Outline

• Introduction

• Integer Programming Formulations

• Cost Problem
• Network Design Problem
• Maximum Delay Problem
• Throughput Problem
• Multicast Packing Problem
• Concluding Remarks

Formulations

• Canonical Formulation
• Flow Formulation
• Level Formulation
• Candidate Tree Formulation

Canonical Formulation (1)

• Multicast is modeled using Steiner tree problem
• For each edge e, there is a variable x

e

indicating

whether e is in the Steiner tree (x

e

= 1) or not (x

e

= 0)

• The formulation uses cuts of the original network

graph G=(V,E), where V denotes set of nodes and

E set of links

• Set T denotes set of terminals (receivers)




(W) denotes the cut induced by WV, i.e., the set

of edges with the source node in W and the

destination node in its complement (V \ W)

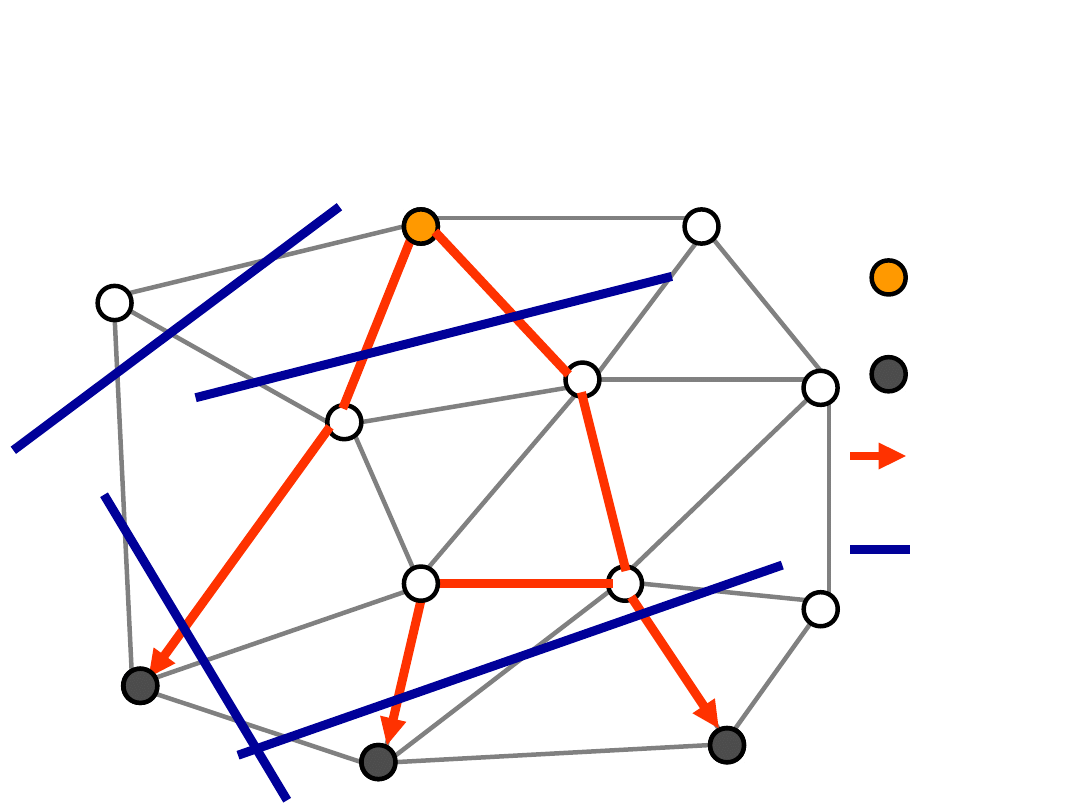
Canonical Formulation (2)

2

1

3

4

11

8

7

6

9

Root
node

Terminal
(receiver)

Multicast
tree

8

9

12

5

10

1

7

Cut

Canonical Formulation (3)

sets
V

network nodes

E

links (directed edges)

T

terminals (receivers)

constants



(W) cut induced by WV, including edges with the

source node in W and end node in its

complement

(V \ W)

s

root node of multicast tree

h

volume (bandwidth requirement) of multicast

c

e

capacity of link e

Canonical Formulation (4)

variables
x

e

= 1, if multicast tree uses link e; 0, otherwise

(binary)

constraints
x(



(W))  1, for all WV, sW, (V \ W)T  0

x(



(W)) = 

e



(W)

x

e

,

x

e

h

 c

e

e = 1,2,…,E.

Flow Formulation (1)

• Node-Link formulation developed for unicast flows

can be modified to be used in multicast flows

• For easy of reference this formulation is named

flow

• The flow to each receiver of the multicasting is

modeled as unicast path

• Additional variable associated with each link is in

the model to assure that the flow goes through

the link at most one time

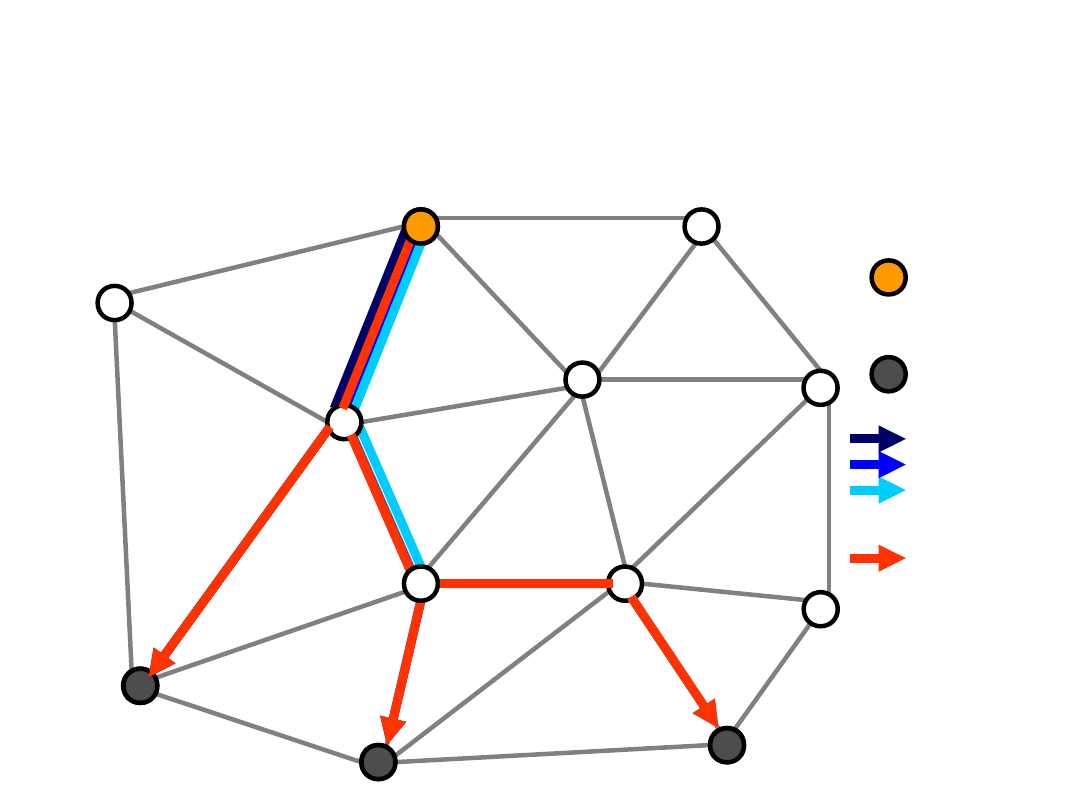
Flow Formulation (2)

2

1

3

4

11

8

7

6

9

Root
node

Receiver
(leaf) node

7

Unicast
path
Multicast
tree

8

9

12

5

10

1

Flow Formulation (3)

indices
v = 1,2,…,V

network nodes

e = 1,2,…,Elinks
k = 1,2,…,K(terminals) receivers
constants
a

ev

= 1, if link e originates at node v; 0, otherwise

b

ev

= 1, if link e terminates in node v; 0,

otherwise

s

root node of multicast tree

h

volume (bandwidth requirement) of multicast

c

e

capacity of link e

Flow Formulation (4)

variables
x

ek

= 1, if multicast flow to receiver k uses link e; 0,

otherwise (binary)

x

e

= 1, if multicast tree uses link e; 0, otherwise

(binary)

constraints


e

 a

ev

x

ek

 – 

e

 b

ev

x

ek

 = 1,   if v = s

v = 1,2,…,V

k =

1,2,…,K



e

 a

ev

x

ek

 – 

e

 b

ev

x

ek

 = –1,   if v = k

v = 1,2,…,V

k = 1,2,

…,K



e

 a

ev

x

ek

 – 

e

 b

ev

x

ek

 = 0,  if v  s,k

v = 1,2,…,V k = 1,2,

…,K

x

ek

 x

e

, e = 1,2,…,E

k = 1,2,…,K

x

e

h

 c

e

, e = 1,2,…,E.

Level Formulation (1)

• We assume that the root of the tree is located on

level 1

• All children of the root (nodes that have a direct

link from the root) are located on level 2

• If a father node of v is on level l, then v is located on

level (l + 1)

• For easy of reference this formulation is named level
• Variable x

wvl

is 1 if the link (w,v) is used in multicast

tree and w is located on level l of the tree t

• In the literature this formulation is also called

Layered Graphs (Gouveia et al.)

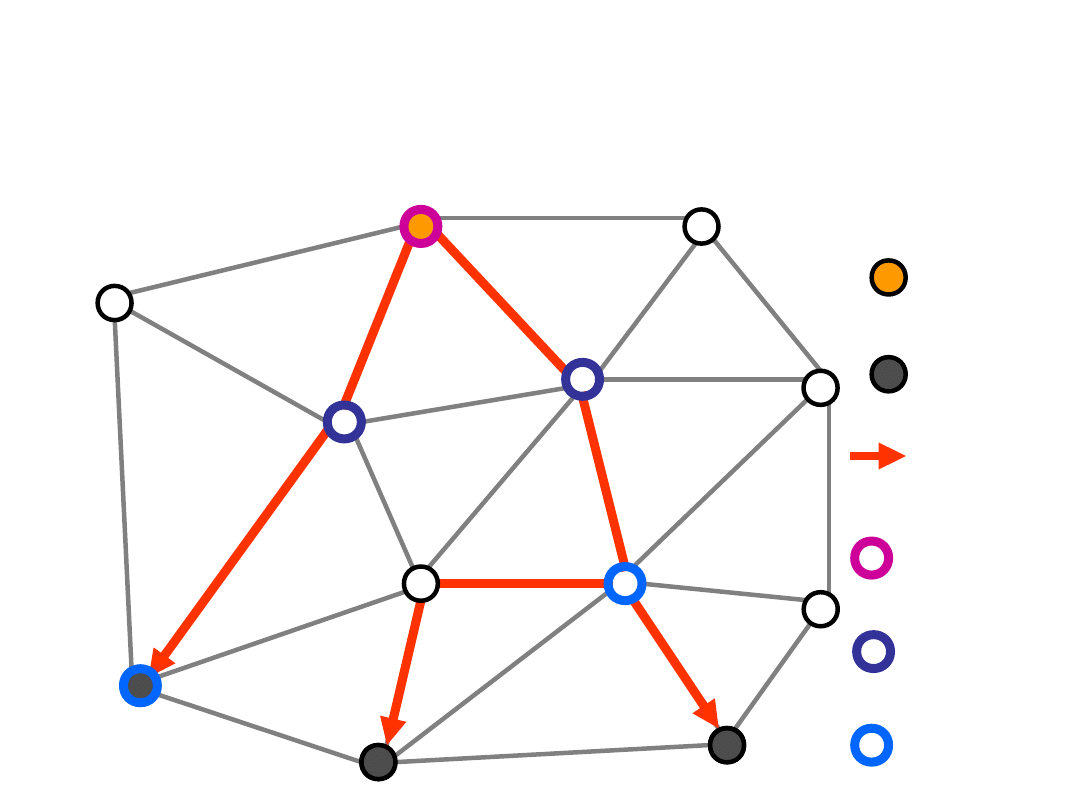
Level Formulation (2)

2

1

3

4

11

8

7

6

9

Root
node

Receiver
(leaf) node

Multicast
tree

8

9

12

5

10

1

Level 1
node

Level 2
node

7

Level 3
node

Level Formulation (3)

indices
v,w,b = 1,2,…,V network nodes
k = 1,2,…,K

receivers

l = 1,2,…,L

levels (parent nodes)

constants
s

root node of multicast tree

e(w,v)

=1, if there is a direct link (w,v) in

graph; 0, otherwise

h

volume (bandwidth requirement) of multicast

c

wv

capacity of link (w,v)

Level Formulation (4)

variables
x

wvl

= 1, if the link (w,v) is used in multicast tree

and w is located on level l of the tree; 0,
otherwise (binary)

x

wv

= 1, if multicast tree uses link (w,v); 0

otherwise

(binary)

Level Formulation (5)

constraints


w:e(w,v)=1



l

 x

wvl

 = 0,   v = s v = 1,2,…,V



w:e(w,k)=1



l

 x

wkl

 = 1,    k = 1,2,…,K



v:e(w,v)=1

x

wv1

 = 0, w  s w = 1,2,…,V

x

wv(l+1)

  

b

 x

bwl

,   e(w,v) = 1 w = 1,2,…,V v = 1,2,

…,V l = 1,2,…,L - 1



l

x

wvl

  x

wv

,  e(w,v) = 1 w = 1,2,…,V  v = 1,2,…,V

x

wv

  

l

x

wvl

, e(w,v) = 1 w = 1,2,…,V  v = 1,2,…,V

x

wv

h

 c

wv

, e(w,v) = 1 w = 1,2,…,V  v = 1,2,…,V.

Candidate Tree Formulation

(1)

• Analogy to Link-Path unicast formulation
• There are candidate trees (topologies) with the

same root node and connecting all terminals
(receivers)

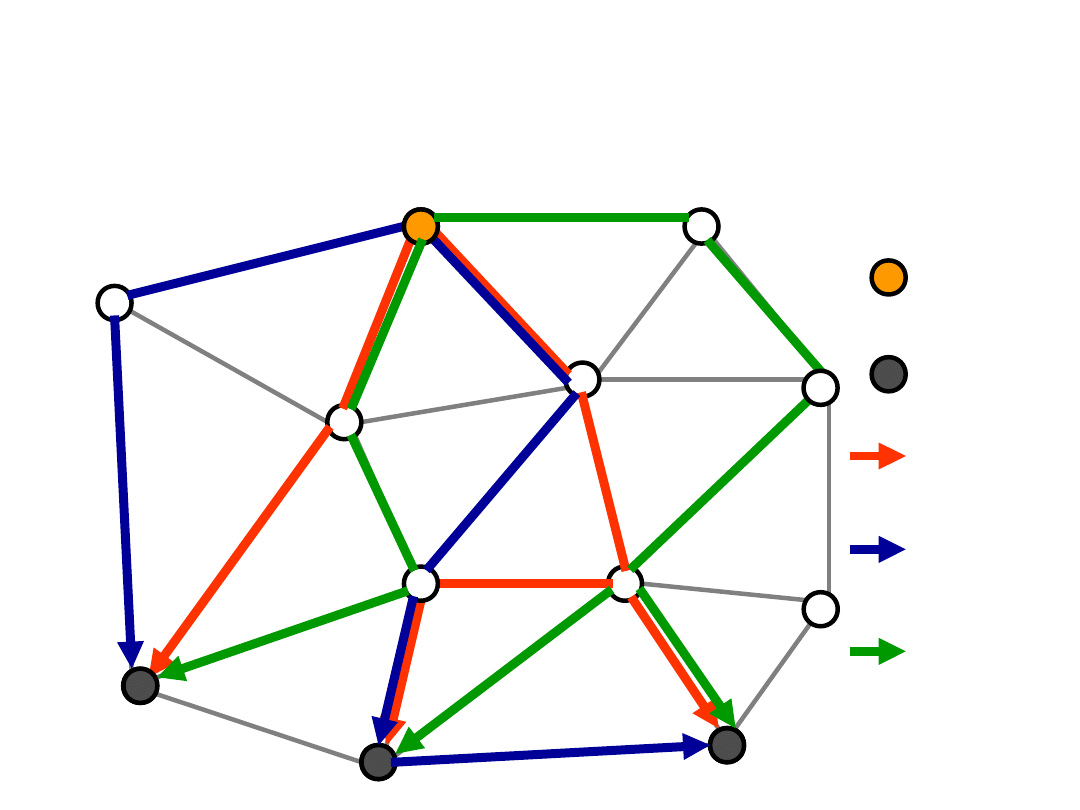
Candidate Tree Formulation

(2)

2

1

4

11

8

7

6

9

Root
node

Terminal
(receiver)

Candidate
tree

8

9

12

5

10

7

Candidate
tree

Candidate
tree

1

3

Candidate Tree Formulation

(3)

indices
e = 1,2,…,Elinks
p = 1,2,…,Pcandidate trees
constants



ep

= 1, if link e belongs to tree p; 0, otherwise

h

volume (bandwidth requirement) of multicast

c

e

capacity of link e

Candidate Tree Formulation

(4)

variables
x

p

flow allocated to tree p (continuous non-

negative)

constraints


p

x

p

= h



p



ep

x

p

 c

e

, e = 1,2,…,E.

Lecture Outline

• Introduction
• Integer Programming Formulations

• Cost Problem

• Network Design Problem
• Maximum Delay Problem
• Throughput Problem
• Multicast Packing Problem
• Concluding Remarks

Cost Problem (1)

• FA (Flow Allocation) problem
• The stream is split and multiple trees are used

to deliver the content to receivers

• Each tree has the same root
• Objective is to minimize overall cost of the

streaming

• Level limit to improve QoS and reliability
• Level formulation

Cost Problem (2)

Given: network topology, link capacity, location of

root, set of receivers, volume of each trees, level
limit, link cost

Minimize: cost

Over: multicast routing

Cost Problem (3)

indices
v,w,b = 1,2,…,V network nodes
k = 1,2,…,K

receivers

t = 1,2,…,T

trees

l = 1,2,…,L

levels (parent nodes)

Cost Problem (4)

constants
s

root node of multicast tree

e(w,v)

=1, if there is a direct link (w,v) in

graph; 0, otherwise

h

t

volume (bandwidth requirement) of tree t

c

wv

capacity of link (w,v)



wv

routing cost of link (w,v)

Cost Problem (5)

variables
x

wvtl

= 1, if the link (w,v) is used in multicast tree t

and w is located on level l of the tree; 0,

otherwise (binary)

x

wvt

= 1, if multicast tree t uses link (w,v); 0

otherwise

(binary)

objective
minimize F = 

w



v



t

x

wvt

h

t



wv

Cost Problem (6)

constraints


w:e(w,v)=1



l

 x

wvtl

 = 0,

v = s v = 1,2,…,V t = 1,2,

…,T



w:e(w,k)=1



l

 x

wktl

 = 1,     k = 1,2,…,K t = 1,2,…,T



v:e(w,v)=1

x

wvt1

 = 0,

w  s w = 1,2,…,V

t = 1,2,…,T

x

wvt(l+1)

  

b

 x

bwtl

,  

e(w,v) = 1 w = 1,2,…,V

v = 1,2,…,V l = 1,2,…,L - 1

t = 1,2,…,T



l

x

wvtl

  x

wvt

,  e(w,v) = 1

w = 1,2,…,V  v = 1,2,

…,V

t = 1,2,…,T

x

wvt

  

l

x

wvtl

, e(w,v) = 1

w = 1,2,…,V  v = 1,2,

…,V

t = 1,2,…,T



t

x

wvt

h

t

 c

wv

, e(w,v) = 1 w = 1,2,…,V   v = 1,2,…,V.

Optimization

• The problem is linear, integer (binary) and

NP-complete (equivalent to Steiner tree
problem)

• To find optimal solutions solvers like CPLEX and

GuRoBi can be used

• Heuristics can be used, e.g., construction

algorithms, greedy approach, evolutionary
algorithm, etc.

Lecture Outline

• Introduction
• Integer Programming Formulations
• Cost Problem

• Network Design Problem

• Maximum Delay Problem
• Throughput Problem
• Multicast Packing Problem
• Concluding Remarks

Network Design Problem (1)

• CFA (Capacity and Flow Allocation) problem for

multicast flows

• A number of multicast demands, each is

defined by the root node, set of receivers and
volume

• Modular links
• Flow formulation of multicast flows

Network Design Problem (2)

Given: network topology, link capacity, multicast

demands (root, receivers and volume)

Minimize: network cost

Over: multicast routing, link allocation

Network Design Problem (3)

indices
v = 1,2,…,V

network nodes

e = 1,2,…,Elinks
d = 1,2,…,D

multicast demands (multicast

group)

k = 1,2,…,K

d

receivers in multicast demand d

Network Design Problem (4)

constants
a

ev

= 1, if link e originates at node v; 0, otherwise

b

ev

= 1, if link e terminates in node v; 0,

otherwise

s

d

root node of multicast demand d

h

d

volume of multicast demand d



e

cost of one capacity module on link e

M

size of the link capacity module

Network Design Problem (5)

variables
x

edk

= 1, if multicast flow of multicast demand d to

receiver k uses link e; 0, otherwise (binary)

x

ed

= 1, if multicast demand d uses link e; 0,

otherwise (binary)

y

e

capacity of link e expressed in the number of
modules (non-negative integer)

objective
minimize F = 

e



e

y

e

Network Design Problem (6)

constraints


e

 a

ev

x

edk

 – 

e

 b

ev

x

edk

 = 1,   

if v = s

d

v = 1,2,…,V

d = 1,2,…,D

k = 1,2,…,K

d



e

 a

ev

x

edk

 – 

e

 b

ev

x

edk

 = –1,    if v = k

v = 1,2,…,V

d = 1,2,…,D

k = 1,2,…,K

d



e

 a

ev

x

edk

 – 

e

 b

ev

x

edk

 = 0, 

if v  s

d

,k

v = 1,2,…,V

d = 1,2,…,D

k = 1,2,…,K

d

x

edk

 x

ed

, e = 1,2,…,E d = 1,2,…,D

k = 1,2,…,K

d



d

x

ed

h

t

 My

e

, e = 1,2,…,E.

Optimization

• The problem is linear, integer, and NP-

complete (equivalent to Steiner tree problem)

• To find optimal solutions solvers like CPLEX and

GuRoBi can be used

• Heuristics can be used

Lecture Outline

• Introduction
• Integer Programming Formulations
• Cost Problem
• Network Design Problem

• Maximum Delay Problem

• Throughput Problem
• Multicast Packing Problem
• Concluding Remarks

Maxium Delay Problem (1)

• FA (Flow Allocation) problem
• Objective is to minimize the maximum (worst)

delay to receiver (QoS requirement)

• Flow formulation, since the level formulation

does not include the path to receiver

Maxium Delay Problem (2)

Given: network topology, link capacity, location of

root, set of receivers, tree volume, link delays

Minimize: maximum delay

Over: multicast routing

Maxium Delay Problem (3)

indices
v = 1,2,…,V

network nodes

e = 1,2,…,Elinks
k = 1,2,…,Kreceivers
constants
a

ev

= 1, if link e originates at node v; 0, otherwise

b

ev

= 1, if link e terminates in node v; 0,

otherwise

s

root node of multicast tree

Maxium Delay Problem (4)

constants
h

volume of multicast transmission t



e

delay of link e

c

e

capacity of link e

variables
x

ek

= 1, if multicast flow to receiver k uses link e;

0, otherwise (binary)

x

e

= 1, if multicast tree uses link e; 0, otherwise

(binary)

x

maximum delay (non-negative continuous)

Maxium Delay Problem (5)

objective
minimize x
constraints


e

 a

ev

x

ek

 – 

e

 b

ev

x

ek

 = 1,   

if v = s

v = 1,2,…,V

k = 1,2,…,K



e

 a

ev

x

ek

 – 

e

 b

ev

x

ek

 = –1,

if v = k

v = 1,2,…,V

k = 1,2,…,K



e

 a

ev

x

ek

 – 

e

 b

ev

x

ek

 = 0, if v  s,k

v = 1,2,…,V

k = 1,2,…,K



e



e

x

ek

 x,

k = 1,2,…,K

x

ek

 x

e

,

e = 1,2,…,E

k = 1,2,…,K

x

e

h

 c

e

, e = 1,2,…,E.

Optimization

• The problem is linear, integer, and NP-

complete (equivalent to Steiner tree problem)

• To find optimal solutions solvers like CPLEX and

GuRoBi can be used

• Heuristics can be used

Lecture Outline

• Introduction
• Integer Programming Formulations
• Cost Problem
• Network Design Problem
• Maximum Delay Problem

• Throughput Problem

• Multicast Packing Problem
• Concluding Remarks

Throughput Problem (1)

• FA (Flow Allocation) problem
• Objective is to maximize the throughput

(streaming rate)

• Multiple trees are used for streaming
• Level limit to improve QoS and reliability
• Level formulation of multicast flows

Throughput Problem (2)

Given: network topology, link capacity, location of

root, set of receivers, number of trees

Maximize: throughput

Over: multicast routing

Throughput Problem (3)

indices
v,w,b = 1,2,…,V network nodes
k = 1,2,…,K

receivers

t = 1,2,…,T

trees

l = 1,2,…,L

levels (parent nodes)

Throughput Problem (4)

constants
s

root node of multicast tree

e(w,v)

=1, if there is a direct link (w,v) in

graph; 0, otherwise

c

wv

capacity of link (w,v)

M

large number

Throughput Problem (5)

variables
x

wvtl

streaming rate on an overlay link (w,v) (no

other

peer nodes in between) in multicast tree

t and w is

located on level l of tree t;

(continuous, non-

negative)

x

wvt

= 1, if multicast tree t uses link (w,v); 0

otherwise

(binary)

q

t

throughput (bandwidth requirement) of tree t
(continuous, non-negative)

objective
maximize F = 

t

q

t

Throughput Problem (6)

constraints


w:e(w,v)=1



l

 x

wvtl

 = 0,

v = s v = 1,2,…,V t = 1,2,

…,T



w:e(w,k)=1



l

 x

wktl

 = q

t

,     k = 1,2,…,K t = 1,2,…,T



v:e(w,v)=1

x

wvt1

 = 0,

w  s w = 1,2,…,V

t = 1,2,…,T

x

wvt(l+1)

  

b

 x

bwtl

,  

e(w,v) =1 w = 1,2,…,V

v = 1,2,…,V l = 1,2,…,L - 1

t = 1,2,…,T



l

x

wvtl

  Mx

wvt

, 

e(w,v) = 1 w = 1,2,…,V

v = 1,2,…,V t = 1,2,…,T

x

wvt

  

l

x

wvtl

,

e(w,v) = 1 w = 1,2,…,V

v = 1,2,…,V t = 1,2,…,T



t



l

x

wvtl

 c

wv

, e(w,v) = 1 w = 1,2,…,V   v = 1,2,…,V.

Optimization

• The problem is linear, integer, and NP-

complete (equivalent to Steiner tree problem)

• To find optimal solutions solvers like CPLEX and

GuRoBi can be used

• Heuristics can be used

Lecture Outline

• Introduction
• Integer Programming Formulations
• Cost Problem
• Network Design Problem
• Maximum Delay Problem
• Throughput Problem

• Multicast Packing Problem

• Concluding Remarks

Multicast Packing Problem

(1)

• FA (Flow Allocation) problem
• Objective is to minimize maximum link

congestion

• Classical problem related to multicasting
• Flow formulation is used
• Level formulation can also be used

Multicast Packing Problem

(2)

Given: network topology, link capacity, location of

root, set of receivers, number of trees

Minimize: maximum link congestion

Over: multicast routing

Multicast Packing Problem

(3)

indices
v = 1,2,…,V

network nodes

e = 1,2,…,Elinks
d = 1,2,…,D

multicast demands (multicast

group)

k = 1,2,…,K

d

receivers in multicast demand d

constants
a

ev

= 1, if link e originates at node v; 0, otherwise

b

ev

= 1, if link e terminates in node v; 0,

otherwise

Multicast Packing Problem

(4)

constants
s

d

root node of multicast demand d

h

d

volume of multicast demand d

M

size of the link capacity module

variables
x

edk

= 1, if multicast flow of multicast demand d to

receiver k uses link e; 0, otherwise (binary)

x

ed

= 1, if multicast demand d uses link e; 0,

otherwise

(binary)



maximum link congestion

Multicast Packing Problem

(5)

objective
minimize



constraints


e

 a

ev

x

edk

 – 

e

 b

ev

x

edk

 = 1,   

if v = s

d

v = 1,2,…,V

d = 1,2,…,D

k = 1,2,…,K

d



e

 a

ev

x

edk

 – 

e

 b

ev

x

edk

 = –1,   

if v = k

v = 1,2,…,V

d = 1,2,…,D

k = 1,2,…,K

d



e

 a

ev

x

edk

 – 

e

 b

ev

x

edk

 = 0, 

if v  s

d

,k

v = 1,2,…,V

d = 1,2,…,D

k = 1,2,…,K

d

x

edk

 x

ed

, e = 1,2,…,E d = 1,2,…,D

k = 1,2,…,K

d



d

x

ed

h

t





,

e = 1,2,…,E.

Optimization

• The problem is linear, integer, and NP-

complete

• To find optimal solutions solvers like CPLEX and

GuRoBi can be used

• Heuristics can be used

Lecture Outline

• Introduction
• Integer Programming Formulations
• Cost Problem
• Network Design Problem
• Maximum Delay Problem
• Throughput Problem
• Multicast Packing Problem

• Concluding Remarks

Concluding Remarks

• Due to growing popularity of various streaming

services in the Internet, the multicast

transmission has been gaining much attention

recently

• Modeling of multicasting makes use of traditional

unicast multicommodity flows, however new

models can be proposed

• Most of problems formulated in the context of

unicast flows can be also formulated for

multicast flows

Further Reading

• Minoli D. , IP Multicast with Applications to IPTV and Mobile DVB-H,

John Wiley & Sons, 2008

• http://www.cisco.com/en/US/tech/tk828/technologies_white_paper09

186a0080092942.shtml

• Koch T. and  Martin A., Solving Steiner tree problems in graphs to

optimality, Networks, vol.32, no. 3, 1998, pp. 207-232

• Oliveira C.A.S., Pardalos P.M. and Resende M.G.C., Optimization

problems in multicast tree construction, Handbook of Optimization in

Telecommunications, Springer, 2006

• Wu C. and Li B., Optimal Rate Allocation in Overlay Content

Distribution, in Proc. of the 6th Networking Conf., 2007, pp. 678-690

• Allen J., Kubat P., Reliable Video Broadcast via Protected Steiner

Trees, IEEE Comm. Magazine, Vol. 48, No. 2, 2010, pp. 70-76

• Gouveia L., Luidi Simonetti L., Uchoa E., Modelling Hop-Constrained

and Diameter-Constrained Minimum Spanning Tree Problems as

Steiner Tree Problems over Layered Graphs, Mathematical

Programming, 2009