Zasady,

prawa,

teorie

Zapis konstrukcji

27.06.21

Zasady, prawa, teorie

2

Przestrzeń euklidesowa

Elementy niewłaściwe

Rzuty

Niezmienniki rzutowania równoległego

Relacje zachodzące pomiędzy elementami

Przynależność elementów w rzucie równoległym

Równoległość i prostopadłość elementów

27.06.21

Zasady, prawa, teorie

3

Przestrzeń euklidesowa

"Elementy" Euklidesa
Aksjomaty Euklidesa
Przestrzeń euklidesowa

27.06.21

"Elementy" Euklidesa

4

Elementy

Euklidesa

Jedno z najsłynniejszych dzieł
naukowych w historii ludzkości,
pochodzące z III wieku p.n.e.
Zostało wydane we wszystkich
językach świata.
Traktat arytmetyczny i
geometryczny, obejmujący swym
zakresem podstawowe zagadnienia
obu tych nauk.
Elementy ukształtowały sposób
myślenia o teoriach matematycznych
i stały się wzorcem do naśladowania
w wielu dziedzinach nauki.
Klasyczny przykład metody
dedukcyjnej i świadectwa siły
rozumowania formalnego opartego na
logice.

27.06.21

"Elementy" Euklidesa

5

Elementy

Euklidesa

Elementy spisane są w postaci wstępu i trzynastu ksiąg:

Wstęp – 35 określeń, 5 aksjomatów, 5 postulatów
Geometria płaska

I – Twierdzenia o trójkątach i prostych
II – Algebra przedstawiona w sposób geometryczny
III, IV – Teoria okręgu. Wielokąty wpisane i opisane na
okręgu

Arytmetyka

V – Teoria proporcji
VI, VII – Teoria podobieństwa
VIII, IX, X – Arytmetyka liczb naturalnych

Stereometria

XI, XII, XIII – Stereometria (geometria przestrzenna)

27.06.21

"Elementy" Euklidesa

6

Aksjomaty Euklidesa

Sformułowany przez Euklidesa zbiór podstawowych
pojęć i twierdzeń geometrycznych dla płaskiej prze-
strzeni oparty jest na systemie pięciu aksjomatów.

1. Dowolne dwa punkty można połączyć odcinkiem.
2. Dowolny odcinek można przedłużyć nieograniczenie.
3. Dla danego odcinka można zaznaczyć okrąg o środku

w dowolnym punkcie i promieniu równym odcinkowi.

4. Wszystkie kąty proste są równe.
5. Dwie proste, które przecinają trzecią w taki sposób,

że suma kątów wewnętrznych po jednej stronie jest
mniejsza od dwu kątów prostych, przetną się z tej
właśnie strony, jeśli się je odpowiednio przedłuży.

27.06.21

"Elementy" Euklidesa

7

Przestrzeń euklidesowa

Przestrzeń euklidesowa to uogólnienie
płaszczyzny i przestrzeni trójwymiarowej

Po wprowadzeniu na płaszczyznę lub w przestrzeń
układu współrzędnych kartezjańskich, każdy
punkt można jednoznacznie identyfikować przy
pomocy jego współrzędnych.

Idea utożsamienia punktu z układem jego współrzędnych
leży u podstaw wspomnianego uogólnienia.

27.06.21

Elementy niewłaściwe

8

Elementy niewłaściwe

Do trójwymiarowej przestrzeni euklidesowej można

dodać tzw. elementy niewłaściwe:
każda prosta posiada punkt niewłaściwy K



utożsamiany z kierunkiem tej prostej;

wszystkie proste równoległe posiadają wspólny

punkt niewłaściwy;

każda płaszczyzna zawiera prostą niewłaściwą,

będącą zbiorem punktów niewłaściwych wszystkich

prostych leżących na tej płaszczyźnie lub

równoległych do tej płaszczyzny;

wszystkie płaszczyzny równoległe posiadają wspólną

prostą niewłaściwą,
prosta równoległa do płaszczyzny przebija tę

płaszczyznę w punkcie niewłaściwym, leżącym na

prostej niewłaściwej tej płaszczyzny;

27.06.21

Elementy niewłaściwe

9

prosta niewłaściwa jest zbiorem samych tylko
punktów niewłaściwych;

jeżeli do prostej należy chociaż jeden punkt
właściwy, to cała ta prosta jest właściwa (posiada
ona tylko jeden punkt właściwy);
dwa różne punkty niewłaściwe jednoznacznie
wyznaczają prostą niewłaściwą;

do całej przestrzeni 3D dołączyć można jedną
płaszczyznę niewłaściwą, będącą zbiorem
punktów niewłaściwych i prostych niewłaściwych
wszystkich prostych i płaszczyzn przestrzeni.

27.06.21

Zasady, prawa, teorie

10

Rzuty

Przestrzeń rzutowa i warunki odwzorowań
Rzut środkowy
Rzut równoległy
Rzut stosowany

27.06.21

Rzuty i warunki odwzorowań

11

Przestrzeń rzutowa

i warunki odwzorowań

Trójwymiarowa przestrzeń euklidesowa
uzupełniona elementami niewłaściwymi
tworzy przestrzeń rzutową.

Podstawową formą zapisu dokumentacji
technicznej trójwymiarowych obiektów
materialnych tworzących daną konstrukcją są
płaskie dwuwymiarowe rysunki zwane rzutami.

27.06.21

Rzuty i warunki odwzorowań

12

Metody odwzorowań obiektów przestrzennych na
płaszczyźnie muszą spełniać następujące warunki:

być jednoznaczne,

tzn. przy ustalonej metodzie

odwzorowania jednemu obiektowi przestrzennemu musi być
przypisany jeden rzut (lub jeden zespół rzutów) i na odwrót -
mając jeden rzut (lub zespół rzutów) powinniśmy na jego
podstawie móc odtworzyć dokładnie ten sam odwzorowany
obiekt w przestrzeni trójwymiarowej;

dawać możliwość restytucji,

tzn. znając rzut (lub

zespół rzutów) obiektu trójwymiarowego powinniśmy mieć
możliwość dokonania analizy jego własności geometrycznych.

27.06.21

Rzut środkowy

13

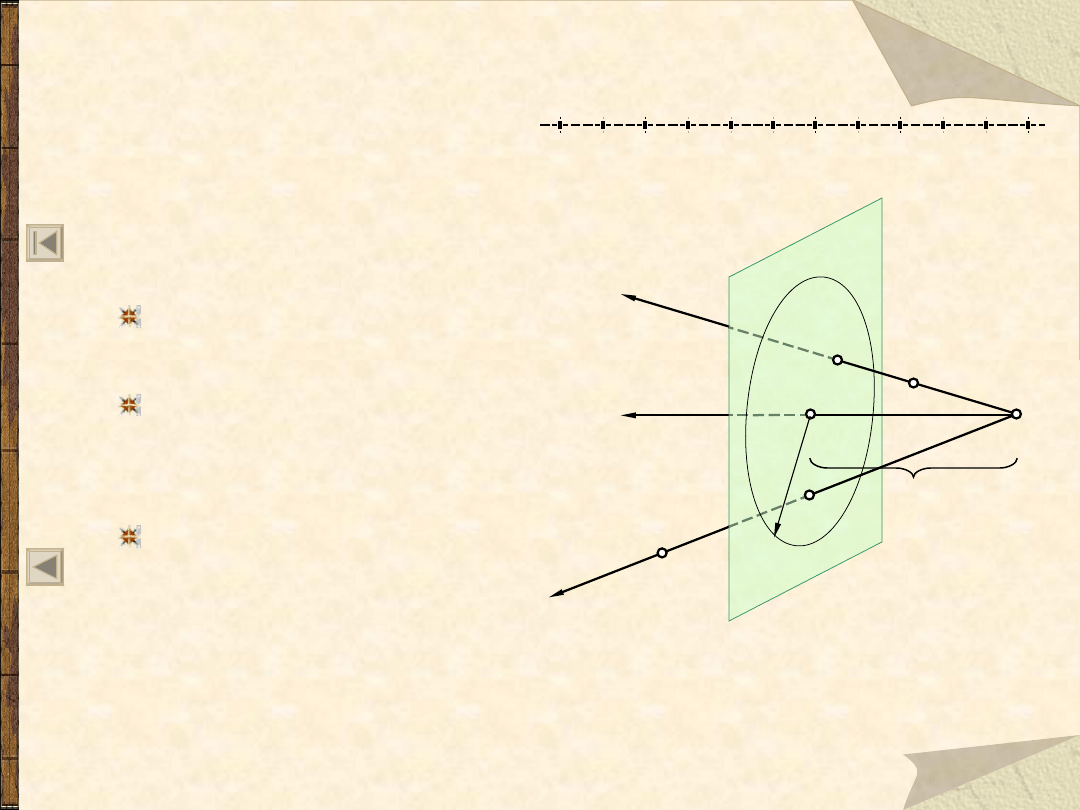
Rzut środkowy

(perspektywa)

Aparat projekcyjny rzutowania
środkowego składa się z umie-
szczonych w trójwymiarowej
przestrzeni euklidesowej:

płaszczyzny



zwanej rzutnią;

a -

promień główny

a

B



środka rzutowania

0

(punktu właściwego
wyznaczającego kierunek
rzutowania);

0



B

S

A

S

A

0

promieni rzutujących
(odwzorowujące w punktach
przebicia z rzutnią punkty,
przestrzeni przez które
przebiegają).

0



-

punkt główny

R -

promień koła oddalenia

R



 -

głębokość

27.06.21

Rzut równoległy

14

Rzut równoległy

Rzutem równoległym nazywamy jednoznaczne
przekształcenie geometryczne przestrzeni
trójwymiarowej na dwuwymiarową przy pomocy
utworzonego w przestrzeni rzutowej aparatu rzutowania
równoległego, zbudowanego z:
płaszczyzny



zwanej rzutnią;

oraz
nie należącego do rzutni



punktu niewłaściwego

K



utożsamianego z kierunkiem rzutowania k



.

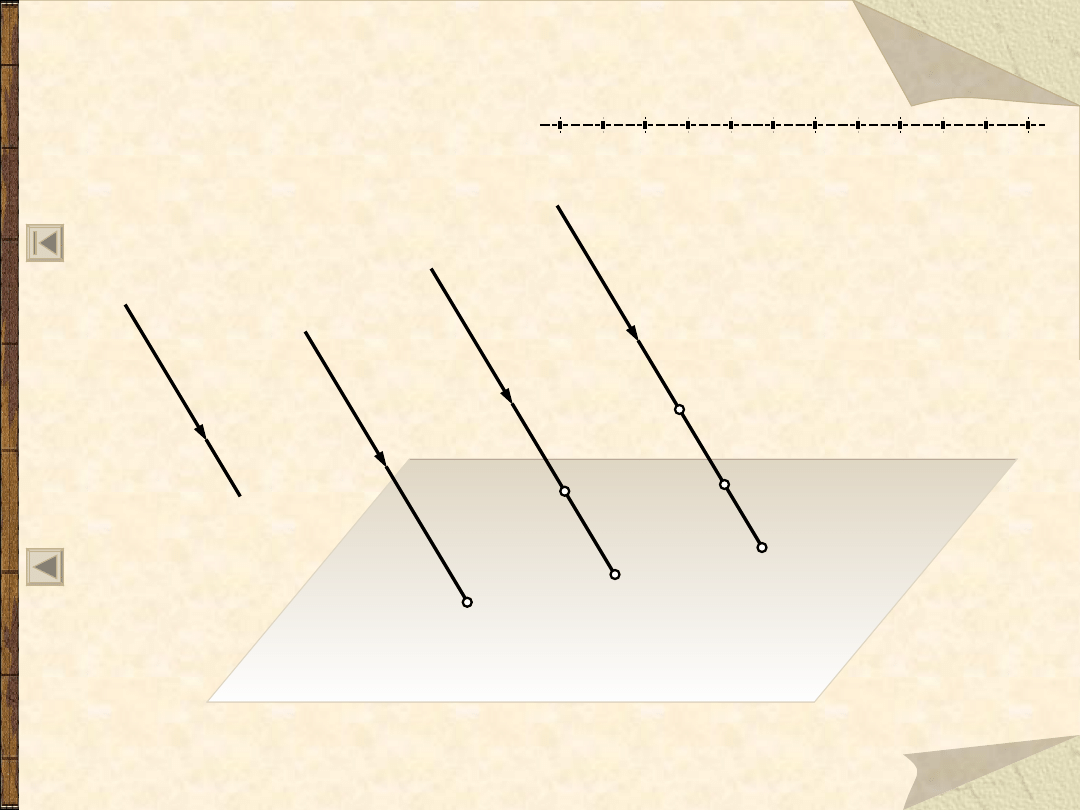
Promienie rzutujące, biegnąc od punktu niewłaściwego będą więc

ustawione do siebie równolegle, a w punktach przebicia z rzutnią 

odwzorować będą rzuty równoległe punktów przestrzeni, przez które

przebiegają.

27.06.21

Rzut równoległy

15

Aparat rzutowania równoległego



T

R

Q

P=P’

Q’

R’=T’

K



k



27.06.21

Rzut stosowany

16

Rzut stosowany

Rzutowanie środkowe i równoległe realizują

jednoznaczne odwzorowania obiektów

przestrzeni trójwymiarowej w figury płaskie

leżące na rzutni, ale te odwzorowania nie są

jednoznaczne, a więc nie są odwracalne.

Aparat rzutowania z dołączoną umową
o odwracalności, nazywamy rzutem
stosowanym.

W ramach przedmiotu Zapis konstrukcji poznamy
dwa rodzaje rzutów stosowanych zbudowanych za
pomocą aparatu rzutowania równoległego:
• aksonometria
• rzuty Monge’a

27.06.21

Zasady, prawa, teorie

17

Niezmienniki rzutowania

równoległego

Określenie
R1 – o zachowaniu współliniowości
R2 – o zachowaniu przynależności
R3 – o zachowaniu równoległości
R4 – o zachowaniu stosunku długości
R5 – o zachowaniu stosunku podziału
R6 – o zachowaniu długości odcinków
R7 – o zachowaniu miary kąta
R8 – o zachowaniu związków miarowych

27.06.21

Niezmienniki rzutowania równoległego

18

Określenie

Niezmiennikami rzutowania równoległego
nazywamy te własności geometryczne
obiektów przestrzennych, które pozostają
niezmienne w procesie tworzenia rzutów i
posługiwania się nimi, a więc przysługiwać
będą również ich obrazom, czyli rzutom.

27.06.21

Niezmienniki rzutowania równoległego

19

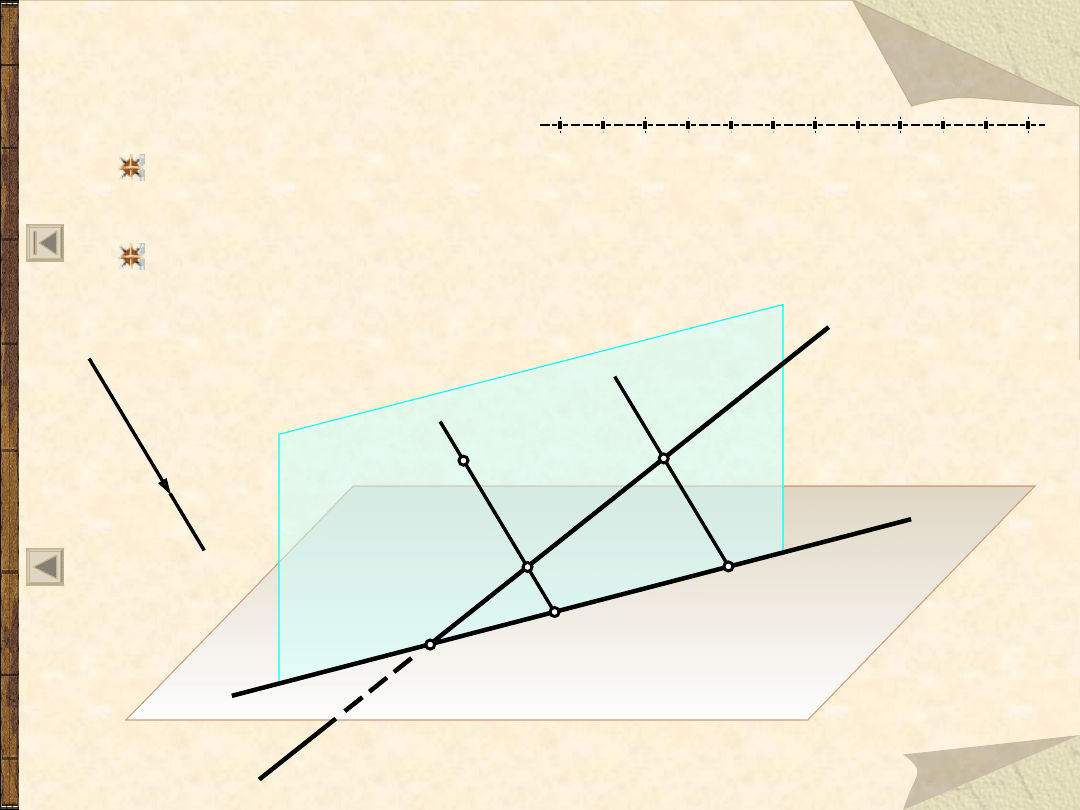
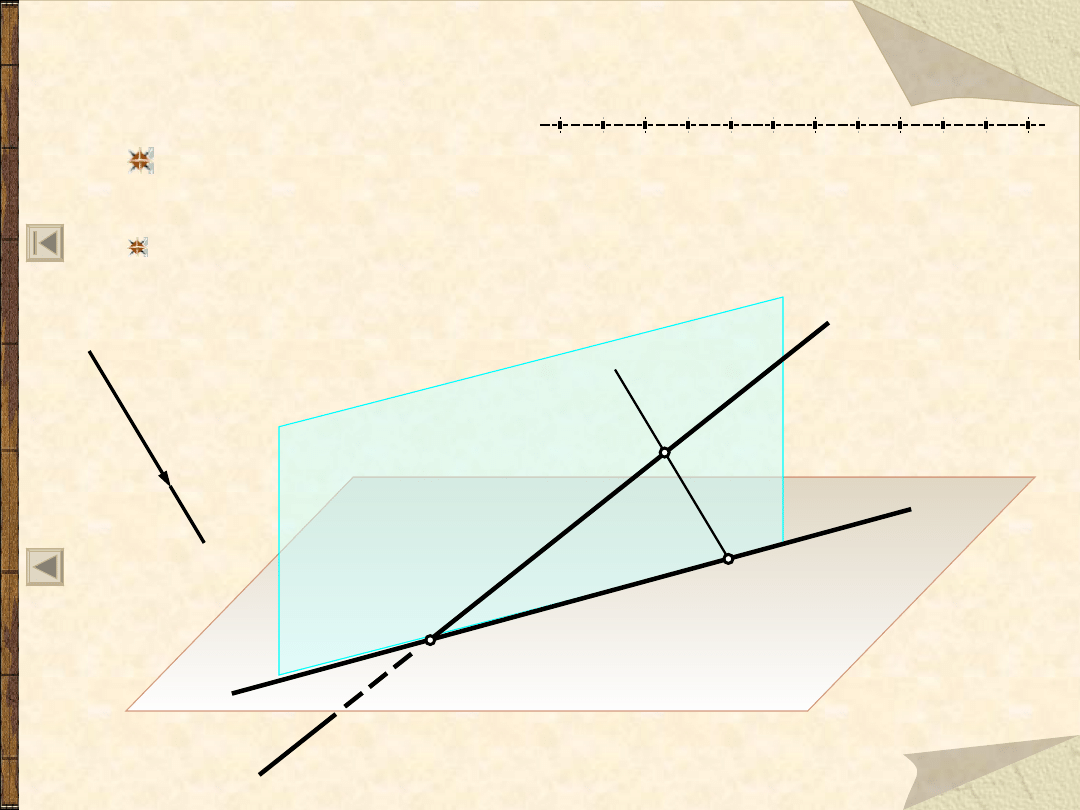
R1 – o zachowaniu współliniowości

Rzutem równoległym prostej (a) w położeniu ogólnym
względem aparatu rzutowania R(, K



) jest prosta (a’).



k



Jeżeli prosta (b) jest równoległa do kierunku rzutowania k



(przechodzi przez punkt niewłaściwy K



) to jej rzutem

równoległym jest punkt (b’).

b

a’

a

C

B’

A’

= C’

= b’

A

B

27.06.21

Niezmienniki rzutowania równoległego

20

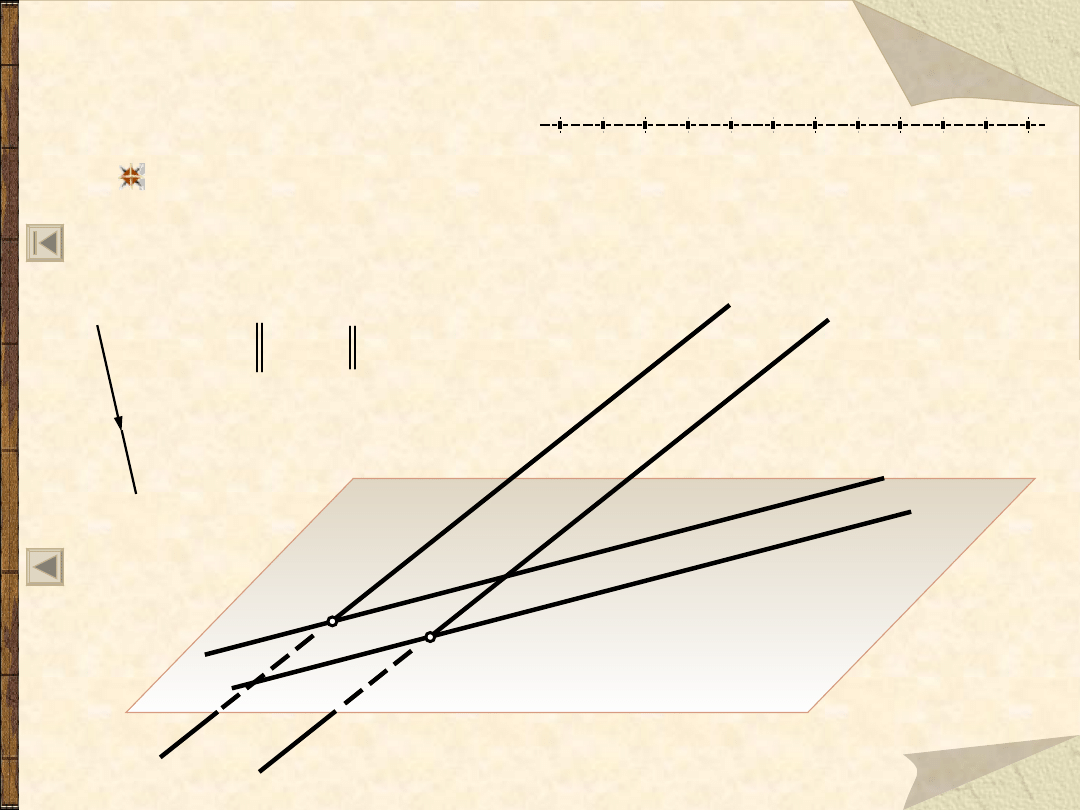
R2 – o zachowaniu przynależności



k



a’

A’

a

Rzut równoległy A’ punktu A leżącego na prostej a,
leży na rzucie równoległym a’ tej prostej.

(Aa)  (A’a’)

Rzut równoległy punktu należącego do zbioru punktów (Aa)

przynależy do rzutu równoległego tego zbioru (A’a’).

A

27.06.21

Niezmienniki rzutowania równoległego

21

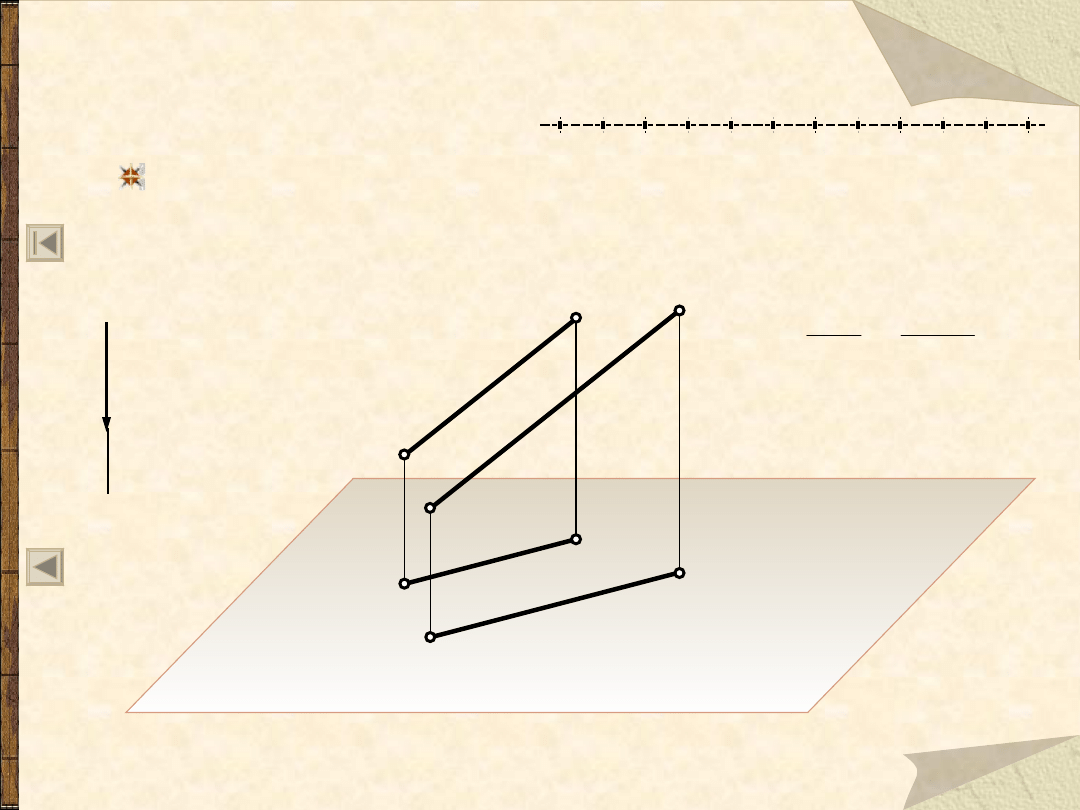
R3 – o zachowaniu równoległości

Rzutem równoległym prostych równoległych będących w
położeniu ogólnym względem aparatu rzutowania (nie
przechodzących przez punkt niewłaściwy K



) są proste

równoległe.



a’

a

k



b’

b

'

' b

a

b

a 

27.06.21

Niezmienniki rzutowania równoległego

22

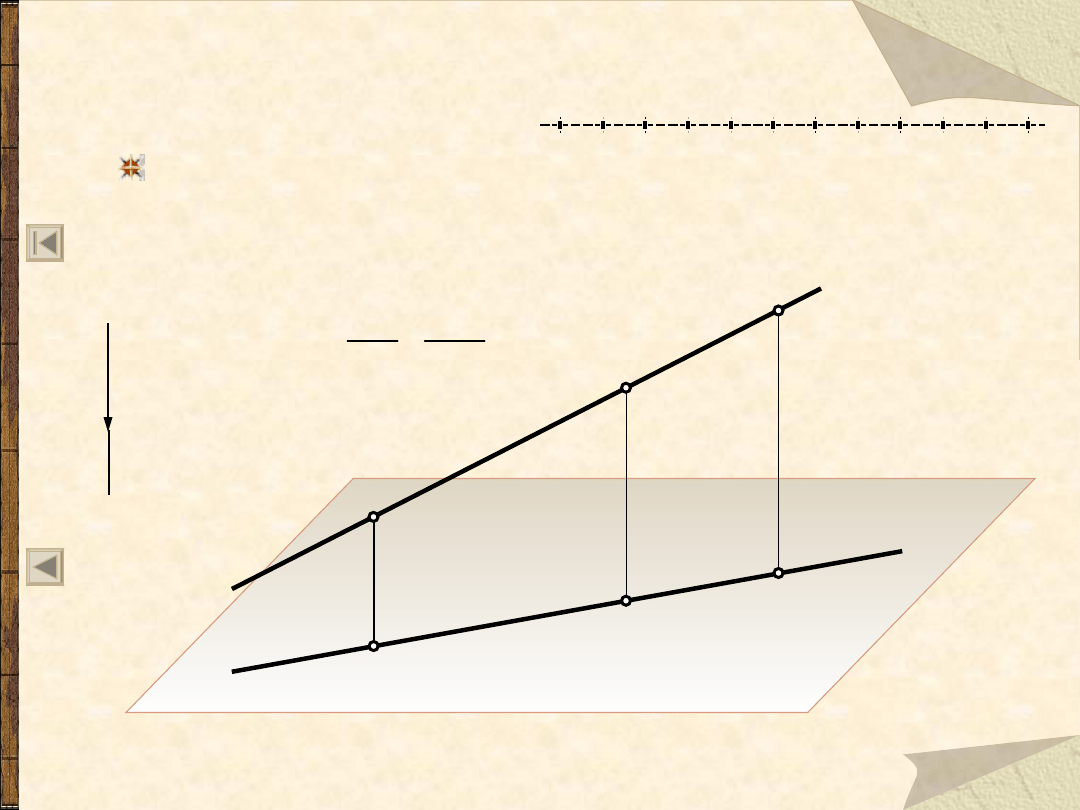
R4 – o zachowaniu stosunku

długości odcinków równoległych

Dla każdej pary odcinków równoległych (lecz nierówno-
ległych do kierunku rzutowania) stosunek ich długości
jest równy stosunkowi długości ich rzutów.

'

'

'

'

D

C

B

A

CD

AB





k



A’

B’

C

D

B

A

C’

D’

27.06.21

Niezmienniki rzutowania równoległego

23

R5 – o zachowaniu stosunku

podziału

Dla każdej prostej przestrzeni nie przechodzącej przez
K



i dla każdej trójki różnych punktów A, B, C tej

prostej oraz trójki ich rzutów równoległych A’, B’, C’
zachodzi równość:

'

'

'

'

C

B

C

A

BC

AC





k



B’

A

C

B

A’

C’

27.06.21

Niezmienniki rzutowania równoległego

24

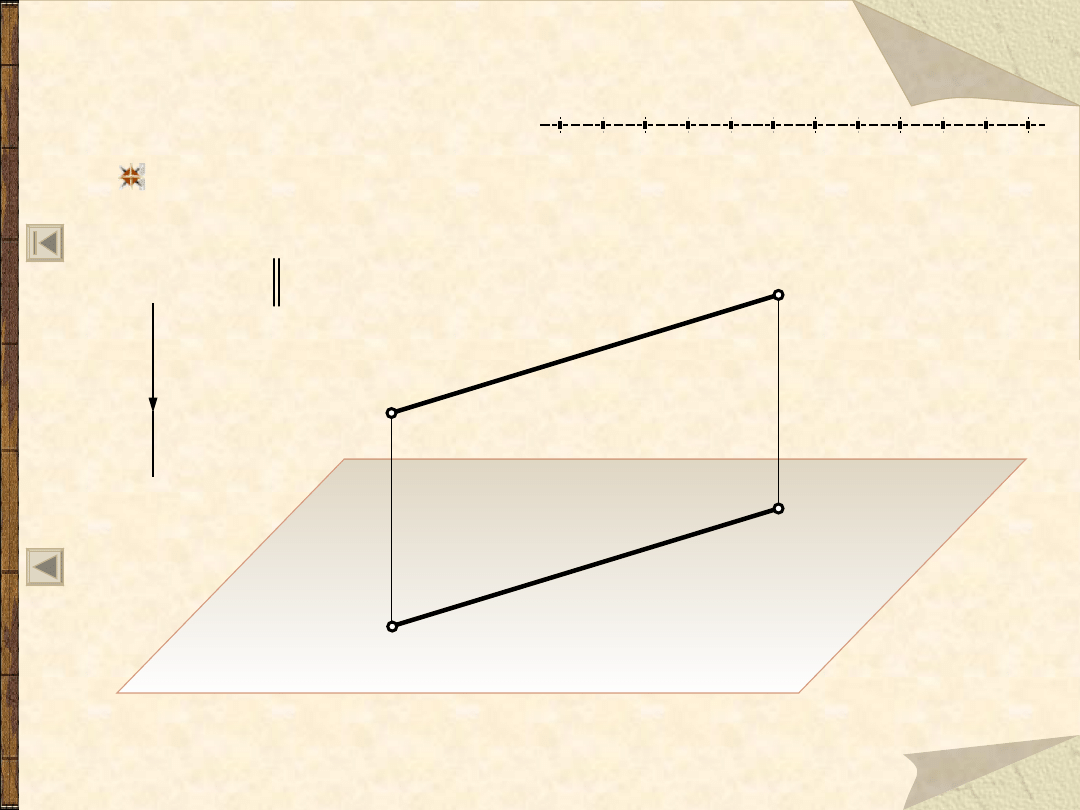
R6 – o zachowaniu długości

odcinków równoległych do rzutni

Długość rzutu równoległego każdego odcinka
równoległego do rzutni, jest równa długości tego odcinka.



k



A’

B’

A

B

'

'B

A

AB

AB







27.06.21

Niezmienniki rzutowania równoległego

25

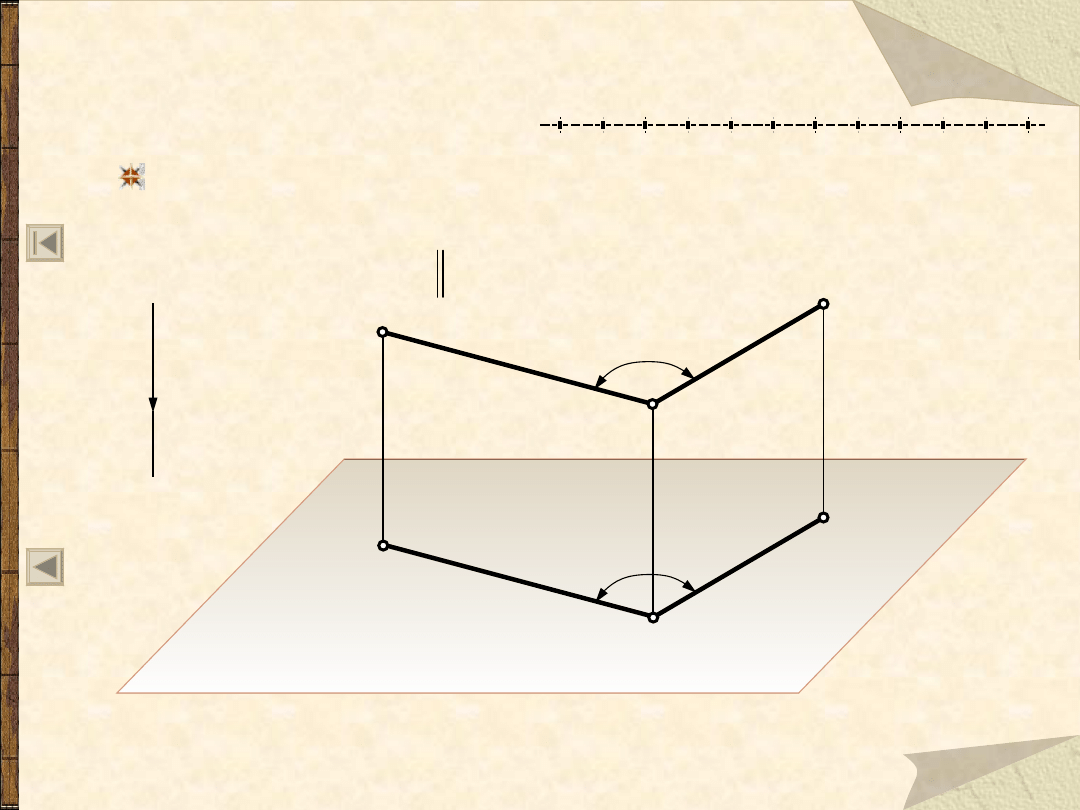
R7 – o zachowaniu miary kąta

o ramionach równoległych do rzutni

Rzutem równoległym kąta o obu ramionach równoległych
do rzutni jest kąt o tej samej mierze.













'

BC

AC



k



B

A

C



'



B’

A’

C’

27.06.21

Niezmienniki rzutowania równoległego

26



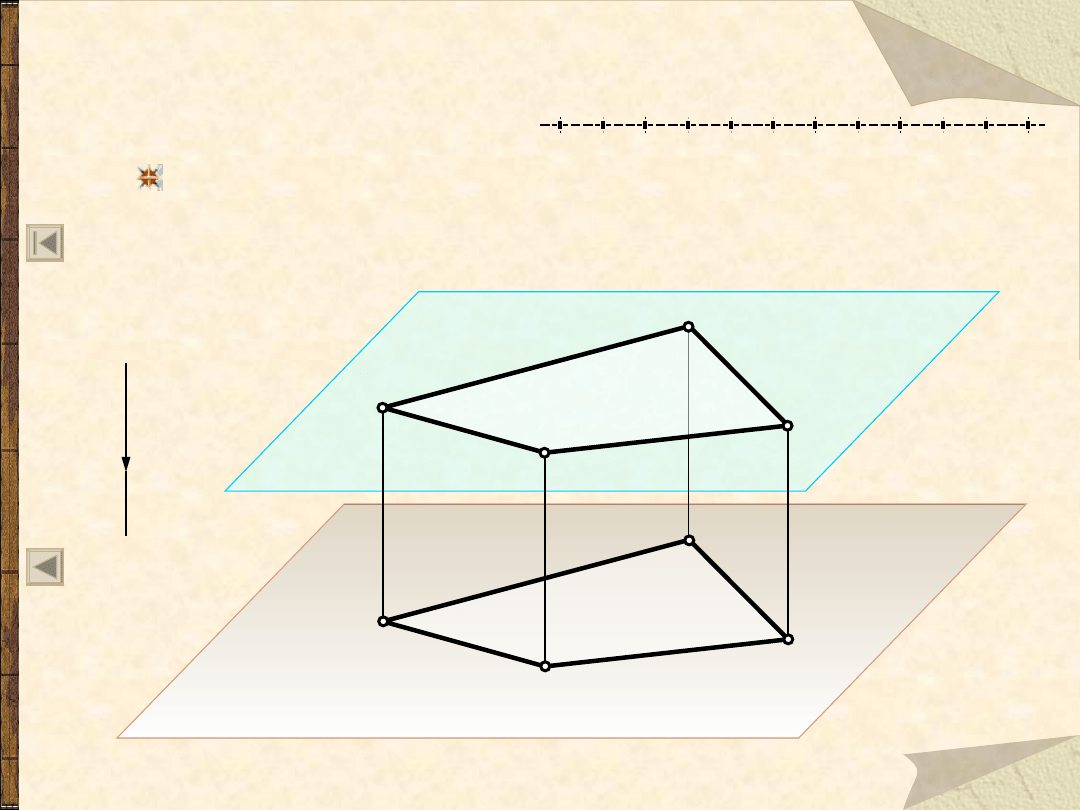
R8 – o zachowaniu związków miarowych

płaszczyzn równoległych do rzutni

k



Dla każdej figury płaskiej F leżącej na płaszczyźnie



równoległej do rzutni, jej rzut F’(A’B’C’D’) jest figurą
przystającą do F(ABCD).



D’

A

B

C

D

A’

B’

C’

27.06.21

Relacje zachodzące pomiędzy prostymi elementami

27

Przynależność elementów

w rzucie równoległym

Punkt i prosta

Punkt na prostej

Punkt i płaszczyzna

Punkt na płaszczyźnie (1)

Punkt na płaszczyźnie (2)

Prosta i płaszczyzna

Prosta na płaszczyźnie (1)
Prosta na płaszczyźnie (1)

27.06.21

Przynależność elementów w rzucie równoległym

28





x

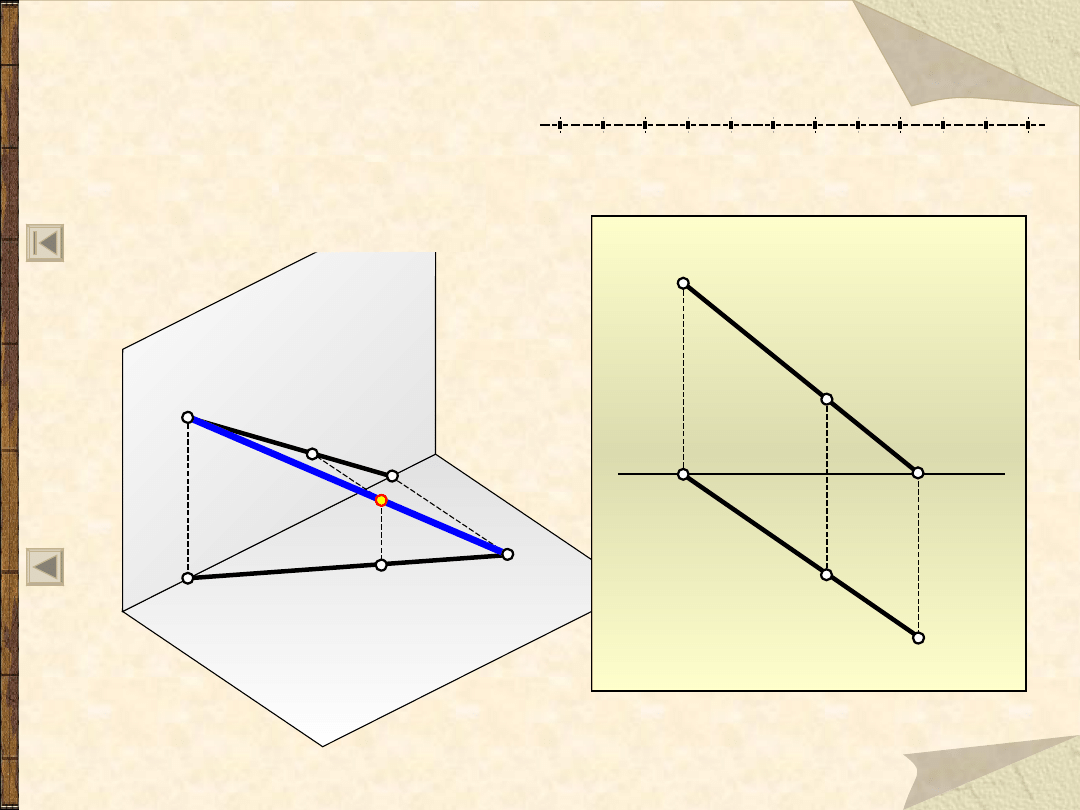
Punkt na prostej

B

A

x

A
”

B=B
”

A=A
’

B’

C
”

C’

Punkt C należy do prostej, jeżeli odpowiednie rzuty
punktu leżą na odpowiednich rzutach tej prostej.

AB

C

B

A

C

B

A

C











"

"

"

'

'

'

B’

C’

=A
’

A
”

C
”

=B
”

C

27.06.21

Przynależność elementów w rzucie równoległym

29

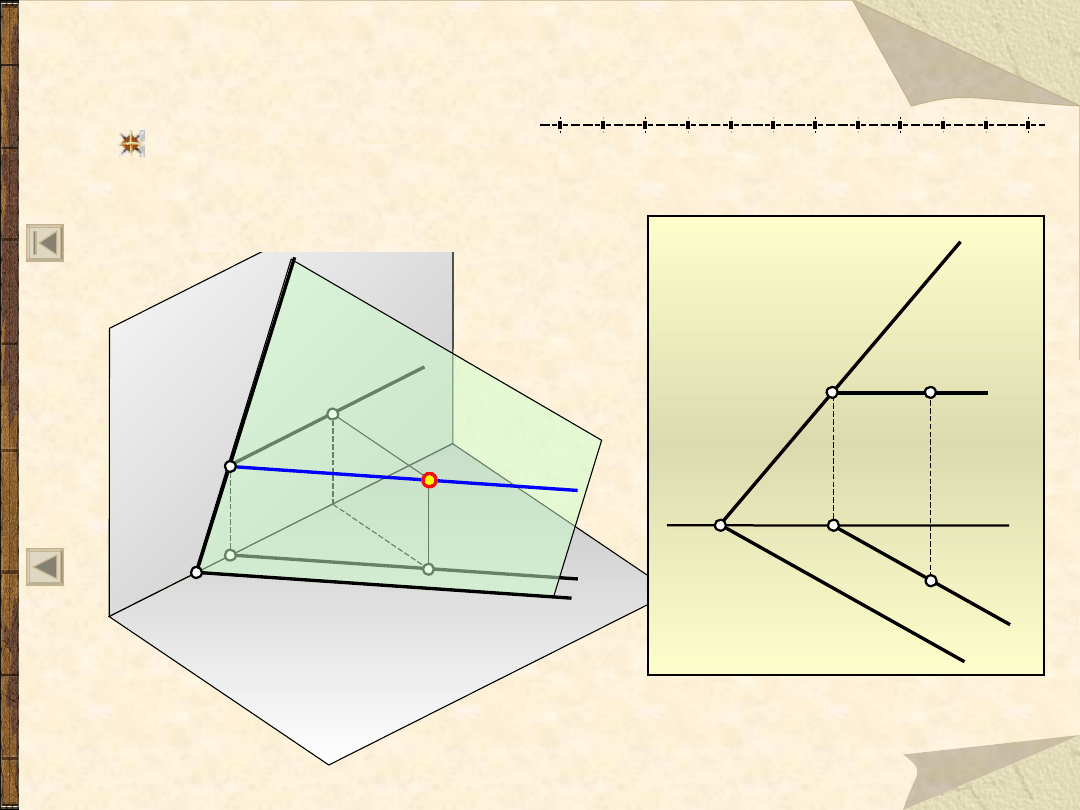
Punkt na płaszczyźnie

(1)





x

x

Punkt P leży na płaszczyźnie



, jeżeli jego rzuty leżą

na odpowiednich rzutach prostej należącej do tej
płaszczyzny.

b”

b’

P”

P’

h



v



b

P

b

P

b

P











"

"

'

'



h



v



V

b

b

P

b
”

b’

V

b

P’

P”

27.06.21

Przynależność elementów w rzucie równoległym

30

b”

b’

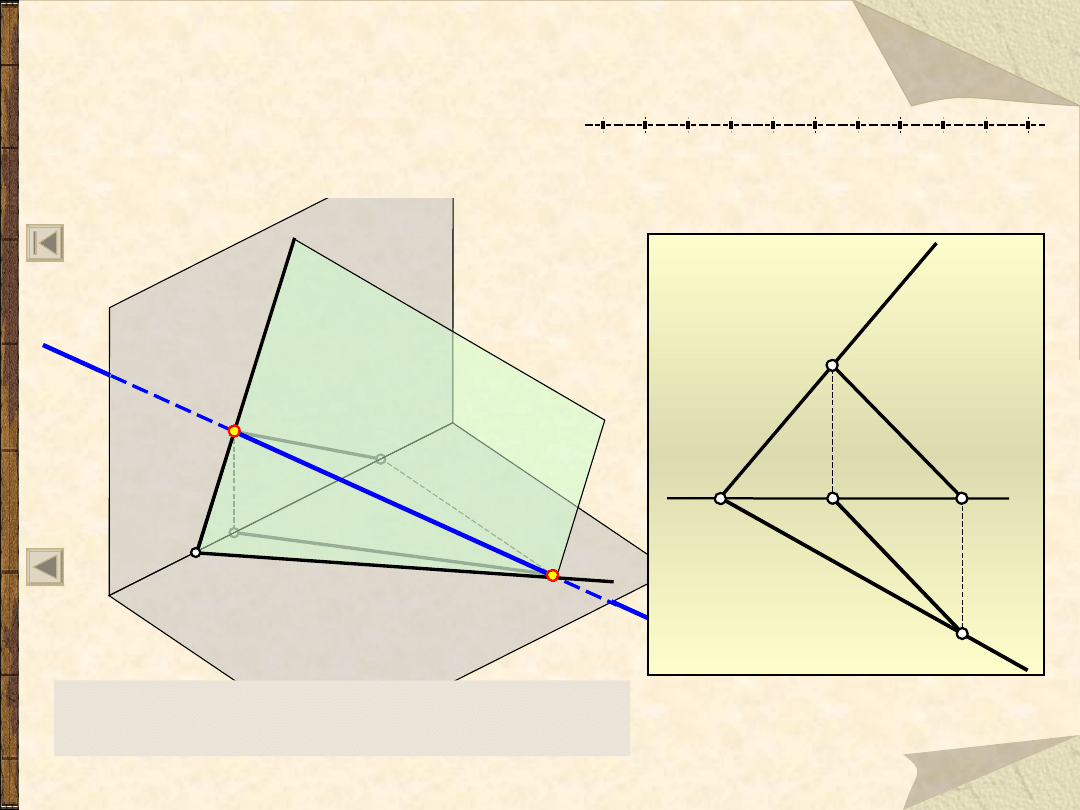
Prosta na płaszczyźnie

(1)





x



V

b

b

v



h



H

b

Prosta b leży na płaszczyźnie,
jeżeli jej ślady

V

b

i H

b

leżą na odpowiednich śladach

v



i

h



płaszczyzny



.

















b

h

H

v

V

b

b

... jeżeli ma z nią, co najmniej,

dwa punkty wspólne.

x

h



v



b
”

b’

V

b

H

b

27.06.21

Przynależność elementów w rzucie równoległym

31

b”

b’

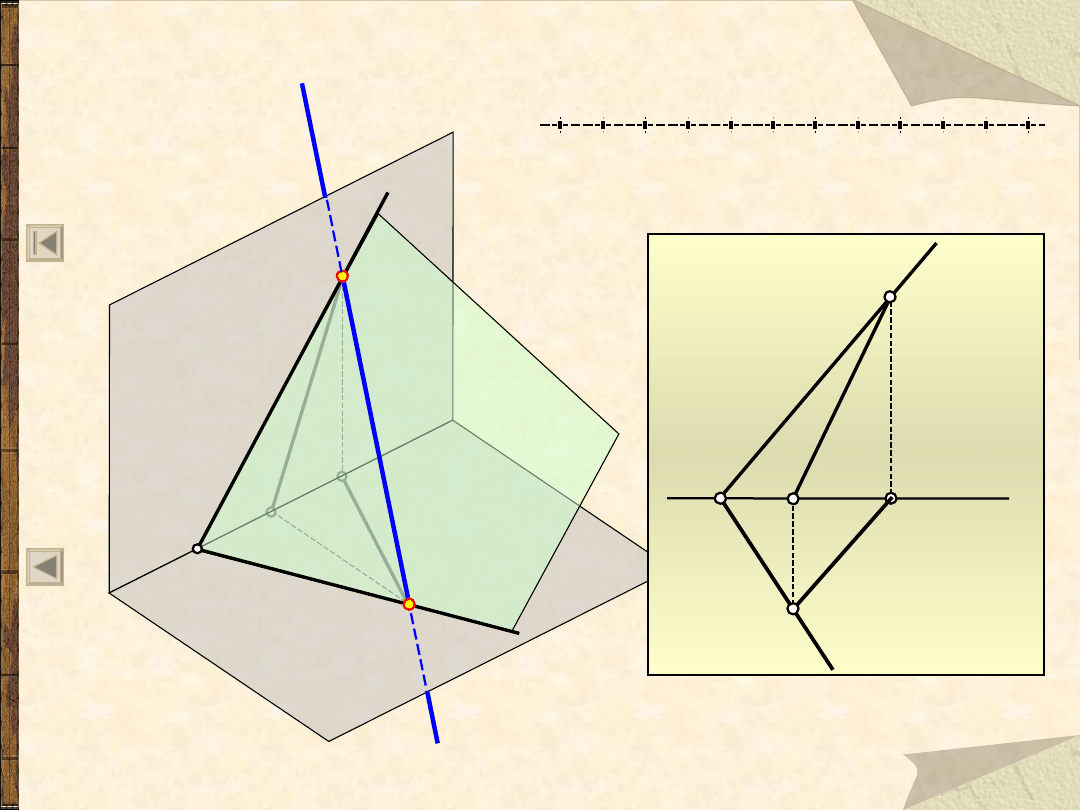
Prosta na płaszczyźnie

(2)





x



v



h



V

b

b

H

b

x

b’

h



v



b
”

V

b

H

b

27.06.21

Relacje zachodzące pomiędzy prostymi elementami

32

Równoległość i prostopadłość

elementów

Równoległość

Równoległość prostej i płaszczyzny
Równoległość płaszczyzn

Prostopadłość

Prostopadłość prostej i płaszczyzny
Prostopadłość płaszczyzn

27.06.21

Równoległość

33





x

b”

b’

a’

Równoległość prostej i płaszczyzny

Prosta a jest równoległa
do płaszczyzny



, jeżeli

jest równoległa do co
najmniej jednej prostej
tej płaszczyzny lub jeżeli
leży na płaszczyźnie.

v



V

b

b



h



H

b

a

a”

27.06.21

Równoległość prostej i płaszczyzny

34

x

h



v



b
”

b’

V

b

H

b

a’

a
”

b

a

b

a

b

a





"

"

'

'

















b

h

H

v

V

b

b



a





27.06.21

Równoległość

35

x



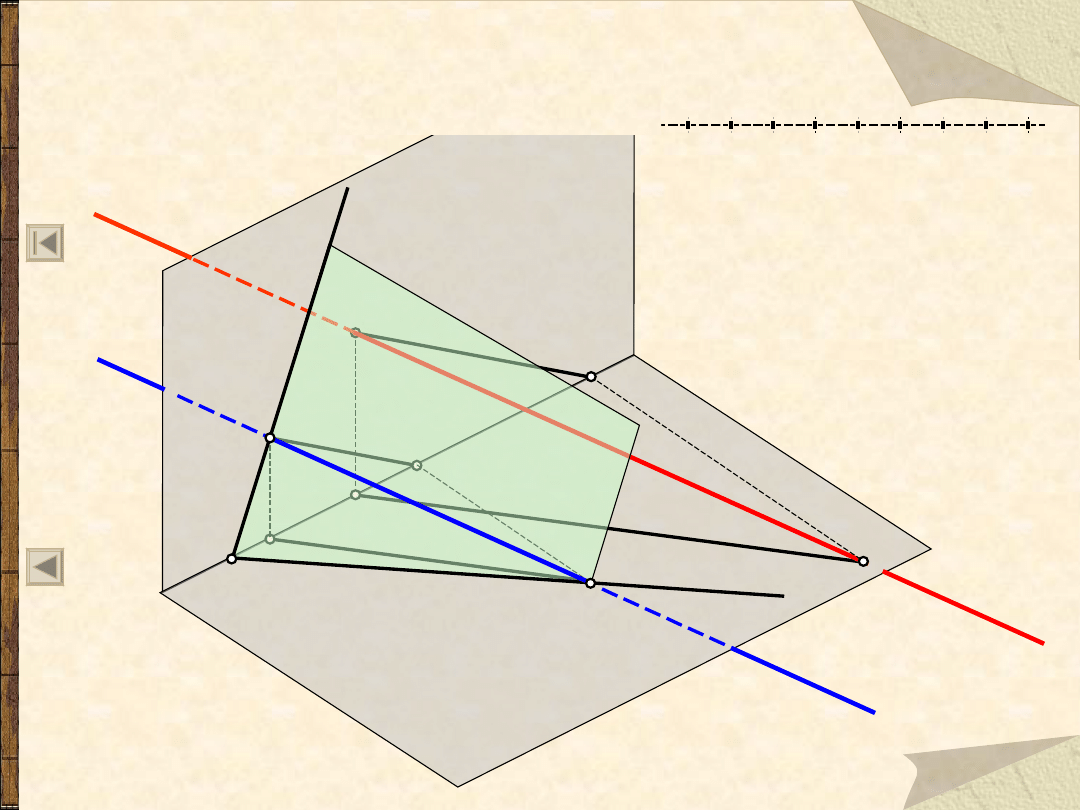
Równoległość płaszczyzn

Płaszczyzna



jest równoległa

do



, jeżeli dwie proste

przecinające się jednej

płaszczyzny są odpowiednio

równoległe do co najmniej

dwu prostych przecinających

się drugiej płaszczyzny.

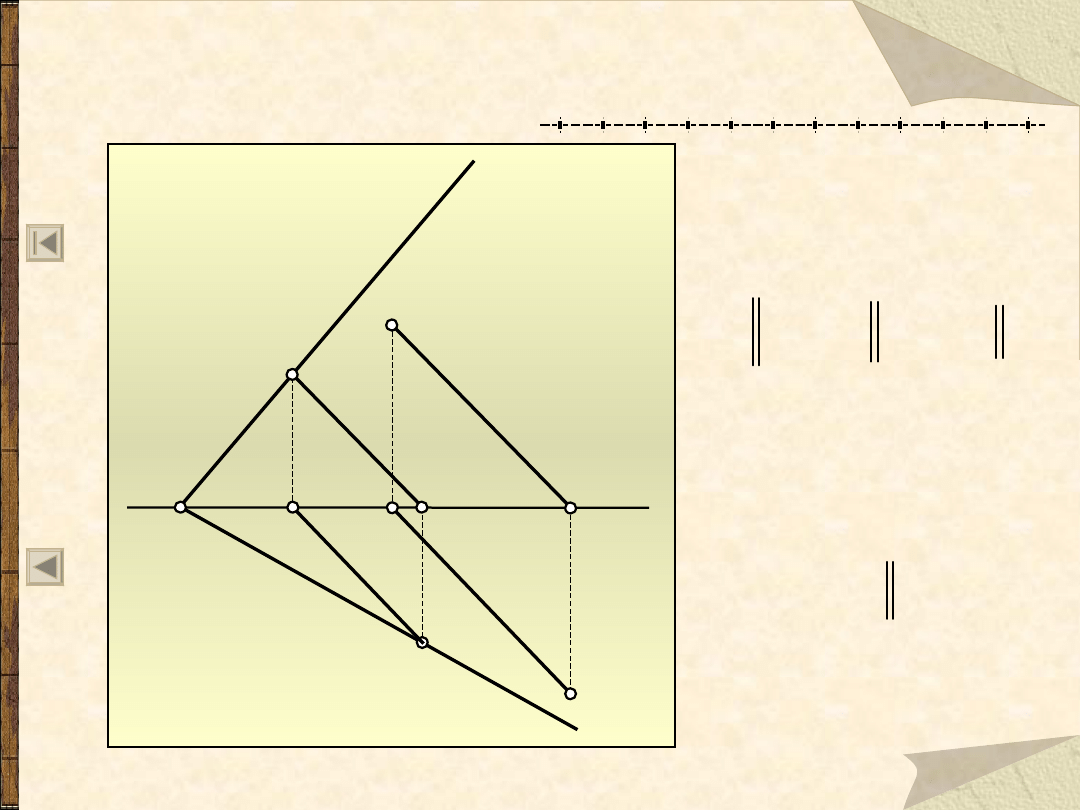
Dwie płaszczyzny



i



są równoległe,

jeżeli jednoimienne
ich ślady są do
siebie równoległe.















 h

h

v

v

v





h



v



h



27.06.21

Prostopadłość

36

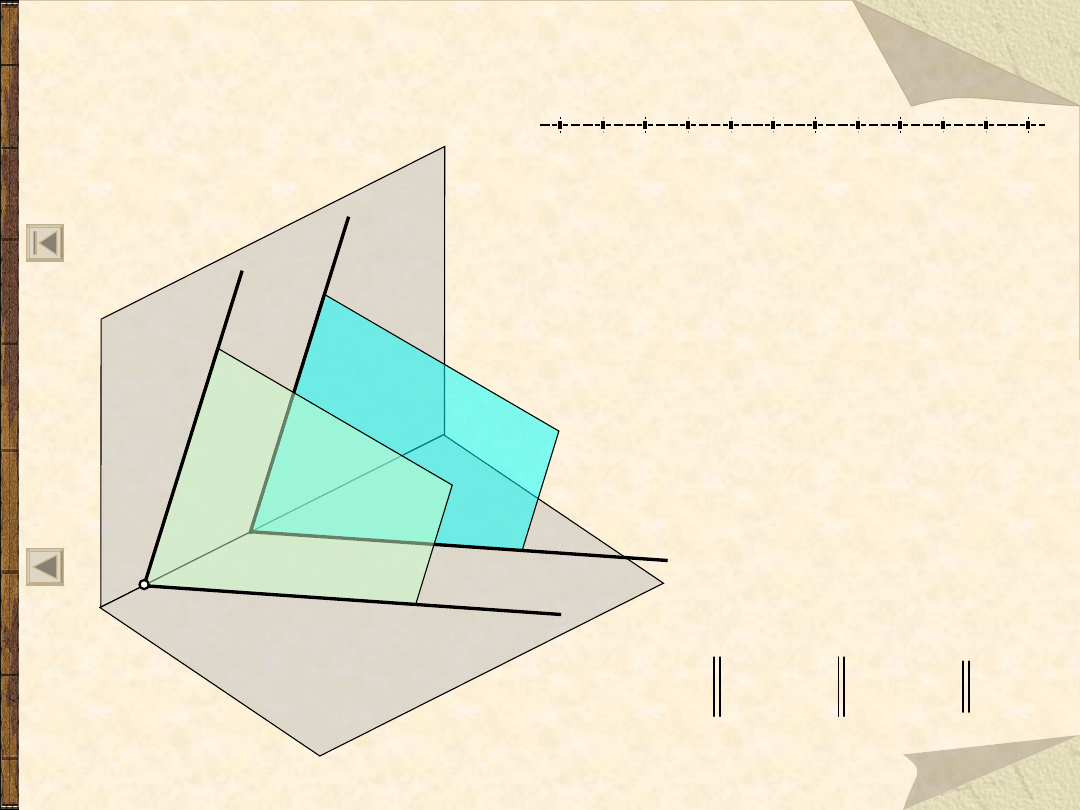
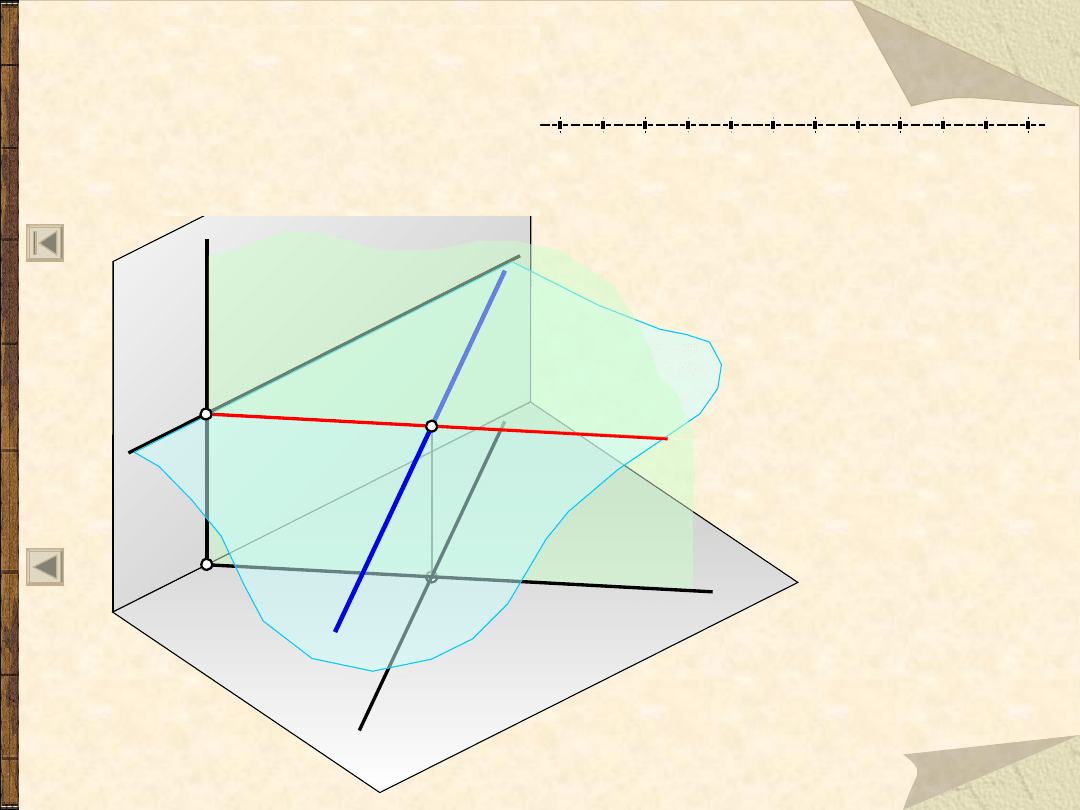
Prostopadłość prostej i płaszczyzny

Prosta jest prostopadła do płaszczyzny gdy jest
prostopadła do co najmniej dwóch prostych
przecinających się, należących do tej płaszczyzny.

Prosta przebija płaszczy-
znę pod kątem prostym,
jeżeli jej rzuty są prosto-
padłe do odpowiednich
śladów płaszczyzny.

Warunek konieczny

i wystarczający.

x

h



v



b
”

b’

h





















b

h

b

v

b

"

'

27.06.21

Prostopadłość

37





h



v



b’

x



b”

b

v





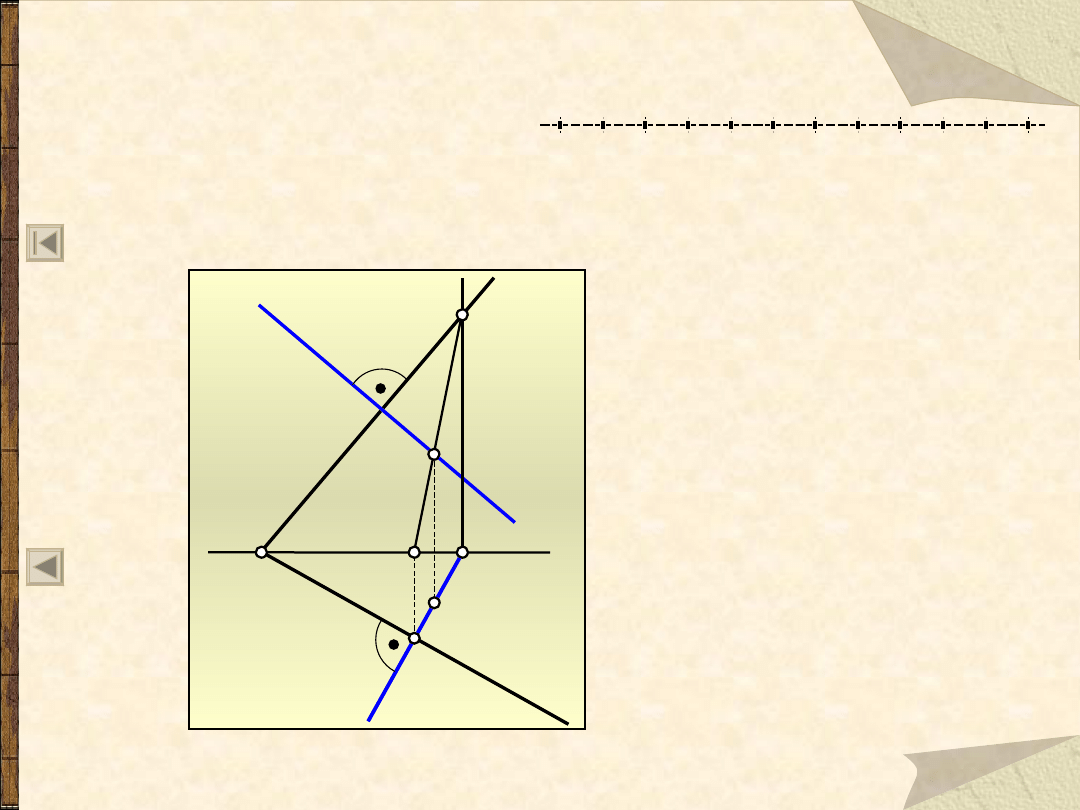
Prostopadłość płaszczyzn

















b

h

b

v

b

"

'











b

v

b'







Płaszczyzna



jest prostopadła do płaszczyzny



,

jeżeli



zawiera co najmniej jedną prostą

prostopadłą do płaszczyzny



.