WNIOSKOWANIE STATYSTYCZNE

 W ZAKRESIE STRUKTURY ZJAWISK

• WPROWADZENIE
Aby móc uogólnić wyniki otrzymane w próbie na całą populację, próba musi być 

losowa.

Próba losowa prosta
Ciąg  n  zmiennych  losowych  X

1

,  X

2

,…,X

n

,  które  są  niezależne  i  mają  jednakowe 

rozkłady, takie jak zmienna X w populacji.

Wnioskowanie  o  parametrach  populacji  na  podstawie  próby  losowej  bazuje  na 

pewnych  funkcjach  zmiennych  losowych  X

1

,  X

2

,…,X

n

,  które  tworzą  próbę. 

Funkcje te nazywa się statystykami z próby.

Przykładami statystyk z próby są następujące funkcje:

Czyli średnia z próby i wariancja z próby.  







n

i

i

X

n

X

1

1















n

i

i

X

X

n

S

1

2

2

1

1

 

 

Dysponując wynikami konkretnej próby, tj. ciągiem liczb x

1

, x

2

,…,x

n

, i 

podstawiając do wzoru

Otrzymuje się realizację statystyki, czyli konkretną wartość średniej z 

próby, którą oznacza się       .

Powtarzanie  procesu  pobierania  prób  i  obliczania  na  ich  podstawie 

realizacji  statystyki  prowadzi  do  otrzymania  zbioru  różnych 
wartości  średnich,  który  służy  do  ustalenia  rozkładu  średniej  z 
próby      .

Rozkłady statystyk z próby







n

i

i

X

n

X

1

1

x

x

X

 

 

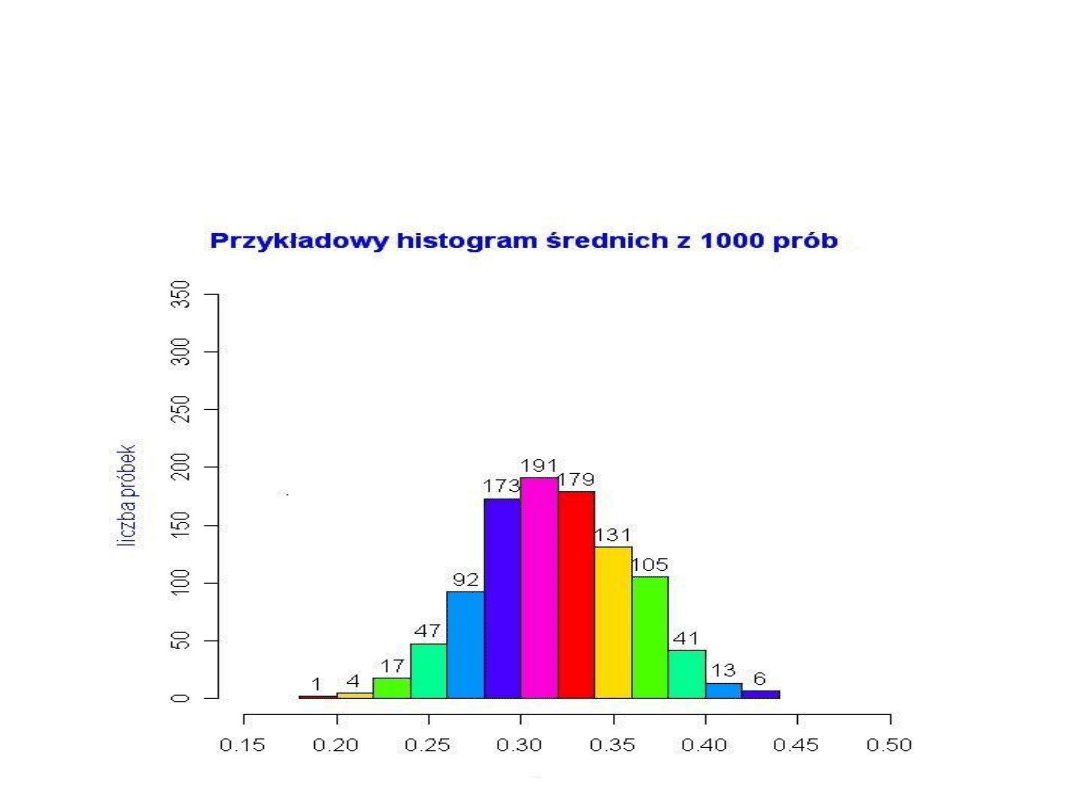
Gdybyśmy  posiadali  wiele  n-elementowych  próbek,  to 

histogram średnich z tych próbek przybliżałby tzw. rozkład 
średniej z próby.

Przykład  histogramu  dla  1000  próbek  (każda  o  liczności  n  = 

150)  przybliżającego  rozkład  średniej  z  próby  przedstawia 
wykres.

 

 

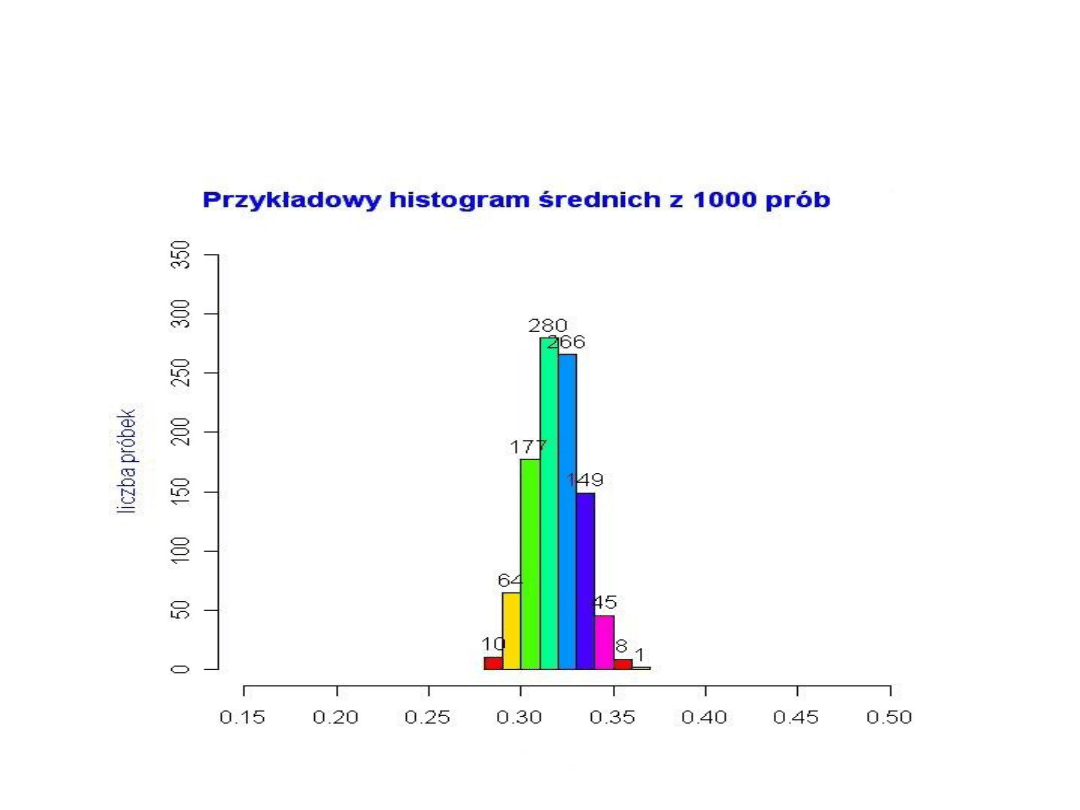
Jeśli  zwiększymy  liczebność  każdej  próbki,  np.  do  n  =  1000, 

wówczas  histogram  średnich  obliczonych  z  tych  próbek 
będzie  bardziej  ”skupiony”  wokół  średniej  z  populacji  (tu 
średnia  z  populacji=  0,32).  Histogram  poniżej  wykonano 
dla 1000 próbek.

 

 

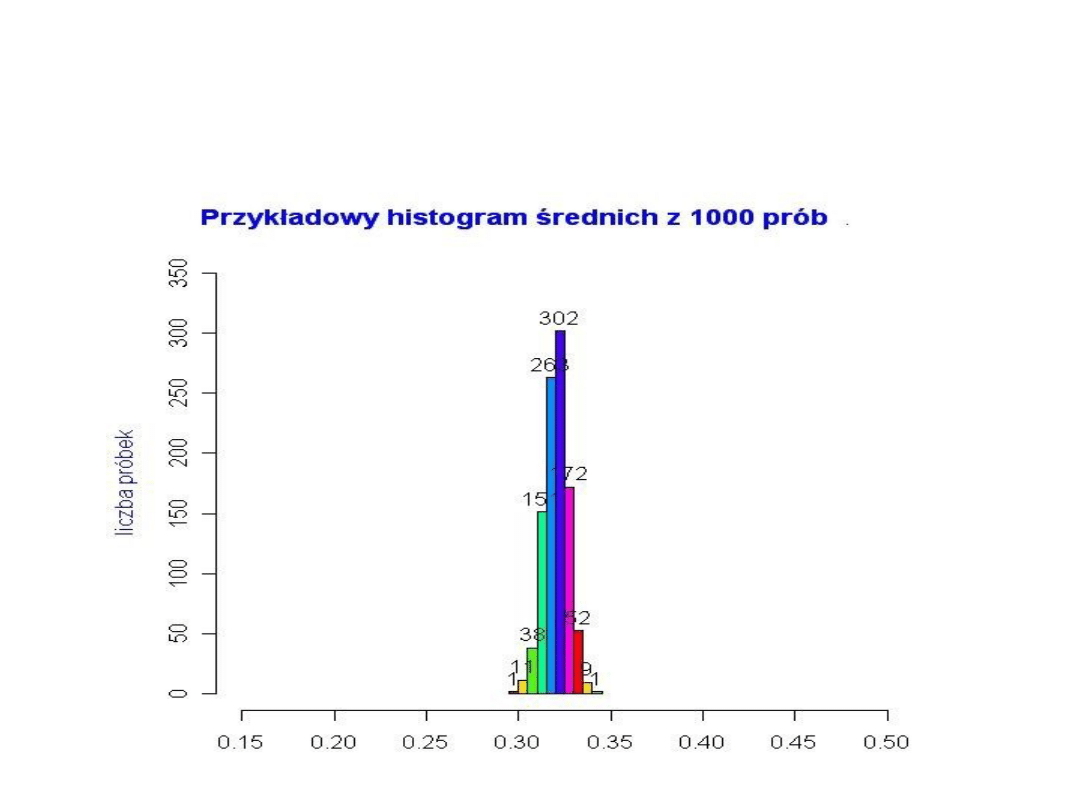
• Załóżmy teraz, że n = 5000. Koncentracja średnich z próbek 

wokół średniej z populacji jest tu jeszcze bardziej wyraźna. 
W tym przypadku średnie dla większości próbek są bardzo 
bliskie  wartości  średniej  dla  całej  populacji  (równej  nadal 
0,32).

 

 

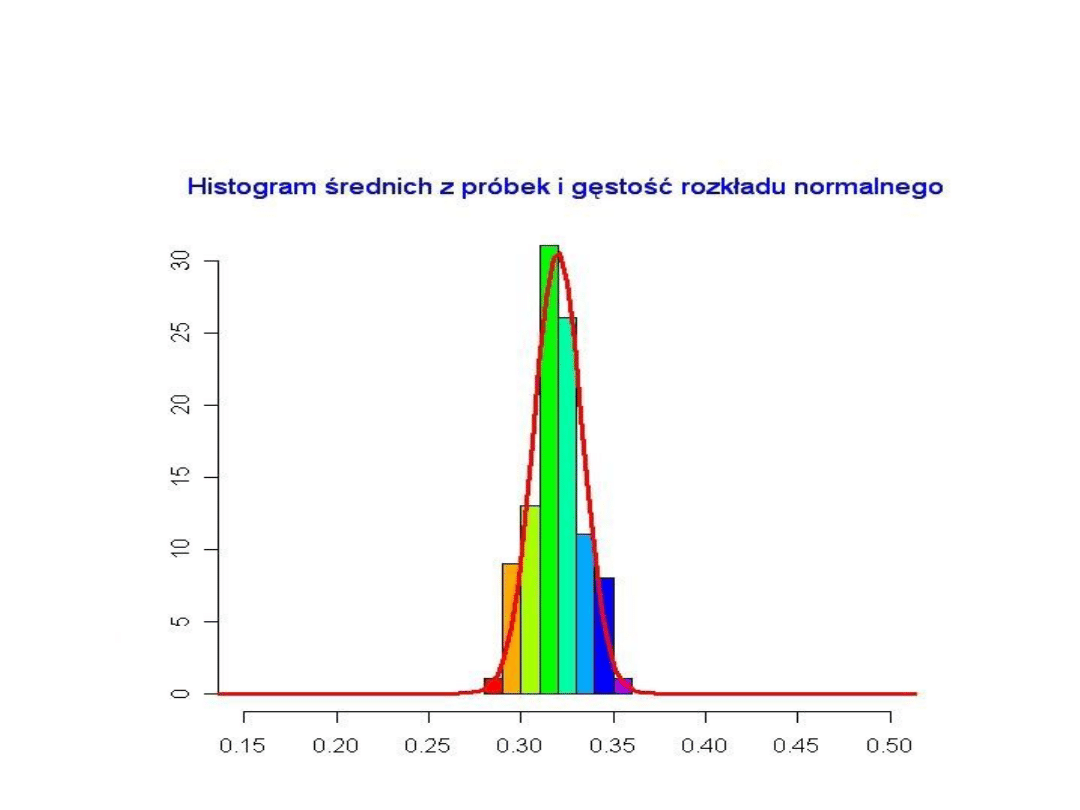
Zauważymy,  że  wykreślona  krzywa  przypomina  krzywą 

gęstości  rozkładu  normalnego.  Wykres  ten  ilustruje  w 
uproszczeniu  sens  centralnego  twierdzenia  granicznego 
przedstawionego dalej.

 

 

Centralne 

twierdzenie 

graniczne 

jest 

ważnym 

twierdzeniem    rachunku  prawdopodobieństwa.  W  skrócie 
mówi  ono,  iż  średniej  arytmetycznej  z  próby  dąży  do 
rozkładu  normalnego  N(μ                    ),  gdy  liczebność  n  próby 
dąży do nieskończoności,

Dotychczasowe  rozważania  pokazują,  że  możliwe  jest 

przybliżanie  rzeczywistych  wartości  pewnych  wskaźników 
(parametrów) populacji na podstawie próby losowej.

Prawdopodobieństwo  ”trafienia”  w  prawdziwą  wartość 

parametru  jest  tym  większe,  im  większa  jest  liczność  n 
próby.

Jeśli  szukanym  parametrem  jest  średnia  określonej  cechy  w 

populacji i jeśli dysponujemy dużą próbą (często wystarczy 
n>=30),  wówczas  możemy  odwołać  się  do  własności 
rozkładu  normalnego,  w  celu  wyznaczenia  oszacowania 
szukanej średniej.

n

/



 

 

Weryfikacja statystyczna

Weryfikacją  hipotez  nazywamy  sprawdzanie  sądów  o  populacji, 

sformułowanych bez zbadania jej całości.

Każdy  sąd  (założenie,  przypuszczenie)  o  parametrach  populacji  lub 

o rozkładzie cechy w populacji, o prawdziwości lub fałszywości, 
którego  wnioski  są  na  podstawie  pobranej  próby,  nazywamy 
hipotezą statystyczną.

Wyróżnia się 2 rodzaje hipotez:
•

hipotezy  parametryczne  –  dotyczące  wybranych  parametrów 
populacji,

•

hipotezy  nieparametryczne  –  dotyczą  postaci  rozkładu  czy 
zgodności dystrybuanty.

Ze zbioru hipotez dopuszczalnych wybiera się jedną, która podlega 

weryfikacji.  Tę  wybraną  do  weryfikacji  hipotezę  nazywa  się 
hipotezą  zerową  i  oznacza  H0.  Procedura  weryfikacyjna 
wymaga,  aby  sformułować  także  hipotezę  przeciwną  do 
zerowej.  Hipotezę  przeciwną  do  hipotezy  zerowej  nazywa  się 
hipotezą alternatywną i oznacza H1.

 

 

Hipoteza zerowa ma miejsce wówczas, kiedy domniemamy, że 

pomiędzy  rozpatrywanymi  parametrami  lub  rozkładami 
dwóch lub więcej populacji nie ma różnic.

Za  pomocą  hipotezy  zerowej,  w  przypadku  hipotezy 

nieparametrycznej,  robi  się  założenie,  że  nie  ma  istotnej 
różnicy  pomiędzy  rozkładem  empirycznym  a  danym 
rozkładem teoretycznym, co można zapisać:

                                 

Gdzie: G(x) – dystybuanata obliczona na podstawie próby,

F(x) – dystybuanata teoretyczna,

Hipoteza  dopuszczająca  istnienie  istotnych  różnic  pomiędzy 

rozkładem empirycznym z próby a rozkładem teoretycznym 
nosi  nazwę  hipotezy  alternatywnej.  Hipotezę  alternatywną 
w tym przypadku formułuje się jako:

 

 

x

F

x

G

H



:

0

   

x

F

x

G

H



:

1

 

 

Podobnie  formułuje  się  hipotezę  zerową  i  alternatywną  przy 

weryfikacji  założenia,  że  parametr  zbiorowości  generalnej 
(Q)  nie  różni  się  istotnie  od  danej  wielkości  hipotetycznej 
(Q

0

):

Oraz, że parametr zbiorowości generalnej istotnie różni się od 

danej wielkości hipotetycznej:

W  przypadku  weryfikacji  hipotezy  parametrycznej  hipotezę 

alternatywną H

1

 można jeszcze sformułować dwojako:

Hipotezy  statystyczne  sprawdza  się  (weryfikuje)  za  pomocą 

tzw. testów statystycznych.

0

0

:

Q

Q

H



0

1

:

Q

Q

H



0

1

:

Q

Q

H



0

1

:

Q

Q

H



 

 

Test statystyczny

Test  statystyczny  –  jest  to  pewna  reguła  postępowania,  która 

prowadzi do decyzji przyjęcia lub odrzucenia hipotezy zerowej.

Sprawdzenie hipotezy zerowej za pomocą odpowiedniego testu nie 

daje całkowitej pewności, czy postawiona hipoteza jest słuszna 
czy nie.

Weryfikując  hipotezę  zerową  za  pomocą  odpowiedniego  testu 

można popełnić dwa rodzaje błędów:

1.

Odrzucić hipotezę zerową (H

0

) wtedy, kiedy ona jest prawdziwa 

(błąd I rodzaju),

2.

Przyjąć  hipotezę  zerową  (H

0

)  wtedy,  kiedy  ona  jest  fałszywa 

(błąd II rodzaju).

Prawdopodobieństwo popełnienia błędu I rodzaju określa się jako:     

  , gdzie α – dowolnie mała liczba zawarta w przedziale <0,1> 
nosi  nazwę  poziomu  istotności  i  ustalona  jest  a  priori,  w 
przypadku 

hipotez 

dotyczących 

zjawisk 

społeczno-

ekonomicznych, na poziomie od 0,01 do 0,1.





P

 

 

Prawdopodobieństwo  popełnienia  błędu  II  rodzaju  określa  się 

jako:

W  postępowaniu  weryfikacyjnym  dąży  się  do  tego,  aby 

prawdopodobieństwo  popełnienia  błędów  I  i  II  rodzaju  było 

jak najmniejsze.

Można  jednak  udowodnić,  że  przy  tej  samej  liczebności  próby 

zmniejszenie  prawdopodobieństwa  α  powoduje  wzrost 

prawdopodobieństwa β i odwrotnie.

Sprzeczność  ta  prowadzi  do  rozstrzygnięcia  kompromisowego, 

które  polega  na  tym,  że  uznając  błąd  I  rodzaju  za  bardziej 

niebezpieczny zmniejsza się α do wymaganego poziomu i do 

weryfikacji określonej hipotezy statystycznej stosuje taki test, 

który przy pożądanym prawdopodobieństwie α daje najniższe 

prawdopodobieństwo β.

Testy, które przy pożądanym prawdopodobieństwie α pozwalają 

na zminimalizowanie prawdopodobieństwa β, określa się jako 

testy najmocniejsze.

Moc  testu:  prawdopodobieństwo  1-β,  tj.  prawdopodobieństwo 

odrzucenia  hipotezy  zerowej,  gdy  jest  ona  fałszywa,  a 

hipoteza alternatywna jest prawdziwa.





P

 

 

Specjalną grupą testów, najczęściej używaną w postępowaniu 

weryfikacyjnym,  stanowią  tzw.  testy  istotności.  Testy 
istotności  to  taki  rodzaj  testów,  które  uwzględniają 
prawdopodobieństwo  popełnienia  błędu  I  rodzaju,  nie 
biorąc pod uwagę prawdopodobieństwa błędu II rodzaju.

Decyzje 

weryfikacyjne 

dla 

hipotezy 

zerowej, 

przy 

zastosowaniu testów istotności, formułuje się dwojako:

1.

Odrzucić  hipotezę  zerową  (H

0

)  i  przyjąć  hipotezę 

alternatywną (H

1

) bądź

2.

Nie ma podstaw do odrzucenia hipotezy zerowej (H

0

) – co 

jednak- nie oznacza jej przyjęcia.

Testy  istotności  stosuje  się  wówczas,  gdy  interesuje  nas 

pytanie-  czy  hipotezę  zerową  można  odrzucić.  Stąd  też   
hipotezę  H

0

  formułuje  się  w  taki  sposób,  że  jest  ona 

przeciwieństwem  hipotezy,  która  ma  być  sprawdzona. 
Przez odrzucenie hipotezy zerowej przyjmuje się hipotezę 
alternatywną.

 

 

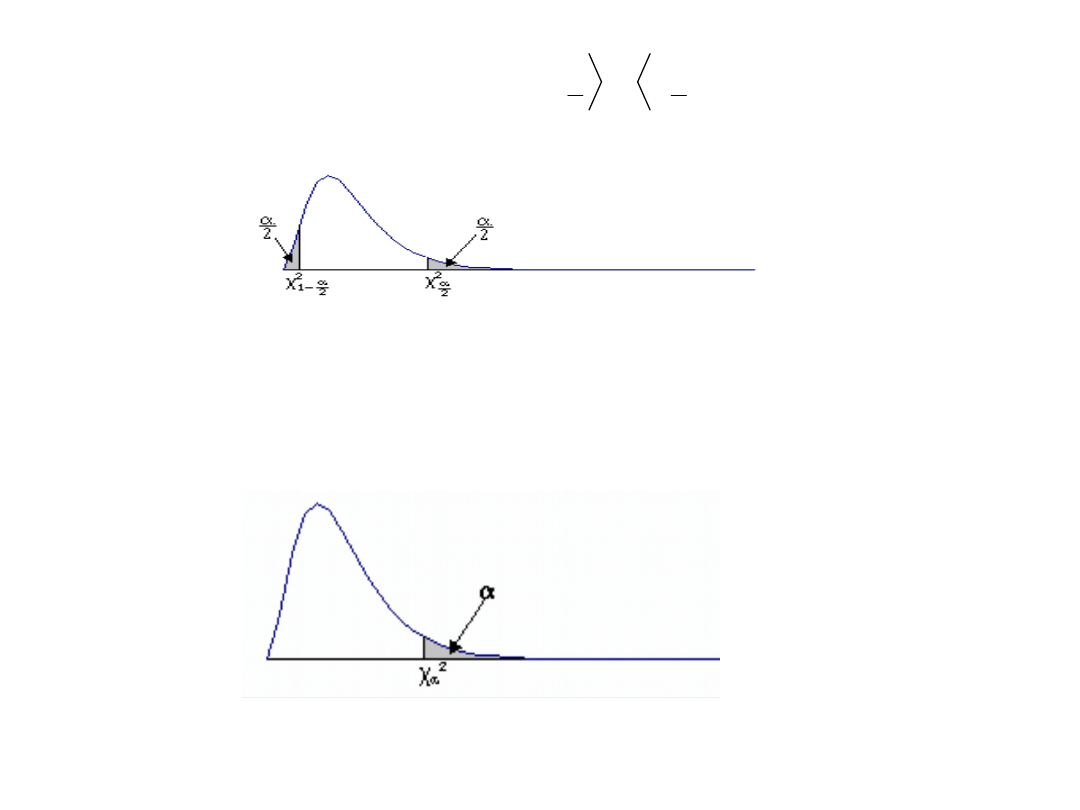
Testy  istotności  konstruuje  się  następująco:  jeżeli  różnicę 

pomiędzy  wartością  parametru  populacji  generalnej  (Q)  a 
wartością  hipotetyczną  (Q

0

)  lub  różnicę  pomiędzy 

dystrybuantą  empiryczną  G(x)  a  dystrybuantą  teoretyczną 
F(x) oznaczy się symbolem ogólnym D, to przy ustalonym z 
góry współczynniku α można dobrać taką wartość krytyczną 
D

α

, która będzie spełniała równość:

Jeżeli przy weryfikacji okaże się, że          ,  wtedy różnica jest 

nieistotna i hipoteza H

0

 zostaje utrzymana ( nie ma podstaw 

do odrzucenia hipotezy zerowej), ponieważ D znajduje się w 
tzw.  obszarze  przyjęć.  Natomiast  jeżeli                          ,  wtedy 
różnica  jest  istotna  obliczona  wartość  D  znajduje  się  w 
obszarze  krytycznym  i  hipoteza  zerowa  zostaje  odrzucona, 
a przyjęta hipoteza alternatywna.











D

D

P



D

D 



D

D 

 

 

Testami  istotności  najczęściej  używanymi  do  sprawdzania 

hipotez  zerowych  są  pewne  zmienne  losowe,  które  mają 
określony rozkład oraz parametry tych rozkładów. Zmienne 
te ( jak np. u, t,      ) nazywane są krótko statystykami lub 
testami.

Z  całego  zbioru  wartości  statystyki  testowej  wyodrębnia  się 

tzw.  obszar  krytyczny  hipotezy  zerowej  i  obszar  przyjęć 
hipotezy zerowej.

Obszar  krytyczny  jest  to  taki  zbiór  wartości  statystyki 

testowej,  których  wystąpienie  jest  mało  prawdopodobne 
jeżeli 

hipoteza 

zerowa 

jest 

prawdziwa. 

Prawdopodobieństwo,  że  statystyka  testowa  przyjmie 
wartość  z  obszaru  krytycznego  hipotezy  zerowej  równa  się 
założonemu  poziomowi  istotności  α.  Prawdopodobieństwo, 
że  statystyka  testowa  przyjmie  wartość  z  obszaru  przyjęć 
hipotezy zerowej równa się 1-α.

2



 

 

Weryfikacja parametryczna

Etapy sprawdzania hipotezy

–

określić hipotezę zerową H0 i alternatywną H1;

–

określić poziom istotności   oraz wielkość próby 

n (lub prób), a w pewnych przypadkach wielkości 

zbiorowości generalnej N;

–

wybrać  odpowiedni  test  statystyczny  dla  oceny 

hipotezy zerowej;

–

obliczyć  wartość  charakterystyki  testu  na 

podstawie  danych  uzyskanych  z  próby  (lub 

prób);

–

znaleźć  w  tablicach  statystycznych  wartość 

krytyczną  na  danym  poziomie  istotności    i 

wyznaczyć  obszar  przyjęcia  i  odrzucenia 

hipotezy zerowej;

–

podjąć decyzję.

 

 

Do 

weryfikacji 

hipotez 

parametrycznych 

najczęściej 

wykorzystywanymi testami są: dla dużej próby statystyka u, dla 
małej próby statystyka t-Studenta. Są to tzw. testy istotności, 
które  znajdują  zastosowanie  w  sytuacji,  gdy  interesuje  nas 
pytanie,  czy  hipotezę  zerową  można  odrzucić  –  a  nie  badamy 
innych  hipotez.  Z  tym,  że  statystyka  u  wykorzystuje  rozkład 
normalny, z kolei statystyka t rozkład t-Studenta.
Reguła  decyzyjna  przy  testowaniu  hipotezy  statystycznej 
polega  na  porównaniu  wartości  sprawdzianu  z  wartościami 
rozgraniczającymi  obszary  odrzucenia  i  nieodrzucenia. 
Hipotezę  zerową  odrzucamy  wtedy  i  tylko  wtedy,  gdy 
sprawdzian

 

wpada  w  obszar  odrzucenia  przy  przyjętym 

poziomie istotności .

 

 

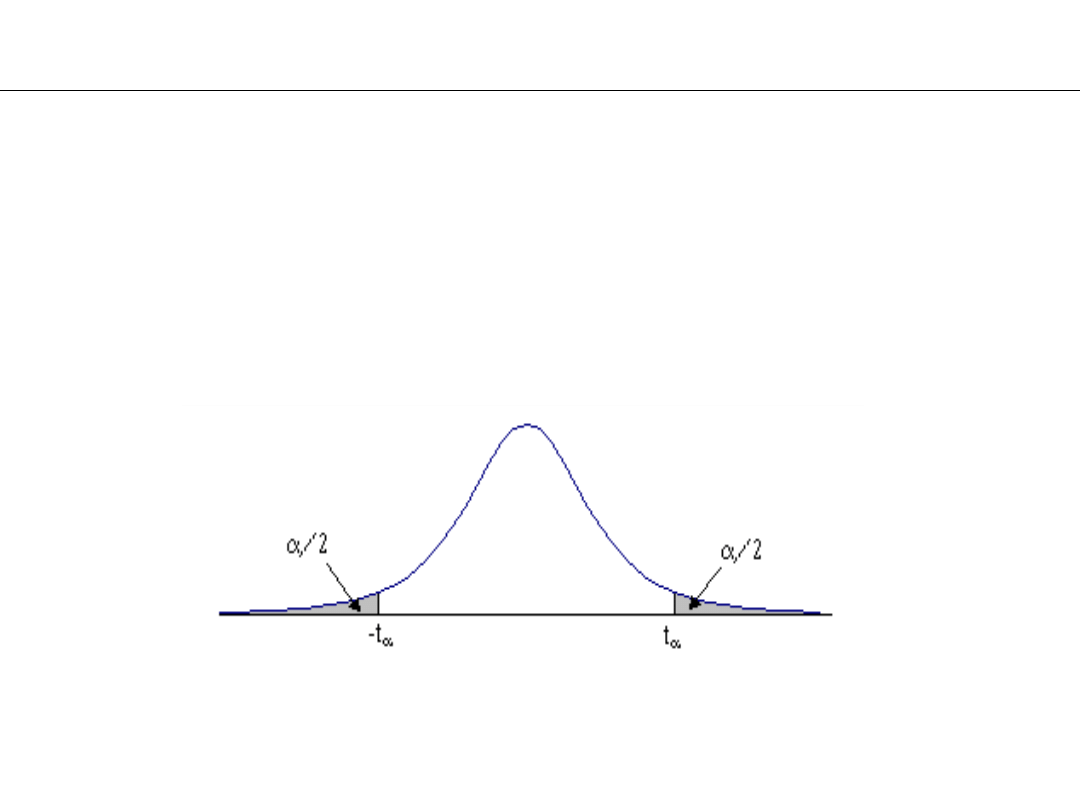
Przed przystąpieniem do testowania muszą być sformułowane 
obie hipotezy: zerowa i alternatywna. 

Testem  dwustronnym  jest  test,  którego  obszar 
odrzucenia składa się z wartości położonych pod dwoma 
„ogonami”  krzywej  gęstości  rozkładu  sprawdzianu  (przy 
założeniu prawdziwości hipotezy zerowej)

 

 

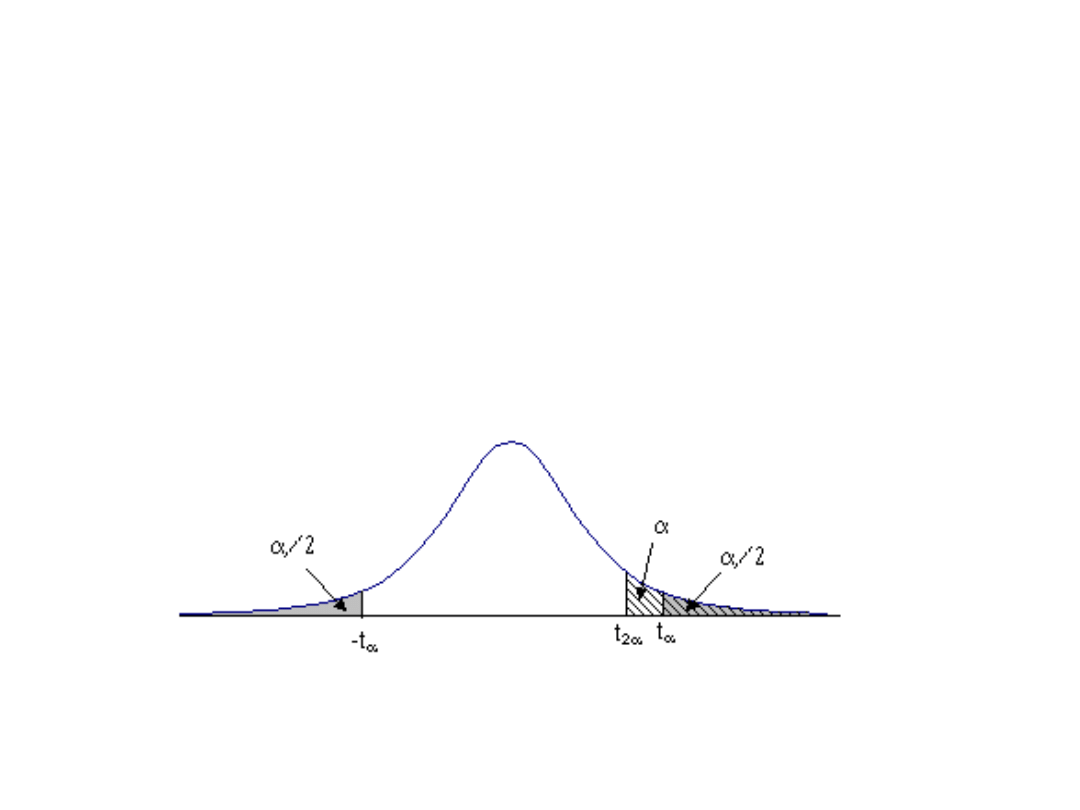
Test  jednostronny  zostanie  zastosowany,  jeżeli  chcemy 

sprawdzić,  czy  parametr  przyjmie  wartość  większą  lub 
mniejszą  od  określonej  liczby.  Wybór  jedno-  lub 
dwustronnego testu hipotezy statystycznej jest wyznaczony 
przez potrzebę działania.

Jeżeli  działanie  będzie  podjęte,  gdy  parametr  przekroczy 

pewną  wartość  a,  to  alternatywną  hipotezą  będzie,  że 
parametr  jest  większy  od  a  i  zastosujemy  test 
prawostronny.

 

 

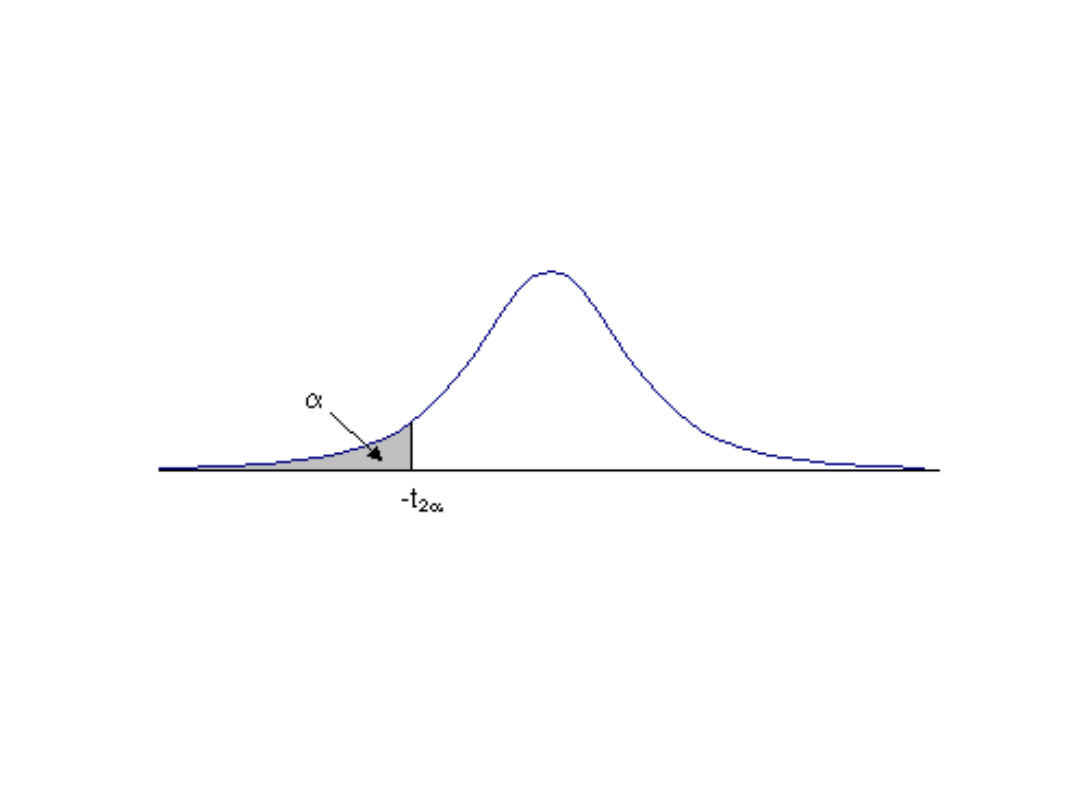
Jeżeli  zaś  działanie  będzie  podjęte,  gdy  parametr  przyjmie 

wartość mniejszą od a, to alternatywną hipotezą będzie, że 
parametr  jest  mniejszy  od  a  i  zastosujemy  test 
lewostronny.

W  przypadku  testów  jednostronnych  prawdopodobieństwo 
popełnienia  błędu  pierwszego  rodzaju,  wyobraża  pole  pod 
jednym „ogonem” krzywej gęstości.

 

 

Wnioskowanie w testach istotności

Jeżeli wartość statystyki z próby należy do obszaru krytycznego

  odrzucamy H

0

 na korzyść H

1

 (przyjmujemy 

H

1

)

Jeżeli wartość statystyki z próby nie należy do obszaru 
krytycznego

  brak podstaw do odrzucenia H

0

 (co nie jest 

jednoznaczne z przyjęciem H

0

)

Jeżeli hipotezę zerową odrzucimy na poziomie istotności , to 
odrzucimy ją na każdym większym poziomie istotności.

Jeżeli hipotezę zerową odrzucimy na poziomie istotności , to 
możemy jej nie odrzucić na mniejszym poziomie istotności.

 

 

Wartością  p  jest  najniższy  poziom  istotności  a,  przy  którym 

hipoteza  zerowa  mogłaby  być  odrzucona  przy  otrzymanej 

wartości sprawdziany.

Wartość  p  to  prawdopodobieństwo  otrzymania  takiej  wartości 

sprawdzianu, jaką otrzymaliśmy – lub wartości skrajniejszej 

– przy założeniu że hipoteza zerowa jest prawdziwa.

W  przypadku  testu  dwustronnego  wartość  p  jest  miarą  sumy 

dwóch  pól  pod  krzywą  gęstości  rozkładu  znajdujących  się 

na  prawo  od  dodatniej  o  na  lewo  od  ujemnej  wartości 

sprawdzianu.  W  przypadku  testów  jednostronnych  jest 

miarą  pola  pod  krzywą  gęstości  rozkładu  na  prawo  od 

wartości sprawdzianu (test prawostronny) lub na lewo (test 

lewostronny).

Przy danym poziomie istotności a odrzucić hipotezę zerową 

można wtedy i tylko wtedy, jeżeli 

a ≥ wartość p. Jeżeli p > a, to brak jest podstaw do 

odrzucenia H0.

Wartość p (p-value)

 

 

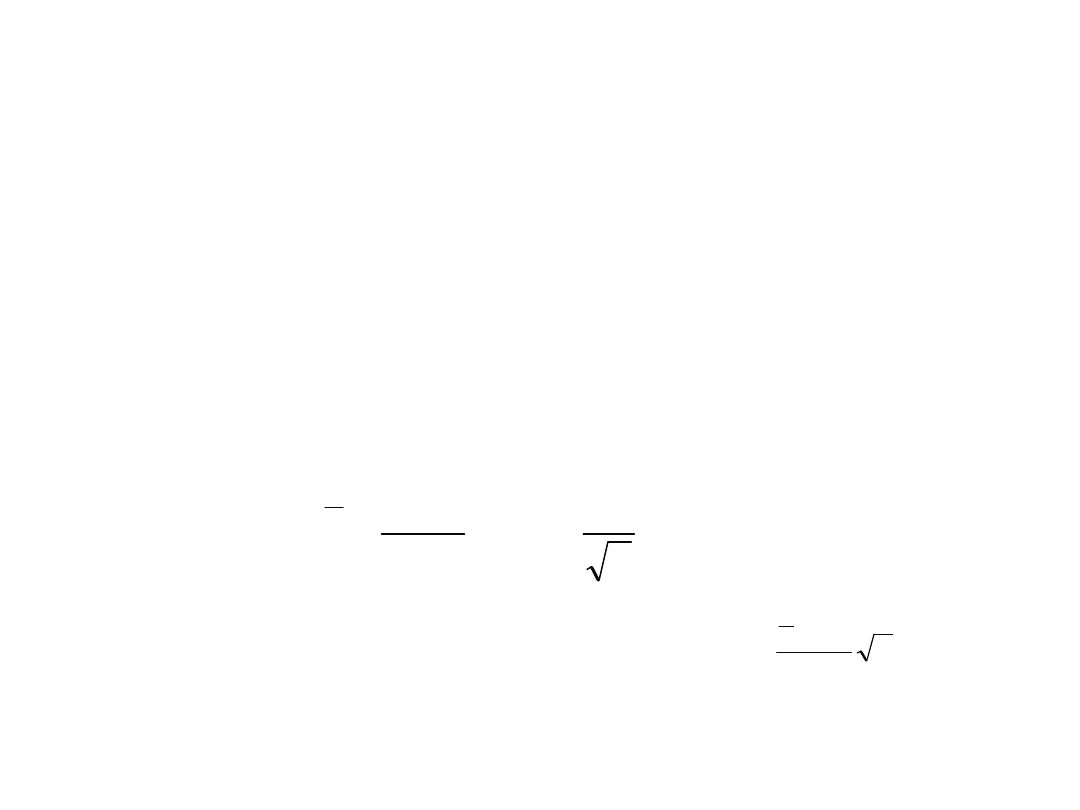
Test dla średniej

H0: μ = μ0
H1: μ ≠ μ0   lub  H1: μ > μ0   lub H1: μ < μ0





















n

,

N

~

n

x

x

i

1°  zakładamy,  że  zmienna  losowa  X  ma  rozkład  normalny  o 
znanym  odchyleniu  standardowym  σ,  próba  jest  dość  duża 
(powyżej  30),  pobrana  z  populacji  o  rozkładzie  N(μ,  σ). 
Estymatorem parametru μ jest

Standaryzując otrzymujemy zmienną 
losową

,

n

x

u

0









która ma rozkład N(0, 1).

 

 















;

;

:





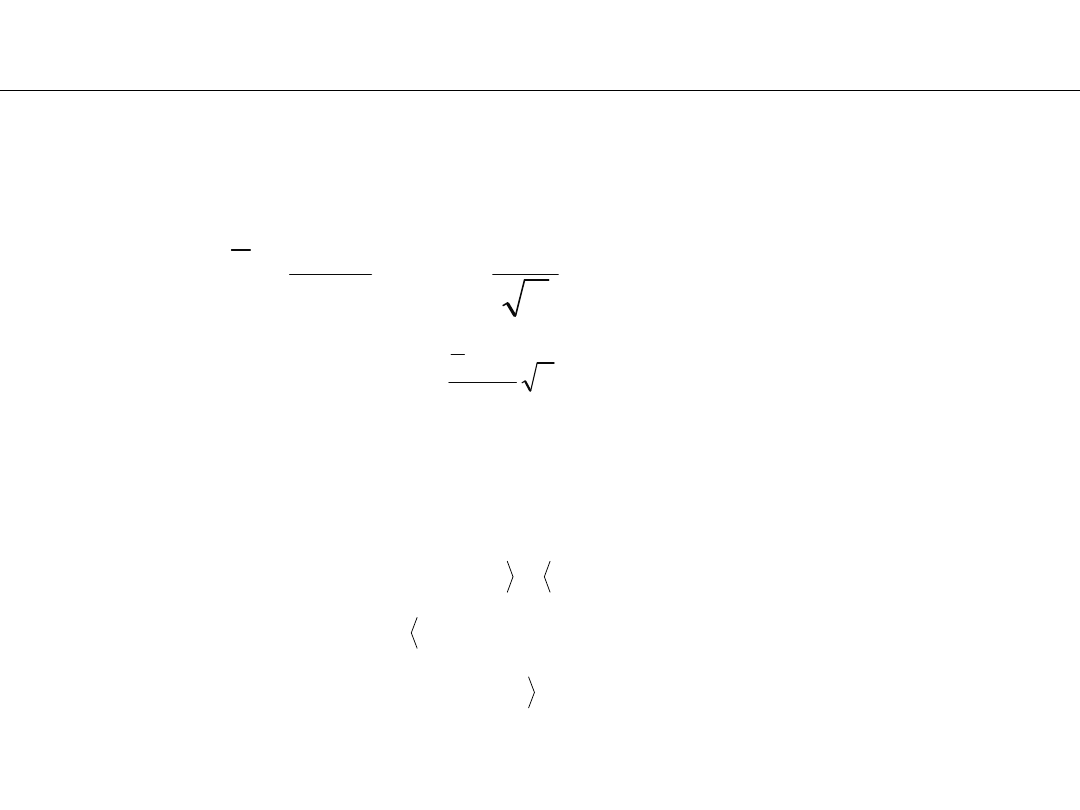
u

u

OK





;

:

2



u

OK

a) jeżeli H

1

:  ≠ 



0

b) jeżeli H

1

:  > 



0

c) jeżeli H

1

:  < 



0

2° zakładamy, że zbiorowość generalna ma dowolny rozkład 

ciągły o nieznanych parametrach, a próba jest duża (n > 50). 

Estymatorem parametru  jest

















n

)

x

(

s

,

N

~

n

x

x

i

Wartość statystyki  
testu:

,

n

)

x

(

s

x

u

0







która ma rozkład 
N(0, 1).

W obu przypadkach obszar krytyczny uzależniony jest od 
postaci hipotezy alternatywnej:





2

;

:

u

OK







 

 

3°  Zbiorowość generalna ma rozkład normalny o parametrach 

N()  o  nieznanych  parametrach,  a  próba  jest  mała  (n  < 
30).  Korzystamy  ze  statystyki  t-  Studenta  z  n-1  stopniami 
swobody. Statystyka testowa ma postać:

Obszary krytyczne mają postać:

.

1

n

)

x

(

s

x

t

0









a) jeżeli H

1

:  

≠ 

0



















;

t

t

;

:

OK

b) jeżeli H

1

:  

> 

0

c) jeżeli H

1

:  < 



0







;

t

:

OK

2











2

t

;

:

OK

 

 

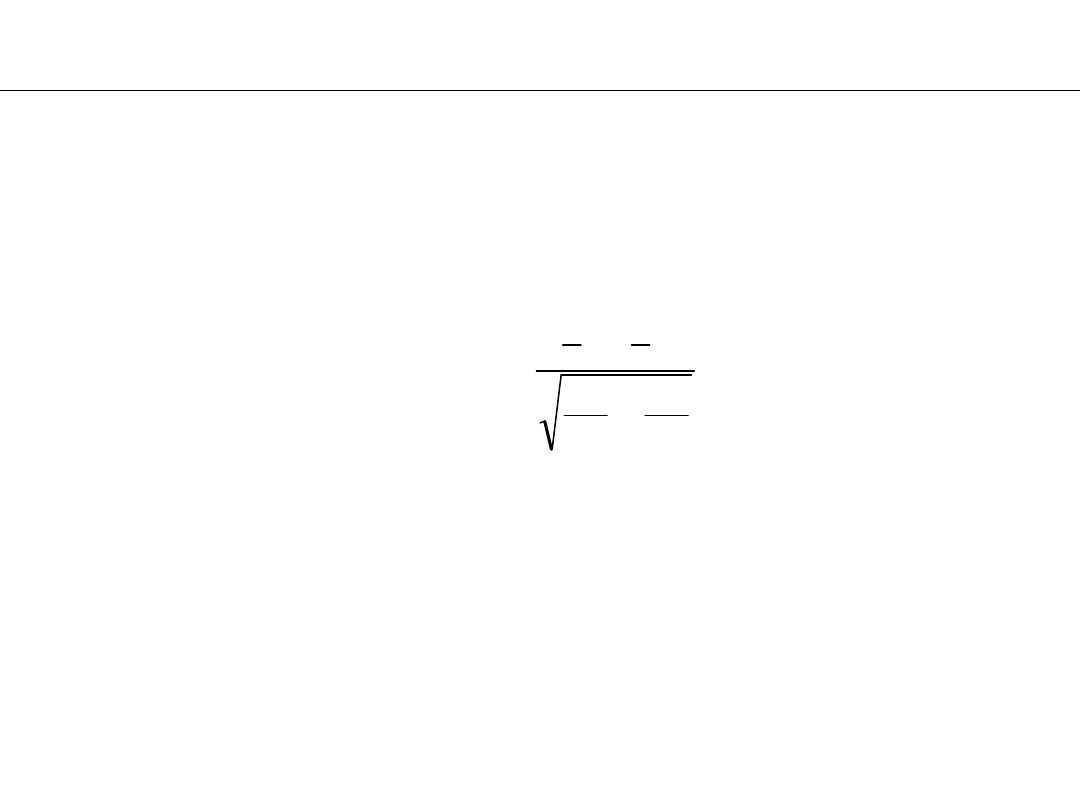
Test dla dwóch średnich

H

0

: 

1

 = 

2

H

1

: 



 ≠ 

2     

lub   



 > 

2

    lub    



 < 



2

 

1°    Badamy  dwie  populacje  generalne  mające  rozkłady 

normalne  N(

1

,  

1

)  i  N(

2

,  

2

),  przy  czym  odchylenie 

standardowe  

1

  i  

2

    są  znane.  Statystyka  testu  ma 

postać:

2

2

2

1

2

1

2

1

n

n

x

x

u











2°    Zmienna  X  ma  w  jednej  populacji  generalnej  ma  rozkład 

N(

1

,  

1

)  i  w  drugiej  populacji  generalnej  ma  rozkład  N(

2

, 



2

)    lub  dowolny  inny  rozkład  o  odpowiednio:  średniej 

wartości  

1

  i o skończonej,  ale  nieznanej  wartości  wariancji 



1

2

  oraz  średniej  wartości  

2

    i  o skończonej,  ale  nieznanej 

wartości  

2

2

. Próby duże. Statystyka testu ma postać:

 

 

 

 

























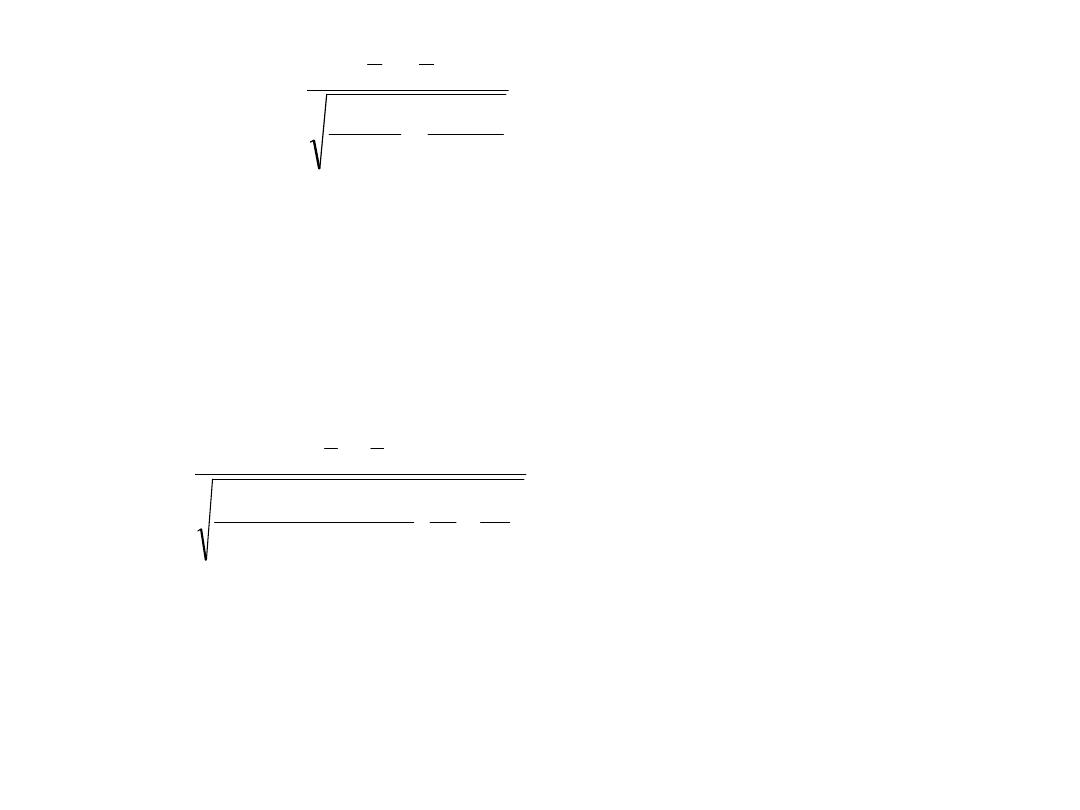
2

1

2

1

2

2

2

2

1

1

2

1

n

1

n

1

2

n

n

x

s

n

x

s

n

x

x

t

3°    Badamy  dwie  populacje  generalne  mające  rozkłady 
normalne  N(m1,  1)  i  N(m2,  2),  przy  czym  odchylenie 
standardowe  nie  są  znane,  ale  wiadomo,  że  1  =  2 
(wariancje  nie  różnią  się  istotnie  między  sobą).  Próby 
małe. Statystyka testu ma postać:

 

 

2

2

2

1

2

1

2

1

n

x

s

n

x

s

x

x

u







 

 

2

0

2

2

)

x

(

s

n









Test dla wariancji

H

0

: 

2

 = 

0

2

H

1

: 



 ≠ 

0

2

     

lub   



 > 

0

2

    lub    



 < 



0

2

 

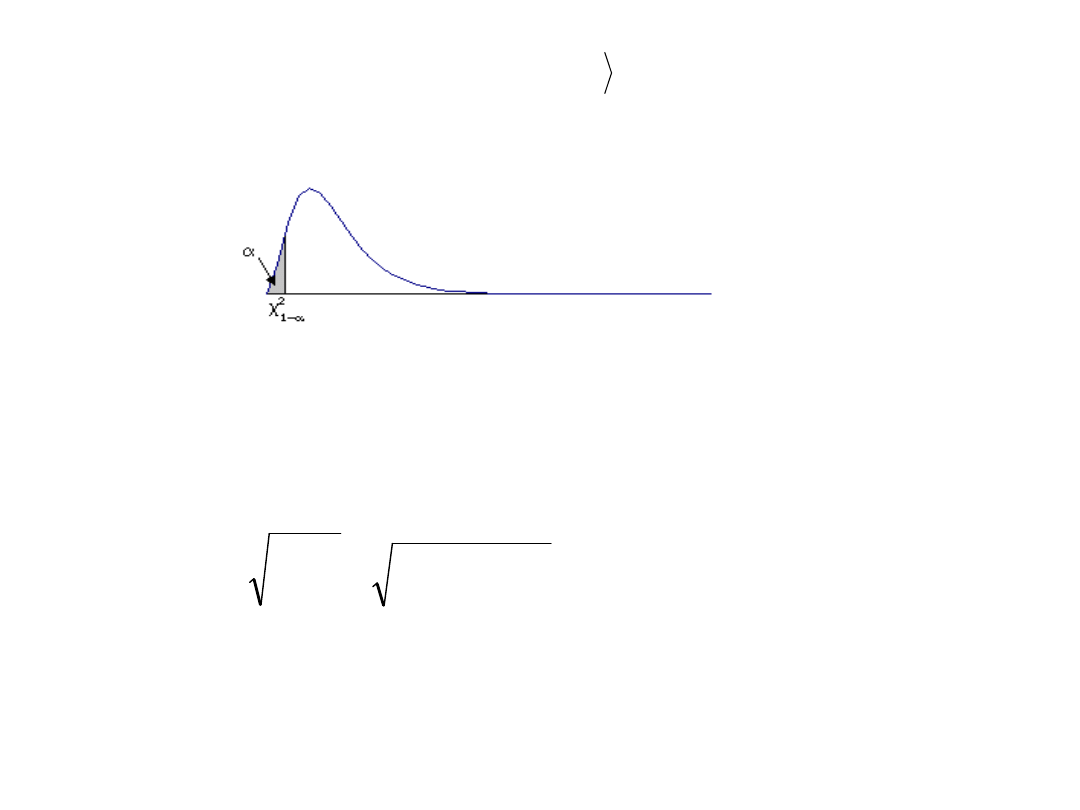
1°  zakładamy,  że  zmienna  losowa  X  ma  rozkład  normalny  o 

nieznanym  odchyleniu  standardowym  średniejpróba 
jest  mała  (poniżej  30),  pobrana  z  populacji  o  rozkładzie 
N(. Estymatorem parametru 



 jest

 

 





























;

;

0

:

OK

2

2

2

2

1

)

,

:

OK

2









a) jeżeli 

b) Jeżeli 

2

0

2

1

:







H

2

0

2

1

:







H

 

 

1

)1

n

(

2

2

u

2













2° zakładamy, że badana cecha populacji ma rozkład N(m, ) o 
nieznanym m  i  .  Duża  próba. Estymatorem parametru jest

c) jeżeli 



2

1

;

0

:

OK







2

0

2

1

:







H