Opcje finansowe

Celem wykładu jest zaznajomienie słuchaczy z opcjami finansowymi i
ich praktyczna rolą. Prezentację ograniczyłem do teorii to jest:
segmentacji rynku opcji, modelowej prezentacji opcji na akcje oraz
czynników mających wpływ na ceny opcji.

W aneksie umieściłem model Blacka - Scholesa - sposób
określania wartości opcji, korzyści i zagrożenia związane ze
stworzeniem rynku opcji w Polsce oraz kombinacje w
handlu

opcjami

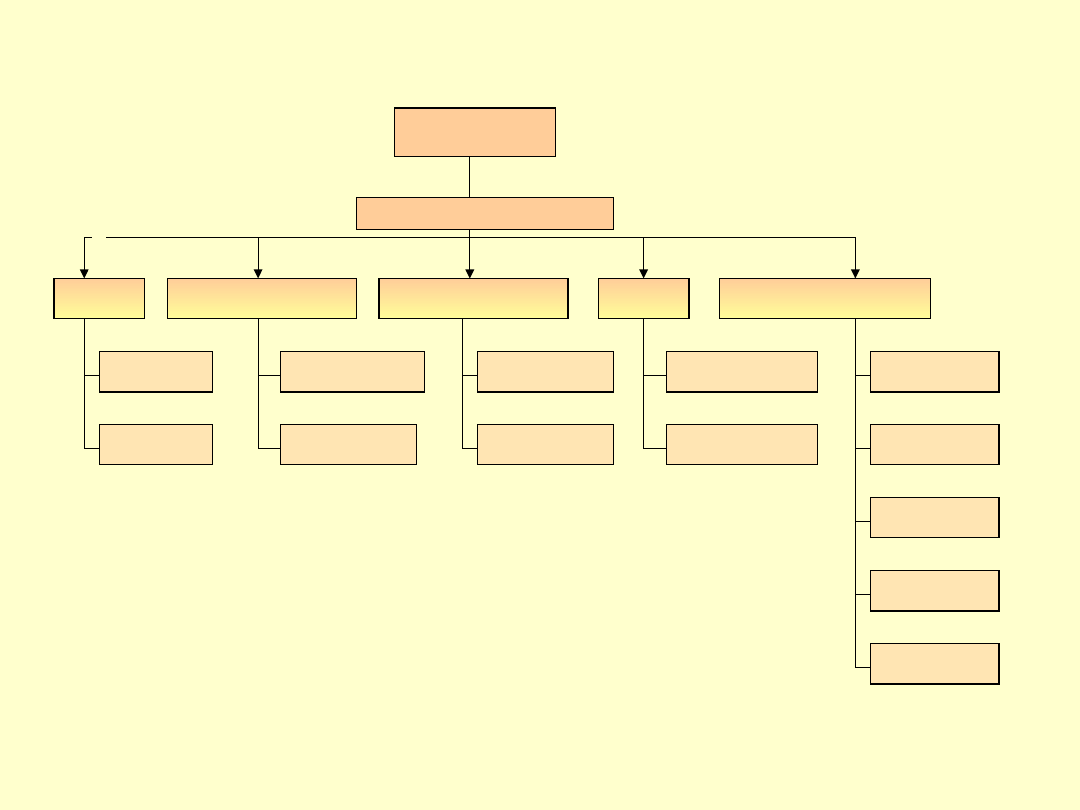
OPCJE

sposób rozliczenia

termin rozliczenia

rodzaj

rynek

instrument bazowy

zakupu

rzeczywiste

pozagiełdowe

giełdowe

sprzedaży

europejska

amerykańska

różniczkowe

terminowe

indeksowe

procentowe

walutowe

akcyjne

podział ze względu na:

Opcje finansowe są powszechnym
przedmiotem obrotu na giełdach

Opcją jest również

warrant

, czyli

prawo poboru.
Jest

to

opcja

zakupu/sprzedaży

instrumentów

finansowych

po

określonej cenie i w ustalonym czasie.

Warrant tym różni się od opcji

zwykłej, tym że (zazwyczaj) jest
wydawany na dłużej niż rok.

Na rynku tworzone są również coraz to nowe,

bardziej skomplikowane instrumenty opcyjne.

Dla przykładu można wymienić:
· opcje złożone - dają nabywcy prawo

kupna/sprzedaży po z góry określonej cenie
innych opcji,

 ·  opcje bermudzkie - można je realizować tylko w

tych terminach, które są z góry określone,

 · opcje azjatyckie - ewentualny zysk zależy od

przeciętnej ceny waloru bazowego, na który
wystawiona jest opcja, w określonym z góry
przedziale czasu,

 · opcje z cap - zysk z nich nie może przekroczyć

określonego górnego poziomu.

 

Wyróżniamy dwa podstawowe typy

opcji:

 

- opcja typu amerykańskiego

- opcja typu europejskiego

Opcja typu amerykańskiego ma

większą

wartość

niż

opcja

typu

europejskiego, gdyż daje posiadaczowi
możliwość rozliczenia w całym okresie, a
opcja typu europejskiego tylko w
określonym dniu.

Premię otrzymuje wystawca opcji za sprzedaż opcji

Rodzaje opcji – (od strony wystawiającego opcję):
-   opcje kupna,
-   opcje sprzedaży,
W przypadku opcji występują zawsze dwie strony:
-   nabywca opcji,
-   wystawiający opcję,
Nabycie opcji jest swego rodzaju ubezpieczeniem się

przed niekorzystnym ruchem cen np. akcji.

Nabywca opcji kupna zabezpiecza się przed wzrostem

cen akcji, gdyż ma zagwarantowaną maksymalną cenę

po jakiej ją kupi (jest to cena rozliczenia).

Z kolei nabywca opcji sprzedaży zabezpiecza się przed

spadkiem cen akcji, gdyż ma zagwarantowaną

minimalną cenę, po jakiej ją sprzeda.

OPCJE NA AKCJE

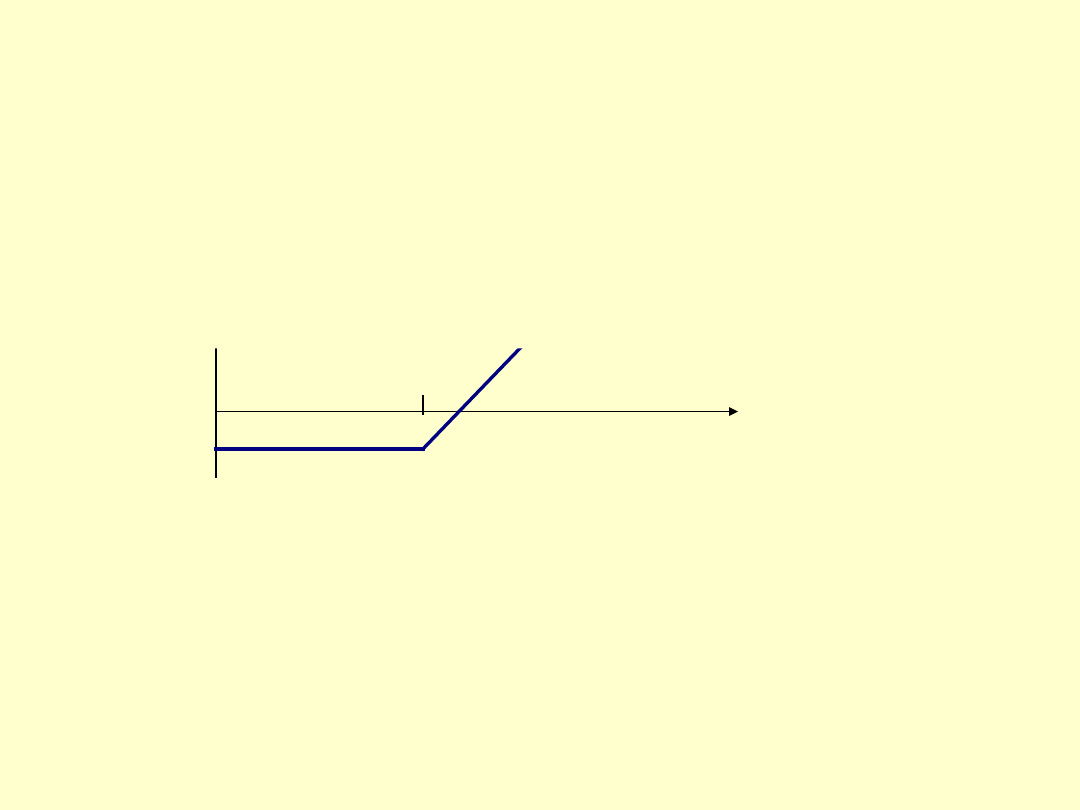
Gdy cena rynkowa akcji (C) < 100, to posiadacz opcji nie rozliczy jej

gdyż cena rozliczenia jest > C (wówczas lepiej opłaca się kupić akcję na
rynku). W tym przypadku posiadacz opcji ponosi stratę równą wartości
premii.

Wartość premii = cenie opcji

Z kolei gdy:
C > 100 opłaca się rozliczyć opcję. Zysk posiadacza opcji rośnie, pozostaje
on jednak ujemny do momentu, gdy C znajduje się w przedziale: 100 < C
<110 (w takim przypadku nadwyżka ceny rynkowej nad ceną rozliczenia nie
rekompensuje premii jaką posiadacz musiał zapłacić za opcję. Dopiero przy
C> 110 posiadacz opcji osiąga zysk dodatni.

0

Kształtowanie się zysku, który wystąpi w momencie

rozliczania opcji można przedstawić na wykresie za pomocą
funkcji:

Z = f(C)

gdzie: Z - zysk, C - cena rynkowa akcji, której ta opcja

dotyczy (w momencie rozliczenia)

W przypadku opcji kupna, zysk ten przedstawia się

następująco:

dla

nabywcy

opcji

:

Zysk

100

110

Cena

-
10

Cena rozliczenia wynosi
100 Premia ( cena
opcji ) wynosi 10

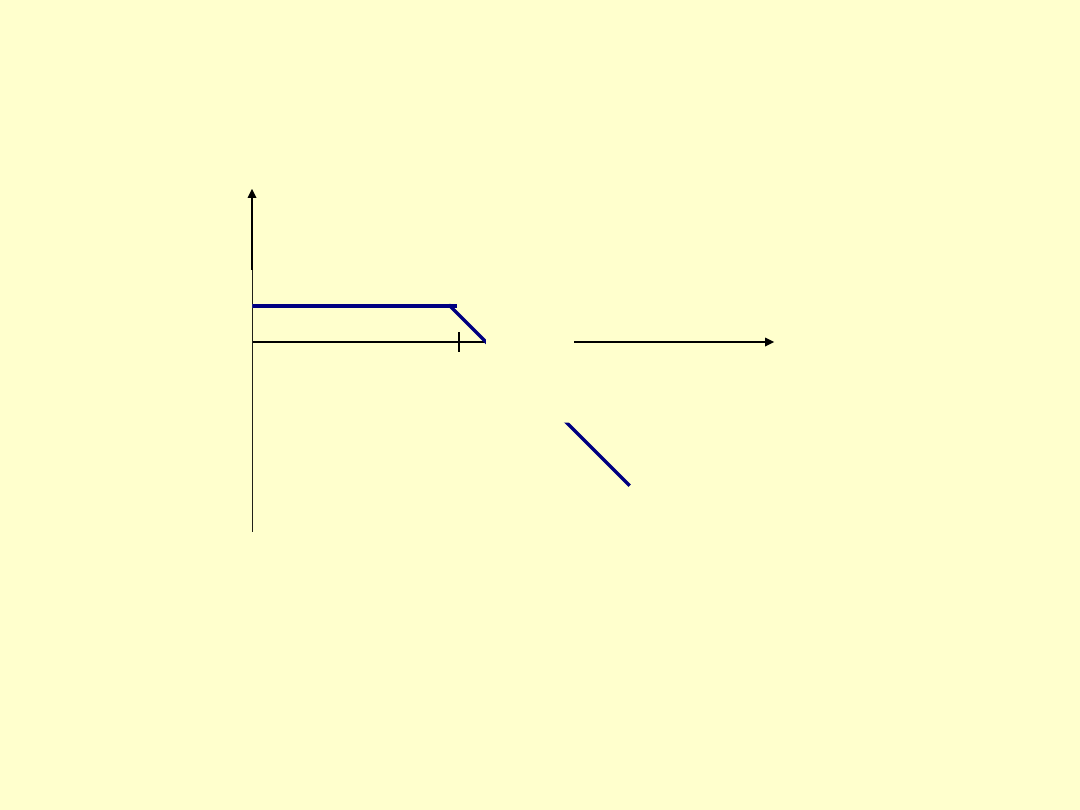
Zysk

dla wystawiającego opcje: 
 

W tym przypadku sytuacja jest odwrotna – zysk nabywcy opcji jest

stratą wystawiającego opcję.

1
0

110

Cena rozliczenia wynosi 100 a
premia 10

100

0

Cena

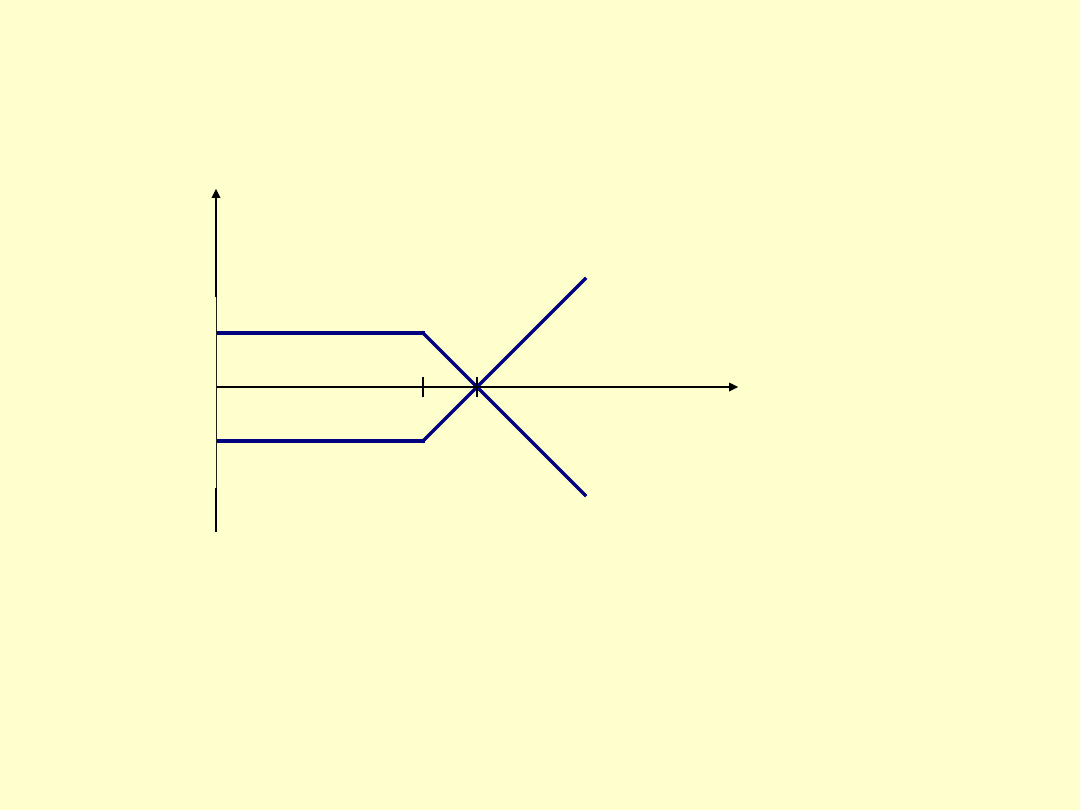
Zysk

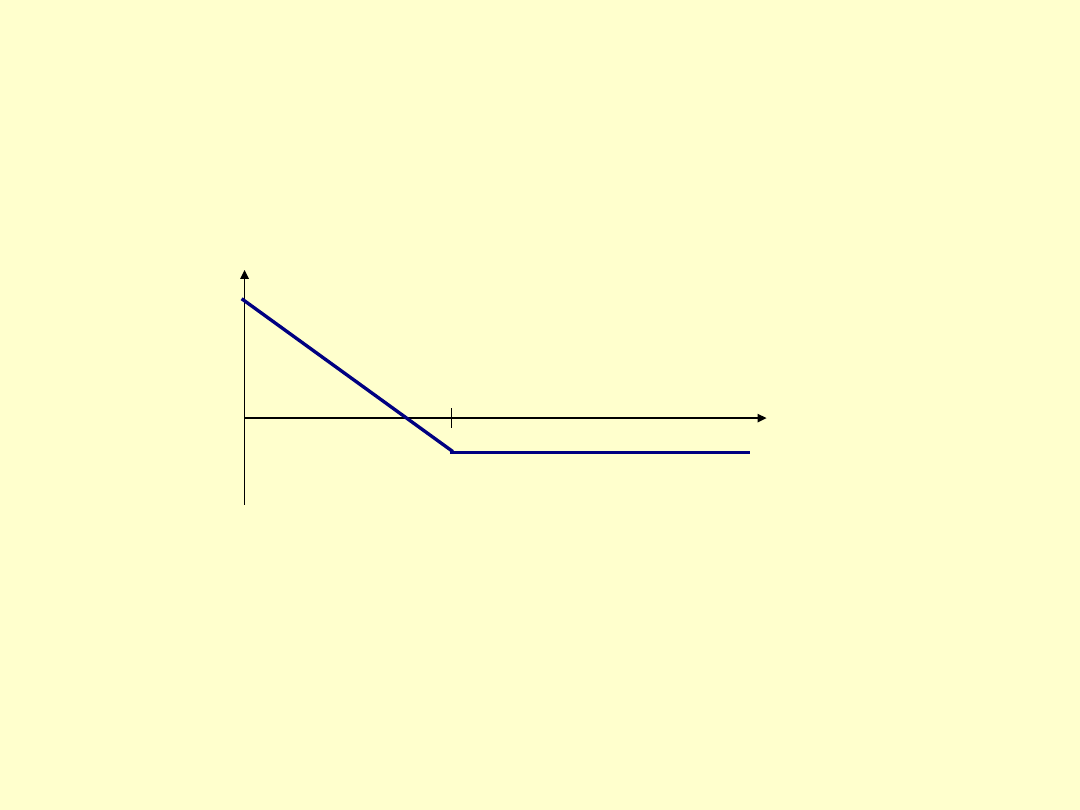
W przypadku opcji kupna, zysk ten przedstawia się następująco:

dla nabywcy opcji i wystawiającego opcje łącznie:
 

Cena rozliczenia w obu przypadkach wynosi 100, a premia ( cena
opcji) wynosi 10.

10

Cena

-10

100 110

Zys
k

W przypadku opcji sprzedaży, zysk ten przedstawia się

następująco:

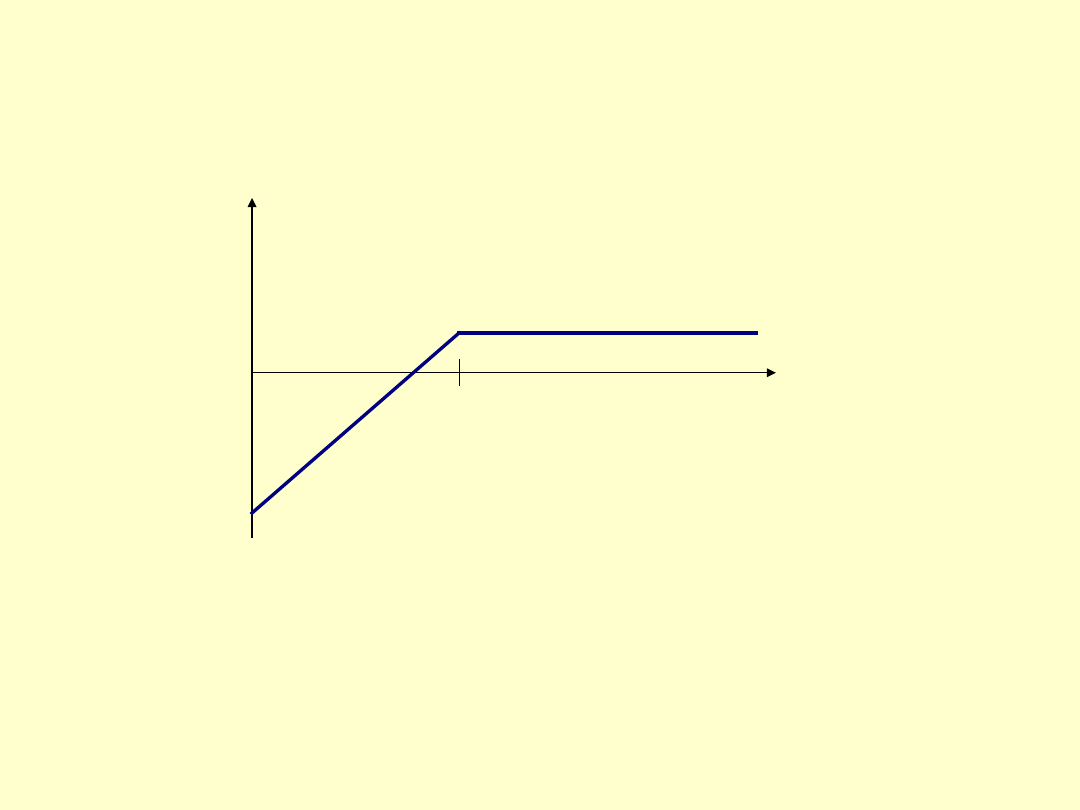
dla nabywcy opcji:

Cena rozliczenia wynosi 100, a premia
10

Gdy C < 100 posiadacz opcji rozliczy ją z zyskiem (czyli sprzeda akcję
wystawiającemu opcję po cenie rozliczenia która jest > C). Jednak gdy
90<C<100 posiadacz opcji przy rozliczeniu poniesie stratę. Gdy zaś
C>100, posiadacz opcji poniesie stratę równą wielkości premii.

Cena

100

90

-10

90

W przypadku wystawiającego opcje:

W przeciwieństwie do poprzedniej sytuacji, w tej maksymalna strata
wystawiającego opcję jest ograniczona.Równa się ona różnicy między
nadwyżką ceny rozliczenia nad "najgorszą ceną rynkową" (wynoszącą
zero) oraz premią.

Zysk

Cena

100

90

10

-90

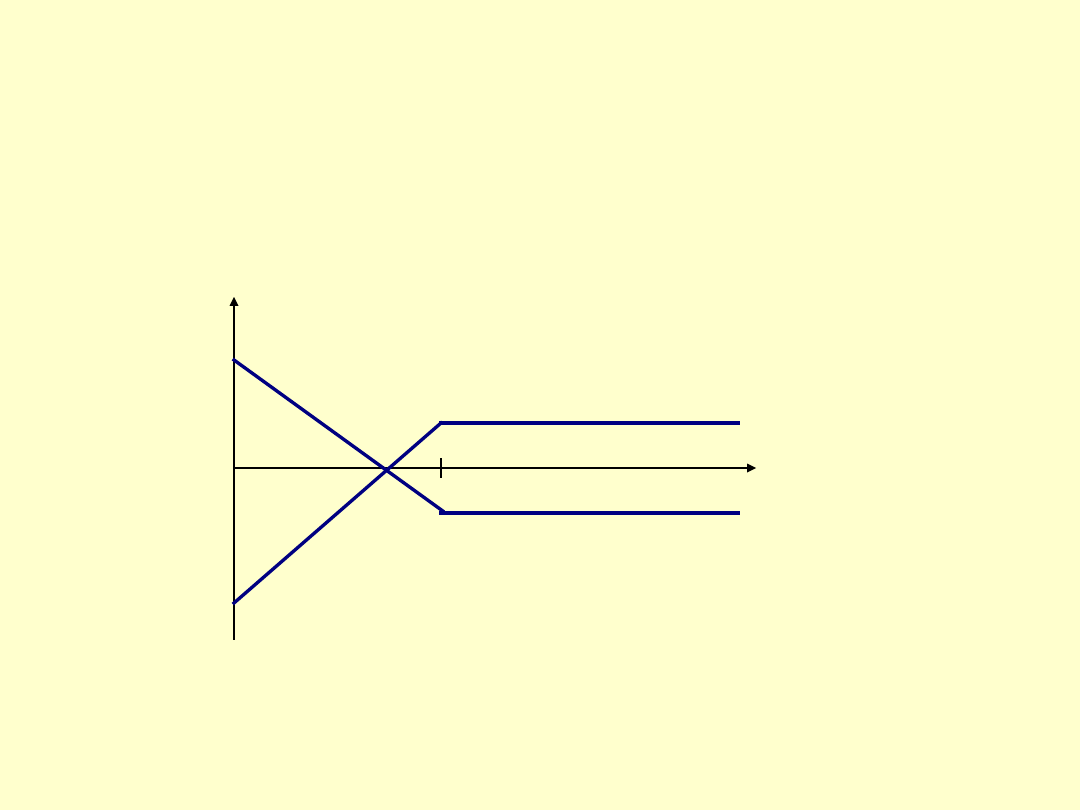
W przypadku opcji sprzedaży, zysk ten przedstawia się następująco:

dla nabywcy opcji i wystawiającego opcje łącznie:

Zysk

90

Cen
a

100

90

10

-10

-90

Do czynników mających wpływ na cenę opcji, należą:
 

• cena instrumentu bazowego (wzrost ceny instrumentu
bazowego prowadzi

do wzrostu ceny opcji kupna i spadku

ceny opcji sprzedaży),

• cena wykonania (wzrost ceny wykonania prowadzi do spadku
ceny opcji kupna i wzrostu ceny opcji sprzedaży),

• zmienność cen instrumentu bazowego (duża zmienność cen
instrumentu bazowego prowadzi do wzrostu ceny zarówno
opcji kupna, jak i sprzedaży),

• czas, pozostający do wygaśnięcia opcji (więcej czasu -
wyższa cena),
 

• poziom stóp procentowych (wzrost stóp prowadzi
pośrednio do spadku ceny opcji kupna i wzrostu ceny opcji
sprzedaży),

• dywidendy spodziewane w czasie ważności opcji.

Na wartość opcji mają wpływ następujące czynniki:

- termin rozliczenia:

a) przy opcji typu amerykańskiego - im dalszy tym wyższa wartość
opcji kupna i sprzedaży,
b) przy opcji typu europejskiego - termin rozliczenia ma niewielki
wpływ na wartość opcji;
 

- cena rozliczenia:

a) w przypadku opcji kupna - cena rozliczenia wpływa ujemnie na
wartość opcji. Im wyższa cena rozliczenia tym niższa wartość opcji,
b) w przypadku opcji sprzedaży - cena rozliczenia wpływa
dodatnio na wartość opcji. Wyższa cena rozliczenia oznacza
większy zysk posiadacza opcji (czyli sprzedającego akcję) w
momencie rozliczenia;

- cena bieżąca akcji, której opcja dotyczy

:

a) w przypadku opcji kupna - cena bieżąca akcji wpływa dodatnio na
wartość opcji (gdyż cena bieżąca akcji w momencie rozliczenia może
być większa od ceny rozliczenia),
b) w przypadku opcji sprzedaży - cena bieżąca akcji wpływa ujemnie
na wartość opcji;
 
 
 

 typ opcji:

- opcja typu amerykańskiego ma większą wartość niż opcja typu
europejskiego, gdyż daje posiadaczowi możliwość rozliczenia w
dłuższym okresie,
- opcja typu europejskiego tylko w określonym dniu;
 

 zmienność cen akcji:

a) w przypadku opcji kupna - duża zmienność cen akcji oznacza
dużą szansę wystąpienia wysokiej ceny rynkowej akcji w momencie
rozliczenia, co zwiększa zysk posiadacza opcji,
b) w przypadku opcji sprzedaży - duża zmienność cen akcji oznacza
dużą szansę wystąpienia niskiej ceny rynkowej akcji w momencie
rozliczenia, co zwiększa zysk posiadacza opcji;



stopa procentowa (stopa dyskontowa):

wzrost stopy procentowej oznacza mniejszą wartość bieżącą (po
zdyskontowaniu) ceny rozliczenia,
w przypadku:
 a) opcji kupna - prowadzi to do wzrostu wartości opcji,
b) opcji sprzedaży - prowadzi to do spadku wartości opcji.

Korzyści i zagrożenia związane ze
stworzeniem rynku opcji w Polsce:

 

1)dla przedsiębiorstw:
-    możliwość zarządzania ryzykiem rynkowym,
-     restrukturyzację struktury czasowej przepływów pieniężnych,
-     redukcję kosztów finansowania;
 
2)dla instytucji finansowych:
-    możliwość zarządzania ryzykiem rynkowym,
- restrukturyzację struktury czasowej przepływów pieniężnych,
-     zwiększenie konkurencyjności;
 
3)dla rynku:
-    zmniejszenie odległości od rynku światowego,
-    alokację i rozproszenie ryzyka na rynku,
-    zwiększenie świadomości i wiedzy uczestników rynku,

-poprawa efektywności, w szczególności zmniejszenie możliwości
arbitrażu, polegającego na wykorzystaniu niedoskonałości w zakresie
cen, który to arbitraż powoduje uzyskiwanie ponadprzeciętnych
dochodów przez niektórych uczestników rynku.

-Ryzyko związane z stosowaniem mało znanego
instrumentu

ANEKS

SPOSÓB OKREŚLANIA WARTOŚCI OPCJI

Model Blacka - Scholesa

 

 

C = S

0

N (d

1

) – E e

-rt

N (d

2

)

d

1

= [ ln (S

0

/ E) + ( r + 0.5 s

2

) * t ] / (s * t

0.5

)

d

2

= [ ln (S

0

/ E ) + ( r - 0.5 s

2

) * t ] / (s * t

0.5

)

gdzie:

C - wartość opcji kupna,
S

0

- cena bieżąca akcji, której dotyczy opcja,

E - cena rozliczenia opcji,
r - tzw. stopa pozbawiona ryzyka,
t - czas pozostały do momentu rozliczenia opcji, wyrażony w latach,
s - odchylenie standardowe stopy zysku akcji,
N(d) - wartość dystrybuanty standaryzowanego rozkładu normalnego dla
argumentu d, (odczytywana dla wartości"d" z tablic rozkładu normalnego o
wartości oczekiwanej 0 i odchyleniu standardowym l).

Stopa pozbawiona ryzyka jest to stopa zysku obligacji rządowych,
otrzymana przy założeniu ciągłej kapitalizacji odsetek (r). Z reguły
dysponuje się informacjami dotyczącymi stopy pozbawionej ryzyka
przy założeniu rocznej kapitalizacji odsetek (r

0

).

Między tymi dwiema stopami zachodzi zależność:

r = ln ( 1 + r

0

)

Przykład

Rozważamy opcję kupna akcji A. Termin rozliczenia wynosi 6 miesięcy. Bieżąca
cena rynkowa akcji wynosi 90, a cena rozliczenia 100. Wiadomo również, że
stopa pozbawiona ryzyka, oszacowana na podstawie stopy zysku obligacji
emitowanych przez rząd, dla których to obligacji odsetki płacone są raz w roku,
wynosi 10 % . Firma analizująca rynek papierów wartościowych udostępniła
informację o odchyleniu standardowym akcji A - wynosi ono 1.
Obliczyć wartość opcji kupna.
 
Rozwiązanie:

1. Obliczamy stopę zysku pozbawianą ryzyka, otrzymaną przy ciągłej kapitalizacji
odsetek:

 

r = In ( l + r

0

) = In ( l + 0.1 ) = 0.095

 

podstawiając dane do wzorów (1) i (2) :

d

1

= [ In ( So / E ) + ( r + 0.5 s

2

) * t ] / ( s * t

0.5

)

(1)

d

2

= [ In ( So / E ) + ( r - 0.5 s

2

) * t ] / ( s * t

0.

5

)

(2)

 

otrzymujemy:

d

1

= [ ln ( 90/ 100 ) + ( 0.095 + 0.5 *1

2

) * 0.5 ] / ( s * 0.5

0,.5

) = 0.272

d

2

= [ ln ( 90/ 100 ) + ( 0.095 - 0.5 *1

2

) * 0.5 ] / ( s * 0.5

0,5

) = - 0.435

Po skorzystaniu z tablic standaryzowanego rozkładu normalnego otrzymujemy w przybliżeniu:
N(d

1

) = N(0.272)= 0.6072

N(d

2

) = N(-0.435)= 0.3318

podstawiając wszystko do wzoru:
C = S

0

N (d

1

) – E e

– r t

N (d

2

)

 

otrzymujemy wartość opcji (premię):
C = 90 * 0.6072 – 100 (2.7183)

- 0,095 * 0,5

* 0.3318 = 23

 

Oznacza to, że warto kupić opcję, jeśli jej cena (premia) nie przekracza 23 jednostek

pieniężnych.

Przedstawiony model służy do określenia opcji kupna. Jeśli chodzi o wartość opcji sprzedaży,

to wykorzystać tu

można tzw. parytet sprzedaż-kupno wyrażony za pomocą następującej formuły:

wartość akcji + wartość opcji sprzedaży + wartość opcji kupna = wartość bieżąca

ceny rozliczenia

czyli:

wartość opcji sprzedaży = wartość bieżąca ceny rozliczenia - wartość akcji -

wartość opcji kupna

Powyższa formuła umożliwia obliczenie wartości opcji sprzedaży przy znajomości ceny akcji,

ceny rozliczenia i wartości opcji kupna (wyznaczonej z

modelu Blacka-Scholesa

).

Zys
k

KOMBINACJE W HANDLU OPCJAMI

 
W praktyce na rynkach kapitałowych inwestorzy dokonują zakupu różnych

kombinacji opcji. Czynią to w celu zmniejszenia możliwości strat i zwiększenia
możliwości zysków. Przy tworzeniu różnych kombinacji opcji biorą oni pod uwagę jak
kształtuje się zysk nabywcy opcji wchodzących w skład kombinacji.

Jest to oczywiście

jednocześnie strata wystawiającego kombinację opcji.

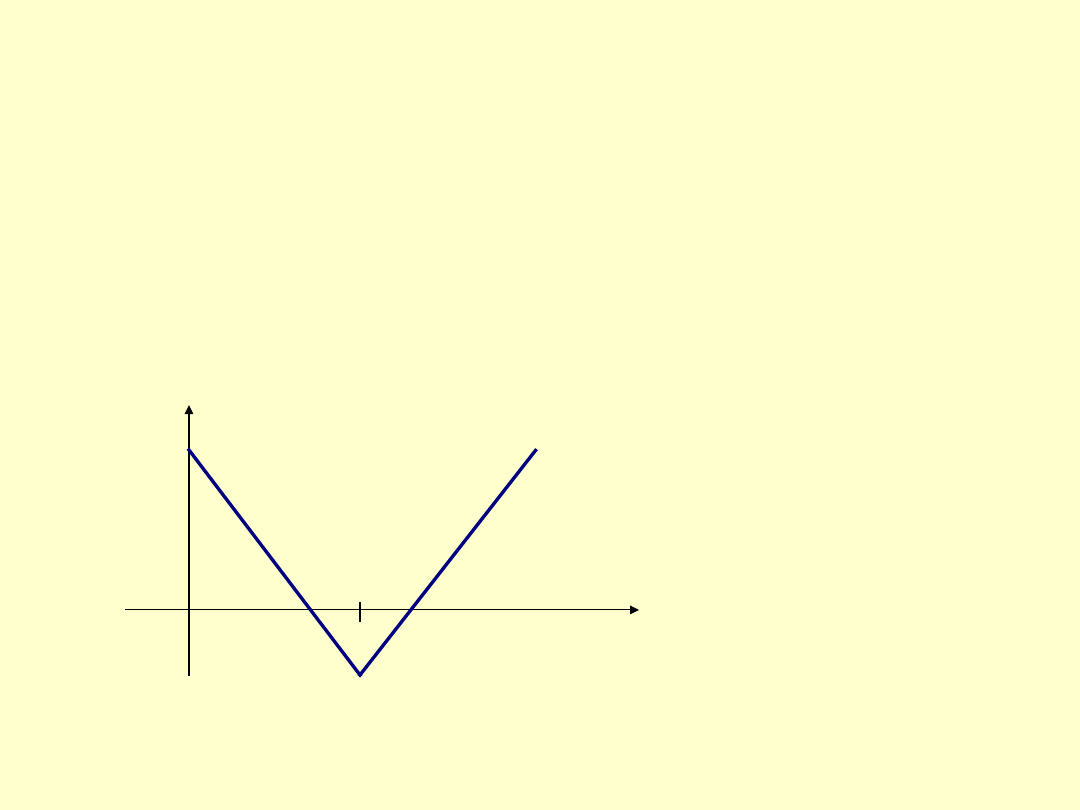
Straddle

jest to kombinacja opcji sprzedaży i opcji kupna z tą samą ceną

rozliczenia i tym samym terminem rozliczenia. Ilustruje ją rys. 6.5.

Nabywca kombinacji straddle oczekuje dużej zmiany ceny akcji, nie będąc przy tym

pewien, czy będzie to spadek czy wzrost ceny.

Rys.1

Straddle

.

Cena
akcji

x

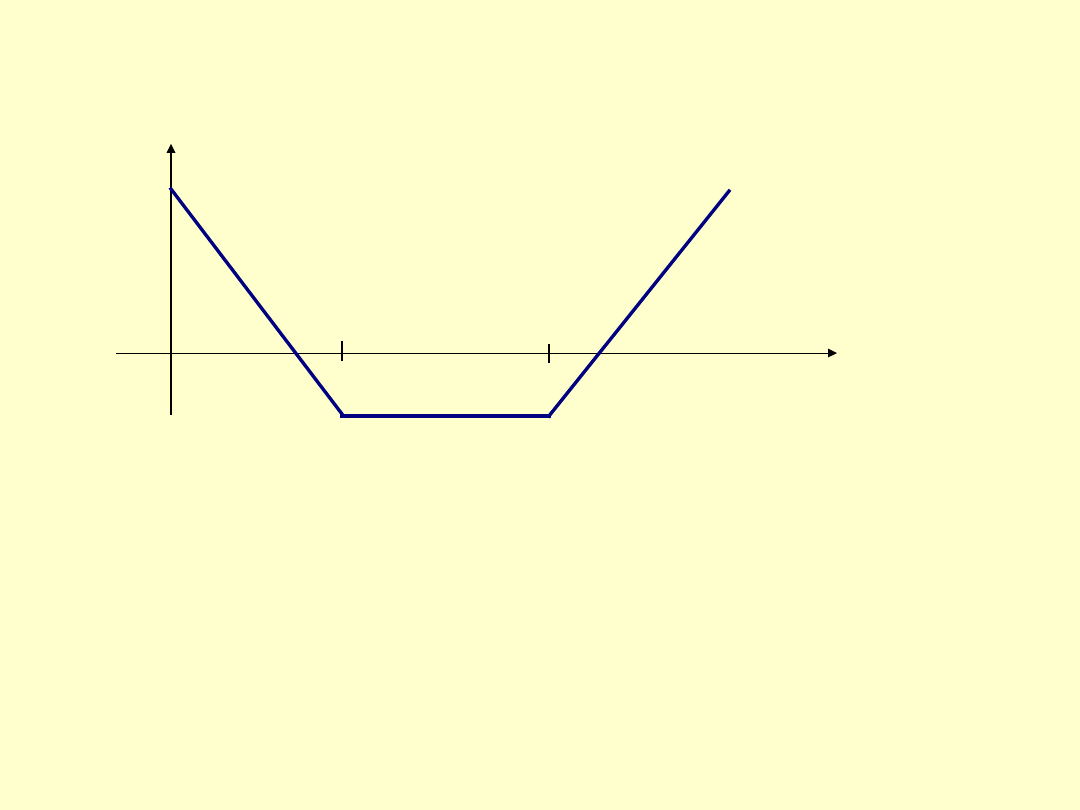
Rys.2.

Strangle

.

 

Strangle

jest to kombinacja opcji sprzedaży i opcji kupna z rożnymi

cenami rozliczenia i tym samym terminem rozliczenia. Ilustruje ją
rys.2.

Cena akcji

Zysk

x

1

x

2

Zysk

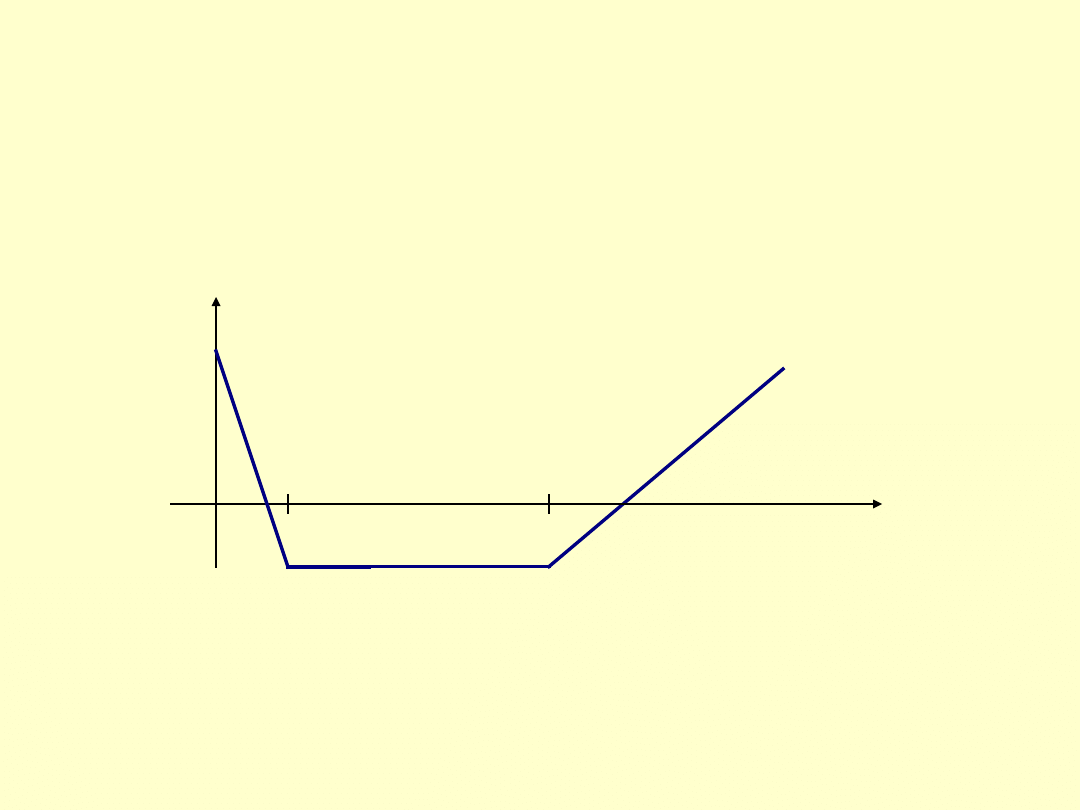
Strap

jest to kombinacja dwóch opcji kupna i jednej opcji sprzedaży. Przy tym

terminy rozliczenia są te

same,a ceny rozliczenia mogą być te same lub różne. Ilustruje ją rys.3

Cena akcji

Rys.3.

Strap.

x

Cena

akcji

Zysk

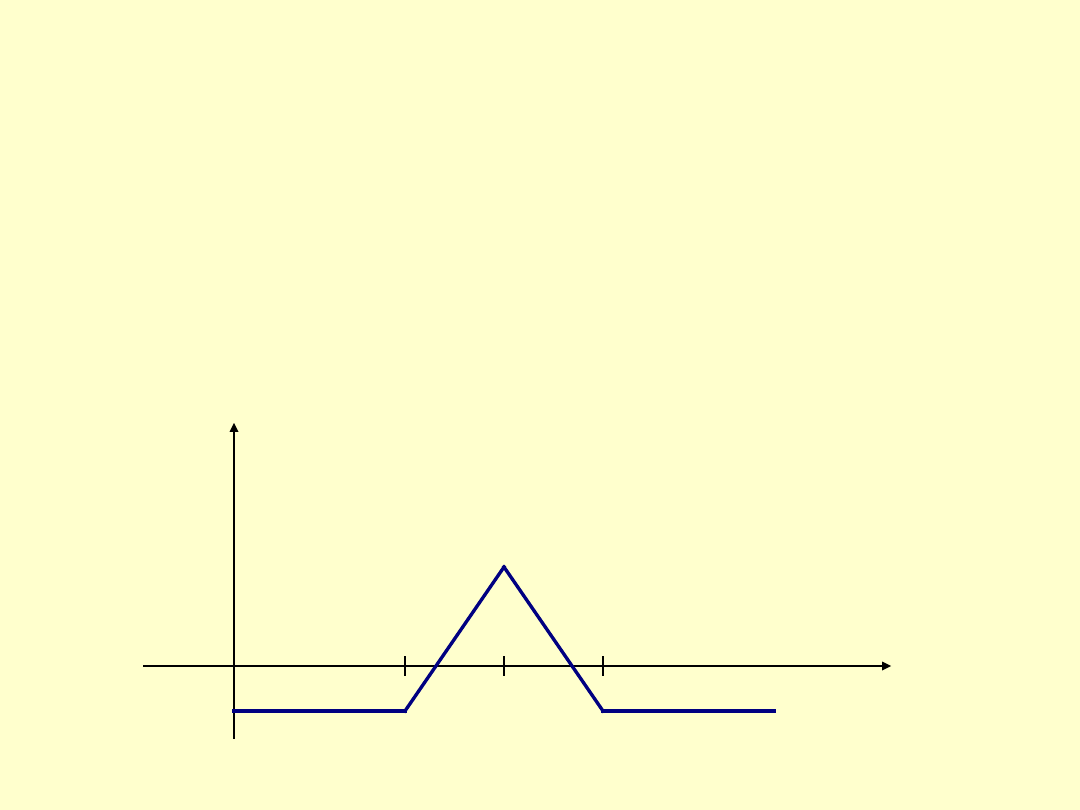
Strip

jest to kombinacja dwóch opcji sprzedaży i jednej opcji kupna. Przy tym

terminy rozliczenia są te

same, a ceny rozliczenia mogą być te same lub różne. Ilustruje ją rys.4

x

1

x

2

Rys. 4.

Strip

Wszystkie powyższe kombinacje dotyczyły sytuacji, gdy osoba była nabywcą

kombinacji lub wystawiającym kombinację. Na rynku występują również
kombinacje, w których jedne opcje są wystawiane (sprzedawane), a drugie
nabywane. Nazywa się je

spread

. Na przykład, horyzontalny spread to

kombinacja opcji (sprzedawanych i nabywanych) z tymi samymi cenami
rozliczenia lecz różnymi terminami rozliczenia. Z kolei diagonalny spread to
kombinacja opcji (sprzedawanych i nabywanych) z różnymi cenami rozliczenia i
różnymi terminami rozliczenia.

Przedstawimy teraz kilka szczególnych przypadków kombinacji typu spread.

Przy tym dla każdej kombinacji istnieje jej odpowiednik, poprzez zastąpienie
zakupu opcji jej sprzedażą a sprzedaży opcji jej zakupem.

Butterfly spread

jest to kombinacja, oznaczająca zakup opcji kupna z ceną

rozliczenia X

1

, zakup opcji kupna z ceną rozliczenia X

3

i sprzedaż dwóch opcji

kupna z ceną rozliczenia X

2

, przy czym X

1

<X

2

<X

3

. Ilustruje ją rys.5.

Zys
k

Cen
a
akcj
i

x

1

x

2

x

3

Rys.5.

Butterfly

spread.

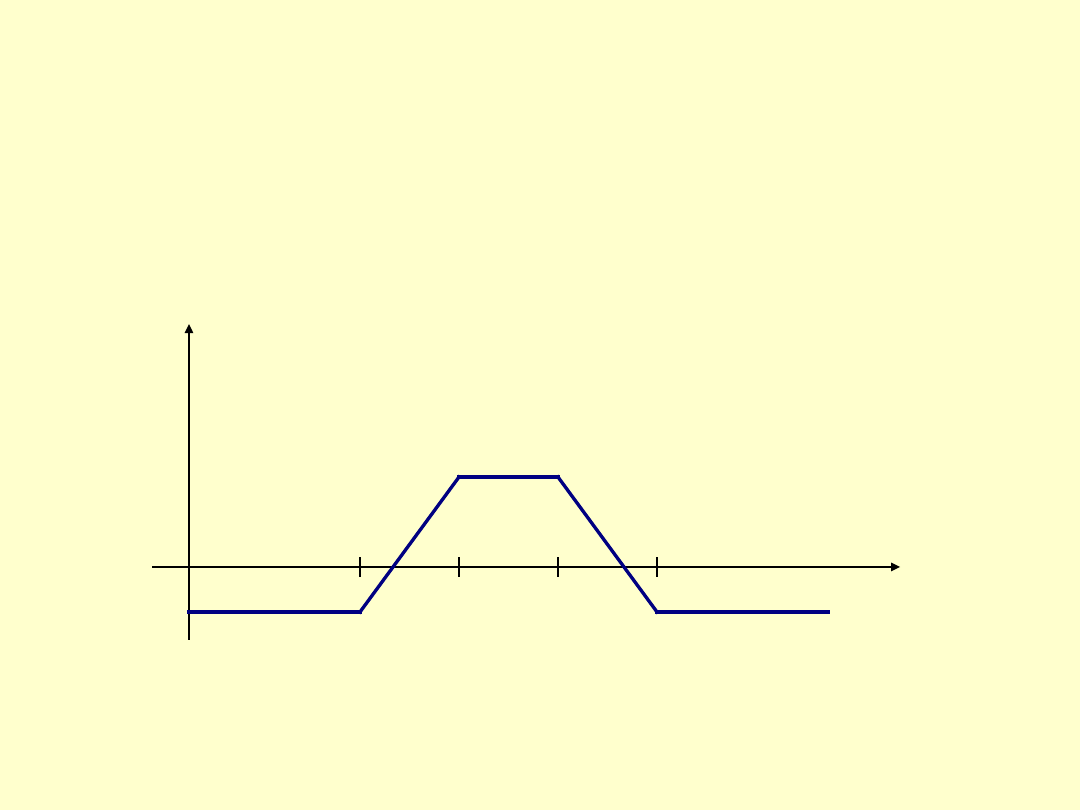
Tego typu postępowanie stosuje się w przypadku, gdy inwestor oczekuje stabilizacji

cen akcji.

 
 
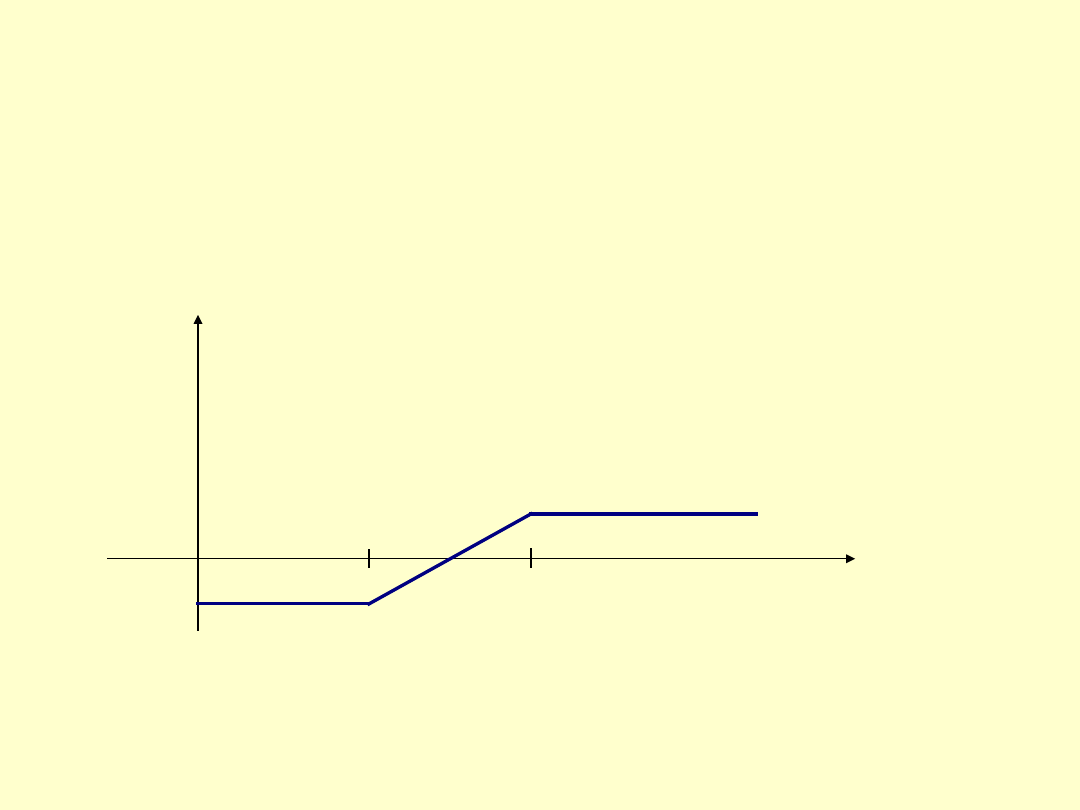
Condor

jest to kombinacja, oznaczająca zakup opcji kupna z ceną rozliczenia X

4

,

sprzedaż opcji kupna z

ceną rozliczenia X

2

i sprzedaż opcji kupna z ceną rozliczenia X

3

, przy czym X

1

<X

2

<X

3

.

Ilustruje ją rys.6.

x

1

x

2

Cena akcji

x

3

x

4

Zysk

Rys.6.

Condor.

Zys
k

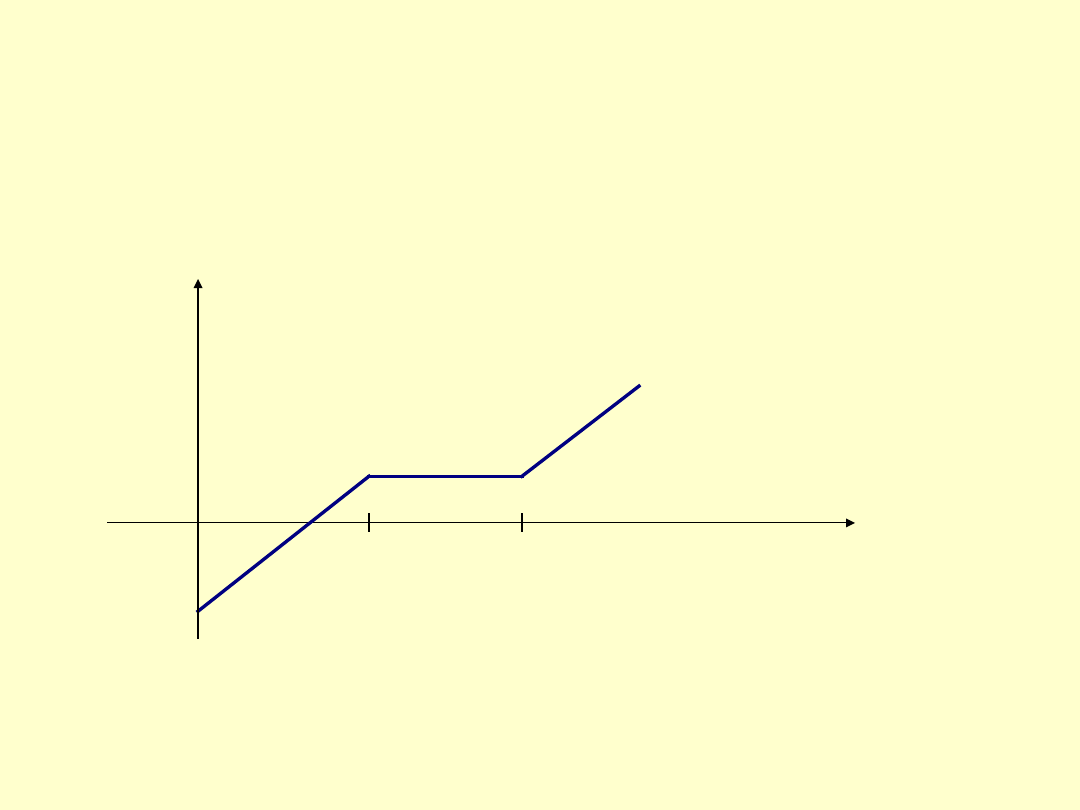
Vertical bull call spread

jest to kombinacja, oznaczająca zakup opcji kupna z

ceną rozliczenia X

1

i sprzedaż opcji kupna z ceną rozliczenia X

2

, przy czym X

1

<X

2

.

Ilustruje ją rys.7. Analogicznie konstruuje się kombinację

vertical bull put spread

(w

tej kombinacji występują opcje sprzedaży).

x

1

x

2

Cena akcji

Rys.7.

Vertical bull call

spread

Zysk

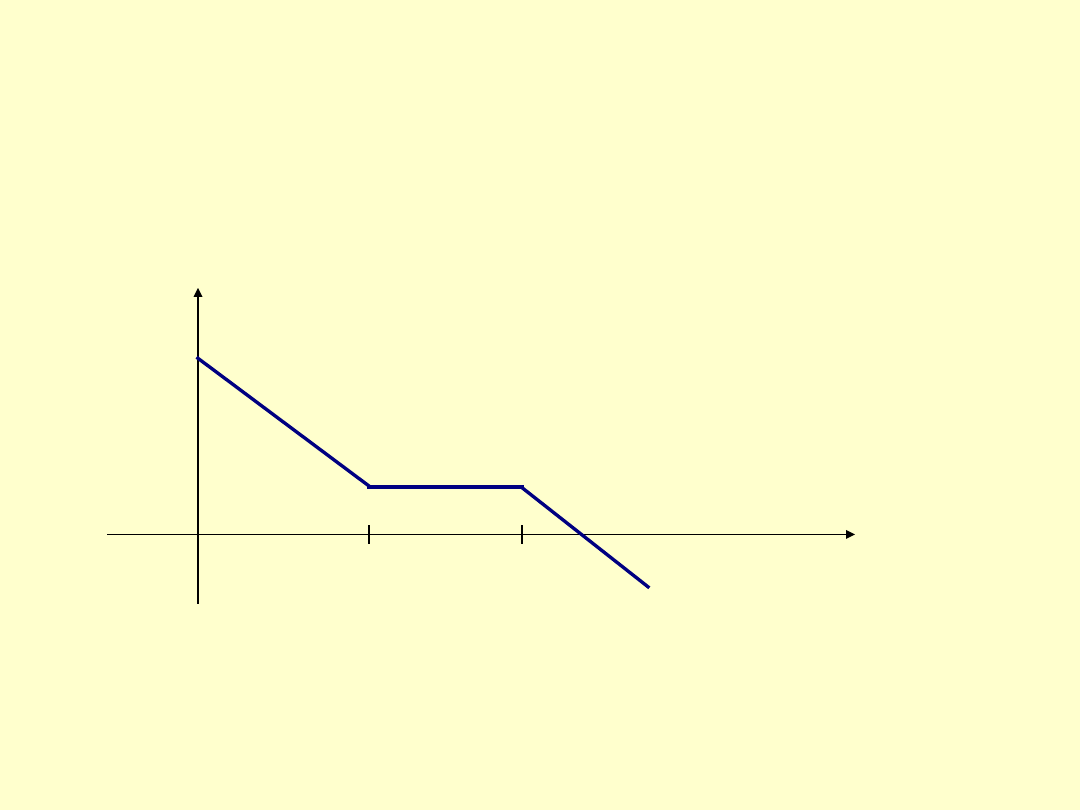
Vertical bear call spread

jest to kombinacja, oznaczająca sprzedaż kupna z

ceną rozliczenia X

1

i zakup opcji kupna z ceną rozliczenia X

2

, przy czym X

1

<X

2

.

Ilustruje ją rys.8. Analogicznie konstruuje się kombinację

vertical bear put spread

(w tej kombinacji występują opcje sprzedaży).

 
 

x

1

x

2

Cena akcji

Rys.8.

Vertical bear call

spread.

Zys
k

Rotated vertical bull spread

jest to kombinacja oznaczająca sprzedaż opcji

sprzedaży z ceną rozliczenia X

1

i zakup opcji kupna z ceną rozliczenia X

2

, przy

czym X

1

<X

2

. Ilustruje ją rys.9.

 
 
 

x

1

x

2

Cena

akcji

Rys.9.

Rotated vertical bull

spread

.

Rotated vertical bear spread

jest to kombinacja oznaczająca zakup opcji sprzedaży

z ceną rozliczenia X

1

i sprzedaż opcji kupna z ceną rozliczenia X

2

,

przy czym X

1

<X

2

.

Ilustruje ją rys.10.

Zysk

x

1

x

2

Cena akcji

Rys.10.

Rotated vertical bear

spread.