Analiza obwodów liniowych

metodą

rachunku operatorowego

Klasa SLS

Dla dwójników SLS przy zerowych
warunkach początkowych,
równanie operatorowe ma postać

)

(

)

(

)

(

s

I

s

Z

s

U



)

(

)

(

)

(

s

U

s

Y

s

I



Z(s), Y(s) - funkcja wymierna
rzeczywista
(o współczynnikach rzeczywistych)

0

1

0

1

...

...

)

(

)

(

)

(

b

s

b

s

b

a

s

a

s

a

s

M

s

L

s

Z

m

m

l

l

















Z(s) – impedancja operatorowa
Y(s) - admitancja operatorowa

(immitancje operatorowe)

0

)

( 



t

i

k

0

)

( 



s

I

k



0

)

(s

U

k

Równania operatorowe

Opornik

)

(

)

(

s

I

R

s

U



R

s

Z

R



)

(

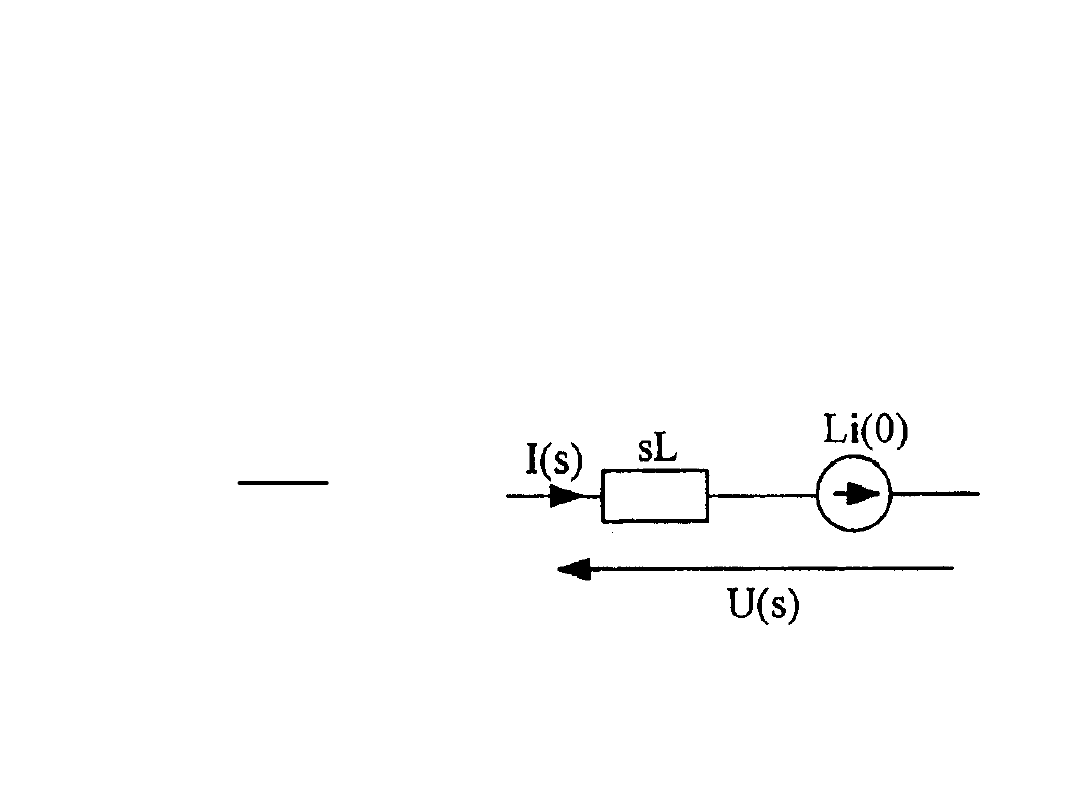
Cewka

t

i

L

u

d

d



(0)

-

)

(

)

(

Li

s

I

sL

s

U



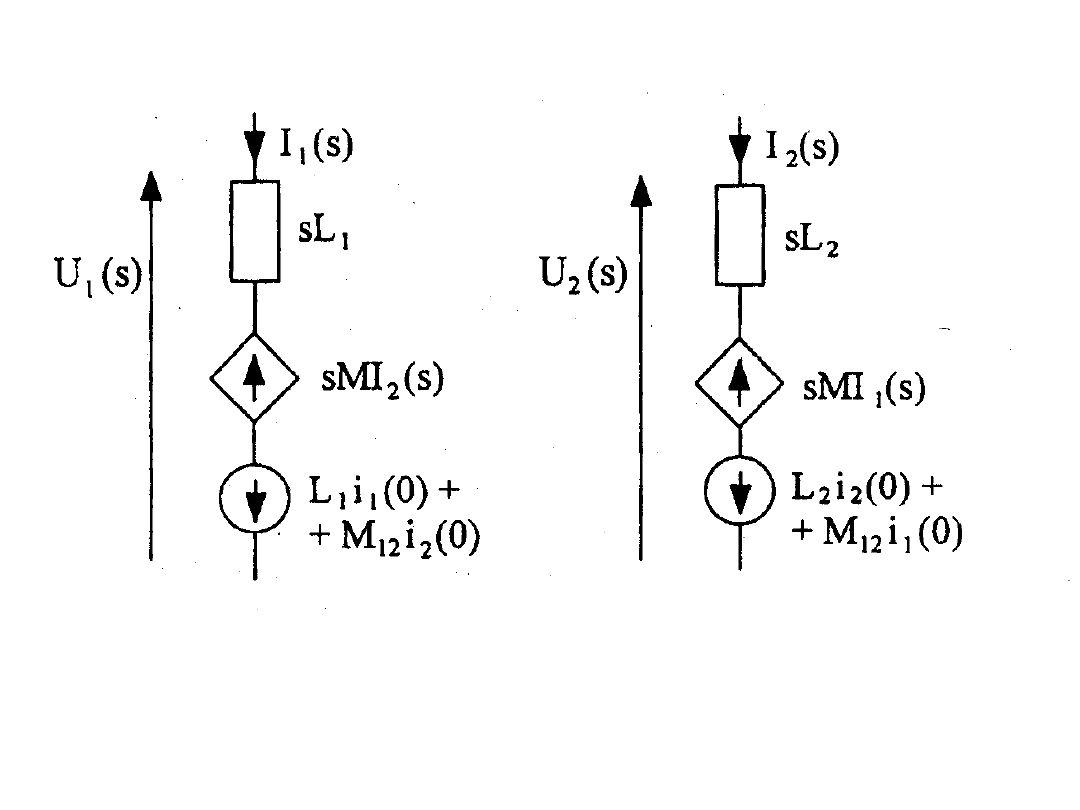
k-ta cewka sprzężona magnetycznie z
(n-1) cewkami

t

i

M

t

i

L

u

l

n

k

l

l

l

k

k

k

k

d

d

d

d

1











)

0

(

)

0

(

)

(

)

(

)

(

1

1

l

n

k

l

l

kl

n

k

l

l

k

k

l

kl

k

k

k

i

M

i

L

s

I

M

s

s

I

sL

s

U





















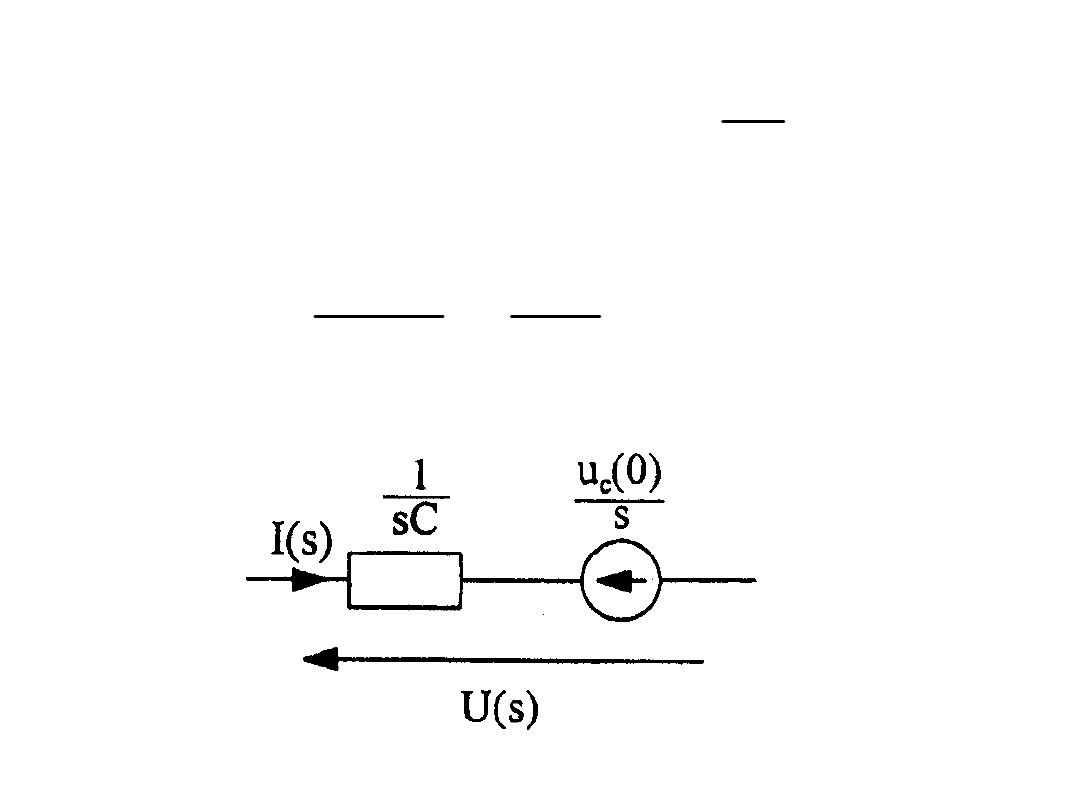
Kondensator











d

)

(

1

)

0

(

0

t

i

C

u

u

)

(

1

)

0

(

)

(

s

I

sC

s

u

s

U





Źródła sterowane

x

y





)

(

)

(

s

X

s

Y





Przy zerowych warunkach
początkowych, cewkę i kondensator w
pełni charakteryzują impedancje
operatorowe

sL

s

Z

L



)

(

sC

s

Z

c

1

)

( 

Prawa Kirchhoffa dla wartości
operatorowych mają taką samą postać
jak dla wartości symbolicznych.

Reguły dotyczące wyznaczania
zastępczej impedancji (admitancji)
operatorowej połączeń są takie same
jak w przypadku impedancji
(admitancji) zespolonych.

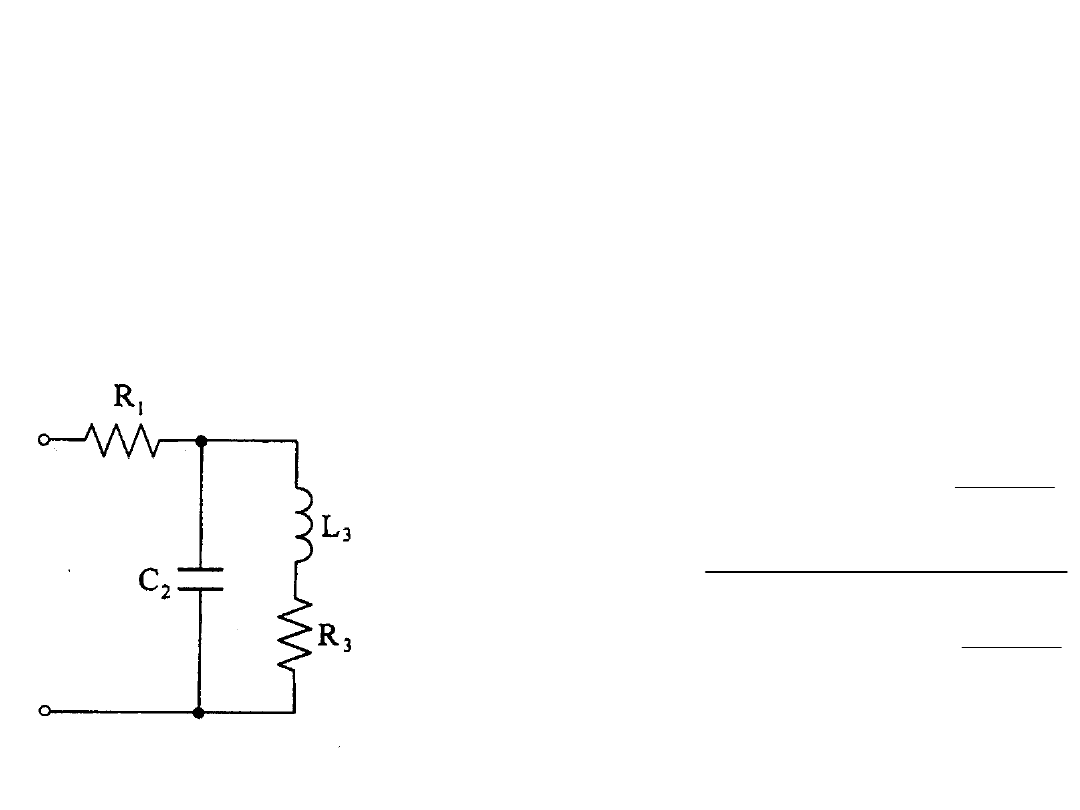
Przykład





2

3

3

2

3

3

1

1

1

)

(

sC

sL

R

sC

sL

R

R

s

Z











Analiza obwodów metodą
operatorową

W procesie analizy obwodów
posługujemy się znanymi metodami.
Otrzymane równania operatorowe
obwodu są równaniami algebraicznymi
o współczynnikach zależnych od
zmiennej zespolonej s.
W wyniku rozwiązania tych równań
otrzymujemy transformaty prądów i
napięć, które następnie poddajemy
przekształceniu odwrotnemu
otrzymując pełne rozwiązania,
obejmujące składową wymuszoną i
swobodną.

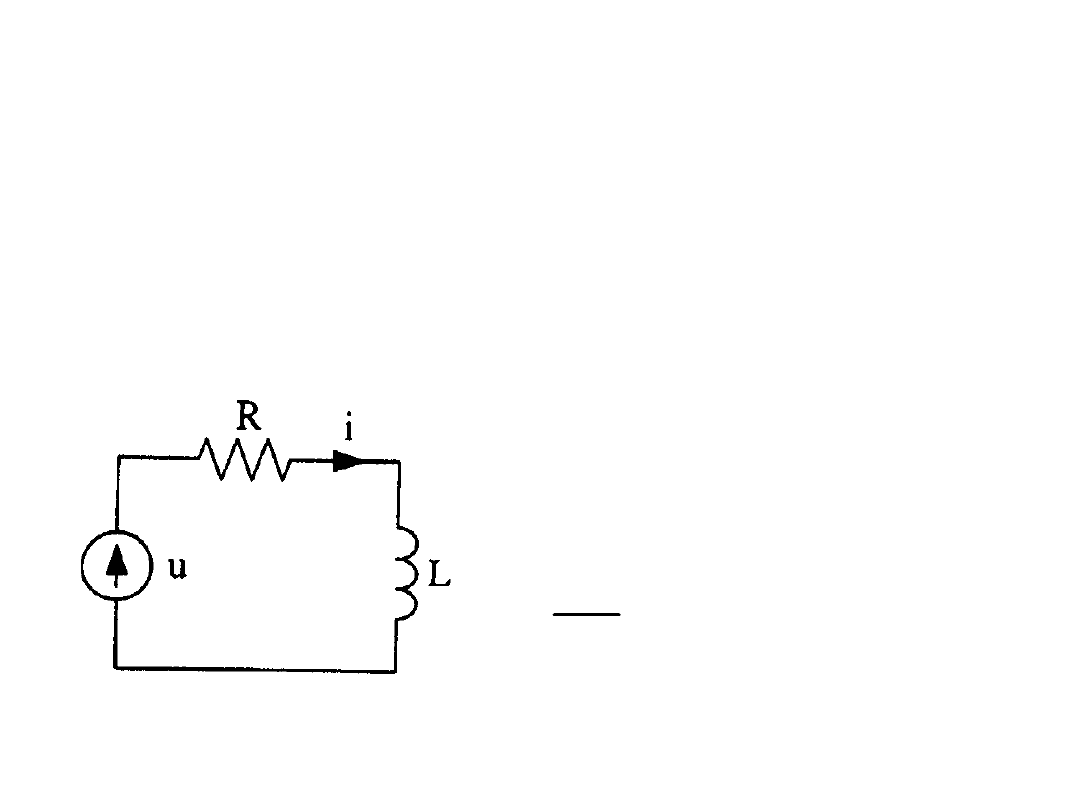
Przykład

Obliczyć prąd i przy zerowych
warunkach początkowych,

 

t

E

u

1



sL

R

s

Z





)

(

)

(

)

(

s

I

s

Z

s

E













 



L

R

s

s

L

E

s

I

1

)

(



























































 











t

L

R

e

k

k

L

E

L

R

s

s

L

E

s

I

t

i

1

)

(

)

(

2

1

1

1

L

L

R

L

L

R

s

s

s

k

s





































 





lim

0

1

R

L

L

R

s

s

L

R

s

k

L

R

s







































 









lim

2





















t

L

R

e

R

E

i

1

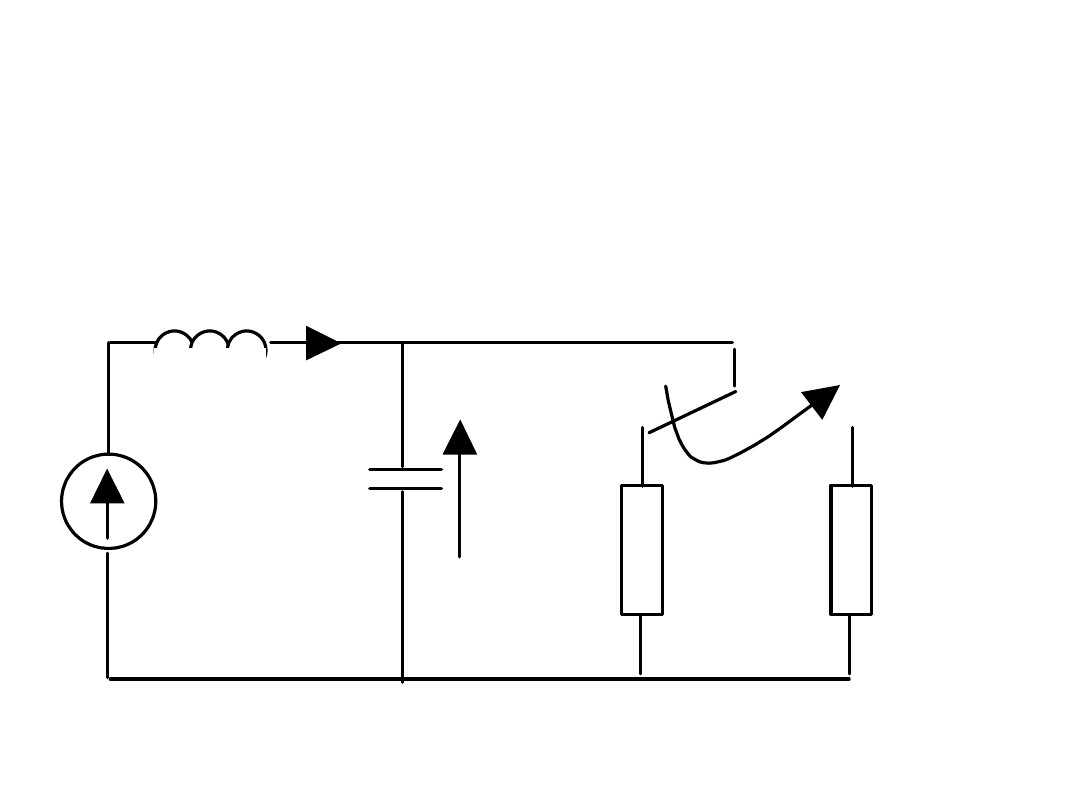
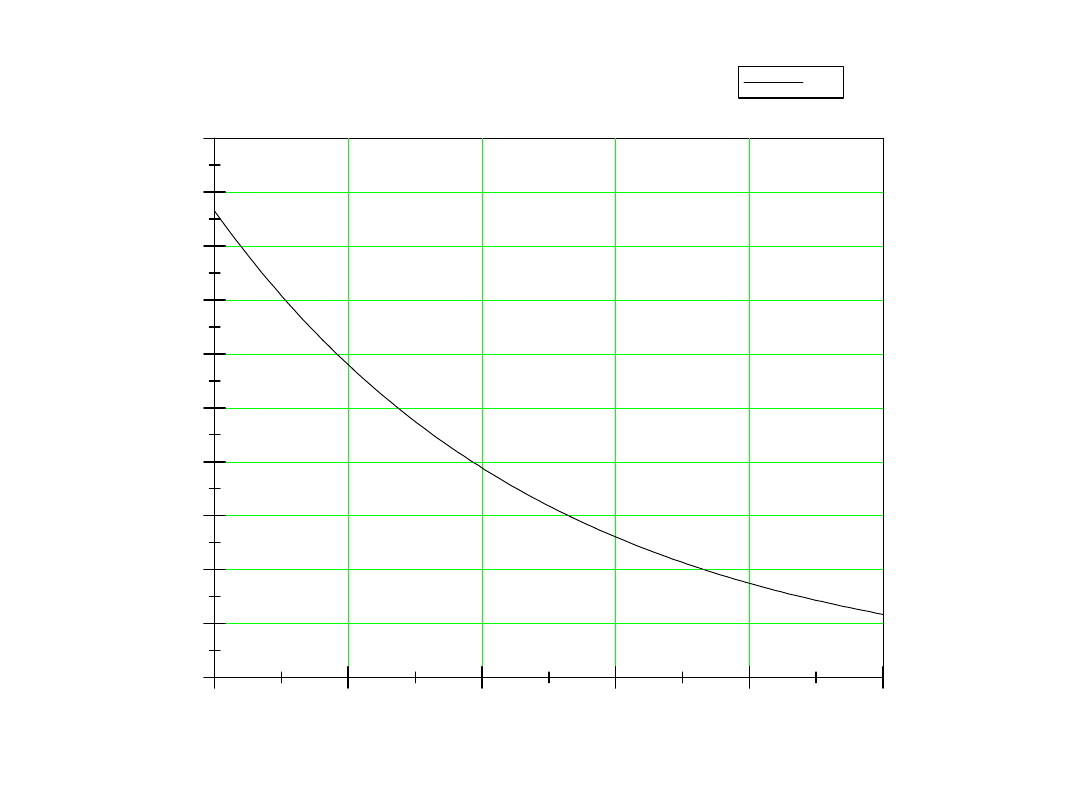
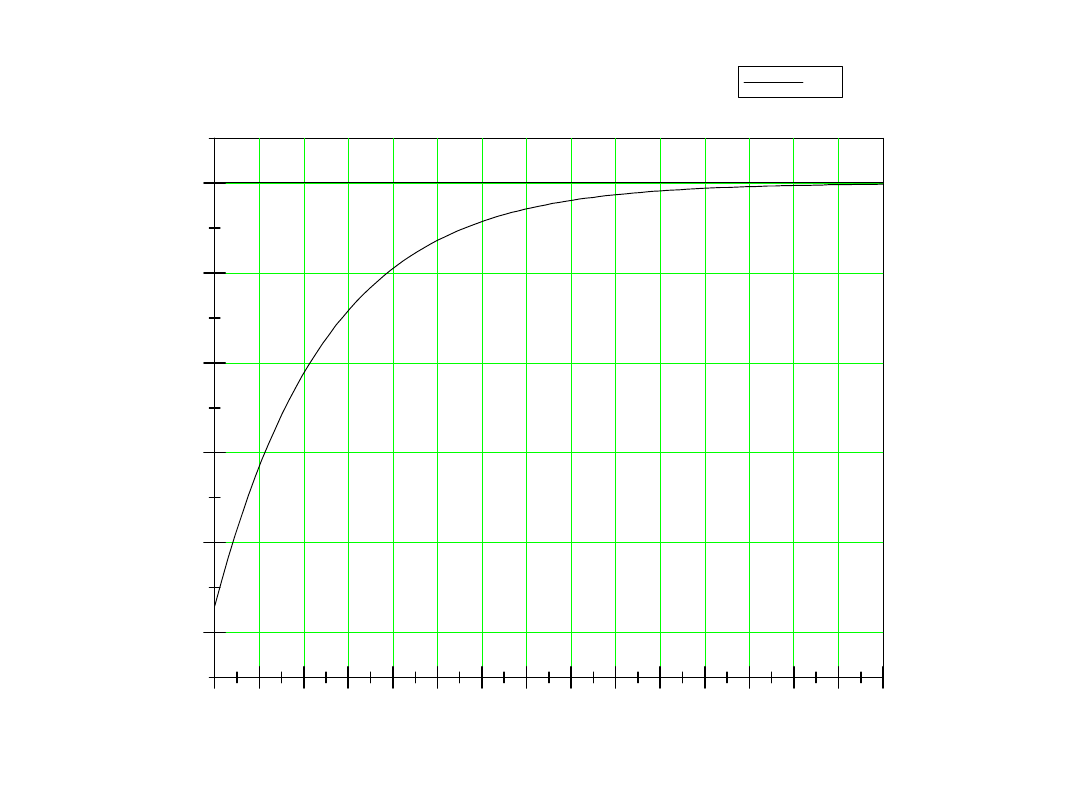
Przykład

Obliczyć u

C

(t) po przełączeniu

e=10V, L=1H, C=1mF, R

1

=5,

R

2

=50

e

L

C

R

1

R

2

t=0

warunki początkowe

 

 

V

E

u

A

R

i

C

L

10

0

2

10

0

1













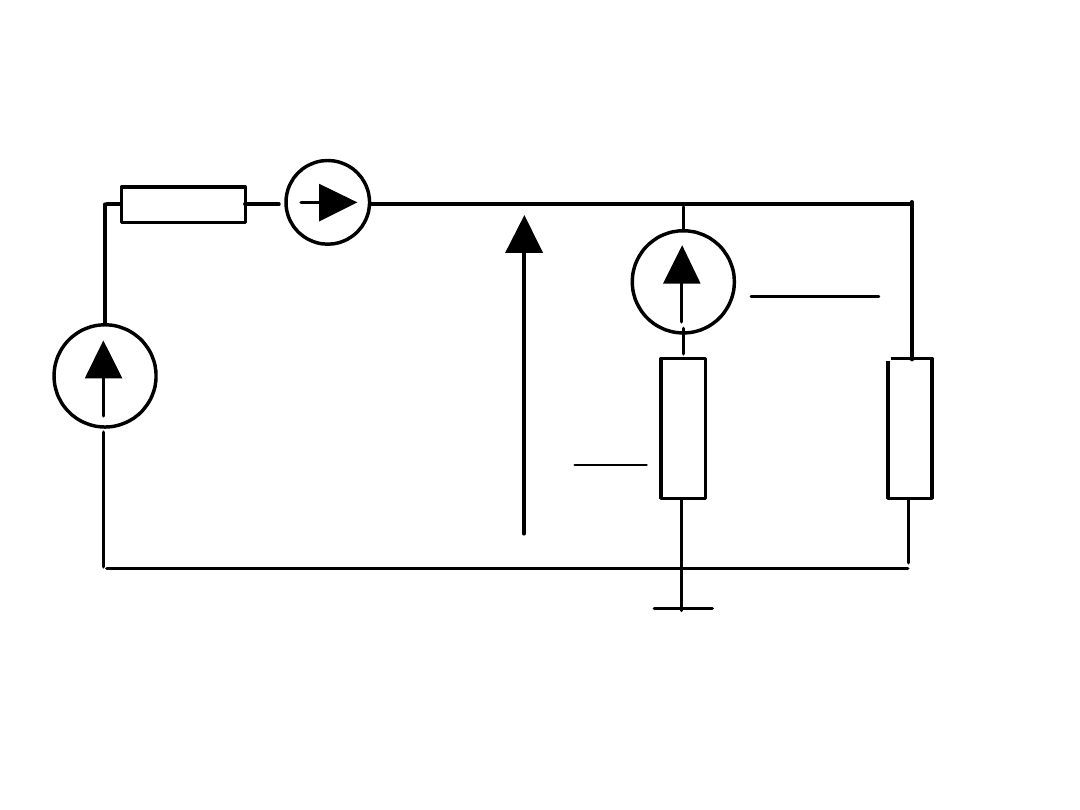
schemat operatorowy

E

(s

)

s

L

sC

1

R

2

L

i

L

(0

)

 

s

u

C

0

U

C

(s

)

   

 

 

 

 

0

1

0

0

2

















R

s

U

sC

s

u

s

U

sL

Li

s

E

s

U

C

C

C

L

C

 





1000

20

10000

2000

10

2

2











s

s

s

s

s

s

U

C

j

s

j

s

s

30

10

30

10

0

3

2

1















 

t

e

t

u

t

C

30

sin

60

10

10







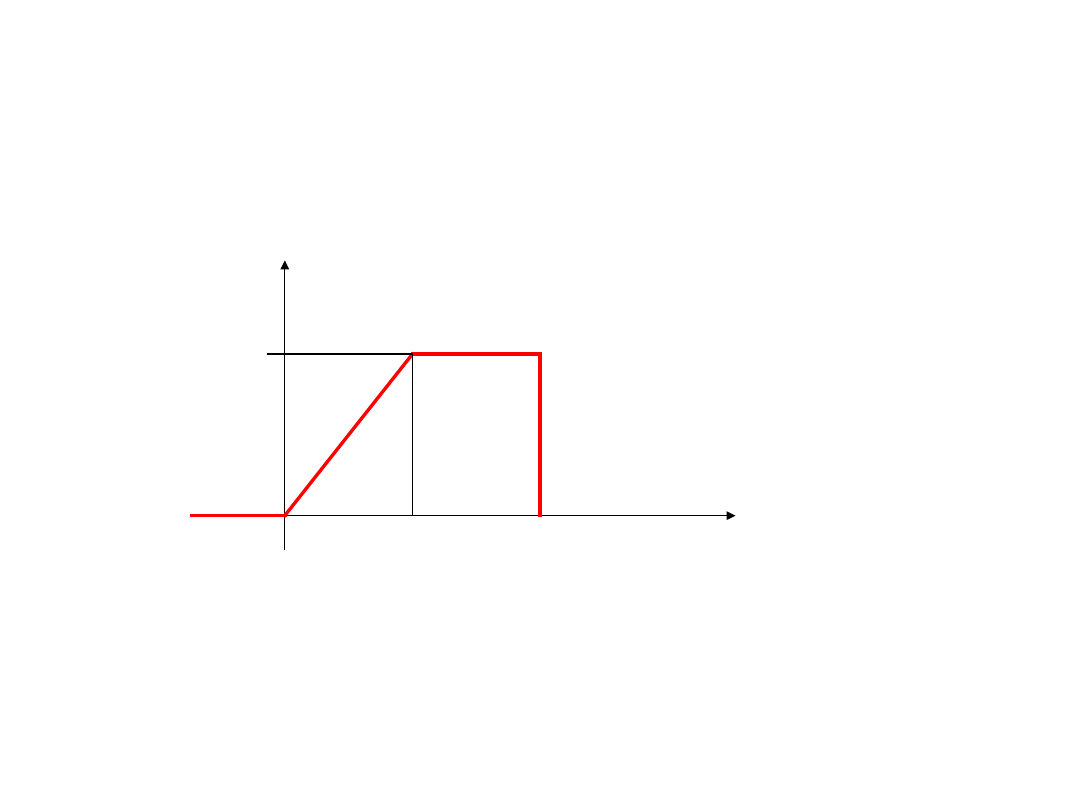
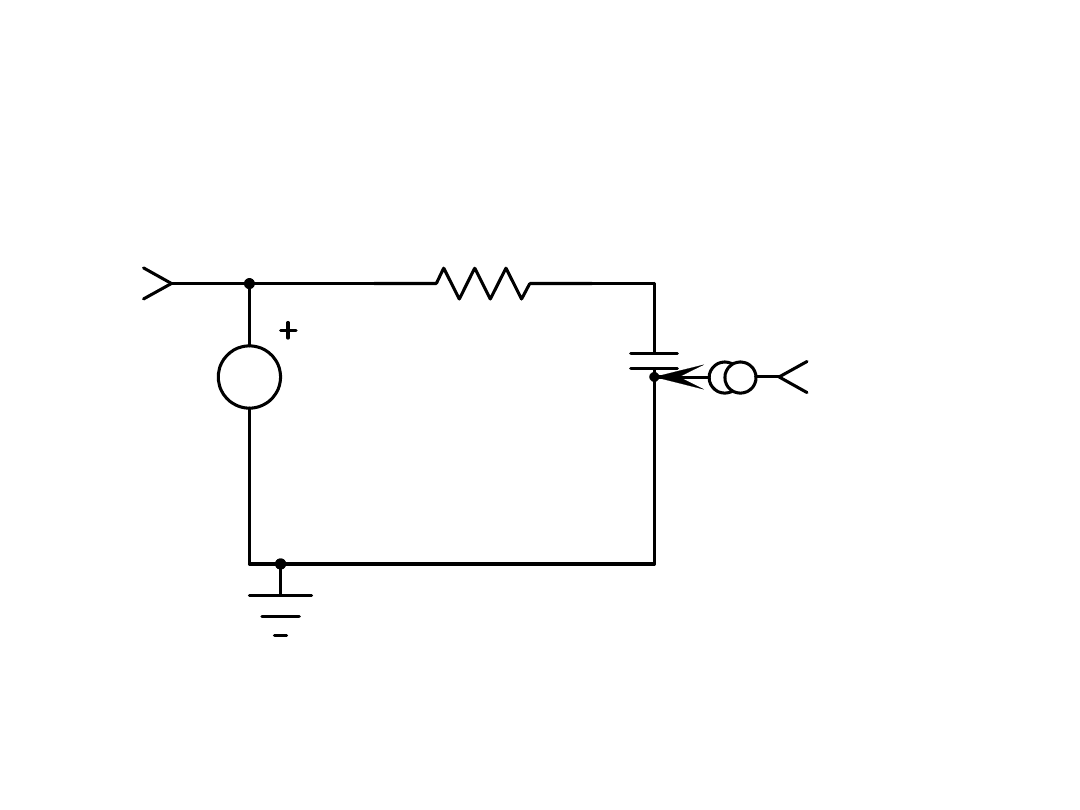
Wyznacz prąd płynący przez szeregowe
połączenie RC, jeżeli układ zasilono napięciem
trapezoidalnym pokazanym na rysunku

u(t)

t

2

1

0

10

R=1 C=0.5F

1. Wyznaczamy transformatę napięcia u(t)

 

 

dt

dt

t

dt

t

u

s

U

st

st

st





















e

10

e

10

e

2

1

1

0

0

pierwszą z całek liczymy przez części

2

2

1

0

2

1

0

1

0

1

0

1

0

1

0

10

e

10

e

10

e

1

10

e

10

e

1

10

e

10

1

e

1

e

e

10

e

10

s

s

s

s

s

t

dt

s

s

t

g

h

gh

g

t

g

s

h

h

dt

t

dt

t

s

s

st

st

st

st

st

st

st

st



















 













 















 













 











































































liczymy drugą całkę

s

s

st

st

s

s

s

dt





















e

10

e

10

e

1

10

e

10

2

2

1

2

1

ostatecznie

 

s

s

s

s

s

s

s

s

s

s

s

s

s

s

s

U

2

2

2

2

2

2

e

10

e

10

10

e

10

e

10

10

e

10

e

10

































Ponieważ u(t)=0 dla t<0, więc

 

0

0 

C

u

i impedancja układu wynosi

 

s

.

s

.

sC

sRC

sC

R

s

Z

5

0

1

5

0

1

1













prąd płynący przez obwód

 

 

 

s

s

s

.

s

.

s

s

.

s

.

s

s

.

s

.

s

s

Z

s

U

s

I

2

2

2

e

1

5

0

5

0

10

e

1

5

0

5

0

10

1

5

0

5

0

10





















 

 

 



 







s

s

s

s

s

s

s

s

Z

s

U

s

I

2

e

2

10

e

2

10

2

10



















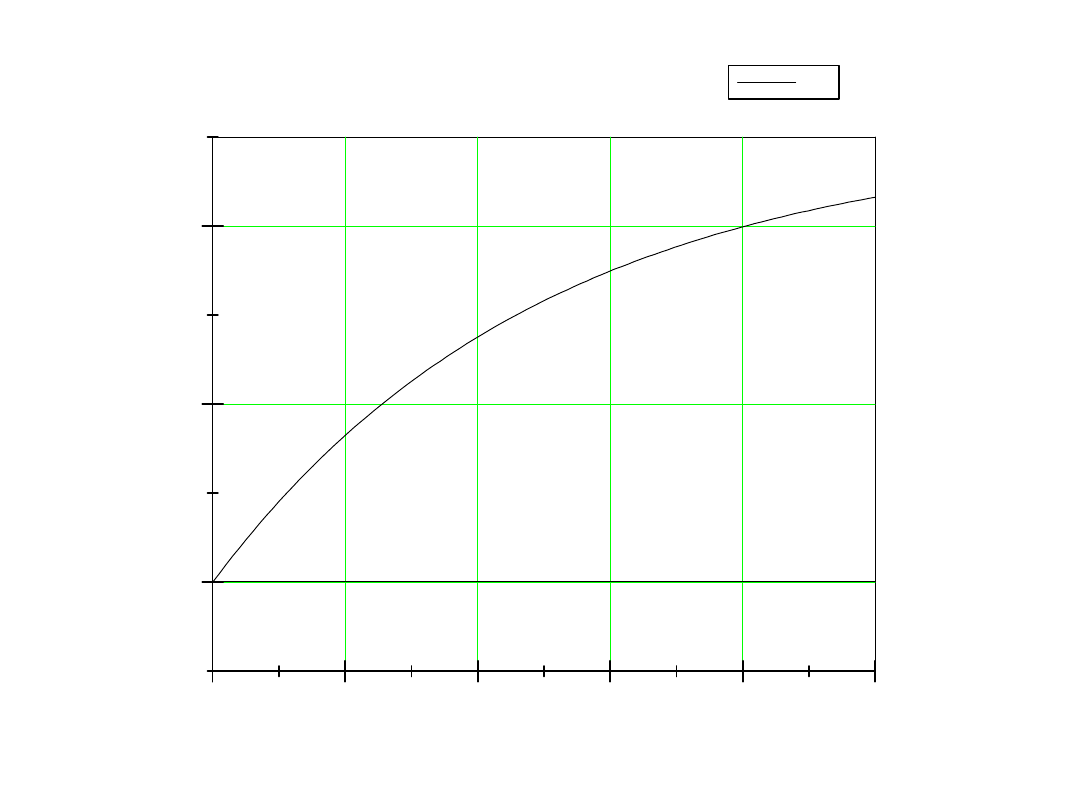
wyznaczamy transformatę odwrotną

 

 

 

 

 





2

1

e

10

1

1

e

5

1

1

5

e

5

5

2

2

1

2

2



































t

t

t

t

i

t

t

t

0,0

0,2

0,4

0,6

0,8

1,0

0

2

4

I

t

F1

1,0

1,2

1,4

1,6

1,8

2,0

0,0

0,5

1,0

1,5

2,0

2,5

3,0

3,5

4,0

4,5

5,0

I

t

F1

2,0 2,2 2,4 2,6 2,8 3,0 3,2 3,4 3,6 3,8 4,0 4,2 4,4 4,6 4,8 5,0

-10

-8

-6

-4

-2

0

I

t

F1

1

V1

2

R1
1

C1
0.5

Ic
amps

v1
volts

SPICE

1

500M

1.50

2.50

3.50

4.50

WFM.1 V1 vs. TIME in Secs

12.0

8.00

4.00

0

-4.00

V

1

in

V

o

lts

1

500M

1.50

2.50

3.50

4.50

WFM.1 IC vs. TIME in Secs

6.00

2.00

-2.00

-6.00

-10.00

IC

in

A

m

p

s

i(t)

u(t)