DYNAMIKA

1.Zasady dynamiki Newtona

2.Prawo ruchu i zachowania środka

masy

3.Zasada zachowania pędu

4.Zderzenia

Kinematyka

- znając przyspieszenie (

a = f(t)

) każdego punktu

materialnego przewidujemy jego przyszłe położenie (

x

).

Dynamika

- informuje, że aby znać przyspieszenie (

a

), trzeba znać siłę

(

F

) działającą na cząstkę oraz masę cząstki (

m

), czyli bada siły i ich

źródła tzn. bada oddziaływania między ciałami powodujące zmiany

ruchu.

Dynamika

zajmuje się przyczyną ruchu (duże masy, małe

prędkości v<<c), tzn:

1) Mamy ciało o masie

m

,

2) Ciału nadajemy prędkość początkową

v

0

w otoczeniu, które

znamy,

3) Pytanie – jaki będzie ruch ciała?

Ad. 1 Zasady dynamiki Newtona

I zasada

-

PRAWO BEZWŁADNOŚCI

Ciało pozostaje w stanie spoczynku lub porusza się ze

stałą prędkością (v = const, a = 0), gdy działa na nie siła

wypadkowa równa zeru.

Ciało pozostaje w spoczynku lub porusza się ruchem jednostajnie

prostoliniowym (v = const, a = 0), dopóki działanie na niego

innych ciał nie spowoduje zmiany tego stanu.

F

wyp

– siła wypadkowa, jeżeli na ciało działa więcej sił F

1

… F

n

, to ich

działanie jest takie samo jak działanie jednej siły wypadkowej F

wyp

równej wektorowej sumie wszystkich działających sił, czyli







m

i

i

wyp

F

F

1





0

F

gdy

0

a

wyp









Inercjalny układ odniesienia

(jego istnienie wynika z I

zasady dynamiki)

I zasada dynamiki

-

jeżeli na badane ciało nie działają siły

zewnętrzne, to istnieje taki układ odniesienia (układ
inercjalny) w którym to ciało spoczywa lub porusza się
ruchem jednostajnym prostoliniowym (bez przyspieszenia).

W układach inercjalnych ruchami ciał rządzą dokładnie te
same prawa.

Bezwładność ciał

Zgodnie z I zasadą dynamiki

ciało zachowuje swój stan ruchu,

dopóki oddziaływanie innych ciał nie zmieni tego stanu

. Tę

własność ciał nazywamy

bezwładnością

.

Jeżeli

chcemy

stosować

zasady

dynamiki

w

układach

nieinercjalnych

, konieczne jest uwzględnienie sił bezwładności

(pozornych),

np. obserwator w jadącym pociągu lub windzie (ruch postępowy),

siły odśrodkowej i Coriolisa (ruch obrotowy).

Zasady dynamiki Newtona spełnione są w układach

inercjalnych, tj. w układach poruszających się ruchem

jednostajnym

prostoliniowym

względem

układu

nieruchomego.

Siła

Miarą oddziaływania między ciałami jest

wielkość

wektorowa zwana siłą

:

jedn.

(N =

kgm/s

2

)

a

m

F







Masa ciała

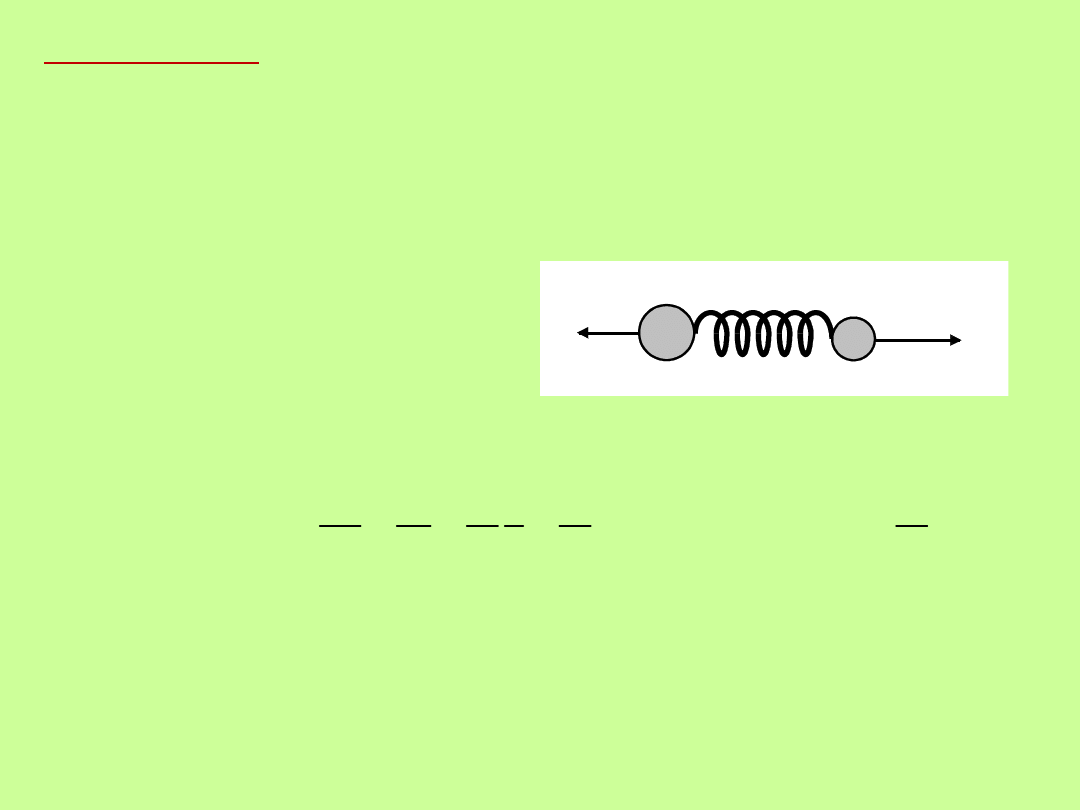
Gdy dwa ciała działają na siebie, to zmieniają nawzajem swój stan

ruchu; poruszają się w przeciwnych kierunkach z pewnymi

prędkościami (np. masy na sprężynie, m

0

- masa znana, m – masa

nieznana).

m

0

m

v

0

v

Nieznaną masę definiujemy jako:

v

v

m

m

const

v

v

v

t

t

v

a

a

m

m

a

m

ma

0

0

0

0

0

0

0

0

















Prędkość będzie tym większą, im mniejsza jest bezwładność ciała.

Dla danych dwóch ciał stosunek uzyskanych prędkości jest

wielkością stałą.

Tak zdefiniowaną wielkość m nazywaną

masą ciała

(jedn.

kg

).

Gęstość ciała

Gęstość ciała

ρ nazywamy stosunek jego masy m do objętości V:

Jednostka

(kg/m

3

)

.

V

m





Pęd ciała

Pęd ciała

definiujemy jako iloczyn jego masy m i prędkości v:

v

m

p







Tempo zmiany pędu ciała jest równe sile wypadkowej

działającej na to ciało.

dt

p

d

dt

v

m

d

a

m

F

czyli

m

F

a

wyp

wyp





















)

(

II zasada

Ciało, na które działają stałe siły, porusza się ruchem

jednostajnie przyspieszonym z przyspieszeniem a, którego

wartość i kierunek są określone stosunkiem siły wypadkowej F

do masy ciała m.

lub

a

m

dt

dm

v

dt

v

d

m

dt

dm

v

v

m

dt

d

F

const

m

gdy

a

m

dt

v

d

m

v

m

dt

d

dt

p

d

F

const

m

gdy













































)

(

)

(

II zasadę dynamiki Newtona można zapisać za pomocą pędu następująco:

układy o
stałej masie

Układy o
zmiennej masie
np. rakieta

III zasada

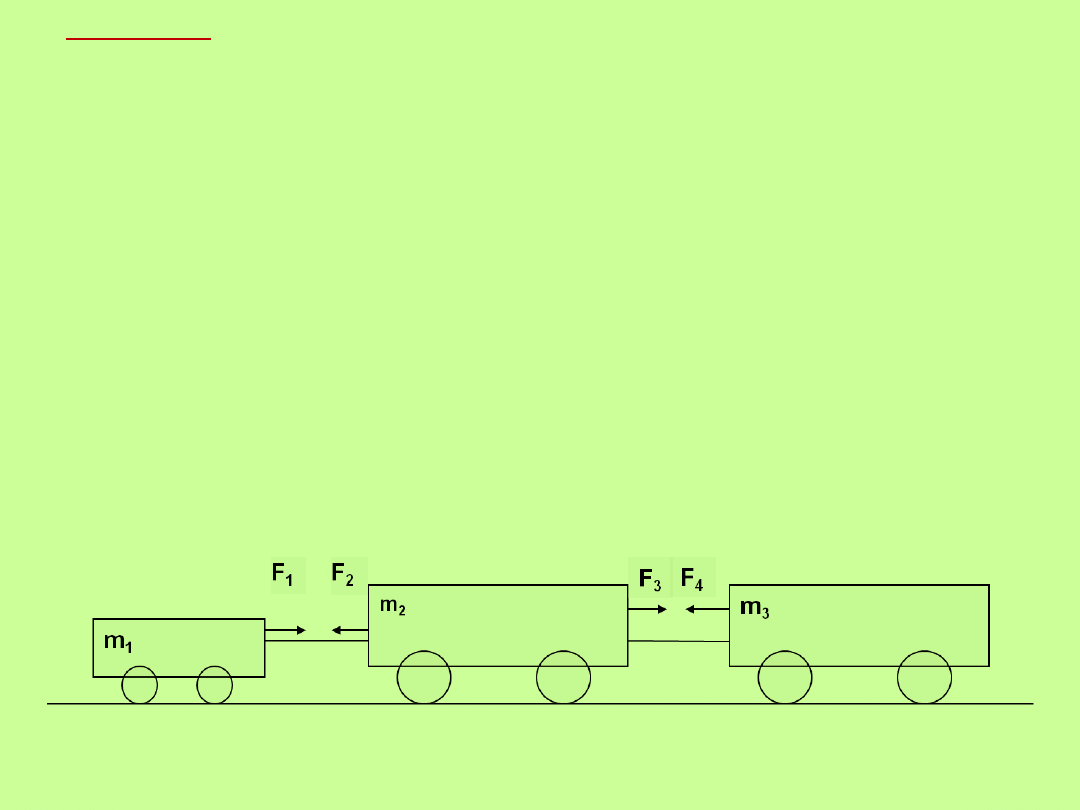
– PRAWO AKCJI I REAKCJI

Siły są zawsze wynikiem oddziaływania dwóch ciał. Dwa ciała

działają na siebie siłami równymi co do wartości i przeciwnymi

co do zwrotu.

lub

Gdy dwa ciała oddziałują wzajemnie, to siła wywierana przez ciało
drugie na ciało pierwsze jest równa i przeciwnie skierowana do siły
jaką ciało pierwsze działa na ciało drugie.

B

A

F

F









Rys.1

np. F

1

= -F

2

F

3

= -F

4

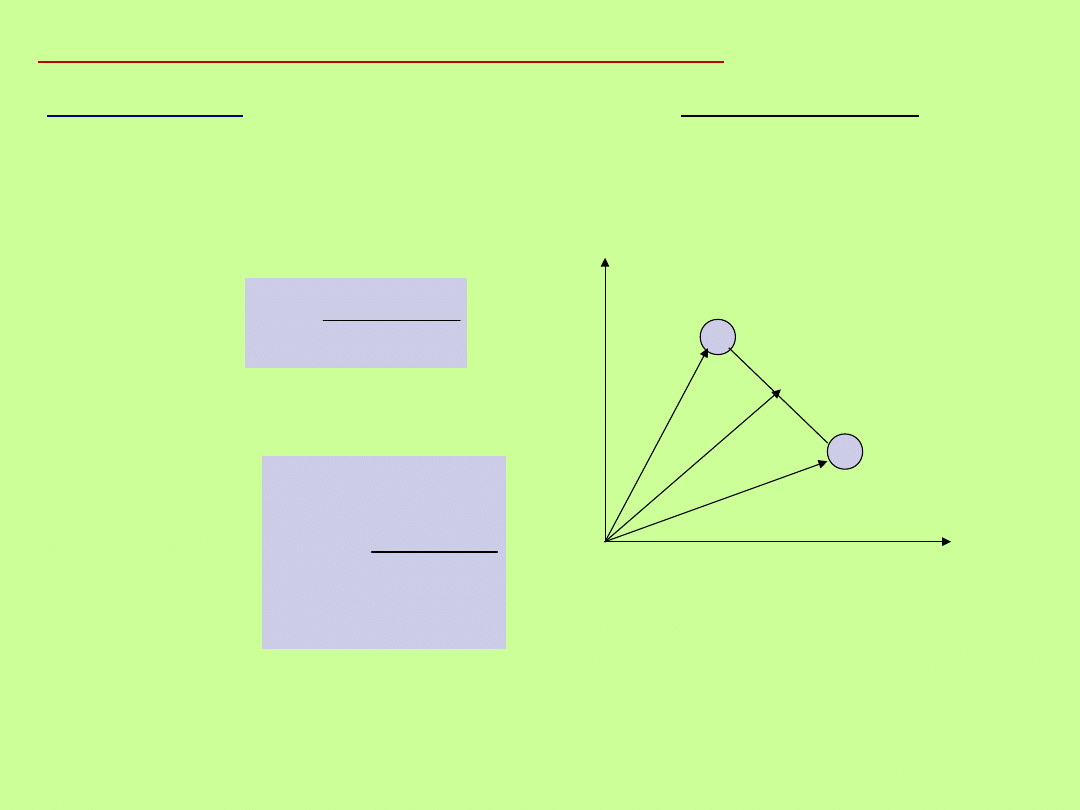
Ad. 2 Prawo ruchu i zachowania środka masy







i

i

i

i

i

śrm

m

r

m

r





r

i

– wektor wodzący i-tego punktu względem danego punktu

odniesienia
m

i

– masa i-tego punktu

r

śrm

– położenie środka masy

m

2

m

1

r

2

r

1

r

śrm

x

y

2

1

2

2

1

1

m

m

r

m

r

m

r

śrm









dla n – mas (m

i

)

Środek masy

układu punktów materialnych - średnie położenie, przy

czym masa jest czynnikiem ważącym (średnia ważona – wagami są

masy).

dla dwóch mas (n = 2)

Jeśli M = m

i

– masa całkowita











i

i

i

śrm

i

i

i

śrm

r

m

r

M

M

r

m

r









czyli

Środek masy

układu punktów materialnych zależy od mas tych

punktów i ich wzajemnego rozmieszczenia (nie zależy od wyboru
układu odniesienia).

i różniczkując to równanie dwukrotnie względem czasu, otrzymamy

Dla ciała o ciągłym rozkładzie masy wyrażenie opisujące środek masy ma postać:

dV

dm

m

V

gdzie

dV

dV

r

dm

dm

r

r

śrm

































ρ – gęstość ciała
r – jest odległością elementu masy dm ciała o ciągłej budowie od
wybranego początku układu





i

i

i

śrm

r

m

r

M





Korzystając z def. środka masy

i różniczkując to równanie dwukrotnie względem czasu, otrzymamy

dt

r

d

m

dt

r

d

M

i

i

i

śrm









2

2

2

2

dt

r

d

m

dt

r

d

M

i

i

i

śrm









stąd

Środek masy

układu punktów materialnych (ciała) porusza się w

taki sposób, jakby cała masa układu była skupiona w środku masy i

jakby wszystkie siły zewnętrzne nań działały.

Wprowadzamy duże uproszczenie zastępując ruch całego ciała

ruchem jego środka masy.

Prawo to obowiązuje dla każdego układu pkt. materialnych.

Gdy siłą zewnętrzną jest siła ciężkości, to wtedy działa ona na

środek ciężkości

.

W rozważanych przypadkach środki masy i ciężkości pokrywają się.

zew

i

i

i

śrm

F

a

m

a

M











Prawo ruchu środka masy

Prawo zachowania środka masy

Jeżeli suma sił zewnętrznych jest równa zeru czyli siły zewnętrzne
nie działają (układ izolowany), to położenie środka masy nie ulega
zmianie.

Układ odosobniony (zamknięty lub izolowany) - układ, na który nie
działają żadne siły zewnętrzne.

Całkowity pęd

układu punktów materialnych jest równy iloczynowi

całkowitej masy i prędkości środka jego masy.

Prawo zachowania pędu

- jeżeli wypadkowa sił zewnętrznych

działających na układ wynosi zero (F

zew

= 0), wtedy całkowity

pęd układu pozostaje stały.

const

P

wtedy

dt

P

d

dt

v

m

d

dt

v

d

m

a

m

F

zew

























0

)

(

1) Gdy mamy do czynienia z układem pkt. materialnych o masach m

1

…m

n

i

2) P – całkowity pęd układu pkt. - suma wektorowa pojedynczych

pędów

Zasada zachowania pędu

czyli

całkowity pęd układu odosobnionego jest wielkością stałą w
każdym czasie

.

śrm

v

M

P







const

v

m

p

P

i

i

i





















i

m

M

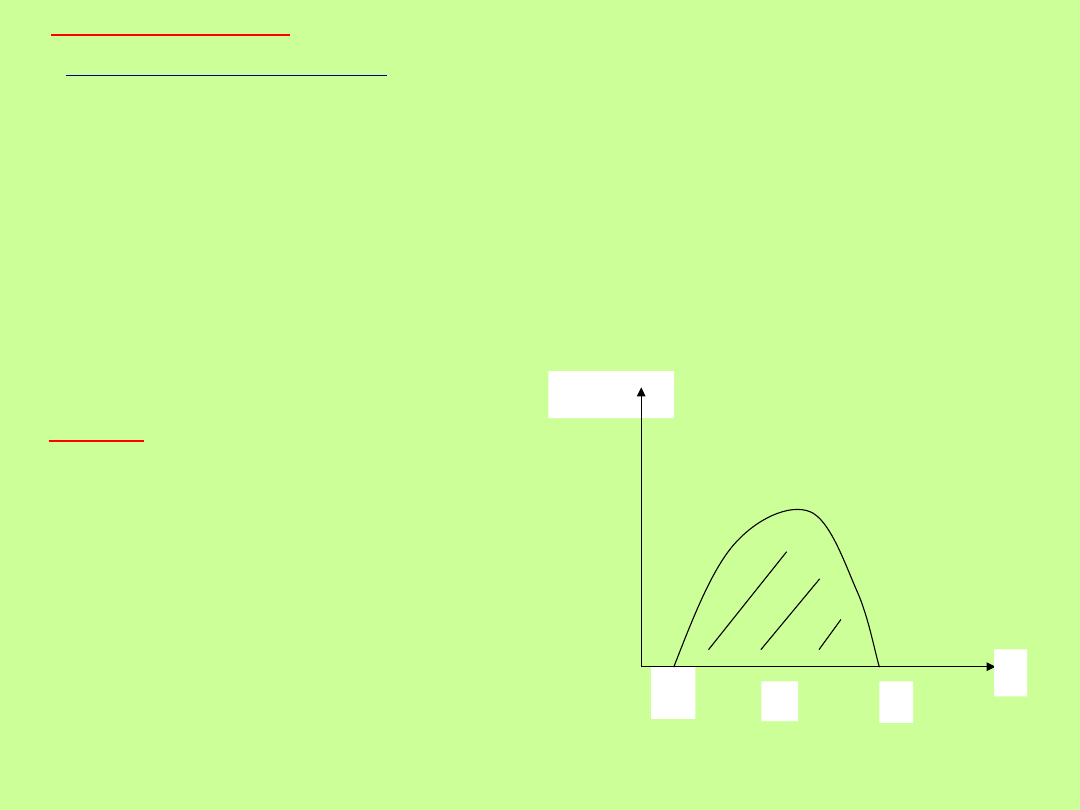
Popęd

Podczas zderzenia na każdy
punkt materialny działa wielka
siła, ale przez krótki czas (np. kij
uderzający w piłkę).

Siła ta zmienia się w czasie w
bardzo złożony sposób – siły
tego typu nazywamy

siłami

impulsowymi
(zderzeniowymi).

t

1

F(x)

t

t

2

∆t

Ad. 4 Zderzenia

Klasyfikacja zderzeń:

-

elastyczne

(sprężyste) – gdy energia kinetyczna jest

zachowana

w

zderzeniu

-

nieelastyczne

– ozn., że początkowa energia kinetyczna jest

tracona

podczas zderzenia.

Na podstawie II zasady dynamiki

dt

F

p

d

F

dt

p

d















)

0

(

2

1

2

1

1

2

























t

const

F

dla

dt

F

p

d

p

p

p

t

t

p

p













Popęd siły

- zmiana (przyrost) pędu ciała.

Miara popędu siły - powierzchnia zawarta pod krzywą

(całka).

t

F

p

















Prawo pędu i popędu

Suma wszystkich sił zewnętrznych działających na poszczególne

punkty układu jest równa pochodnej całkowitego pędu układu

względem czasu















i

i

i

i

zew

zew

v

m

p

P

f

F

gdy

dt

P

d

F









,

Ruchem układu punktów materialnych ciał rządzą prawa:

- ruchu środka masy

- zachowania środka masy

- pędu i popędu.