4.2.4. Rozkład Weibulla

Rozkład Weibulla jest jednym z wniosków statystycznej teorii wartości ekstremalnych

[2]. Jest to jeden z najbardziej elastycznych - jeśli nie najelastyczniejszy - rozkład

statystyczny. Oznacza to, że może zastąpić wiele innych popularnych dotąd rozkładów.

Szczególną zaletą tego rozkładu jest posiadanie dolnej lub górnej granicy dziedziny zmiennej

losowej. Istnienie granicy dolnej jest nieocenioną właściwością przy rozpatrywaniu wszelkich

zagadnień wytrzymałościowych czy to mechanicznych czy elektrycznych. Dystrybuanta

rozkładu Weibulla w wersji dostosowanej do zagadnień wytrzymałości elektrycznej ma

postać:





















































0

0

0

0

exp

1

0

)

(

X

x

dla

X

X

X

x

X

x

dla

x

F

k

m

gdzie:
X

0

- parametr przesunięcia [próg wytrzymałości F(X

0

) = 0] wyrażony w jednostkach

zmiennej losowej;

X

m

- parametr skali [F(X

m

)= 1 - e

-1



0.632] wyrażony w jednostkach zmiennej losowej;

k - bezwymiarowy parametr kształtu.

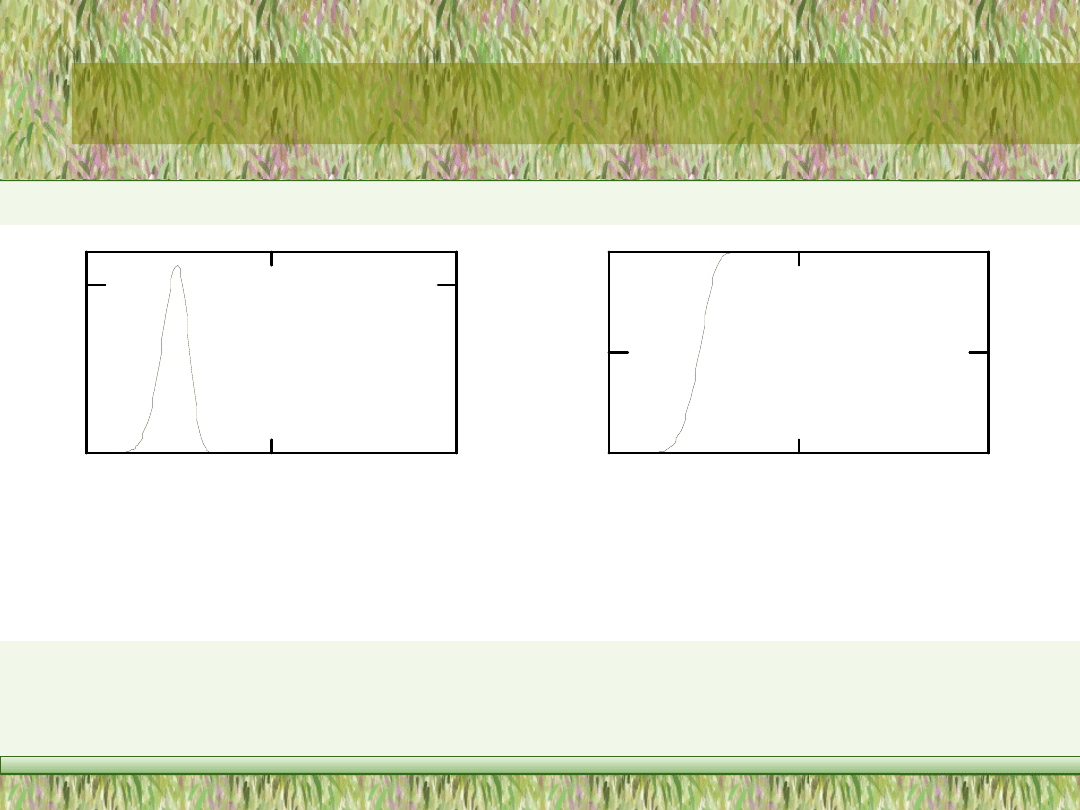
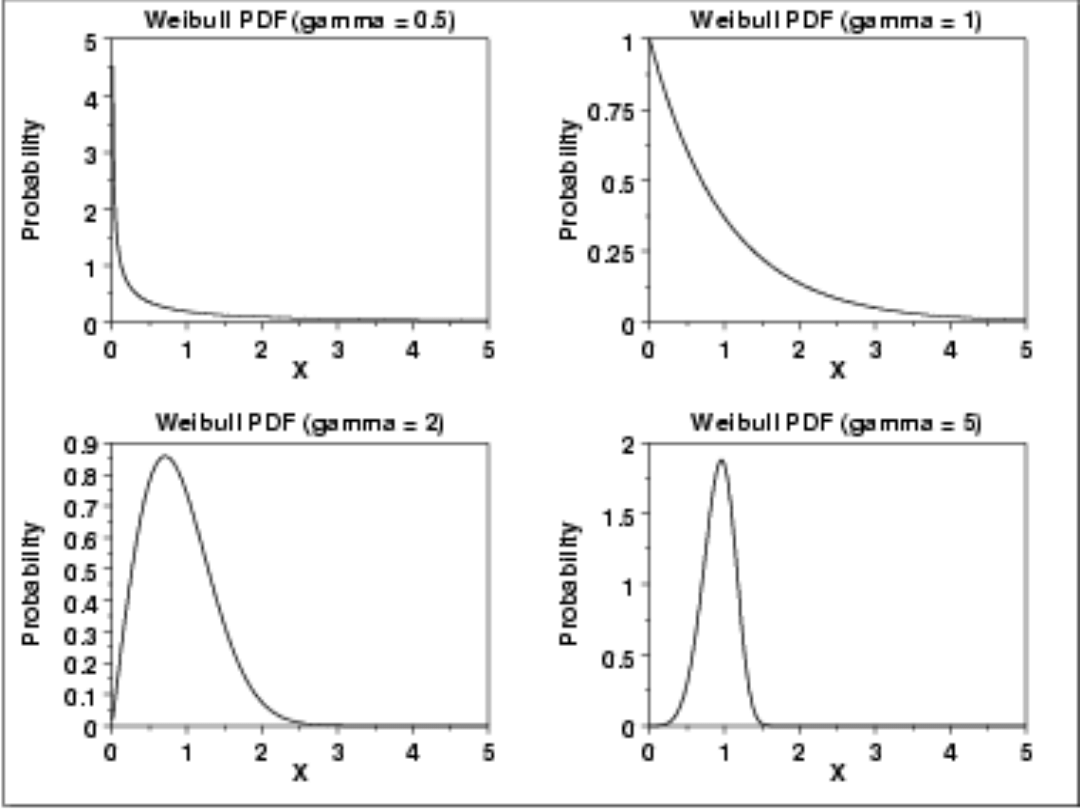
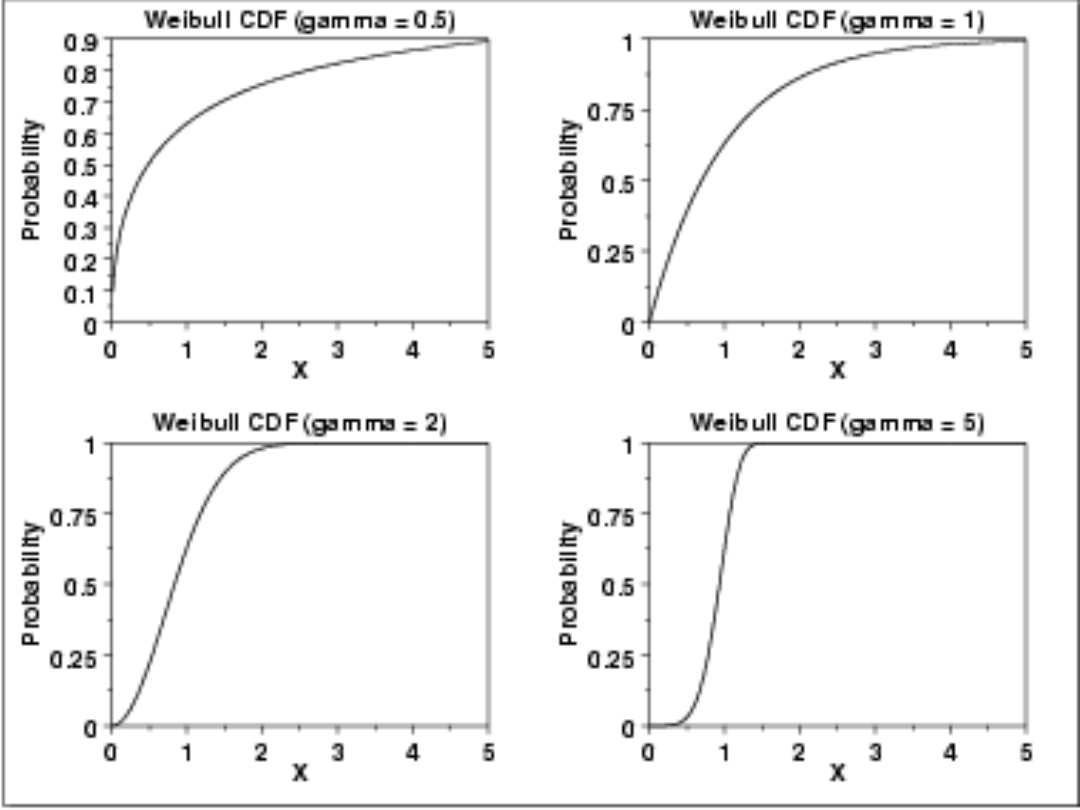
Przykłady funkcji gęstości i dystrybuanty rozkładu Weibulla dla różnych parametrów

kształtu pokazano odpowiednio na rys. 4.15 i 4.16.

0

100

200

0

0.05

0

100

200

0

0.5

1

R

y

s

. 4

.1

5

. F

u

n

k

c

je

g

ę

s

to

ś

c

i r

o

z

k

ła

d

u

W

e

ib

u

lla

d

la

tr

ze

c

h

p

a

r

a

m

e

tr

ó

w

k

s

z

ta

łtu

k

=

1

(lin

ia

p

r

z

e

r

y

w

a

n

a

d

łu

g

a

), 3

.5

(lin

ia

p

r

z

e

r

y

w

a

n

a

k

r

ó

tk

a

), 6

(lin

ia

c

ią

g

ła

).

R

y

s

. 4

.1

6

. D

y

s

tr

y

b

u

a

n

ty

r

o

z

k

ła

d

u

W

e

ib

u

lla

d

la

tr

z

e

c

h

p

a

r

a

m

e

tr

ó

w

k

s

zta

łtu

k

=

1

(lin

ia

p

r

z

e

r

y

w

a

n

a

d

łu

g

a

), 3

.5

(lin

ia

p

r

ze

r

y

w

a

n

a

k

r

ó

tk

a

), 6

(lin

ia

c

ią

g

ła

).

Wprowadzając przekształcenie:

0

0

X

X

X

X

Z

m







uzyskuje się rozkład zredukowany do postaci:

0

)

exp(

1

)

(









z

dla

z

z

F

k

Dla k = 1 rozkład powyższy, a więc i rozkład Weibulla w postaci pierwotnej, jest funkcją

wykładniczą, czyli bardzo ważny - wykorzystywany szeroko w teorii niezawodności - rozkład

wykładniczy jest szczególnym przypadkiem rozkładu Weibulla. Jeśli k = 2 oraz X

0

= 0 to

uzyskuje się funkcję zwaną rozkładem Rayleigha.

Ponieważ dziedzina zmiennej losowej rozkładu Weibulla o postaci danej powyższym

wzorem jest ograniczona lewostronnie a nieograniczona prawostronnie to rozkład jest

asymetryczny. Jednakże usytuowanie względem siebie miar wartości centralnych: mediany,

mody i wartości oczekiwanej (średniej) oraz znak trzeciego momentu (określającego

asymetrię) zmieniają się w funkcji parametru kształtu k. W związku z tym istnieją przypadki

pseudosymetrii rozkładu gdy „wydaje się”, że jest on symetryczny. W tablicy 4.1 zestawiono

parametry charakteryzujące rozkład Weibulla. W tablicy 4.2 zestawiono wartości

zredukowanych miar wartości centralnych z tablicy 4.1 dla tych wartości k, dla których dwie

lub trzy z nich są sobie równe i gdy zanika trzeci moment centralny (zanika asymetria).

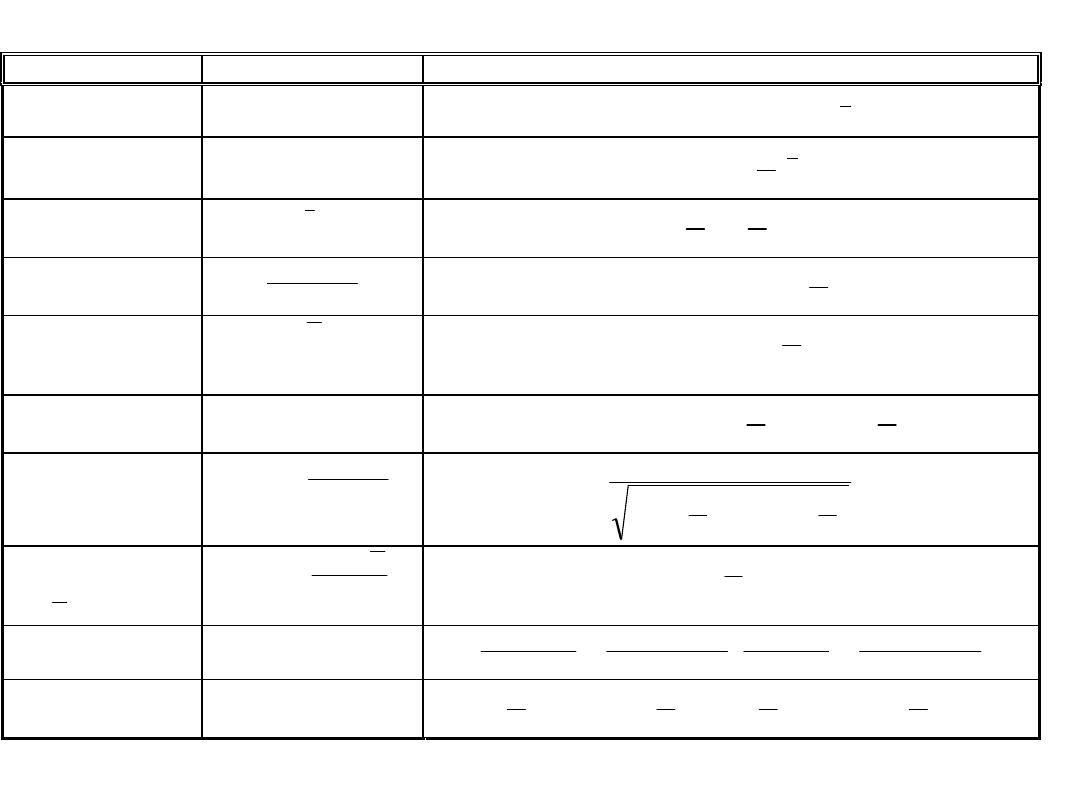
T a b e l a 4 . 1
P a r a m e t r y z w i ą z a n e z r o z k ł a d e m W e i b u l l a

P a r a m e t r

S y m b o l

W z ó r

M e d i a n a



X

X

X

X

m

k

0

0

1

2







(

) ( l n )

M o d a

~

X

X

X

X

k

d l a

k

m

k

0

0

1

1

1

1





 



(

) (

)

Z r e d u k o w a n y
m o m e n t r z ę d u l

z

l

l

k

l

k

  ( )

M o m e n t r z ę d u l

(

)

x

X

l



0

(

)

(

)

X

X

l

k

m

l







0

1



P i e r w s z y
m o m e n t
( ś r e d n i a )

X

X

X

X

l

k

d l a l

m

0

0

1

1











(

)

(

)



W a r i a n c j a



2

(

)

[ (

)

(

) ]

X

X

k

k

m











0

2

2

1

2

1

1





S t a n d a r y z o w a n a
r ó ż n i c a o d X

m

d o X

0

B k

X

X

m

( ) 



0



1

1

2

1

1

2





(

)

(

)







k

k

S t a n d a r y z o w a n a
r ó ż n i c a o d X

m

d o

X

A k

X

X

m

( ) 





)

(

1

1

1

)]

(

[

k

B

k









T r z e c i m o m e n t
c e n t r a l n y



3

(

)

(

)

(

)

(

)

x

X

x

X

x

X

x

X



















0

3

0

2

0

0

3

3

2

W s p ó ł c z y n n i k
a s y m e t r i i



[ (

)

(

)

(

)

(

) ]

( )









1

3

3

1

2

1

1

2

1

1

2

3

3





















k

k

k

k

B

k

U w a g a :

 ( )

z

x

e

d x

z

x















1

0

j e s t f u n k c j ą G a m m a - E u l e r a ; z - l i c z b a r z e c z y w i s t a .

T a b l i c a 4 . 2 .

C z t e r y p s e u d o s y m e t r y c z n e p r z y p a d k i r o z kł a d u W e i b u l l a

W a r u n e k

P a r a m e t r

M e d i a n a

M o d a

Ś r e d n i a

W s p ół c z y n n i k

s k oś n o ś c i

k

1 / k

z

~z

z



z

=

~z

3 . 2 5 8 8 9

0 . 3 0 6 8 5

0 . 8 9 3 6 3

0 . 8 9 3 6 3

0 . 8 9 6 4 6

0 . 0 9 3 5 0

~z

=

z

3 . 3 1 1 2 5

0 . 3 0 1 8 9

0 . 8 9 5 2 5

0 . 8 9 7 1 9

0 . 8 9 7 1 9

0 . 0 7 4 4 7

z

=

z

3 . 4 3 9 3 8

0 . 2 9 0 7 5

0 . 8 9 8 9 2

0 . 9 0 4 9 4

0 . 8 9 8 9 2

0 . 0 4 0 5 7

 = 0

3 . 6 0 2 3 2

0 . 2 7 7 6 0

0 . 9 0 3 2 6

0 . 9 1 3 6 9

0 . 9 0 1 1 4

0 . 0 0 0 0 0

U w a g a :

O d p o w i e d n i e

w a r t oś c i

w y r a ż o n e

w

j e d n o s t k a c h

z m i e n n e j

l o s o w e j

u z y s k u j e

s i ę

z

w z o r u :





(

 )

x

z X

z

X

m

 







1

0

Jak wynika z tablicy 4.2, gdy dwie z wartości centralnych mają tę

samą wartość to trzecia różni się od nich nieznacznie. Podobnie wówczas
gdy współczynnik asymetrii jest równy zeru to wszystkie trzy miary
wielkości centralnych mają wartości zbliżone. We wszystkich tych
przypadkach rozkład „wydaje się” być symetryczny. Ogólnie wrażenie
symetrii rozkładu Weibulla jest zachowane jeśli parametr kształtu jest
zawarty w przedziale 3.2 < k < 3.7. W przedziale tym rozkład Weibulla
jest „podobny” do rozkładu normalnego i z powodzeniem może rozkład
normalny zastąpić, eliminując jego wady takie jak nieograniczoność
dziedziny zmiennej losowej. W ten sposób zachowując zgodność
rozkładu zmiennej losowej z dotychczas obserwowaną jego
normalnością można uzyskać zgodność teorii statystycznej z fizyką
zjawisk. Na rys.4.17 wykreślono rozkłady Weibulla o parametrach
kształtu k = 3.27 i k = 3.445 w normalnej (Gaussowskiej) siatce
prawdopodobieństwa. Na takiej siatce dystrybuanta rozkładu normalnego
jest linią prostą (o siatkach funkcyjnych rozkładów statystycznych
będzie mowa w następnym rozdziale).

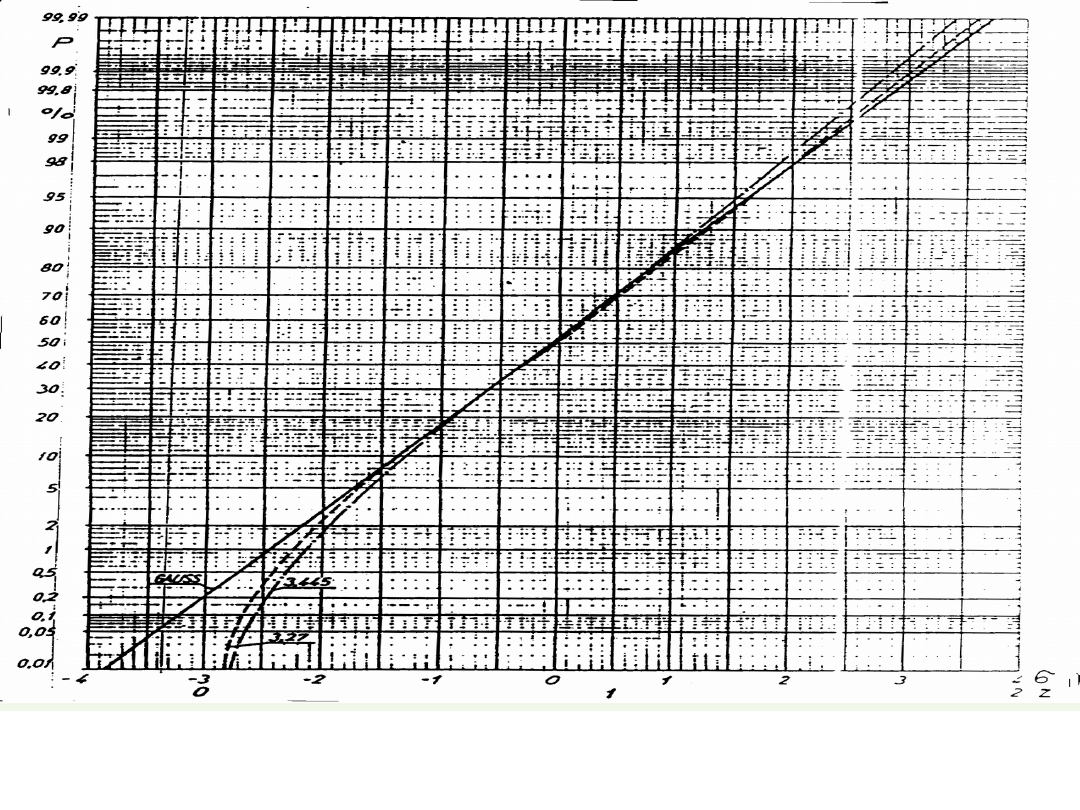
Rys. 4.17. Dystrybuanta rozkładu normalnego (linia prosta) i dystrybuanty rozkładu Weibulla

o parametrach kształtu k = 3.27 i k = 3.445 wykreślone w normalnej (Gaussowskiej) siatce

prawdopodobieństwa.

Jak widać rozkłady Weibulla niewiele odbiegają od
rozkładu

normalnego i to jedynie w zakresie

prawdopodobieństw poniżej 10%, który to zakres jest
stosunkowo trudny do weryfikacji eksperymentalnej.
Minimalne różnice między rozkładami Gaussa i Weibulla
stanowią, że w oparciu o ograniczoną liczbę obserwacji
zmiennej losowej, trudno jest dokonać wyboru rozkładu
przy zastosowaniu jedynie statystycznych kryteriów.
Wybór powinien w takich przypadkach być dodatkowo
wsparty argumentami wynikającymi ze znajomości
fizycznych właściwości badanego zjawiska. Przykładowo
aby zniszczyć mechanicznie element maszyny potrzebna
jest siła większa od zera, lub aby nastąpiło przebicie
elektryczne izolacji konieczne jest napięcie większe (co
do wartości bezwzględnej) od zera. W obu przypadkach, z
fizyki zjawisk wynika, że istnieje progowa, różna od zera,
wartość zmiennej losowej (siły czy napięcia). Zatem
rozkład Weibulla będzie lepszym narzędziem nawet
wówczas gdy do tej pory posługiwano się - z dobrym
wynikiem - rozkładem normalnym. Rozkład Weibulla jest
bowiem w zgodzie z fizyką zjawisk.

Jeżeli przyjąć za kryterium, że dla wartości

średniej prawdopodobieństwo ma wynosić 0.5
(50%) to rozkład Weibulla odpowiadający
rozkładowi normalnemu ma parametr kształtu k
= 3.5. Ten rozkład najczęściej stosuje się jako
pokrywający się praktycznie z rozkładem
normalnym w zakresie dostępnym do obserwacji
eksperymentalnych. Jest to rozkład o średniej
bliskiej medianie (tab. 4.2) i o bardzo małym
współczynniku asymetrii





0.04.