Jądro atomowe

Jądro atomowe charakteryzuje się dodatnim ładunkiem
elektrycznym. Wartość liczbowa tego ładunku Z stanowi
wielokrotność bezwzględnej wartości ładunku elektronu
Q = Ze; wiel kość Z, zwana liczbą atomową (liczbą
ładunku),

równa

się

numerowi

porządkowemu

pierwiastka w układzie okresowym Mendelejewa.

Inną cechę charakterystyczną jądra atomowego stanowi
jego masa m

j

. Jest ona związana z masą atomową

pierwiastka. W rzeczywistości większość pierwiastków
ma po kilka izotopów, tj. po kilka rodzajów atomów o
różnych masach przy tej samej liczbie atomowej Z.

Większość pierwiastków chemicznych występuje w
postaci dwu lub większej liczbie typów atomów,
różniących się między sobą liczbą atomów w jądrze.

Wyróżniamy np. trzy typy atomów wodoru (H), pięć
typów atomów węgla (C) oraz 16 typów ołowiu (Pb) .
Te różne typy atomów jednego i tego samego pierwiastka
nazywane są IZOTOPAMI (isos = równy, topos =
miejsce), ponieważ zajmują one to samo miejsce w
układzie okresowym pierwiastków

.

Wszystkie izotopy danego pierwiastka mają taką samą
liczbę protonów, lecz różnią się liczbą neutronów w
jądrze.

Aczkolwiek izotopy danego pierwiastka mają takie same
właściwości chemiczne, można je rozróżnić stosując
właściwości fizyczne.

Niektóre są radioaktywne, wobec tego można je
wykrywać

i

określić

ilościowo

na

podstawie

intensywności promieniowania.

Inne

izotopy

można

rozróżniać

na

podstawie

nieznacznych różnic w masie atomowej spowodowanych
obecności dodatkowego neutronu w jądrze.

Przez masę atomową M jakiegoś czystego izotopu danego
pierwiastka będziemy rozumieć stosunek masy m

M

jego

atomu do 1/16 m

0

, gdzie m

0

oznacza masę najbardziej

rozpowszechnionego (a zarazem najlżejszego) izotopu
tlenu.

Masę atomową tego izotopu tlenu przyjmuje się w ten
sposób za równą 16,00000. Określone w ten sposób masy
atomowe czystych izotopów wyznacza się przy pomocy
pomiarów na spektrografie masowym.

Wartość bezwzględna (w gramach) masy izotopu tlenu o
masie ato mowej M = 16 można wyznaczyć, znając jego
masę cząsteczkową  (równą 16) i liczbę Avogadra,

m

0

= /N = 16.00/6.023 x 10

23

= 26.576 x 10

-27

[kg]

Jednostce masy atomowej odpowiada masa:

26.576 x 10

-24

/ 16 = 1.662 x 10

-27

[kg]

jest to tzw. jednostka masy atomowej.

Stad wartość bezwlędna masy m

M

atomu danego izotopu

wyznacza się ze wzoru:

m

M

= 1.662 x 10

-27

M [kg]

Ponieważ masa elektronu jest prawie dwa tysiące razy
mniejsza od masy jądra, więc masa jądra m

j

dowolnego

izotopu niewiele różni się od masy całego atomu m

M

.

m

e

= 9.31 x 10

-31

kg

Ponieważ E = mc

2

i biorąc pod uwagę zależności

powyższe możemy określić zależność, że jednostka masy
równoważna jest 931 MeV energii; znajomość tej
wielkości pozwala nam przeliczać bilanse masy na
bilanse energii i odwrotnie

PROMIENIOWANIE

JONIZUJĄCE

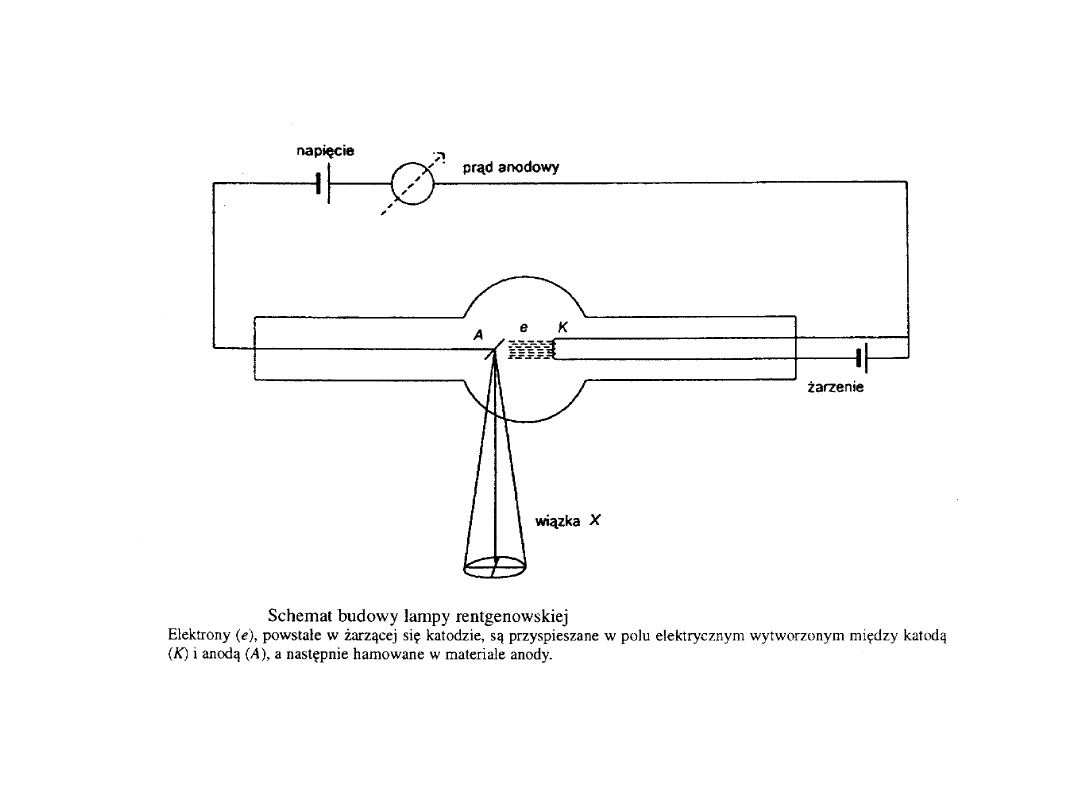
POWSTAWANIE PROMIENIOWANIA

RENTGENOWSKIEGO

E = eU

min

max

c

h

h

eU









eU

hc

min





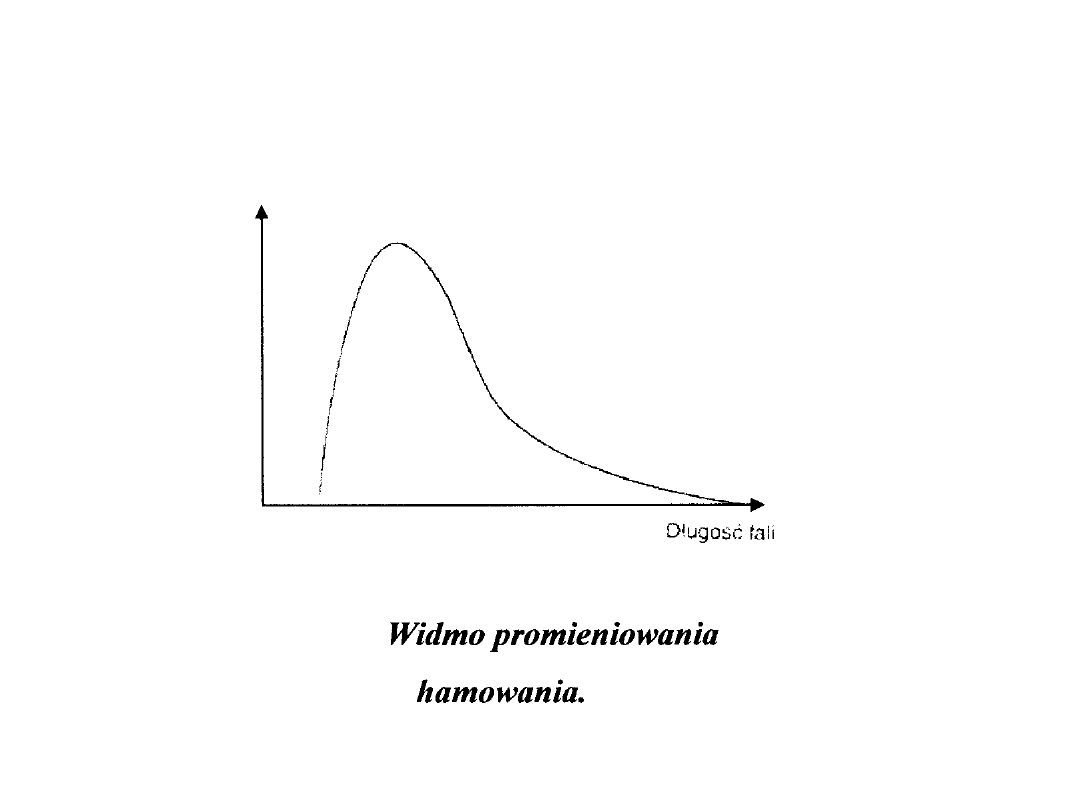
WIDMO PROMIENIOWANIA X

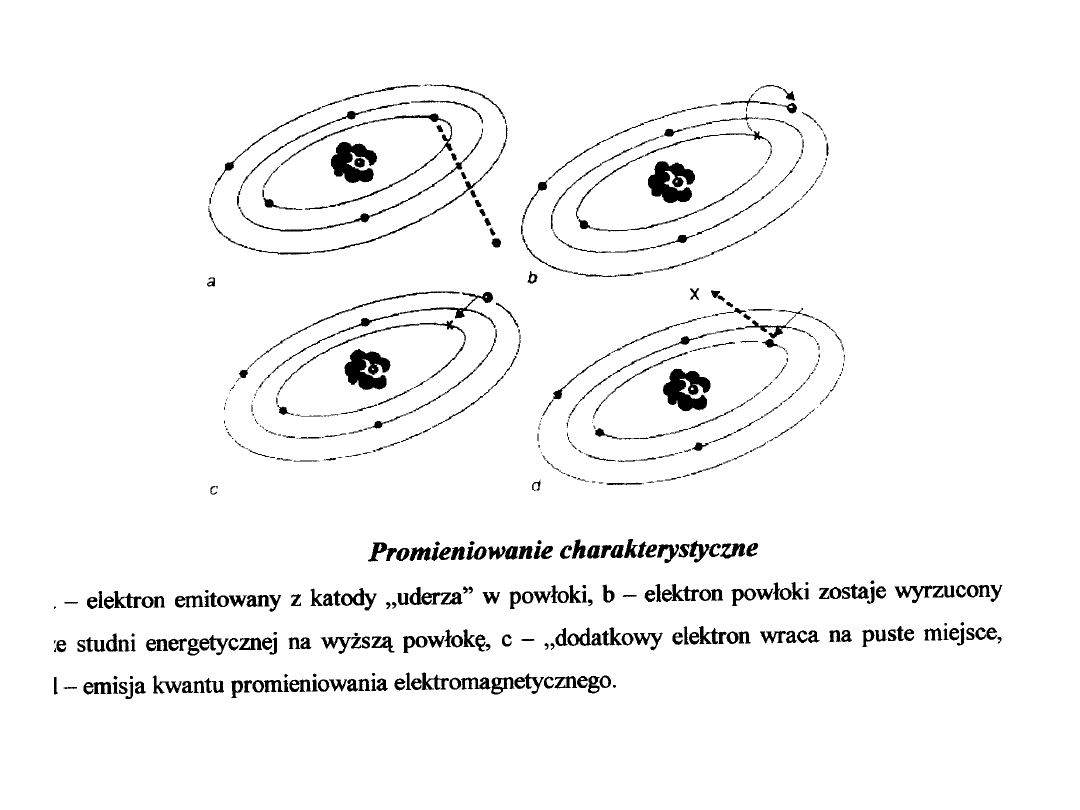
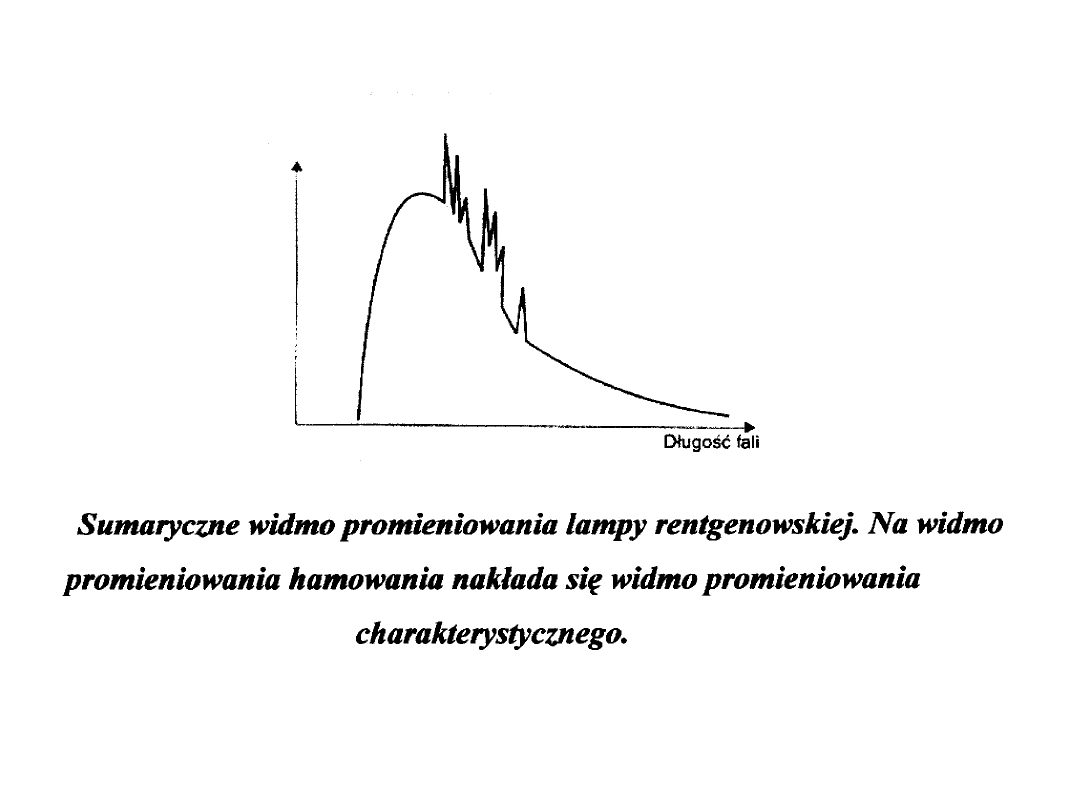
WŁASNOŚCI PROMIENIOWANIA X

d

-

0

e

I

I





I

x

= A Z I

a

U

2

a

I

x

– strumień fotonów prom. X;

A – stała zależna od konstrukcji lampy;
Z - liczba atomowa materiału tarczy;
I

a

- natężenie prądu anodowego;

U

a

- napięcie na lampie rentgenowskiej.

 

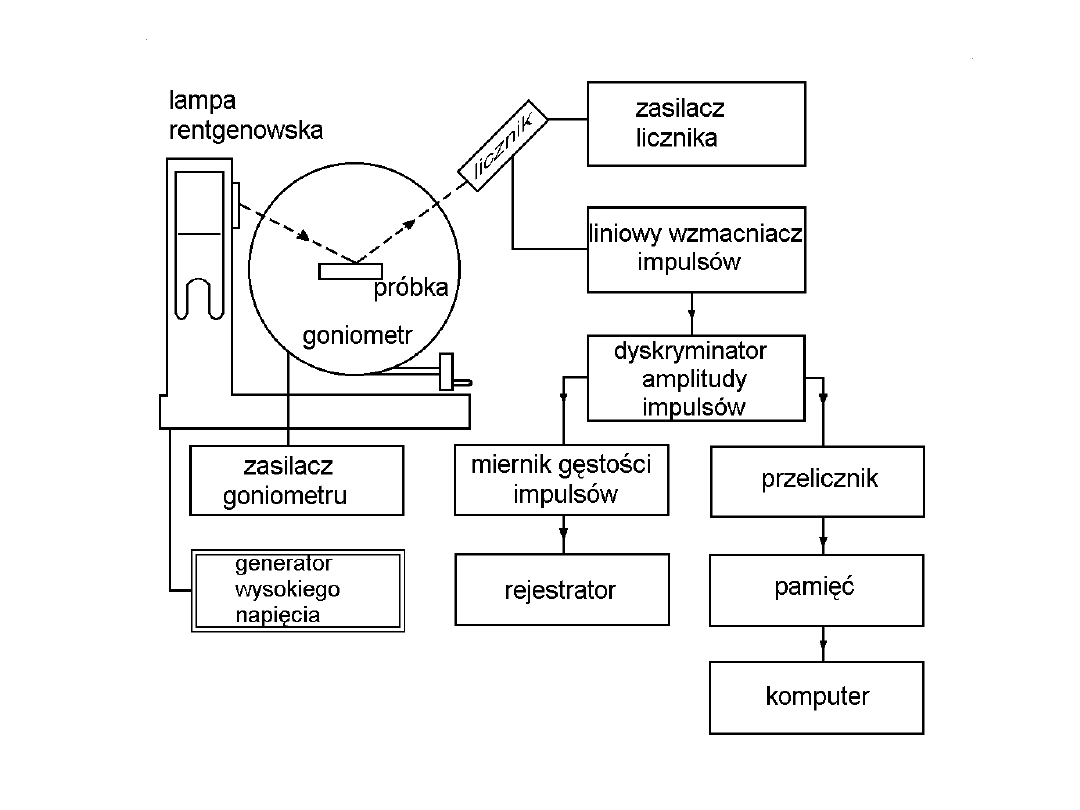
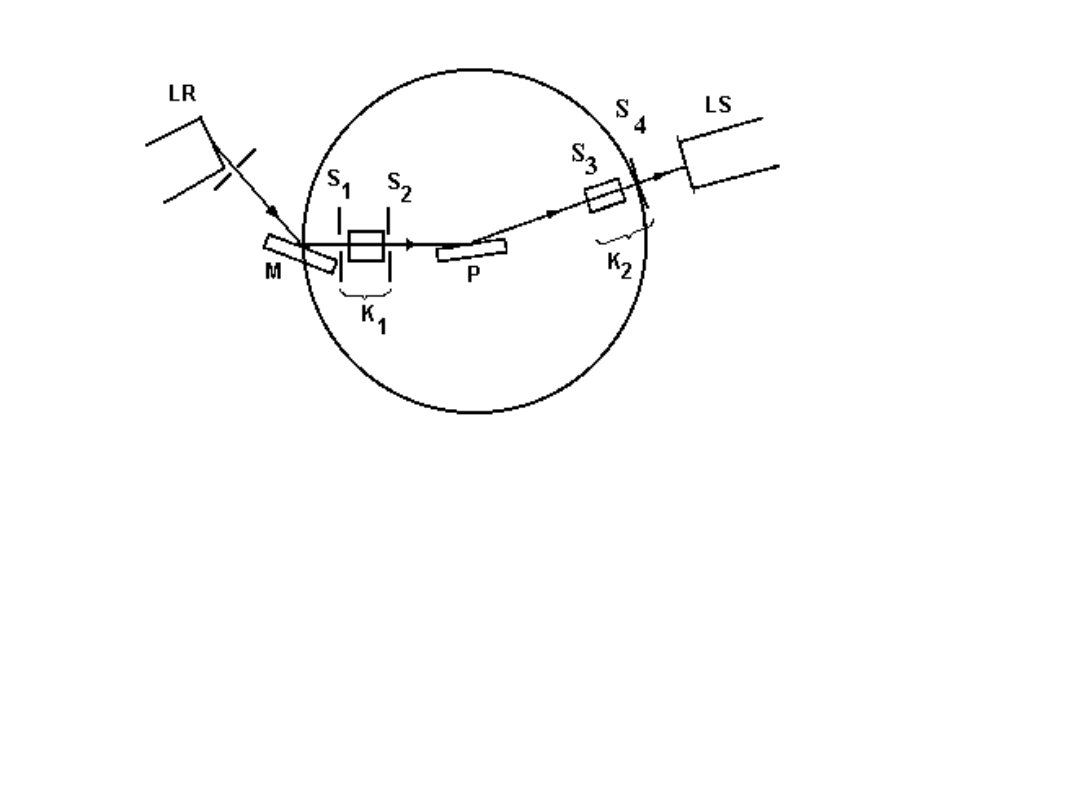
LR

- lampa rentgenowska,

K

1

- kolimator wiązki pierwotnej,

K

2

- kolimator wiązki wtórnej,

M

- monochromator grafitowy,

LS

- licznik scyntylacyjny,

P

- badana próbka,

S

1

, S

2

, S

3

, S

4

- szczeliny.

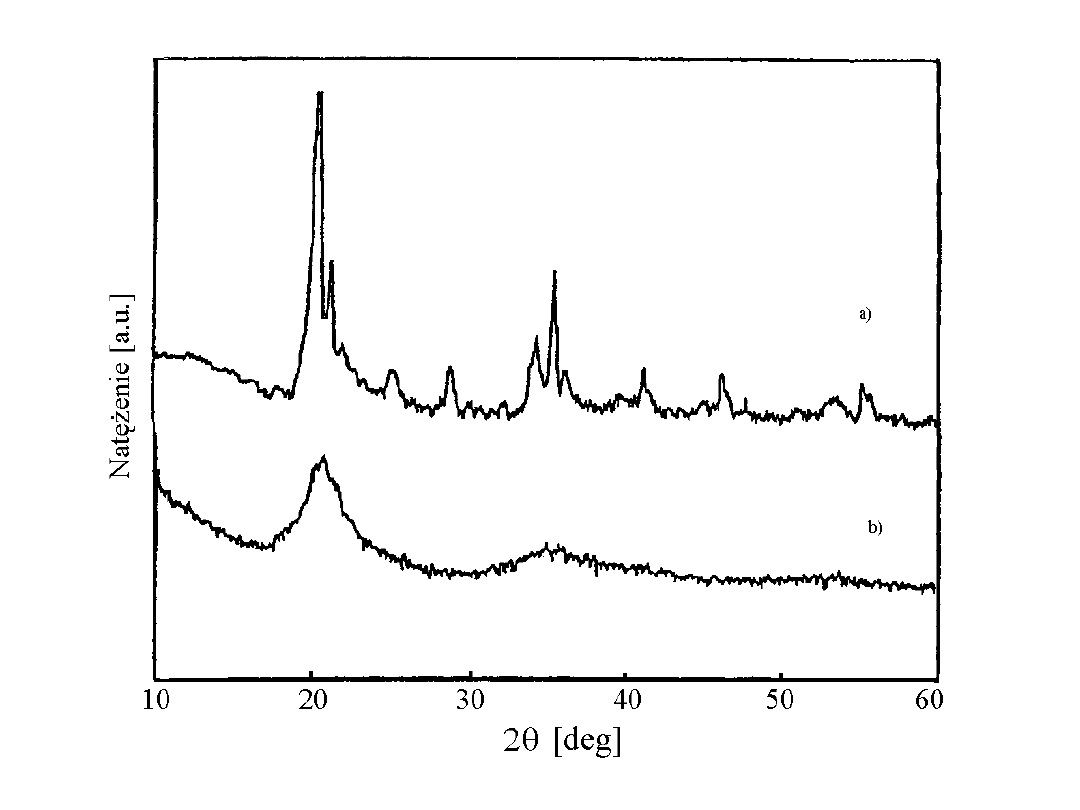
PROMIENIOTWÓRCZOŚĆ

NATURALNA

W roku 1896 francuski fizyk, A. Becquerel, badając sole
uranu stwierdził, że emitują one niewidzialne promienie,
wywołujące zaczernienie kliszy fotograficznej. Badanie
promieni uranu w polu magnetyczym wykazało, że
występują w nich trzy składowe.

Jedna odchyla się w polu magnetycznym tak, jak
powinien odchylić się strumień cząstek naładowanych
dodatnio. Składową tę nazwano promieniami a.

Druga składowa odchyla się jak strumień cząstek
naładowanych ujemnie, a trzecia — w ogóle nie doznaje
odchylenia w polu magnetycznym. Te składowe nazwano
odpowiednio promieniami  i .

Dwa lata później Pierre Curie i Maria Curie-Skłodowska
odkryli; dwa nowe pierwiastki rad i polon wysyłające
promieniowanie analogiczne do promieniowania uranu,
ale o większym natężeniu. Odkryli oni ponadto, że
własności promieniotwórcze wykazuje znany dawniej
pierwiastek tor.

Dalsze badania wykazały, że odkryte promieniowanie:

a) może

wywoływać

działanie

biologiczne

i

chemiczne, w szczególności zaczernienie kliszy
fotograficznej,

b) jonizuje gazy,

c) wzbudza luminescencję licznych ciał stałych i

ciekłych,

d) jest bardzo przenikliwe

.

Najbardziej przenikliwe są promienie , przenikają one

przez grube warstwy ciał stałych, zatrzymywane są
dopiero przez ciężkie metale takie jak ołów.

Najmniej przenikliwe są promienie , ale i one mogą

przenikać przez cienkie warstwy ciał stałych, całkowicie
są pochłaniane przez 2-3 milimetrową warstwę papieru.

Promieniowanie , jest praktycznie monoenergetyczną

wiązką

elektronów,

jest

średnio

przenikliwym

promieniowaniem, które praktycznie może być całkowicie
zaabsorbowane przez kilku milimetrową warstwę
lekkiego metalu np. aluminium.

PRAWO ROZPADU

PROMIENIOTWÓRCZEGO

Jeśli

m

0

oznacza

masę

pierwotną

pierwiastka

promieniotwórczego, to empirycznie prawo zaniku tej
ilości z czasem ma postać:

m = m

0

e

t

gdzie  jest stałą rozpadu promieniotwórczego.

Prawo to łatwo można objaśnić, jeśli przyjąć, że liczba
atomów —dN, rozpadających się w czasie dt jest
proporcjonalna do liczby wszystkich atomów:

 dN =  N dt

Biorąc pod uwagę liczbę atomów pierwiastka
promieniotwórczego:

N = N

0

e

-t

Całkowanie prowadzi do wzoru:

lnN =  t + C

gdzie C jest stałą całkowania.

To ostatnie równanie możemy zapisać w postaci:

dN/N =  dt

Dla (t = 0) mamy lnN

0

= C,

gdzie N

0

jest pierwotną liczbą atomów

.

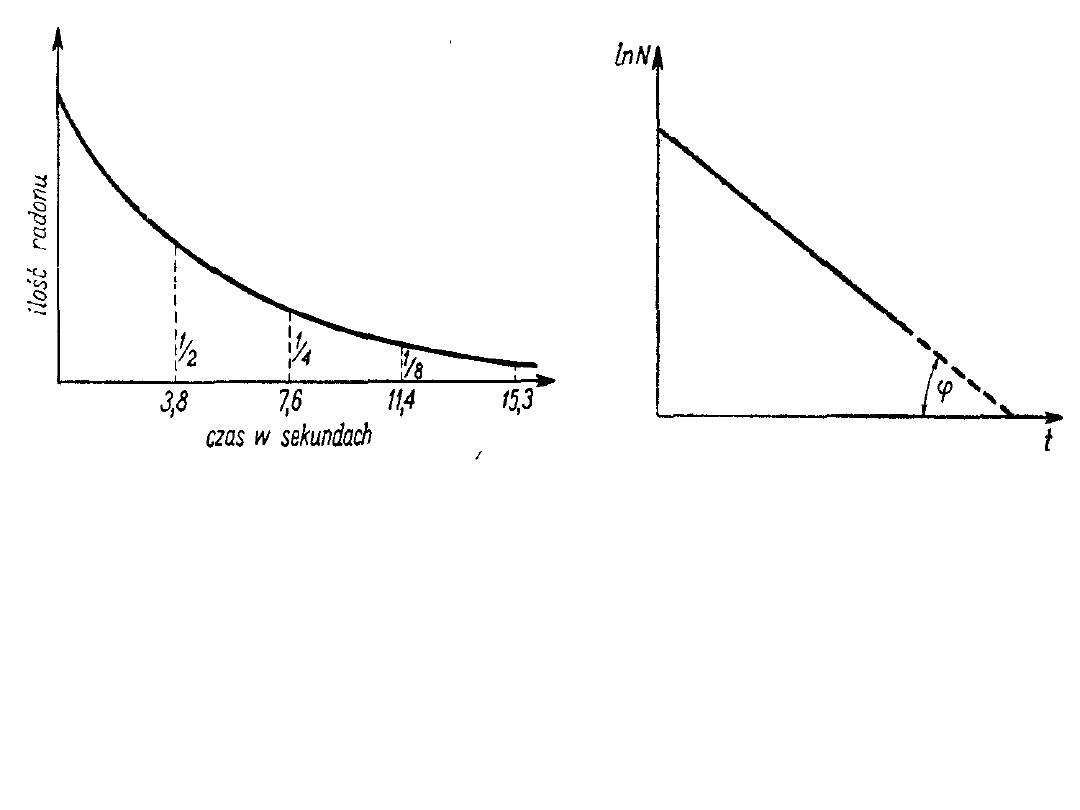
Krzywa rozpadu radonu Krzywa

zależności ln N od czasu

Korzystając z otrzymanej wartości C (lnN

0

= C), możemy

napisać, że:

lnN/N

0

=  t lub N = N

0

e

 t

Prawo rozpadu jest słuszne dla wszystkich
pierwiastków promieniotwórczych.

Stałą rozpadu  łatwo możemy powiązać z czasem

połowicznego zaniku T

1/2

.

Zgodnie z definicją dla t = T

1/2

mamy N = ½ N

0

, a stąd

po uwzględnieniu:

N = N

0

e

 t

otrzymamy:

½

=

e

 t

Logarytmując to wyrażenie uzyskamy:

 T

1/2

= ln2

a więc

T

1/2

= ln2/ = 0.693/

Drugą

ważną

wielkością

charakteryzującą izotop

promieniotwórczy jest aktywność izotopu A.

A = dN/dt

Jednostką aktywności w układzie SI jest

1Bq = 1 rozpad/s.

Ponadto używa się także jednostki Kiur [Ci]:

1 Ci = 3.7 x 10

10

rozpadów/s

RAZPADY PROMIENIOTWÓRCZE.

REGUŁA PRZESUNIĘĆ

Rozpad promieniotwórczy, odbywa się zgodnie z prawem
zachowania

ładunków

elektrycznych

i

prawem

zachowania energii całkowitej.

W myśl pierwszego z tych praw - suma ładunków
powstających cząstek równa się ładunkowi jądra
wyjściowego.

Drugie prawo można zapisać w następujący sposób:

jeśli m

j

oznacza masę jądra wyjściowego, a m

i

masę

powstających cząstek:

2

i

j

c

E

m

m







gdzie E jest ilością energii, która wydzieliła się podczas
rozpadu,
c zaś — prędkością światła w próżni.

Ponieważ w zjawisku promieniotwórczości naturalnej E
odpowiada masie

(E = mc

2)

,

wyrażającej się niewielkim

ułamkiem jednostki masy atomowej, więc z równania
wynika, że
suma liczb masowych powstających cząstek równa się
liczbie masowej jądra wyjściowego.

Wykazano, że przemiany promieniotwórcze radu polegają
na wyrzucaniu cząstek ; taki proces nazywa się

rozpadem



.

Następny typ rozpadu wiąże się z emisją promieni .

Doświadczenia

nad

odchylaniem

promieni

ciał

promieniotwórczych w polu magnetycznym wykazały, że
promienie  stanowią strumień bardzo szybkich

elektronów.

Okazuje się więc, że rozpad  polega na wyrzucaniu

elektronu z jądra pierwotnego.

Trzeci rodzaj promieniowania — promienie  są

promieniowaniem elektromagnetycznym; natura ich jest
identyczna z naturą krótkofalowego promieniowania
rentgenowskiego.

Promieniowanie



towarzyszy rozpadowi



lub



.

Prawo zachowania ładunków i prawo stałości sum liczb
masowych prowadzą do tak zwanych reguł przesunięć,

które pozwalają określić| jaki nowy pierwiastek powstaje
w wyniku danego rozpadu  lub rozpadu 

+

i 



oraz 

.

Podczas rozpadu  z jądra wyjściowego zostaje

wyrzucone jądro atomu helu

2

He

4

, tj. cząstka o liczbie

atomowej 2 i liczbie masowej 4.

Dlatego też powstający pierwiastek powinien mieć liczbę
atomową (numer porządkowy w tablicy Mendelejewa) o
dwie jednostki mniejszą i liczbę masową o cztery
jednostki mniejszą niż jądro wyjściowe.

Oznaczając jądro wyjściowe symbolem X,
a jądro powstające — symbolem Y,
zapiszemy rozpad  w postaci następującego schematu

Q

He

X

4

2

4

-

A

2

-

Z

A

Z





 Y

Ponieważ liczba atomowa wyznacza miejsce pierwiastka
w tablicy okresowej Mendelejewa, więc ze schematu
wynika, że:

wskutek rozpadu powstaje nowy pierwiastek,
stojący w układzie okresowym Mendelejewa o dwa
miejsca przed pierwiastkiem wyjściowym.

Podczas rozpadu 



z jądra pierwiastka wyjściowego

zostaje wyrzucony elektron.

Masa elektronu jest prawie dwa tysiące razy mniejsza od
masy atomu wodoru; można więc w przybliżeniu przyjąć
liczbę masową elektronu za zero.

Ładunek elektronu równy jest co do wartości
bezwzględnej ładunkowi protonu, jednak ma znak
ujemny, więc należy przyjąć Z = l.

W związku z tym będziemy oznaczać elektron symbolem

e

0

1



i schemat rozpadu 

-

przybierze postać:

Q

e

Y

X

0

1

A

1

Z

A

Z











Liczba masowa nowego jądra równa się liczbie masowej
jądra wyjściowego, a jego liczba atomowa jest o jedność
większa.

Wskutek rozpadu



--

powstaje nowy pierwiastek,

stojący w układzie okresowym Mendelejewa o jedno
miejsce za pierwiastkiem wyjściowym.

Podczas rozpadu 

+

z jądra pierwiastka wyjściowego

zostaje wyrzucony pozyton.

Masa pozytonu jest taka sama jak masa elektronu.
Ładunek pozytonu jest także równy co do wartości
bezwzględnej ładunkowi elektronu.

m

e

+

= m

e

-

q

e

-

= q

e

+



W związku z tym będziemy oznaczać pozyton symbolem:

e

0

1



schemat rozpadu 

+

przybierze postać:

Q

e

Y

X

0

1

A

1

Z

A

Z











Liczba masowa nowego jądra równa się liczbie masowej
jądra wyjściowego, a jego liczba atomowa jest o jedność
mniejsza.

Wskutek rozpadu



-+

powstaje nowy pierwiastek, stojący

w układzie okresowym Mendelejewa o jedno miejsce
przed pierwiastkiem wyjściowym.

Przytoczone dwie reguły przesunięć pozwalają całkowicie
zorientować się we wszystkich kolejnych przemianach,
występujących

w

procesie

promieniotwórczości

naturalnej pierwiastków ciężkich, spotykanych w
skorupie ziemskiej.

Okazuje się, że istnieją trzy szeregi albo trzy rodziny
pierwiastków promieniotwórczych,

które biorą swój początek odpowiednio od uranu

92

U

288

,

toru

90

Th

232

i izotopu uranu

92

U

235

zwanego także aktyno-

uranem (AcU).
Ostatni szereg nazywa się szeregiem aktynowym.

Wszystkie trzy szeregi zaczynają się od pierwiastków o
bardzo dużym okresie połowicznego zaniku:

92

U

288

ma okres połowicznego zaniku

 = 4.4 •10

9

lat

dla toru

90

Th

232

 = 1.8 •10

10

lat

Dla aktyno-uranu (AcU)

92

U

235

= 4,4 •10

8

lat.

Te długie okresy tłumaczą fakt występowania w skorupie
ziemskiej pierwiastków promieniotwórczych. W odległych
epokach

powstawały

zapewne

te

pierwiastki

z

pierwiastków lżejszych. Znalazłszy się w skorupie
ziemskiej

pierwiastki

te

zapoczątkowały

szeregi

wszystkich

naturalnych

pierwiastków

promieniotwórczych.

W czasie, który upłynął od ich powstania, nie zdążyły się
one rozpaść całkowicie.

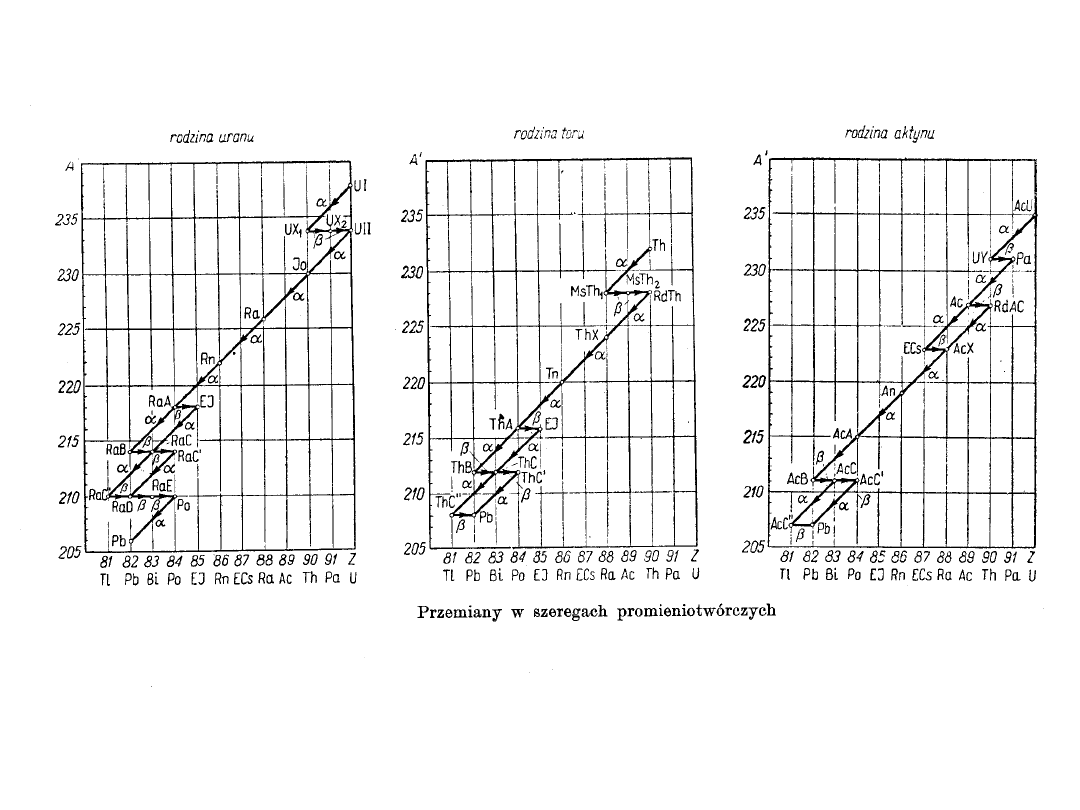
Naturalnym złożom pierwiastków promieniotwórczych
towarzyszy zawsze ołów, który jest końcowym produktem
ich rozpadu.

szereg uranowy kończy się izotopem Pb

206

,

torowy — izotopem Pb

208

aktynowy — izotopem Pb

207

.

w rudach uranowych (zawierających U

238

i U

235

)

występuje ołów, stanowiący mieszaninę dwóch izotopów
Pb

208

i Pb

207

zaś w rudach torowych — ołów, będący czystym izotopem
Pb

208

.

Jest to jedyny przypadek, gdy trwałe izotopy występują w
skorupie ziemskiej rozdzielone.

Prócz wymienionych pierwiastków promieniotwórczych
słabą promieniotwórczość wykazuje jeszcze:
potas

(



= 1.3 • 10

9

lat),

rubid

(



== 6.5 • 10

10

lat)

samar

(



= 6,7 • 10

11

lat).

Wiemy obecnie, że istnieje również dużo izotopów
promieniotwórczych innych pierwiastków, które nie
występują jednak w postaci naturalnej w skorupie
ziemskiej i mogą być otrzymane jedynie w drodze
sztucznych przemian.

Tłumaczy się to w ten sposób, że dla wszystkich tych
izotopów okres połowicznego zaniku jest stosunkowo
krótki, i dlatego jeśli one nawet występowały
kiedykolwiek w skorupie ziemskiej, to zdążyły już rozpaść
się całkowicie.

Rozpad promieniowania :

 



h

X

X

*

A

Z

*

A

Z



