PROJEKT Z METOD

NUMERYCZNYCH

Wykonali:

Daniel Królikiewicz

Łukasz Gwóźdź

Zadanie nr 14

Dana jest funkcja x-9

-x

=0. Równanie ma

rozwiązania w przedziale [0,1]. Napisać procedurę
wyznaczającą wielomian interpolacyjny
Lagrange`a dla lewej strony równania w punktach:
x=0, x=0.25, x=0.5, x=0.75, x=1 i na podstawie
tego wielomianu wyznaczyć przybliżone
rozwiązania przyrównując wielomian do zera. Do
znajdowania pierwiastka można wykorzystać
procedury MATLAB`a (np. Aitken, lub Newton)
Sporządzić wykresy funkcji x i 9

-x

i określić wartość

rozwiązania graficznie.

INTERPOLACJA

Interpolowanie funkcji f(x) polega na

znalezieniu funkcji F(x) określonej
klasy (np. wielomian), która na
zadanym przedziale [a,b] w zbiorze
dyskretnych punktów, tzw. węzłów
interpolacji, przyjmuje wartości
funkcji f(x), a pomiędzy węzłami
aproksymuje tę funkcję.

Zastosowanie interpolacji

• Obliczanie przybliżonych wartości danej funkcji w

punktach różnych od węzłów interpolacji:

- Wewnątrz przedziału interpolacji,
- Poza przedziałem interpolacji

• Zastępowanie skomplikowanych wzorów funkcji

prostszymi (wygodniejszymi dla oblicze,

przetwarzania, itp.);

• Konstruowanie nowych metod rozwiązania

różnych zagadnień numerycznych.

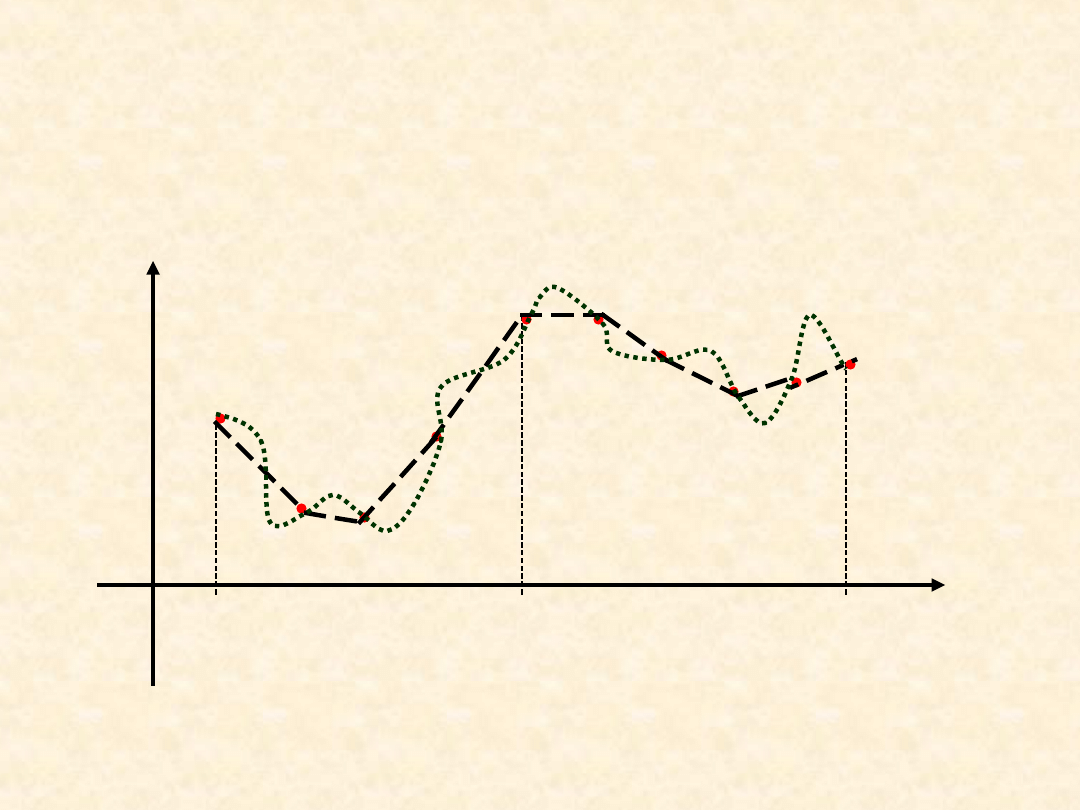
Graficzna interpretacja

x

y

x

0

y

0

x

n

y

n

x

N-1

y

N-1

INTERPOLACJA LAGRANGE’A

Innym sposobem szukania wielomianu

interpolacyjnego p. dla zadanego zbioru {x

i

,

y

i

},

0≤i≤n, jest interpolacja Lagrange’a. W tym

miejscu należy wyraźnie zaznaczyć, że
istnieje

tylko jeden wielomian stopnia n interpolujący

zbudowany na punktach {x

i

, y

i

}, nie

zależnie od

sposobu jego konstrukcji.

Postać wielomianu interpolacyjnego

)

)...(

)(

(

)

)....(

)(

(

y

y

y

p(x)

1

0

1

0

0

n

1

1

0

0

n

i

i

i

n

i

n

k

k

k

n

x

x

x

x

x

x

x

x

x

x

x

x

L

gdzie

L

y

L

L

L





























