4.4.2.6.

Rozkład

równomierny

Rozkład równomierny nazywany bywa również rozkładem jednostajnym lub rozkładem

prostokątnym. Jest to najprostszy rozkład zmiennej losowej ciągłej X w przedziale (c, d)

określony gęstością:

f x

d c

dla c x d
dla x corazx d

( ) 

 












1

0

Dystrybuanta tego rozkładu jest dana wzorem:

F x

dla

x c

x c

d c

dla c x d
dla

x d

( ) 







 












0

1

a jej wartość oczekiwana i wariancja są określone wzorami:

E X

d c

V X

d c

( )

( )

(

)









2

12

2

Graficzną postać gęstości i dystrybuanty rozkładu równomiernego pokazano na rys. 4.20.

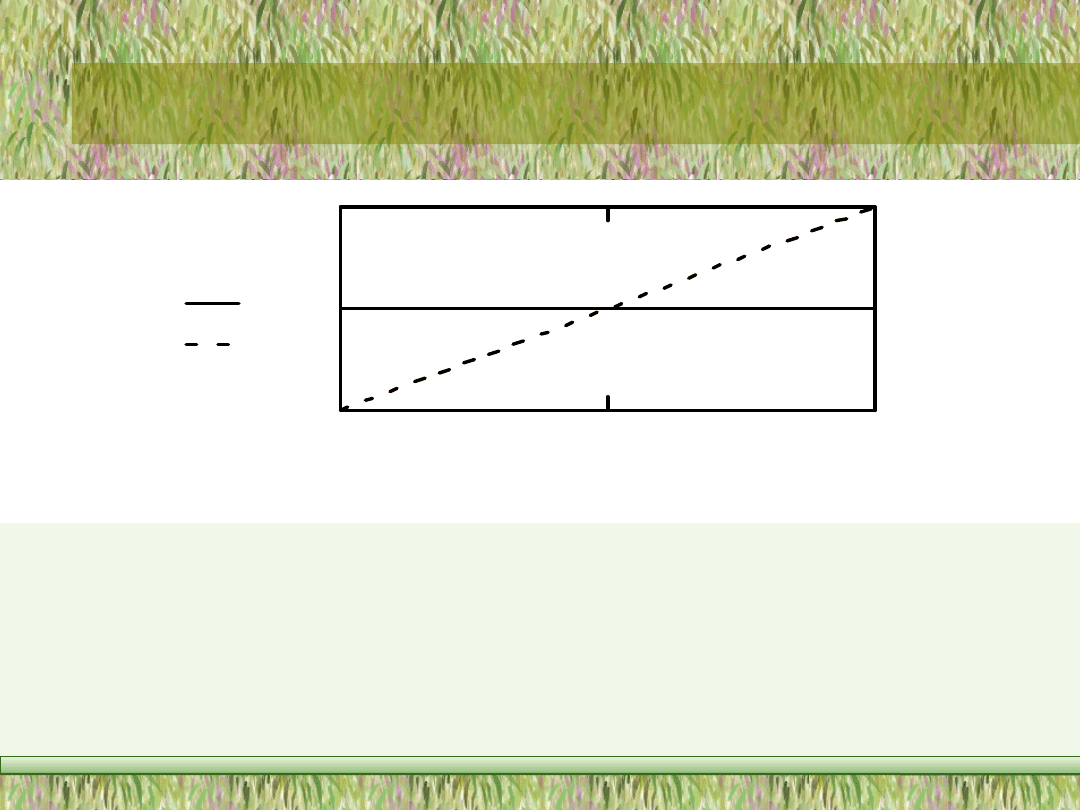
0

1

2

0

0.5

1

f(

)

x

F(

)

x

x

R

y

s

. 4

.2

0

. Gę

s

t

o

ś

ć

(lin

ia

c

ią

g

ła

) i d

y

s

t

r

y

b

u

a

n

t

a

r

o

z

k

ła

d

u

r

ó

w

n

o

m

ie

r

n

e

g

o

Rozkład równomierny ma następujące właściwości:

 Jeżeli zmienna losowa X ma rozkład równomierny w przedziale (0, d) to zmienna

losowaZ

d

X

ln( ) ma rozkład wykładniczy o wartości oczekiwanej 1;

 Jeżeli zmienna losowa X ma rozkład równomierny w przedziale (c, d) to zmienna losowa

Y

x c

d c







ma rozkład równomierny w przedziale (0, 1) określony gęstością i dystrybuantą:

f y

dla

y

dla

y oraz y

( ) 

 











1

0

1

0

0

1

F x

dla

y

y dla

y

dla

y

( ) 



 



0

0

0

1

1

1

Wartość oczekiwana i wariancja zmiennej losowej Y o rozkładzie równomiernym w

przedziale (0, 1) są określone wzorami:

E Y

V Y

( )

( )





1
2

1

12

 Jeżeli zmienne Y

1

, Y

2

, ..... , Y

n

są niezależne i mają jednakowy rozkład równomierny w

przedziale (0, 1) to przy wzroście n rozkład ich sumy dąży do rozkładu normalnego

N

n n

( ;

)

2 12

, a rozkład ich średniej arytmetycznej dąży do rozkładu normalnego N( ;

)

1
2

1

12

.

Zbieżność rozkładu statystyki Y = Y

1

+ Y

2

+ ..... + Y

n

do rozkładu normalnego jest bardzo

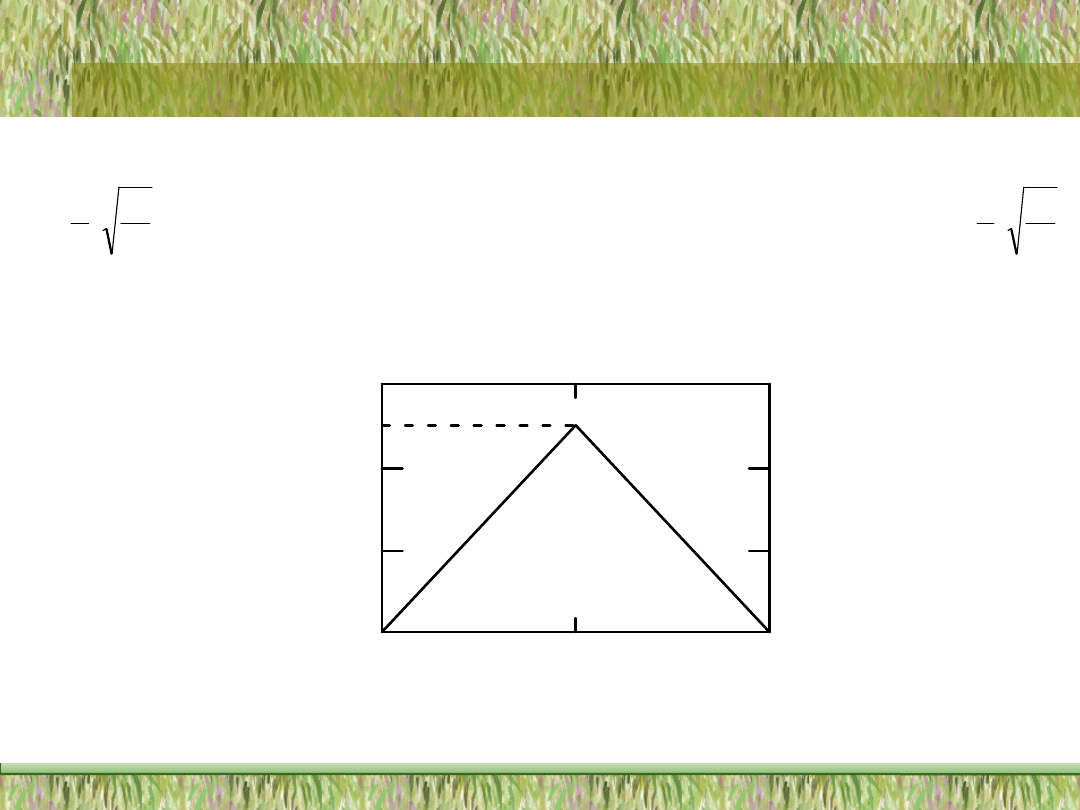
szybka. Dla n = 2 uzyskuje się rozkład trójkątny, a dla n = 3 uzyskuje się już kształt rozkładu

normalnego (rys. 4.21).

0

1

2

0

0. 2

0. 4

0. 6

Rys. 4.21. Gęstość rozkładu równomiernego w przedziale (0, 1) (linia przerywana)

i gęstość sumy dwóch niezależnych zmiennych o rozkładach równomiernych

w przedziale (0,1) (lina ciągła)

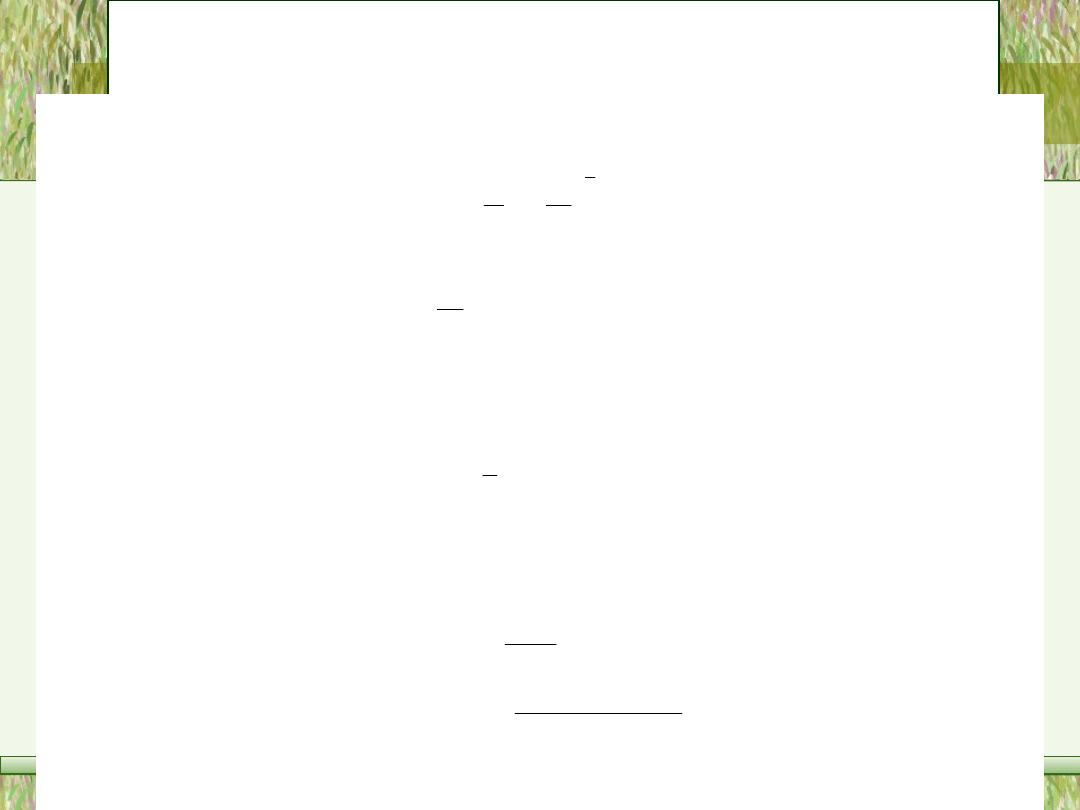
4.2.6.

4.2.6.

Rozkład potęgowy

Rozkład potęgowy

Z ałóżm y , że zm ienna losow a X m a rozkład rów nom ierny w przedziale (0, c) i jest dana

w artość stała



> 0. W ów czas zm ienna losow a T określona w zorem :

T

c

X

c









1



m a rozkład potęgowy o funkcji gęstości:

f t

c

t

dla

t c

dla t

t c

( )

;





 


















 1

0

0

0

i dy strybuancie:

F t

dla

t

t

c

dla

t

c

dla

t

c

( ) 









 















0

0

0

1



gdzie c>0 to param etr skali, a



>0 to param etr kształtu rozkładu. W artość oczekiw ana i w ariancja

tego rozkładu m ają odpow iednio postać:

E T

c

V T

c

( )

( )

(

) (

)

 









 











1

1

2

2

2

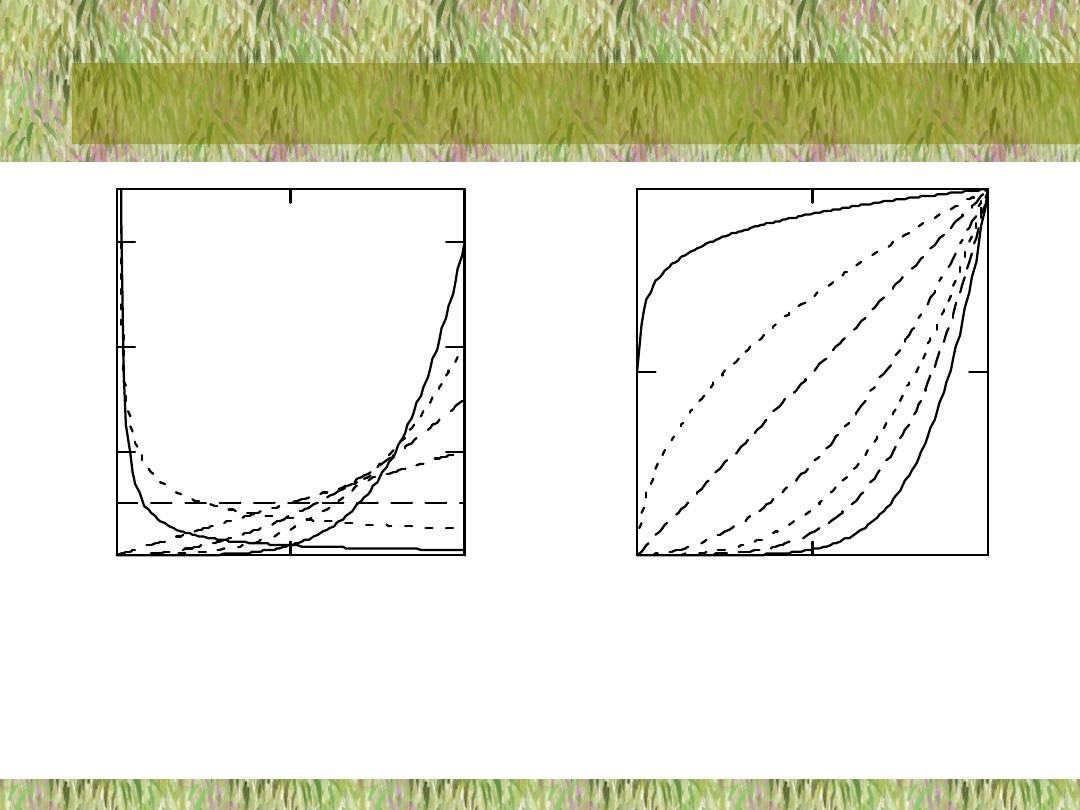
Przy kłady gęstości rozkładu potęgow ego pokazano na ry s. 4.22 a przy kłady dy stry buanty tego

rozkładu pokazano na rys. 4.23.

0

0.5

1

0

2

4

6

0

0.5

1

0

0.5

1

R

y

s

. 4

.2

2

. Gę

s

to

ś

c

i r

o

z

k

ła

d

u

p

o

tę

g

o

w

e

g

o

, d

la

c

=

1

i r

óż

n

y

c

h

p

a

r

a

m

e

tr

ó

w

, o

d

=

0

.1

d

la

le

w

e

j lin

ii c

ią

g

łe

j p

o

p

r

z

e

z

w

a

r

to

ś

c

i

=

0

.5

i 0

.6

(lin

ia

p

o

z

io

m

a

), 2

, 3

, 4

aż

d

o

6

(p

r

a

w

a

lin

ia

c

ią

g

ła

)

R

y

s

.

4

.2

3

.

D

y

s

tr

y

b

u

a

n

ty

r

o

z

k ła

d

u

p

o

tę

g

o

w

e

g

o

, d

la

c

=

1

i r

óż

n

y

c

h

p

a

r

a

m

e

tr

ó

w

,

o

d

=

0

.1

d

la

g

ó

r

n

e

j lin

ii c

ią

g

łe

j p

o

p

r

z

e

z

w

a

r

toś

c

i

=

0

.5

, 0

.6

, 2

, 3

, 4

aż

d

o

6

(d

o

ln

a

lin

ia

c

ią

g

ła

)

Podstawowe właściwości rozkładu potęgowego można zestawić w następujących

punktach:
 Rozkład potęgowy o parametrze skali c i parametrze kształtu



= 1 jest rozkładem

równomiernym w przedziale (0, c) (patrz rys. 4.22 i 4.23 wykresy dla



= 1).

 Jeżeli zmienna losowa T ma rozkład potęgowy o parametrach c i



to zmienna losowa T/c ma

rozkład potęgowy o parametrze skali 1 i parametrze kształtu



.

 Rozkład potęgowy o parametrach c i



jest przypadkiem granicznym uogólnionego rozkładu

gamma (pominiętego w tym wykładzie) o parametrach c; p i



przy

 

i p



= const =



.