MODELE WYBORU

MODELE WYBORU

KONSUMENTA

KONSUMENTA

PROF. DR HAB. GRAŻYNA KARMOWSKA

Literatura: T. Tokarski. Ekonomia matematyczna. PWE
2011

1

POJĘCIA WSTĘPNE



Modele ekonomii matematycznej zazwyczaj
mają charakter modeli teoretycznych.



Całkowita użyteczność konsumpcji, to
satysfakcja, zadowolenie które czerpie
konsument z realizacji określonej kombinacji
dostępnych mu dóbr i usług.



Zakładamy, ze poziom użyteczności całkowitej
jest mierzalny.



Funkcja użyteczności opisuje relacje
zachodzące pomiędzy realizowaną przez
konsumenta kombinacją konsumpcji a
poziomem realizowanej uzyskiwanej
użyteczności.

2

FUNKCJA UŻYTECZNOŚCI

FUNKCJA UŻYTECZNOŚCI



x – wielkość konsumpcji danego dobra
(usługi)



dziedzina funkcji:



funkcja u jest dwukrotnie różniczkowalna



zachodzi nierówność:

Jeśli wielkość konsumpcji i-tego dostępnego
konsumentowi dobra (usługi) rośnie, przy
stałej wielkości dobra j, to użyteczność
całkowita u, którą czerpie konsument z
konsumpcji tych dóbr lub usług rośnie.

)

,

(

2

1

x

x

u

u

0

,

:

2

1



x

x

D

u

0

2

,

1

)

,

(

2

1















i

u

x

u

i

D

x

x

3

KRAŃCOWA UŻYTECZNOŚĆ

KRAŃCOWA UŻYTECZNOŚĆ

KONSUMPCJI

KONSUMPCJI



jest dodatnia:

0

2

,

1

)

,

(

2

1

















i

i

u

x

u

mu

i

D

x

x

u

const

x

X

j

i



const

x

X

j

i



mu

i

4



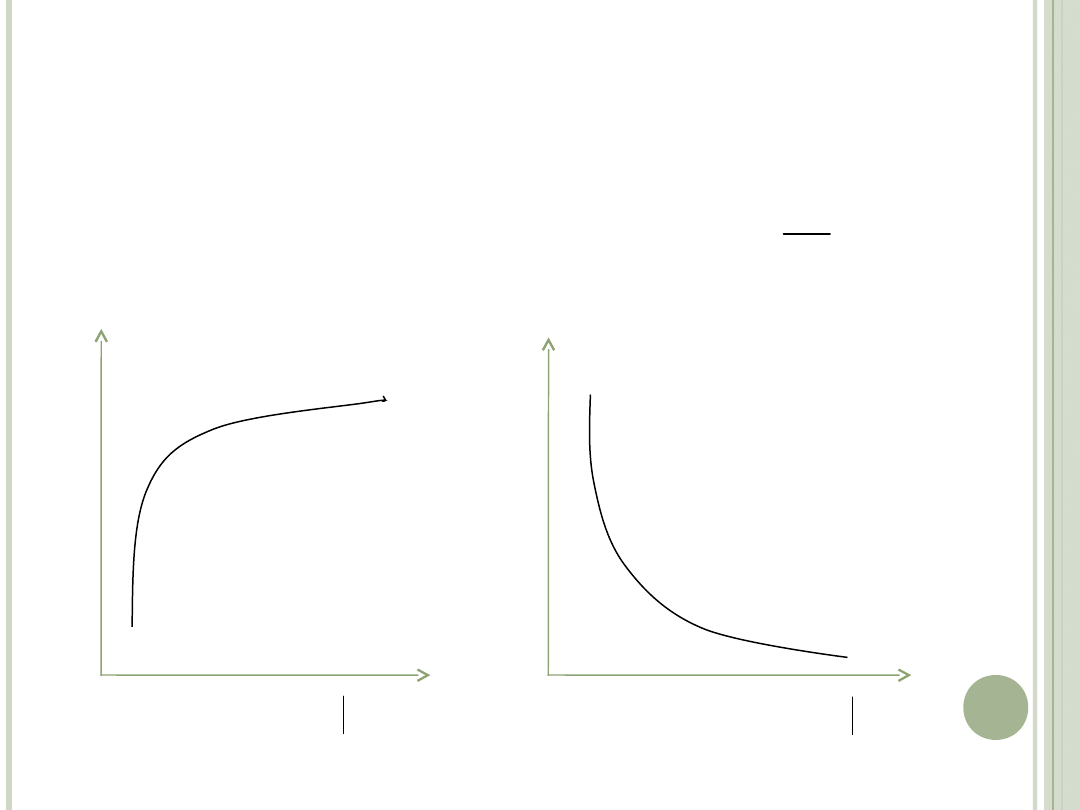
Krzywa użyteczności całkowitej u konsumpcji x
i-tego z konsumowanych dóbr lub usług, przy
stałej konsumpcji j tego dobra (usługi) jest
wklęsła.



Wzrost konsumpcji i-tego dobra prowadzi do
spadku krańcowej użyteczności jego
konsumpcji.



Stąd spełnione jest I prawo Gossena (malejącej
użyteczności krańcowej): wraz ze wzrostem
konsumpcji danego dobra (usługi)



użyteczność całkowita każdego z dostępnych
konsumentowi dóbr (usług) rośnie coraz wolniej,



użyteczność krańcowa spada.

0

2

,

1

2

2







































i

i

i

i

i

x

u

x

u

x

x

mu

i

KRAŃCOWA UŻYTECZNOŚĆ KONSUMPCJI

5

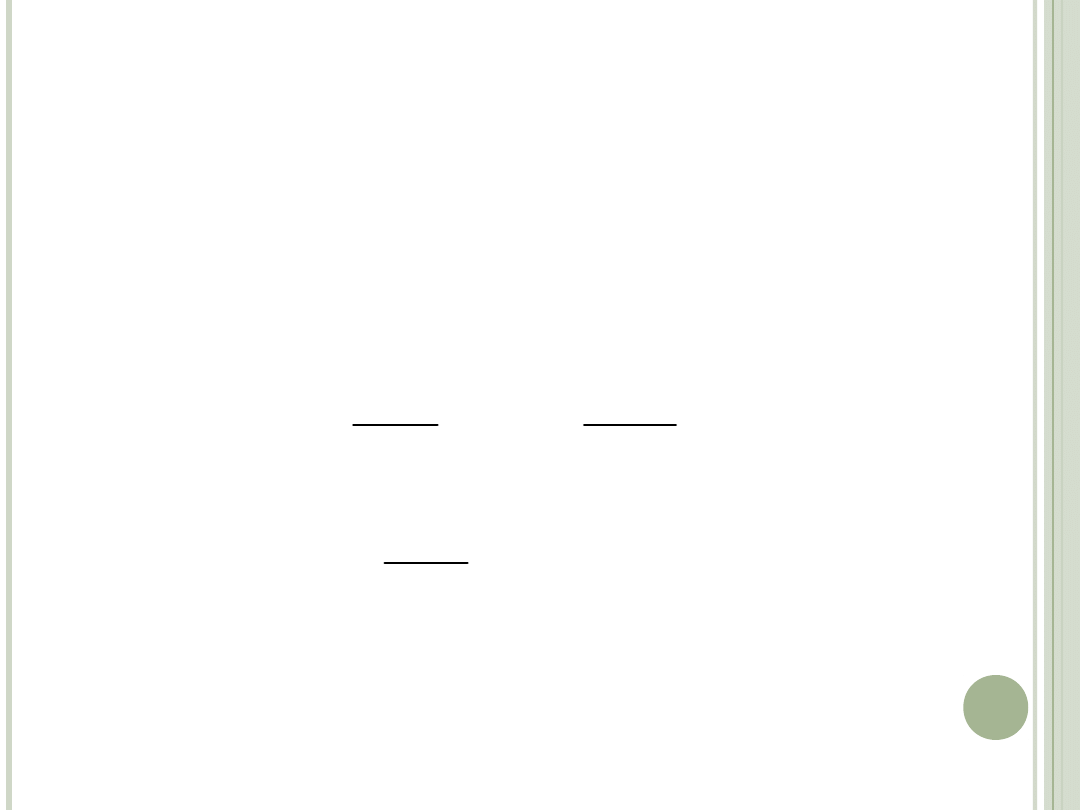
PRZYROST UŻYTECZNOŚCI

PRZYROST UŻYTECZNOŚCI

CAŁKOWITEJ

CAŁKOWITEJ

jest sumą krańcowych użyteczności
konsumpcji tych dóbr (usług) ważonych
przyrostami wielkości konsumpcji tych dóbr
(usług):

2

2

1

1

2

2

1

1

dx

mu

dx

mu

du

x

u

mu

dx

x

u

dx

x

u

du

i

i























6

KRZYWA OBOJĘTNOŚCI

KRZYWA OBOJĘTNOŚCI



Poziom realizowanej przez konsumenta

użyteczności jest stały, więc przyrosty

użyteczności są zerowe:

krańcowa stopa substytucji



Jeśli konsument zmniejsza wielkość

konsumpcji jednego z dostępnych mu dóbr

(usług), to by zachować poziom użyteczności

całkowitej, wielkość konsumpcji drugiego

dobra (usługi) musi wzrosnąć.

0

0

2

1

1

2

1

1

2

2

2

2

1

1















mu

mu

dx

dx

dx

mu

dx

mu

dx

mu

dx

mu

7

ZBIÓR BUDŻETOWY

ZBIÓR BUDŻETOWY

zbiór wiązek towarowych, spośród których
konsument może dokonać wyboru.

1. Zmniejszy się gdy jedna z cen rośnie, a

pozostałe czynniki pozostają bez zmian.

2. Zwiększy się, gdy dochód rośnie, a reszta

czynników pozostaje bez zmian.

8

ZBIÓR BUDŻETOWY

dochód nominalny



Wszystkie dostępne kombinacje konsumpcji
przy danym nominalnym dochodzie i
wektorze cen:

2

2

1

1

x

p

x

p

m





0

0

0

2

1

1

2

1

2

1

2

2

1

1

2

2

1

1

2

2

2

1



























p

p

dx

dx

x

p

p

p

m

x

x

p

m

x

p

p

m

x

x

p

m

x

x

nachylenie ograniczenia
budżetowego

9

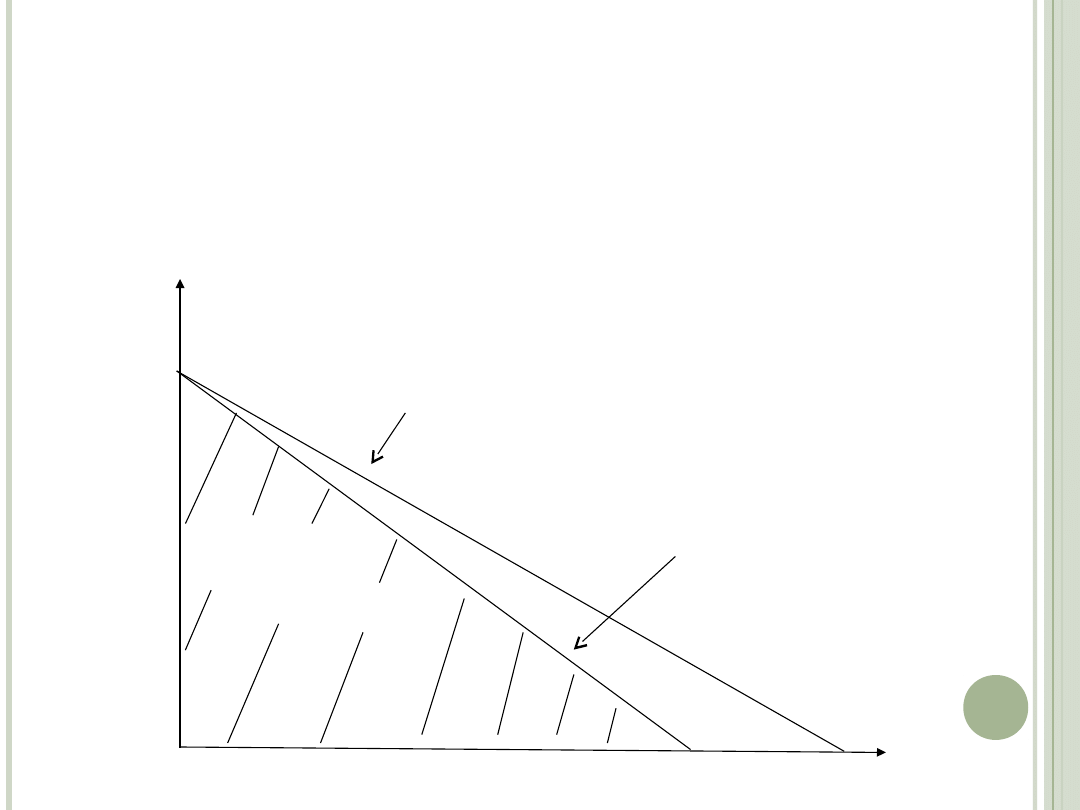
Zbiór
budżetowy

nowa linia
budżetowa

m

x

p

x

p





2

2

1

1

m/p

1

x

2

x

1

m/p

2

poprzednia
linia budżetowa

10



Konsument szuka takiej kombinacji
konsumpcji

która maksymalizuje

funkcję użyteczności

przy ograniczeniu budżetowym



Problem decyzyjny:



Można rozwiązać z wykorzystaniem funkcji
Lagrange’a:

11

MODEL Z OGÓLNĄ FUNKCJĄ

MODEL Z OGÓLNĄ FUNKCJĄ

UŻYTECZNOŚCI

UŻYTECZNOŚCI





2

1

,x

x





2

1

,x

x

u

m

x

p

x

p





2

2

1

1



















0

)

,

(

max

2

2

1

1

2

1

)

,

(

2

1

m

x

p

x

p

x

x

u

u

D

x

x





)

(

,

)

,

,

(

2

2

1

1

2

1

2

1

m

x

p

x

p

x

x

u

x

x

L













SPEŁNIONE MUSZĄ BYĆ WARUNKI: KONIECZNE
I DOSTATECZNE



Warunek konieczny istnienia maksimum
warunkowego:



Warunek dostateczny: wyznacznik Hesjanu
obrzeżonego jest dodatni w punkcie
stacjonarnym

12



















m

x

p

x

p

p

p

mu

mu

2

2

1

1

2

1

2

1

Krańcowa stopa substytucji

Linia ograniczenia budżetowego

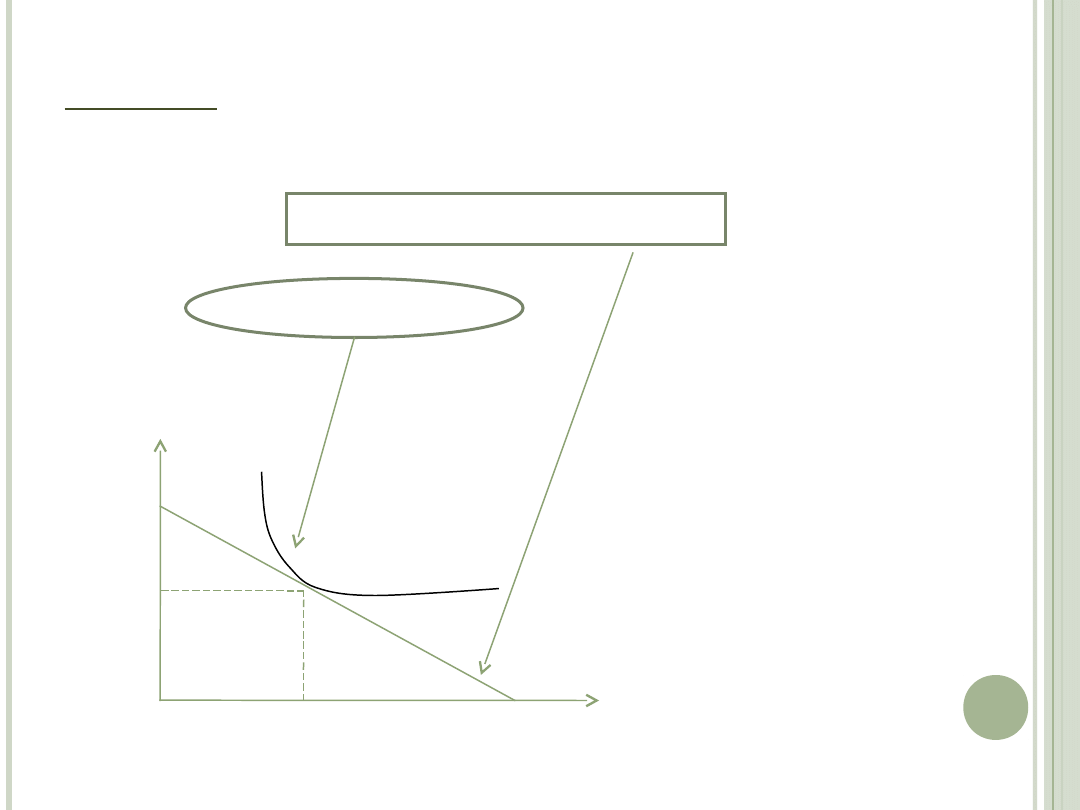
WARUNKI:



W.K

. Linia ograniczenia budżetowego jest

styczna do krzywej obojętności.



W.D.

Krzywa obojętności jest wypukła w

otoczeniu punktu styczności z linią
ograniczenia budżetowego.

13

MODEL Z POTĘGOWĄ FUNKCJĄ

MODEL Z POTĘGOWĄ FUNKCJĄ

UŻYTECZNOŚCI

UŻYTECZNOŚCI



elastyczność

14

)

1

;

0

(

,

)

,

(

2

1

2

1

2

1

2

1















x

x

x

x

u

u

2

2

2

1

1

1

2

1





























x

u

x

u

x

u

x

u

ux

ux



Konsument szuka takiej kombinacji
konsumpcji

która maksymalizuje

funkcję użyteczności

przy ograniczeniu budżetowym



Problem decyzyjny:



można rozwiązać z wykorzystaniem funkcji
Lagrange’a:

15

EKSTREMUM WARUNKOWE





2

1

,x

x





2

1

2

1

,





x

x

u

m

x

p

x

p





2

2

1

1





















0

)

,

(

max

2

2

1

1

2

1

)

,

(

2

1

2

1

m

x

p

x

p

x

x

u

u

D

x

x









)

(

,

)

,

,

(

2

2

1

1

2

1

2

1

2

1

m

x

p

x

p

x

x

u

x

x

L

















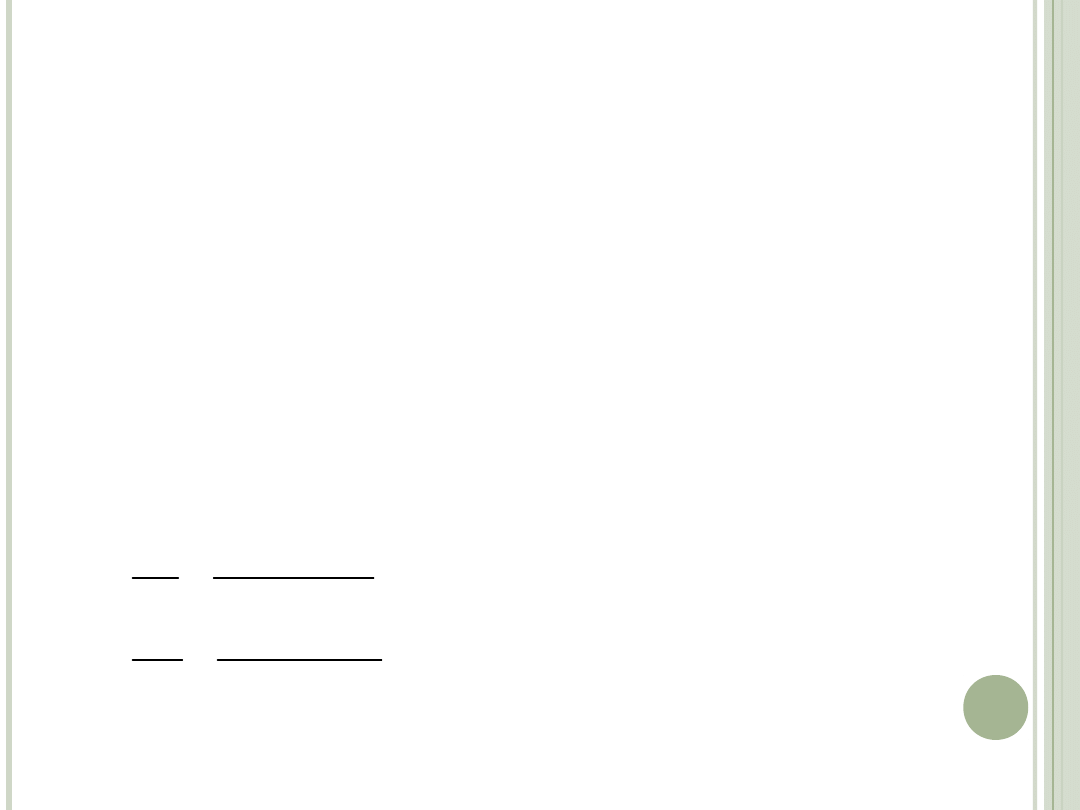
WNIOSKI:



Optymalna wielkość konsumpcji dobra
(usługi) x

1

zależy od dochodu nominalnego

m, ceny p

1

oraz elastyczności cząstkowych

funkcji użyteczności.



Analogiczny wniosek wyciągamy dla dobra
(usługi) 2.



Im wyższy dochód nominalny konsumenta,
tym wyższe są wielkości konsumpcji obu
dóbr:

16

0

)

(

0

)

(

2

2

1

2

2

1

2

1

1

1





















p

m

x

p

m

x













WNIOSKI



Wzrostowi ceny dobra (usługi) 1. odpowiada
spadek wielkości konsumpcji tego dobra, w
warunkach równowagi konsumenta.



Im wyższa jest elastyczność użyteczności
względem konsumpcji pierwszego dobra
(usługi), tym niższa jest optymalna wielkość
konsumpcji tego dobra.

17

0

)

(

0

)

(

2

2

2

1

2

2

2

2

1

2

1

1

1

1

























p

m

p

x

p

m

p

x













PODSUMOWANIE



Wnioski, które płyną z analiz optymalnych
zachowań na rynku dwóch dóbr konsumenta
dokonującego wyboru dóbr (usług) można
uogólnić na n skończonych dóbr (usług).

18

MODELE DWUOKRESOWE

MODELE DWUOKRESOWE

ZAŁOŻENIA:
Konsument funkcjonuje w dwóch okresach:



bieżącym t

1

; o wielkości konsumpcji c

1

,



przyszłym t

2

; o wielkości konsumpcji c

2

.

Funkcja użyteczności:



u jest dwukrotnie różniczkowalna,

0

,

)

,

(

2

1

2

1





c

c

c

c

u

u

19

MODELE DWUOKRESOWE



wzrost wielkości konsumpcji prowadzi do
wzrostu użyteczności całkowitej:



Drugie pochodne cząstkowe funkcji
użyteczności są ujemne:

0

2

,

1

)

,

(

2

1

















i

i

u

c

u

mu

i

D

c

c

20

0

2

,

1

)

,

(

2

2

2

1





















i

i

i

u

c

u

c

mu

i

D

c

c



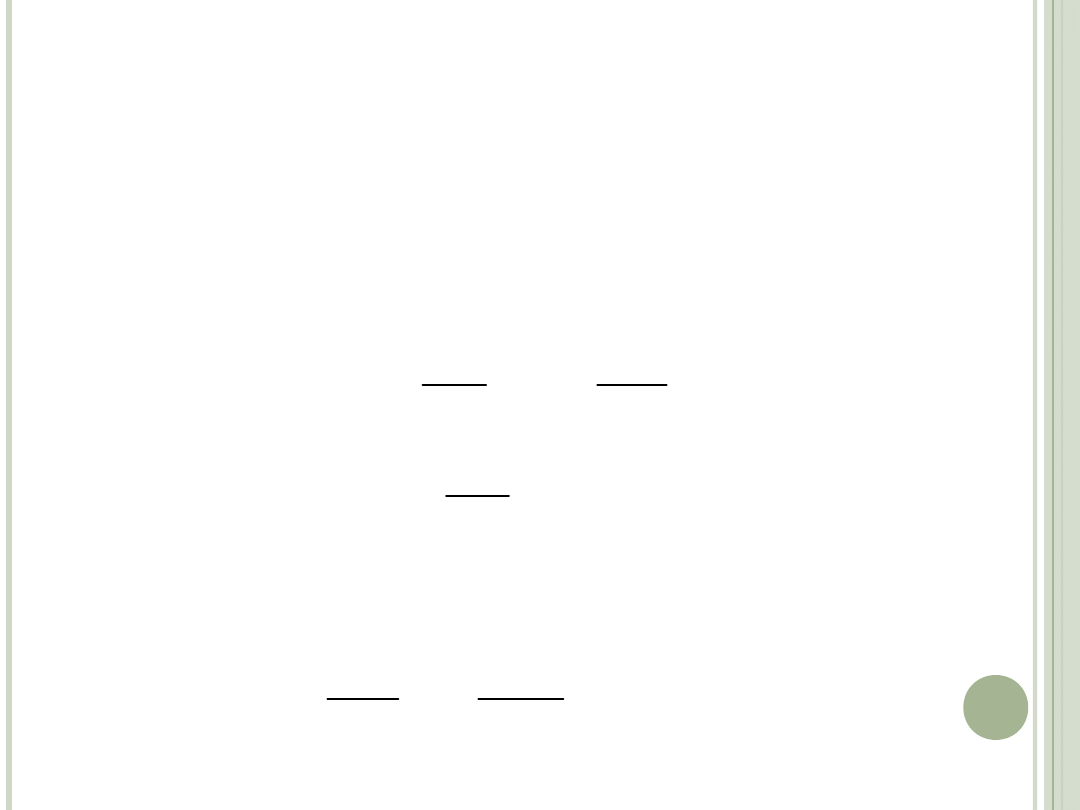
Międzyokresowa krzywa obojętności
wyznacza wszystkie kombinacje konsumpcji
bieżącej c

1

i przyszłej c

2

, które pozwalają

konsumentowi na realizację określonego
(stałego) poziomu użyteczności u

21

0

0

2

1

1

2

1

1

2

2

2

2

1

1

2

2

1

1



































mu

mu

dc

dc

dc

mu

dc

mu

dc

mu

dc

mu

du

c

u

mu

dc

c

u

dc

c

u

du

i

i

MODEL Z DOSTĘPEM DO RYNKU

MODEL Z DOSTĘPEM DO RYNKU

KREDYTOWEGO

KREDYTOWEGO

Założenia:



Konsument, z międzyokresową funkcją
użyteczności, może dokonać transferów
konsumpcji w czasie jedynie za pośrednictwem
rynku kredytowego.



W okresie bieżącym konsument uzyskuje
dochody



, a w okresie przyszłym spodziewa się
dochodów . Dochody te są w całości
przeznaczone na konsumpcje w okresie t

1

=1 i

t

2

=2



bieżące dochody są przeznaczone na bieżącą
konsumpcję i bieżące oszczędności:

22

0

1



y

0

2



y

s

c

y





1

1



Na rynku kredytowym jest stopa procentowa
r (niezależna od konsumenta)
oprocentowania kredytów i depozytów.



Przyszła konsumpcja c

2

może być

finansowana z jego przyszłych dochodów y

2

,

bieżące oszczędności s oraz odsetek rs od
owych oszczędności:



Bieżące oszczędności s stanowią
nieskonsumo-waną część bieżących
dochodów konsumenta y

1

.

23

1

1

2

2

2

)

1

(

c

y

s

r

s

y

rs

s

y

c

















1

1

c

y 



Poziom oszczędności s nie może być wyższy
od bieżącego dochodu y

1

24

2

1

2

1

1

1

2

1

1

2

2

)

1

(

)

1

(

)

1

(

)

1

(

)

)(

1

(

y

y

r

c

c

r

c

r

y

r

s

y

c

y

r

s

y

c































WNIOSKI



Na ograniczeniu budżetowym suma
zdyskontowanych (realna stopą procentową
r) wydatków konsumpcyjnych

musi

być równa sumie zdyskontowanych
dochodów

konsumenta.



Przy rezygnacji z konsumpcji bieżącej:



Przy rezygnacji z konsumpcji przyszłej

25

2

1

)

1

(

c

c

r





2

1

)

1

(

y

y

r





2

1

2

1

)

1

(

0

y

y

r

c

c











r

y

y

c

y

y

r

c

r

c





















1

)

1

(

)

1

(

0

2

1

1

2

1

1

2

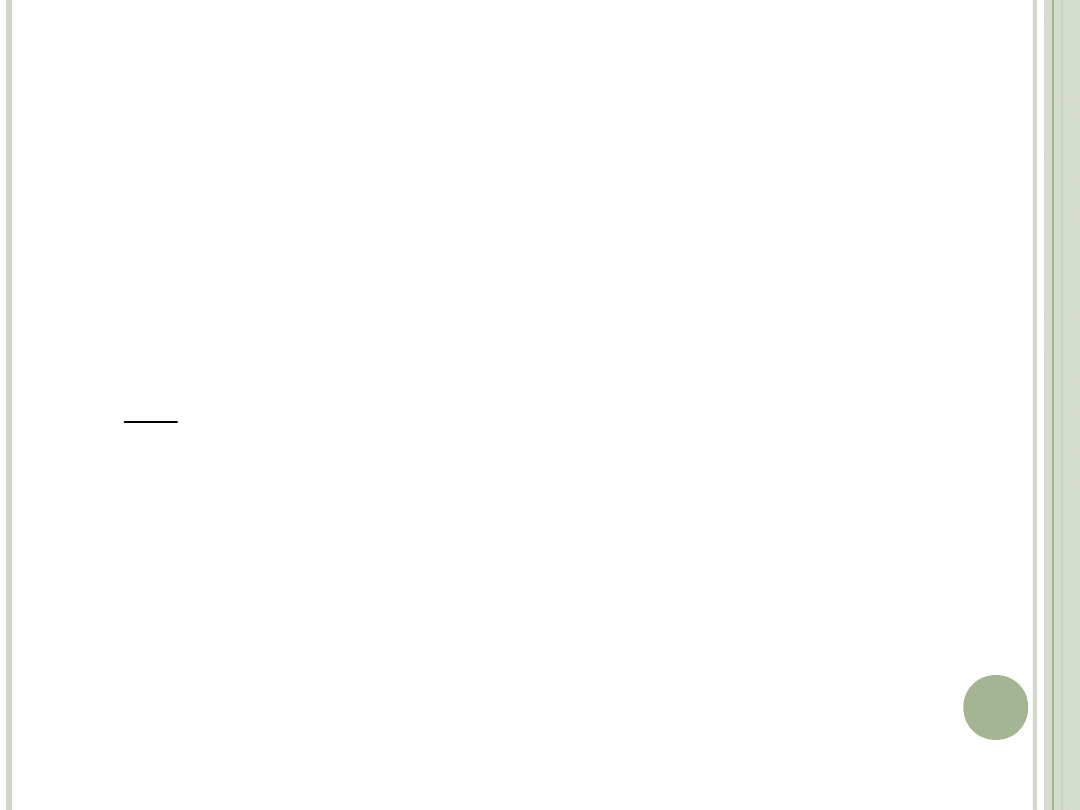
WNIOSKI



Przy równej konsumpcji bieżącej bieżącym
dochodom:



Jeśli konsument zwiększy konsumpcję
bieżącą o dc

1

to musi ograniczyć konsumpcję

przyszłą o

26

0

)

1

(

)

1

(

)

1

(

)

1

(

)

1

(

1

2

1

2

1

2

2

2

2

1

2

1

1

1





































r

dc

dc

c

r

y

y

r

c

y

c

y

y

r

c

y

r

y

c

1

)

1

(

dc

r



PROBLEM DECYZYJNY



Maksimum funkcji użyteczności:

27





























0

)

1

(

)

1

(

)

,

(

max

2

1

2

1

2

1

)

,

(

2

1

y

y

r

c

c

r

c

c

u

u

D

c

c





)

)

1

(

)

1

((

,

)

,

,

(

2

1

2

1

2

1

2

1

y

y

r

c

c

r

c

c

u

c

c

L



















WARUNKI



W.K

. Międzyokresowa krzywa obojętności jest

styczna do międzyokresowego ograniczenia
budżetowego.

w punkcie ekstremalnym nachylenie krzywej

obojętności=

= nachyleniu ograniczenia budżetowego

konsument musi znajdować się na jego

ograniczeniu

budżetowym



W.D.

Międzyokresowa krzywa obojętności, w

otoczeniu punktu styczności z
międzyokresowym ograniczeniem budżetowym,
jest wypukła.

28



























2

1

2

1

2

1

)

1

(

)

1

(

)

1

(

y

y

r

c

c

r

r

mu

mu

MODEL Z DOSTĘPEM DO RYNKU

MODEL Z DOSTĘPEM DO RYNKU

INWESTYCYJNEGO

INWESTYCYJNEGO

x=f(i) funkcja przychodu od inwestycji
Założenia:



Dziedzina R+,



Różniczkowalna co najmniej dwukrotnie,



Zerowym nakładom inwestycyjnym
odpowiada zerowy przyszły przychód z
inwestycji f(0)=0.



Bardzo dużym nakładom inwestycyjnym
odpowiadają duże przyszłe dochody

29









)

(

lim i

f

i

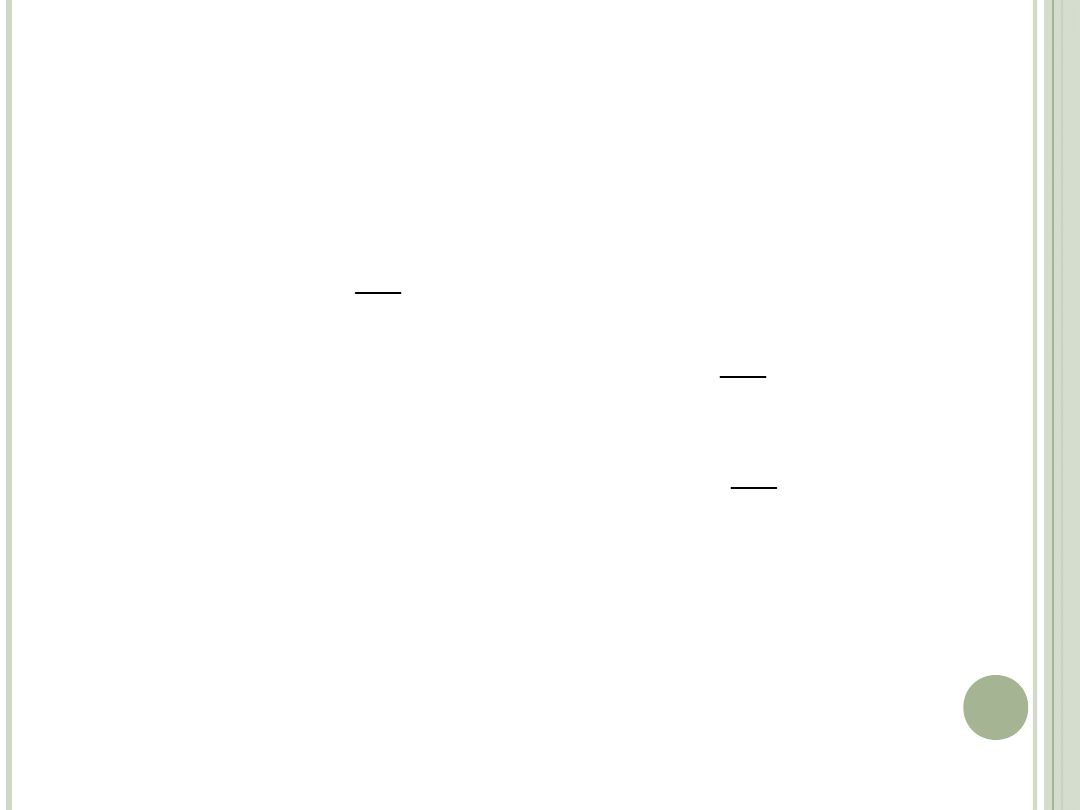
CD ZAŁOŻEŃ



Ze wzrostem nakładów inwestycyjnych rośnie
przychód z inwestycji



Spełnione są warunki:

Bardzo małym nakładom inwestycyjnym i odpowiada

bardzo duży krańcowy przychód od inwestycji mpi.

Analogiczne wnioski są dla dużych nakładów.

30

0









di

df

mpi

D

i

f

0

lim

lim

lim

lim

0

0



























di

df

mpi

di

df

mpi

i

i

i

i

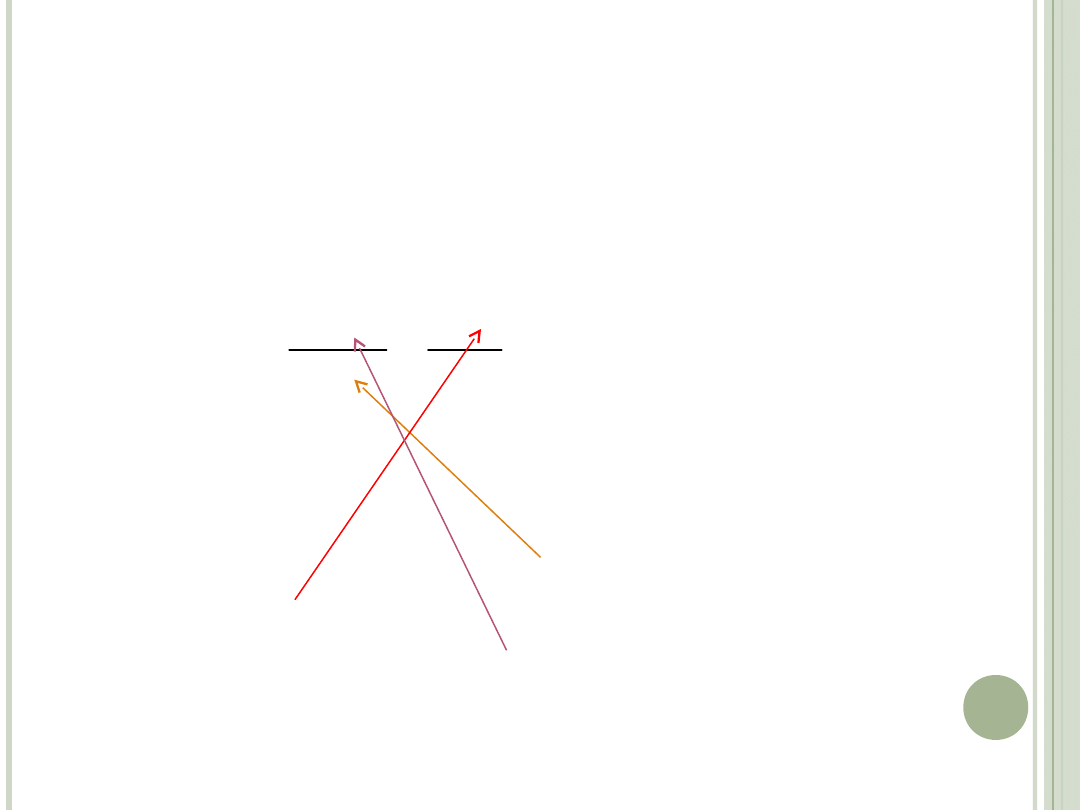
CD ZAŁOŻEŃ



Druga pochodna funkcji przychodu od
inwestycji jest ujemna:

spełnione jest prawo malejących przychodów

krańcowych od inwestycji, tj. ze wzrostem
nakładów inwestycyjnych i przychód od
inwestycji f(i) rośnie coraz wolniej, zaś
krańcowy przychód od inwestycji mpi maleje

31

0

2

2









di

f

d

di

mpi

d

D

i

f



Międzyokresowe ograniczenie budżetowe
konsumenta

32

)

(

)

(

1

1

2

2

1

1

2

2

2

1

1

c

y

f

y

c

c

y

i

i

f

y

x

y

c

i

c

y























WNIOSKI



Jeśli konsument zwiększy (zmniejszy)
konsumpcję bieżącą o k jednostek, to będzie
musiał ograniczyć (zwiększyć) konsumpcję
przyszłą o jednostek



Międzyokresowe ograniczenie budżetowe
konsumenta są funkcją wklęsłą

33

di

df

k

0

2

2

2

1

2

2





di

f

d

dc

c

d

PROBLEM DECYZYJNY



Funkcja opisująca preferencje konsumpcji w
czasie z ograniczeniem budżetowym

34



























0

)

(

)

,

(

max

1

1

2

2

2

1

0

,

2

1

c

y

f

y

c

c

c

u

u

c

c





))

(

(

,

)

,

,

(

1

1

2

2

2

1

2

1

c

y

f

y

c

c

c

u

c

c

L















MODEL Z DOSTĘPEM DO RYNKU

MODEL Z DOSTĘPEM DO RYNKU

KREDYTOWEGO I INWESTYCYJNEGO

KREDYTOWEGO I INWESTYCYJNEGO



Założenia jak przy poprzednich modelach

35

)

(

)

1

(

)

,

(

)

,

(

)

(

)

1

(

2

2

1

1

2

2

1

1

i

f

s

r

y

i

s

c

i

s

y

i

s

c

i

f

s

r

y

c

i

s

c

y





























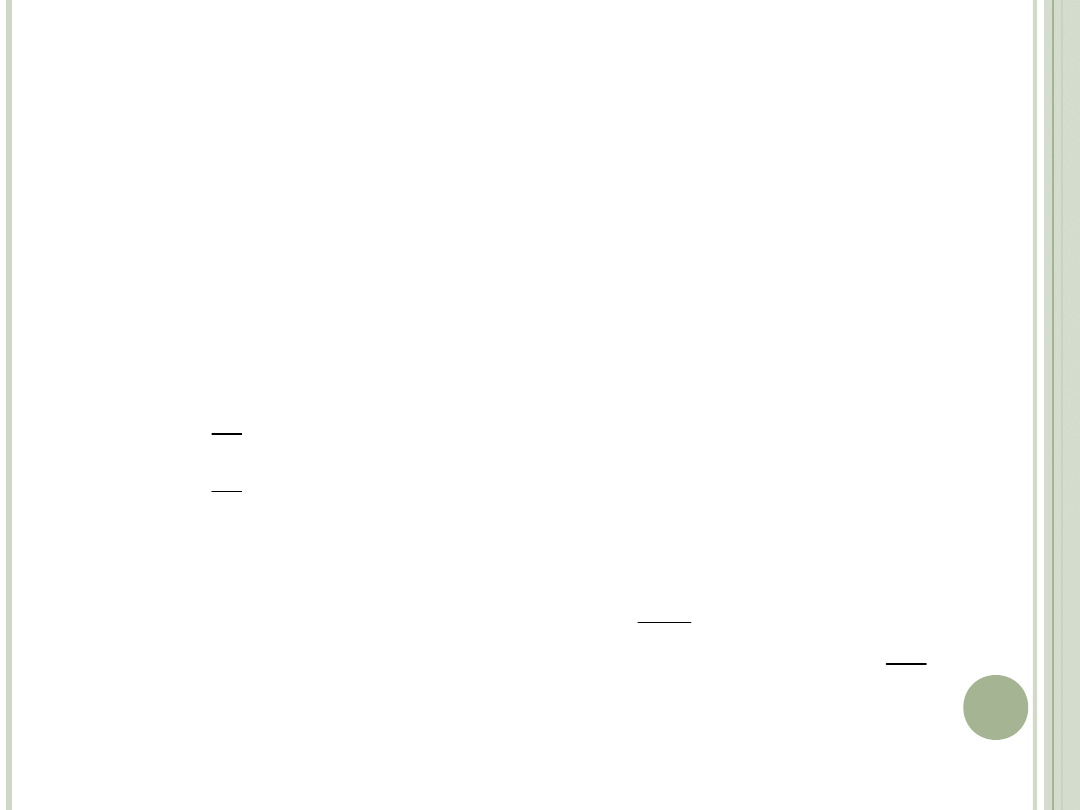
PROBLEM DECYZYJNY



maksymalizacja funkcji użyteczności
względem bieżących oszczędności oraz
inwestycji



W.K.

Przychód od oszczędności 1+r musi być
równy relacji krańcowych użyteczności ,
ta zaś krańcowemu przychodowi od inwestycji

36

))

,

(

),

,

(

(

)

,

(

2

1

2

1

i

s

c

i

s

c

u

c

c

u

u



























0

0

i

u

s

u

2

1

mu

mu

di

df



W.D.

Hesjan jest ujemnie określony w punkcie w

którym

37

di

df

mu

mu

r







2

1

1

PODSUMOWANIE



Jeśli konsument ma dostęp do rynku
kredytowego i inwestycyjnego, to
ograniczenie budżetowe zdeterminowane
jest przez kombinację dochodów w czasie,
realną stopę procentową jak i przez funkcję
przychodu od inwestycji.



Warunki konieczne maksymalizacji
użyteczności konsumenta funkcjonującego
na obu rynkach sprowadzają się do
zrównania relacji krańcowej użyteczności
konsumpcji bieżącej i krańcowej użyteczności
przyszłej zarówno z przychodem od
oszczędności, jak i krańcowym przychodem
od inwestycji.

38