
PODSTAWY
METROLOGII
Wykład 1
Niepewność
pomiarowa

Wprowadzenie
Przy omawianiu błędów wygodnie jest
przypomnieć na wzór terminologii
stosowanej w literaturze zachodniej
rozróżnienie pomiędzy pojęciami
dokładność
i
precyzja
.
Wynik pomiaru określamy wówczas jako
dokładny
, gdy jest on wolny od błędów
systematycznych, natomiast jako
precyzyjny
, gdy jego błąd przypadkowy
jest bardzo mały.

Dokładność pomiaru
- określa, jak bardzo rezultat
pomiaru jest zbliżony do wartości prawdziwej.
Wyniki o dużej dokładności otrzymuje się stosując
mierniki i wzorce o małej niepewności wzorcowania
Precyzja pomiaru
- określa, jak dobrze został
określony rezultat pomiaru, bez odnoszenia się do
wartości prawdziwej.
Wyniki o dużej precyzji otrzymuje się poprzez taką
modyfikację warunków pomiaru, aby niepewności
przypadkowe były jak najmniejsze.
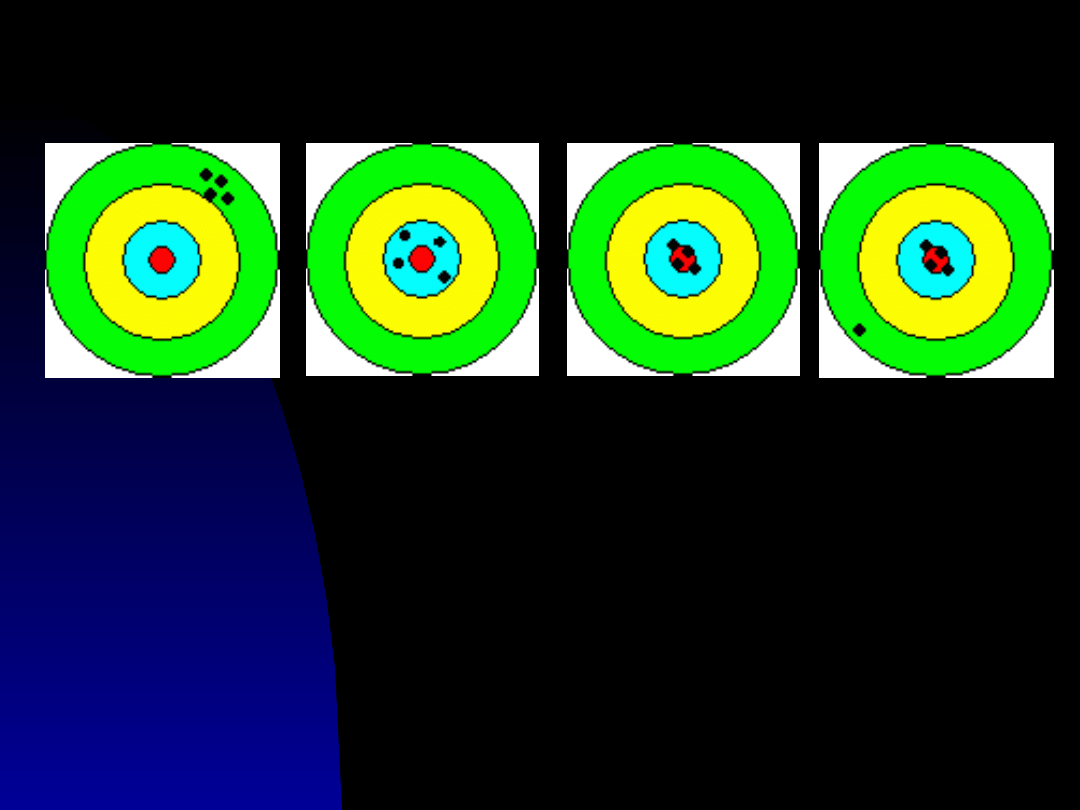
Precyzja
Dokładność
Precyzja i
dokładność
Precyzja i dokładność z
grubym błędem
.
precyzja
mówi nam coś o jakości działania
przyrządu.
dokładność
mówi nam coś o jakości lub
poprawności otrzymanego wyniku.
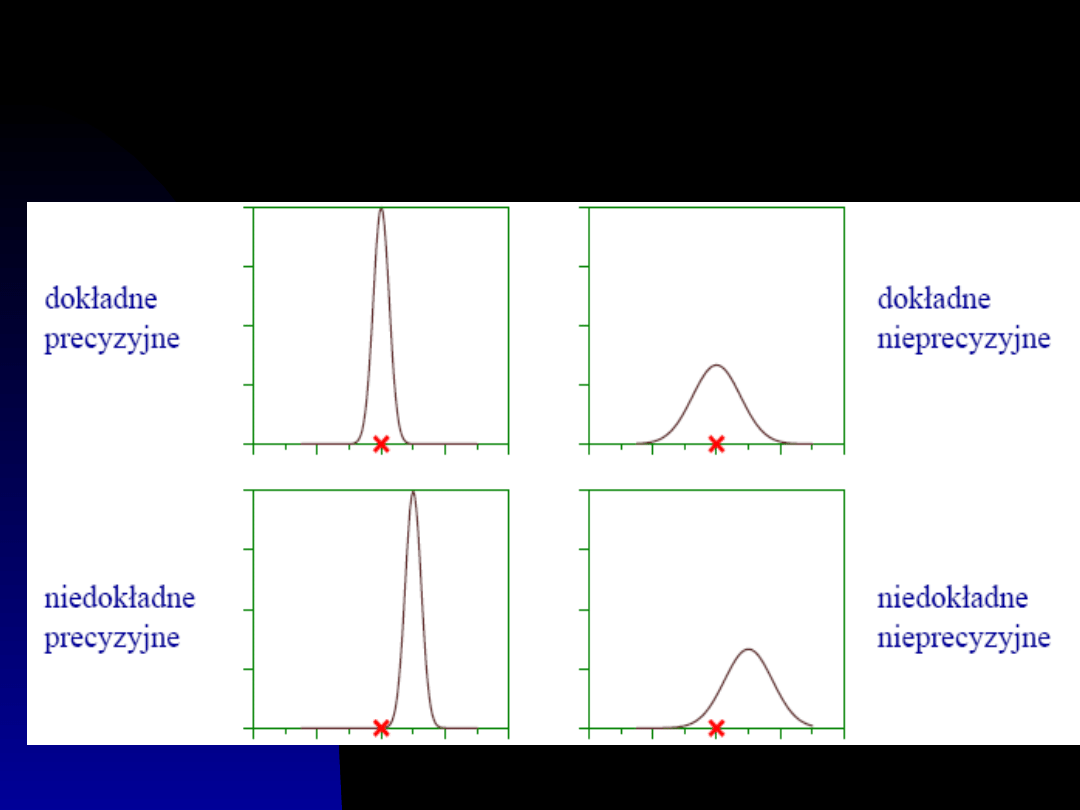
Dokładność i
precyzja

Każdy eksperyment, każdy pomiar i prawie
każda operacja składowa pomiaru daje wyniki
obarczone różnymi typami błędów
– dlatego podanie wyniku pomiaru bez wartości
oszacowanego przedziału niepewności jest błędem

Pomiar
Pomiar
— pewna sekwencja czynności
doświadczalnych i obliczeniowych, prowadząca do
wyznaczenia liczbowej wartości wielkości fizycznej.
Pomiar jest zawsze operacją niedokładną, to znaczy
estymata wartości prawdziwej mezurandu
otrzymana jako wynik pomiaru różni się na ogół od
wartości prawdziwej, równość estymaty i
estymowanej wartości jest zdarzeniem
wyjątkowym, a fakt jego zajścia pozostaje nieznany.

Istotą pomiaru jest jednak to, że niedokładność
wyniku pomiaru można zawsze oszacować, to
znaczy można zawsze określić graniczną
odległość między znanym wynikiem pomiaru a
nieznaną wartością prawdziwą mezurandu.
Szacowanie niedokładności pomiaru jest jedną
z podstawowych czynności, która powinna być
wykonywana w procesie mierzenia.

Wynik pomiaru
wartość pomiaru
±
błąd
pomiarowy

Błąd pomiaru
Błąd pomiarowy niepewność pomiarowa,
dokładność pomiaru
Błąd w pomiarach = pomyłka
.

Rodzaje błędów
Rozróżnia się trzy rodzaje miar
błędu:
błędy prawdziwe,
błędy umownie prawdziwe
błędy graniczne

Błąd pomiaru
Bezwzględny błąd pomiaru -
jest różnicą
miedzy wynikiem pomiaru a wartością
prawdziwą wielkości mierzonej:
X = Xs - Xp ,
gdzie:
Xs — wynik surowy,
Xp — wartość prawdziwa wielkości mierzonej.
Ma on jakąś konkretną wartość, ale niestety nie zawsze jest ona
znana, ponieważ we wzorze definicyjnym występuje nie zawsze
znana wartość prawdziwa
.
Błąd pomiaru jest wskaźnikiem stopnia zgodności wyniku pomiaru i
wartości prawdziwej.

Wynik surowy
jest to wynik pomiaru przed
korekcją błędu systematycznego.
Przy powtarzaniu pomiarów wartość błędu będzie
się zmieniała, co uwidoczni się w zmienności,
ponieważ błąd pomiaru jest wypadkową dwóch
składowych:
•
błędu systematycznego
sX,
•
błędu przypadkowego
pX,
czyli:
X = sX + pX

Podział błędów
Wyniki pomiarów podlegają pewnym
prawidłowościom, tzw. rozkładom typowym dla
zmiennej losowej. Z tego względu błędy
dzielimy na:
•
Błędy grube
(pomyłki), które należy
eliminować
•
Błędy systematyczne
, które można
ograniczyć udoskonaląjąc pomiar
•
Błędy przypadkowe
, które podlegają prawom
statystyki i rachunku prawdopodobieństwa,
wynikają z wielu losowych przyczynków i nie
dają się wyeliminować

Błąd systematyczny
Błąd systematyczny
zdefiniowany jest następująco:
„Błąd systematyczny jest różnicą między wartością
średnią Χśr z nieskończonej liczby wyników
pomiarów tej samej wielkości mierzonej,
wykonanych w warunkach powtarzalności, a
wartością prawdziwą wielkości mierzonej Χp ":
sΧ = Χśr − Χp .

Błąd przypadkowy
Błąd przypadkowy
ma następującą definicję:
„Błąd przypadkowy jest różnicą między
wynikiem pomiaru X a średnią Χśr z
nieskończonej liczby wyników pomiarów tej
samej wielkości mierzonej, wykonanych w
warunkach powtarzalności"
pΧ = Χ − Χśr .
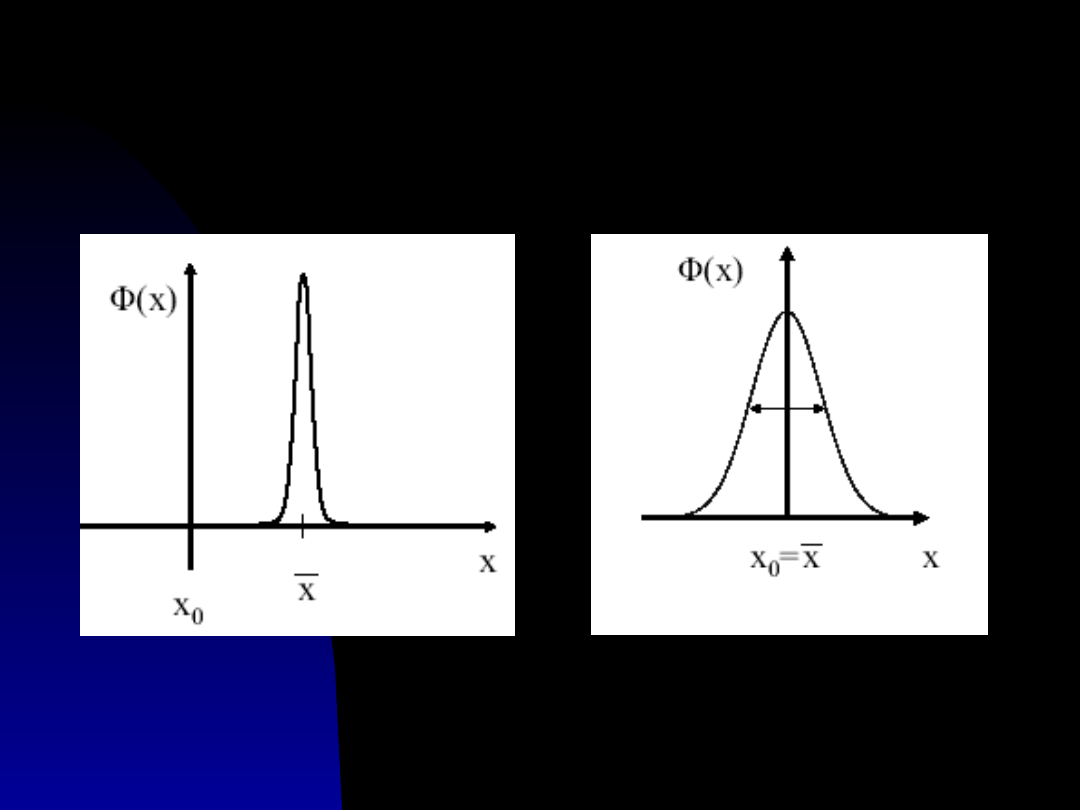
Krzywe rozkładu
błędu
Błąd systematyczny Błąd przypadkowy


Rodzaje błędów
Wartość oczekiwana błędu
przypadkowego jest równa
zeru
,
- właściwość ta nie zawsze jest zgodna z
sensem fizycznym błędów przypadkowych.

Całkowity błąd pomiaru
Χ = sΧ + pΧ .
Względny błąd pomiaru
zdefiniowany jest
jako stosunek bezwzględnego błędu
pomiaru do wartości prawdziwej, czyli:

Poprawka
Jeżeli znana jest wartość błędu systematycznego, to
można go wyeliminować z wyniku pomiaru poprzez
wprowadzenie
poprawki
.
Poprawka ma wartość błędu systematycznego, ale ze
znakiem przeciwnym
:
p(X) = - sX
Poprawka jest wartością dodawaną algebraicznie do surowego wyniku
pomiaru w celu skompensowania błędu systematycznego.
Wynik pomiaru po korekcji błędu systematycznego nazywamy wynikiem
poprawionym.

Rodzaje błędów
Podział błędów ze względu na fizyczne
przyczyny powstawania błędu - wyróżnia się tu
m.in.:
błąd wzorcowania,
błąd niestałości,
błędy kwantowania,
błędy próbkowania,
błędy zliczania,
itd.
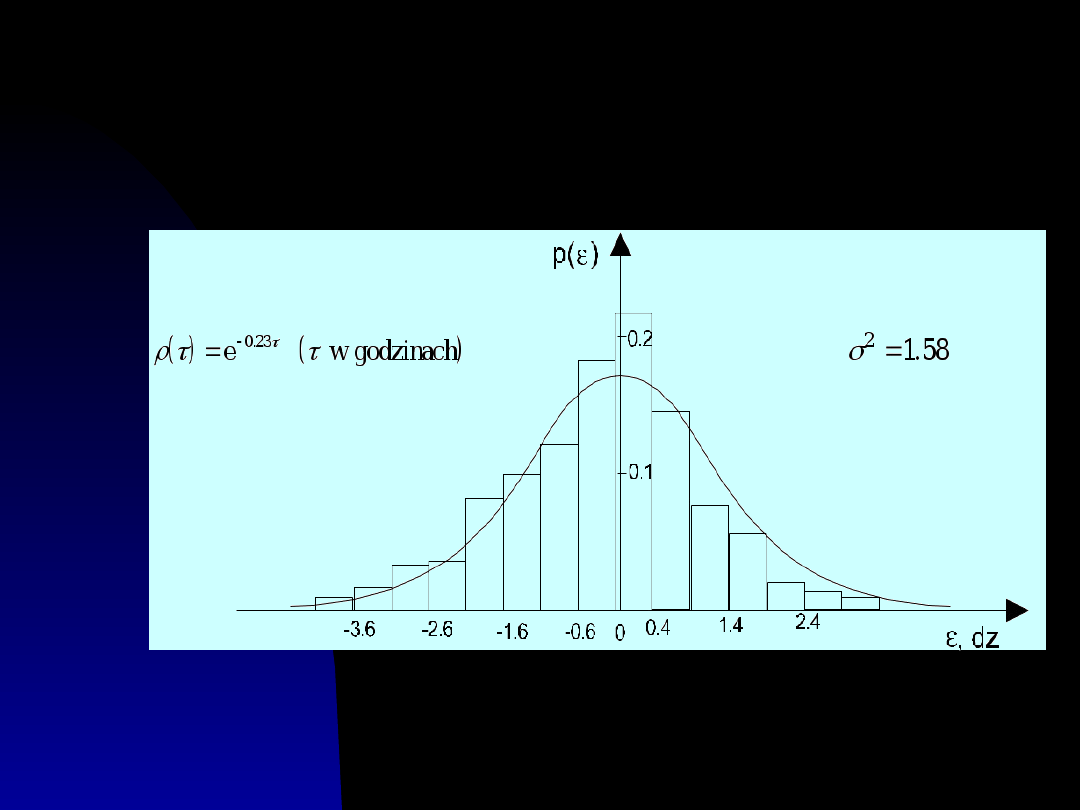
Charakterystyka
metrologiczna
Rozkład prawdopodobieństwa błędu
niestałości
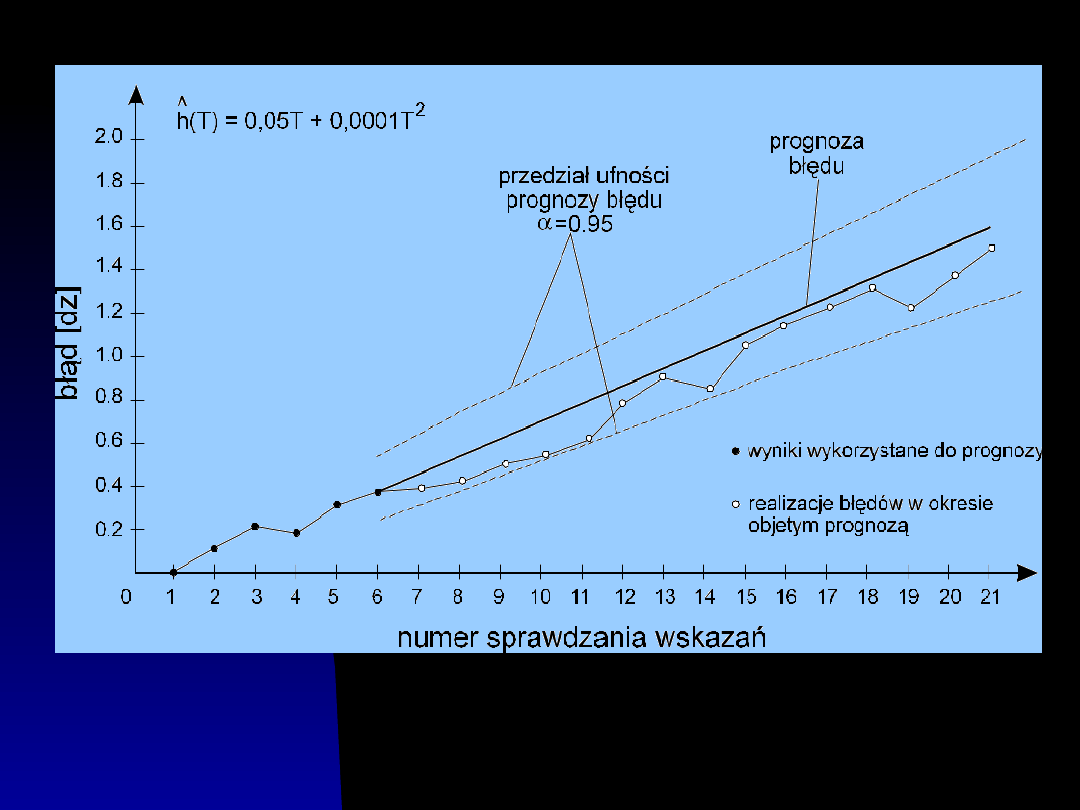
Przebieg błędu niestałości i jego
prognoza
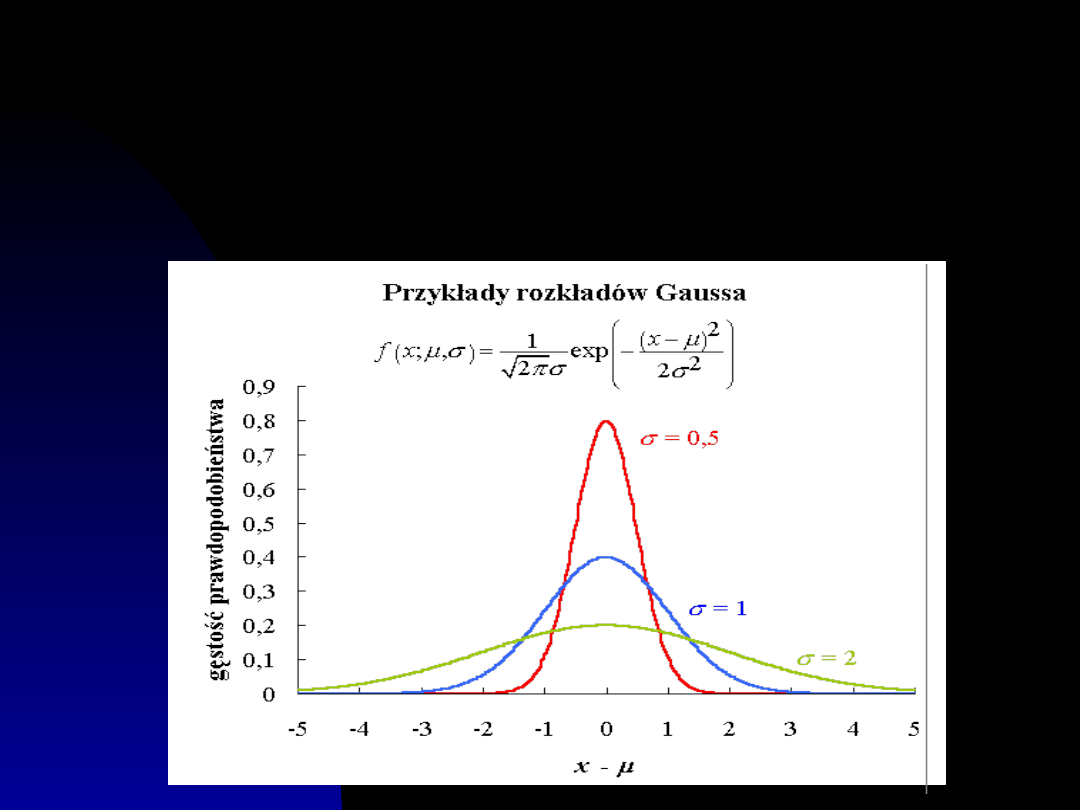
Jeżeli pomiary pewnej wielkości x narażone są
na wpływ wielu niewielkich i przypadkowych
zaburzeń, to rozkład wyników jest rozkładem
normalnym lub rozkładem Gaussa.

Niepewność
pomiaru
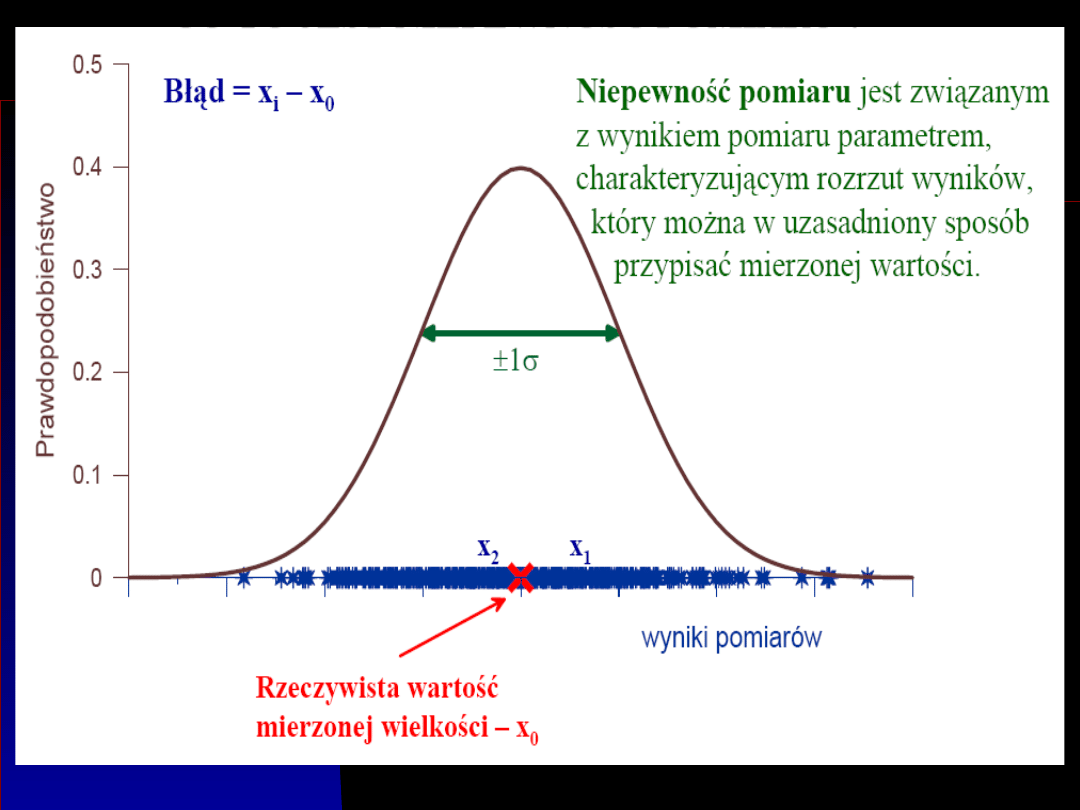
Niepewność możemy określić w rożny
sposób:
-przyjmując model statystyczny,
- posługując się deterministyczną teorią niepewności
maksymalnej.
Międzynarodowa Norma Oceny Niepewności Pomiaru zawarta w
dokumencie
Guide to the Expression of Uncertainty
Measurements
opracowanym przez ISO)posługuje się w opisie
niepewności
modelem statystycznym.

Podstawowe terminy i
definicje
•
wartość oczekiwana
– wartość
zgodna ze zdefiniowana, jest nazywana
często wartością rzeczywista; jest to
wartość, która może być uzyskana w
wyniku doskonałego pomiaru;
•
wartość oznaczana
– wartość
uzyskana w wyniku zastosowania danej
procedury analitycznej; wynik pomiaru
to najczęściej średnia arytmetyczna z
uzyskanych wartości oznaczanych;

•
dokładność pomiaru
– stopień zgodności
pomiędzy wynikiem pojedynczego
pomiaru a wartością rzeczywista;
•
poprawność pomiaru
– stopień
zgodności pomiędzy wynikiem analizy
(średnią) a wartością rzeczywistą;
•
precyzja pomiaru
– zgodność pomiędzy
uzyskiwanymi niezależnymi pomiarami;

niepewność pomiaru
(uncertainty) –
parametr związany z wynikiem pomiaru,
który określa przedział wokół wartości
średniej, w którym może (na założonym
poziomie istotności) znaleźć się wartość
oczekiwana;
standardowa niepewność pomiaru
(standard uncertainty) –
u(xi)
-
niepewność pomiaru przedstawiona i
obliczona jako odchylenie standardowe;

złożona standardowa niepewność
(combined standard uncertainty) –
uc(y)
–
standardowa niepewność wyniku
y
pomiaru,
której wartość jest obliczona na podstawie
niepewności parametrów wpływąjących na
wartość wyniku analizy z zastosowaniem prawa
propagacji niepewności;
rozszerzona niepewność
(expanded
uncertainty) -
U
– wielkość określająca przedział
wokół uzyskanego wyniku analizy, w którym
można, na odpowiednim, przyjętym poziomie
istotności (prawdopodobieństwa) oczekiwać
wystąpienia wartości rzeczywistej;

•
współczynnik rozszerzenia
(coverage
factor) –
k
– wartość liczbowa użyta do
wymnożenia złożonej standardowej
niepewności pomiaru w celu uzyskania
rozszerzonej niepewności, wartość
współczynnika zależy od przyjętego
poziomu prawdopodobieństwa (np.: dla 95
% wynosi 2) i najczęściej jest wybierana z
przedziału liczb 2-3;

Niepewność
W praktyce nie znamy wartości rzeczywistych
wielkości mierzonych i szacujemy
niepewności pomiarowe wynikające ze
statystycznych praw rozrzutu pomiarów
.
Niepewność pomiaru jest związanym
rezultatem pomiaru parametrem,
charakteryzującym rozrzut wyników, który
można w uzasadniony sposób przypisać
wartości mierzonej.
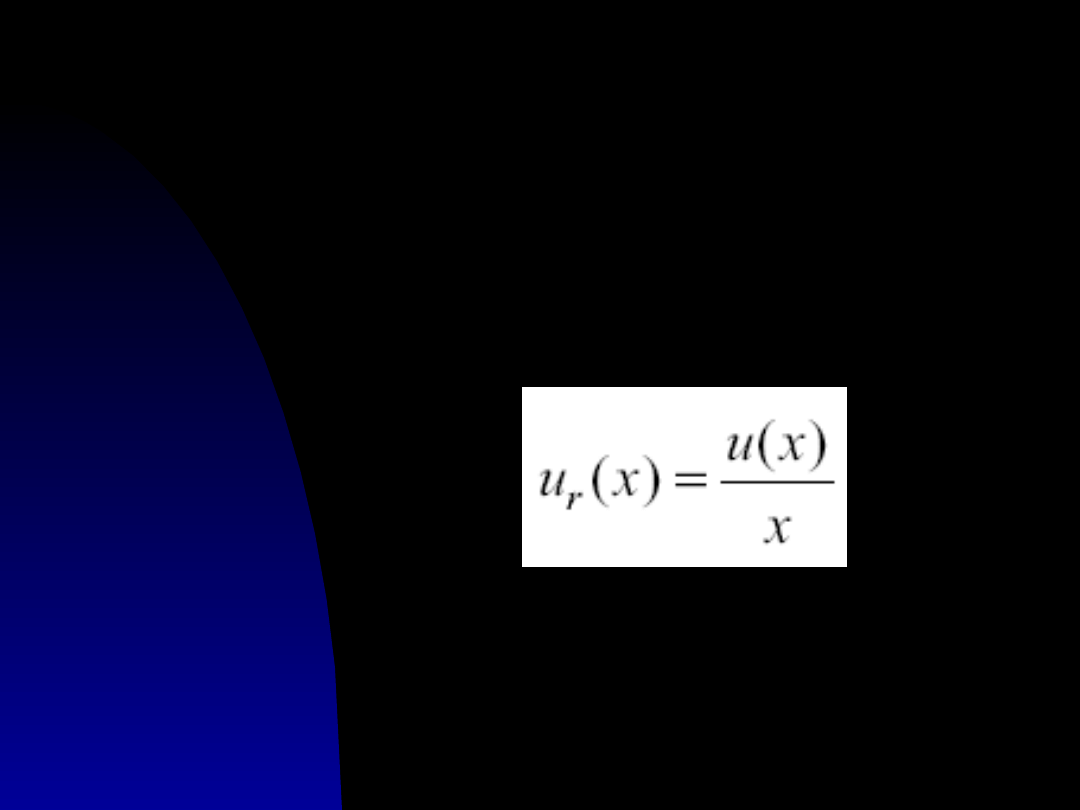
Niepewność u
lub
u(x)
(ang.
uncertainty) posiada wymiar, taki sam
jak wielkość mierzona
Niepewność względna ur(x)
to
stosunek niepewności (bezwzględnej) do
wielkości mierzonej:
Niepewność względna
jest wielkością
bezwymiarową i może być wyrażona w %
Niepewność
Istnieją dwie miary niepewności
pomiaru:
niepewność standardowa
u(x)
niepewność maksymalna
Δx
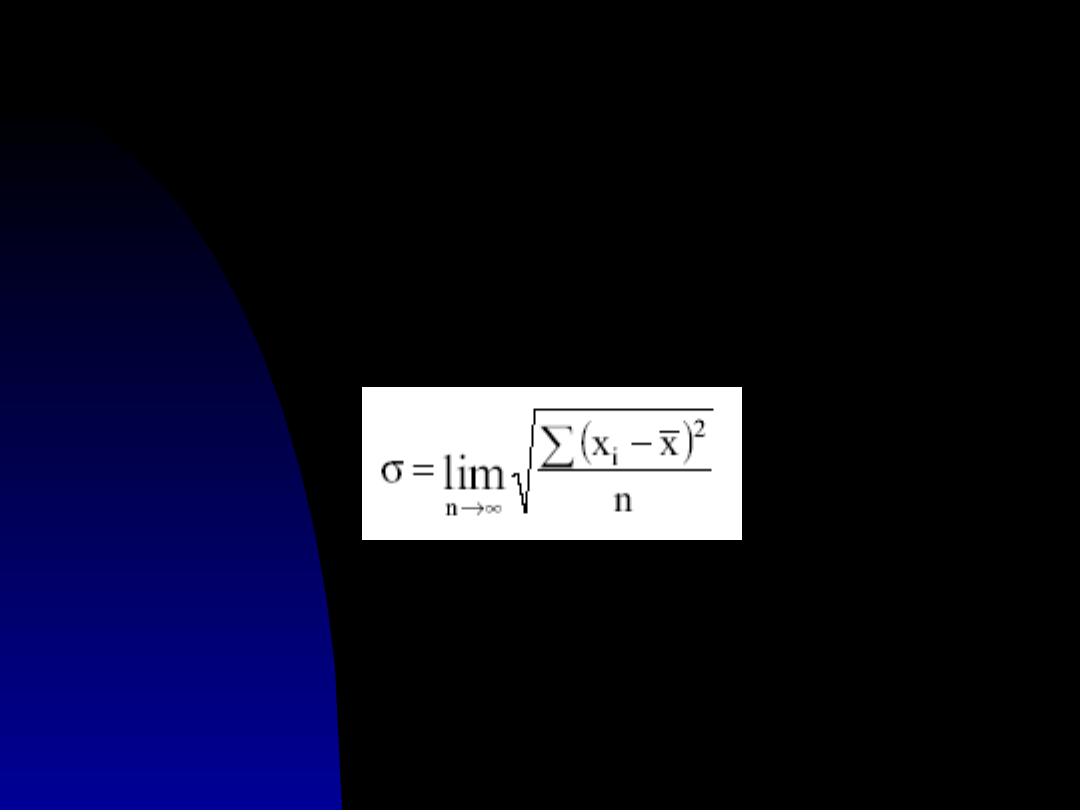
Niepewność
standardowa
Rezultat pomiaru jest zmienną losową
x
i
, której
rozrzut wokół wartości średniej
x
charakteryzuje parametr zwany odchyleniem
standardowym
Dokładnej wartości odchylenia standardowego
nie znamy. Niepewność standardowa jest jego
niezbyt dokładnym oszacowaniem
(estymatorem, oceną).

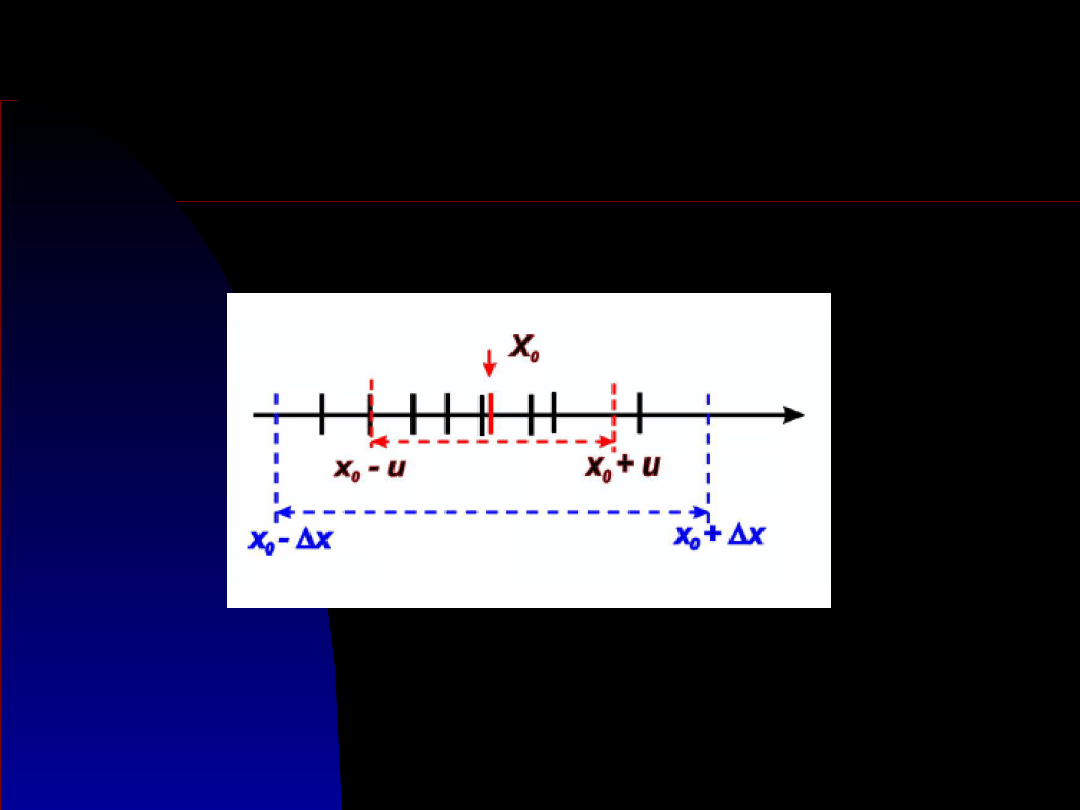
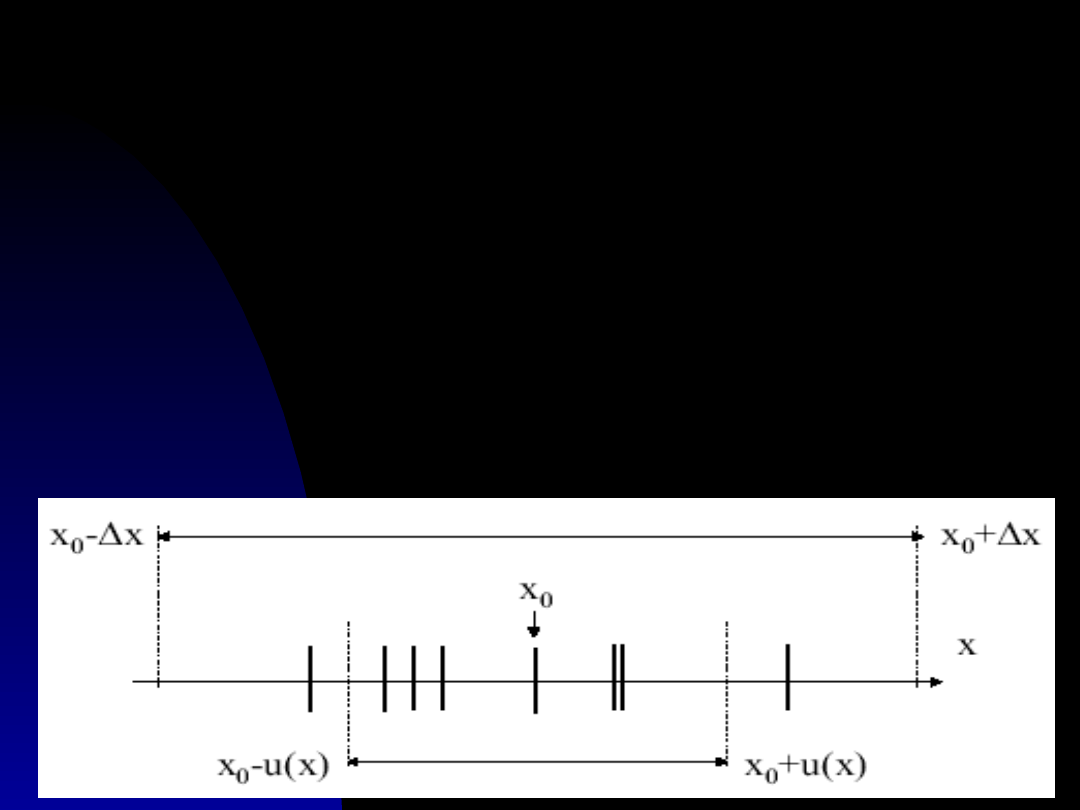
Niepewność
maksymalna
Jest miarą deterministyczną, gdyż zakłada, że można
określić przedział wielkości mierzonej x, w którym
na pewno znajdzie się wielkość rzeczywista.
W tym przypadku staramy się określić przedział,
x
o
- Δx < x
i
< x
o
+ Δx
w którym mieszczą się wszystkie wyniki pomiaru xi,
aktualnie wykonane i przyszłe.
Zaleca się obecnie niepewność maksymalną
specyfikowaną przez producenta zamieniać na
niepewność standardową wg wzoru:

Typy oceny
niepewności
Typ A
Metody wykorzystujące statystyczną analizę serii
pomiarów:
•wymaga odpowiednio dużej liczby powtórzeń pomiaru
• ma zastosowanie do błędów przypadkowych
Typ B
Opiera się na naukowym osądzie eksperymentatora
wykorzystującym wszystkie informacje o pomiarze i
źródłach jego niepewności
•
stosuje się gdy statystyczna analiza nie jest możliwa
•dla błędu systematycznego lub dla jednego wyniku
pomiaru
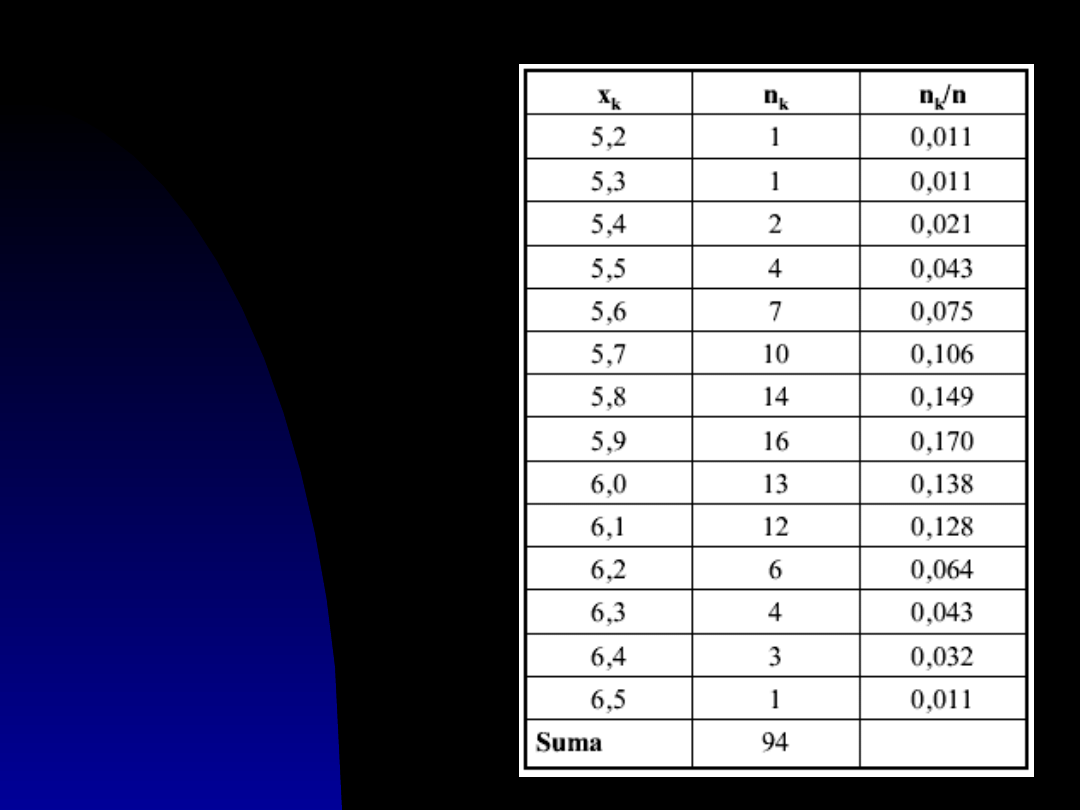
Typ A
Seria wyników (próba)
x
1
,x
2
, ….x
n
obarczonych
niepewnością
przypadkową jest duża
gdy 30<n<100. W
próbie takiej wyniki się
powtarzają:
n
k
jest
liczbą pomiarów, w
których wystąpił wynik
x
k
,
n
k
/n
jest częstością
występowania wyniku
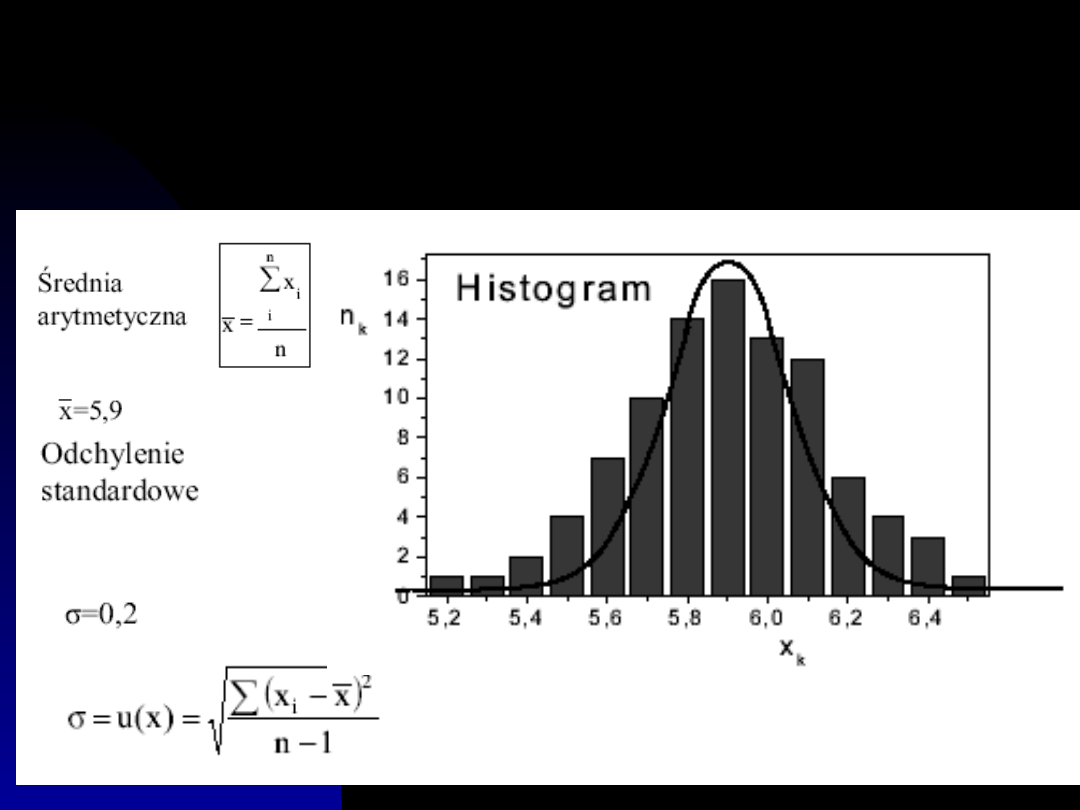
Opracowanie serii
pomiarów
bezpośrednich dużej
próby
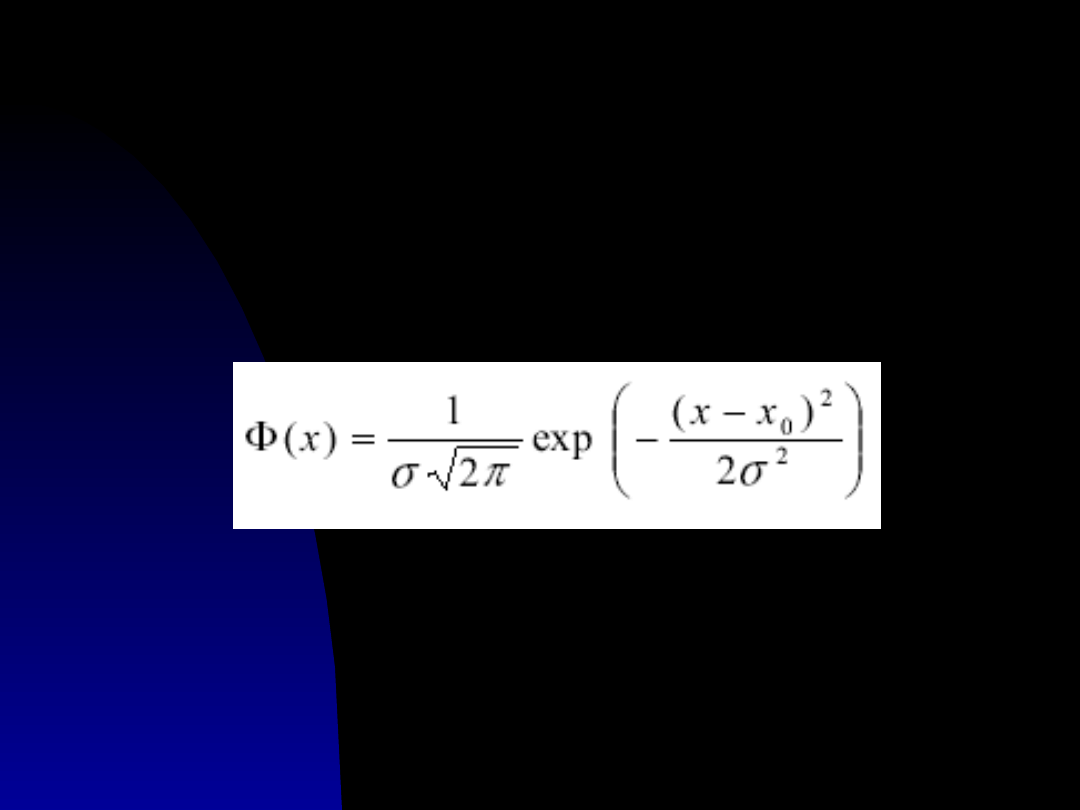
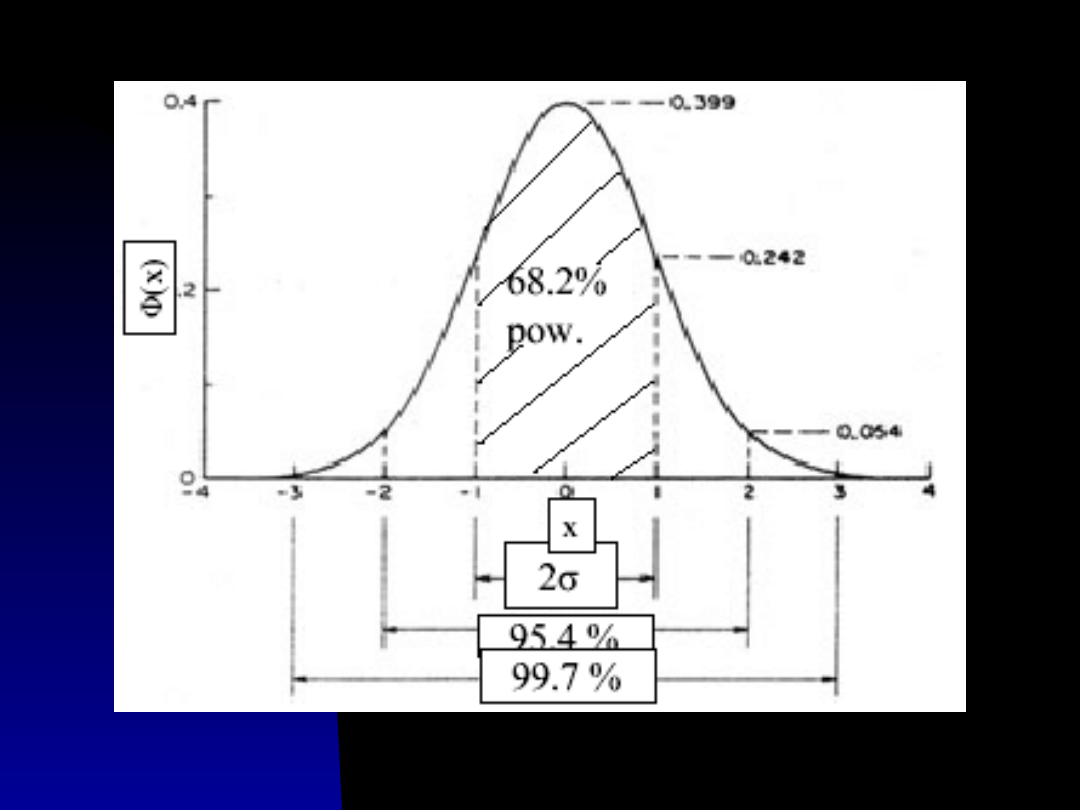
Rozkład normalny
Gaussa
Gęstość prawdopodobieństwa wystąpienia
wielkości x lub jej błędu Δx podlega rozkładowi
Gaussa
x
0
jest wartością najbardziej prawdopodobną i
może być nią średnia arytmetyczna, jest
odchyleniem standardowym, jest wariancją
rozkładu
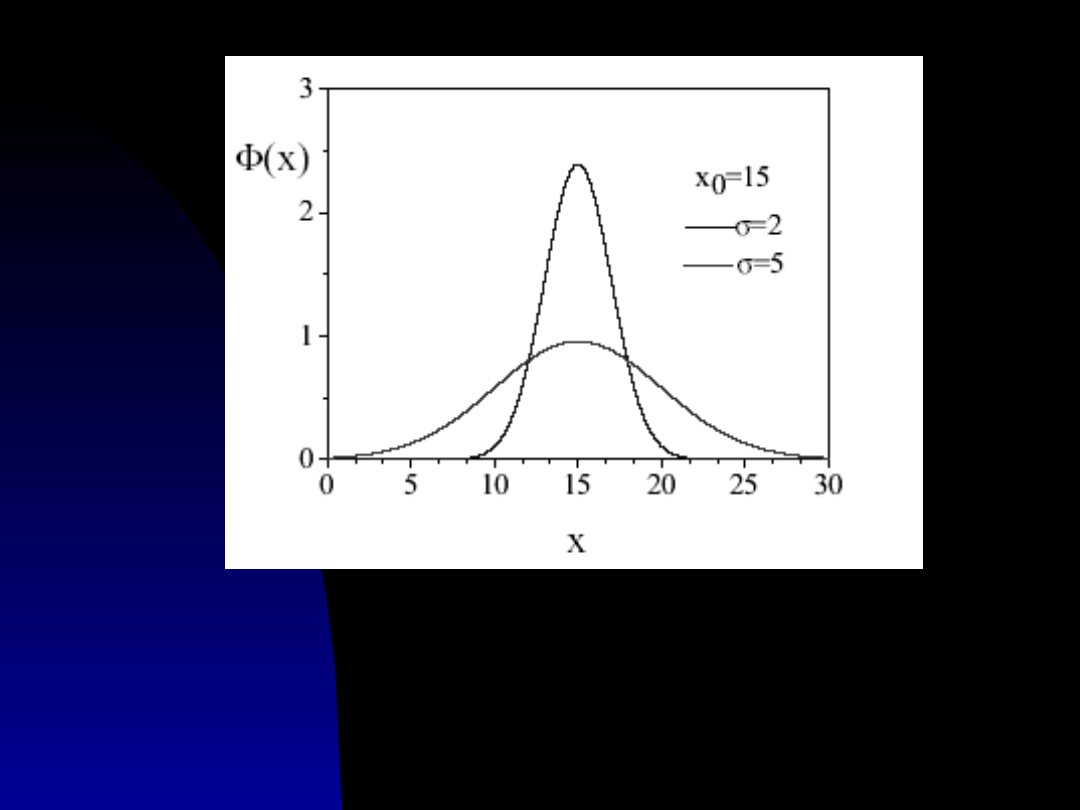
Pomiar o większym
σ
charakteryzuje się
większym rozrzutem wyników wokół
wartości średniej a zatem mniejszą
precyzją

Typ B
Dla oceny typu B wykorzystać można
m.in.:
•
dane z pomiarów poprzednich,
• doświadczenie i wiedzę na temat
przyrządów
i obiektów mierzonych,
• informacje producenta przyrządów,
• niepewności przypisane danym z
literatury.
Gdy informacja o pomiarze i źródle jego niepewności
jest dobra, dokładność oceny typu B jest
porównywalna z dokładnością oceny typu A.
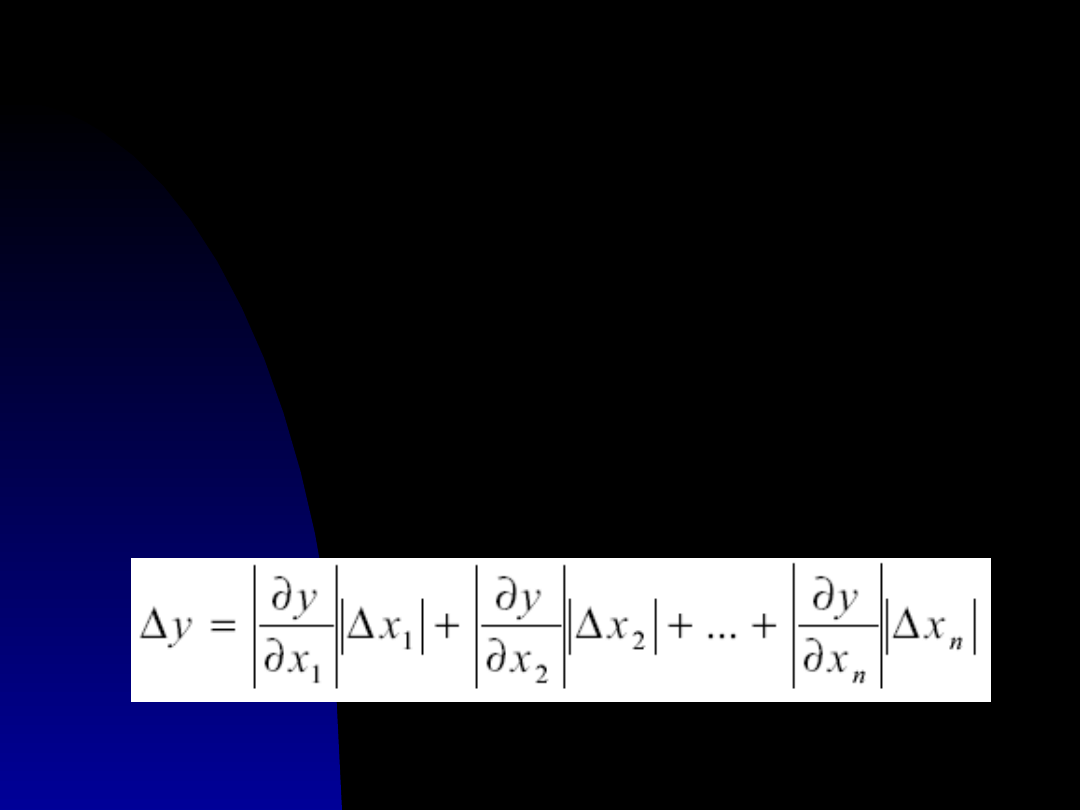
Metoda różniczki
zupełnej
Dla wielkości złożonej y=f(x
1
,x
2
,...x
n
)
gdy niepewności maksymalne Δx
1
,
Δx
2
, ... Δx
n
są małe w porównaniu z
wartościami zmiennych x
1
,x
2
, ... x
n
niepewność maksymalną wielkości y
wyliczamy z praw rachunku
różniczkowego:

Prawo przenoszenia
niepewności
Niepewność standardową wielkości złożonej
y=f(x
1
,x
2
,...x
n
) obliczamy z tzw.
prawa
przenoszenia niepewności
jako sumę
geometryczną różniczek cząstkowych

Zasady wyznaczania niepewności
pomiaru
Wyznaczanie niepewności pomiaru składa się z
następujących kroków:
Określenie wielkości mierzonej (wielkość wyjściowa), wielkości
wpływających na wynik pomiaru i jego niepewność (wielkości wejściowe)
oraz zależności pomiędzy wielkościami wejściowymi a wielkością
wyjściową (model pomiaru)
Zebranie informacji o wartościach i niepewności wielkości wejściowych (np.
błędy graniczne przyrządów pomiarowych, niepewności wzorców lub
materiałów odniesienia, serie wyników powtarzalnych pomiarów)
Wyrażenie niepewności związanych z wielkościami wejściowymi za pomocą
odchyleń standardowych (niepewności standardowe wielkości
wejściowych). Stosowane są metody: A – statystyczne oraz B – inne
Przeliczenie standardowych niepewności wielkości wejściowych na
standardowe niepewności składowe wielkości wyjściowej (wyniku
pomiaru) z wykorzystaniem modelu pomiaru i obliczanych
automatycznie pochodnych cząstkowych
Połączenie standardowych niepewności składowych w standardową
niepewność złożoną wyniku pomiaru
Obliczenie niepewności rozszerzonej wyniku pomiaru

Normy
PN-EN ISO 10012:2004
Systemy zarządzania
pomiarami. Wymagania dotyczące procesów
pomiarowych i wyposażenia pomiarowego
PN-ISO 497:2002
Przewodnik wyboru ciągu liczb
normalnych i ciągów zawierających kolejne
zaokrąglone wartości liczb normalnych
PN-ISO 5725-1:2002
Dokładność (poprawność i
precyzja) metod pomiarowych i wyników
pomiarów. Część 1: Ogólne zasady i definicje
PN-ISO 5725-2:2002
Dokładność (poprawność i
precyzja) metod pomiarowych i wyników
pomiarów. Część 2: Podstawowa metoda
określania powtarzalności i odtwarzalności
standardowej metody pomiarowej

Normy
PN-ISO 5725-3:2002
Dokładność (poprawność i
precyzja) metod pomiarowych i wyników pomiarów.
Część 3: Pośrednie miary precyzji standardowej metody
pomiarowej
PN-ISO 5725-4:2002
Dokładność (poprawność i
precyzja) metod pomiarowych i wyników pomiarów.
Część 4: Podstawowe metody wyznaczania poprawności
standardowej metody pomiarowej
PN-ISO 5725-5:2002
Dokładność (poprawność i
precyzja) metod pomiarowych i wyników pomiarów.
Część 5: Alternatywne metody wyznaczania precyzji
standardowej metody pomiarowej
PN-ISO 5725-6:2002
Dokładność (poprawność i
precyzja) metod pomiarowych i wyników pomiarów.
Część 6: Stosowanie w praktyce wartości określających
dokładność

Normy
PN-ISO 7976-1:1994
Tolerancje w budownictwie. Metody pomiaru
budynków i elementów budowlanych. Metody i przyrządy
PN-ISO 11095:2001
Kalibracja liniowa z zastosowaniem
materiałów odniesienia
PN-ISO 11843-1:2003
Zdolność wykrywania. Część 1:
Terminologia
PN-ISO 11843-2:2003
Zdolność wykrywania. Część 2:
Metodologia w przypadku kalibracji liniowej
PN-ISO 11843-3:2007
Zdolność wykrywania. Część 3:
Metodologia określania wartości krytycznej zmiennej odpowiedzi
bez użycia danych z kalibracji
PN-ISO 11843-4:2007
Zdolność wykrywania. Część 4:
Metodologia porównywania minimalnej wartości. wykrywalnej z
wartością podaną
PN-71/N-02050
Metrologia. Nazwy i określenia

Przykład 1
Zaokrąglić liczbę 1953,5091 do formatów z
ostatnią cyfrą znaczącą kolejno na miejscach od
trzeciego po przecinku do czwartego przed
przecinkiem.
Stosując zasady mamy kolejno:
1953,509; 1953,51; 1953,5; 1954;
Przykład 2
Mierzymy rezystancję opornika R z rozdzielczością
pozwalającą na otrzymanie wyniku
czterocyfrowego, podanie wyniku w postaci:
R = 29,82 ±0,02385 Ω -
źle!!!
jeśli błąd dx = 0,02385 Ω, wynik ten powinien być zaokrąglony do dx =
0,02 Ω
R = 29,82 ±0,02 Ω - dobrze!!!

Warunek minimum funkcji dwu zmiennych:
Otrzymuje się układ równań liniowych dla
niewiadomych a i b
Rozwiązując ten układ równań otrzymuje
się wyrażenia na a i b
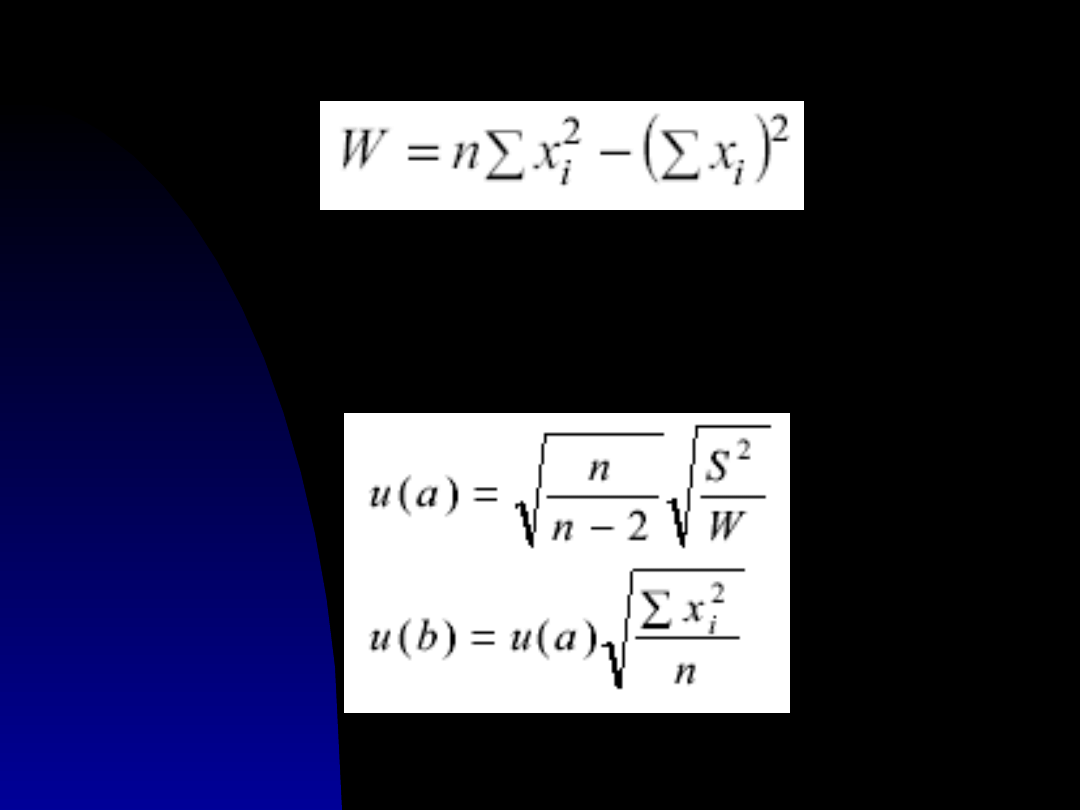
Z praw statystyki można wyprowadzić
wyrażenia na odchylenia standardowe obu
parametrów prostej:
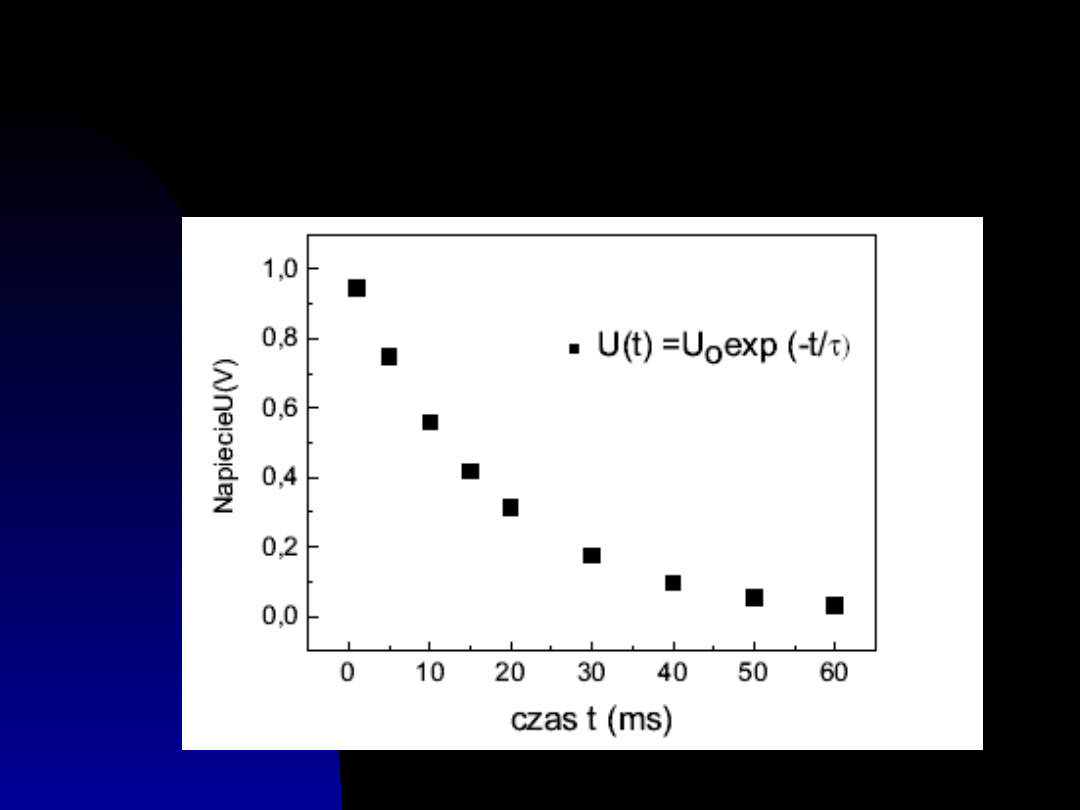
Linearyzacja danych
eksperymentalnych

Zaokrąglanie
liczb
Zaokrąglanie
jest operacją zastępowania cyfrowej
reprezentacji x liczby rzeczywistej x& cyfrową
reprezentacją y tejże liczby x& , ale o mniejszej
ilości cyfr znaczących.
Liczbę x będziemy nazywali liczbą zaokrąglaną, a
liczbę y – liczbą zaokrągloną.
Niech liczba zaokrąglona y ma ostatnią cyfrę
znaczącą na pozycji J, niech dalej liczba
zaokrąglana x jest zapisana w postaci ciągu cyfr
(dK-1 dK-2 ... dJ+1 dJ , dJ-1 dJ-2 ...)×10J .

Zaokrąglanie normalne
jest określone zależnością:
gdzie roundJ () – operator zaokrąglania normalnego do
ostatniej cyfry znaczącej na pozycji J.
Zaokrąglanie w górę
polega na utworzeniu y przez
odrzucenie wszystkich cyfr x po dJ i dodaniu doń 10J
(jeżeli któraś z odrzuconych cyfr jest różna od zera) lub
pozostawieniu tak otrzymanej reprezentacji (jeżeli
wszystkie odrzucone cyfry są zerami).
Zaokrąglanie w dół
czyli obcinanie polega na utworzeniu
y przez odrzucenie wszystkich cyfr x po dJ .

Ogólna reguła może więc przyjąć następującą formę:
Ostatnia cyfra znacząca w każdym wyniku
powinna być tego samego rzędu (stać na tym
samym miejscu dziesiętnym) co błąd.
Na przykład:
Wynik
92,81
z błędem
0,3
powinien być
zaokrąglony do
92,8 ±0,3
.
Jeśli błąd równy jest
3
, to ten sam rezultat
należałoby zapisać jako
93±3
,
jeśli zaś błąd wynosi
30
, to zapis powinien być
90
±30
.

Jest wyjątek od podanej tu reguły.
Jeśli pierwsza cyfra błędu jest mała (l lub być może
2), to mogłoby być właściwe pozostawienie w
odpowiedzi jeszcze jednej cyfry znaczącej.
Przykładowo, wynik taki jak:
L = 27,6 ± l cm
jest zupełnie rozsądny.
jego zaokrąglenie do
28 ± l
powodowałoby utratę
informacji.

PODSUMOWANIE
• Każdy pomiar w laboratorium jest obarczony
niepewnością pomiarową, którą eksperymentator
musi określić zgodnie z pewnymi zasadami.
• W pierwszej kolejności należy przeanalizować
źródła błędów, pamiętając, aby wyeliminować
wyniki obarczone błędem grubym. W
laboratorium studenckim błędy systematyczne z
reguły przewyższają błędy przypadkowe.

•
Wielokrotne powtarzanie pomiarów, gdy
dominuje błąd systematyczny, nie ma
sensu. W takim przypadku dokonujemy tylko
3-5 pomiarów w tych warunkach w celu
sprawdzenia powtarzalności.
• Gdy błąd przypadkowy dominuje w
eksperymencie, należy sprawdzić czy
rozkład wyników może być opisany funkcją
Gaussa czy też należy spodziewać się
innego rozkładu. W tym celu dokonujemy
wielokrotnego (np. 100 razy) pomiaru w
tych samych warunkach, obliczamy średnią i
wariancję rozkładu, rysujemy histogram,
etc.)

•
Jako miarę niepewności stosujemy raczej
niepewność standardową, rzadziej
niepewność maksymalną.
• W przypadku wielkości złożonej, stosujemy
prawo przenoszenia błędu. Staramy się
przeprowadzić analizę niepewności wielkości
złożonej tak, aby uzyskać informacje
dotyczące wagi przyczynków, jakie wnoszą do
całkowitej niepewności pomiary
poszczególnych wielkości prostych. W tym
celu należy analizować niepewności
względne.

•
Ważnym elementem sprawozdania z
przebiegu eksperymentu (i to nie tylko w
laboratorium studenckim) jest wykres.
Wykresy sporządzamy zgodnie z dobrymi
zasadami, pamiętając o jednoznacznym
opisie.
• Zawsze, gdy to możliwe, dokonujemy
linearyzacji danych eksperymentalnych, np.
rysując y i ln (x), lub log y i log x, lub y i 1/x
itp. Do tak przygotowanych danych można
zastosować metodę regresji liniowej

•
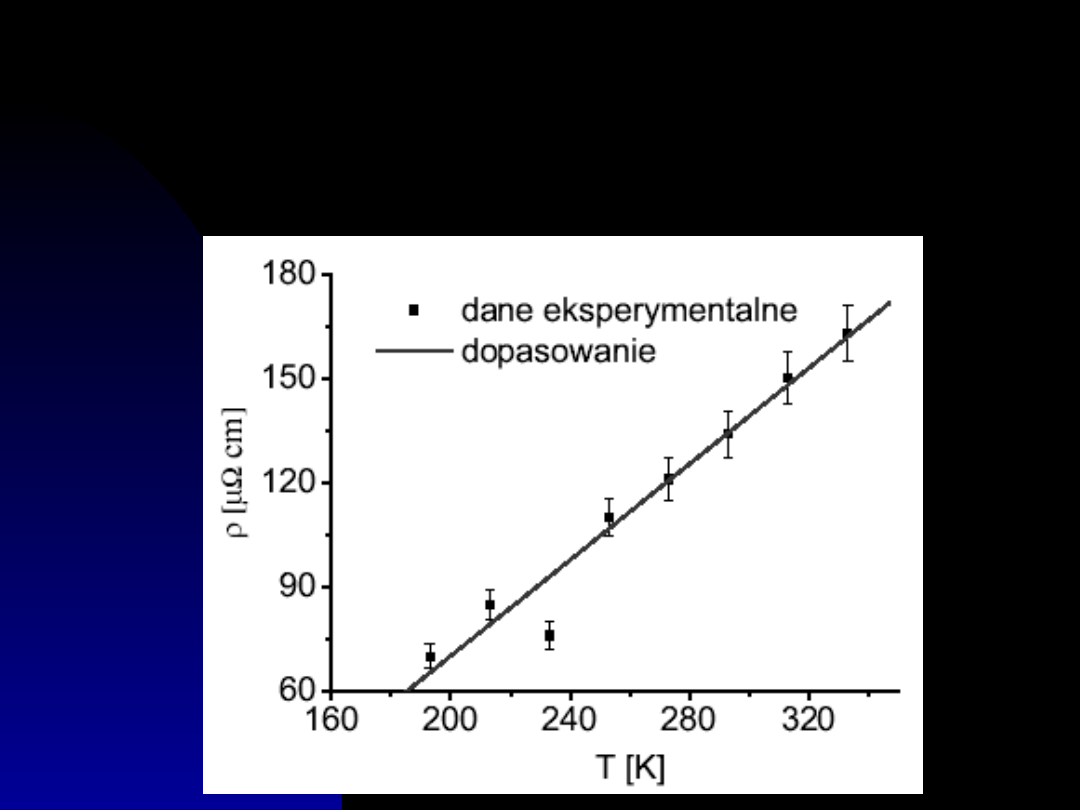
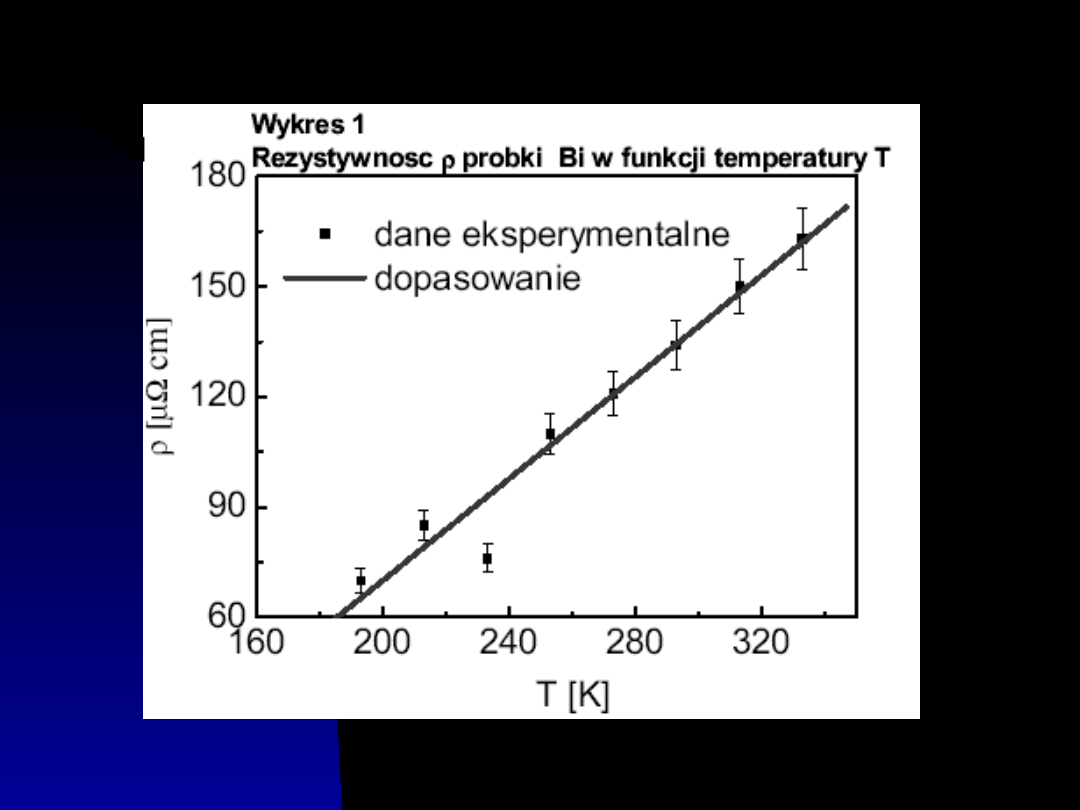
Jeżeli znane są podstawy teoretyczne
badanego zjawiska, na wykresie
zamieszczamy krzywą teoretyczną (linia
ciągła) na tle wyraźnych punktów
eksperymentalnych (dobieramy
odpowiednie symbole i nanosimy
niepewności eksperymentalne). Możemy
wcześniej dokonać dopasowania
parametrów przebiegu teoretycznego w
oparciu o znane metody „dopasowania”
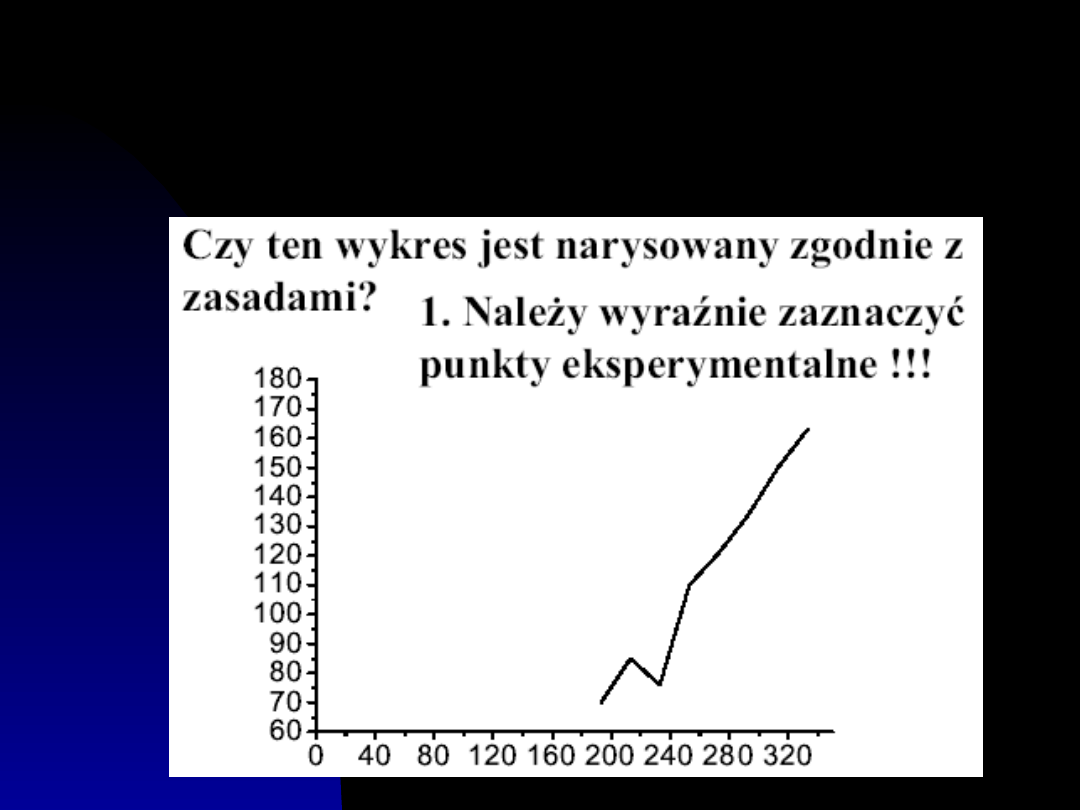
Zasada rysowania
wykresów
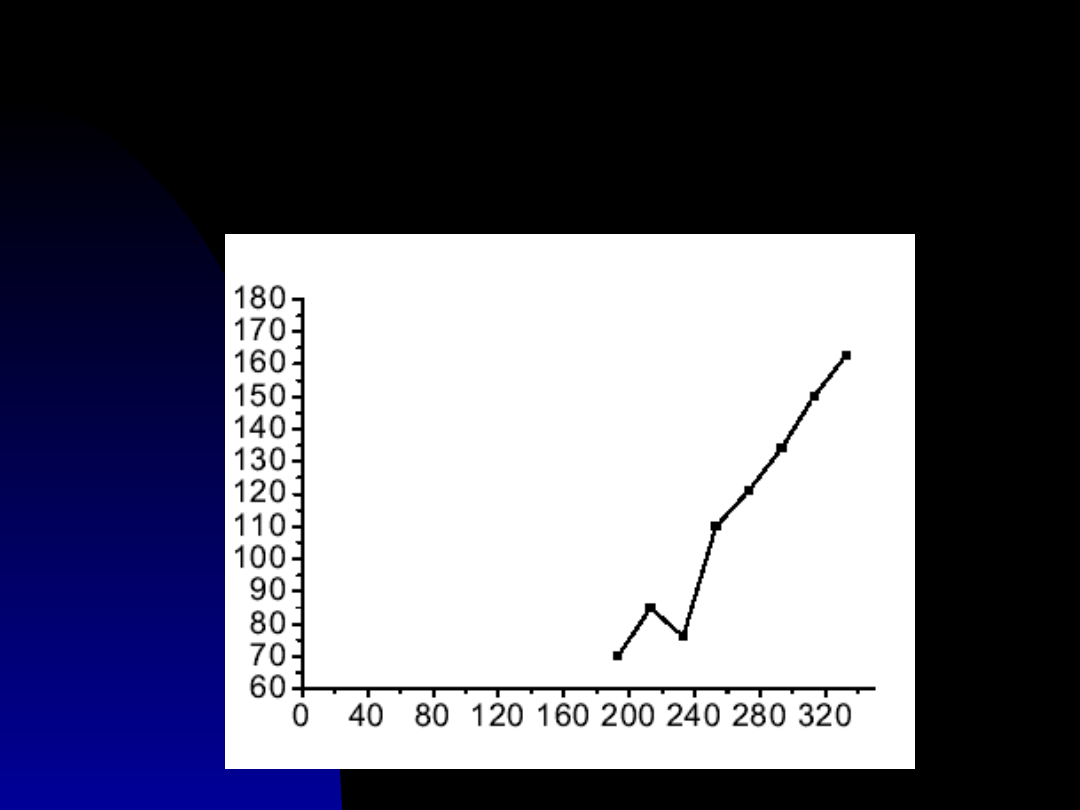
2. Trzeba nanieść błąd pomiaru
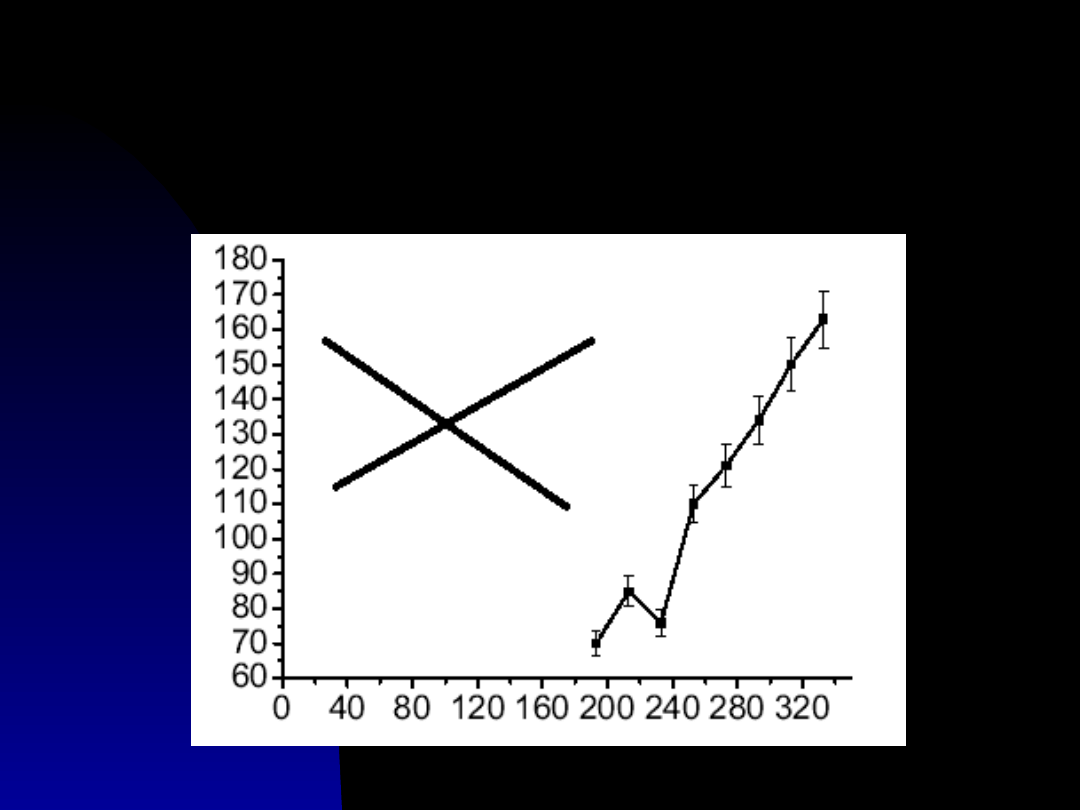
3. Dobrać zakresy osi współrzędnych
odpowiednio do zakresu zmienności danych
pomiarowych !!!
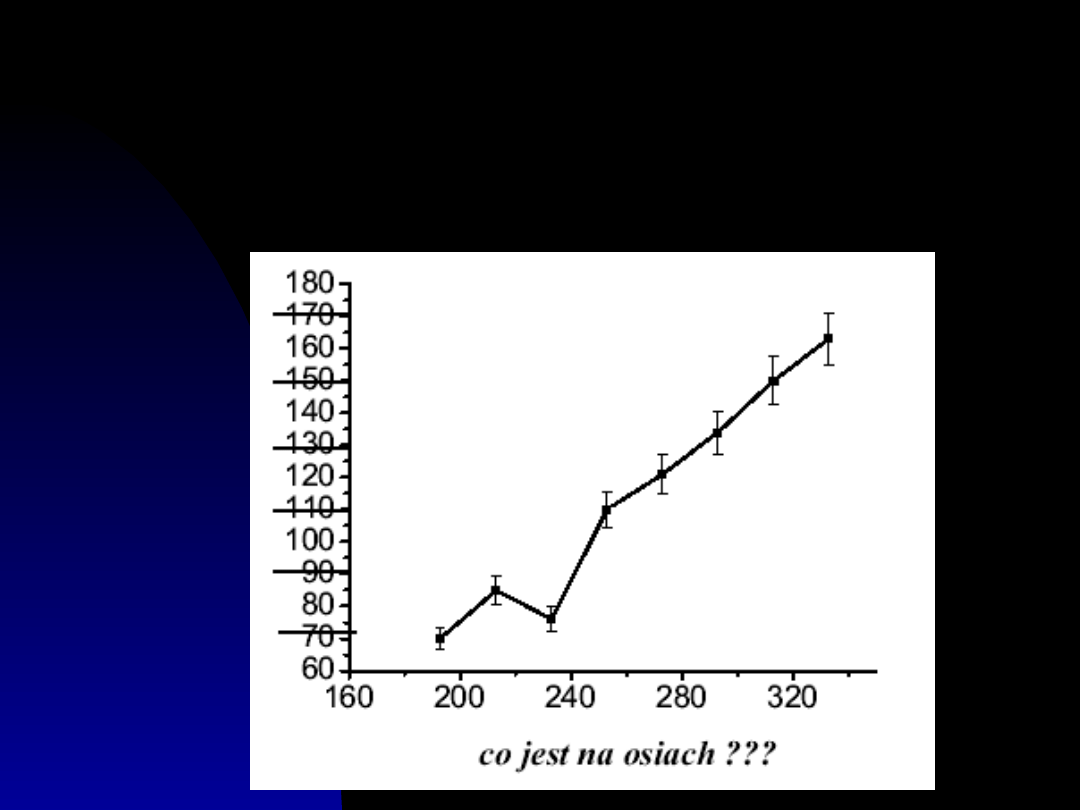
4. Właściwie opisać osie współrzędnych i
dobrać skalę, tak aby łatwo można było
odczytać wartości zmierzone.
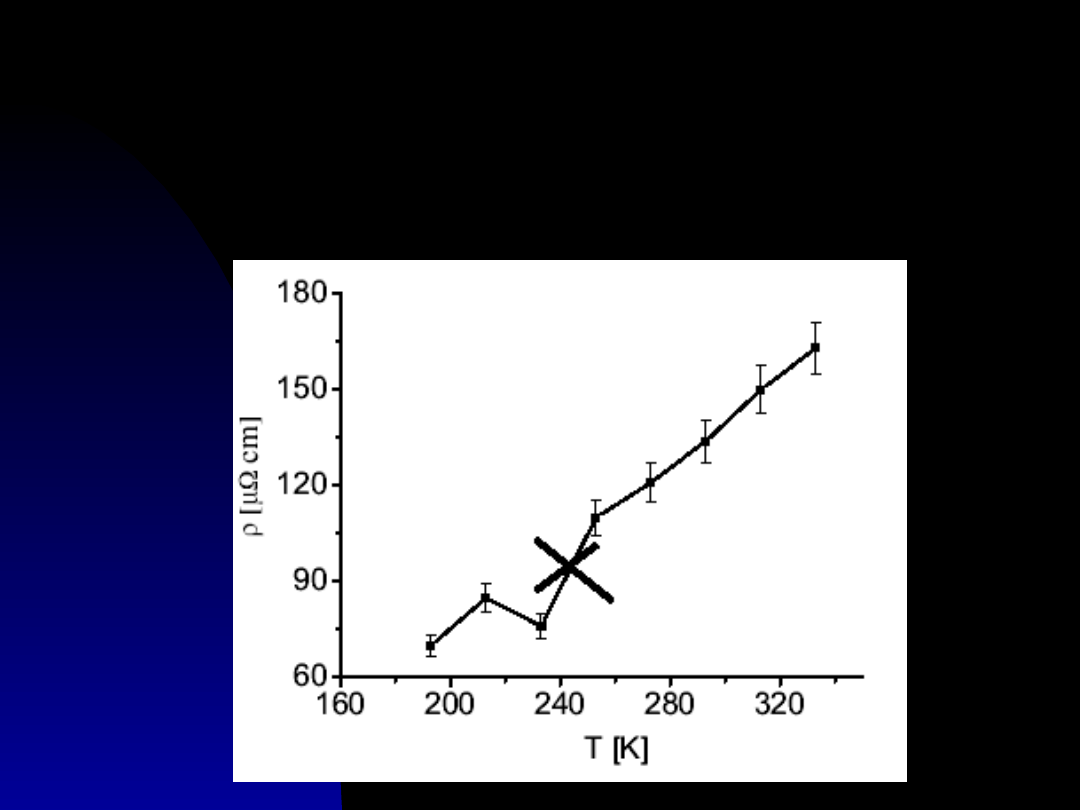
5. Nie łączyć punktów eksperymentalnych
linią łamaną!!! Jeśli znany jest przebieg
teoretyczny to dokonać dopasowania teorii
do doświadczenia
6. Zadbać o aspekt estetyczny wykresu (opis,
zamknięcie ramką, itp.)
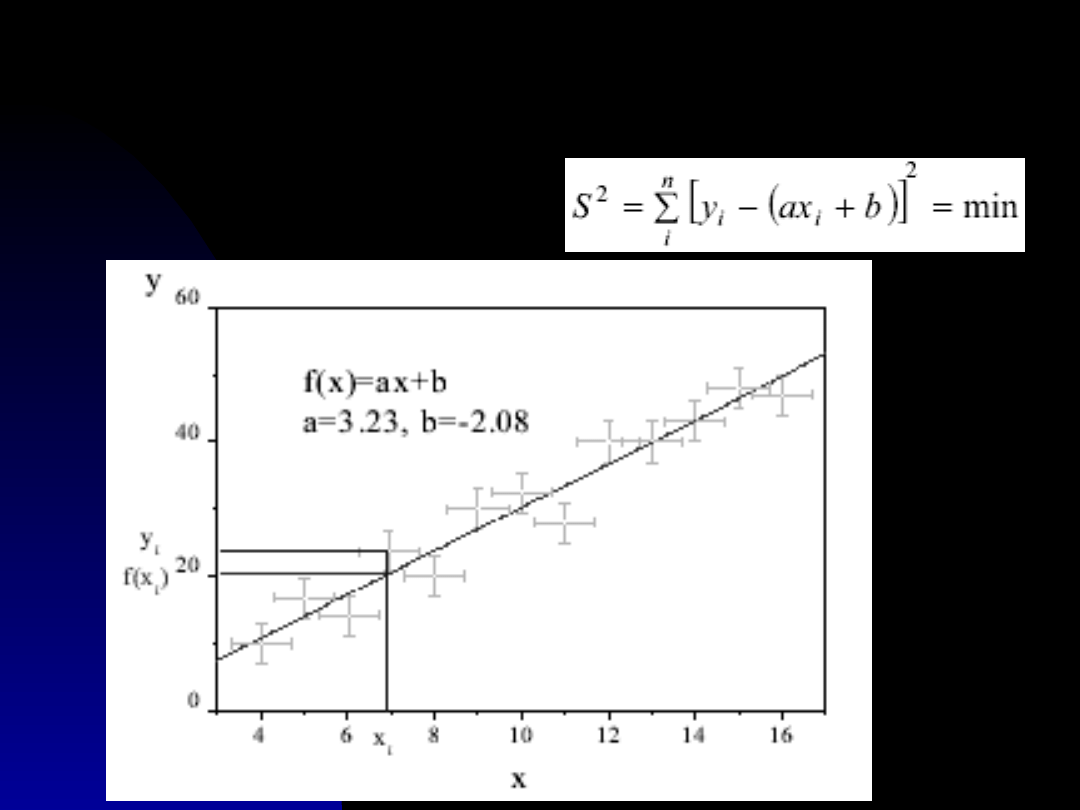
Metoda najmniejszych
kwadratów
Regresja liniowa
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
- Slide 38
- Slide 39
- Slide 40
- Slide 41
- Slide 42
- Slide 43
- Slide 44
- Slide 45
- Slide 46
- Slide 47
- Slide 48
- Slide 49
- Slide 50
- Slide 51
- Slide 52
- Slide 53
- Slide 54
- Slide 55
- Slide 56
- Slide 57
- Slide 58
- Slide 59
- Slide 60
- Slide 61
- Slide 62
- Slide 63
- Slide 64
- Slide 65
- Slide 66
- Slide 67
- Slide 68
- Slide 69
- Slide 70
- Slide 71
- Slide 72
Wyszukiwarka
Podobne podstrony:
Podstawy metr wykł11 2008
Podstawy metr wykł1 2008
Podstawy metr wykł10
Podstawy metr wykł6 2008
Podstawy metr wykł13 2008 Gwinty, koła zębate
Podstawy metr wykł13 2008
Podstawy metr wykł3 2008
Podstawy metr wykł 4 2008
Podstawy metr wykł 5 2008
Podstawy metr wykł2Jednostki 2008
więcej podobnych podstron