23.06.21

IMSiIS

1.1

Uniwersytet Kazimierza Wielkiego

Arytmetyka komputerowa

23.06.21

IMSiIS

1.2

Systemy dziesiętny



Najpopularniejszym z systemów liczbowych 
jest system dziesiętny

234

(10)

 = 2 * 10

2 

+3 * 10

1 

+ 4 * 

10

0

Podstawa 

systemu 

liczbowego

L

(10)

 = C

k

 * 10

n 

+ C

k-1

 * 10

k-1 

+...+ C

0

 * 

10

0

przykład



Uwaga !

W systemie dziesiętnym wykorzystuje 
się 10 cyfr (0, 1,2,3,4,5,6,7,8,9)

23.06.21

IMSiIS

1.3

System dwójkowy



Dwójkowy

 zwany 

binarnym

 systemem liczbowym jest  

pozycyjnym systemem zapisu liczb opartym na 
potęgach liczby 2. Wykorzystuje dwie cyfry (

0

,

1

)

1010

(2)

 = 1 * 2

3 

+0 * 2

2 

+ 1 * 2

1 

+ 0 * 2

0 

= 

10

(10)

przykład



Cyframi tego systemu są: 

0

 i 

1

. Symbolizują one dwa 

stany tzw. stan niski i stan wysoki. Podstawą systemu jest 

2

. Stąd też i nazwa - układ dwójkowy. A ponieważ jest to 

również system pozycyjny, to możemy w znany już sposób 
dokonywać konwersji liczby z systemu dziesiątkowego na 
dwójkowy

23.06.21

IMSiIS

1.4

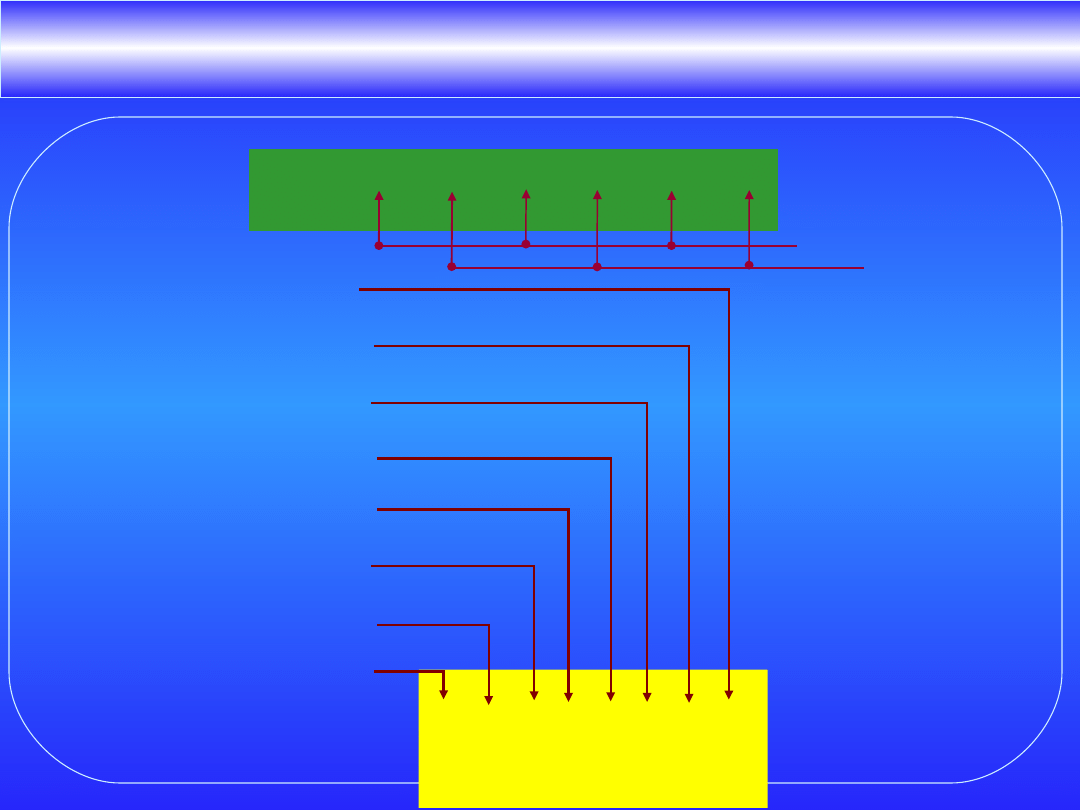
Zmiana liczb dziesiętnych na binarne

236 = 2 · 10

2

+ 3 · 10

1

+ 6 · 10

0

Cyfra

Waga

236 : 2 =118 reszta 

0

 118 : 2 =59 reszta 

0

  59 : 2 = 29 reszta 

1

  29 : 2 = 14 reszta 

1

  14  : 2 = 7 reszta 

0

    7  : 2 = 3 reszta 

1

    3  : 2 = 1 reszta 

1

     1  : 2 = 0 reszta 

1

1 1 1 0 1 1 

0 0

23.06.21

IMSiIS

1.5

Zalety układu binarnego



Mnożenie przez 2 - wystarczy przesunąć wszystkie bity 
w liczbie w lewo o jedną pozycję, 



Dzielenie całkowite przez 2 - poprzez przesunięcie bitów 
w prawo - bit najmniej znaczący (tzw. najmłodszy) jest 
tracony, 



mnożenie i dzielenie całkowite przez potęgi dwójki - 
przesunięcia odbywają się o określoną wykładnikiem 
potęgi liczbę miejsc - na przykład mnożenie przez 8 
odbywa się przez przesunięcie bitów o 3 pozycje w lewo 
(8=2<<3), 



inne, złożone z powyższych.

23.06.21

IMSiIS

1.6

Wady



podany powyżej sposób dotyczy tylko zapisu liczb 
całkowitych dodatnich, w przypadku liczb rzeczywistych 
należy użyć innych metod.



w celu binarnego zapisania dużej liczby potrzebujemy 
znacznie dłuższego ciągu znaków 0/1 niż w przypadku 
zapisu dziesiętnego.



Zapis liczb ujemnych wymaga stosowania dodatkowego 
mechanizmu

23.06.21

IMSiIS

1.7

System szesnastkowy



System szesnastkowy

 zwany 

heksadecymalnym

 

wykorzystuje do zapisu liczby 16 cyfr (dziesięć 

cyfr podstawowych (

0

 – 

9

) oraz litery 

A

, 

B

, 

C

, 

D

, 

E

, 

F

 odpowiadające kolejno wartości 10, 11, 12, 

13, 14, 15



Każdej cyfrze systemu szesnastkowego 

odpowiada cztero-pozycyjna liczba systemu 

dwójkowego. Zamiana liczby dwójkowej na 

szesnastkową polega na przypisaniu każdym 

kolejnym czterem pozycjom zerojedynkowym 

odpowiedniej cyfry układu szesnastkowego

1011 0011 1010

(2)

 = 

B3A

(16)

przykład

11

(10

)

3

(10)

10

(10

)

23.06.21

IMSiIS

1.8

Jednostki informacji



Komputer przechowuje dane w postaci 

liczb binarnych

 (2);



Pojedyncza cyfra systemu dwójkowego mogąca 
przechowywać informację o jednym z dwóch możliwych 
stanów – może przybierać wartość 

0

 lub 

1

, oznacza 

najmniejszą i niepodzielną jednostkę informacji cyfrowej – 
zwanej 

bit

bit

-em (1 

b

b

);



Bity grupuje się w 

bajt

bajt

 (1 

B)

B)

, którego tworzy 8 bitów.



1 kB =2

10

 B = 1024 B                      (

kilobajt

)



1 MB =2

20 

B = 1024 kB                   (

megabajt

)



1 GB =2

30 

MB = 1024 MB               (

gigabajt

)



1 TB =2

40

B = 1024 GB                    (tera

bajt

)



1 PB =2

50

B = 1024 TB                     (

peta bajt

)



1 EB =2

60

B = 1024 PB                     (

eksabajt

)

23.06.21

IMSiIS

1.9

Reprezentacja liczb naturalnych



Liczby naturalne

 przechowywane są dokładnie tak, jak 

zapisuje się je w systemie dwójkowym. 



Każdy bit stanowi pojedynczą cyfrę w tym systemie;



Liczba zapisana w postaci binarnej jest określona przez 
ilość możliwych kombinacji bitów zajmując przy tym 
określony obszar pamięci komputera

2

8

 = 256

przykład

Dla 1 B (8b) możliwych liczb 
będzie:

Przyjmując za pierwszą liczbę 0 otrzymujemy zakres liczb 0 - 
255

bit

7

6

5

4

3

2

1

0

waga

128 64

32

16

8

4

2

1

23.06.21

IMSiIS

1.10

Reprezentacja liczb całkowitych



Reprezentację 

liczb całkowitych

 w komputerze 

wymaga zastosowania pewnego mechanizmu do 
najpopularniejszych rozwiązań należy:



reprezentacja 

znak-moduł

 – polega ona na tym, że 

informację o tym czy mamy do czynienia z liczbą 
dodatnią czy ujemną określamy poprzez wartość 
najbardziej znaczącego bitu ( jeśli 

0

 to 

+

, jeśli 

1

 to 

-

)



reprezentacja 

uzupełnienia do dwóch 

(

U2

), 

podobnie jak poprzednia notacja używa najbardziej 
znaczącego bitu jako bitu znaku, różni się natomiast 
interpretowaniem pozostałych bitów.

23.06.21

IMSiIS

1.11

Reprezentacja znak-moduł



Reprezentacja znak-moduł ma kilka wad:



odejmowanie i dodawanie wymaga rozważania znaków 

liczb jaki i ich modułów;



występowanie dwóch reprezentacji liczby 0; 

0

0 1 0 0 1 0 0

zna
k

moduł

1 
bit

N-1 bitów

Słowo 8 bitowe

Możliwe jest zakodowanie 256 liczb 

od –128 (10000000)

(2)

 do 127 

(01111111)

(2)

 

Uwaga !

10000000
00000000

23.06.21

IMSiIS

1.12

Arytmetyka liczb całkowitych



Negowanie



Dodawanie



Odejmowanie



Mnożenie



Dzielenie

23.06.21

IMSiIS

1.13

Negowanie



Negowanie realizuje się za pomocą następujących 
czynności:



 należy zanegować wszystkie bity liczby negowanej 
(negacja bitowa:



Do otrzymanego wyniku dodać 1 stosując normalne 
dodawanie dla liczb binarnych

1

0

0

1

1

1

0

1

~

0

1

1

0

0

0

1

0

0

1

1

0

0

0

1

0

+

0

0

0

0

0

0

0

1

wynik

0

1

1

0

0

0

1

1

Negacja 
bitowa

Liczba 
przeciwna

23.06.21

IMSiIS

1.14

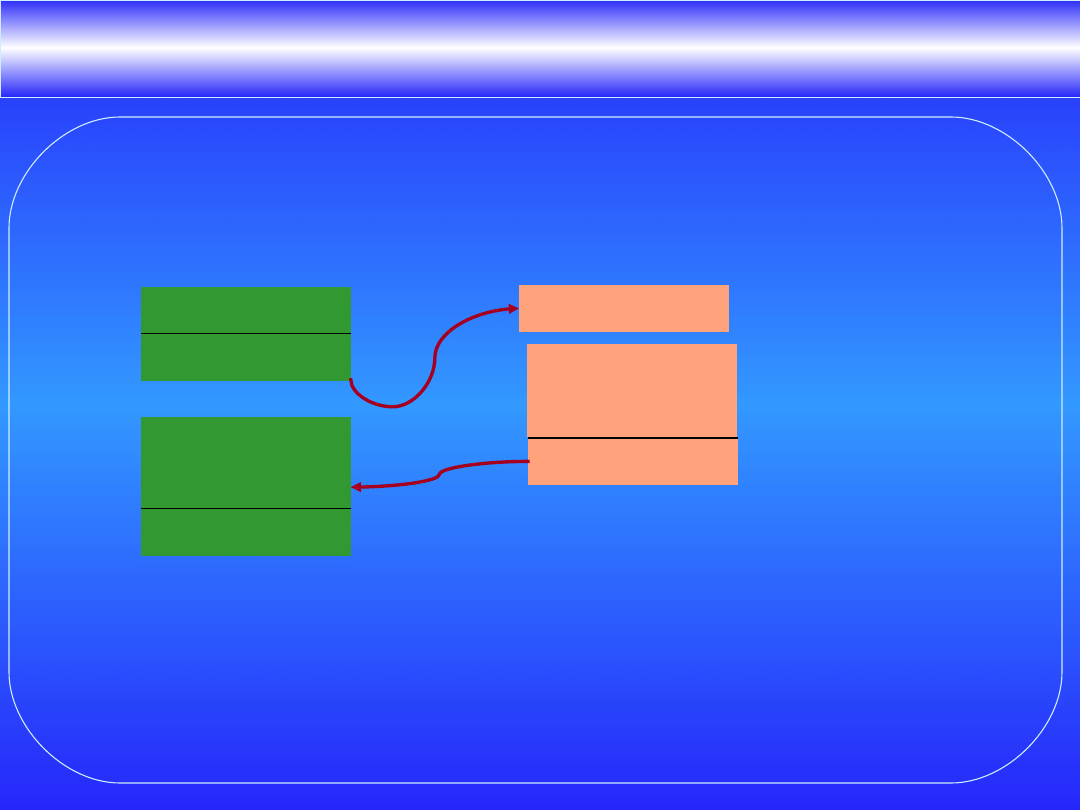
Dodawanie



Dodawanie liczb binarnych z uzupełnieniem do dwóch 

realizowane jest podobnie do dodawanie w układzie dziesiętnym 



Uwaga podobnie, ale nie identyczne

0 0 1 1

0 1 0 0

0 1 1 1

3

4

7

przepełnienie

1 +

1
= 0

23.06.21

IMSiIS

1.15

Odejmowanie



W celu odjęcia od jednej liczby (odjemnej) drugiej liczby 

(odjemnika) wyznaczamy liczbę przeciwną w uzupełnieniu 

do dwóch odjemnika i dodajemy ją do odjemnej

0 1 1

1

0 0 1

0

0 1 1

1

2

7

2-7=2+(-

7)=-5

1 0 0

0

negacja bitowa

0 0 0

1

Dodawana 
jedynka

1 0 0

1

+

Wynik jest liczbą 

przeciwną

0 0 1

0

1 0 0

1

1 0 1

1

-5

+

W przypadku odejmowania 
tez może wystąpić 
przepełnienie

23.06.21

IMSiIS

1.16

Reprezentacja liczb rzeczywistych



W postaci kodu stałoprzecinkowego 
(stałopozycyjnego)



W postaci kodu zmiennoprzecinkowego 
(zmiennopozycyjnego)

Liczby rzeczywiste można przedstawić:

Nie jest możliwe przedstawienie nieskończonych zbiorów za 
pomocą skończonej liczby bitów. Do obliczeń w komputerach 
stosuje się reprezentację skończonych podzbiorów liczb 
rzeczywistych.
Zgodne jest to ze standardem 

IEEE – 754

, gdzie określony został 

standard zapisu i działań arytmetycznych na liczbach 
zmiennoprzecinkowych