Elementy kombinatoryki.



Twierdzenie o mnożeniu.



Permutacje.



Kombinacje.



Wariacje bez powtórzeń.



Wariacje z powtórzeniami.

Sposób na prawie każde zadanie.

Twierdzenie o mnożeniu.

Jeżeli dane są dwa skończone zbiory

A = { x

1

, x

2

, ... x

n

} i B = { y

1

, y

2

, ...

y

m

}, to liczba różnych par ( x, y ), takich, że xA

oraz yB jest równa m•n.

Uwaga

: Twierdzenie to można uogólnić na skończoną

ilość zbiorów.

Przykład:

Niech A = { a

1

, a

2

, a

3

} i B = { b

1

, b

2

}. Liczba par ( x, y )

takich, że xA oraz yB jest równa 3 •2 = 6.

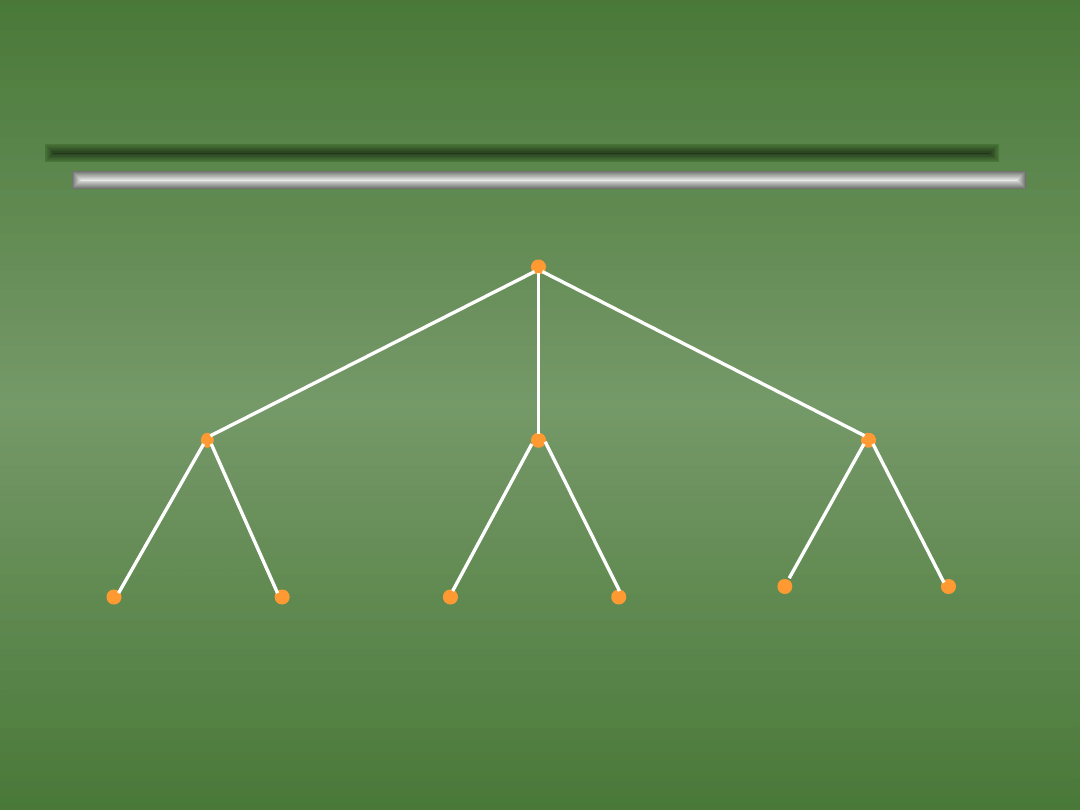
Ilustracja twierdzenia o mnożeniu.

a

1

a

3

a

2

b

1

b

1

b

1

b

2

b

2

b

2

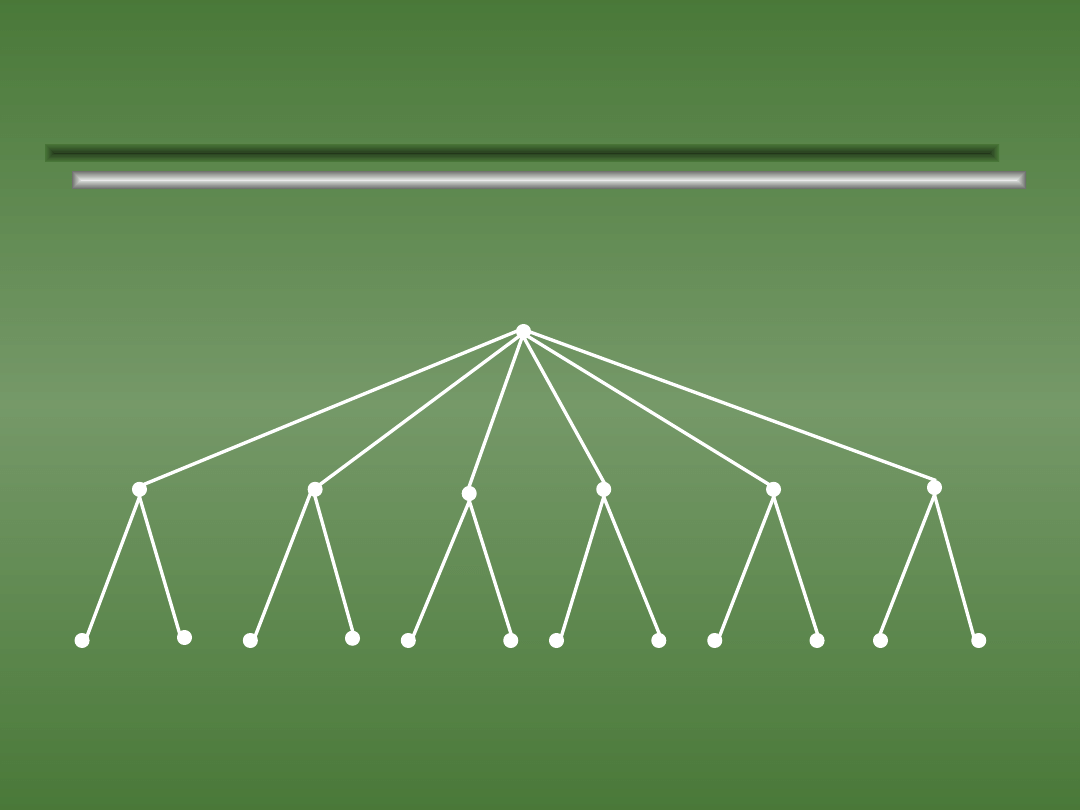
Przykład zastosowania twierdzenia o
mnożeniu

.

Rzucamy sześcienną kostką i symetryczną monetą. Ile
jest wszystkich możliwych wyników?

1

6

5

4

3

2

R

O

R

R

R

R

R

O

O

O

O

O

Permutacja

.

Permutacją zbioru n-elementowego nazywamy

każdy

ciąg

n-elementowy utworzony

z

wszystkich

elementów tego zbioru, czyli jest to pewne
uporządkowanie elementów tego zbioru.

Liczba wszystkich różnych permutacji zbioru n-
elementowego jest równa:























N

n

;

n

1

n

...

2

1

!

n

P

n

Przykład permutacji.

Ile wyrazów mających lub nie sens można ułożyć
przestawiając litery wyrazu KAT?

K A T

A K T

T A K

K T A

A T K

T K A

Są to permutacje zbioru trzyelementowego, a zatem
ich ilość wynosi :

P

3

= 3!

=

1•2•3 = 6

Kombinacja.

Kombinacją k-elementową ze zbioru n-elementowego
nazywamy

każdy

podzbiór

k-elementowy

danego

zbioru.

Liczba wszystkich różnych kombinacji k-
elementowych zbioru n-elementowego jest równa:

k

n

,

N

k

,

n

;

)!

k

n

(

!

k

!

n

k

n

C

k

n



























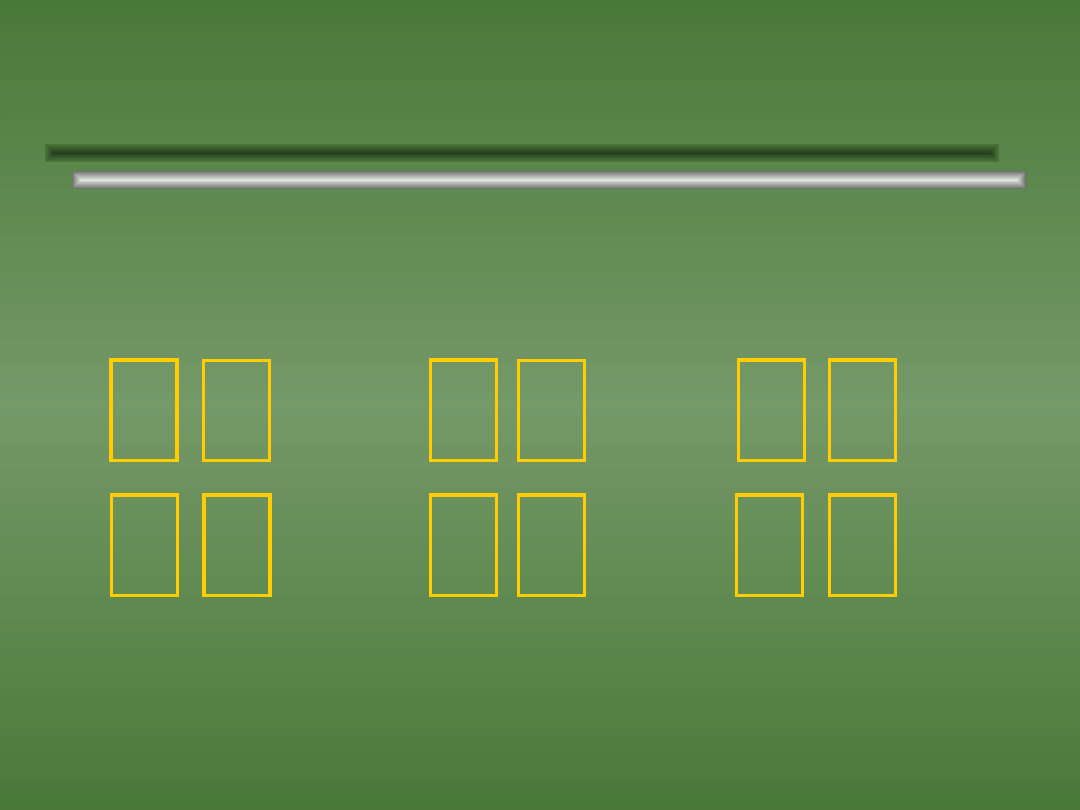
Przykład kombinacji.

1.

Ile jest możliwości wyboru dwóch różnych

kolorów kart z czterech?

































Są to kombinacje dwuelementowe ze zbioru czteroelementowego.

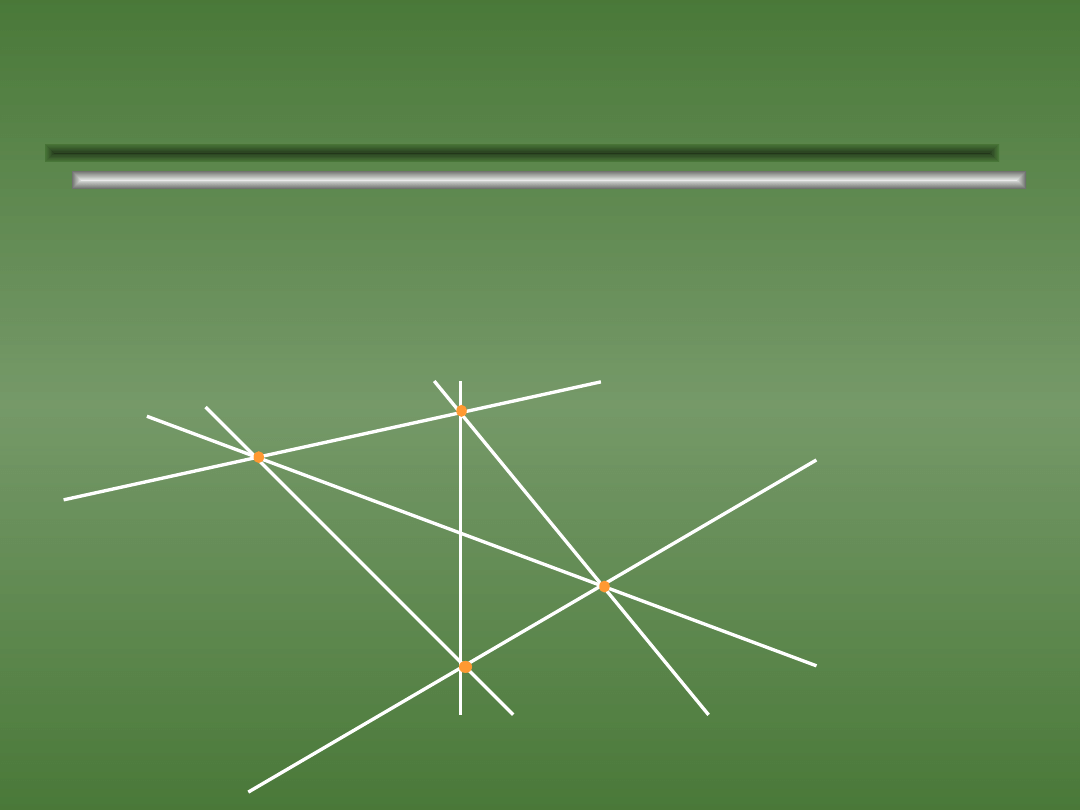
Przykład kombinacji.

2.

Ile można narysować na płaszczyźnie prostych

przechodzących przez: a) dwa, b) trzy, c) cztery

punkty
( jeżeli żadne trzy z nich nie są współliniowe ) ?

A

C

D

B

Wariacja bez powtórzeń

.

Wariacją k-elementową bez powtórzeń zbioru
n-elementowego nazywamy

każdy

ciąg różnowartościowy

k-wyrazowy utworzony z

elementów danego zbioru.

Liczba wszystkich różnych k-elementowych wariacji
bez powtórzeń zbioru n-elementowego jest równa:















N

k

,

n

k

n

;

!

k

n

!

n

V

k

n

Przykład wariacji bez powtórzeń.

1.

Ile liczb dwucyfrowych można utworzyć używając

dwóch

różnych

cyfr ze zbioru { 2,5,7,9 }?

2
5

2
7

2
9

7
9

7
2

7
5

5
9

5
7

5
2

9
2

9
7

9
5

Są to dwuwyrazowe wariacje bez powtórzeń ze
zbioru zawierającego cztery elementy.

Przykład wariacji bez powtórzeń..

2.

Na ile sposobów z czteroosobowej reprezentacji

klasy można wybrać kapitana i jego zastępcę :

























K Z

K Z

K Z

K Z

K Z

K Z

























K Z

K Z

K Z

K Z

K Z

K Z

Są to wariacje dwuelementowe bez powtórzeń ze zbioru
czteroelementowego.

Wariacja z powtórzeniami.







N

k

,

n

;

n

V

k

k
n

Wariacją k-elementową z powtórzeniami
zbioru n-elementowego
nazywamy

każdy

ciąg

k-wyrazowy utworzony

z elementów danego zbioru.
Liczba wszystkich różnych k-elementowych
wariacji z powtórzeniami
zbioru n-elementowego jest równa:

Przykład wariacji z powtórzeniami.

1.

Ile liczb dwucyfrowych można utworzyć używając

cyfr ze zbioru { 2,5,7,9 }?

2
9

7
9

5
9
9
7

2
7

7
5

5
7

9
5

2
5

7
2

5
2

9
2

9
9

7
7

5
5

2
2

Są to dwuwyrazowe wariacje z powtórzeniami ze
zbioru zawierającego cztery elementy.

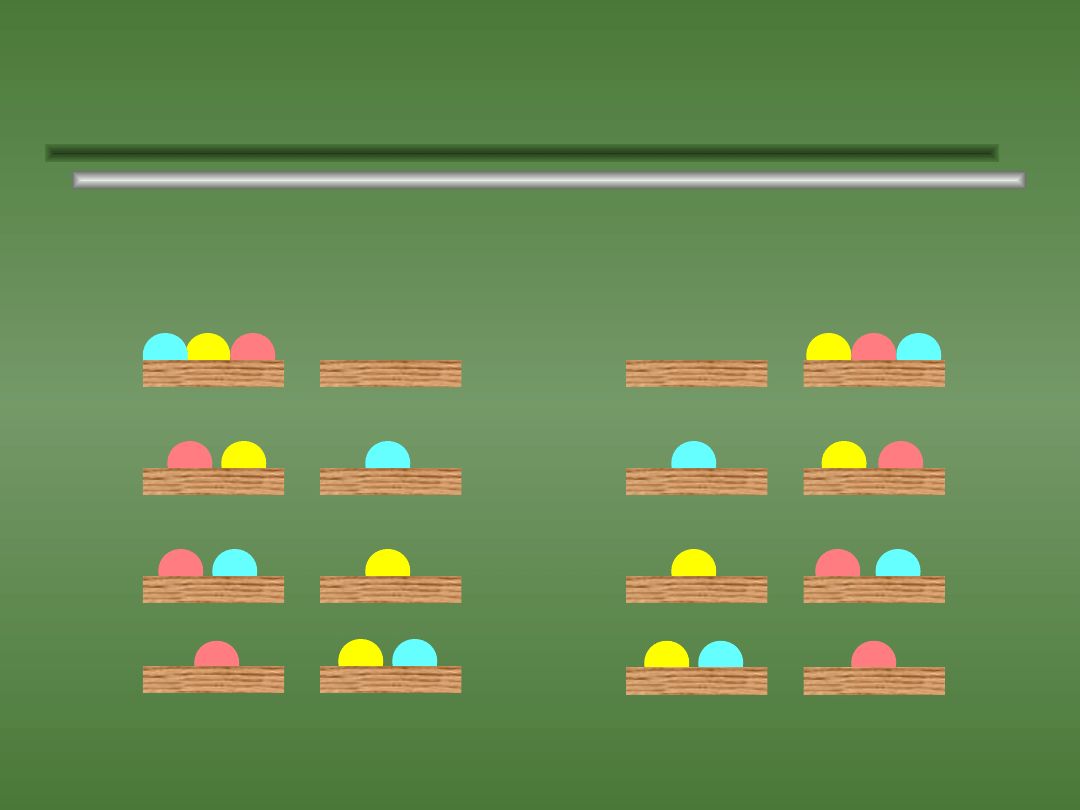
Przykład wariacji z powtórzeniami.

2.

Na ile sposobów można włożyć trzy różne piłeczki

do dwóch ponumerowanych pudełek ?

1

2

1

2

1

2

1

2

1

2

1

2

1

2

1

2

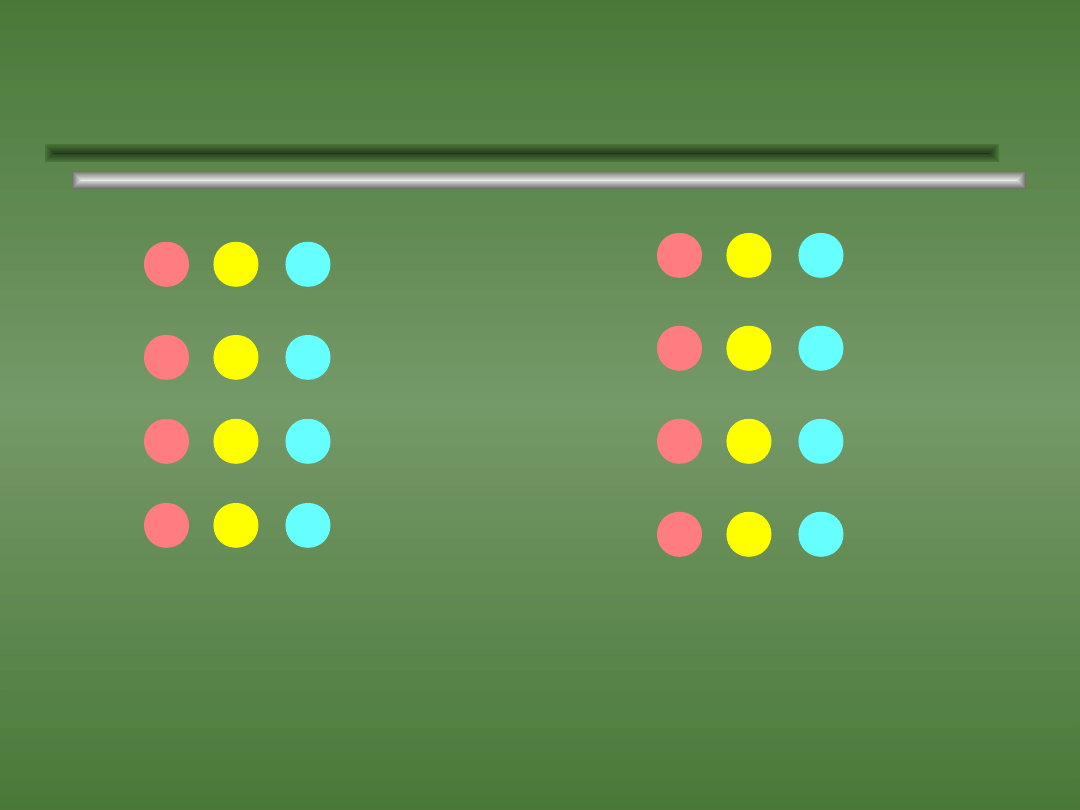
Przykład wariacji z powtórzeniami.

Są to trzywyrazowe wariacje z powtórzeniami ze
zbioru zawierającego dwa elementy, a zatem ich
ilość wynosi 2

3

= 8.

1

1

1

1

1

2

1

2

1

1

2

2

2

1

1

2

1

2

2

2

1

2

2

2

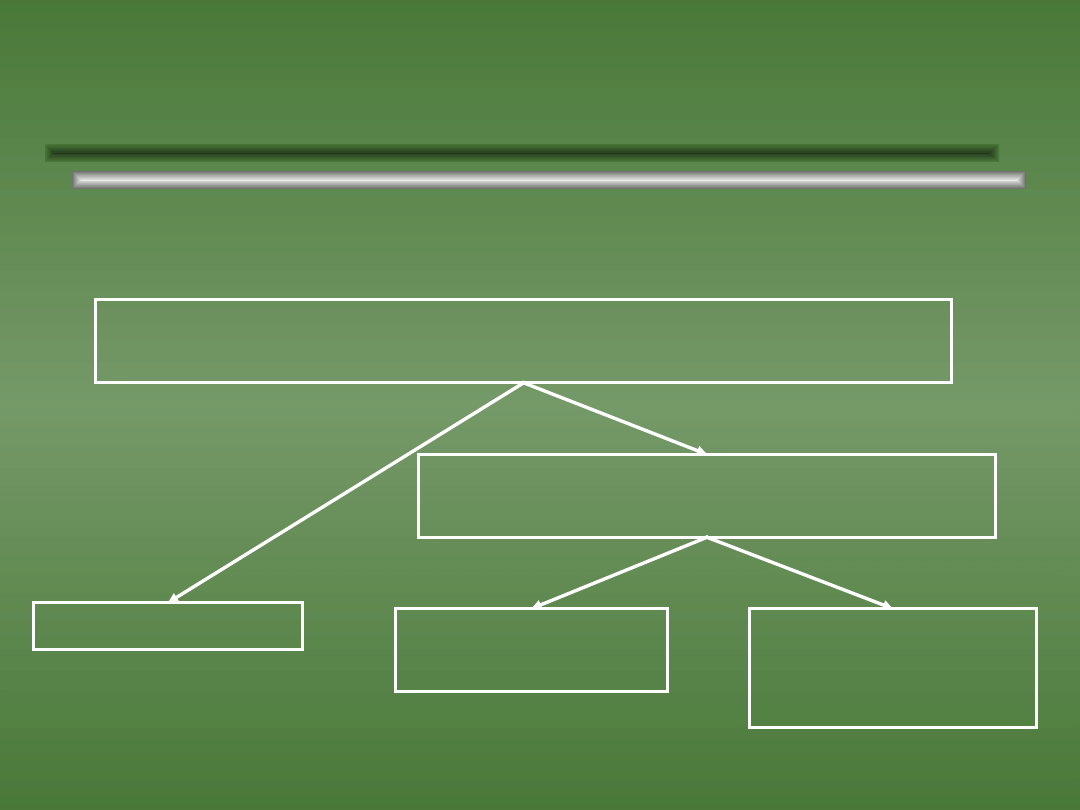
Sposób na zadanie.

Doświadczenie polega na wylosowaniu k-elementów ze zbioru n-
elementowego

Czy istotna jest kolejność wylosowanych

elementów?

Kombinacja.

Wariacja bez

powtórzeń.

Czy elementy mogą się

powtarzać?

Wariacja

z

powtórzeniami.

nie

tak

tak

nie

Zadania

Ćwiczenie 1

Rozwiąż zadania ze stron 91-95 oraz 99-101 z
podręcznika