C 01 p
1
ILOCZYNY WEKTORÓW
cos ( , )
a b ab
a b
� =
r
r
r
r
S
Iloczyn skalarny dwu
wektorów:
(
) (
)
x x
y y
z z
x x
y y
z z
x x
y y
z z
a b
a i
a i
a i
b i
b i
bi
a b a b a b
� =
+
+
�
+
+
=
+
+
r
r
r
r
r
r
r
r
• W kartezjańskim układzie współrzędnych prostokątnych:
Iloczyn skalarny dwu wektorów w układzie
współrzędnych
cylindrycznych ρ, φ, z:
(
) (
)
z z
z z
a b
a i
a i
a i
b i
b i
bi
r r
j j
r r
j j
� =
+
+
�
+
+
r
r
r
r
r
r
r
r
i
a b
r
r
z z
a b a b
a b
a b
r r
j j
� =
+
+
r
r
Iloczyn skalarny dwu wektorów w układzie
współrzędnych
sferycznych r, θ, φ :
(
) (
)
r r
r r
a b
a i
a i
a i
bi
b i
b i
q q
j j
q q
j j
� =
+
+
�
+
+
r
r
r
r
r
r
r
r
i
a b
r
r
r r
a b a b a b
a b
q q
j
j
� =
+
+
r
r
C 01 p
2
ILOCZYNY WEKTORÓW (2)
|
|
sin ( , )
a b ab
a b
� =
r
r
r
r
S
Iloczyn wektorowy jest wektorem,
którego:
1. moduł wynosi
a b
�
r
r
2. kierunek jest prostopadły do płaszczyzny
rozpiętej na wektorach
i
a b
r
r
3. zwrot taki, że trójka uporządkowana ma taką
orientację jak przestrzeń, w której definiujemy iloczyn
wektorowy
, ,
a b a b
�
r
r
r
r
Podstawowe własności iloczynu
wektorowego
• Podstawowe związki
(
)
a b
b a
� =-
�
r
r
r
r
0
a a
� =
r
r r
(
)
(
) 0
a a b
b a b
=
״ =
״
r
r
r
r r
r
(
)
(
)
ma b m a b
� =
�
r
r
r
r
(
)
a b c
a b a c
� + = � + �
r
r
r
r
r
r r
[(
) ]
(
)(
)
(
)
(
)
m n a b
m n a b
m a b
n a b
+
� =
+
� =
� +
�
r
r
r
r
r
r
r
r
C 01 p
3
ILOCZYNY WEKTORÓW (3)
• Związki wyrażone przez wektory
bazy
1 2 3
, ,
i i i
r r r
1 1
2 2
3 3
a a i a i
a i
=
+
+
r
r
r
r
1 1
2 2
3 3
b bi b i
bi
=
+
+
r
r
r
r
2
3
3
1
1
2
1
2
3
1
2
3
i i
i i i i
a b
a
a
a
b
b
b
�
�
�
� =
r r r r r r
r
r
• Związki w kartezjańskich współrzędnych
prostokątnych
0
x
x
y
y
z
z
i
i
i
i
i i
� = � = � =
r
r r
r r
r r
x
y
z
i
i
i
� =
r r
r
z
x
y
i i
i
� =
r r
r
y
z
x
i
i
i
� =
r r
r
?
a b
� =
r
r
C 01 p
4
ILOCZYNY WEKTORÓW (4)
x x
y y
z z
a a i
a i
a i
=
+
+
r
r
r
r
x x
y y
z z
b b i
b i
b i
=
+
+
r
r
r
r
x
y
z
y
z
x
y
z
x
x
y
z
x
y
z
y
z
x
y
z
x
x
y
z
i
i
i
a
a
a
a
a
a
a b a
a
a
i
i
i
b
b
b
b
b
b
b
b
b
� =
=
+
+
=
r
r
r
r
r
r
r
r
(
)
(
)
(
)
y z
z y
x
z x
x z
y
x y
y x
z
a b a b i
a b a b i
a b
a b i
=
-
+
-
+
-
r
r
r
• Wybrane, podstawowe tożsamości
algebraiczne
(
)
(
)
(
)
A B C
B C A
C A B
״ =
״ =
״
r
r
r r
r r
r
r
r
(
) (
)
(
)
A B C
C A B
A B C
� � = �
-
�
r
r
r r
r
r
r
r
r
C 01 p
5
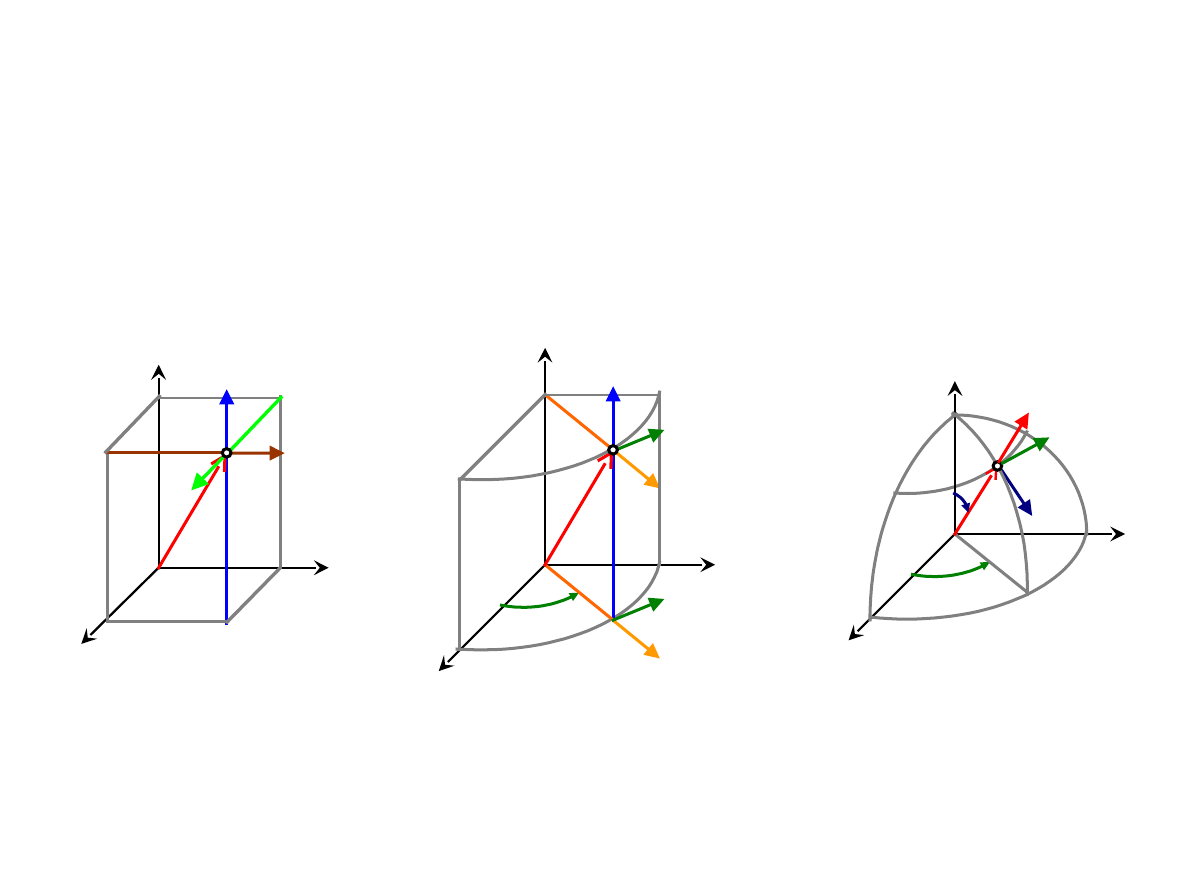
UKŁADY WSPÓŁRZĘDNYCH
x
y
z
i
q
r
r
i
r
r
j
i
j
r
q
Współrzędne
sferyczne
(r, θ, φ):
P
x
y
z
i
r
r
i
r
r
i
j
r
z
i
r
r
r
r
j
i
j
r
z
P
Współrzędne
cylindryczne
(ρ, φ, z):
Współrzędne
prostokątne
(x, y, z):
x
y
z
y
i
r
x
i
r
z
i
r
r
r
y
z
P
x
x
y
z
r xi
yi
zi
=
+
+
r
r
r
r
cos
x r
j
=
sin
y r
j
=
z z
=
sin cos
x r
q
j
=
sin sin
y r
q
j
=
cos
z r
q
=
C 01 p
6
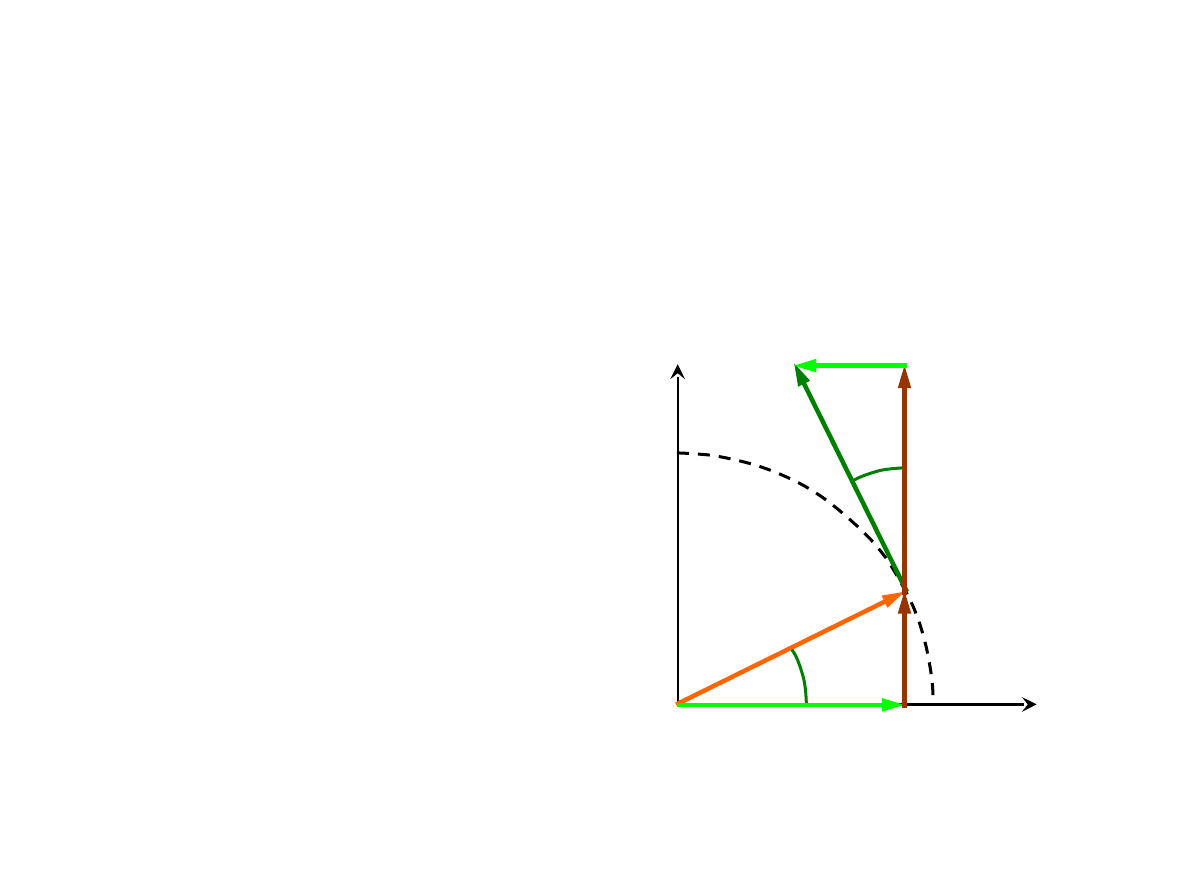
TRANSFORMACJA WEKTORÓW
A
A i
r
r
= �
r r
• Obliczyć należy następujące iloczyny:
• Iloczyn skalarny wektora przez wersor to składowa tego wektora
w kierunku wersora.
• Powyższa cecha iloczynu skalarnego wektorów
pozwala
na
transformację
wektora
z
jednego
układu
współrzędnych
do
drugiego.
Transformacja wektora
z współrzędnych prostokątnych do współrzędnych
cylindrycznych:
z z
A A i
A i
A i
r r
j j
=
+
+
r
r
r
r
x x
y y
z z
A A i
A i
A i
=
+
+
r
r
r
r
A
r
A
A i
j
j
= �
r r
C 01 p
7
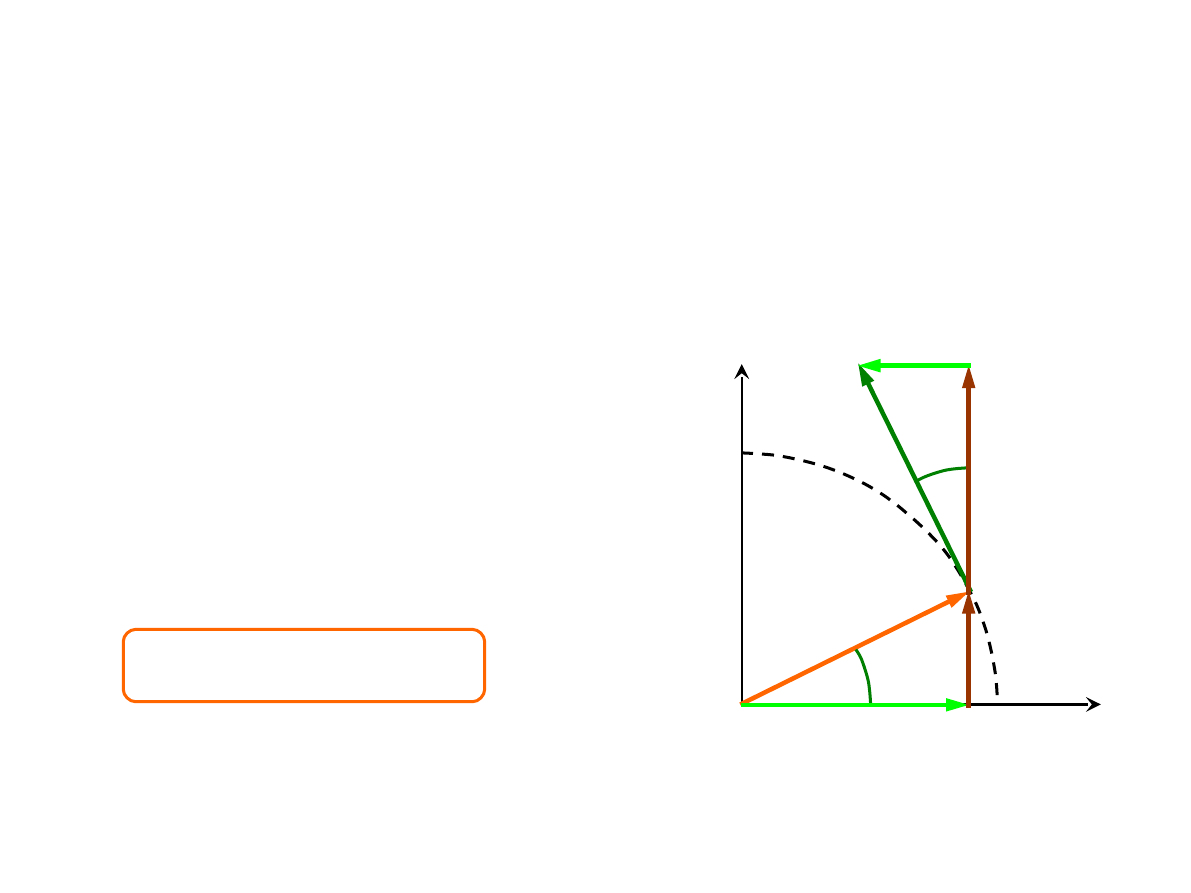
TRANSFORMACJA WEKTORÓW (2)
(
)
(
)
(
)
(
)
x x
y y
z z
x x
y
y
z z
A
A i
A i
A i
Ai
i
A i i
A i i
A i i
r
r
r
r
r
r
= � =
+
+
� =
� +
� +
�
r r
r
r
r r
r r
r r
r r
?
x
i i
r
� =
r r
?
z
i i
r
� =
r r
?
y
i i
r
� =
r r
i
r
r
i
j
r
j
x
y
j
1
1
?
?
x
y
i
i
i
r
=
+
r
r
r
C 01 p
8
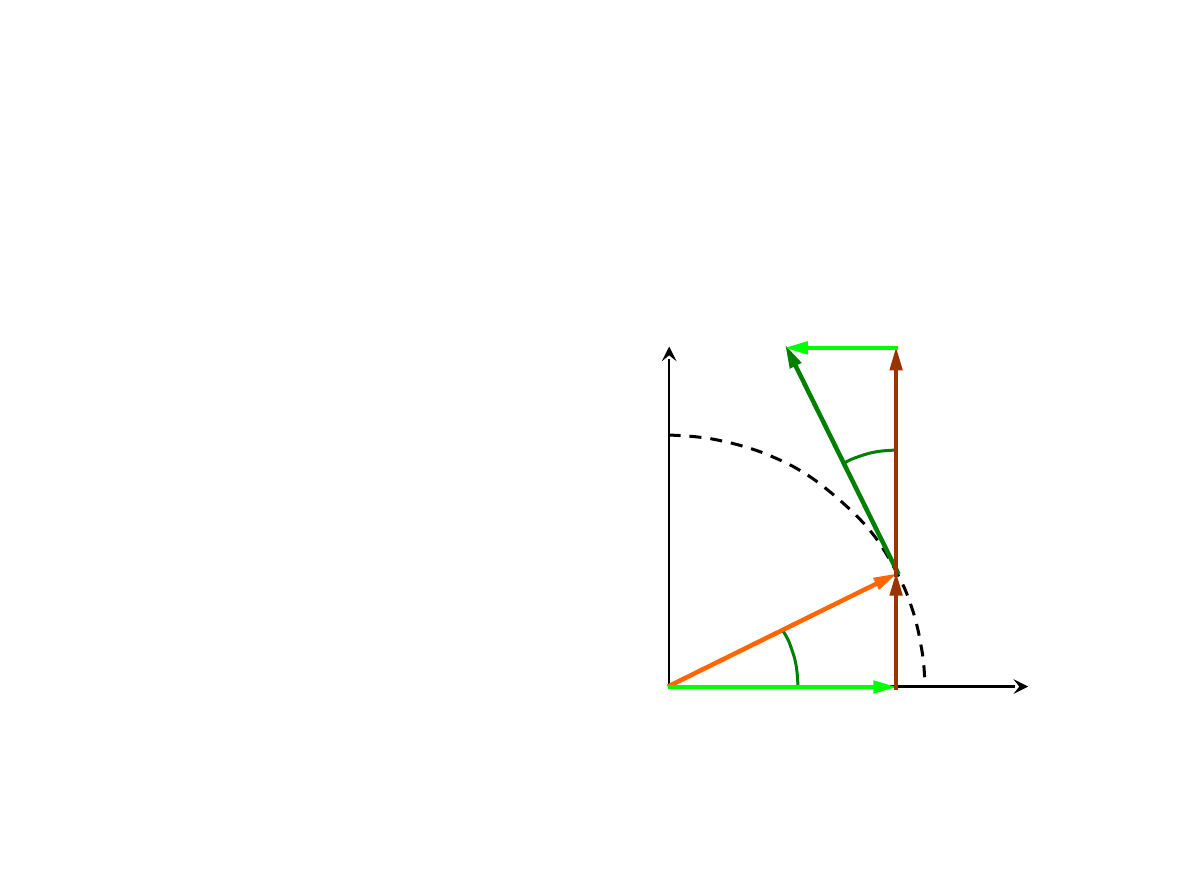
TRANSFORMACJA WEKTORÓW (3)
(
)
(
)
(
)
(
)
x x
y y
z z
x x
y
y
z z
A
A i
A i
A i
Ai i
A i i
A i i
A i i
r
r
r
r
r
r
= � =
+
+
� =
� +
� +
�
r r
r
r
r r
r r
r r
r r
(cos
sin
) cos
x
x
x
y
i i
i
i
i
r
j
j
j
� = �
+
=
r r
r
r
r
0
z
i i
r
� =
r r
(cos
sin
) sin
y
y
x
y
i i
i
i
i
r
j
j
j
� = �
+
=
r r
r
r
r
cos
sin
x
y
A
A
A
r
j
j
=
+
i
r
r
i
j
r
j
x
y
cos
x
i
j
r
sin
y
i
j
r
j
1
1
C 01 p
9
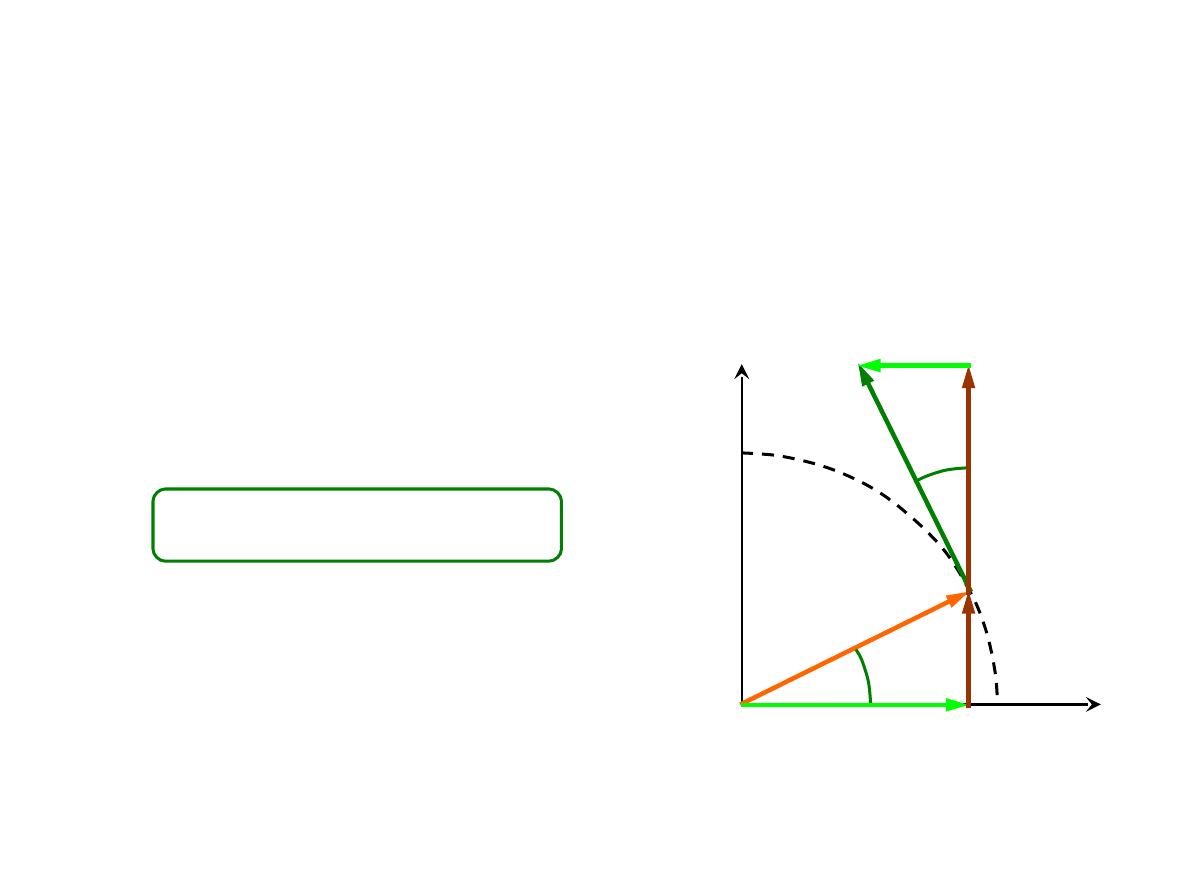
TRANSFORMACJA WEKTORÓW (4)
(
)
(
)
(
)
(
)
x x
y y
z z
x x
y
y
z z
A
A i
A i
A i
A i
i
A i i
A i i
A i i
j
j
j
j
j
j
= � =
+
+
� =
� +
� +
�
r r
r
r
r r
r r
r r
r r
?
x
i i
j
� =
r r
?
z
i i
j
� =
r r
?
y
i i
j
� =
r r
?
?
x
y
i
i
i
j
=
+
r
r
r
i
r
r
i
j
r
j
x
y
cos
x
i
j
r
sin
y
i
j
r
j
1
1
C 01 p
10
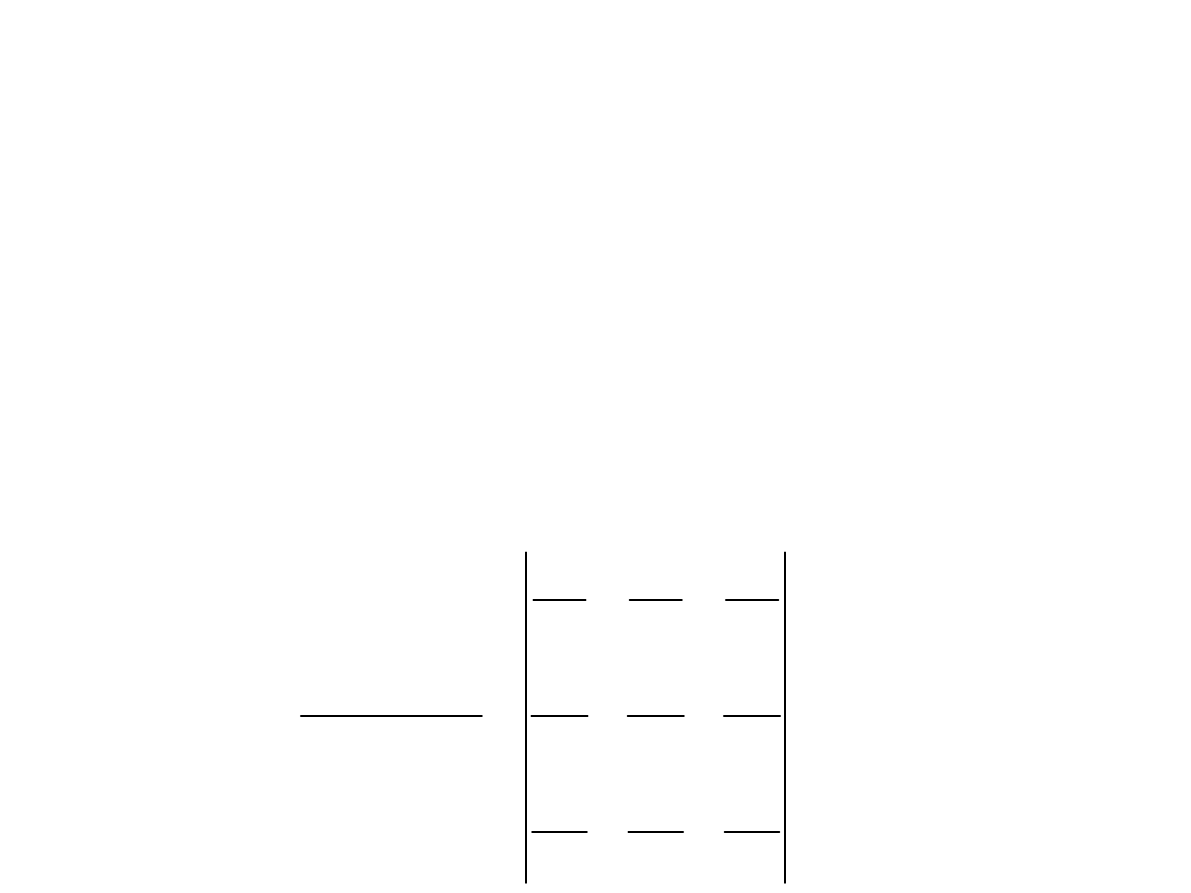
TRANSFORMACJA WEKTORÓW (5)
(
)
(
)
(
)
(
)
x x
y y
z z
x x
y
y
z z
A
A i
A i
A i
A i
i
A i i
A i i
A i i
j
j
j
j
j
j
= � =
+
+
� =
� +
� +
�
r r
r
r
r r
r r
r r
r r
( sin
cos
)
sin
x
x
x
y
i i
i
i
i
j
j
j
j
� = �-
+
=-
r r
r
r
r
0
z
i i
j
� =
r r
( sin
cos
) sin
y
y
x
y
i i
i
i
i
j
j
j
j
� = �-
+
=
r r
r
r
r
( sin )
cos
x
y
A
A
A
j
j
j
=
-
+
cos
sin
0
sin
cos
0
0
0
1
x
y
z
z
A
A
A
A
A
A
r
j
j
j
j
j
� � �
�� �
� � �
�� �
= -
� � �
�� �
�
�
� �
� �
�
�
� �
� �
i
r
r
i
j
r
j
x
y
cos
x
i
j
r
sin
y
i
j
r
j
sin
x
i
j
-
r
cos
y
i
j
r
1
1
C 01 p
11
ANALIZA WEKTORÓW
1
1
1
1
2
3
2
2
2
3
3
3
( , , )
0
( , , )
u
u
u
x
y
z
u u u
u
u
u
J
x y z
x
y
z
u
u
u
x
y
z
�
�
�
�
�
�
�
�
�
�
=
=
�
�
�
�
�
�
�
�
�
�
�
1
1
( , , ),
u
u x y z
=
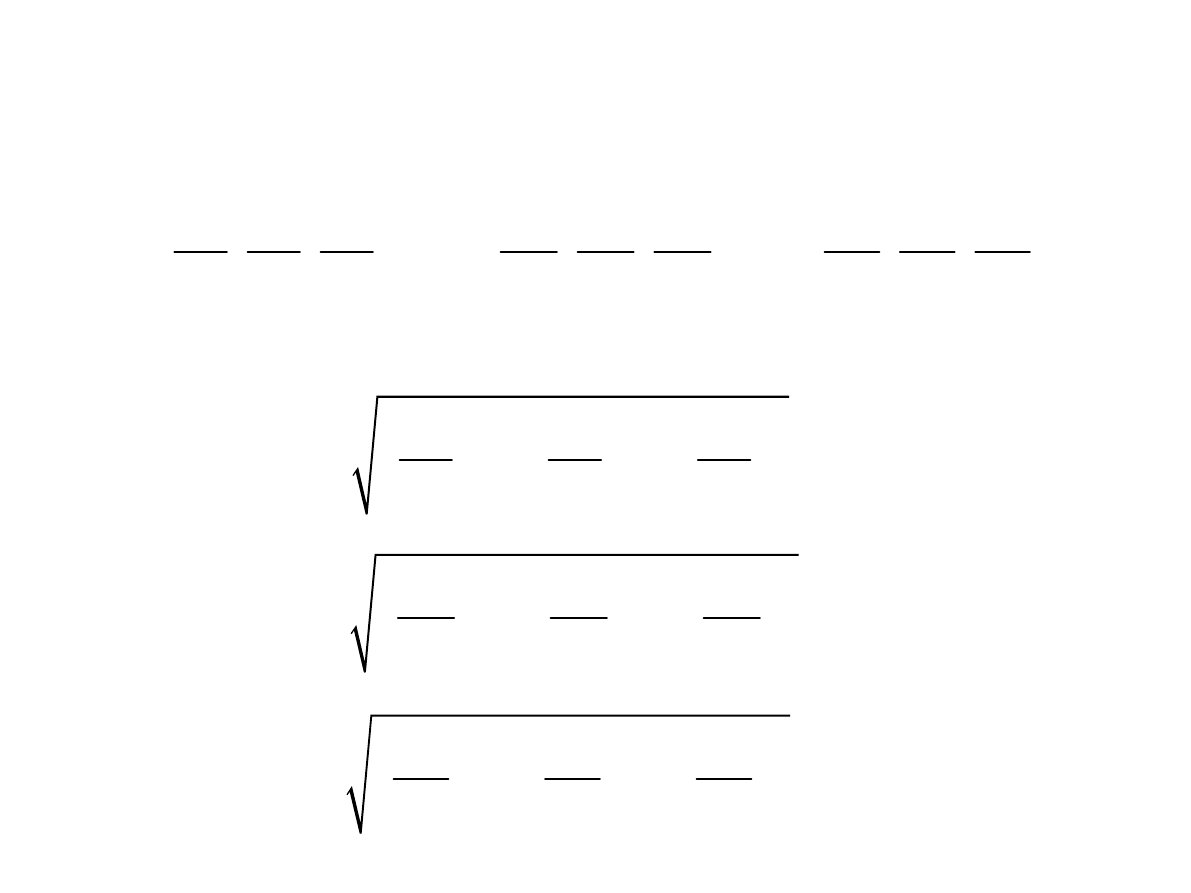
Operacje różniczkowe wektorowe we współrzędnych
krzywoliniowych
• W przestrzeni trójwymiarowej oprócz układu
współrzędnych
prostokątnych wprowadzamy układ krzywoliniowy za
pomocą
związków klasy C
1
2
2
( , , ),
u
u x y z
=
3
3
( , , )
u
u x y z
=
przy czym powyższy układ jest lokalnie odwracalny
1
2
3
( , , ),
x x u u u
=
1
2
3
( , , ),
y y u u u
=
1
2
3
( , , )
z z u u u
=
co wynika z założenia, że
C 01 p
12
ANALIZA WEKTORÓW
1
1
1
,
,
,
x
y
z
u
u
u
� � �
�
�
�
�
� � �
�
�
• Wektory styczne do linii współrzędnych układu
krzywoliniowego
są następujące:
o długościach (zwanych współczynnikami
Lamégo):
2
2
2
,
,
,
x
y
z
u
u
u
� � �
�
�
�
�
� � �
�
�
3
3
3
,
,
x
y
z
u
u
u
� � �
�
�
�
�
� � �
�
�
2
2
2
1
1
1
1
x
y
z
h
u
u
u
�
�
�
� � � � � �
=
+
+
� � � � � �
�
�
�
� � � � � �
2
2
2
2
2
2
2
x
y
z
h
u
u
u
�
�
�
� � � � � �
=
+
+
� � � � � �
�
�
�
� � � � � �
2
2
2
3
3
3
3
x
y
z
h
u
u
u
�
�
�
� � � � � �
=
+
+
� � � � � �
�
�
�
� � � � � �
C 01 p
13
ANALIZA WEKTORÓW
• Zakładamy, że układ krzywoliniowy jest układem
ortogonalnym
o wektorach jednostkowych (wersorach) wektorów
stycznych
do
linii współrzędnych:
1 2 3
, ,
i i i
r r r
• Elementy skierowane we współrzędnych krzywoliniowych
d ,d
l s
r r
1
1 1
2
2 2
3
3 3
d
d
d
d
l
h ui
h u i
h u i
=
+
+
r
r
r
r
2 3
2
3 1
1 3
1
3 2
1 2
1
2 3
d
d d
d d
d d
s h h u u i
hh u u i
hh u u i
=
+
+
r
r
r
r
• Element objętości we współrzędnych krzywoliniowych
1 2 3
1
2
3
d
d d d
v hh h u u u
=
• Równanie linii sił pola
3
3
1
1
2
2
1
2
3
d
d
d
h u
h u
h u
A
A
A
=
=
gdzie
1 1
2 2
3 3
A Ai
A i
Ai
=
+
+
r
r
r
r
- pole wektorowe
C 01 p
14
TRANSFORMACJE WEKTORÓW
• Wyznaczanie składowych wektora w układzie
współrzędnych
prostokątnych gdy znamy współrzędne wektora w
układzie
współrzędnych krzywoliniowych
1
1
1
2
2
3
3
2
1
1
2
2
3
3
3
1
1
2
2
3
3
1
1
1
1
1
1
1
1
1
x
y
z
x
x
x
A
A
h u
h u
h u
y
y
y
A
A
h u
h u
h u
z
z
z
A
A
h u
h u
h u
�
�
�
�
�
� �
� �
�
�
�
�
�
� �
� �
�
�
� �
� �
�
�
�
�
�
=
� �
� �
�
�
�
�
�
� �
� �
�
�
� �
� �
�
�
�
�
�
� �
� �
� �
� � �
�
�
�
�
�
�
C 01 p
15
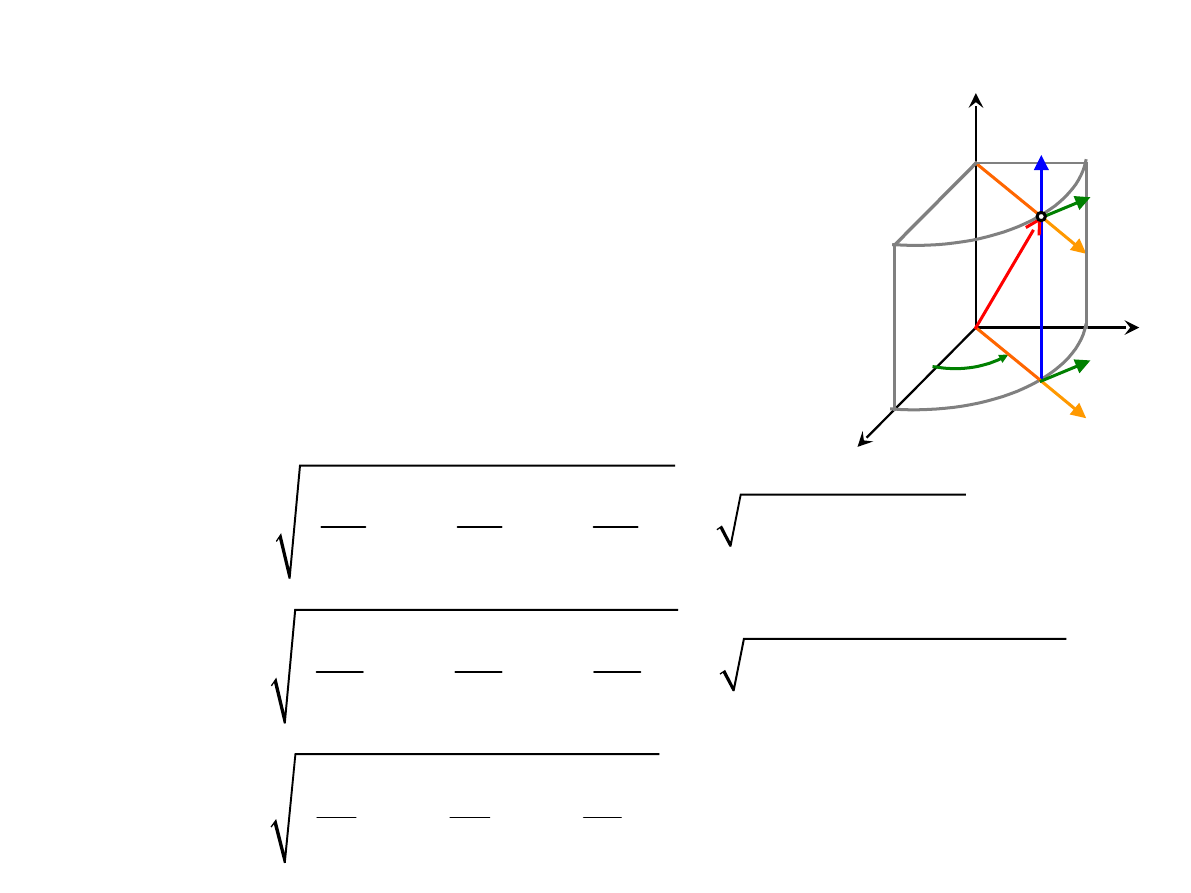
TRANSFORMACJE WEKTORÓW
• Wyznaczanie składowych wektora w układzie
współrzędnych
krzywoliniowych gdy znamy współrzędne wektora w
układzie
współrzędnych prostokątnych
1
1
1
1
1
1
1
2
2
2
2
2
2
2
3
3
3
3
3
3
3
1
1
1
1
1
1
1
1
1
x
y
z
x
y
z
A
A
h u
h u
h u
x
y
z
A
A
h u
h u
h u
x
y
z
A
A
h u
h u
h u
�
�
�
�
�� �
� � �
�
�
�
� � �
� � �
�� �
� �
�
�
�
�
�
=
� �
� � �
�
�
�
� � �
� � �
�� �
� �
�
�
�
�
�� �
� �
� �
� �
�
�
�
�
�
�
�
C 01 p
16
TRANSFORMACJE WEKTORÓW
Transformacja współrzędnych z prostokątnych
(x, y, z)
do cylindrycznych (ρ, φ, z):
cos
sin
x
y
z z
r
j
r
j
=
=
=
2
2
2
2
2
cos
sin
1
x
y
z
h
r
j
j
r
r
r
�
�
�
� � � � � �
=
+
+
=
+
=
� � � � � �
�
�
�
� � � � � �
2
2
2
2
2
2
2
sin
cos
x
y
z
h
j
r
j
r
j
r
j
j
j
�
�
�
� � � � � �
=
+
+
=
+
=
� � � � � �
�
�
�
� � � � � �
2
2
2
1
z
x
y
z
h
z
z
z
�
�
�
� � � � � �
=
+
+
=
� � � � � �
� � � � � �
�
�
�
•
Współczynnikami
Lamégo:
x
y
z
i
r
r
i
r
r
i
j
r
z
i
r
r
r
r
j
i
j
r
z
P
C 01 p
17
TRANSFORMACJE WEKTORÓW
• Wektor we współrzędnych prostokątnych wyrażony
przez
współrzędne wektora w układzie współrzędnych
cylindrycznych
1
1
1
1
1
1
1
1
1
x
z
y
z
z
z
z
x
x
x A
A
h
h
h z
y
y
y
A
A
h
h
h z
z
z
z
A
A
h
h
h z
r
r
j
j
r
j
r
j
r
j
r
j
r
j
�
�
�
�
�� �
� � �
�
�
�
� � �
� � �
�� �
� � �
�
�
�
� � �
=
=
� � �
�
�
�
� � �
� � �
�� �
� � �
�
�
�
� � �
� � �
�� �
� �
�
�
�
�
�
cos
sin
0
sin
cos
0
0
0
1
z
A
A
A
r
j
j
j
j
j
-
�
�� �
�
�� �
�
�� �
�
�� �
�
�� �
1
1
1
1
1
1
1
1
1
x
y
z
z
z
z
z
x
y
z
A
A
h
h
h
x
y
z
A
A
h
h
h
x
y
z
A
A
h z
h z
h z
r
r
r
r
j
j
j
j
r
r
r
j
j
j
�
�
�
�
�
� �
� �
�
�
�
�
�
� �
� �
�
�
� �
� �
�
�
�
�
�
� �=
=
� �
�
�
�
�
�
� �
� �
�
�
� �
� �
�
�
�
�
�
� �
� �
�
�
� �
� �
�
�
�
�
�
cos
sin
0
sin
cos
0
0
0
1
x
y
z
A
A
A
j
j
j
j
�
�� �
�
�� �
-
�
�� �
�
�� �
�
�� �
• Wektor we współrzędnych cylindrycznych wyrażony
przez
współrzędne wektora w układzie współrzędnych
prostokątnych
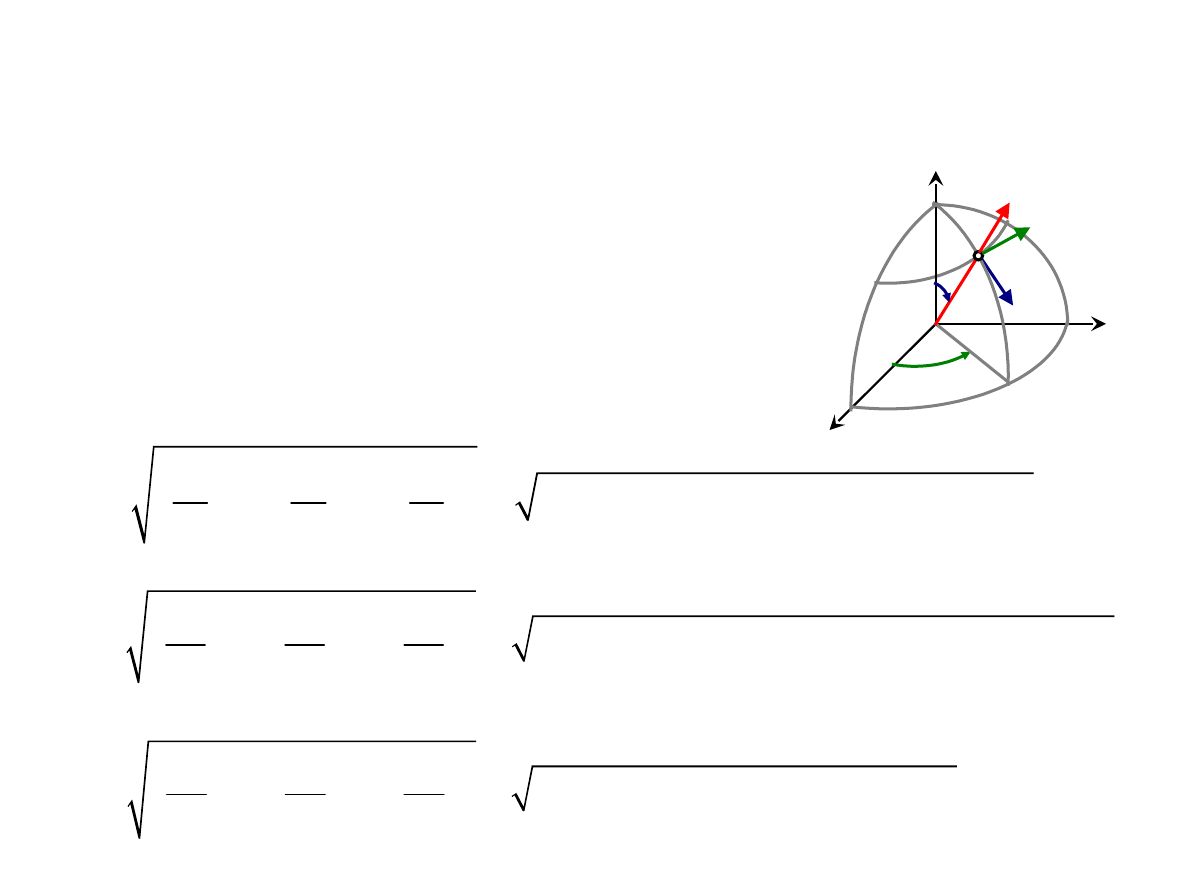
C 01 p
18
TRANSFORMACJE WEKTORÓW
Transformacja współrzędnych z prostokątnych
(x, y, z)
do sferycznych (r, θ, φ):
sin cos
sin sin
cos
x r
y r
z r
q
j
q
j
q
=
=
=
2
2
2
2
2
2
2
2
sin cos
sin sin
cos
1
r
x
y
z
h
r
r
r
q
j
q
j
q
�
�
�
� � � � � �
=
+
+
=
+
+
=
� � � � � �
� � � � � �
�
�
�
2
2
2
2
2
2
2
2
2
2
2
cos cos
cos sin
sin
x
y
z
h
r
r
r
r
q
q
j
q
j
q
q
q
q
�
�
�
� � � � � �
=
+
+
=
+
+
=
� � � � � �
� � � � � �
�
�
�
•
Współczynnikami
Lamégo:
2
2
2
2
2
2
2
2
2
sin sin
sin cos
sin
x
y
z
h
r
r
r
j
q
j
q
j
q
j
j
j
�
�
�
� � � � � �
=
+
+
=
+
=
� � � � � �
�
�
�
� � � � � �
x
y
z
i
q
r
r
i
r
r
j
i
j
r
q
P
C 01 p
19
TRANSFORMACJE WEKTORÓW
• Wektor we współrzędnych prostokątnych wyrażony
przez
współrzędne wektora w układzie współrzędnych
sferycznych
1
1
1
1
1
1
1
1
1
x
r
r
y
r
z
r
x
x
x
A
A
h r h
h
y
y
y
A
A
h r h
h
z
z
z
A
A
h r h
h
q
j
q
q
j
j
q
j
q
j
q
j
q
j
�
�
�
�
�
� �
� �
�
�
�
�
�
� �
� �
�
�
� �
� �
�
�
�
�
�
=
=
� �
� �
�
�
�
�
�
� �
� �
�
�
� �
� �
�
�
�
�
�
� �
� �
�
�
� �
� �
�
�
�
�
�
sin cos
cos cos
sin
sin sin
cos cos
cos
cos
sin
0
r
A
A
A
q
j
q
j
q
j
j
q
j
q
j
j
q
q
-
� �
�
�
� �
�
�
� �
�
�
� �
-
�
�
�
�� �
1
1
1
1
1
1
1
1
1
x
r
r
r
r
y
z
x
y
z
A
A
h r
h r
h r
x
y
z
A
A
h
h
h
x
y
z
A
A
h
h
h
q
q
q
q
j
j
j
j
q
q
q
j
j
j
�
�
�
�
�� �
� � �
�
�
�
� � �
� � �
�� �
� �
�
�
�
�
�
=
=
� �
� � �
�
�
�
� � �
� � �
�� �
� �
�
�
�
�
�� �
� �
� �
� �
�
�
�
�
�
�
�
• Wektor we współrzędnych sferycznych wyrażony przez
współrzędne wektora w układzie współrzędnych
prostokątnych
sin cos
sin sin
cos
cos cos
cos sin
sin
sin
cos
0
x
y
z
A
A
A
q
j
q
j
q
q
j
q
j
q
j
j
�
�� �
�
�� �
-
�
�� �
-
�
�� �
�
�� �
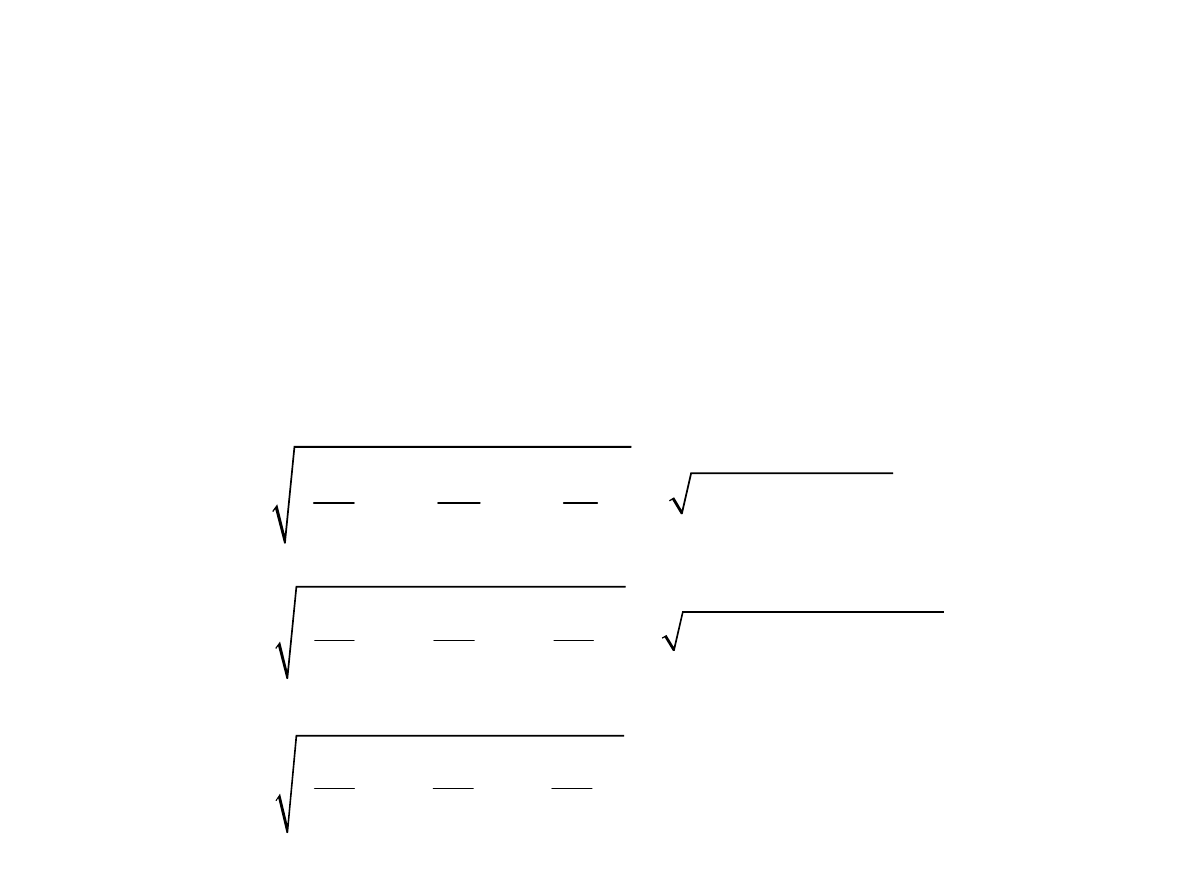
C 01 p
20
TRANSFORMACJE WEKTORÓW
Transformacja współrzędnych z cylindrycznych (ρ,
φ, z) do
sferycznych (r, θ, φ):
sin
cos
r
z r
r
q
j
j
q
=
=
=
2
2
2
2
2
sin
cos
1
r
z
h
r
r
r
r
j
q
q
�
�
�
� � � � � �
=
+
+
=
+
=
� � � � � �
� � � � � �
�
�
�
2
2
2
2
2
2
2
cos
sin
z
h
r
r
r
q
r
j
q
q
q
q
q
�
�
�
� � � � � �
=
+
+
=
+
=
� � � � � �
� � � � � �
�
�
�
•
Współczynnikami
Lamégo:
2
2
2
1
z
h
j
r
j
j
j
j
�
�
�
� � � � � �
=
+
+
=
� � � � � �
�
�
�
� � � � � �
C 01 p
21
TRANSFORMACJE WEKTORÓW
• Wektor we współrzędnych cylindrycznych wyrażony
przez
współrzędne wektora w układzie współrzędnych
sferycznych
1
1
1
1
1
1
1
1
1
r
r
r
z
r
A
A
h r h
h
A
A
h r h
h
z
z
z
A
A
h r h
h
r
q
j
j
q
q
j
j
q
j
r
r
r
q
j
j
j
j
q
j
q
j
�
�
�
�
�
� �
� �
�
�
�
�
�
� �
� �
�
�
� �
� �
�
�
�
�
�
� �=
=
� �
�
�
�
�
�
� �
� �
�
�
� �
� �
�
�
�
�
�
� �
� �
�
�
� �
� �
�
�
�
�
�
sin
cos
0
0
0
1
cos
sin
0
r
A
A
A
q
j
q
q
q
q
� �
�
�
� �
�
�
� �
�
�
� �
-
�
�
�
�� �
• Wektor we współrzędnych sferycznych wyrażony przez
współrzędne wektora w układzie współrzędnych
cylindrycznych
sin
0 cos
cos
0
sin
0
1
0
z
A
A
A
r
j
q
q
q
q
�
�� �
�
�� �
-
�
�� �
�
�� �
�
�� �
1
1
1
1
1
1
1
1
1
r
z
z
z
z
r
A
A
h
h
h
r
A
A
h
h
h
r
A
A
h z h z h z
r
r
r
r
q
j
j
j
j
j
q
j
r
r
r
q
j
j
j
j
q
j
�
�
�
�
�� �
� � �
�
�
�
� � �
� � �
�� �
� � �
�
�
�
� � �
=
=
� � �
�
�
�
� � �
� � �
�� �
� � �
�
�
�
� � �
� � �
�� �
� �
�
�
�
�
�
C 01 p
22
WEKTORY ZESPOLONE
• Wektor zespolony we współrzędnych
prostokątnych
( , , )
( , , )
( , , )
( , , )
x
x
y
y
z
z
A x y z
A x y z i
A x y z i
A x y z i
=
+
+
r
r
r
r
( )
( )
( )
( )
x
x
y
y
z
z
A r
A r i
A r i
A r i
=
+
+
r
r
r
r
r
r
r
r
lub
przy
czym
{
}
{
}
( ) Re
( )
Im
( )
( )
( ) cos
( ) sin
x
x
x
x
j
x
x
x
x
x
A r
A r
j
A r
A r e
A r
j A r
a
a
a
=
+
=
=
=
+
r
r
r
r
r
r
{
}
{
}
( ) Re
( )
Im
( )
( )
( ) cos
( ) sin
y
y
y
y
j
y
y
y
y
y
A r
A r
j
A r
A r e
A r
j A r
a
a
a
=
+
=
=
=
+
r
r
r
r
r
r
{
}
{
}
( ) Re
( )
Im
( )
( )
( ) cos
( ) sin
z
z
z
z
j
z
z
z
z
z
A r
A r
j
A r
A r e
A r
j A r
a
a
a
=
+
=
=
=
+
r
r
r
r
r
r
C 01 p
23
WEKTORY ZESPOLONE (2)
• Wektory zespolone nie mają sensu fizycznego i nie
należy
przypisywać im własności geometrycznych.
• Działania na wektorach zespolonych definiuje się tak jak
na
wektorach rzeczywistych, przy czym w wyniku tam gdzie
mamy
kwadrat jednostki urojonej należy wstawić minus
jedność.
• Wektor zespolony spełnia
zależności:
( )
( )
( )
A r
A r A r
*
=
�
r
r
r
r
r
r
{
}
( )
( )
A( ) Re ( )
2
A r
A r
r
A r
*
+
=
=
r
r
r
r
r
r
r
r
• Aby poznać własności fizyczne i geometryczne pól
należy
zawsze wyznaczyć wektory rzeczywiste.
C 01 p
24
WEKTORY ZESPOLONE (3)
• Obliczmy iloczyn wektorowy następujących wektorów
zespolonych:
C
r
( ) (
)
(
)
x
y
A r
x jy i
y jx i
= +
+ +
r
r
r
r
( ) (
)
(
)
x
y
B r
y jx i
x jy i
= -
+ +
r
r
r
r
?
C A B
= � =
r
r r
• Rzeczywisty wektor
:
{ }
C Re
?
C
=
=
r
r
C 01 p
25
WEKTORY ZESPOLONE (4)
• Obliczmy iloczyn wektorowy następujących wektorów
zespolonych:
C
r
( ) (
)
(
)
x
y
A r
x jy i
y jx i
= +
+ +
r
r
r
r
( ) (
)
(
)
x
y
B r
y jx i
x jy i
= -
+ +
r
r
r
r
2
2
2
2
2
(
2
)
( 2
2 )
z
z
x
j xy y
y
x i
y
j xy i
=
+
-
-
-
= -
+
r
r
(
)
2
0
(
)(
)
0
x
y
z
z
i
i
i
C A B
x jy y jx
x jy
y jx y jx i
y jx x jy
�
�
�
� �
�
= � = +
+
=
+
-
+
-
�
� �
�
�
�
-
+
�
�
r
r
r
r
r r
r
• Rzeczywisty wektor
:
{ }
2
C Re
2
z
C
y i
=
=-
r
r
r
C 01 p
26
WEKTORY ZESPOLONE (5)
• Dany jest wektor
zespolony:
(
)
(
)
(1
)
j t
z
j t
z
x
y
A
j i e
ji e
w b
w b
-
-
= +
+
r
r
r
?
z
B i
A
= � =
r
r r
• Obliczmy wektory:
?
C A B
*
= � =
r
r r
C 01 p
27
WEKTORY ZESPOLONE (6)
• Dany jest wektor
zespolony:
(
)
(
)
(1
)
j t
z
j t
z
x
y
A
j i e
ji e
w b
w b
-
-
= +
+
r
r
r
z
B i
A
= �
r
r r
(
)
(
)
(
)
2
2
1
0
1
3
1
0
x
y
z
j t
z
j t
z
z
z
i
i
i
C A B
e
e
j
j
j
j i
i
j
j
w b
w b
*
-
-
-
�
�
�
�
= � =
+
= -
-
=
�
�
�
�
-
�
�
r
r
r
r
r r
r
r
• Obliczmy wektory:
C A B
*
= �
r
r r
(
)
(
)
0
0 1
(1
)
1
0
x
y
z
j t
z
j t
z
z
x
y
i
i
i
B i
A e
ji
j i e
j
j
w b
w b
-
-
�
�
�
� �
�
= � =
= -
+ +
�
�
�
�
�
�
+
�
�
r
r
r
r
r r
r
r
(
)
(1
)
j t
z
x
y
B
ji
j i e
w b
*
-
-
�
�
=
+ -
�
�
r
r
r
C 01 p
28
WEKTORY ZESPOLONE (7)
• Wyznaczmy wektory rzeczywiste
odpowiadające
wektorom zespolonym:
(
)
(
)
(1
)
j t
z
j t
z
x
y
A
j e
i
je
i
w b
w b
-
-
= +
+
r
r
r
(
)
(
)
(1
)
j t
z
j t
z
x
y
B
je
i
j e
i
w b
w b
-
-
=-
+ +
r
r
r
A, B
r r
A Re{ } ?
A
=
=
r
r
B Re{ } ?
B
=
=
r
r
C 01 p
29
WEKTORY ZESPOLONE (8)
• Wyznaczmy wektory rzeczywiste
odpowiadające
wektorom zespolonym:
(
)
(
)
(1
)
j t
z
j t
z
x
y
A
j e
i
je
i
w b
w b
-
-
= +
+
r
r
r
(
)
(
)
(1
)
j t
z
j t
z
x
y
B
je
i
j e
i
w b
w b
-
-
=-
+ +
r
r
r
A, B
r r
(
/4)
(
/2)
2
j t
z
j t
z
x
y
A
e
i
e
i
w b p
w b p
-
+
-
+
=
+
r
r
r
2cos(
/4)
2sin(
/4)
x
A
t
z
j
t
z
i
w b
p
w b
p
�
�
=
-
+
+
-
+
�
�
r
r
[
]
cos(
/2)
sin(
/2)
y
t
z
j
t
z
i
w b
p
w b
p
+
-
+
+
-
+
r
A Re{ }
2cos(
/4)
cos(
/2)
x
y
A
t
z
i
t
z
i
w b
p
w b
p
=
=
-
+
+
-
+
r
r
r
r
B Re{ } cos(
/ 2)
2cos(
/4)
x
y
B
t
z
i
t
z
i
w b
p
w b
p
=
=
-
-
+
-
+
r
r
r
r
C 01 p
30
OPERATORY RÓŻNICZKOWE
A
A
div
Operatory różniczkowe:
gradient
dywergencja
rotacja
laplasjan skalarny
laplasjan wektorowy
A
A
rot
A
A
A
A
)
(
2
x
y
z
i
i
i
x
y
z
�
�
�
Ѻ
+
+
�
�
�
r
r
r
;
x
y
z
r xi
yi
zi
=
+
+
r
r
r
r
( )
( , , )
U U r
U x y z
�
�
r
gdzie
- skalarna funkcja położenia
( )
( , , )
A A r
A x y z
�
�
r
r
r
r
- wektorowa funkcja położenia
( , , )
( , , )
( , , )
( , , )
x
x
y
y
z
z
A x y z
A x y z i
A x y z i
A x y z i
=
+
+
r
r
r
r
Operator nabla:
2
2
2
2
2
2
2
x
y
y
�
�
�
D=Ѻ��Ѻ++
�
�
�
Operator Laplace’a:
grad U
U
��
2
(
)
(
)
U
U
U
U
D �� = ��
� =���
C 01 p
31
OPERATORY RÓŻNICZKOWE - GRADIENT
Gradient w kartezjańskich współrzędnych
prostokątnych
x
y
z
U
U
U
U
i
i
i
x
y
z
�
�
�
� =
+
+
�
�
�
r
r
r
Gradient we współrzędnych
cylindrycznych
1
z
U
U
U
U
i
i
i
z
r
j
r
r j
�
�
�
� =
+
+
�
�
�
r
r
r
Gradient we współrzędnych
sferycznych
1
1
sin
r
U
U
U
U
i
i
i
r
r
r
q
j
q
q j
�
�
�
� =
+
+
�
�
�
r
r
r
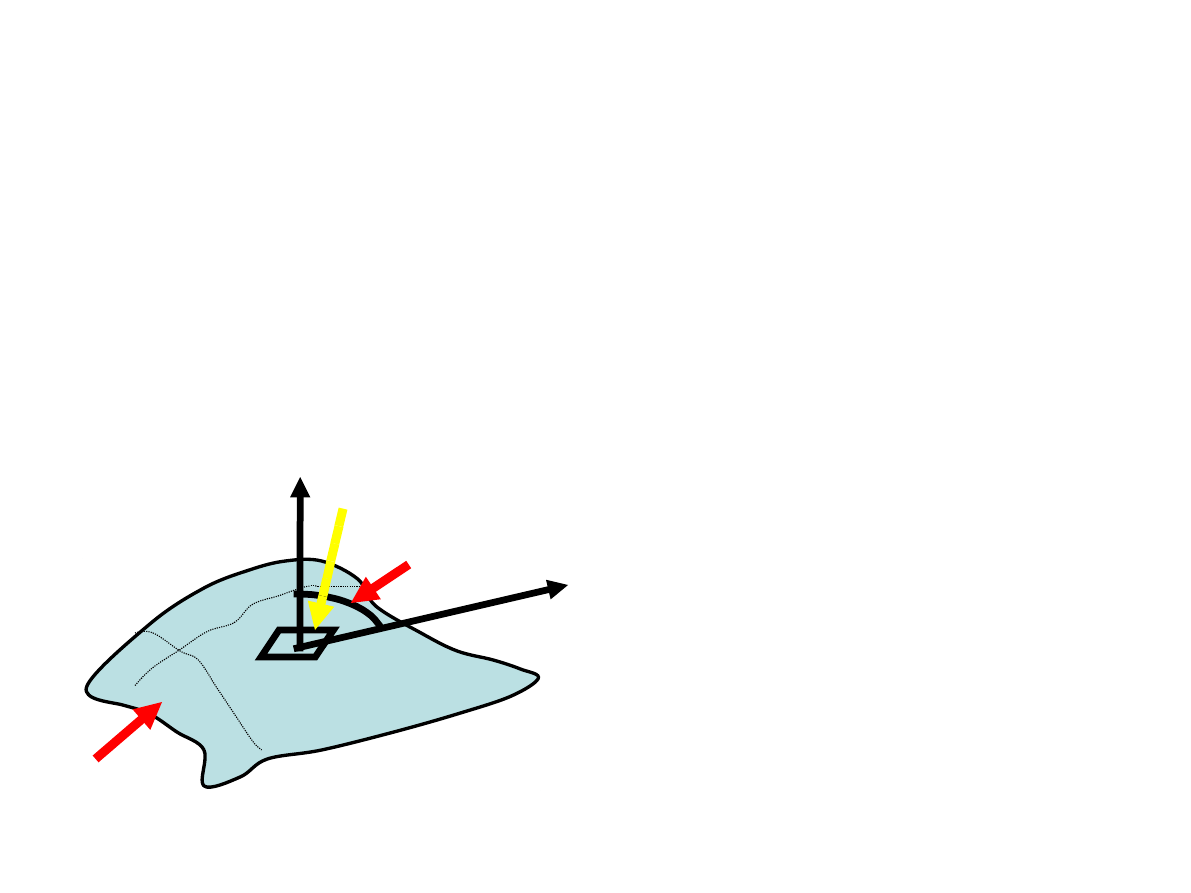
C 01 p
32
STRUMIEŃ WIELKOŚCI WEKTOROWEJ
S
q
ds
A
r
d
d
s n s
=
r r
• Elementarny strumień wielkości wektorowej
przez
element powierzchni reprezentowanej przez
wektor
(normalny do powierzchni i skierowany na zewnątrz
zamkniętej powierzchni) jest równy
iloczynowi
składowej
normalnej wektora przez pole powierzchni
A
r
ds
ds
r
dF
A
r
ds
d
d
d
d
n
A s A n s A s
F = � = � =
r
r
r
r
• Strumień wektora
przez
powierzchnię
S
:
F
A
r
d
S
A s
F =
�
�
�
r r
C 01 p
33
OPERATORY RÓŻNICZKOWE – DYWERGENCJA
0
d
lim
S
V
A s
A
V
�
�
�� =
�
�
r r
r
�
Dywergencję wektora , w oparciu o twierdzenie
Gaussa
d
S
A s
�
�
�
r r
�
przy
czym
- strumień wektora wypływający z
obszaru
o objętości V
A
r
S - powierzchnia zamknięta ograniczająca objętość V
A
r
• Jeżeli w punkcie przestrzeni znajduje się skalarne źródło pola ,
to dywergencja jest różna od zera.
A
r
• Pole wektorowe, którego dywergencja jest różna od
zera,
jest
polem źródłowym
.
• Pole wektorowe o zerowej dywergencji jest
polem
bezźródłowym
albo
solenoidalnym
.
możemy przedstawić
jako:
d
d ,
V
S
A V
A s
��
=
�
�
�
�
�
�
r
r r
�
0
A
�
r
0
A
�� =
r
C 01 p
34
OPERATORY RÓŻNICZKOWE – DYWERGENCJA (2)
Dywergencja w kartezjańskich współrzędnych
prostokątnych
y
x
z
x
y
z
A
A
A
A
A
A
A i
i
i
x
y
z
x
y
z
�
�
�
�
�
�
�� =
+
+
=
+
+
�
�
�
�
�
�
r
r
r
r r
r
r
Dywergencja we współrzędnych
cylindrycznych
(
)
1
1
z
A
A
A
A
z
r
j
r
r
r
r j
�
�
�
�� =
+
+
�
�
�
r
Dywergencja we współrzędnych
sferycznych
(
)
2
2
(sin
)
1
1
1
sin
sin
r
A
r A
A
A
r
r
r
r
j
q
q
q
q
q j
�
�
�
�� =
+
+
�
�
�
r
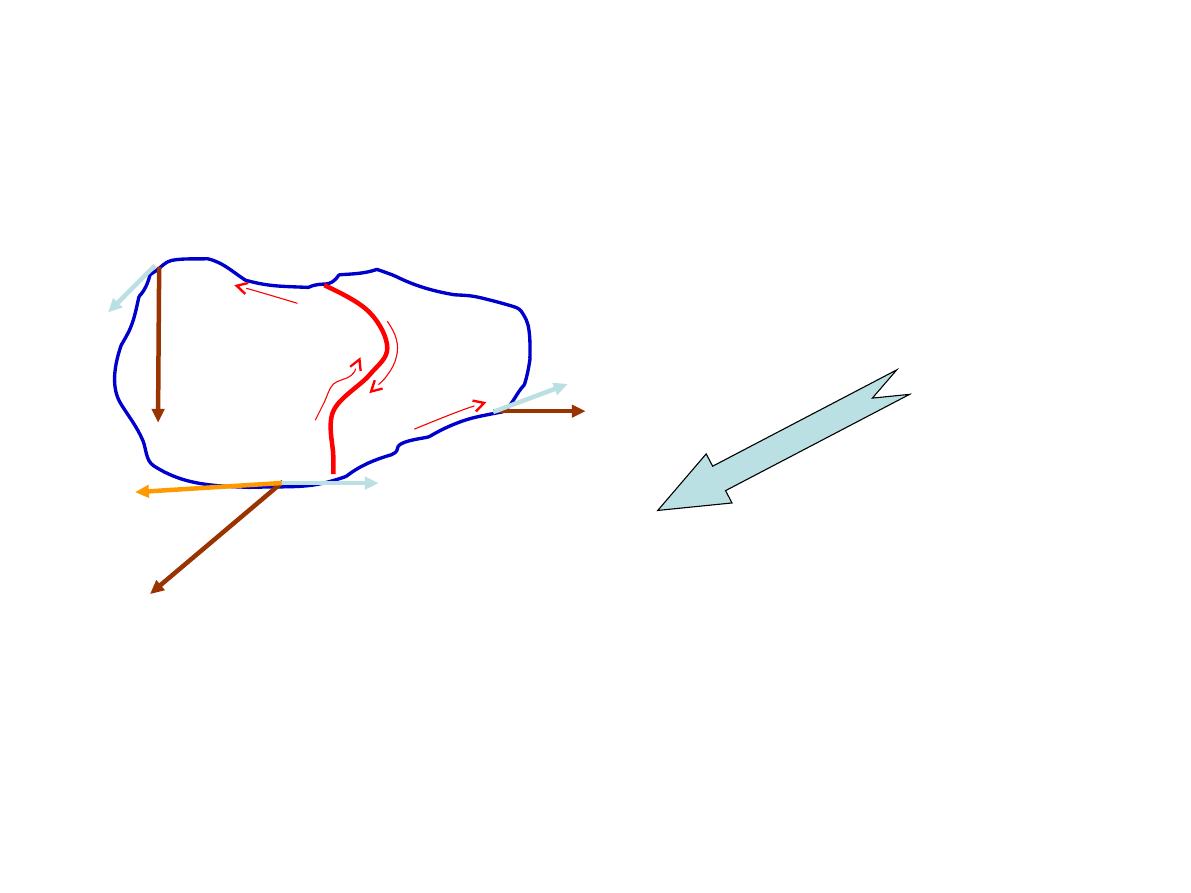
C 01 p
35
CYRKULACJA (KRĄŻENIE) POLA WEKTOROWEGO
A
r
A
r
A
r
t
A
r
L
A
r
d
d
t
L
L
C
A l
A l
=
� =
�
�
r
r
�
�
• Niech będzie dowolnym polem wektorowym, a
dl
r
niech będzie styczną
do
krzywej
wtedy całkę
krzywoliniową
L
dl
r
dl
r
dl
r
cyrkulacją pola wektorowego po krzywej
zamkniętej.
nazywamy
C 01 p
36
OPERATORY RÓŻNICZKOWE – ROTACJA
0
d
(
)
lim
L
S
A l
A n
S
�
�
Ѵ�=
�
r
r
r r
�
Rotację wektora , w oparciu o twierdzenie
Stokesa
d
L
A l
�
�
r
r
�
przy
czym
- cyrkulacja pola wektorowego po
zamkniętej
dodatnio zorientowanej krzywej L
A
r
S - powierzchnia płaska
A
r
• Jeżeli rotacja pola wektorowego w określonym obszarze
jest
różna od zera
, to pole nazywa się
wirowym
.
• Pole wektorowe, którego rotacja jest
równa zero
w danym obszarze,
jest polem
bezwirowym
lub
potencjalnym
.
L – linia zamknięta będąca brzegiem
powierzchni S
możemy przedstawić w postaci:
(
) d
d
S
L
A n s
A l
Ѵ�=�
�
�
�
r
r
r
r
�
- wersor normalny do powierzchni
płaskiej S
n
r
0
A
�Ѵ�
r r
0
A
�Ѵ=
r r
C 01 p
37
OPERATORY RÓŻNICZKOWE – ROTACJA (2)
Rotacja w kartezjańskich współrzędnych
prostokątnych
Rotacja we
współrzędnych
cylindrycznych
Rotacja we
współrzędnych
sferycznych
x
y
z
y
y
x
x
z
z
x
y
z
x
y
z
i
i
i
A
A
A
A
A
A
A
i
i
i
x
y
z
y
z
z
x
x
y
A
A
A
�
�
�
�
�
�
�
�
�
�
� � �
�
�
Ѵ
=
=
-
+
-
+
-
�
�
�
�
�
�
� � �
�
�
�
�
�
�
�
�
�
�
�
�
r
r
r
r
r
r
r
z
z
i
i
i
A
z
A
A
A
r
j
r
j
r
r
r
j
r
�
�
�
Ѵ
=
�
�
�
r
r
r
r
2
sin
sin
sin
r
r
i
i
i
r
r
r
A
r
A
rA
r
A
j
q
q
j
q
q
q
j
q
�
�
�
Ѵ
=
�
�
�
r
r
r
r
Document Outline