DRGANIA WŁASNE

DRGANIA WŁASNE

BELKI

BELKI

MATLAB

MATLAB

DRGANIA WŁASNE BELKI- MATLAB

DRGANIA WŁASNE BELKI- MATLAB

Zagadnienie własne

Zagadnienie własne

dotyczące drgań

dotyczące drgań

swobodnych, nietłumionych, opisuje ruch

swobodnych, nietłumionych, opisuje ruch

układu dynamicznego bez sił

układu dynamicznego bez sił

wymuszających i bez uwzgędnienia

wymuszających i bez uwzgędnienia

tłumienia.

tłumienia.

Rozwiązanie zagadnienia własnego

Rozwiązanie zagadnienia własnego

prowadzi

prowadzi

do określenia częstości własnych i

do określenia częstości własnych i

wektorów własnych, które to wielkości

wektorów własnych, które to wielkości

odgrywają główną rolę w wyznaczeniu

odgrywają główną rolę w wyznaczeniu

reakcji dynamicznej liniowych układów

reakcji dynamicznej liniowych układów

poddanych działaniu sił wymuszających.

poddanych działaniu sił wymuszających.

DRGANIA WŁASNE BELKI- MATLAB

DRGANIA WŁASNE BELKI- MATLAB

Równanie ruchu drgań własnych otrzymuje

Równanie ruchu drgań własnych otrzymuje

się z równania ruchu:

się z równania ruchu:

)

(t

F

Kδ

δ

C

δ

B





 



Po pominięciu członu zawierającego macierz
tłumienia C oraz wektora obciążeń zewnę-
trznych F.

(1)

W równaniu (1) B jest macierzą bezwładności
(macierzą mas),

δ

δ 

 ,

-odpowiednio wektorem przyśpieszeń i
prędkości,

δ

- wektorem przemieszczeń węzłowych

DRGANIA WŁASNE BELKI- MATLAB

DRGANIA WŁASNE BELKI- MATLAB

Równanie drgań własnych przyjmuje

Równanie drgań własnych przyjmuje

zatem postać:

zatem postać:

0

Kδ

δ

B







(2)

Zakładając, że drgania własne są ruchem
harmonicznym

t

t



sin

)

(

0

δ

δ 

Po dwukrotnym zróżniczkowaniu zal. (3):

(3)

t

t



sin

)

(

0

2

δ

ω

δ





(4)

DRGANIA WŁASNE BELKI- MATLAB

DRGANIA WŁASNE BELKI- MATLAB

I podstawieniu do równania (2)

I podstawieniu do równania (2)

otrzymujemy:

otrzymujemy:

2

0

)

(

ω

0

δ

B

K











(5)

Jest to układ liniowych jednorodnych równań
algebraicznych, który ma rozwiązanie tylko
wtedy gdy

0

)

det(

2





B

K



(6)

DRGANIA WŁASNE BELKI- MATLAB

DRGANIA WŁASNE BELKI- MATLAB

Równanie to nazywa się równaniem

Równanie to nazywa się równaniem

charakterystycznym zagadnienia

charakterystycznym zagadnienia

własnego. Z punktu widzenia matematyki,

własnego. Z punktu widzenia matematyki,

jest to równanie na znalezienie wartości

jest to równanie na znalezienie wartości

własnych macierzy.

własnych macierzy.

PRZYKŁAD

Dana jest belka wspornikowa o długości 3m.
Dane belki są następujące:
E=2e09 Pa
v=0.2
hb=0.269 m
b=0.2 m

DRGANIA WŁASNE BELKI- MATLAB

DRGANIA WŁASNE BELKI- MATLAB

I=3.25e-4 m^-4

I=3.25e-4 m^-4

ro=7.8e3 kg/m^3

ro=7.8e3 kg/m^3

1.

1.

WPROWADZENIE DANYCH

WPROWADZENIE DANYCH



E=2.0e9

E=2.0e9



E =

E =



2.0000e+009

2.0000e+009



I=3.25e-4

I=3.25e-4



I =

I =



3.2500e-004

3.2500e-004



b=0.2

b=0.2



b =

b =



0.2000

0.2000



hb=0.269

hb=0.269



hb =

hb =



0.2690

0.2690

DRGANIA WŁASNE BELKI- MATLAB

DRGANIA WŁASNE BELKI- MATLAB



l=1

l=1



l =

l =



1

1

Belkę podzielono na trzy elementy o długości
1 m każdy.

le=3

le =
3

lw=le+1

lw =
4

DRGANIA WŁASNE BELKI- MATLAB

DRGANIA WŁASNE BELKI- MATLAB



l=1

l=1



l =

l =



1

1



Ee=[E,E,E]

Ee=[E,E,E]



Ee =

Ee =



1.0e+009 *

1.0e+009 *



2.0000 2.0000 2.0000

2.0000 2.0000 2.0000



lE=[l,l,l]

lE=[l,l,l]



lE =

lE =



1 1 1

1 1 1



Ie=[I,I,I]

Ie=[I,I,I]



Ie =

Ie =



1.0e-003 *

1.0e-003 *



0.3250 0.3250 0.3250

0.3250 0.3250 0.3250



ien=[1 2;2 3;3 4]'

ien=[1 2;2 3;3 4]'



ien =

ien =



1 2 3

1 2 3



2 3 4

2 3 4

DRGANIA WŁASNE BELKI- MATLAB

DRGANIA WŁASNE BELKI- MATLAB



N=8

N=8



N =

N =



8

8



rob=7.8e3

rob=7.8e3



rob =

rob =



7800

7800

2. OBLICZENIE MACIERZY SZTYWNOŚCI
ELEMENTÓW

DRGANIA WŁASNE BELKI- MATLAB

DRGANIA WŁASNE BELKI- MATLAB



e=1

e=1



e =

e =



1

1



k1=sztywelbelki(e,Ee,Ie,lE)

k1=sztywelbelki(e,Ee,Ie,lE)



k1 =

k1 =



7800000 3900000 -7800000 3900000

7800000 3900000 -7800000 3900000



3900000 2600000 -3900000 1300000

3900000 2600000 -3900000 1300000



-7800000 -3900000 7800000 -3900000

-7800000 -3900000 7800000 -3900000



3900000 1300000 -3900000 2600000

3900000 1300000 -3900000 2600000

DRGANIA WŁASNE BELKI- MATLAB

DRGANIA WŁASNE BELKI- MATLAB



e=2;

e=2;



k2=sztywelbelki(e,Ee,Ie,lE)

k2=sztywelbelki(e,Ee,Ie,lE)



k2 =

k2 =



7800000 3900000 -7800000 3900000

7800000 3900000 -7800000 3900000



3900000 2600000 -3900000 1300000

3900000 2600000 -3900000 1300000



-7800000 -3900000 7800000 -3900000

-7800000 -3900000 7800000 -3900000



3900000 1300000 -3900000 2600000

3900000 1300000 -3900000 2600000

e=3

e =
3

k3=sztywelbelki(e,Ee,Ie,lE)

k3 =
7800000 3900000 -7800000 3900000
3900000 2600000 -3900000 1300000
-7800000 -3900000 7800000 -3900000
3900000 1300000 -3900000 2600000

DRGANIA WŁASNE BELKI- MATLAB

DRGANIA WŁASNE BELKI- MATLAB

2

. OBLICZENIE MACIERZY MAS

ELEMENTÓW

Konsystentna macierz mas elementu

belkowego ma postać:

































2

2

2

4

22

156

3

13

4

13

54

22

156

420

L

SYM

L

L

L

L

L

L

L

B

e



DRGANIA WŁASNE BELKI- MATLAB

DRGANIA WŁASNE BELKI- MATLAB



e=1

e=1

m

m

1=macmasbelka(e,lE,rob,b,hb)

1=macmasbelka(e,lE,rob,b,hb)



m1 =

m1 =



155.8663 21.9811 53.9537 -12.9889

155.8663 21.9811 53.9537 -12.9889



21.9811 3.9966 12.9889 -2.9974

21.9811 3.9966 12.9889 -2.9974



53.9537 12.9889 155.8663 -21.9811

53.9537 12.9889 155.8663 -21.9811



-12.9889 -2.9974 -21.9811 3.9966

-12.9889 -2.9974 -21.9811 3.9966

e=2;

m2=macmasbelka(e,lE,rob,b,hb)

m2 =

155.8663 21.9811 53.9537 -12.9889

21.9811 3.9966 12.9889 -2.9974

53.9537 12.9889 155.8663 -21.9811

-12.9889 -2.9974 -21.9811 3.9966

DRGANIA WŁASNE BELKI- MATLAB

DRGANIA WŁASNE BELKI- MATLAB

e=3

e=3

;

;



m3=macmasbelka(e,lE,rob,b,hb)

m3=macmasbelka(e,lE,rob,b,hb)



m3 =

m3 =



155.8663 21.9811 53.9537 -12.9889

155.8663 21.9811 53.9537 -12.9889



21.9811 3.9966 12.9889 -2.9974

21.9811 3.9966 12.9889 -2.9974



53.9537 12.9889 155.8663 -21.9811

53.9537 12.9889 155.8663 -21.9811



-12.9889 -2.9974 -21.9811 3.9966

-12.9889 -2.9974 -21.9811 3.9966

Funkcja własna macmasbelka ma postać:

DRGANIA WŁASNE BELKI- MATLAB

DRGANIA WŁASNE BELKI- MATLAB



% macierz mas belka



function me=macmasbelka(e,lE,rob,b,hb)



%Dznaczniki_stanu;



me=zeros(4);



me(1,1)=(13/35)*rob*b*hb*lE(1,e);



me(1,2)=(11/210)*rob*b*hb*(lE(1,e))^2;



me(1,3)=(9/70)*rob*b*hb*lE(1,e);



me(1,4)=(-13/420)*rob*b*hb*(lE(1,e))^2;



me(2,2)=(1/105)*rob*b*hb*(lE(1,e))^3;



me(2,3)=(13/420)*rob*b*hb*(lE(1,e))^2;



me(2,4)=(-1/140)*rob*b*hb*(lE(1,e))^3;



me(3,3)=(13/35)*rob*b*hb*lE(1,e);



me(3,4)=(-11/210)*rob*b*hb*(lE(1,e))^2;



me(4,4)=(1/105)*rob*b*hb*(lE(1,e))^3;



% symetryczne odbicie



for i=1:4



for j=1:4



me(j,i)=me(i,j);



end;



end;

DRGANIA WŁASNE BELKI- MATLAB

DRGANIA WŁASNE BELKI- MATLAB

3. PRZYGOTOWANIE DO AGREGACJI

3. PRZYGOTOWANIE DO AGREGACJI

MACIERZY SZTYWNOŚCI I MACIERZY

MACIERZY SZTYWNOŚCI I MACIERZY

MAS

MAS



lm=pomocagregacji(2,2,lw,ien,le)

lm=pomocagregacji(2,2,lw,ien,le)



lm =

lm =



1 3 5

1 3 5



2 4 6

2 4 6



3 5 7

3 5 7



4 6 8

4 6 8





K=zeros(N,N);

K=zeros(N,N);



M=zeros(N,N);

M=zeros(N,N);

DRGANIA WŁASNE BELKI- MATLAB

DRGANIA WŁASNE BELKI- MATLAB

4.

4.

AGREGACJA MACIERZY SZTYWNOŚCI ELEMENTÓW DO

AGREGACJA MACIERZY SZTYWNOŚCI ELEMENTÓW DO

MACIERZY GLOBALNEJ K I MACIERZY MAS

MACIERZY GLOBALNEJ K I MACIERZY MAS

ELEMENTÓW DO MACIERZY GLOBALNEJ M

ELEMENTÓW DO MACIERZY GLOBALNEJ M



e=1;

e=1;



K=agregacjamacglob(K,e,k1,2,2,le,lw,lm);

K=agregacjamacglob(K,e,k1,2,2,le,lw,lm);



M=agregacjamacglob(M,e,m1,2,2,le,lw,lm

M=agregacjamacglob(M,e,m1,2,2,le,lw,lm

);

);



e=2;

e=2;





K=agregacjamacglob(K,e,k2,2,2,le,lw,lm);

K=agregacjamacglob(K,e,k2,2,2,le,lw,lm);



M=agregacjamacglob(M,e,m2,2,2,le,lw,lm);

M=agregacjamacglob(M,e,m2,2,2,le,lw,lm);



e=3;

e=3;



K=agregacjamacglob(K,e,k3,2,2,le,lw,lm);

K=agregacjamacglob(K,e,k3,2,2,le,lw,lm);



M=agregacjamacglob(M,e,m3,2,2,le,lw,lm);

M=agregacjamacglob(M,e,m3,2,2,le,lw,lm);

DRGANIA WŁASNE BELKI- MATLAB

DRGANIA WŁASNE BELKI- MATLAB

5. UWZGLĘDNIENIE WARUNKÓW

5. UWZGLĘDNIENIE WARUNKÓW

BRZEGOWYCH

BRZEGOWYCH

Kąt obrotu i ugięcie na podporze typu

Kąt obrotu i ugięcie na podporze typu

zamocowanie są równe zeru.

zamocowanie są równe zeru.

Tak więc w naszym przypadku

Tak więc w naszym przypadku

0

0

1

1







w

Należy więc wykreślić z macierzy K i M
odpowiednio pierwszy i drugi wiersz i pierwszą i
drugą kolumnę.

- Pierwsze równanie

- Drugie równanie

DRGANIA WŁASNE BELKI- MATLAB

DRGANIA WŁASNE BELKI- MATLAB



K(1,:)=[];

K(1,:)=[];



K(:,1)=[];

K(:,1)=[];





M(1,:)=[];

M(1,:)=[];



M(:,1)=[];

M(:,1)=[];





K(1,:)=[];

K(1,:)=[];



K(:,1)=[];

K(:,1)=[];





M(1,:)=[];

M(1,:)=[];



M(:,1)=[];

M(:,1)=[];

DRGANIA WŁASNE BELKI- MATLAB

DRGANIA WŁASNE BELKI- MATLAB

6. OBLICZENIE WARTOŚCI I WEKTORÓW

6. OBLICZENIE WARTOŚCI I WEKTORÓW

WŁASNYCH

WŁASNYCH



[V,D]=eig(K,M)

[V,D]=eig(K,M)



V =

V =



0.0093 0.0335 -0.0421 0.0154 -0.0174 0.0149

0.0093 0.0335 -0.0421 0.0154 -0.0174 0.0149



0.0170 0.0333 0.0314 -0.1962 -0.3239 0.1526

0.0170 0.0333 0.0314 -0.1962 -0.3239 0.1526



0.0308 0.0240 0.0372 0.0071 0.0306 0.0233

0.0308 0.0240 0.0372 0.0071 0.0306 0.0233



0.0246 -0.0559 0.0240 0.2010 -0.2130 0.4291

0.0246 -0.0559 0.0240 0.2010 -0.2130 0.4291



0.0564 -0.0567 -0.0566 -0.0609 0.0659 0.1237

0.0564 -0.0567 -0.0566 -0.0609 0.0659 0.1237



0.0259 -0.0905 -0.1501 -0.2597 0.4366 1.2370

0.0259 -0.0905 -0.1501 -0.2597 0.4366 1.2370



D =

D =



1.0e+006 *

1.0e+006 *



0.0002 0 0 0 0 0

0.0002 0 0 0 0 0



0 0.0093 0 0 0 0

0 0.0093 0 0 0 0



0 0 0.0746 0 0 0

0 0 0.0746 0 0 0



0 0 0 0.3784 0 0

0 0 0 0.3784 0 0



0 0 0 0 1.3403 0

0 0 0 0 1.3403 0



0 0 0 0 0 5.3270

0 0 0 0 0 5.3270

DRGANIA WŁASNE BELKI- MATLAB

DRGANIA WŁASNE BELKI- MATLAB

Macierz

Macierz

D

D

jest macierzą diagonalną; na diagonali

jest macierzą diagonalną; na diagonali

zawarte są kolejne wartości

zawarte są kolejne wartości

Macierz

Macierz

V

V

jest macierzą pełną, jej kolumny są

jest macierzą pełną, jej kolumny są

odpowiednimi dla danych wartości własnych

odpowiednimi dla danych wartości własnych

wektorami własnymi.

wektorami własnymi.



omega=sqrt(D)

omega=sqrt(D)



omega =

omega =



1.0e+003 *

1.0e+003 *



0.0154 0 0 0 0 0

0.0154 0 0 0 0 0



0 0.0967 0 0 0 0

0 0.0967 0 0 0 0



0 0 0.2732 0 0 0

0 0 0.2732 0 0 0



0 0 0 0.6151 0 0

0 0 0 0.6151 0 0



0 0 0 0 1.1577 0

0 0 0 0 1.1577 0



0 0 0 0

0 0 0 0

0 2.3080

0 2.3080

2







DRGANIA WŁASNE BELKI- MATLAB

DRGANIA WŁASNE BELKI- MATLAB

7.

7.

WYZNACZENIE PI

WYZNACZENIE PI

E

E

RWSZEJ POSTACI

RWSZEJ POSTACI

DRGAŃ WŁASNYCH

DRGAŃ WŁASNYCH

Wektory własne:

Wektory własne:











































0259

.

0

0564

.

0

0246

.

0

0308

.

0

0170

.

0

0093

.

0

01



wektor własny odpowiadający
pierwszej częstości własnej

Wektory przemieszczeń (amplitud)
węzłowych dla pierwszej postaci w
układzie globalnym:

DRGANIA WŁASNE BELKI- MATLAB

DRGANIA WŁASNE BELKI- MATLAB

.

.















































































0259

.

0

0564

.

0

0246

.

0

0308

.

0

,

0246

.

0

0308

.

0

0170

.

0

0093

.

0

,

0170

.

0

0093

.

0

0

0

13

12

11







Przemieszczenie każdego punktu opisuje
zależność:































2

2

1

1

4

3

2

1

]

[





w

w

N

N

N

N

w

δ

N

(7)











































0259

.

0

0564

.

0

0246

.

0

0308

.

0

0170

.

0

0093

.

0

01



W2
fi2
W3
fi3
W4
fi4

DRGANIA WŁASNE BELKI- MATLAB

DRGANIA WŁASNE BELKI- MATLAB

gdzie funkcje kształtu elementu belkowego

gdzie funkcje kształtu elementu belkowego

mają postać:

mają postać:

)

(

1

)

3

2

(

1

)

2

(

1

)

3

2

(

1

2

2

3

3

4

2

3

3

3

3

2

2

3

3

2

3

2

3

3

1

l

x

x

l

l

N

lx

x

l

N

l

x

l

x

lx

l

N

l

lx

x

l

N























DRGANIA WŁASNE BELKI- MATLAB

DRGANIA WŁASNE BELKI- MATLAB

Po podstawieniu danych macierze funkcji

Po podstawieniu danych macierze funkcji

kształtu dla poszczególnych elementów

kształtu dla poszczególnych elementów

mają postać:

mają postać:

]

0

1

0

0

[

)

1

(

]

125

.

0

5

.

0

125

.

0

5

.

0

[

)

5

.

0

(

]

0

0

0

1

[

)

0

(















x

x

x

N

N

N

Po podstawieniu do wzoru (7) otrzymamy:

DRGANIA WŁASNE BELKI- MATLAB

DRGANIA WŁASNE BELKI- MATLAB

-

-

dla elementu pierwszego

dla elementu pierwszego

0093

.

0

0170

.

0

0093

.

0

0

0

]

0

1

0

0

[

)

1

(

)

1

(

002525

.

0

0170

.

0

0093

.

0

0

0

]

125

.

0

5

.

0

125

.

0

5

.

0

[

)

5

.

0

(

)

5

.

0

(

0

0170

.

0

0093

.

0

0

0

]

0

0

0

1

[

)

0

(

)

0

(

11

1

1

11

1

1

11

1

1









































































































δ

N

δ

N

δ

N

x

x

w

x

x

w

x

x

w

DRGANIA WŁASNE BELKI- MATLAB

DRGANIA WŁASNE BELKI- MATLAB

-

-

dla elementu drugiego

dla elementu drugiego

0308

.

0

0246

.

0

0308

.

0

0107

.

0

0093

.

0

]

0

1

0

0

[

)

1

(

)

1

(

0183

.

0

0246

.

0

0308

.

0

0107

.

0

0093

.

0

]

125

.

0

5

.

0

125

.

0

5

.

0

[

)

5

.

0

(

)

5

.

0

(

0093

.

0

0246

.

0

0308

.

0

0107

.

0

0093

.

0

]

0

0

0

1

[

)

0

(

)

0

(

12

2

2

12

2

2

12

2

2









































































































δ

N

δ

N

δ

N

x

x

w

x

x

w

x

x

w

DRGANIA WŁASNE BELKI- MATLAB

DRGANIA WŁASNE BELKI- MATLAB

-

-

dla elementu trzeciego

dla elementu trzeciego

0564

.

0

0259

.

0

0564

.

0

0246

.

0

0308

.

0

]

0

1

0

0

[

)

1

(

)

1

(

0434

.

0

0259

.

0

0564

.

0

0246

.

0

0308

.

0

]

125

.

0

5

.

0

125

.

0

5

.

0

[

)

5

.

0

(

)

5

.

0

(

0308

.

0

0259

.

0

0564

.

0

0246

.

0

0308

.

0

]

0

0

0

1

[

)

0

(

)

0

(

13

3

3

13

3

3

13

3

3









































































































δ

N

δ

N

δ

N

x

x

w

x

x

w

x

x

w

DRGANIA WŁASNE BELKI- MATLAB

DRGANIA WŁASNE BELKI- MATLAB

8.

8.

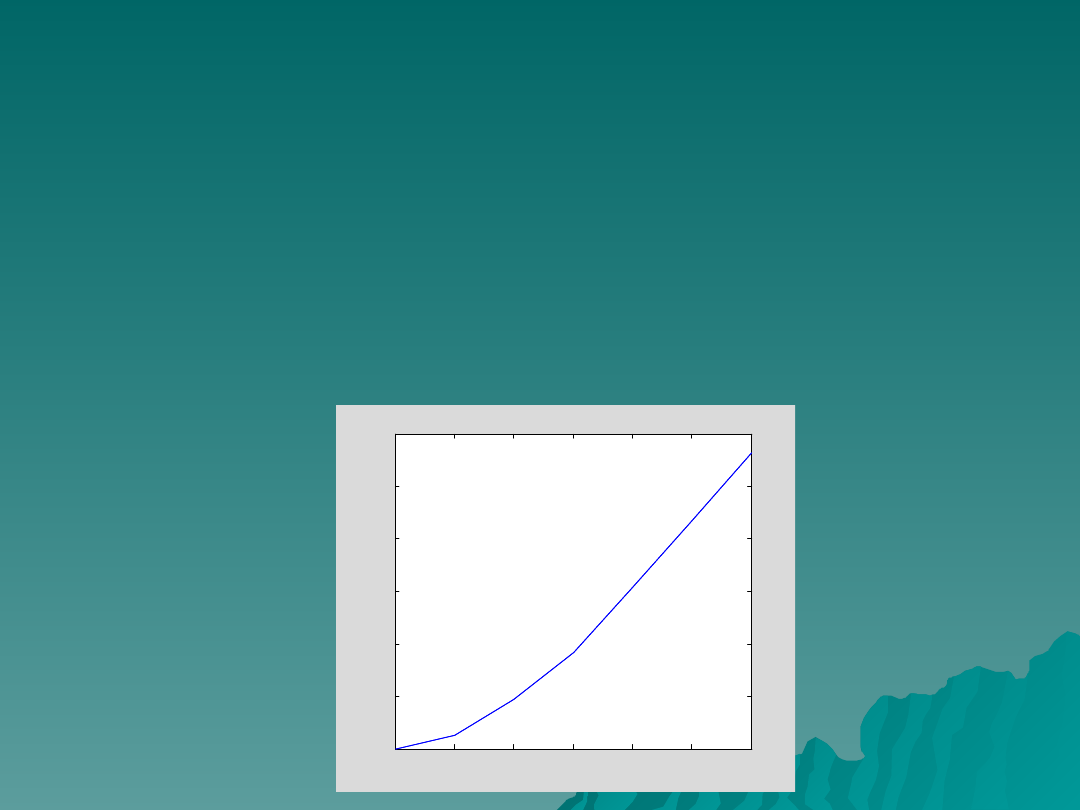
WIZUALIZACJA

WIZUALIZACJA

x=[0 0.5 1 1.5 2 2.5 3]

x=[0 0.5 1 1.5 2 2.5 3]

y=[0 0.002525 0.0093 0.0183 0.0308 0.0434 0.0564]

y=[0 0.002525 0.0093 0.0183 0.0308 0.0434 0.0564]

plot(x, y); hold on;title('PIERWSZA POSTAĆ DRGAŃ

plot(x, y); hold on;title('PIERWSZA POSTAĆ DRGAŃ

WŁASNYCH');xlabel('m')

WŁASNYCH');xlabel('m')

0

0.5

1

1.5

2

2.5

3

0

0.01

0.02

0.03

0.04

0.05

0.06

PIERWSZA POSTAĆ DRGAŃ WŁASNYCH

m