51

Ponieważ cztery wielkości występujące w powyższych formułach, tzn. pęd p, siła F,

kręt K

C

i moment M

C

względem środka masy lub punktu nieruchomego, są wektorami,

więc metodę bilansową można również nazwać metodą wektorową. Nazywamy ją

także, przez wzgląd na autorów formuł (2.47) i (2.48), metodą Newtona - Eulera.

Warto

zauważyć, że z równania (2.47), po wykorzystaniu definicji pędu p = mv

i przy założeniu, że m = const, można otrzymać II zasadę Newtona, czyli równanie

m a = F

(2.51)

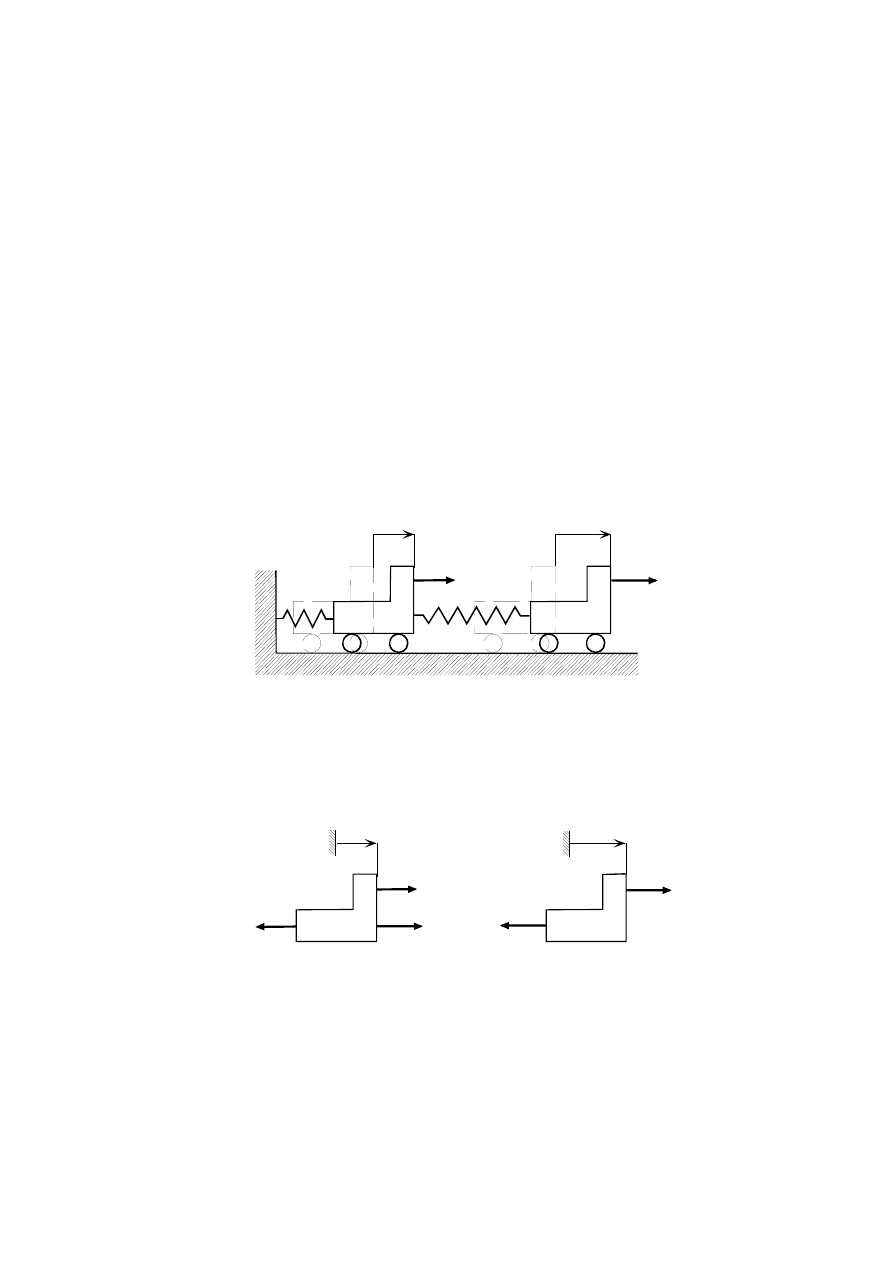
Przykład 2.1. W celu ilustracji metody bilansowej wyprowadzimy równania ruchu dla

układu, którego schemat przedstawiony jest na rys.2.19. Na rysunku tym symbole q

1

i

q

2

oznaczają współrzędne punktów materialnych mierzone od położenia równowagi.

Przyjmujemy ponadto, że koła wagoników jak i sprężyny są pozbawione masy.

q

1

q

2

F

1

(t)

F

2

(t)

k

1

k

2

m

1

m

2

Rys.2.19

Wyprowadzając równania ruchu metodą bilansową w pierwszej kolejności uwalniamy

obie masy od więzów, czyli m.in. od sprężyn, zastępując ich działanie siłami, co

przedstawia rys.2.20

q

2

F

2

(t)

m

2

k

2

(q

2

-q

1

)

q

1

F

1

(t)

k

1

q

1

k

2

(q

2

-q

1

)

m

1

Rys. 2.20

Następnie zapisujemy równanie (2.51) kolejno dla każdej masy:

(

)

( )

t

F

q

q

k

q

k

q

m

1

1

2

2

1

1

1

1

+

−

+

−

=

&&

(P.2.1a)

(

)

( )

t

F

q

q

k

q

m

2

1

2

2

2

2

+

−

−

=

&&

(P.2.1b)

52

Po uporządkowaniu równań (P.2.1) można je zapisać w następującej postaci

standardowej

(

)

( )

t

F

q

k

q

k

k

q

m

1

2

2

1

2

1

1

1

=

−

+

+

&&

(P.2.2a)

( )

t

F

q

k

q

k

q

m

2

2

2

1

1

2

2

=

+

−

&&

(P.2.2b)

2.5.3 Równania Lagrange’a II rodzaju

Równania te w najbardziej ogólnym zapisie mają postać

σ

σ

σ

=

∂

∂

−

∂

∂

Q

q

L

q

L

dt

d

&

σ = 1,...,s

(2.52)

gdzie wielkość L, zwana funkcją Lagrange’a albo lagranżianem, jest zdefiniowana jako

L = T - V

(2.53)

czyli jest różnicą energii kinetycznej T i potencjalnej V. Wielkość Q

σ

jest siłą

uogólnioną niepotencjalną, którą wyznacza się ze wzoru

σ

ν

=

ν

ν

σ

∂

∂

⋅

=

∑

q

Q

n

r

F

1

σ = 1,...,s

(2.54)

Wielkości q

σ

w liczbie stopni swobody s są współrzędnymi uogólnionymi, F

ν

są

wektorami głównymi sił przyłożonymi w punktach określonych wektorami

pozycyjnymi r

ν

,

ν = 1,...,n.

Aby

skorzystać ze wzoru (2.54) należy wektory r

ν

wyrazić za pomocą

współrzędnych uogólnionych, tj. skorzystać ze związków

(

)

σ

ν

ν

=

q

;

t

r

r

ν = 1,..., n ; σ = 1,...,s

(2.55)

Tradycyjny zapis równań Lagrange’a pochłania zbyt dużo miejsca. Przedstawiamy więc

alternatywny, zwarty zapis równań (2.52)

σ

•

=

−

σ

σ

Q

,

L

)

,

L

(

q

q&

σ = 1,...,s

(2.56)

z którego w dalszym ciągu będziemy wielokrotnie korzystać.

W (2.56) symbole

σ

q

,

L

&

i

σ

q

,

L oznaczają pochodne cząstkowe funkcji L względem

odpowiednio prędkości uogólnionej

σ

q& oraz współrzędnej uogólnionej q

σ

. Operator

•

(*) oznacza pochodną zupełną względem czasu wielkości w nawiasie. Analogiczną

symbolikę stosować będziemy także w odniesieniu do innych funkcji.

53

Jeżeli na układ drgający działają tylko siły potencjalne, to równania (2.52) wygodnie

jest wziąć w postaci, która uwzględnia fakt, że energia potencjalna nie jest funkcją

prędkości uogólnionych

0

,

V

,

T

)

,

T

(

q

q

q

=

+

−

σ

σ

σ

•

&

σ = 1,...,s

(2.57)

Przy stosowaniu metody Lagrange’a należy przestrzegać następującej kolejności

działań:

1. Ustalić liczbę stopni swobody układu drgającego;

2. Wybrać współrzędne uogólnione;

3. Wyrazić energię kinetyczną i potencjalną w funkcji współrzędnych i prędkości

uogólnionych;

4. Wykonać operacje różniczkowania występujące w równaniu (2.52);

5. Obliczyć niepotencjalne siły uogólnione ze wzoru (2.54);

6. Ułożyć równania ruchu w liczbie równej liczbie stopni swobody.

Przykład 2.2. W celu ilustracji metody Lagrange’a, a także jej porównania z metodą

bilansową, rozważmy ponownie model przedstawiony na rys.2.19. Ustalamy, że układ

ten ma dwa stopnie swobody. Jako współrzędne uogólnione przyjmujemy

przemieszczenia q

1

i

q

2

odmierzane od położenia równowagi. Energia kinetyczna i

potencjalna wyrażają się odpowiednio wzorami:

2
2

2

2

1

1

q

m

5

,

0

q

m

5

,

0

T

&

& +

=

;

(

)

2

1

2

2

2

1

1

q

q

k

5

,

0

q

k

5

,

0

V

−

+

=

(P.2.3a,b)

Równania (2.52), po uwzględnieniu wzoru (2.53), przybiorą dla rozważanego układu

postać:

σ

•

=

+

−

σ

σ

σ

Q

,

V

,

T

)

,

T

(

q

q

q&

σ = 1,2 (P.2.4)

W czwartym etapie wykonujemy wymagane różniczkowania. Mamy:

1

1

1

q

m

q

/

T

&

& =

∂

∂

,

1

1

1

q

m

)

q

/

T

(

&&

&

=

∂

∂

•

,

0

q

/

T

1

=

∂

∂

,

)

q

q

(

k

q

k

q

/

V

1

2

2

1

1

1

−

−

=

∂

∂

(P.2.5)

2

2

2

q

m

q

/

T

&

& =

∂

∂

,

2

2

2

q

m

)

q

/

T

(

&&

&

=

∂

∂

•

,

0

q

/

T

2

=

∂

∂

,

)

q

q

(

k

q

/

V

1

2

2

2

−

=

∂

∂

(P.2.6)

Do wyznaczenia niepotencjalnych sił uogólnionych ze wzoru (2.54) potrzebne są

pochodne cząstkowe

σ

ν

∂

∂

q

/

r

. W celu ich wyznaczenia, zauważmy, że

ν

ν

ν

q

C

r

+

=

,

54

gdzie C

ν

jest pewną stałą zależną od długości swobodnych sprężyn i długości wózka

(rys.2.21).

q

1

F

1

(t)

m

1

r

1

C

1

Rys.2.21

Mamy zatem

,

1

/

1

1

=

∂

∂

q

r

,

0

/

2

1

=

∂

∂

q

r

,

0

/

1

2

=

∂

∂

q

r

,

1

/

2

2

=

∂

∂

q

r

a stąd, po

wykorzystaniu wzoru (2.54), otrzymujemy

( )

t

F

Q

1

1

=

,

( )

t

F

Q

2

2

=

.

(P.2.7)

Po podstawieniu do (P.2.4) pochodnych (P.2.5) i (P.2.6) oraz sił (P.2.7) otrzymujemy

dokładnie te same równania ruchu, co w wyniku zastosowania metody bilansu pędu,

czyli (P.2.2a,b).

Na pierwszy rzut oka wydaje się, że metoda Lagrange’a nie wykazuje żadnej

przewagi nad metodą bilansową. Otóż zalety metody Lagrange’a demonstrują się w

dwóch sytuacjach:

1) gdy modelujemy układy bardziej złożone (niż w powyższych przykładach),

np. o większej liczbie stopni swobody lub, gdy nałożone na układ więzy

dopuszczają złożone ruchy ciał tworzących układ .

2) kiedy rozważamy układy o innej naturze niż mechaniczna.

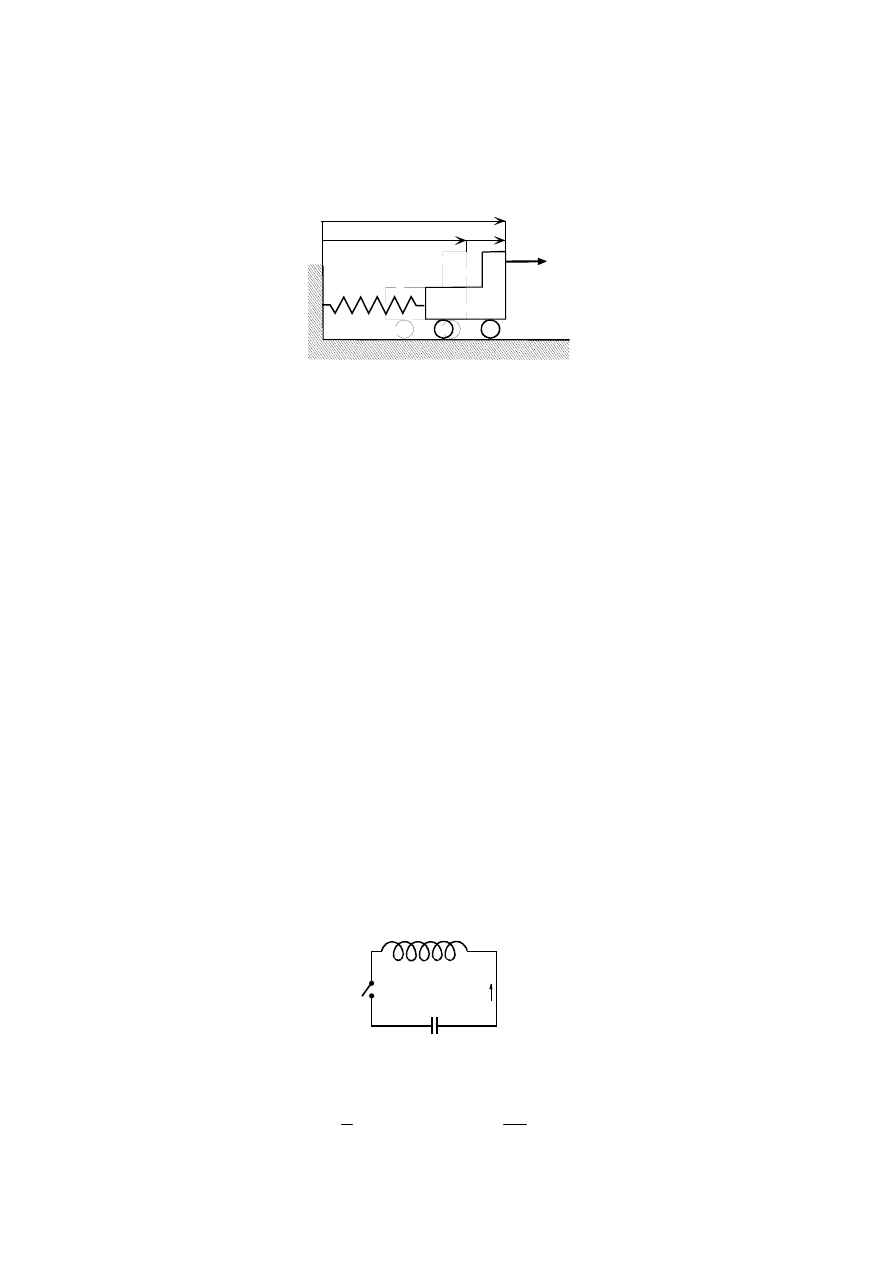
Dla ilustracji możliwości metody Lagrange’a w drugiej sytuacji rozważmy układ

elektryczny złożony z cewki o indukcyjności L i kondensatora o pojemności C (rys.

2.22).

L

C

e&

Rys.2.22

Dla przedstawionego układu mamy

2

2

1

e

L

T

&

=

,

2

2

1

e

C

V

=

(2.58a,b)

55

gdzie

e jest ładunkiem przepływającym przez obwód (zatem &e jest natężeniem prądu).

Równanie Lagrange’a ma postać

0

,

V

)

,

T

(

e

e

=

+

•

&

(2.59)

skąd, po podstawieniu wzorów (2.58a,b), mamy równanie

0

1 =

+

e

C

e

L &&

(2.60)

Równanie (2.60) można wprawdzie otrzymać z II prawa Kirchhoffa, ale tutaj istotny

jest fakt, że otrzymujemy je bez znajomości tego prawa, co podkreśla uniwersalny

charakter metody Lagrange’a. Innymi słowy metoda Lagrange’a daje możliwość

uogólnień.

2.6 ZABIEGI UPRASZCZAJĄCE

2.6.1 Dyskretyzacja

Bardzo wiele drgających układów fizycznych, z którymi mają do czynienia

inżynierowie, nie daje się opisać za pomocą równań różniczkowych zwyczajnych, jak

to było do tej pory. Jak zobaczymy w dalszej części niniejszego preskryptu naturalnym

modelem układów ciągłych są równania różniczkowe cząstkowe. Skoro jednak

znacznie prościej rozwiązuje się równania zwyczajne, to istnieje naturalna skłonność do

tworzenia modeli dyskretnych dla układów ciągłych. Zabieg taki nazywamy

dyskretyzacją. Ze względu na wynik dyskretyzacji zabieg ten bywa także nazywany

skupianiem. Znane są różne sposoby dyskretyzacji: Można spotkać się z poglądem, że

do najbardziej rozpowszechnionych należy metoda różnic skończonych i metoda

elementów skończonych (MES). Mówi się wówczas o komputerowych metodach

dyskretyzacji, gdyż są to metody nastawione na „produkowanie” modeli, które można

rozwiązywać tylko za pomocą komputera.

Warto w tym kontekście napomknąć, że na długo przed zastosowaniem w/w metod,

a w szczególności MESu, inżynierowie z powodzeniem stosowali dyskretyzację, którą z

braku lepszej nazwy nazywiemy dyskretyzacją inżynierską. Polega ona na tym, że

obiekt rzeczywisty dzieli się na kawałki, przypisując im odpowiednią masę na

podstawie pomiarów lub obliczeń (rys.2.25a). Masy te lokuje się na elemencie

modelowym, który cechuje się pewną sztywnością (np. na zginanie), ale pozbawiony

jest masy (rys. 2.25 b).

56

a)

b)

Rys. 2.25

Ponieważ w dalszych rozdziałach MES-em nie będziemy się zajmowali, więc

już tutaj podamy istotę tej metody dyskretyzacji, ale bez szczegółów, gdyż jest ona

wykładana jako oddzielny przedmiot. Istnieje też obszerna, wyspecjalizowana literatura

dotycząca MESu.

Metoda elementów skończonych (ang. finite element method) jest obecnie najczęściej

stosowaną metodą dyskretyzacji i znalazła powszechne zastosowanie w praktyce

inżynierskiej. Polega ona na podziale układu ciągłego na podukłady o prostych

kształtach, zwanych elementami skończonymi. Współrzędne uogólnione tych elementów

określa się w skończonej liczbie punktów leżących na ogół (choć niekoniecznie) na

brzegach elementów. Punkty te nazywa się węzłami. Przemieszczenia wewnątrz

elementów uzależniamy od przemieszczeń węzłów aproksymując je za pomocą tzw.

funkcji kształtu, które są przyjętymi z góry (a priori) wielomianami. Wzajemne

oddziaływanie między elementami odbywa się tylko poprzez węzły leżące na brzegach

sąsiadujących ze sobą elementów. Oddziaływanie to musi spełniać pewne związki

podstawowe (np. warunki równowagi) i równania ciągłości przemieszczeń węzłów.

W wyniku dyskretyzacji otrzymuje się układ równań różniczkowych zwyczajnych (dla

dynamiki) lub algebraicznych (dla statyki). Wielkościami poszukiwanymi są wielkości

węzłowe.

Z punktu widzenia dynamiki maszyn podstawową zaletą MESu jest możliwość

odtwarzania szczegółów konstrukcji, np. karbów czy niejednorodności.

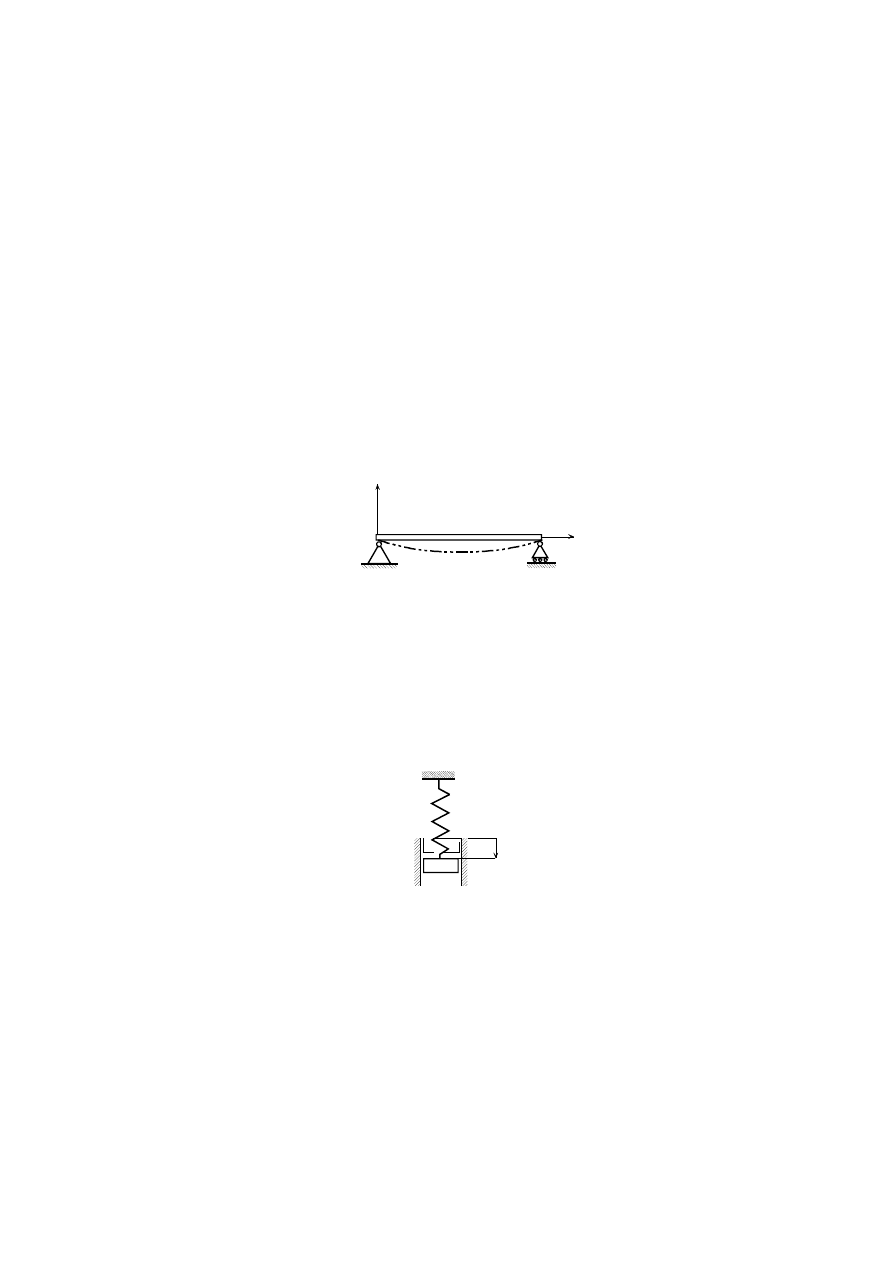
57

Na zakończenie warto stwierdzić, że dyskretyzacja dotyczy na ogół przestrzeni,

przy jednoczesnym traktowaniu czasu jako wielkości ciągłej. Wyjątek stanowi tzw.

metoda elementów czasoprzestrzennych, w której dyskretyzacji podlega również czas.

Należy też wspomnieć, że MES jest stosowany nie tylko dla układów

mechanicznych, ale także elektrycznych , cieplnych, przepływowych, itp.

Istnieje jeszcze jeden sposób dyskretyzacji, popularny zwłaszcza w dynamice

konstrukcji lotniczych, który dla całości obrazu wstępnie omówimy. Otóż elementy

konstukcyjne samolotów (skrzydła, usterzenia, kadłuby) często modelujemy za pomocą

belek. Dyskretyzacja takich elementów wymaga założenia krzywej ugięcia belki

podczas drgań. Taką dyskretyzację nazwiemy matematyczną (ścislej: dyskretyzacją za

pomocą postaci drgań). Dla ustalenia uwagi zajmiemy się drganiami belki swobodnie

podpartej na obu końcach (rys. 2.26).

y

x

Rys.2.26

Załóżmy, że aktualne ugięcie belki y(x,t) można opisać iloczynem

y(x

,t)

=

f(x)q(t)

(2.66)

gdzie f(x) jest funkcją o postaci dostosowanej do rzeczywistej sytuacji (w rozważanym

wypadku może to być np. parabola, albo połówka sinusoidy), zaś q(t) jest nieznaną

funkcją czasu. Tym sposobem wyrażenie (2.66) opisuje przejście do modelu o jednym

stopniu swobody, przy czym q(t) jest współrzędną uogólnioną (rys. 2.27).

k

q(t)

m

Rys.2.27

Oczywiście powstaje pytanie jak się ma masa m punktu materialnego i sztywność k

sprężyny do masy m(x) rozłożonej wzdłuż długości belki oraz jej sztywność na zginanie

EI(x).

Linearyzacja

Niniejszy preskrypt jest poświęcona zagadnieniom podstawowym, przez co

rozumiemy, że będziemy przede wszystkim zajmować się modelami liniowymi. Jest

jednak faktem, że układy rzeczywiste mają elementy o charakterystykach nieliniowych

i zachodzi pytanie, co wówczas robić? Otóż jest także prawdą, że często dobre

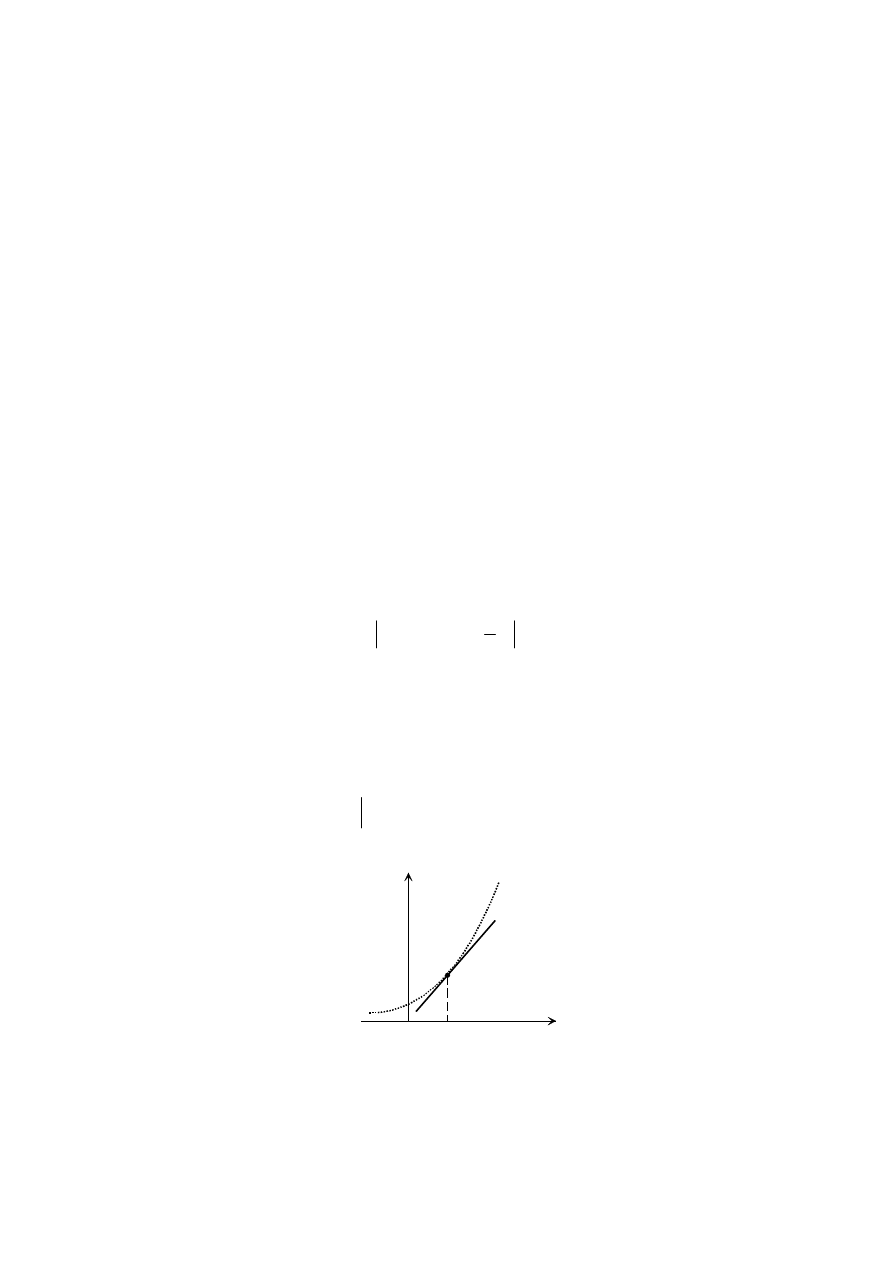
58

przedstawienie własności dynamicznych, wystarczających do podjęcia decyzji

projektowych, można otrzymać zastępując rzeczywiste (nieliniowe) elementy

konstrukcyjne ich modelem liniowym o stałych parametrach. Taki sposób upraszczania

nosi nazwę

linearyzacji.

Choć istnieje wiele metod linearyzacji, to w niniejszym skrypcie omówimy tylko

jedną, ale za to bardzo ważną, a mianowicie linearyzację wokół wybranego punktu (tę

metodę często nazywa się linearyzacją w punkcie pracy).

Jeżeli charakterystyka elementu opisana jest za pomocą pewnej funkcji nieliniowej

y = f(x), to w pewnym punkcie tej charakterystyki, np. przy x = x

0

, można poprowadzić

styczną do charakterystyki i uznać, że w pobliżu tego punktu charakterystyka pokrywa

się ze styczną, a więc ma postać

y = c

1

x + c

0

(2.67)

przy czym współczynnik c

1

odpowiada nachyleniu stycznej, zaś

c

0

jest przesunięciem

względem początku układu współrzędnych. Wzór (2.67) można też uzyskać

analitycznie po rozwinięciu funkcji f(x) w szereg Taylora

( ) ( )

(

)

(

)

....

x

x

f

x

x

f

x

f

x

f

x

x

x

x

+

−

′′

+

−

′

+

=

=

=

2

0

0

0

0

0

2

1

(2.68)

Jeżeli w szeregu (2.68) pominie się wszystkie wyrazy oprócz dwóch pierwszych, to

otrzymuje się przybliżenie liniowe funkcji f(x) jak poniżej

c

f

x x

1

0

= ′

=

,

( )

c

f x

c x

0

0

1 0

=

−

(2.69)

co, można zilustrować graficznie (rys. 2.28)

y

x

x

0

y = f(x)

y = c

1

x + c

0

Rys. 2.28

59

Na to, aby można było zaakceptować wzory (2.68), powinny być spełnione pewne

warunki: odchylenie (

x-x

0

) punktu aktualnego od punktu ustalonego

x

0

, wokół którego

dokonujemy linearyzacji, musi być dostatecznie małe. Innymi słowy oznacza to, że

wyrazy wyższego rzędu w szeregu (2.67) są pomijalnie małe wobec wyrazów

liniowych. Ponadto, aby przybliżenie liniowe miało sens, powinna istnieć pochodna

′

f

w punkcie

x

0.

Warunek ten oznacza „gładkość” charakterystyki

f(x) w punkcie x

0

, tzn.

brak załamań lub skoków w tym punkcie.

Rozważmy teraz przypadek bardzo częsty w praktyce, tzn. taki, kiedy ruch

odbywa się wokół punktu „zero”. Linearyzacja polega tutaj na zastosowaniu wzoru

(

)

(

)

....

1

!

2

1

1

1

2

+

−

+

+

=

+

ξ

ξ

ξ

m

m

m

m

(2.70)

i zachowaniu tylko wyrazu liniowego.

Dla ilustracji rozważmy:

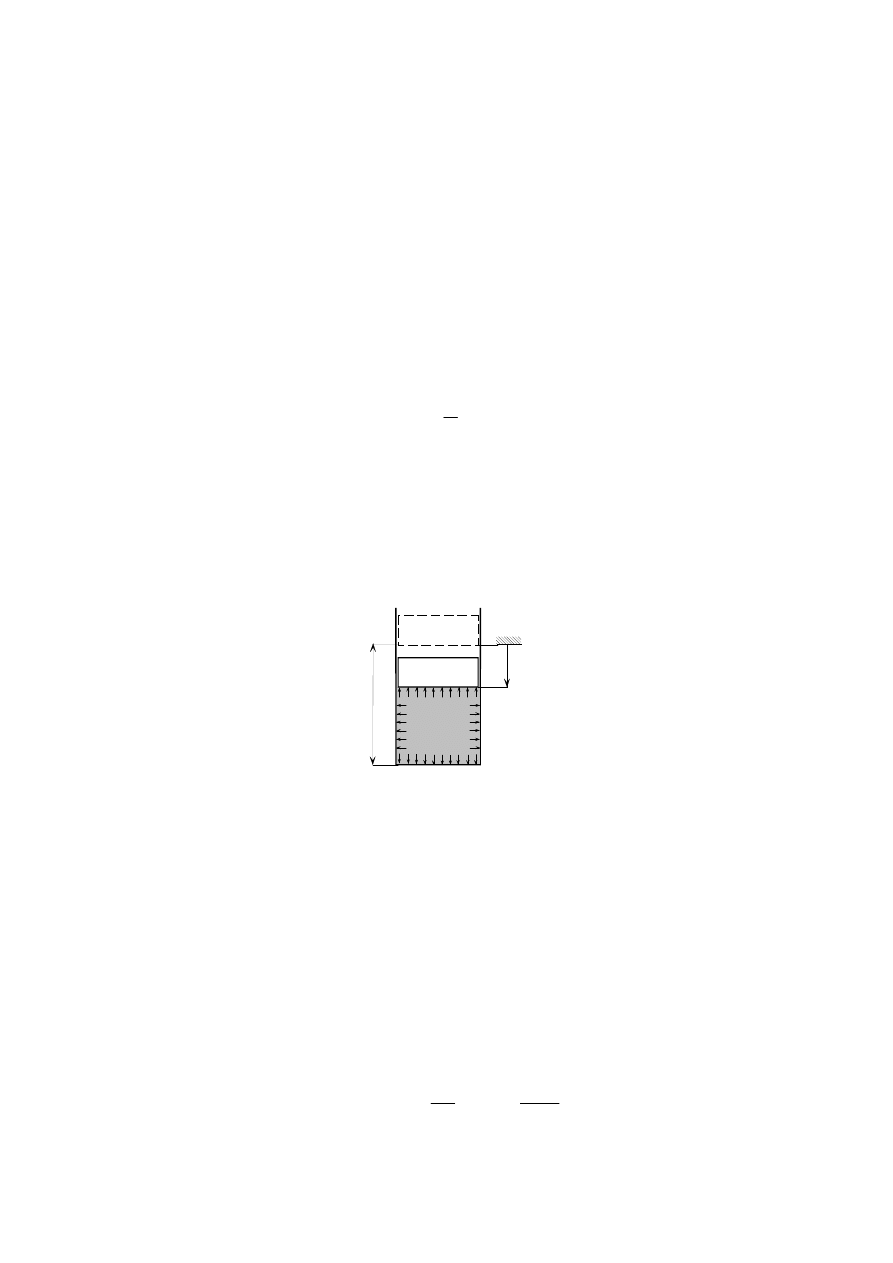
Przykład 2.4. Tłok o masie m zamyka szczelnie w zbiorniku o kształcie walca pewną

objętość V gazu izentropowego (zob.rys.2.29). Należy napisać równanie małych drgań

tłoka przy założeniu, że proces sprężania ma charakter adiabatyczny.

h

p

x

γ

m

x

Rys.2.29

Siła działająca na tłok „od spodu” jest p

x

A, gdzie A – pole powierzchni tłoka, p

x

– nieznane ciśnienie gazu po przesunięciu tłoka o x. Według II zasady Newtona mamy

mx

mg p A

x

&& =

−

(P.2.12)

Dla adiabatycznego sprężania gazu mamy równanie

p

x

V

γ

= c (P.2.13)

gdzie V jest objętością gazu w zbiorniku , a

γ

oznacza wykładnik adiabaty (dla

powietrza

γ

= 1,4). Zapiszmy równanie (P.2.13) dla dwóch stanów (równowagi i ruchu):

γ

γ

=

x

x

V

p

V

p

0

0

. Stąd, po uwzględnieniu faktu, że

V =Ah, zaś V

x

= A(h - x) otrzymujemy

γ

γ

⎟

⎠

⎞

⎜

⎝

⎛

−

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

x

h

h

p

V

V

p

p

x

x

0

0

0

(P.2.14)

60

Po podstawieniu wzoru (P.2.14) do równania (P.2.12) otrzymujemy

mx p

h

h x

A

mg

&& +

−

⎛

⎝⎜

⎞

⎠⎟

=

0

γ

(P.2.15)

czyli równanie ruchu tłoka ma jest nieliniowe. Źródłem nieliniowości jest oczywiście

równanie stanu (P.2.13). Linearyzacja polega tutaj na zastosowaniu wzoru (2.70), co

daje nam zależność

p

p

h

x

x

=

+

⎛

⎝⎜

⎞

⎠⎟

0

1

γ

(P.2.16)

a w konsekwencji, po uwzględnieniu, że mg = p

0

A, równanie (P.2.15) przybiera postać

mx

p A

h

x

&& +

=

0

0

γ

(P.2.17)

Równanie (P.2.17) jest już równaniem liniowym. Ponieważ powstało w wyniku

linearyzacji wyrazu nieliniowego mówimy też często, że jest to równanie

zlinearyzowane.

2.6.3 Agregacja

W konstrukcjach rzeczywistych elementy mechaniczne występują w różnych

kombinacjach, przez co rozumiemy, przede wszystkim, ich wzajemne usytuowanie.

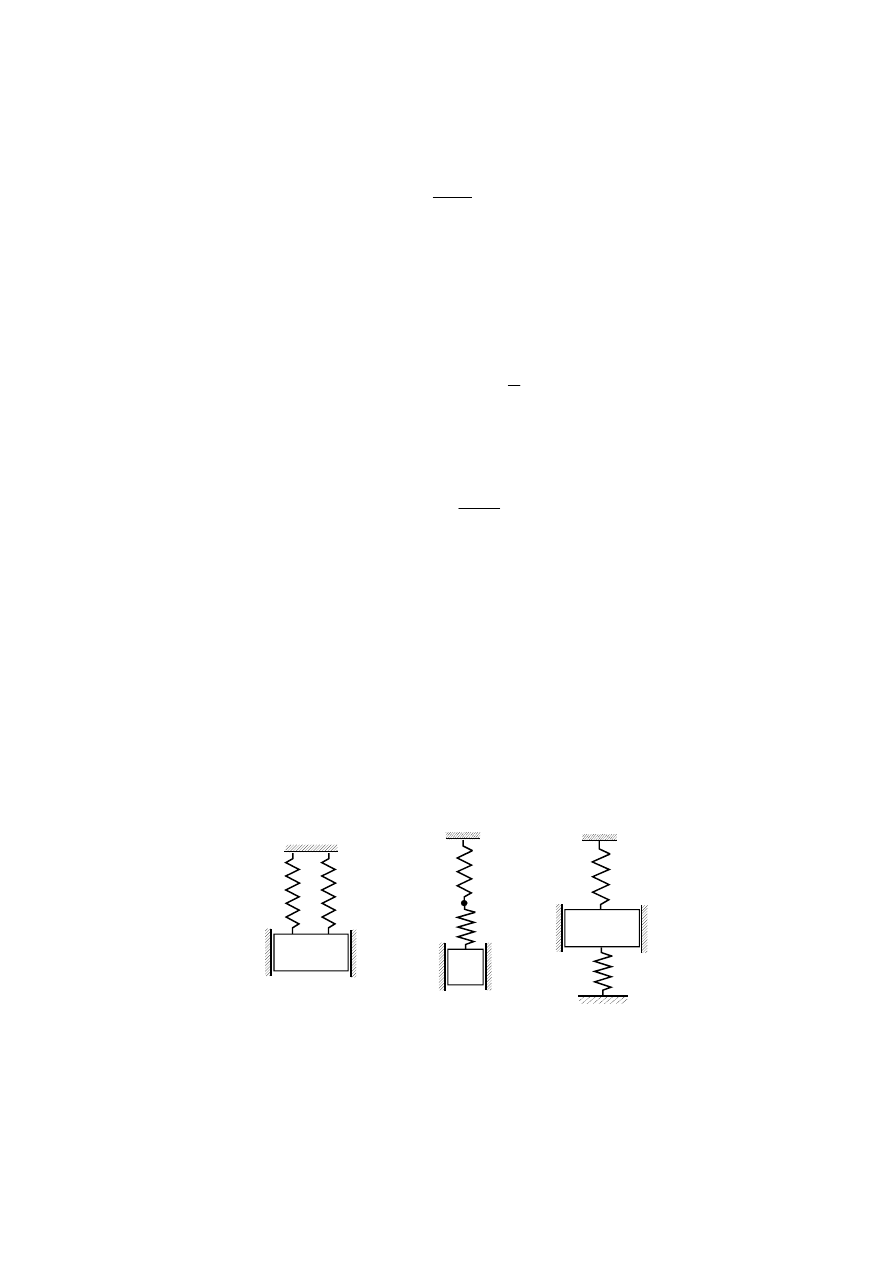
Rysunek 2.30 przedstawia trzy różne usytuowania dwu sprężyn o sztywnościach k

1

i

k

2

względem ruchomej masy i ostoi.

a)

b)

c)

k

1

k

2

k

2

k

1

m

m

m

k

2

k

1

Rys.2.30

.

Podobnie jak sprężyny mogą być usytuowane tłumiki, dlatego nie przedstawiamy

odpowiedniego rysunku.

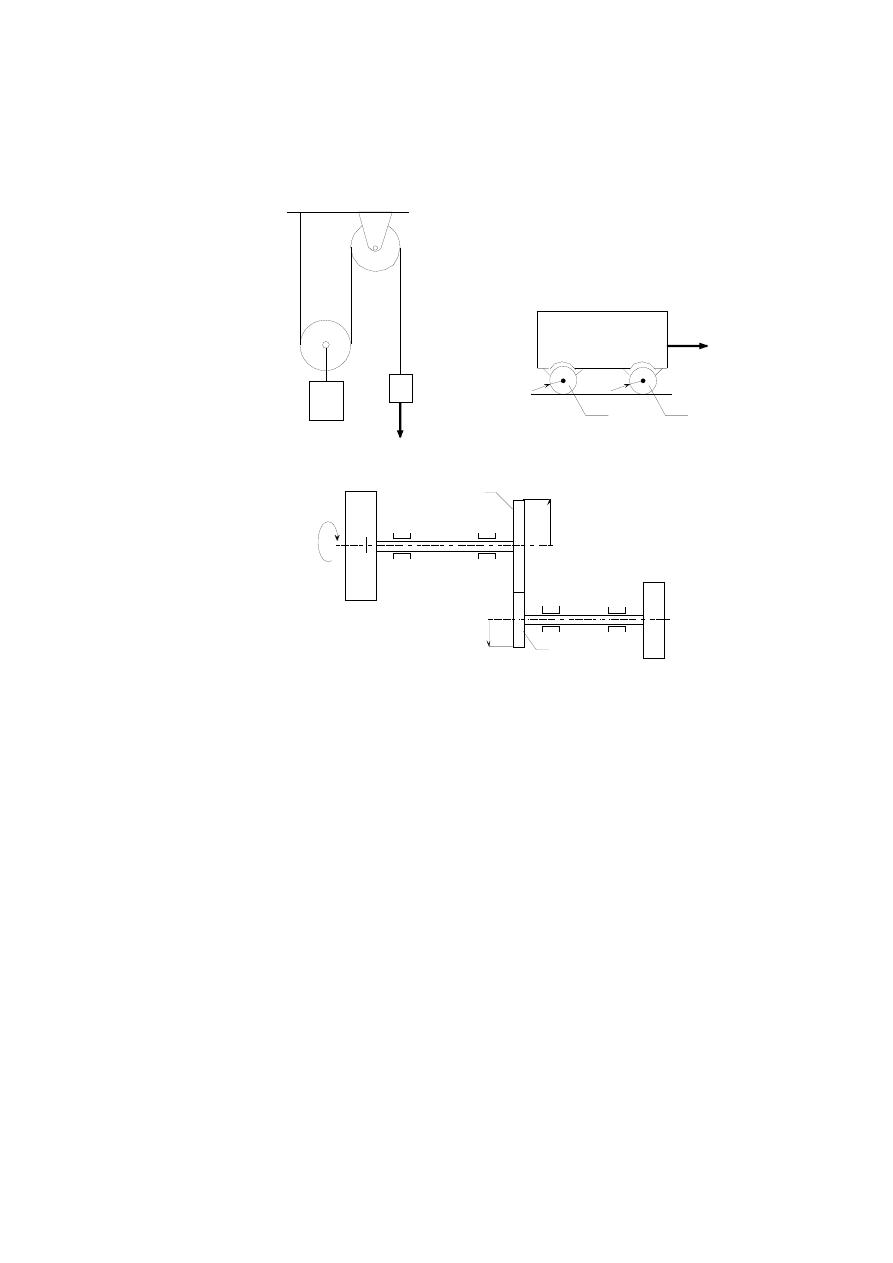
61

Także elementy bezwładnościowe występują w takich zestawach, że ruch

jednego z nich determinuje ruch innych elementów bezwładnościowych. Rys. 2.31

przedstawia trzy przykłady takich sytuacji.

(c)

b)

a)

I

1

I

2

M

o

(t)

R

1

G

R

2

D

r

r

M

F(t)

m

1

m

2

F(t)

m

m

k

2

k

1

Rys.2.31

W przykładzie z rys. 2.31a, który może być uważany za model windy, ruch

przeciwwagi o masie m

2

pod wpływem siły

F(t) wywołuje ruch masy m

1

.

W przykładzie z rys.2.31b wózek o masie M na czterech kołach o masie m i promieniu r

każde porusza się po linii prostej pod wpływem siły F(t). Jeśli założymy, że koła toczą

się, to ruch wózka determinuje ruch kół.

W przykładzie z rys.2.31c dwa koła zamachowe o momentach bezwładności I

1

i

I

2

połączone są przekładnią zębatą o przełożeniu n = R

1

/

R

2

. Zakładamy, że osiowe

momenty bezwładności wałów i kół przekładni są pomijalnie małe. Jeśli dodatkowo

założymy, że wałki są idealnie sztywne, to ruch koła zamachowego I

1

pod wpływem

momentu M

0

(

t) determinuje ruch koła I

2

. Wszystkie układy z rys.2.31 charakteryzują się

tym, że mimo iż układ składa się z wielu elementów bezwładnościowych, to są to

układy o jednym stopniu swobody. W każdej sytuacji, zresztą niezależnie od liczby

stopni swobody układu, możemy spytać, czy układ wyjściowy da się zastąpić innym

62

równoważnym o mniejszej liczbie elementów. Taką redukcję nazywać będziemy

agregacją. W niniejszym punkcie rozważać będziemy tylko układy o jednym stopniu

swobody i wówczas zadanie agregacji można sformułować nieco dokładniej. Pytamy

więc, czy zespół dwu lub większej liczby elementów danego typu daje się zastąpić

jednym elementem równoważnym, zwanym elementem zastępczym (tzn. sprężyną

zastępczą, masą zastępczą lub tłumikiem zastępczym). Gdy pojawia się pojecie

równoważności natychmiast pytamy „w jakim sensie?”. Tu odpowiedź jest prosta.

Żądamy mianowicie, aby zdolności magazynowania energii lub jej rozpraszania przez

odpowiednie elementy zastępcze były identyczne jak zespołu elementów podlegających

agregacji układu wyjściowego. To energetyczne sformułowanie warunków

równoważności można zastąpić sformułowaniem przyczynowym: te same bodźce

działające na układ zastępczy i układ wyjściowy winny powodować te same skutki.

W szczególności oznacza to, że pod działaniem danej siły winny być identyczne:

a) deformacja sprężyny zastępczej i danego układu sprężyn;

b) spadek prędkości na biegunach tłumika zastępczego i w zespole tłumików

układu wyjściowego;

c) przyspieszenie masy zastępczej i masy, której ruch jest przedmiotem

rozważań.

Przejdźmy zatem do konkretów i w pierwszej kolejności wyznaczymy sztywność

sprężyny zastępczej (lub krócej sztywność zastępczą) dla układów przedstawionych na

rys. 2.30.

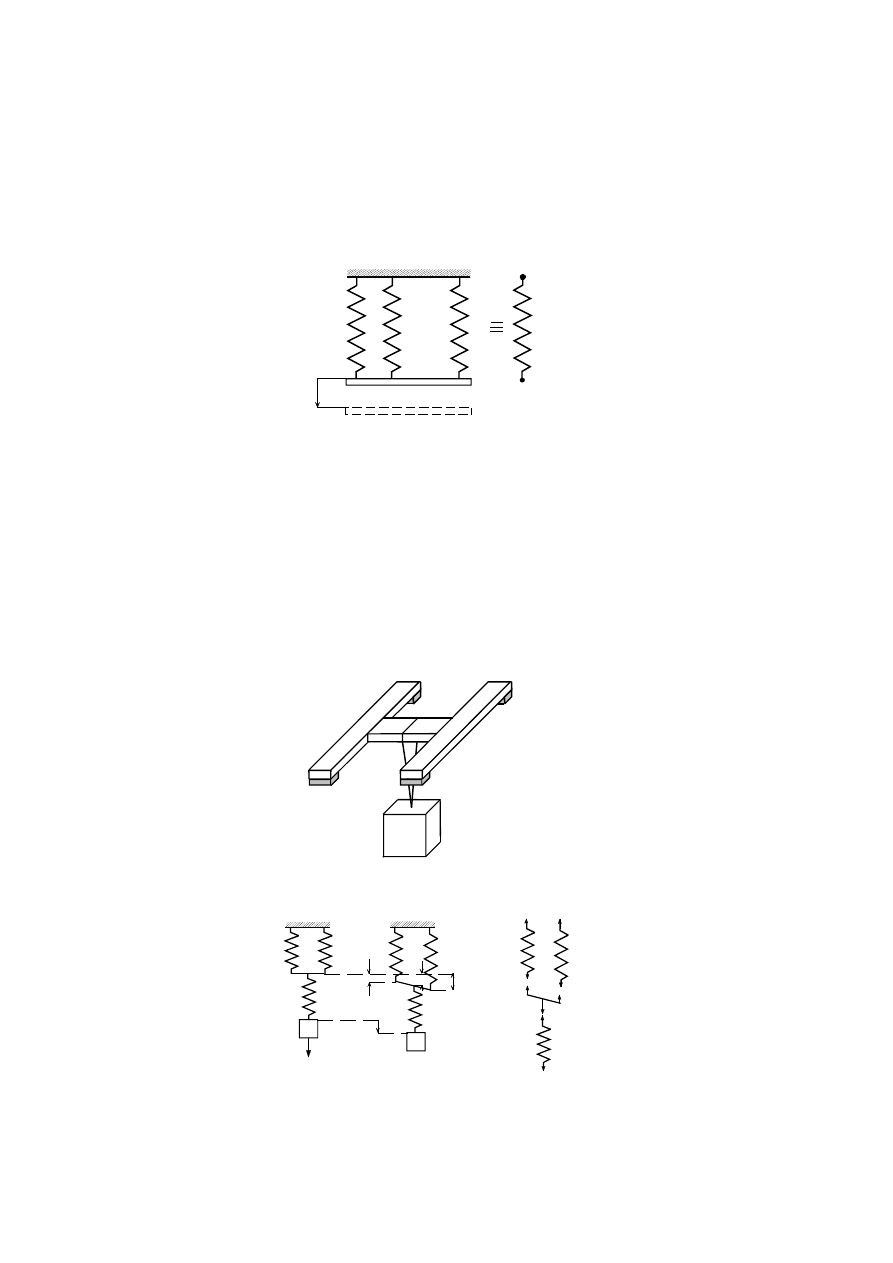
W wypadku równoległego połączenia sprężyn (rys.2.30a) obciążonych pewną siłą, np.

mg ich wydłużenia są identyczne i oznaczamy je symbolem

δ

.

Na rys.2.32a pokazany jest układ sił

mg

mg

a)

b)

δ

2

k

δ

1

k

δ

z

k

Rys.2.32

działających na ciało podtrzymywane przez układ dwu sprężyn równoległych, a na rys.

2.32b siły działające na to samo ciało podtrzymywane przez jedną sprężynę zastępczą.

Na podstawie rys. 2.32 wnioskujemy, że k

z

δ

= k

1

δ

+ k

2

δ

, co po podzieleniu przez

δ

daje

k

z

= k

1

+ k

2

(2.71)

63

W wypadku ogólnym n sprężyn równoległych o sztywnościach k

1

, k

2

,..., k

n

, (zob.

rys.2.33) sztywność zastępcza wyraża się wzorem

∑

=

=

n

i

i

z

k

k

1

(2.72)

k

1

k

2

k

n

...........

A

B

k

z

δ

Rys.2.33

Powyższy wzór jest ważny tylko wtedy, gdy sprężyny podlegają identycznym

odkształceniom, tzn. powierzchnie A i B pozostają równoległe. Takie milczące

założenie zostało w istocie uczynione, co miało swe odzwierciedlenie na rys.2.32a i w

dalszych obliczeniach. Jakie skutki niesie uchylenie tego założenia zobaczymy

rozważając przykład 2.5.

Przykład 2.5. Wyznaczmy sztywność zastępczą układu belek z rys.2.34 przy

obciążeniu układu siłą F w środku belki 3. Długości i sztywności belek podane są na

rysunku.

m

l

1

EI

1

l

3

EI

3

l

2

EI

2

Rys.2.34

m

A

B

k

1

k

2

m

x

x

δ

1

δ

12

δ

2

a)

b)

c)

k

3

k

1

k

2

F/2

F/2

F/2

F/2

F

F

F

k

3

F/2

F/2

Rys.2.35

64

Rozwiązanie. Model sztywnościowy układu belek przedstawiony jest na rys.2.35a .

Każda z belek obciążona jest siłą w środku, a wobec tego sztywności belek, zgodnie ze

wzorem (2.21), wynoszą k

i

= 48EI

i

/l

i

3

.

Oznaczmy symbolem x przemieszczenie pionowe

środka belki 3.

Jest ono wynikiem odkształceń środków belek

δ

i

. Na podstawie warunków zgodności

odkształceń (rys. 2.35b) i rozkładu sił (rys.2.35c) mamy

,

k

F

1

1

2

=

δ

,

k

F

2

2

2

=

δ

3

3

k

F

=

δ

(P.2.18)

oraz

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

=

δ

+

δ

=

δ

2

1

2

1

2

1

12

4

2

k

k

k

k

F

,

(P.2.19)

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

+

=

δ

+

δ

=

3

2

1

2

1

3

12

1

4

k

k

k

k

k

F

x

(P.2.20)

Z definicji sztywność układu jest ilorazem siły i odkształcenia wywołanego tą siłą.

Mamy więc

(

)

2

1

3

2

1

3

2

1

4

4

k

k

k

k

k

k

k

k

x

F

k

+

+

=

=

(P.2.21)

Przy okazji zauważmy, że mimo, iż sprężyny 1 i 2 są równoległe, to sztywność

zastępcza jest równa

2

1

2

1

12

4

k

k

k

k

k

+

=

(P.2.22)

co bezpośrednio wynika z (P.2.19).

Zatem, gdy wydłużenia sprężyn

δ

1

≠

δ

2

, to k

12

≠ k

1

+ k

2

.

Rozważmy teraz szeregowe połączenie sprężyn jak na rys. 2.31b. W tym wypadku

obie sprężyny są rozciągnięte tą samą siłą mg, w rezultacie czego sumaryczne

wydłużenie obu sprężyn pod wpływem tej siły jest

δ = δ

1

+

δ

2

(2.73)

gdzie wydłużenia

δ

1

i

δ

2

spełniają związki

k

1

δ

1

= mg,

k

2

δ

2

= mg

(2.74)

Znaleźć sprężynę zastępczą to tyle, co wyznaczyć jej sztywność k

z

taką, aby sprężyna ta

pod wpływem tej samej siły mg wydłużyła się o

δ

. Zatem dla sprężyny zastępczej

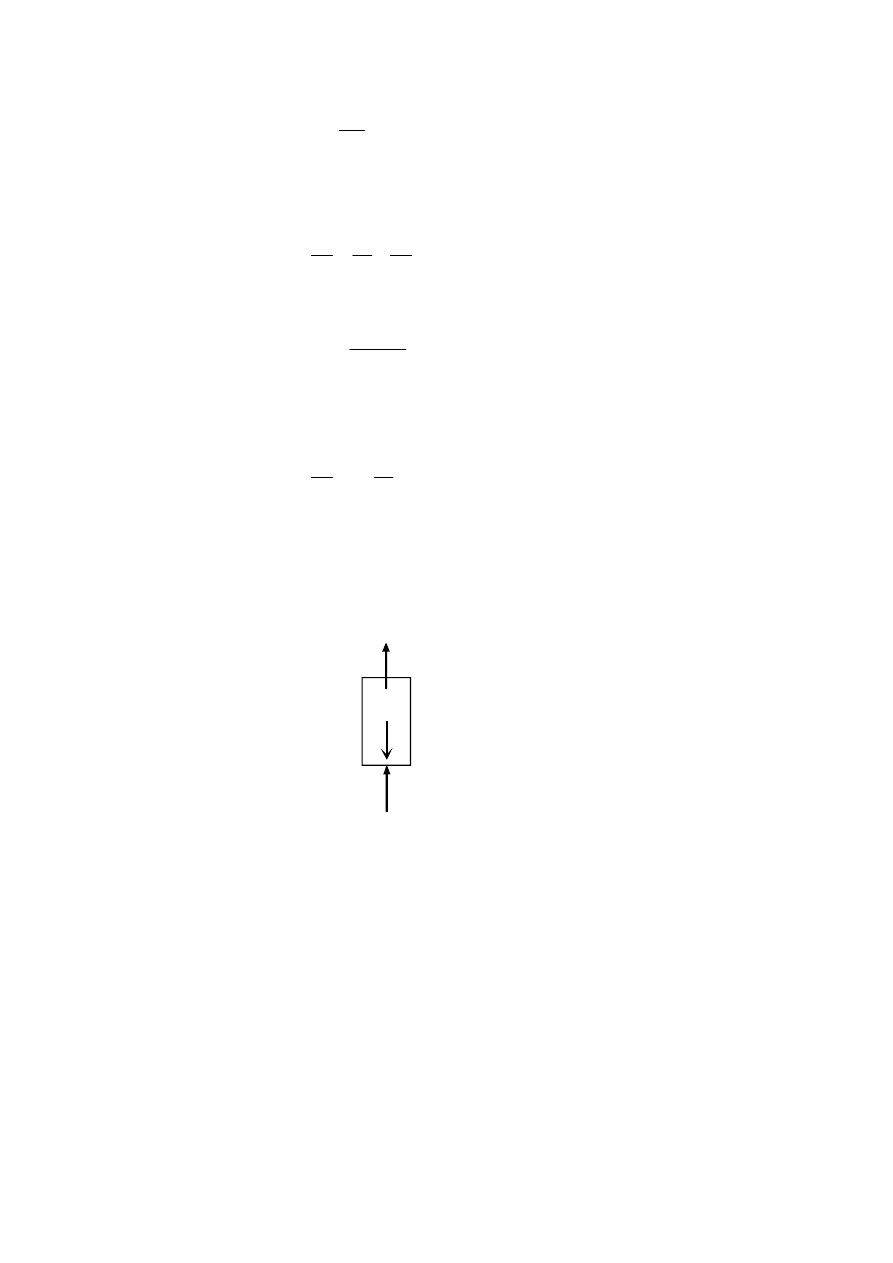
65

z

k

mg

=

δ

(2.75)

Po podstawieniu (2.74) i (2.75) do (2.75) i podzieleniu obu stron wyrażenia przez mg

otrzymujemy

2

1

1

1

1

k

k

k

z

+

=

(2.76)

Zatem dla dwu sprężyn połączonych szeregowo sztywność sprężyny zastępczej wynosi

2

1

2

1

k

k

k

k

k

z

+

=

(2.77)

W przypadku ogólnym n sprężyn o sztywnościach k

1

, k

2

,..., k

n

połączonych szeregowo,

sztywność zastępczą liczymy ze wzoru

∑

=

=

n

i

i

z

k

k

1

1

1

(2.78)

Zauważmy także, że układ sprężyn przedstawiony na rys. 2.30c jest w istocie

połączeniem równoległym. Łatwo to zrozumieć, gdy rozważymy siły działające na ciało

po jego przemieszczeniu ze stanu równowagi o

δ

, co ilustruje rys. 2.36.

mg

δ

1

k

δ

2

k

Rys.2.36

Ten układ sił jest identyczny jak na 2.32a, więc ta kombinacja sprężyn jest w istocie

połączeniem równoległym.

Wyznaczmy teraz sztywność zastępczą na skręcanie K

z

zespołu przekładniowego z

rys. 2.31c. Sztywności skrętne wałów są dane i wynoszą odpowiednio K

1

i K

2.

Rozważmy zatem układ zastępczy (rys.2.37) złożony z koła o momencie bezwładności

względem osi I oraz wałka o sztywności na skręcanie równej K

z

. Oznacza to, że przy

unieruchomionym kole I

66

I

M

0

K

z

Rys.2.37

moment skręcający M

0

przyłożony na drugim końcu wału spowoduje skręcenie tego

końca o kąt

ϕ

0

taki, że

z

K

M

0

0

=

ϕ

(2.79)

Powtórzmy ten eksperyment myślowy dla zespołu przekładni z rys. 2.31c. Blokujemy

koło I

2

, a do koła I

1

przykładamy moment skręcający M

0

. Ze względu na istniejącą

przekładnię o przełożeniu n, moment skręcający wał dolny o sztywności K

2

jest równy

M

0

/n

, a odpowiadający mu kąt skręcania wału wynosi

2

0

2

nK

M

=

ϕ

(2.80)

Ponieważ koło I

2

jest unieruchomione, koło zębate D obróci się też o kąt

ϕ

2

, a

odpowiedni kąt obrotu koła G jest n razy mniejszy, tzn.

2

2

0

K

n

M

G

=

ϕ

(2.81)

Kąt skręcania wału górnego jest wynikiem przyłożenia momentu skręcającego M

0

i

wynosi

1

0

1

K

M

=

ϕ

(2.82)

a zatem całkowity obrót koła I

1

jest

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

+

=

ϕ

+

ϕ

2

2

1

0

1

1

1

K

n

K

M

G

(2.83)

Zastępcza sztywność na skręcanie to taka, że ten sam moment powoduje ten sam skutek

– tu obrót koła zamachowego o momencie I

1

, czyli

ϕ

0

=

ϕ

1

+

ϕ

G

(2.84)

Zatem, po podstawieniu do (2.84) zależności (2.79) oraz (2.83) i podzieleniu przez M

0

mamy

2

2

1

1

1

1

K

n

K

K

z

+

=

(2.85)

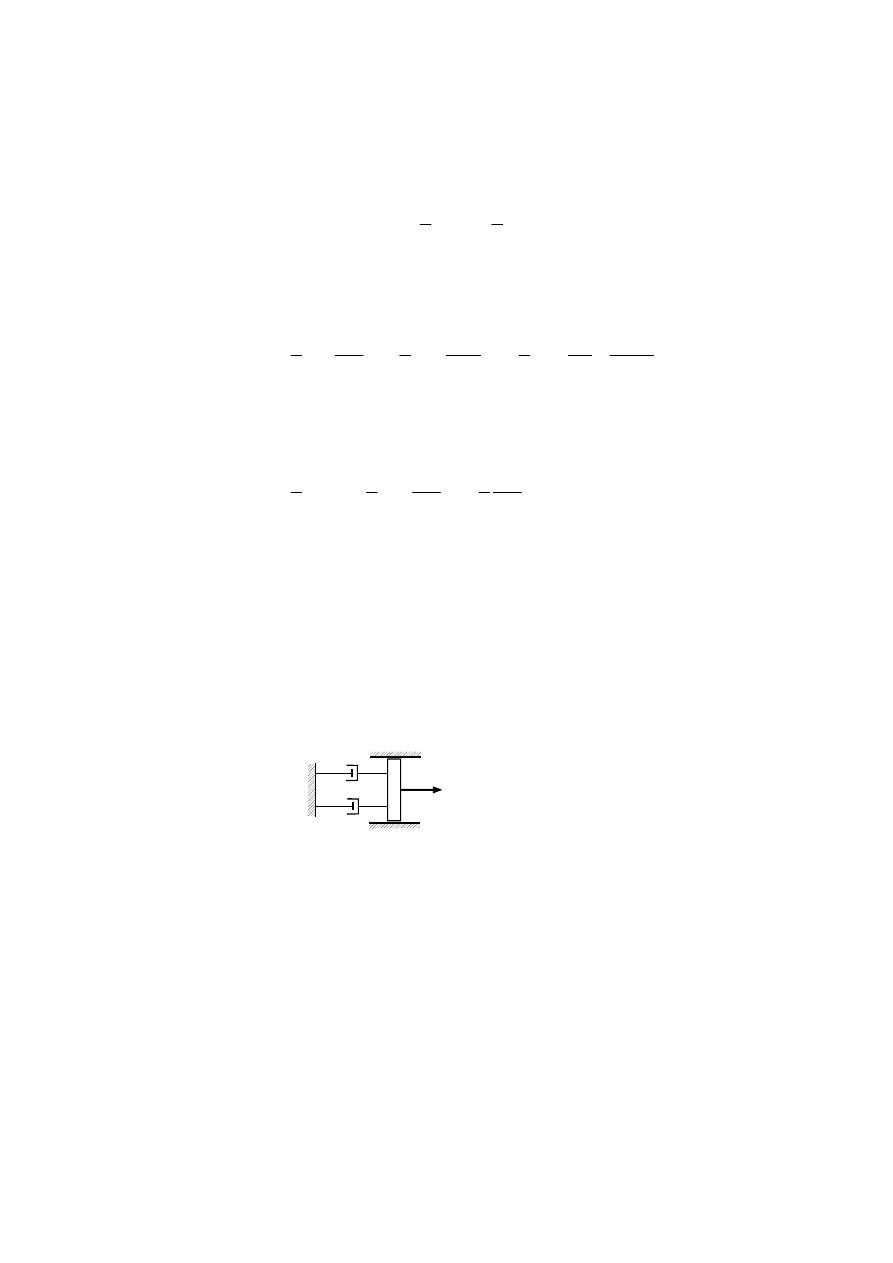
67

Ten sam wynik otrzymamy stosując kryterium energetyczne. Istotnie, energia

potencjalna odkształceń sprężystych wałków w wyniku ich skręcania wyraża się

wzorem:

2

2

2

2

1

1

2

1

2

1

2

1

ϕ

+

ϕ

=

+

=

K

K

V

V

V

(2.86)

Pod działaniem momentu skręcającego M

0

, kąty

ϕ

1

i

ϕ

2

wyrażają się odpowiednio

wzorami (2.82) i (2.80), czyli

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

+

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

2

2

1

2

0

2

2

0

2

2

1

0

1

1

1

2

1

2

1

2

1

K

n

K

M

nK

M

K

K

M

K

V

(2.87)

Z drugiej strony energia potencjalna wałka o sztywności zastępczej K

z

, z

uwzględnieniem wzoru (2.79), wyraża się wzorem:

z

z

z

z

K

M

K

M

K

K

V

2

0

2

0

2

0

2

1

2

1

2

1

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

ϕ

=

(2.88)

Z porównania prawych stron wyrażeń (2.87) i (2.88) otrzymujemy zależność identyczną

jak (2.85), co wskazuje na możliwość stosowania obu kryteriów równoważności

układu.

Wyznaczenie tłumika zastępczego jest w zasadzie identyczne jak wyznaczanie

sztywności zastępczej. W istocie sprowadza się do rozważenia sił działających na

tłumiki i spadków prędkości na ich biegunach. To podobieństwo postępowania

zilustrujemy tylko jednym przykładem równoległego połączenia tłumików (rys.2.38).

F(t)

c

1

c

2

Rys.2.38

Załóżmy, że do układu dwóch tłumików równoległych przyłożona jest siła F(t), która

wymusza ruch dolnych końcówek tłumików z prędkością

x&

(rys. 2.38a). Siły oporów

ruchu generowane przez tłumiki są

,

x

c

R

&

1

1

=

x

c

R

&

2

2

=

Poszukujemy tłumika zastępczego, który przy ruchu punktu A z prędkością

x&

generować będzie siłę

x

c

x

)

c

c

(

R

R

R

z

&

& =

+

=

+

=

2

1

2

1

Współczynnik tłumienia tłumika zastępczego jest więc

c

z

= c

1

+ c

2

(2.89)

68

Ogólnie dla układu n tłumików o współczynnikach c

1

,c

2

,...,c

n

, połączonych równolegle

tłumienie zastępcze wyraża się wzorem

∑

=

=

n

i

i

z

c

c

1

(2.90)

Tu, podobnie jak w wypadku wzoru (2.72), zwracamy uwagę, że tłumienie zastępcze

można wyznaczać ze wzoru (2.90) tylko wtedy, gdy spadki prędkości na końcówkach

tłumików równoległych są takie same.

W rzadko występującym w praktyce przypadku szeregowego połączenia tłumików,

współczynnik c

z

tłumika zastępczego może być wyliczony z zależności analogicznej do

(2.78) tyle, że w miejsce współczynników sztywności k podstawiamy współczynniki c.

Proces agregacji elementów bezwładnościowych najwygodniej jest prowadzić

metodą energetyczną, tj. przyrównując energię kinetyczną układu wyjściowego do

energii kinetycznej elementu zastępczego. Dla przykładu rozważmy wózek z rys 2.31b.

Przykład 2.6. Należy wyznaczyć masę zastępczą M

z

dla układu z rys.2.31b.

Rozwiązanie. Załóżmy, że wózek porusza się z prędkością

x&

. Z tą samą prędkością

porusza się środek każdego z czterech kół wózka. Stąd wynika, że prędkość kątowa

każdego koła jest

r

/

x&

=

ω

. Energia kinetyczna układu jest więc

(

)

(

)

2

2

2

2

2

2

2

x

m

6

M

2

1

r

x

mr

2

x

m

4

M

2

1

I

2

1

x

m

2

1

4

x

M

2

1

T

&

&

&

&

&

+

=

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

+

+

=

⎟

⎠

⎞

⎜

⎝

⎛

ω

+

+

=

Z drugiej strony energia kinetyczna masy zastępczej wyraża się wzorem

2

2

1

x

M

T

z

&

=

.

Z porównania prawych stron obu wyrażeń na energię kinetyczną wynika, że

M

z

= M + 6m

Proces agregacji w układach o wielu stopniach swobody, a także dla układów ciągłych

jest bardziej skomplikowany. Ponieważ wymaga on wiedzy o własnościach tego typu

układów, więc nie będziemy rozwijać tego tematu.

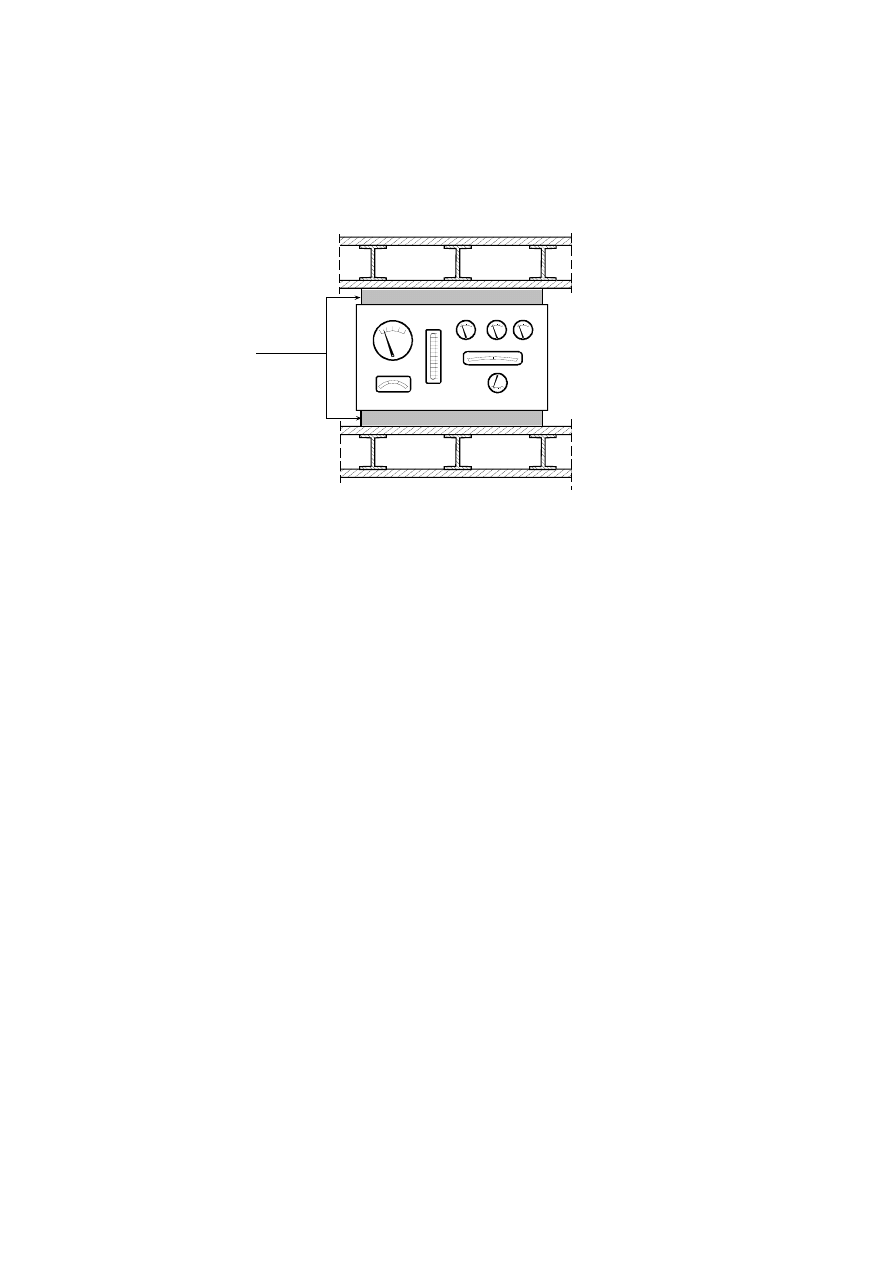
2.7 Przykład budowy modelu fizycznego tablicy przyrządów pokładowych

2.7.1 Do czego model ma służyć?

69

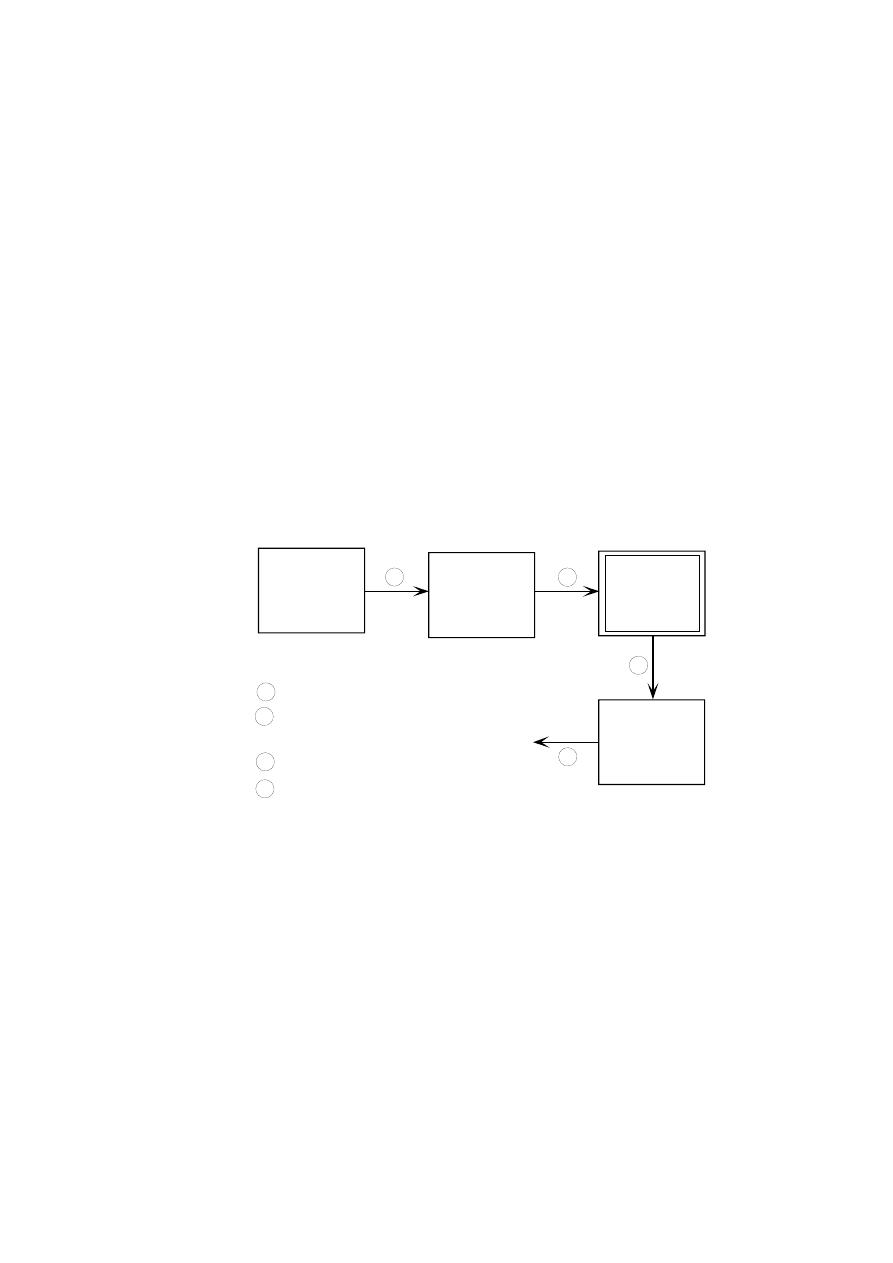
Dla ustalenia uwagi załóżmy, że tablica przyrządów pokładowych ma być zabudowana

na śmigłowcu. Bezpieczeństwo i komfort pilotażu wymaga, by wskazania przyrządów

były czytelne. W tym celu tablica musi być tak zamocowana, by nie udzielały się jej

drgania generowane przez samą maszynę lub jej otoczenie, np. podmuchy wiatru.

Często źródłem tych drgań jest silnik (rys.2.39). Zabiegi zmierzające do osiągnięcia

takiego stanu, w którym na tablicę przyrządów nie mają wpływu (lub ich wpływ jest

ograniczony) drgania innych elementów śmigłowca, nazywane są wibroizolacją.

Wibroizolację tablicy przyrządów realizuje się pomocą elementów podatnych, którymi

są zwykle amortyzatory gumowe o nieliniowej charakterystyce sprężystej i tłumiennej.

Śmigłowiec drga, skutkiem czego tablica poddana jest wymuszeniu kinematycznemu.

Zadanie polega na tym, aby przy znanym wymuszeniu tak dobrać charakterystyki

elementów zawieszenia tablicy, aby jej poziom drgań był akceptowany.

Silnik
śmigłowca

Kadłub

Tablica
przyrządów

Przyrząd
pomiarowy

1

3

1

Drgania silnika

2

Drgania kadłuba w miejscu
zamocowania tablicy

Drgania tablicy

Błąd wskazań przyrządu

3

4

4

2

Rys. 2.39

2.7.2 Założenia do budowy modelu fizycznego

Podstawowym zabiegiem jest dyskretyzacja, czyli zastąpienie tablicy - obiektu

o parametrach rozłożonych modelem o parametrach skupionych. Dochodzi się do tego

w sposób następujący: tablica przyrządów jest zespołem konstrukcyjnym pomyślanym

jako złożona płyta, z licznymi wykrojami (rys. 2.40), „sama w sobie” względnie

sztywna, ale przecież odkształcalna, w której zamocowane są różne przyrządy.

Elementy podatne, za pomocą których tablica jest zamocowana do śmigłowca. są

rozłożone na obwodzie tablicy, a ich podstawową cechą jest podatność oraz zdolność

do absorbcji energii w czasie drgań. Masa tych elementów jest znacznie mniejsza niż

70

masa tablicy (zwykle o dwa rzędy wielkości), dlatego można przyjąć, że są to elementy

pozbawione masy („bezmasowe”), a ich jedynymi cechami mechanicznymi jest

podatność oraz rozpraszanie energii drgań.

tablica przyrządów

elementy
mocujące

Fragment
kadłuba
śmigłowca

Rys. 2.40

Obserwacje tablicy w czasie wstępnej eksploatacji nasuwają spostrzeżenie, że

źródłem dyskomfortu są drgania tablicy "jako całości", a nie drgania przyrządów

będące rezultatem jej odkształceń. Tablicę modelujemy więc jako ciało sztywne o

pewnej masie m. Tak więc wykonaliśmy dekompozycję tablicy, polegającą na

wyodrębnieniu w niej charakterystycznych elementów, którym przypisaliśmy pewne

cechy dominujące, pomijając drugorzędne.

Inną obserwacją ze wstępnej eksploatacji jest to, że dominującym ruchem

tablicy są jej drgania w płaszczyźnie pionowej. Upoważnia to do przyjęcia założenia, że

tablica jest ciałem, zamocowanym podatnie w sposób umożliwiający jej

przemieszczenia w płaszczyźnie pionowej. W ten sposób tablica została sprowadzona

do modelu dyskretnego o jednym stopniu swobody. Mówimy, że dokonana została

redukcja

stopni swobody.

Skoro zgodziliśmy się co do tego, że tablicę wraz z wyposażeniem zastąpić

można ciałem sztywnym, to jej kształt w rozpatrywanym zagadnieniu przestaje

odgrywać istotną rolę. Rozbudowaną formę tablicy redukujemy więc do jej

odwzorowania symbolicznego (rys. 2.41).

71

x(t)

y(t)

Tablica

Rys. 2.41

Stwierdziliśmy powyżej, że drgania tablicy wymuszane są drganiami

konstrukcji, do której jest mocowana. Zachodzi pytanie, na ile jest to oddziaływanie

dwukierunkowe, tj. czy drgania tablicy nie mają wpływu na drgania jej otoczenia. Tu

odpowiedź wydaje się oczywista: sztywna konstrukcja pojazdu oraz jego masa

wielokrotnie większa do masy tablicy (np. więcej niż 100 razy) sprawia, że ruch

względny tablicy w jej otoczeniu nie oddziałuje na to otoczenie, tzn., że ruch pojazdu

jest w pełni niezależny od ruchu tablicy.

Założenie tego rodzaju powinno być jednak starannie przemyślane, bowiem

stosowanie dynamicznego eliminatora drgań wskazuje na możliwość istnienia takiego

sprzężenia.

Jak już wiemy, tablica zamocowana jest za pomocą specjalnych elementów

podatnych, które są kształtowane w taki sposób, że ich charakterystyka sprężysta jest

zwykle nieliniowa, a ponadto charakteryzują się zdolnością do absorbowania energii.

Przykład ich charakterystyki pokazany jest na rys. 2.42.

si

ła

odkształcenie

punkt pracy

Rys.

2.42

W modelu naszym decydujemy się na linearyzację tych charakterystyk, co

polega na ich zastąpieniu przez przybliżenie liniowe w otoczeniu punktu pracy. W

72

efekcie sprowadzamy charakterystyki sprężyste zawieszenia do sztywności k, a jego

własności polegające na absorbcji energii do równoważnego tłumienia lepkiego o

współczynniku c. W rezultacie opisanego postępowania otrzymujemy model fizyczny

tablicy pokazany na rys. 2.43.

x(t)

y(t)

k

b

Rys.

2.43

Budowa modelu fizycznego jest pierwszym etapem modelowania. Dalsze etapy

to: budowa modelu matematycznego i identyfikacja jego parametrów.

2.7.3 Podsumowanie: wykaz działań upraszczających

Rozważony przykład tworzenia modelu tablicy daje asumpt do sporządzenia

listy typowych zabiegów i założeń upraszczających (przy modelowaniu obiektów o

naturze mechanicznej). Oczywiście, ze względu na to, że tablica nie jest obiektem

uniwersalnym, jej modelowanie fizyczne nie mogło zawierać wszystkich

wyszczególnionych haseł.

Tak więc możemy się spotkać z następującymi działaniami:

•

wyodrębnienie elementów podstawowych,

•

podział elementów na grupy o różnych właściwościach (dekompozycja),

•

uproszczenie geometrii wyodrębnionych elementów,

•

zastąpienie właściwości rozłożonych przez skupione,

•

przyjęcie zależności liniowych między przyczynami i skutkami (linearyzacja),

•

pomijanie szumów otoczenia i pomiarów,

•

redukcja liczby stopni swobody.

W trakcie tych działań należy dostrzegać możliwość uwzględniania lub pominięcia w

modelu następujących cech:

73

•

niejednorodność elementów obiektu (gdyż są wykonane z materiałów o różnych

gęstościach),

•

zmienność parametrów w czasie,

•

niedookreślenie wartości parametrów,

•

oddziaływanie obiektu z otoczeniem.

2.8 O SPECYFICE MODELOWANIA UKŁADÓW MECHANICZNYCH

Specyfikę układów mechanicznych najłatwiej dostrzec na tle innych układów

fizycznych. Rozważmy więc na wstępie popularne w technice układy elektryczne.

Każdy z podstawowych elementów tych układów, czyli opornik, cewka indukcyjna i

kondensator może być scharakteryzowany za pomocą tylko jednej stałej odpowiednio

R

, L i C. Działanie tych elementów jest zawsze takie samo niezależnie od usytuowania

elementu w obwodzie elektrycznym (przy pominięciu wpływu wysokich częstości). Są

to, jak wiemy z p.2.4, elementy dwubiegunowe, włączane w obwód przewodowo, a ich

usytuowanie w przestrzeni nie odgrywa żadnej roli. Są to ponadto elementy liniowe, a

zatem podobnie jak elementy układów regulacji automatycznej, mogą być

charakteryzowane za pomocą funkcji przenoszenia sygnału, czyli tzw. transmitancji.

Elementy te kontaktują się z resztą układu w ściśle określonych miejscach zwanych

wejściem i wyjściem. Zmiana przestrzennego położenia elementu regulacji

automatycznej nie wpływa na transmitancję elementu.

Inaczej jest w wypadku elementów układów mechanicznych. Ich usytuowanie w

przestrzeni, w szczególności względem innych elementów układu, nałożone na nie

ograniczenia ruchu, a także sposób definiowania współrzędnych w istotny sposób

zmieniają model matematyczny elementu. Zmiana nie wynika z niestacjonarności

elementu. Przeciwnie, zakładamy, że charakterystyki elementu w ustalonym układzie

odniesienia są niezmienne w czasie. Ale z racji różnych możliwości włączenia

elementu mechanicznego do układu jego model matematyczny w konkretnych

warunkach pracy (a jest ich praktycznie nieskończenie wiele) i przy konkretnych

więzach może dalece odbiegać od podstawowego modelu elementu, czyli od jego

równania biegunowego. Jest jeszcze jeden czynnik, który komplikuje wykorzystanie

równań biegunowych elementów sprężystych i tłumiących. Otóż współrzędne, które

wprowadza się do opisu zjawisk mechanicznych zwykle wiąże się z elementem

bezwładnościowym (punktem materialnym, bryłą sztywną). Współrzędne adekwatne

74

dla opisu położenia elementu bezwładnościowego zastosowane do elementów

sprężystych lub tłumiących mogą powodować znaczną komplikację równań

biegunowych tych elementów. Często ta komplikacja jest tak duża, że nie da się

wykorzystać równań biegunowych elementów sprężystych i tłumiących jako gotowego

składnika modelu matematycznego układu mechanicznego. Aby rozjaśnić te trudne

sprawy weźmy pod uwagę podstawowy element układów mechanicznych - sprężynę

liniową, której równanie (2.16) jest dobrze znane. Teraz jednak współpracuje ona z

elementem bezwładnościowym.

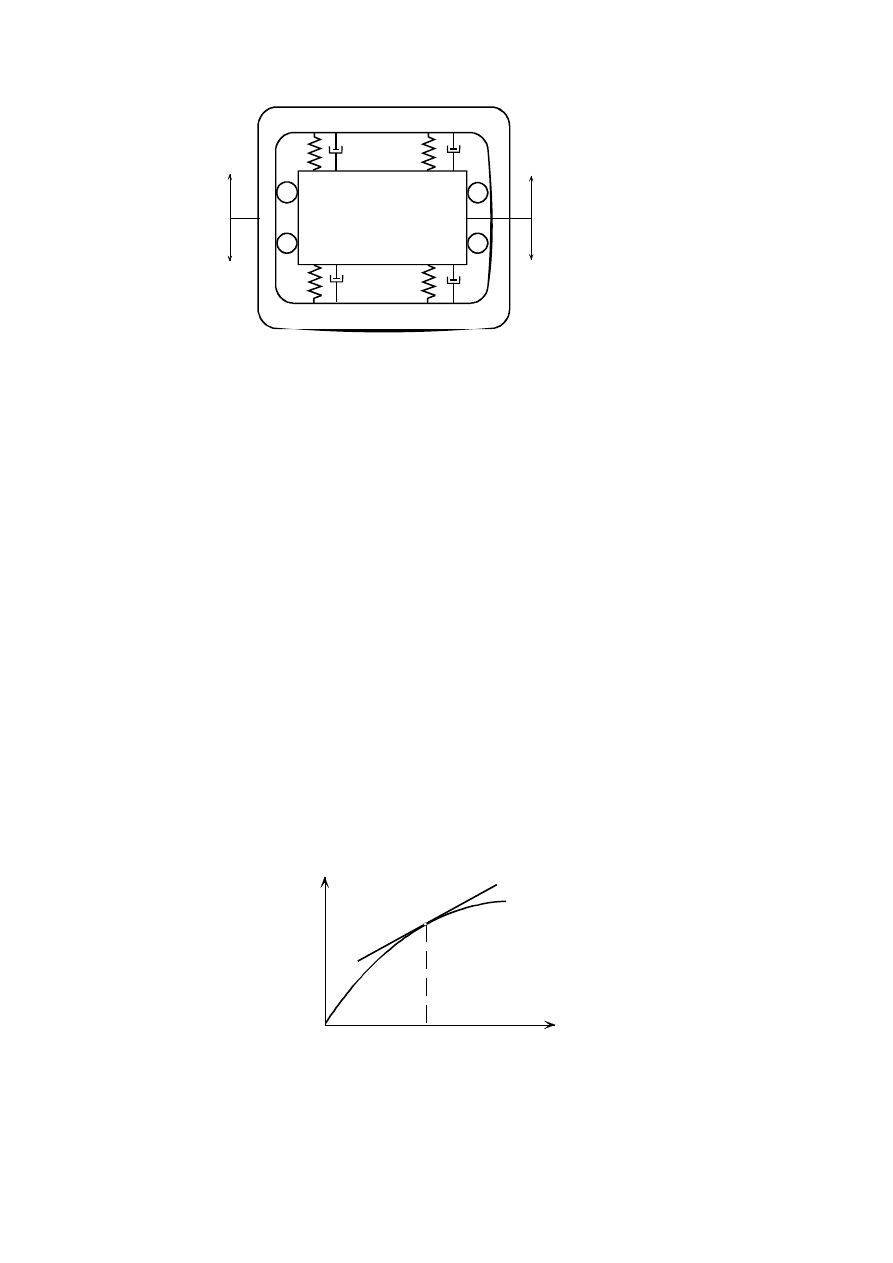
Rozważmy więc trzy układy drgające, w których występuje ta sama sprężyna

liniowa o sztywności k i długości swobodnej l

0

. Układ pierwszy to oscylator

harmoniczny z p.1.2, dwa pozostałe przedstawione są na rys 2.44a i 2.44b.

a)

b)

x

a

P

x

α

B

l

A

0

α

g

a

x

położenie początkowe

Rys.2.44

a,

b

Współrzędna x we wszystkich trzech układach opisuje położenie masy. Pytamy o model

sił sprężystych, czyli o siłę P

x

działającą na masę na kierunku jej ruchu, a pochodzącą

od sprężyny. Aby uniknąć nieporozumień ustalmy, że siłę działającą na sprężynę

oznaczać będziemy symbolem F, zaś siłę oddziaływania sprężyny na masę symbolem

P. Oczywiście zachodzi związek

P

= - F

(2.91)

W układzie oscylatora P

x

= -kx, czyli model oddziaływań sprężystych zachowuje postać

równania (2.16). Zobaczmy jak sprawa wygląda w pozostałych układach.

W układzie z rys. 2.44(a) dopuszczamy napięcie wstępne sprężyny, tzn. przyjmujemy,

że A0 = a > l

0

. Wydłużenie sprężyny w położeniu B suwaka określonym współrzędną x,

jest

Δ

l = l – l

0

= (a

2

+ x

2

)

1/2

– l

0

. Zatem

(

)

0

2

2

l

x

a

k

l

k

F

−

+

=

Δ

=

(2.92)

Siła P

x

= Pcos

α

, gdzie cos

α

= x/l. Wziąwszy pod uwagę te związki oraz (2.91) i (2.92)

mamy

75

P

F

x

l

kx

l

l

kx

l l

l

kx

l

a

x

x

= −

= −

= −

−

= −

−

+

⎛
⎝

⎜

⎞
⎠

⎟

Δ

0

0

2

2

1

(2.93)

Zarówno z (2.93), jak i z (2.92) odczytujemy, że obie siły są nieliniowe, a model

oddziaływań sprężyny jest różny od jej równania biegunowego.

Rozważmy teraz układ z rys.2.44(b). W zakresie x < a wózek może poruszać się

swobodnie. Gdy położenie wózka x przekracza a, napotyka on zderzak umocowany na

sprężynie. Pojawia się oddziaływanie na wózek siłą P

x

pochodzącą od sprężyny. Zatem

(

)

⎩

⎨

⎧

≥

−

−

<

=

a

x

gdy

a

x

k

a

x

gdy

P

x

0

(2.94)

Ponownie model oddziaływań sprężyny w całym zakresie zmian współrzędnej x jest

nieliniowy mimo, że jest liniowy w obu zakresach, tzn., gdy x < a oraz gdy x

≥

a

.

Skąd więc wynikają nieliniowości modelu oddziaływań sprężystych mimo, iż sam

element pozostaje stale liniowy? Otóż w układach mechanicznych istotną rolę odgrywa

geometria, czyli wzajemne usytuowanie elementów względem siebie, pojawianie się

luzów, sposoby odmierzania współrzędnych.

W praktyce, dla konkretnego usytuowania elementu w układzie musimy tworzyć

adekwatny model jego oddziaływań z pozostałą częścią układu. Analogiczna sytuacja

jest z elementami tłumiącymi. Nieskończona liczba sposobów włączenia elementów do

układu mechanicznego czyni praktycznie niemożliwe katalogowanie ich modeli

matematycznych. Porzućmy zatem pomysł przedstawienia pełnego katalogu modeli

elementów mechanicznych na rzecz:

a) znajomości kilku charakterystyk podstawowych elementów mechanicznych;

b) umiejętności wyznaczania sił oddziaływań elementów sprężystych i tłumiących na

ciała;

c) poznania metod generowania równań ruchu ciał.

Nasze rozważania skoncentrowane były dotąd na elementach „modelowych” tj.

takich, które posiadając jedną własność nie zawierają „domieszki” innej własności, np.

bryła sztywna ma masę, ale jej odkształcalność jest zaniedbywalna, sprężyna zaś jest

elementem odkształcalnym którego miarą jest sztywność sprężyny, ale jej masa

i właściwości tłumiące są bliskie zera, a w konsekwencji pomijane.

W rzeczywistych konstrukcjach mechanicznych dość rzadko występują te sterylne

elementy „modelowe”, natomiast mamy do czynienia z belkami wspornikowymi,

powłokami, podkładami, linami, pasami transmisyjnymi, wałami, kołami, itp.

76

Wszystkie one posiadają masę rozłożoną w pewnym podobszarze przestrzeni, a ponadto

nie są pozbawione własności sprężystych i tłumiennych. Innymi słowy elementy

konstrukcji mechanicznych to zazwyczaj układy ciągłe będące konglomeratem trzech

podstawowych własności mechanicznych: bezwładności, odkształcalności i własności

tłumiących.

Specyfika układów mechanicznych przejawia się także w tym, że często zjawiska

odkształceń sprężystych i rozproszenia energii występują łącznie. W konsekwencji

trudno mówić oddzielnie o elementach sprężystych i tłumiących. Z podobną sytuacją

spotykamy się próbując modelować siły w połączeniach elementów konstrukcji,

zwłaszcza w połączeniach nitowanych (rys2.45a,b) i wtłaczanych (rys.2.46a,b)

a)

b)

M

Rys.2.45

a)

b)

M

Rys.2.46

Odkształceniom elementów konstrukcji towarzyszy zjawisko tarcia na połączeniach

elementów. W rezultacie wykres siły w funkcji odkształcenia ma kształt podobny do

przedstawionych na rys.2.47a,b.

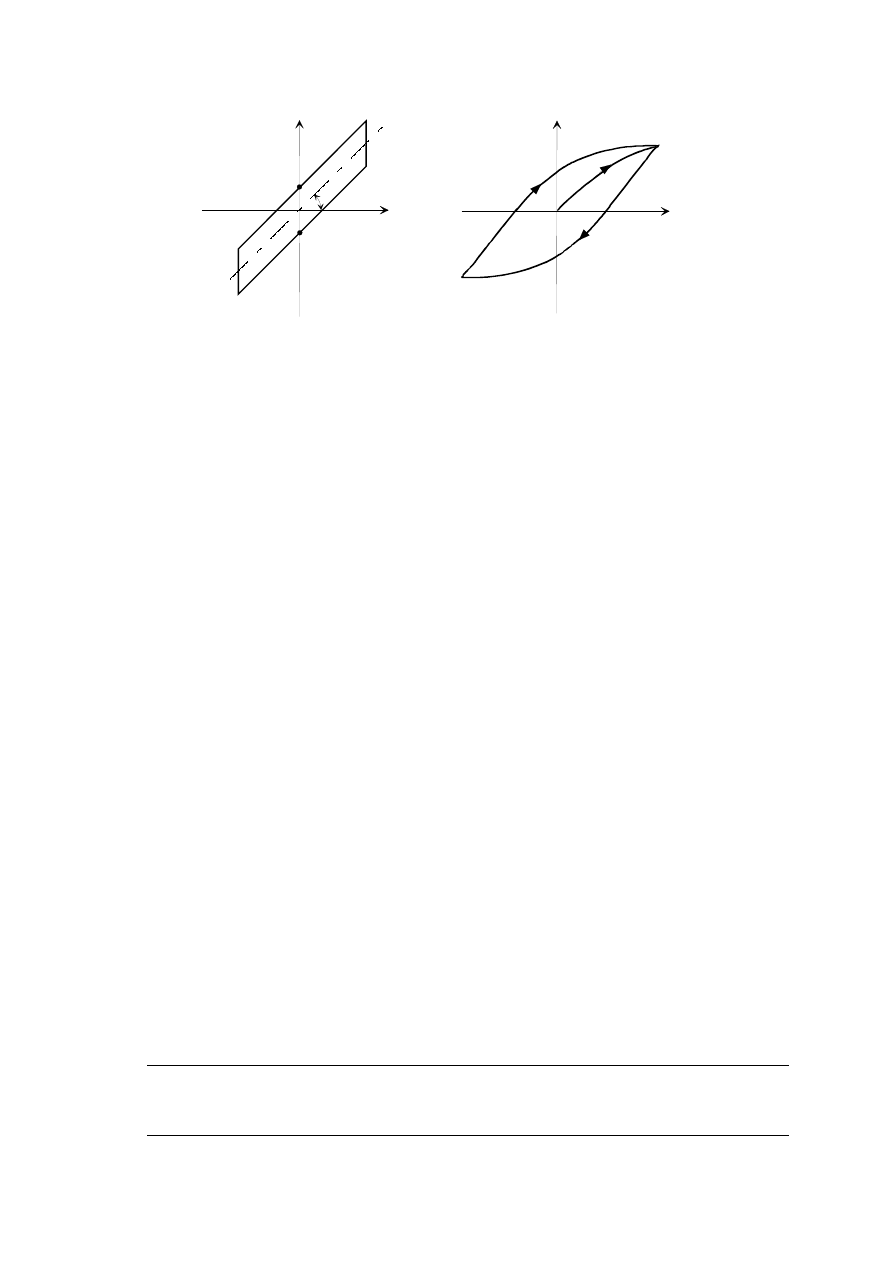
77

a)

T

-T

x

P

α

kx

P

x

b)

k

tg

=

α

Rys.2.47

Wykres siły z rys 2.47(a) odpowiada wzorowi

P

kx T

x

=

+ sgn &,

(2.95)

natomiast pętla histerezy z rys. 2.47(b) przypomina pętlę histerezy dla materiałów

lepkosprężystych i w konsekwencji siła może być też podobnie modelowana, tzn.

(

)

P

k i x

=

+ η

(2.96)

Jak widzimy modelowanie elementów układów mechanicznych i zjawisk z ich

udziałem nie jest sprawą łatwą. Temat modelowania sił tłumiących w połączeniach jest

niezwykle obszerny. Droga, do adekwatnego modelowania wiedzie przez zrozumienie

natury drgań układów o wielu stopniach swobody, drgań układów ciągłych,

rozpoznanie własności materiałów konstrukcyjnych, wreszcie przez ich pomiar

i identyfikację.

ROZDZIAŁ

TRZECI

78

DRGANIA UKŁADÓW LINIOWYCH O JEDNYM STOPNIU

SWOBODY

Celem niniejszego

rozdziału jest poznanie własności układu drgającego liniowego

o stałych parametrach mechanicznych i jednym stopniu swobody, a w szczególności

jego odpowiedzi na najprostsze rodzaje wymuszeń.

3.1 DRGANIA SWOBODNE

3.1.1 Drgania swobodne układu bez tłumienia

Z drganiami tego rodzaju spotkaliśmy się już w p.1.2 rozważając oscylator

harmoniczny. Teraz przypomnimy najważniejsze rezultaty tego punktu na przykładzie

drgań skrętnych zespołu balansu zegarowego, którego schemat przedstawiony jest na

rys.3.1. Balans (1) jest tak ukształtowany, aby jego osiowy moment bezwładności I był

jak największy przy możliwie małej masie. Sprężyna zwrotna (3) o stałej K ma zwykle

kształt spirali Archimedesa i jej wewnętrzny koniec przytwierdzony jest do wałka

balansu (2), a zewnętrzny - do korpusu mechanizmu (4).

3

2

1

θ

4

Rys.3.1

Standardowa procedura uwalniania od więzów wraz z wykorzystaniem twierdzenia

o zmianie krętu pozwala na napisanie równania ruchu balansu w postaci

I

K

&&θ

θ

+

= 0

(3.1)

79

gdzie

θ

jest kątem wychylenia balansu z położenia równowagi. Równanie różniczkowe

(3.1) jest podobne do równania (1.1), zatem jego rozwiązanie jest analogiczne do

(1.17), czyli

( )

(

)

α

+

ω

Θ

=

θ

t

sin

t

0

(3.2)

gdzie amplituda

Θ

i faza drgań

α

zależą od warunków początkowych, tj. θ

0

i &

θ

0

, zaś

ω

0

= (K/I)

1/2

jest częstością drgań swobodnych nietłumionych, czyli krótko częstością

własną.

Kończąc ten punkt przypomnijmy, że rozważona przez nas sytuacja drgań układu

bez tłumienia jest tylko idealizacją, która w rzeczywistości - na poziomie układów

technicznych - nie występuje. Wyłania się więc pytanie: czy warto mówić o częstości

własnej układu technicznego, a więc z definicji obdarzonego tłumieniem? Owszem, tak

i to z dwu powodów:

1. zdarzyć się może, niekiedy celowo, niekiedy przypadkowo, że siły wymuszające

zewnętrzne całkowicie „neutralizują” wpływ tłumienia danego układu i wtedy

drgania układu rzeczywistego zachowują wszelkie własności układu

modelowego nietłumionego;

2. częstość własna jest najbardziej syntetyczną wielkością reprezentującą dowolny

układ drgający (a więc też tłumiony wewnętrznie), jest niejako jego wizytówką,

a nawet podstawowym identyfikatorem, takim jakim dla człowieka są jego linie

papilarne. Częstość własna jest ważnym punktem odniesienia, jest wielkością,

którą można wyznaczyć lub pomierzyć, od niej, w dużym stopniu, zależy

przebieg zjawisk drganiowych realizowanych w danym układzie przy różnych

wymuszeniach. Dlatego warto ją znać.

Zauważmy więc, że w konsekwencji pojęcie częstość własna dotyczy przede

wszystkim modeli, ale może dotyczyć układów rzeczywistych jako ich syntetyczny

reprezentant.

3.1.2 Drgania swobodne układu z tłumieniem

80

Podobnie jak w p. 1.2 rozważać będziemy ruch postępowy i prostoliniowy ciała o masie

m

po idealnie gładkiej płaszczyźnie (rys.3.2). Teraz, oprócz liniowej sprężyny o

sztywności k, do masy dołączony jest tłumik liniowy, którego własności tłumienne

charakteryzuje tzw. współczynnik tłumienia lepkiego (lub inaczej wiskotycznego) c

[kg/s].

m

x

k

c

Rys. 3.2

Równanie ruchu ciała ma postać

mx cx kx

&&

&

+

+

= 0

(3.3)

Dla ułatwienia dalszej analizy równanie (3.3) zapiszemy następująco

&&

&

x

hx

x

+

+

=

2

0

0

2

ω

(3.4)

gdzie

ω

0

2

= k/m, a znormalizowany współczynnik tłumienia 2h wyraża się wzorem

2h

c

m

=

(3.5)

Równanie charakterystyczne dla równania różniczkowego (3.4) ma postać

r

hr

2

0

2

2

0

+

+

=

ω

(3.6)

zaś jego pierwiastki są następujące

r

h

h

1

2

0

2

= − −

− ω , r

h

h

2

2

0

2

= − +

− ω

(3.7)

Rozwiązanie ogólne równania (3.4) jest zatem kombinacją liniową rozwiązań

szczególnych, tj.

( )

x t

C e

C e

r t

r t

=

+

1

2

1

2

(3.8)

gdzie C

1

i C

2

są stałymi dowolnymi.

W

zależności od znaku wyrażenia h

2

0

2

−

ω

we wzorach (3.7) wyróżniamy trzy

przypadki:

1) h >

ω

0

2) h = ω

0

,

3) h <

ω

0

Tłumienie wiskotyczne c, przy którym h =

ω

0

nazywamy tłumieniem krytycznym, tzn.

81

c

kr

= 2m

ω

0

(3.9)

Zdefiniujmy także tzw. względny współczynnik tłumienia zwany też stopniem tłumienia

jako

γ = c c

kr

/

(3.10)

Przy jego użyciu równanie ruchu (3.4) i pierwiastki (3.7) można zapisać w postaci

&&

&

x

x

x

+

+

=

2

0

0

0

2

γω

ω

(3.11)

(

)

r

1

2

0

1

= − −

−

γ

γ

ω

,

(

)

r

2

2

0

1

= − +

−

γ

γ

ω .

(3.12)

Dla przekształcenia (3.4) w (3.11), a (3.7) w (3.12) wystarczy wykazać, że

h c m c

m

c c

kr

=

=

=

=

2

2

0

0

0

0

ω

ω

ω

γω

(

)

(3.13)

Rozważmy szczegółowo każdy z trzech przypadków.

1. Tłumienie nadkrytyczne h >

ω

0

, czyli

γ

> 1.

W tym przypadku pierwiastki (3.12) równania charakterystycznego (3.6) są różne i

ujemne, zaś rozwiązanie x(t) dane jest wzorem (3.8). Stałe C

1

, C

2

wyznaczamy z

układu równań:

x

C

C

0

1

2

=

+

, v

r C

r C

0

1 1

2

2

=

+

(3.14)

gdzie x

0

, v

0

są odpowiednio wychyleniem i prędkością początkową. Z (3.14) mamy

C

x r

v

r

r

1

0 2

0

2

1

=

−

−

, C

v

r x

r

r

2

0

1 0

2

1

=

−

−

(3.15)

Wychylenie x(t) wyraża się więc zależnością

( )

(

)

(

)

[

]

x t

r

r

x r

v e

v

r x e

r t

r t

=

−

−

+

−

1

2

1

0 2

0

0

1 0

1

2

(3.16)

Rozwiązanie (3.16) jest sumą dwu funkcji wykładniczych o wykładnikach

rzeczywistych i ujemnych. Zatem ruch układu nie jest drgający, lecz asymptotycznie

zanikający, tzn. dla t

→ ∞ x(t) → 0. Więcej o charakterze ruchu w warunkach tłumienia

nadkrytycznego dowiemy się wyznaczając chwilę t

m

, w której wychylenie jest

ekstremalne. Wiadomo, że ekstremum wychylenia zachodzi wtedy, gdy prędkość

x&

(t)

jest równa zero. Po zróżniczkowaniu (3.8) i wykorzystaniu warunku

x&

(t

m

) = 0,

otrzymujemy:

r

1

C

1

exp(r

1

t

m

) + r

2

C

2

exp(r

2

t

m

) = 0, czyli exp(r

1

- r

2

)t

m

= - r

2

C

2

/

r

1

C

1

, a stąd

(

)

t

r

r

r C r C

m

=

−

−

1

1

2

2

2

1

1

ln

(3.17)

Dla stałych C

1

i C

2

(wzory (3.15)) ekstremalne wychylenie zachodzi w chwili

82

(

)

(

)

t

r

r

r v

r x

r v

r x

m

=

−

−

−

⎡

⎣

⎢

⎢

⎤

⎦

⎥

⎥

1

1

2

2

0

1 0

1

0

2 0

ln

(3.18)

Czas t

m

jest określony pod warunkiem, że wyrażenie w nawiasie kwadratowym jest

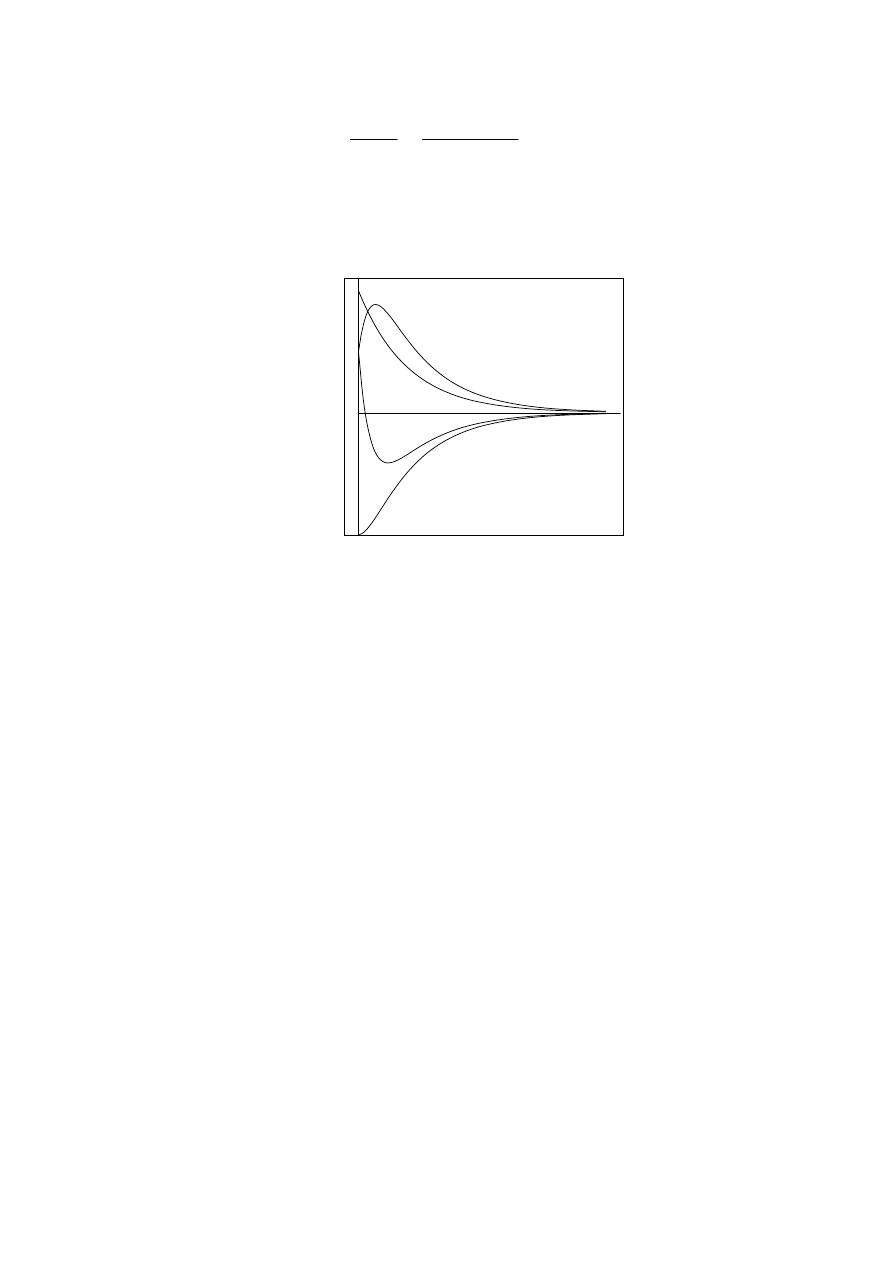
dodatnie. Jeśli wyrażenie podlogarytmiczne jest niedodatnie, to oznacza, że funkcja x(t)

nie posiada ekstremum. Jej przebieg jest więc taki jak np. krzywej 1 na rys 3.3.

Rys. 3.3

Jeśli warunki początkowe mają postać x(0) = x

0

,

v(0) = 0, to iloraz pod znakiem

logarytmu w (3.18) przybiera wartość 1. Ponieważ ln1 = 0, więc t

m

= 0, co oznacza, że

ekstremalne wychyle-nie zachodzi tylko w chwili t = 0. Tę sytuację przedstawia krzywa

2 na rys 3.3.

Krzywe 3 i 4 przedstawiają dwie sytuacje, w których czas t

m

> 0. Warto ponadto

zauważyć, że:

- bez względu na warunki początkowe ciało co najwyżej raz przechodzi przez

położenie x = 0,

- jeśli w trakcie ruchu ciało osiągnie chwilową prędkość zero, to potem zmierza

asymptotycznie

do położenia równowagi

2. Tłumienie krytyczne h =

ω

0

, czyli

γ = 1.

W tym przypadku pierwiastki (3.7) przekształcają się w jeden pierwiastek podwójny,

tzn.

r

1

= r

2

= -h = -

ω

0

(3.19)

Rozwiązanie przybiera wówczas postać:

( )

(

)

x t

e

C

C t

t

=

+

−ω

0

1

2

,

(3.20)

3

1

2

4

t

x

83

gdzie stałe C

1

,

C

2

są wyznaczane na podstawie warunków początkowych. W celu

wyznaczenia tych stałych różniczkujemy (3.20). Mamy

( )

(

)

[

]

&x t

C

C

C t e

t

=

−

+

−

2

0

1

2

0

ω

ω

(3.21)

Na podstawie (3.20) i (3.21) otrzymujemy

x

0

= C

1

oraz

v

0

= C

2

-

ω

0

C

1

, czyli

C

1

= x

0

, C

2

= v

0

+

ω

0

x

0

(3.22)

Ruch jest zatem opisany zależnością

( )

(

)

[

]

x t

x

v

x t e

t

=

+

+

−

0

0

0 0

0

ω

ω

(3.23)

Rozwiązanie to jest iloczynem funkcji liniowej i wykładniczo malejącej funkcji czasu.

Zależy ono od warunków początkowych, ale jego podstawowe cechy są takie same jak

rozwiązania (3.16) dla tłumienia nadkrytycznego. W rozważanym przypadku łatwo

wyznaczyć chwilę t

m

, w której wychylenie

x(t) jest ekstremalne. Na podstawie (3.21)

mamy

(

)

C

C

C t

m

2

0

1

2

0

−

+

=

ω

skąd

t

m

= (C

2

-

ω

0

C

1

)/

ω

0

C

2

. Po podstawieniu wartości stałych

C

1

,

C

2

z (3.22)

otrzymujemy

(

)

t

v

v

x

m

=

+

0

0

0

0 0

ω

ω

(3.24)

3.

Tłumienie podkrytyczne h <

ω

0

, czyli

γ < 1.

W tym przypadku pierwiastki są liczbami zespolonymi, sprzężonymi, tj.

r

1

= - h - i

ω

D

,

r

2

= - h + i

ω

D

(3.25)

gdzie

ω

ω

ω

γ

D

h

=

−

=

−

0

2

2

0

2

1

(3.26)

jest tzw.

częstością drgań swobodnych tłumionych, zwaną krótko częstością naturalną.

Rozwiązanie (3.8) przybiera postać:

( )

(

)

x t

e

C

t C

t

ht

D

D

=

+

−

1

2

cos

sin

ω

ω

(3.27)

Dla warunków początkowych

x(0) = x

0

,

v(0) = v

0

stałe

C

1

,

C

2

są następujące

C

1

= x

0

, C

2

= (v

0

+ hx

0

)/

ω

D

(3.28)

Po zamianie stałych (zob. p.1.2) rozwiązanie (3.27) można zapisać w postaci:

( )

(

)

x t

Ae

t

ht

D

=

+

−

sin

ω

α

(3.29)

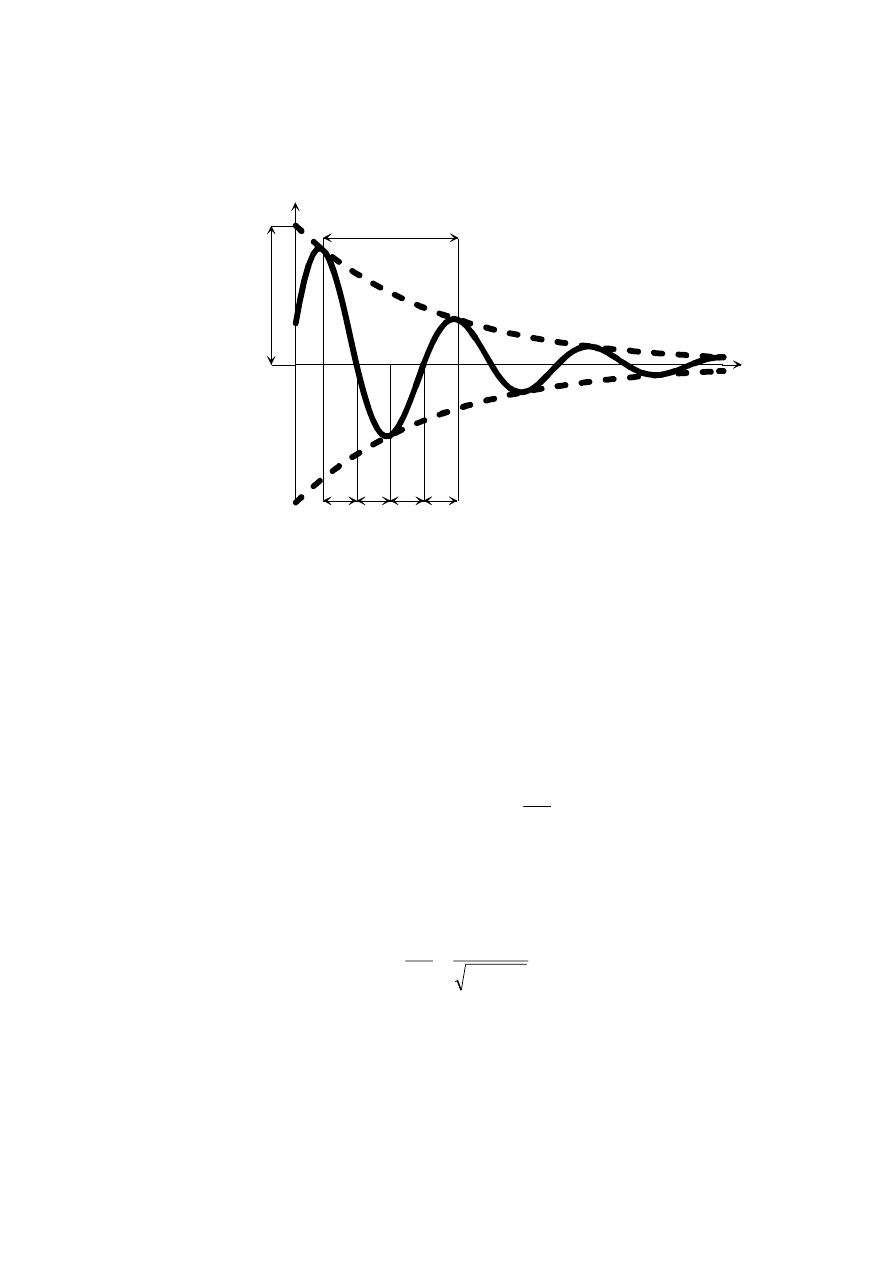
84

gdzie stałe A - amplituda początkowa i

α

- kąt przesunięcia fazowego są wyznaczane z

wa-runków początkowych. Ruch opisany zależnością (3.29) przedstawiony jest na rys.

3.4

x

Ae

-ht

T

D

/4

T

D

/4

T

D

/4

T

D

/4

A

T

D

t

Rys. 3.4

Drgania tłumione nie są okresowe, gdyż nie istnieje taka stała czasowa

τ

, dla

której

x(t +

τ)

=

x(t). Można jednak wprowadzić wielkość T

D

, zwaną okresem

umownym, którą definiujemy jako odstęp czasu, między dwoma kolejnymi

maksymalnymi wychyleniami w tę samą stronę. Dla ustalenia zależności między T

D

a

innymi parametrami układu zbadajmy ekstrema funkcji (3.29). W tym celu

przyrównajmy do zera pochodną funkcji (3.29), czyli

( )

(

)

(

)

&

sin

cos

x t

Ahe

t

A

e

t

ht

D

D

ht

D

= −

+

+

+

=

−

−

ω

α

ω

ω

α

0

a stąd

(

)

tg

t

h

D

D

ω

α

ω

+

=

Wzór ten wyznacza wartości t, dla których funkcja (3.29) ma ekstrema. Jeśli jednak

ekstremum występuje dla t = t

1

, to występuje ono również dla

t

2

=

t

1

+

n

π

/

ω

D

.

Dla

n = 1 mamy więc t

2

-

t

1

= 0.5

T

D

=

π

/

ω

D

, a stąd

T

h

D

D

=

=

−

2

2

0

2

2

π

ω

π

ω

`

(3.30)

Jest widoczne, że wartość T

D

nie zmienia się wraz z upływem czasu, tzn. kolejne

skrajne wychylenia występują po tym samym czasie T

D

. Porównując wzory (3.30) i

(1.19) widzimy, że T

D

>

T, tzn. umowny okres drgań tłumionych jest większy od okresu

drgań nietłumionych.

3.1.3 Dekrement drgań

85

Dla ruchu swobodnego układu tłumionego danego wzorem (3.29) rozważmy iloraz

wychylenia w danej chwili i wychylenia po czasie T

D

od chwili danej, czyli

( )

(

)

q

x t

x t T

e

D

hT

D

=

+

=

Widzimy, że iloraz ten nie zależy od czasu t. Skoro jest to wielkość niezależna od czasu

t

można ją traktować jako dobrą miarę zanikania drgań. Definiujemy więc wielkość

( )

(

)

δ

π

ω

=

+

=

=

−

ln

x t

x t T

hT

h

h

D

D

2

0

2

2

(3.31)

którą nazywamy logarytmicznym dekrementem drgań lub krótko dekrementem drgań.

Wielkość ta stosowana jest jako miara tłumienia drgań, przy użyciu której szczególnie

prosto dają się wyrazić zmiany zachodzące w układzie tłumionym.

Biorąc pod uwagę wzory (3.13) i (3.26), dekrement drgań może być przedstawiony jako

δ

πγ

γ

=

−

2

1

2

(

3.32)

Jeśli

γ

<< 1 (co jest typowe dla licznych materiałów i zespołów mechanicznych), to

wówczas dekrement przybiera szczególnie prostą postać

δ

πγ

= 2

(3.33

)

Istnieje jeszcze jedna miara tłumienia drgań stosowana bardzo często w lotnictwie. Jest

to czas stłumienia amplitudy do połowy T

1/

2

. Tę wartość wyznaczymy wykorzystując

warunek

( )

(

)

x t

x t T

e

hT

+

=

=

1 2

1 2

2

/

/

Zatem po uwzględnieniu wzoru (3.5)

T

h

m

c

1 2

2

2

2

/

ln

ln

=

=

(3.34)

3.1.4 Straty energii podczas drgań tłumionych

Rozważmy straty energetyczne w układzie spowodowane tłumieniem. Uczynimy to

zakładając, że tłumienie jest małe. O ilości rozproszonej energii można wnosić na

podstawie maksymalnych wychyleń od położenia równowagi w kolejnych fazach

drgań. W warunkach maksymalnego wychylenia, energia potencjalna jest równa

całkowitej energii układu, bowiem wówczas prędkość równa jest zeru. Wyznaczmy

zatem najpierw względną zmianę energii miedzy kolejnymi maksymalnymi

wychyleniami o wartościach odpowiednio x

i

oraz

x

i+1

. Przez

U

i

oraz

U

i+1

oznaczmy

86

energie zmagazynowane w układzie w tych szczególnych chwilach. Wówczas

całkowita energia równa jest energii potencjalnej, czyli

U

kx

i

i

=

1

2

2

oraz

U

kx

i

i

+

+

=

1

1

2

1

2

Strata energii

Δ

U w pełnym cyklu miedzy kolejnymi maksimami wynosi

(

)

(

)(

)

1

1

2

1

2

1

2

2

1

1

+

+

+

+

−

+

=

−

=

−

=

Δ

i

i

i

i

i

i

i

i

x

x

x

x

k

x

x

k

U

U

U

(3.35

)

Policzmy względną stratę energii

Δ

U/U

i

wykorzystując przy tym definicję dekrementu

drgań (3.31) oraz wzór (3.35). Mamy

(

)(

)

(

)(

)

ΔU

U

k x

x

x

x

kx

x

x

x

x

e

e

e

i

i

i

i

i

i

i

i

i

i

=

+

−

=

+

⎛
⎝

⎜

⎞
⎠

⎟ −

⎛
⎝

⎜

⎞
⎠

⎟ = +

−

= −

+

+

+

+

−

−

−

0 5

0 5

1

1

1

1

1

1

1

2

1

1

2

.

.

δ

δ

δ

(3.36

)

Wyznaczymy teraz energię rozproszoną w pojedynczym cyklu zakładając przy

tym, że w przybliżeniu, w tym czasie ruch jest harmoniczny, tj. x = Asin

ω

t, gdzie A jest

amplitudą wyróżnionego cyklu. Strata energii w pierwszej ćwiartce cyklu (na drodze od

0 do A) równa jest w przybliżeniu jednej czwartej strat energii w całym cyklu. Mamy

więc

∫

=

Δ

A

dx

x

c

U

0

4

&

(3.37

)

gdzie &

cos .

x

A

t

=

ω

ω

Ponieważ &

/

,

x

dx dt

=

więc dx

xdt

= & , to całkę (3.37) można

zapisać jako

ΔU

cx dt

cA

tdt

c A

=

=

=

∫

∫

4

4

2

0

2

2

0

2

2

2

2

&

cos

/

/

π ω

π ω

ω

ω

π ω

(3.38

)

Zależność (3.38) może posłużyć do wyznaczania zastępczego współczynnika tłumienia

dla elementów o nieliniowej charakterystyce tłumiennej.

3.2 DRGANIA WYMUSZONE SIŁĄ HARMONICZNĄ

87

3.2.1 Drgania wymuszone układu bez tłumienia

Rozważmy układ drgający nietłumiony (rys.1.1) pod działaniem siły

F(t) = F

0

sin

ωt

skierowanej wzdłuż osi

x. Ruch masy opisany jest wówczas równaniem różniczkowym

niejednorodnym

t

sin

F

kx

x

m

ω

=

+

0

&&

(3.39)

Rozwiązanie równania (3.39) jest sumą rozwiązania x

s

równania jednorodnego

(drgań

swobodnych) i rozwiązania szczególnego

x

w

równania niejednorodnego (tj. drgań

wymuszonych), tzn.

x = x

s

+ x

w

(3.40)

Do wyznaczenia rozwiązania szczególnego

x

w

posłużymy się procedurą standardową -

w tym wypadku, ze względu na postać prawej strony równania (3.39), zastosujemy tzw.

metodę przewidywania. Poszukujemy zatem tego rozwiązania w postaci

x

w

= A

1

sin

ωt + A

2

cos

ωt

(3.41)

Rozwiązanie (3.41) i jego drugą pochodną

&&

sin

cos

x

A

t

A

t

x

w

w

= −

−

= −

ω

ω ω

ω

ω

2

1

2

2

2

(3.42)

podstawiamy do (3.39), grupujemy wyrazy przy funkcjach sin

ω

t i cos

ω

t i otrzymujemy

(

)

(

)

t

sin

F

t

cos

m

k

A

t

sin

m

k

A

ω

=

ω

ω

−

+

ω

ω

−

0

2

2

2

1

(3.43)

Skoro x

w

dane wzorem (3.41) ma być rozwiązaniem równania (3.39), to (3.43) musi

być tożsamością. A zatem współczynniki stojące przy liniowo niezależnych funkcjach

sin

ω

t i cos

ω

t po obu stronach (3.43) muszą być sobie równe. Z tego warunku wynika,

że

A

2

= 0 oraz

)

(

2

0

1

ω

m

k

F

A

−

=

. Skoro

A

2

= 0, to amplituda

A drgań równa jest stałej

A

1

. Mamy zatem

t

sin

m

k

F

t

sin

A

x

w

ω

ω

−

=

ω

=

2

0

(3.44)

Przedstawione rozwiązanie jest ważne pod warunkiem, że k

≠ m

ω

2

, co oznacza,

że

ω

≠

ω

0

.

Dla siły wymuszającej o częstości

ω

rozwiązanie

x

w

(3.44) jest ruchem

harmonicznym o tej samej częstości i są to tzw.

drgania ustalone. Amplitudę drgań

ustalonych (3.44) można zapisać na kilka różnych sposobów.

Mianowicie

88

(

)

2

2
0

0

2

0

m

F

m

k

m

F

A

ω

−

ω

=

⎟

⎠

⎞

⎜

⎝

⎛

ω

−

=

2

st

2
0

2

0

2

0

1

A

1

k

F

k

m

1

k

F

ν

−

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

ω

ω

−

=

⎟

⎠

⎞

⎜

⎝

⎛

ω

−

=

(3.45)

gdzie ostatni ułamek wyrażony został za pomocą ilorazu częstości

ν = ω/ω

0

oraz

wydłużenia statycznego sprężyny

A

st

pod działaniem siły F

0

. Zachodzi bowiem związek

A

st

= F

0

/k .

Amplituda drgań A może być wyrażona także jako:

A

A

st

=

β

(3.46)

gdzie

2

1

1

ν

−

=

β

(3.47)

jest współczynnikiem zwielokrotnienia amplitudy zwanym także współczynnikiem

wzmocnienia dynamicznego

. Jego wartość,

a w konsekwencji amplituda drgań

ustalonych (3.46), zależy od ilorazu częstości

ν.

Dla

ν

<< 1,

β

≈ 1, dla

ν

= 1,

β

dąży do nieskończoności, zaś dla

ν

>>1,

β

dąży do zera.

Współczynnik

β

jest dodatni, gdy

ω

<

ω

0

, a ujemny gdy

ω

>

ω

0

. Oznacza to, że

wychylenie x

w

jest tego samego znaku co siła F(t), gdy

ω

<

ω

0

, zaś przeciwnego,

gdy

ω

>

ω

0

. Innymi słowy częstość drgań własnych

ω

0

jest granicą zmiany fazy

wychylenia względem siły wymuszającej. Dla

ω

<

ω

0

wychylenie jest w fazie z siłą, zaś

powyżej przesunięcie fazy jest

π

. Rys. 3.5 przedstawia zależność wartości

bezwzględnej

współczynnika

β

od ilorazu częstości

ω

/

ω

0

.

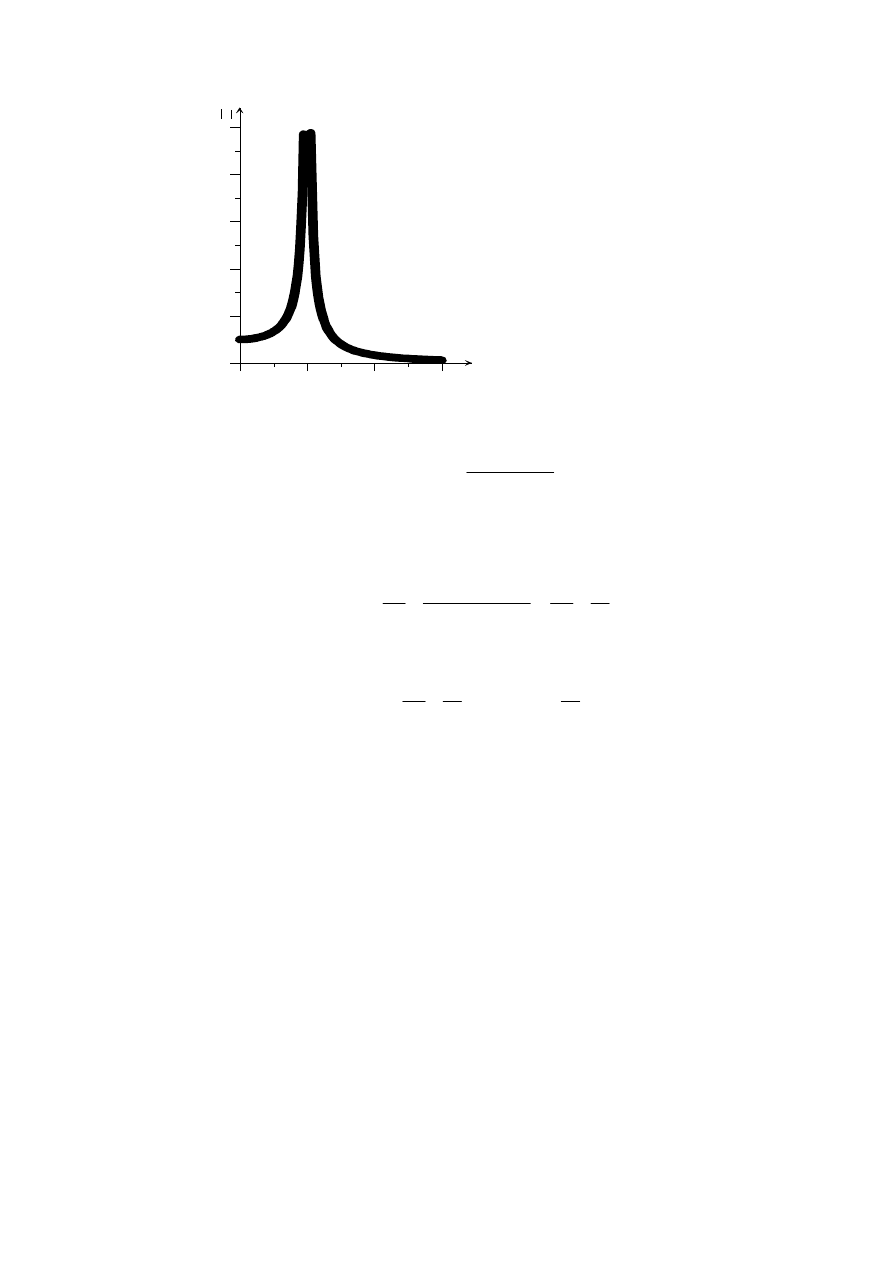
89

0 .0 0

1 .0 0

2 .0 0

3 .0 0

0 .0 0

2 .0 0

4 .0 0

6 .0 0

8 .0 0

1 0 .0 0

β

ω /ω

0

R y s .3 .5

Rys.3.5

Pełne rozwiązanie równania (3.40) ma postać

)

(

m

t

sin

F

t

sin

C

t

cos

C

x

2

2
0

0

0

2

0

1

ω

−

ω

ω

+

ω

+

ω

=

(3.48)

Stałe C

1

i C

2

wyznaczamy na podstawie warunków początkowych. Dla najbardziej

ogólnego zestawu tych warunków, tj. x(0) = x

0

oraz

( )

&x

v

0

0

=

mamy

C

1

= x

0,

βν

−

ω

=

ω

−

ω

ω

ω

−

ω

=

k

F

v

)

(

m

F

v

C

0

0

0

2

2
0

0

0

0

0

2

(3.49)

a zatem pełne rozwiązanie można zapisać jako:

( )

t

sin

k

F

t

sin

k

F

v

t

cos

x

t

x

0

0

0

0

0

0

0

ω

β

+

ω

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

βν

−

ω

+

ω

=

(3.50)

Warto zwrócić uwagę, że odpowiedź układu nietłumionego na wymuszenie siłą

harmoniczną zawiera jeden nieco nieoczekiwany składnik. O ile bowiem składnik

pierwszy spowodowany jest wychyleniem początkowym x

0

, składnik drugi prędkością

masy v

0

, w chwili t = 0, składnik czwarty to odpowiedź ustalona na siłę F

0

sin

ω

t

, o tyle

nie tak łatwo podać przyczynę pojawienia się trzeciego składnika rozwiązania (3.50), tj.

-(F

0

/k)

β

νsin

ω

0

t

Otóż zauważmy, że składnik ten to drgania z częstością własną

ω

0

, których amplituda

jest proporcjonalna do amplitudy F

0

siły wymuszającej. Składnik ten występuje

niezależnie od warunków początkowych x

0

,

v

0

. Drgania te wzbudzane są tylko dlatego,

że na układ o częstości drgań własnych

ω

0

działa siła o innej częstości. Działanie tej

siły jakby zaburza naturalny stan dynamiczny układu, tj. drgania z częstością

ω

0

i stad

pojawia się w odpowiedzi składnik, który jest „reakcją” na to zaburzenie.

3.2.2 Drgania wymuszone układu z tłumieniem

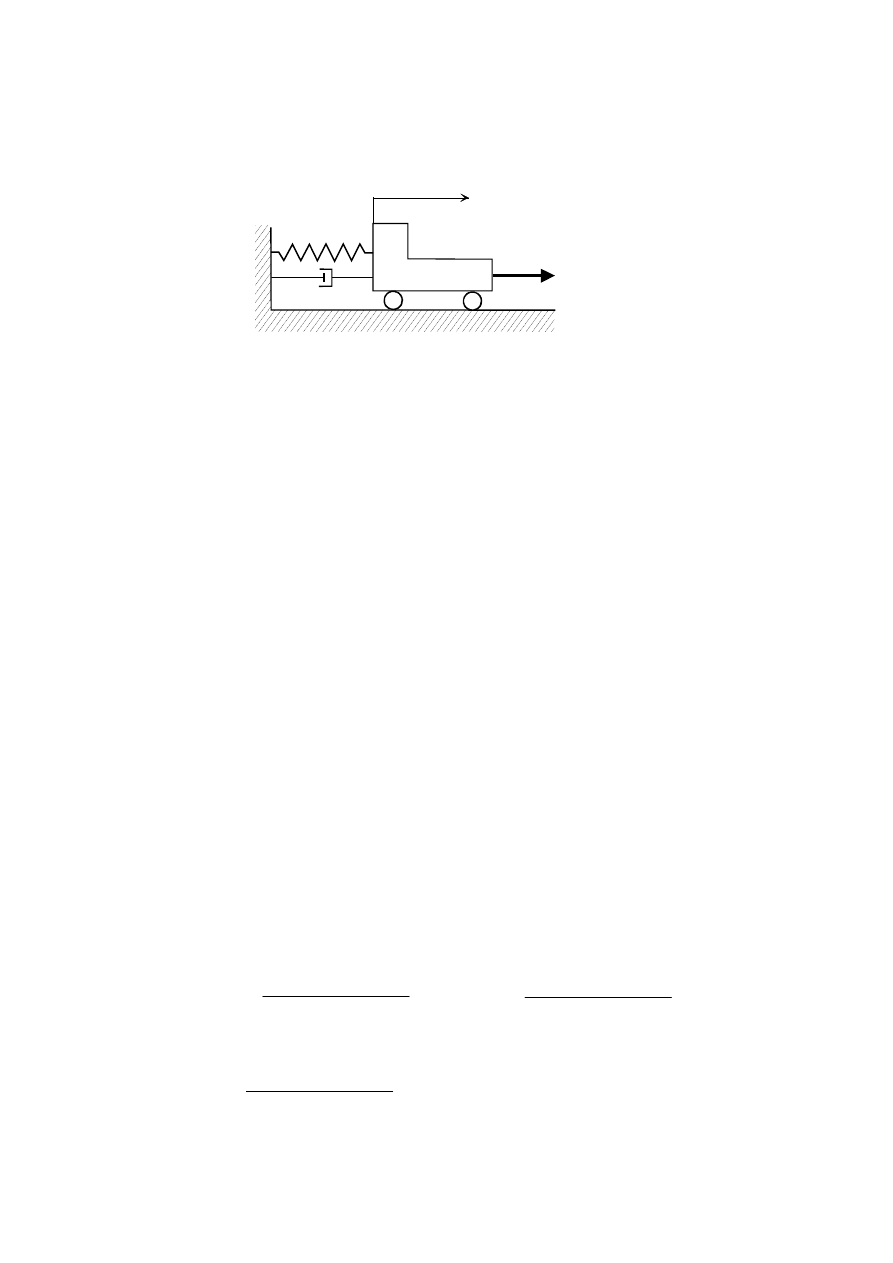
90

Rozważmy teraz drgania wymuszone siłą harmoniczną F(t) = F

0

sin

ω

t

działającą na

układ przedstawiony na rys. 3.6.

Fsin ω

m

k

c

0

t

X

Rys.3.6

Ruch tego układu opisany jest równaniem

,

t

sin

F

kx

x

c

x

m

ω

=

+

+

0

&

&&

(3.51)

które, po wprowadzeniu symbolu f

0

= F

0

/m i użyciu oznaczeń (1.6) i (3.5) można

zapisać jako

t

sin

f

x

x

h

x

ω

=

ω

+

+

0

2

0

2 &

&&

(3.52)

Rozwiązanie tego równania jest, tak jak w wypadku równania (3.39),

sumą (3.40). Tym razem mamy jednak do czynienia z układem tłumionym, zatem

składnik

x

s

(

t) rozwiązania jest funkcją zanikającą w czasie (zob. (3.27)). Składnik x

w

(

t)

reprezentujący drgania ustalone pod wpływem siły harmonicznej z czasem dominuje w

rozwiązaniu x(t), dlatego tylko ta część rozwiązania pozostanie przedmiotem dalszych

rozważań.

Jak zwykle postulujemy rozwiązania w postaci (3.41) tzn.

x

w

= A

1

sin

ω

t + A

2

cos

ω

t

W wyniku standardowej procedury dla równań różniczkowych niejednorodnych,

otrzymujemy:

0

2

1

2

2
0

f

A

h

2

A

)

(

=

ω

−

ω

−

ω

,

0

A

)

(

A

h

2

2

2

2
0

1

=

ω

−

ω

+

ω

(3.53)

z którego to układu wyznaczamy stałe A

1

i

A

2

:

2

2

2

2

2
0

2

2
0

0

1

h

4

)

(

)

(

f

A

ω

+

ω

−

ω

ω

−

ω

=

,

2

2

2

2

2
0

0

2

h

4

)

(

h

f

2

A

ω

+

ω

−

ω

ω

−

=

, (3.54)

a zatem rozwiązanie x

w

przybiera postać

[

]

t

cos

h

2

t

sin

)

(

h

4

)

(

f

x

2

2
0

2

2

2

2

2
0

0

w

ω

ω

−

ω

ω

−

ω

ω

+

ω

−

ω

=

(3.55)

91

Znak minus poprzedzający składnik z kosinusem wskazuje, że przesunięcie fazy

odpowiedzi względem wymuszenia jest ujemne, dlatego z wykorzystaniem pomysłu

zastąpienia dwu stałych A

1

i

A

2

stałymi A i

ε

(zob.p.1.2), rozwiązanie (3.55) daje się

wyrazić w postaci

(

)

x

A

t

w

=

−

sin

ω

ε

(3.56)

gdzie

2

2

2

2

2
0

0

h

4

)

(

f

A

ω

+

ω

−

ω

=

,

2

2
0

h

2

tg

arc

ω

−

ω

ω

=

ε

(3.57a,b)

Zwracamy uwagę, że tym razem kąt fazowy oznaczyliśmy inną literą (

ε

) niż uprzednio

w p.1.2 (

α

) dla podkreślenia innej przyczyny tego przesunięcia w fazie.

Zazwyczaj więcej możemy powiedzieć o wpływie tłumienia, gdy operujemy

wielkościami względnymi. Podzielmy zatem (3.57a

) przez A

s

t

. Po niezbędnych

przekształceniach z wy-korzystaniem definicji (3.5), (3.10) i (3.46) otrzymujemy

β =

2

2

2

2

st

4

)

1

(

1

A

A

ν

γ

+

ν

−

=

(3.58)

Kąt przesunięcia fazowego jako funkcja wielkości względnych

γ

oraz ν wyraża się

wzorem

2

1

2

tg

arc

ν

−

γν

=

ε

(3.59)

Wzory (3.58) i (3.59) są podstawą dwu ważnych wykresów: 1) współczynnika

rezonansu

β

w funkcji ilorazu częstości

ν

(rys.3.7), 2) kąta przesunięcia fazy

ε

w

funkcji ilorazu częstości

ν

(rys.3.8). Oba wykresy podane są dla kilku wartości

względnego współczynnika tłumienia

γ

.

92

st

A

A

=

β

0.00

2.00

4.00

0.00

2.00

4.00

γ=0

γ=0.2

γ=0.4

γ=0.8

γ=1

0

ω

ω

=

ν

Rys. 3.7

Ze wzoru (3.57a) wynika, że gdy h

≠ 0, tzn. gdy występuje tłumienie,

amplituda

A tych drgań pozostaje zawsze skończona, niezależnie od częstości

ω

siły

wymuszającej. Jednak dla małych tłumień, w warunkach, gdy częstość ta jest bliska

częstości drgań własnych

ω

0

, amplituda drgań może wielokrotnie przewyższać ugięcie

statyczne

A

s

t

.

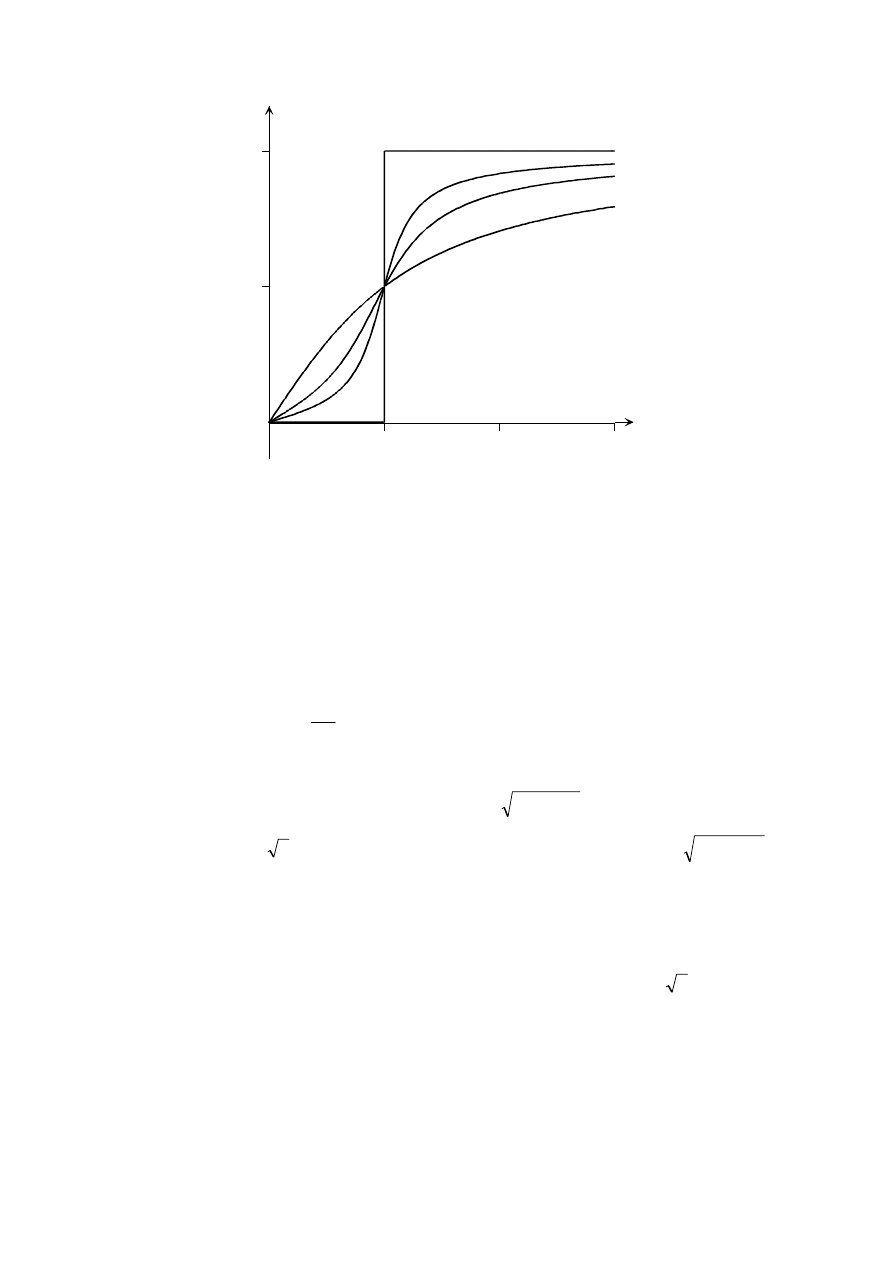
93

ε

ν

0

1

2

3

π

π/2

γ=0

γ=0.2
γ=0.4

γ=1

Rys. 3.8

Takie warunki pracy mogą być niepożądane, a nawet niebezpieczne dla

konstrukcji. Dlatego warto wiedzieć kiedy występuje maksimum amplitudy i jakie jest

jej zwielokrotnienie

β

w tym maksimum. Wyznaczmy więc ekstrema amplitudy

A

traktowanej jako funkcja częstości wymuszenia

ω

. Funkcja ta przybiera maksima, gdy

mianownik (3.57a) przybiera wartość minimalną. Zróżniczkujmy zatem wyrażenie

podpierwiastkowe ze wzoru (3.57a). Mamy

(

)

[

]

(

)

d

d

h

h

ω

ω

ω

ω

ω ω

ω

0

2

2 2

2

2

2

0

2

2

4

4

2

−

+

=

−

+

Pochodna ta jest równa zeru, gdy

ω = 0 oraz

2

2
0

h

2

−

ω

=

ω

(3.60)

Kiedy h

<

ω

0

2

/

, wówczas amplituda

A osiąga maksimum dla

ω

ω

=

−

0

2

2

2h , a

wiec dla częstości wymuszenia mniejszej od częstości drgań własnych. Tzw. pik

rezonansowy (maksimum amplitudy) pojawia się w pobliżu rezonansu dla małych

współczynników tłumienia, ale wraz ze wzrostem tłumienia coraz bardziej przesuwa się

w lewo, czyli w kierunku małych częstości wymuszenia, aż dla

h

≥ 2

0

ω

amplituda

osiąga maksimum dla

ω

= 0 i maleje wraz ze wzrostem częstości

ω

. Z tego powodu

maksimum amplitudy nie może być brane pod uwagę jako kryterium rezonansu, tj.

dostrojenia się częstości wymuszenia do częstości własnej.

94

Dla tłumień małych, tj. dla h <

ω

0

2

/

występuje jednostronne minimum lokalne

dla

ω

=

0. Wówczas A = A

st

. Ale nie oznacza to, że w tym punkcie wartość amplitudy

jest najmniejsza. Jak to widać z wykresu na rys. 3.7 dla dużych częstości

ω amplituda

zmierza do zera. Po podstawieniu

ω

ω

=

−

0

2

2

2h , czyli częstości odpowiadającej

maksimum, do (3.57a) otrzymujemy wzór na amplitudę maksymalną

2

2
0

0

max

h

hm

2

F

A

−

ω

=

(3.61)

Analogicznie, wyznaczając minimum mianownika wzoru (3.58), można określić

maksymalną wartość współczynnika wzmocnienia dynamicznego. Mamy

2

1

2

1

γ

−

γ

=

β

max

(3.62)

Zwróćmy jeszcze uwagę na prosty związek między współczynnikiem

β

a

stopniem tłumienia

γ

zachodzący w warunkach rezonansu, czyli dla

ν

= 1. Z (3.58)

mamy wówczas

β

γ

ν=

=

1

1

2

(3.63)

Zależność ta może być podstawą identyfikacji tłumienia układu drgającego.

Spójrzmy teraz na rys. 3.8. Widzimy, że bez względu na tłumienie dla

rezonansu, tj. gdy

ω

=

ω

0

, opóźnienie fazy wychylenia

x względem siły F(t) jest

π

/2.

Wynika stąd, że przesunięcie fazy jest dobrym kryterium dla doświadczalnego

wyznaczenia rezonansu.

3.2.3 Rezonans i dudnienie

Rezonans. W zakończeniu p.1.2 poznaliśmy pojęcie rezonansu jako zjawiska

zwielokrotnienia amplitudy drgań wymuszonych oscylatora pozbawionego tłumienia

pod działaniem siły okresowej o częstości równej częstości własnej oscylatora. Takie

pojmowanie rezonansu, jakkolwiek precyzyjne, jest zbyt wąskie. W żargonie

technicznym jak i w literaturze przedmiotu spotykamy szersze, ale też nieco rozmyte

pojmowanie rezonansu. Otóż rezonansem nazywamy zjawisko wzmocnienia amplitudy

drgań wymuszonych w stanie ustalonym dowolnych układów rzeczywistych (a więc z

tłumieniem i o dowolnej liczbie stopni swobody), co ma miejsce wtedy, gdy częstość

wymuszenia jest dostatecznie bliska częstości własnej układu.

95

W

układach modelowych (pozbawionych tłumienia) przy częstości wymuszenia

ω

=

ω

0

, amplituda rośnie do nieskończoności, w układach z tłumieniem amplituda

pozostaje skończona i jest tym mniejsza im większe jest tłumienie układu.

Dysponując wzorem (3.60) lub choćby wykresem z rys.3.7 łatwo zauważyć, że

maksimum amplitudy w układach tłumionych przypada dla częstości mniejszych od

częstości własnej. Jeśli więc częstość rezonansową zdefiniujemy jako odpowiadającą

maksimum amplitudy drgań wymuszonych, to dla układów rzeczywistych (czyli z

tłumieniem) jest ona mniejsza od częstości własnej i zmienia się w zależności od

stopnia tłumienia układu. Widzimy więc, że przy takim pojmowaniu pojęcia rezonans

zatraca ono swą precyzję.

Jak wygląda zjawisko narastania drgań w warunkach rezonansu? Sprawę tę

wyjaśnimy dla modelu bez tłumienia. Zauważmy najpierw, że nie możemy posłużyć się

rozwiązaniem (3.44), bo w warunkach rezonansu,

czyli dla

ω

=

ω

0

, traci ono ważność.

Zgodnie z teorią równań różniczkowych zwyczajnych rozwiązania poszukujemy wtedy

w postaci:

x

At

t

w

=

cos

ω

0

(3.64)

Po podstawieniu (3.64) do równania (3.39) otrzymujemy

t

sin

F

t

cos

kAt

t

cos

Amt

t

sin

Am

0

0

0

0

2

0

0

0

2

ω

=

ω

+

ω

ω

−

ω

ω

−

skąd po uwzględnieniu, że m

ω

0

2

=

k otrzymujemy

0

0

m

2

/

F

A

ω

−

=

(3.65)

Pełne rozwiązanie przybiera więc postać:

t

cos

t

m

F

t

sin

C

t

cos

C

x

0

0

0

0

2

0

1

2

ω

ω

−

ω

+

ω

=

(3.66)

Ostatni wyraz przedstawia drgania o nieskończenie rosnącej amplitudzie. Charakter

rozwiązania w warunkach rezonansu pokazuje rys. 3.9.

96

x

t

Rys.

3.9

Dudnienia. Przedyskutujmy teraz przypadek szczególny drgań wymuszonych układu

bez tłumienia. Niech na układ pozostający w spoczynku zacznie działać siła

harmonicznie zmienna o częstości

ω

mało różniącej się od częstości

ω

0

układu.

Wówczas równanie (3.50) można zapisać w postaci

( )

(

)

t

sin

t

sin

k

F

t

x

0

0

ω

ν

−

ω

β

=

(3.67)

Skoro

ω

≈

ω

0

, to

ν

≈ 1,

ω

+

ω

0

≈ 2

ω

0

, zaś różnica częstości

ω

0

−

ω

jest wielkością

małą, którą oznaczymy 2

α,

czyli

ω

0

−

ω

= 2a. Współczynnik

β

może być teraz

wyrażony jako:

(

)(

)

α

ω

=

α

ω

ω

≈

ω

−

ω

ω

+

ω

ω

=

ω

−

ω

ω

=

ν

−

=

β

4

4

1

1

0

0

2

0

0

0

2

0

2

2

0

2

0

2

zaś rozwiązanie (3.50) przybiera wtedy postać:

( )

(

)

t

sin

t

cos

k

F

t

sin

t

sin

k

F

t

x

α

⎟

⎠

⎞

⎜

⎝

⎛

ω

α

ω

=

ω

−

ω

α

ω

=

2

4

0

0

0

0

0

(3.68)

Ruch opisany równaniem (3.68) nosi nazwę dudnień i może być interpretowany jako

drgania z częstością

ω

, których amplituda zmienia się powoli tak jak funkcja sin

α

t,

której okres

2

π

/

α

jest duży w porównaniu z okresem funkcji cos

ω

t, czyli 2

π/ω

.

Charakter ruchu obrazuje rys 3.10

97

0.00

1.00

2.00

3.00

4.00

5.00

-0.80

-0.40

0.00

0.40

0.80

Rys. 3.10

Dudnienia niektórych urządzeń technicznych, np. generatorów lub turbin są słyszalne

i na ogół nie wywołują przyjemnych wrażeń.

3.3 TEN PODROZDZIAŁ OPUSZCZAMY

3.4 DRGANIA WYMUSZONE KINEMATYCZNIE

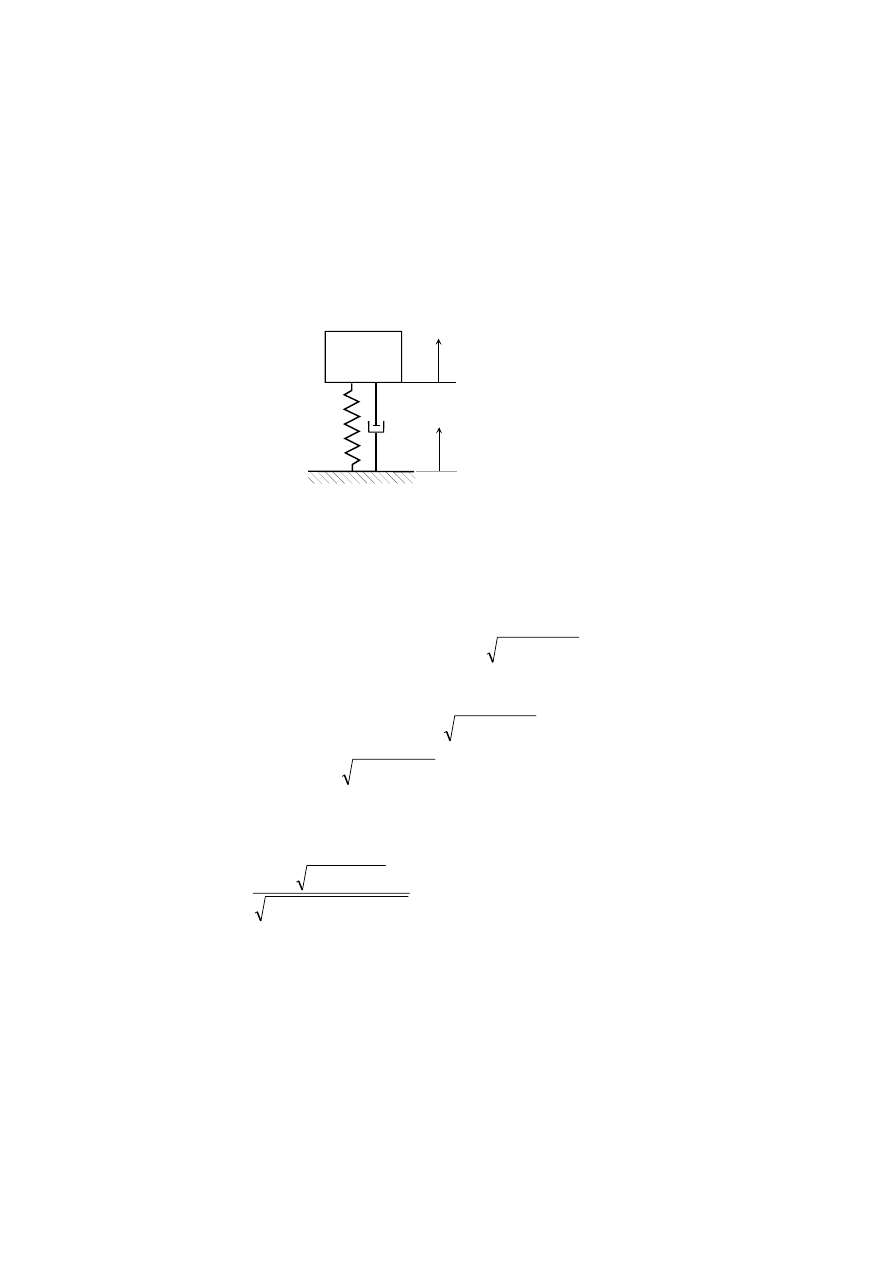
98

Wymuszeniem kinematycznym nazywać będziemy takie oddziaływanie z zewnątrz na

układ, które przejawia się zadanym (wymuszonym) ruchem wybranego punktu lub

zespołu układu. Rozważymy dwa przypadki tego rodzaju wymuszenia.

3.4.1 Wymuszenie ruchem harmonicznym punktu zamocowania sprężyny

Weźmy pod uwagę układ z rys. 3.17, którego podstawa porusza zgodnie z równaniem:

y

y

t

=

0

sin

ω

(3.87)

x

y = y

0

sin t

k

c

m

ω

Rys.3.17

Równanie ruchu masy ma zatem postać

(

) (

)

mx

c x y

k x y

&&

& &

= −

−

−

−

, czyli

mx cx kx cy ky

&&

&

&

+

+

=

+

(3.88)

Ale na podstawie (3.87) i po zabiegach analogicznych jak w p.1.2 otrzymujemy

( )

(

)

cy ky cy

t ky

t

y

k

c

t

&

cos

sin

sin

+

=

+

=

+

+

0

0

0

2

2

ω

ω

ω

ω

ω

α

(3.89)

gdzie )

k

/

c

(

tg

arc

ω

=

α

. Równanie ruchu ma zatem postać

( )

(

)

mx cx kx

y

k

c

t

&&

&

sin

+

+

=

+

+

0

2

2

ω

ω

α

(3.90)

Utożsamiając wielkość

( )

y

k

c

0

2

2

+

ω

z amplitudą

F

0

z równania (3.51) możemy też

wykorzystać jego rozwiązanie (3.56) wraz z (3.57a,b). Z porównania otrzymujemy

zatem

(

)

(

)

α

+

ε

−

ω

=

α

+

ε

−

ω

ω

+

ω

−

ω

+

=

t

sin

x

t

sin

)

c

(

)

m

k

(

)

c

(

k

y

)

t

(

x

0

2

2

2

2

2

0

(3.91)

Na podstawie (3.91) można wyznaczyć stosunek amplitudy

x

0

odpowiedzi

x(t) do

amplitudy wymuszenia kinematycznego

y

0

. Iloraz

x

0

/

y

0

nazywany jest

kinematycznym

współczynnikiem przenoszenia lub zdolnością przenoszenia ruchu i można go wyrazić

zarówno za pomocą wielkości wymiarowych

m, c, k i

ω

jak i wielkości

bezwymiarowych

γ

i

ν

(zob. (3.46)). Mamy:

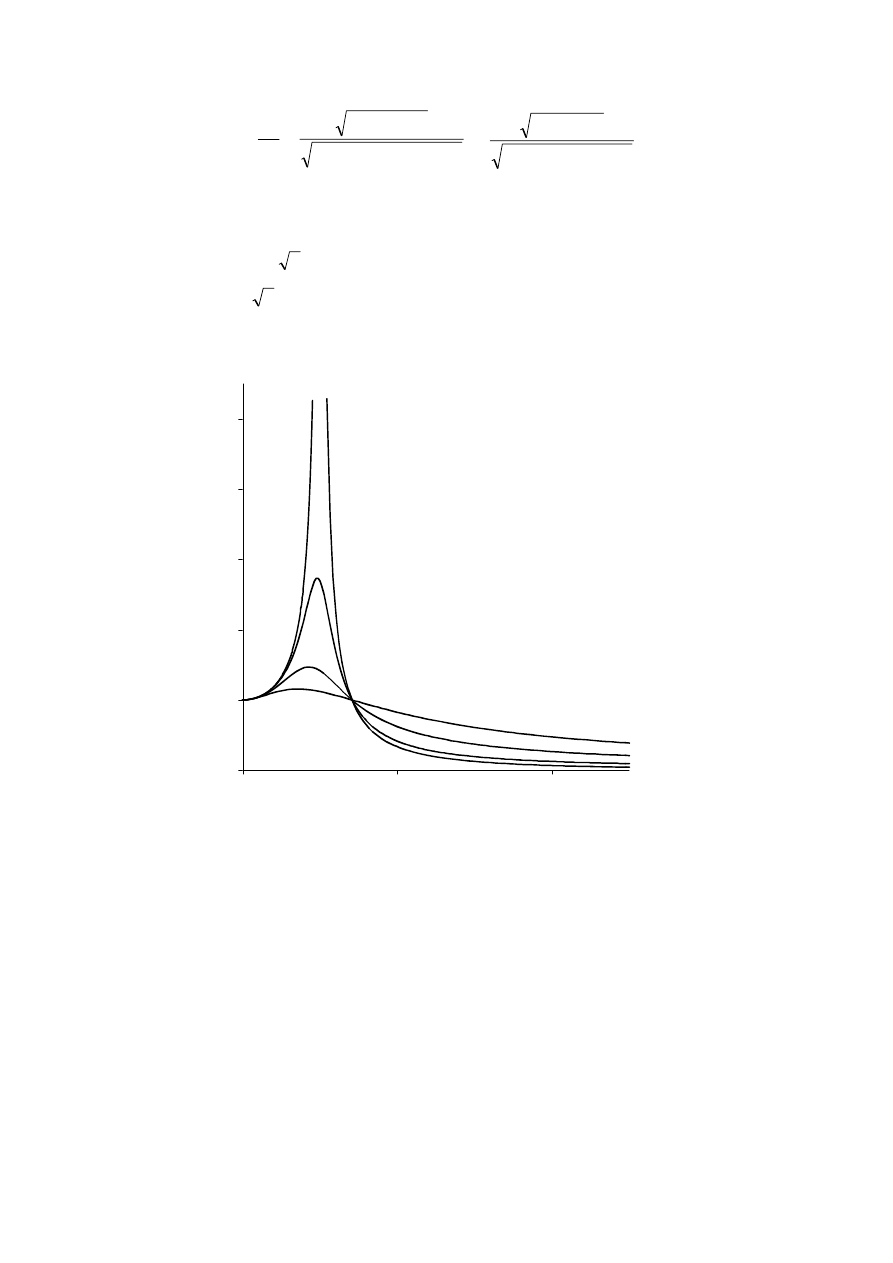
99

( )

x
y

k

c

k m

c

0

0

2

2

2 2

2

=

+

−

+

ω

ω

ω

(

)

(

)

2

2

2

2

)

2

(

)

1

(

)

2

(

1

γν

+

ν

−

γν

+

=

(3.92)

Na rys. 3.18 przedstawiony jest wykres kinematycznego współczynnika przenoszenia

dla różnych współczynników tłumienia

γ

. Pokazuje on, że o ile w zakresie wymuszeń o

częstościach

ω ≤

2

ω

0

tłumienie w układzie powoduje zmniejszenie amplitudy drgań,

o tyle dla

ω >

2

ω

0

tłumienie przyczynia się do zwiększenia amplitudy x

0

odpowiedzi.

Projektując zatem układy wibroizolacji musimy, w zależności od celu i zakresu

częstości wymuszeń, odpowiednio dobierać tłumienie układu.

0.00

2.00

4.00

0.00

1.00

2.00

3.00

4.00

5.00

γ = 0

γ = 0.2

γ = 0

γ = 0.5

γ = 1

Rys

.3.18

3.4.2 Wymuszenie bezwładnościowe (ruchem obrotowym masy niewyważonej)

W licznych maszynach występują pojedyncze elementy lub podzespoły wirujące.

Jednym z przejawów ich niewyważenia jest niewłaściwe położenie środka masy takiego

elementu, jak np. wał lub koło zębate. Tę sytuację możemy zobrazować w sposób

pokazany na rys. 3.19.

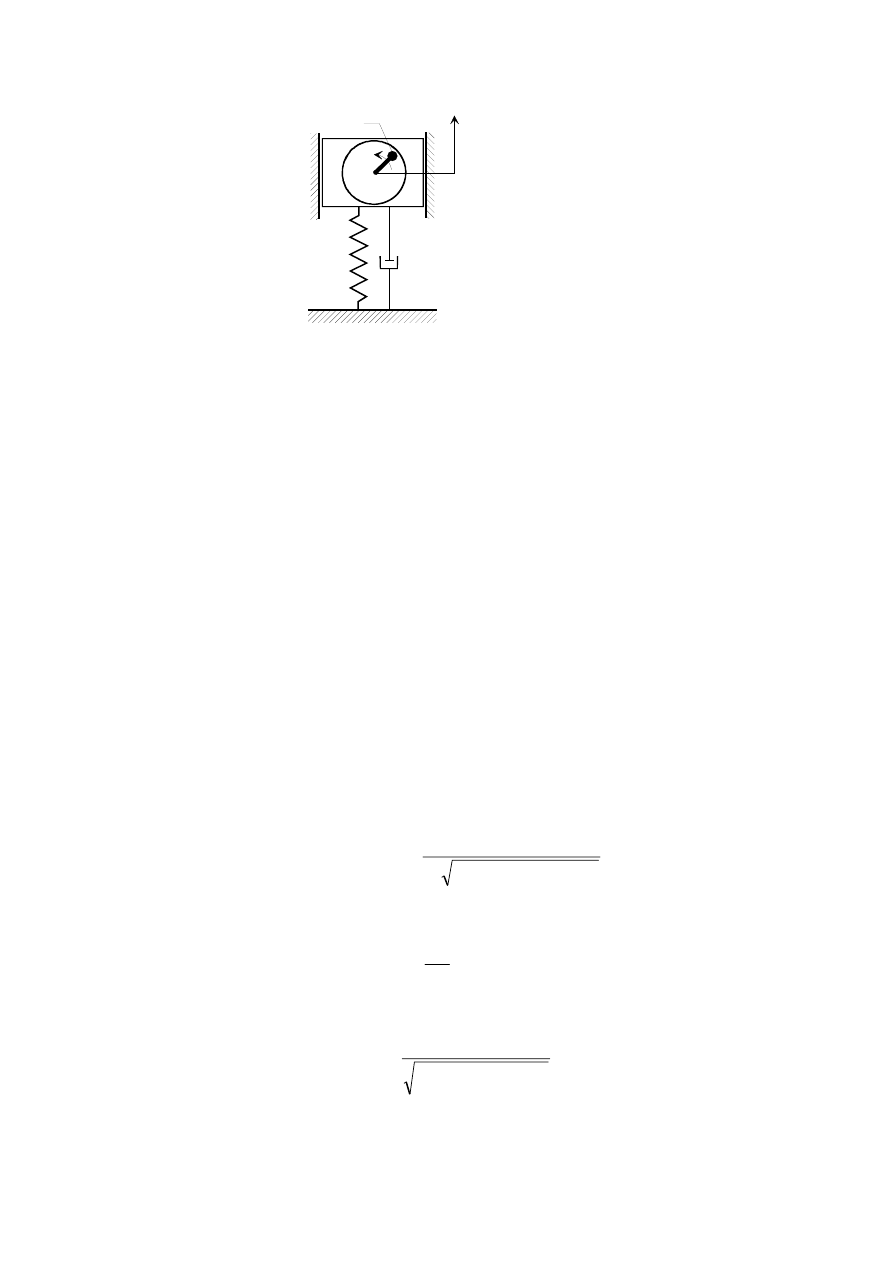
100

x

e

m

k

c

Μ

0

ω

Rys. 3.19

Maszyna o całkowitej masie

M jest podparta na elementach sprężystych o sztywności k

i tłumiku o współczynniku tłumienia wiskotycznego

c. Niejednorodność materiałowa

części wirujących przejawia się w mimośrodowym położeniu masy

m. Wartość

mimośrodu jest

e, a prędkość kątowa części wirujących jest

ω

.

Przemieszczenie masy

m w kierunku pionowym wyraża się więc

wzorem

x

x e

t

m

= + sin

ω

, skąd

&&

&&

sin

x

x

e

t

m

= − ω

ω

2

(3.93)

Równanie ruchu korpusu maszyny (bez wirującej masy

m) ma więc postać;

(

)

M m x mx

cx kx

m

−

+

= − −

&&

&&

&

(3.94)

Po podstawieniu (3.93) do (3.94) i uporządkowaniu otrzymujemy równanie:

Mx cx kx

me

t

&&

&

sin

+

+

=

ω

ω

2

(3.95)

które przypomina (3.51). Utożsamiając

F

0

z równania (3.51) z

me

ω

2

możemy

zaadoptować wyniki uzyskane w p. 3.2.2. W szczególności drgania ustalone mają

postać

( )

(

)

ε

−

ω

ω

+

ω

−

ω

ω

=

t

sin

h

4

)

(

M

me

t

x

2

2

2

2

2
0

2

w

(3.96)

gdzie

ω

0

2

=

k/M. Rozwiązanie (3.97) może być wyrażone w następujący zwięzły sposób

( )

(

)

x t

me

M

t

w

r

=

−

β

ω

ε

sin

(3.97)

gdzie

β

r

jest współczynnikiem zwielokrotnienia amplitudy, który tym razem ma postać:

(

)

( )

β

ν

ν

νγ

r

=

−

+

2

2 2

2

1

2

(3.98)

Wykres

β

r

dla różnych tłumień

γ

pokazany jest na rys. 3.20.