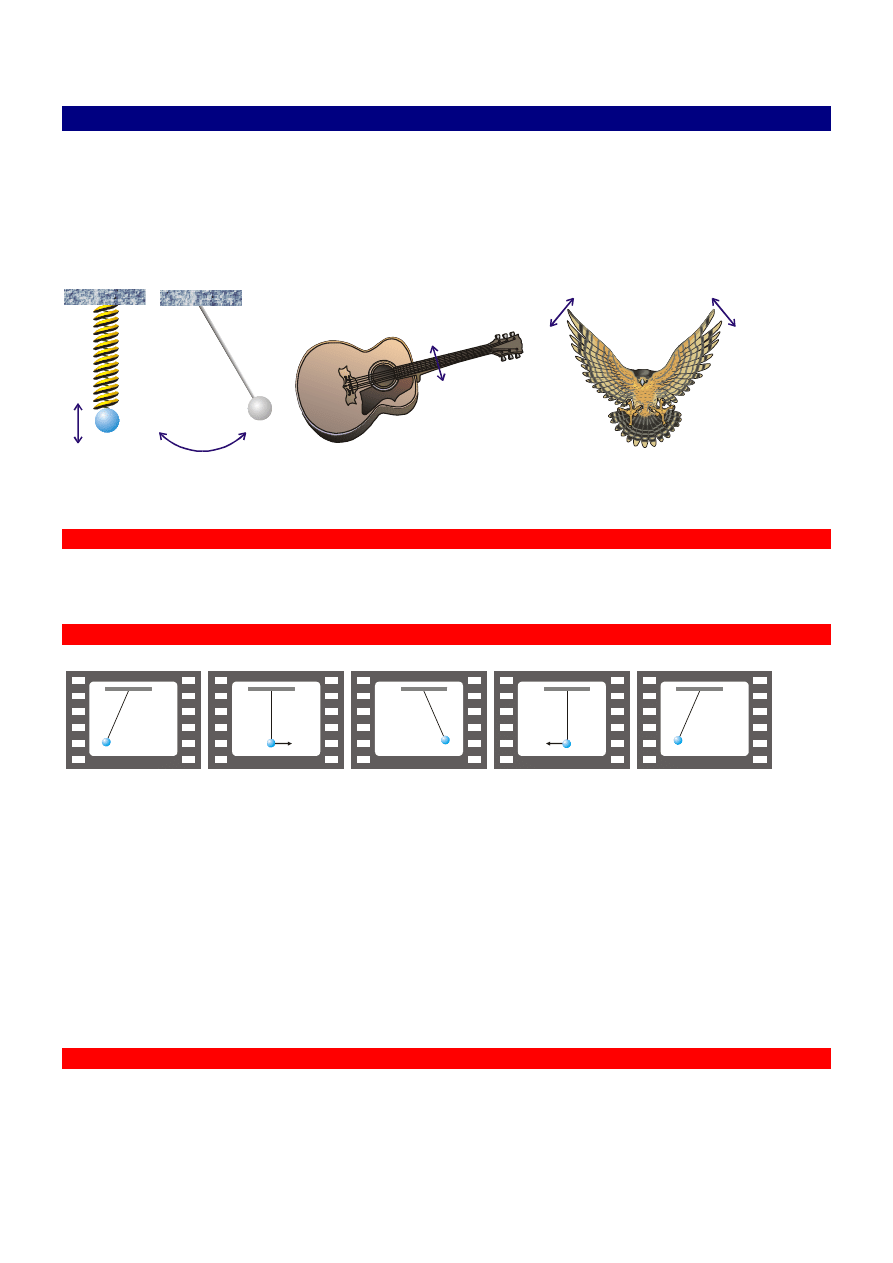
Drgania.
Ruch drgający jest chyba najczęściej występującym w przyrodzie i technice ruchem. Nie wierzysz? Chcesz przy-
kładów? Proszę bardzo. Wahadło starego zegara, metalowa kulka zawieszona na sprężynce, struna gitary, powie-
trze w piszczałce organowej – to wszystko drga. Jeszcze? Most, po którym jadą samochody, szyby w Twoim domu,
gdy ulicą przejeżdża ciężarówka, ziemia podczas trzęsienia, gwiazdy pulsujące (to też drgania tylko powolne),
Twoje serce. Są jeszcze inne drgania. Prądy w telewizorze, radiu, komputerze, elektrony w atomie emitującym
światło, pole elektromagnetyczne w samym świetle. Przykładów można podać bardzo, bardzo wiele.
Czy już mi wierzysz, że drgania występują bardzo powszechnie? Skoro tak jest, to może warto byłoby się czegoś o
nich dowiedzieć?
1. Jak można scharakteryzować ruch drgający?
–
Ruch drgający odbywa się tam i z powrotem po tym samym torze
–
Położenia drgającego ciała powtarzają się okresowo
2. Jakie są przemiany energii w drganiach?
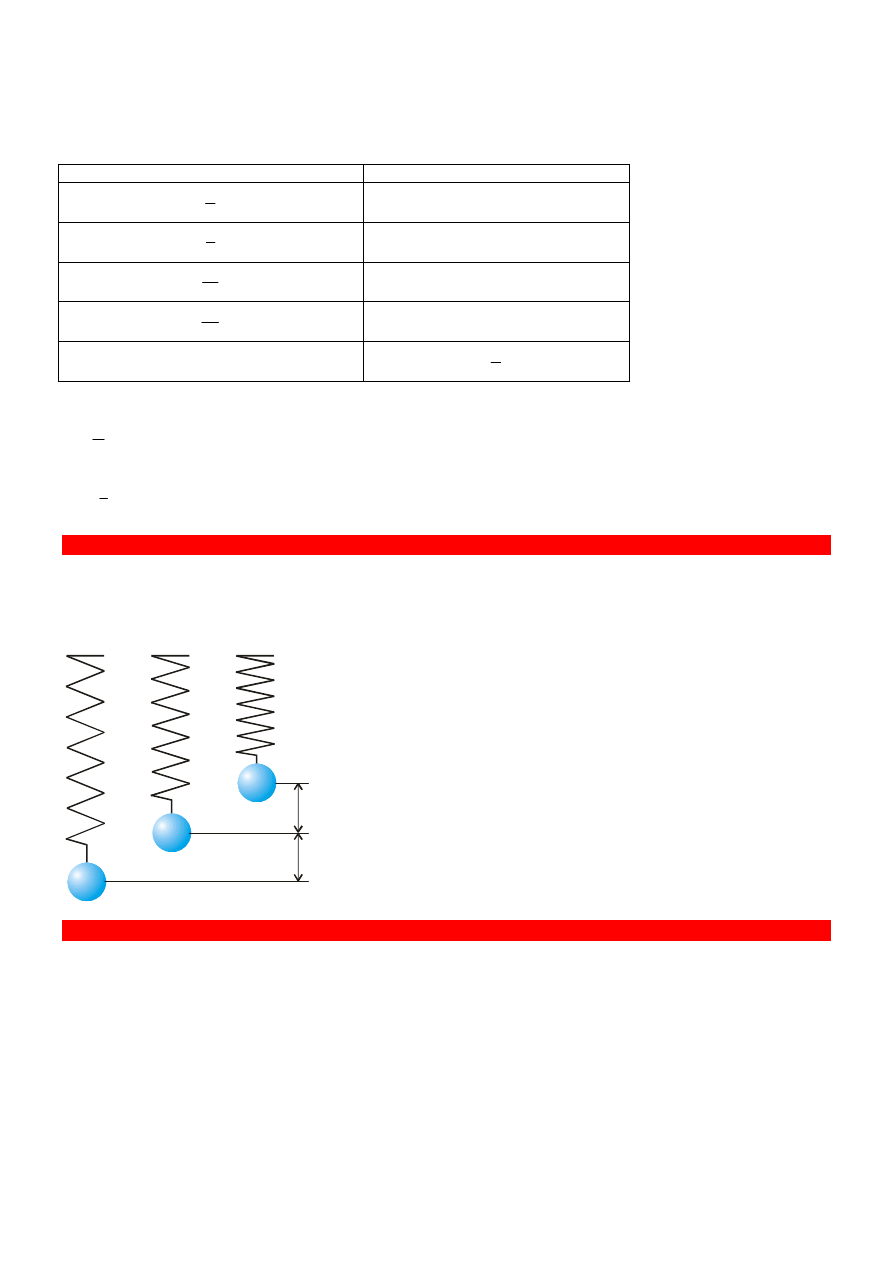
Wyobraź sobie, że puszczasz w ruch wahadełko. Na rysunku widzisz klatki filmowe z kolejnymi stadiami ruchu
wahadełka. Na pierwszej widzimy maksymalnie wychylone wahadełko o zerowej prędkości. Zatem jego energia
kinetyczna jest równa zeru. A co z energią potencjalną? Ma ona największą wartość, jako że kulka jest na maksy-
malnej wysokości. Następnie kulka opada i nabiera prędkości; rozpędza się. Jej energia potencjalna maleje, a kine-
tyczna rośnie. Tak jest do chwili, w której kulka zajmie najniższe położenie. To położenie nosi nazwę położenia
równowagi, bo gdybyśmy kulki nie wprawili w ruch, to tkwiłaby tam w bezruchu. Właśnie tam energia kinetycz-
na osiąga swą największą wartość, a energia potencjalna najmniejszą. Po przekroczeniu położenia równowagi
energia potencjalna wahadła zaczyna rosnąć, zaś kinetyczna maleć. Na trzeciej klatce znów widzimy wahadełko w
stanie maksymalnego wychylenia, tyle że w drugą stronę. Znów energia potencjalna jest największa, a energia
kinetyczna zerowa. Kulka zaczyna wracać zwiększając swą energię kinetyczną, która największą wartość osiąga w
położeniu równowagi. Po wykonaniu pełnego drgania kulka wraca do punktu wyjścia. Widzimy, że następują w
czasie drgań nieustanne przemiany energii potencjalnej w kinetyczną i na odwrót.
3. Co to jest okres drgań? Co to jest częstotliwość?
Czas, po którym ciało drgające wykona jedno pełne drganie nazywamy okresem drgań. Jest to inaczej mówiąc
czas, jaki upływa między sytuacją pokazaną na pierwszej i piątej klatce. Tę wielkość zwykle oznaczamy literą T.
Częstotliwość to liczba drgań wykonanych w ciągu jednostki czasu, np. sekundy. Oznaczymy tę wielkość f. Jak
częstotliwość ma się do okresu drgań? Popatrz w tabelkę.
Okres drgań, czyli jak długo trwa jedno drganie
Częstotliwość, czyli ile drgań na sekundę
2
1
2
3
1
3
10
1
10
50
1
50
2
2
1
Czy zauważasz tu jakąś prawidłowość? Tak! Częstotliwość jest odwrotnością okresu drgań.
T
f
1
=
Częstotliwość mierzymy w odwrotnościach sekundy. Ta jednostka ma swoją nazwę – herc (skrót – Hz).
[ ]
Hz
s
1
=
=
f
4. Czym jest amplituda drgań?
Amplituda to maksymalne wychylenie z położenia równowagi. Na rysunku widzisz kulkę drgającą na sprężynie
w trzech położeniach. Odległości między położeniami skrajnymi a środkowym to właśnie amplituda. Oznaczamy
ją literą A.
położenie równowagi
maksymalne wychylenie
maksymalne wychylenie
amplituda A
amplituda A
5. Co to jest wahadło matematyczne? Jak obliczyć okres jego drgań?
Jeśli niewielką kulkę zawiesisz na nici, otrzymasz wahadło. Takie wahadło nazywamy matematycznym.
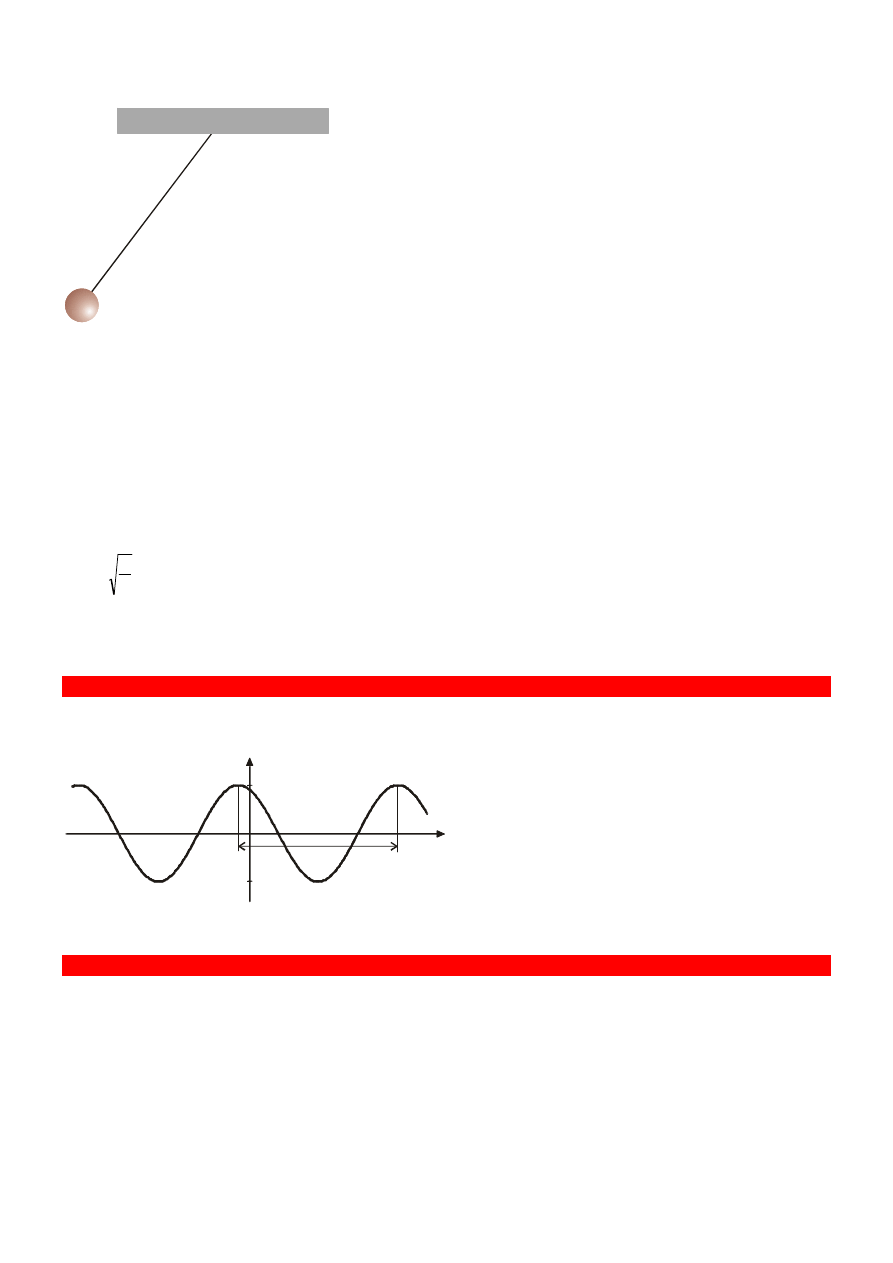
Od czego zależy okres drgań tego wahadła. Zrób doświadczenie: zawieś mały ciężarek najpierw na krótkiej, a
później na długiej nitce. Co obserwujesz? Okres drgań wydłuża się, gdy bierzesz coraz dłuższą nitkę. Jeśli zmienisz
ciężarek na inny (np. o większej masie) zmiany okresu drgań nie zauważysz. Z tego można wysnuć wniosek, że
okres drgań wahadła zależy od jego długości, a nie zależy od masy ciężarka. Na Księżycu to samo wahadło drga-
łoby inaczej – okres jego drgań wydłużyłby się. Zależy on jeszcze od przyspieszenia grawitacyjnego. Tego do-
świadczenia raczej nie zrobisz – nie słyszałem, by jakiś gimnazjalista wybierał się w najbliższym czasie na Księżyc.
Księżyc można jednak zastąpić przyspieszającą lub hamującą windą. W windzie ruszającej z przyspieszeniem do
góry (w której waga łazienkowa wskazałaby zwiększony ciężar) okres wahadła byłby krótszy. A jak dokładnie
wygląda zależność okresu wahadła matematycznego od jego długości i przyspieszenia grawitacyjnego (na Ziemi –
ziemskiego)?
g
l
T
π
2
=
, gdzie
l
– długość wahadła
g
– przyspieszenie ziemskie (na Ziemi, bo na innych planetach nazywa się ono inaczej – ogólnie, jest to przyspie-
szenie grawitacyjne)
6. Jak wygląda zależność wychylenia drgającego ciała od czasu?
Może wyglądać różnie. Wykres zależności położenia od czasu dla najprostszego drgania zwanego harmonicznym
wygląda jak na rysunku
T
t
x
A
- A
Tak jest tylko wtedy, gdy nie ma żadnych oporów ruchu (co się nie zdarza) lub, gdy uzupełniamy traconą (tzn. zmienianą w
energię wewnętrzną) energię mechaniczną wahadła.
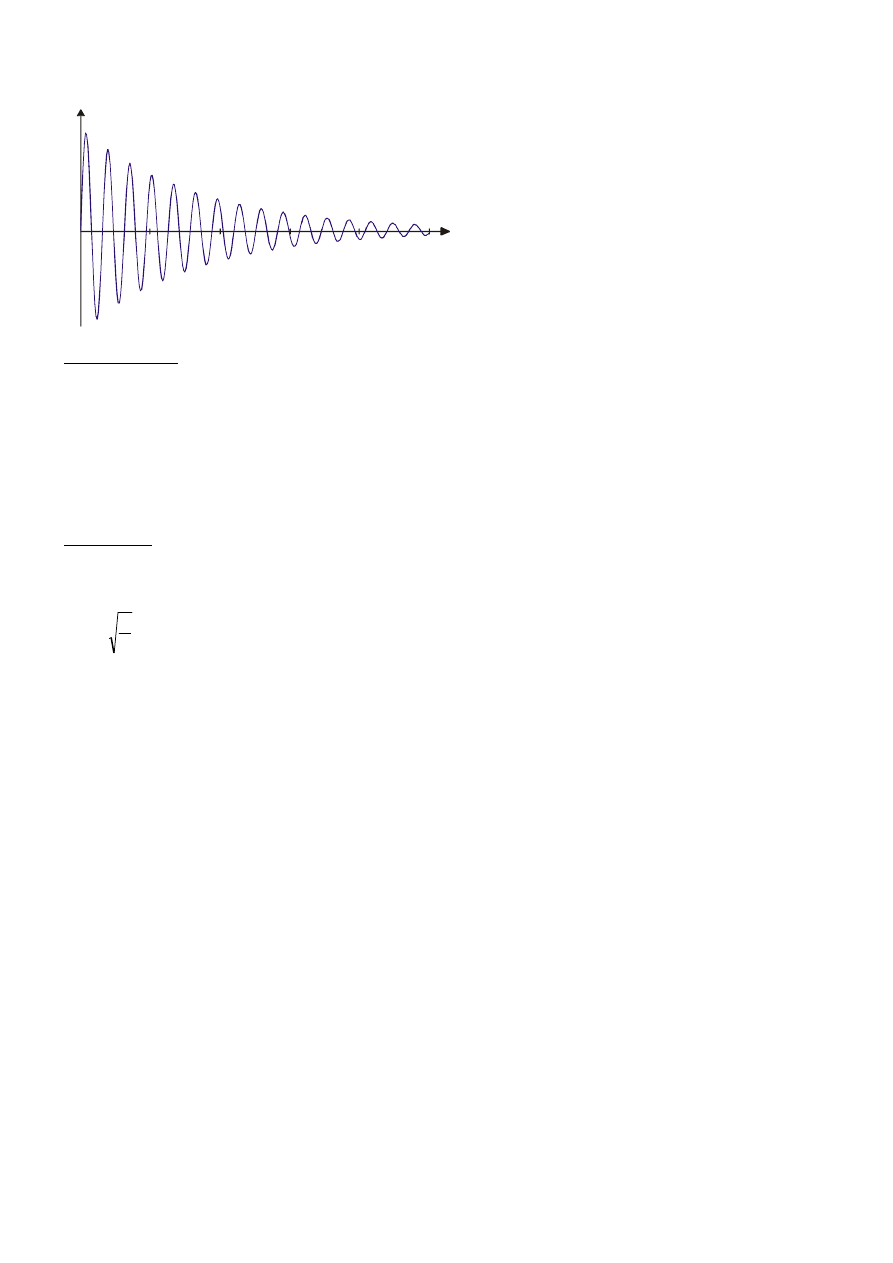
7. Co dzieje się z amplitudą drgań, gdy działa siła oporu?
Amplituda drgań będzie coraz mniejsza. Takie drgania nazywamy tłumionymi.
x
t
Czas na zadanie.
Kasia wyjeżdża do eksperymentalnego miasteczka na Księżycu. Bierze ze sobą swój ulubiony zegar wahadłowy –
pamiątkę po pradziadku, który żył bardzo dawno, bo w XX wieku. Okazało się, że
A) Zegar przestał chodzić
B) Zegar chodzi równie dobrze jak na Ziemi
C) Zegar spieszy się
D) Zegar się późni.
Rozwiązanie
Mowa jest o zegarze wahadłowym, w którym elementem odmierzającym czas jest wahadło. Jak będzie się ono
zachowywać na Księżycu? Co można powiedzieć o okresie jego drgań? Znamy wzór na okres.
g
l
T
π
2
=
W mianowniku pod pierwiastkiem jest przyspieszenie grawitacyjne, które na Księżycu jest ok. 6 razy mniejsze niż
na Ziemi. Skoro mianownik ułamka zmniejszy się, to sam ułamek wzrośnie, z czego mamy wniosek, że okres
drgań wahadła będzie dłuższy. Wahadło będzie wolniejsze, więc wolniej będzie odmierzało czas. Zegar będzie się
późnił.
©
Sławomir Jemielity