Teoria

mnogości

Zbiory

A, B, C

....

x  X

x jest elementem X

x  X

x nie jest elementem

X

Uniwersum

U

Zbiór pusty

, 0

Oznaczenia

zbiorów

{ 1, 3, 4, 6, 7 }

{ ( 1, 2 ), ( 3, 4 ), ( 6, 7 )}

{ 1, 2, 3, 4, 5, 6, 7............} = N

{ x: x  R  1 x < 3 }

{ x: x  N  x = 2n }

{ x: x  N  x = n

2

} = { n

2

: n  N }

= { 1, 4, 9, 16 ........}

{ 1 }

{ }

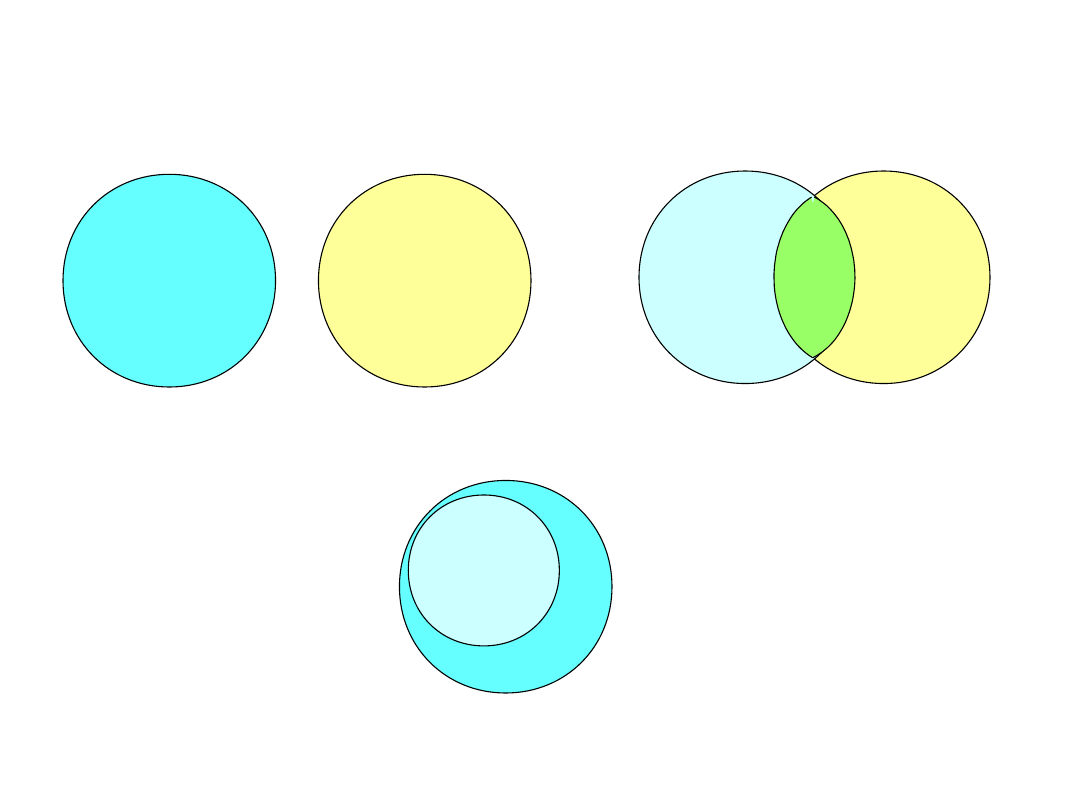
Diagramy Venna

Koła Eulera

B

A

B

A

A

B

Suma zbiorów

A  B

A plus B,

A +

B

Iloczyn zbiorów A  B

A razy B

A •

B

Iloczyn kart.

A  B

Różnica zbiorów A  B

A minus B A \ B

Różnica

A ÷ B

A Δ B
symetryczna

Inkluzja zbiorów A  B

A zawiera się w

B

Działania na zbiorach

Negacja

– A

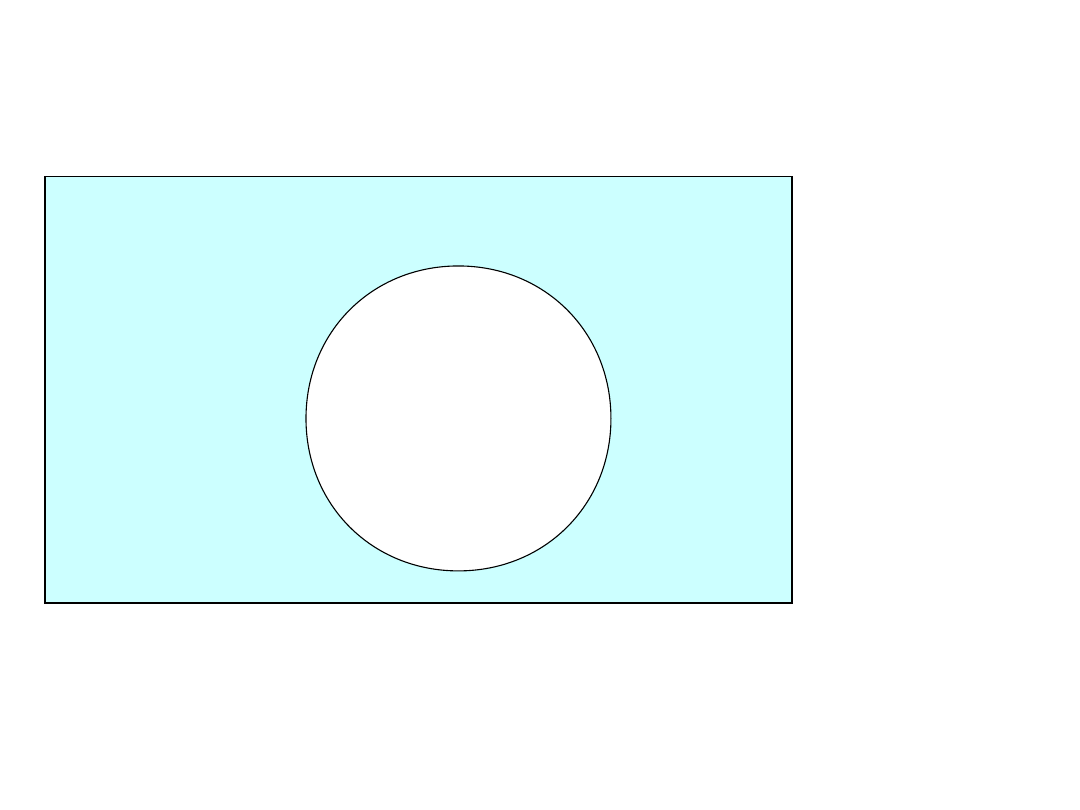
-A

A

Dopełnienie -

uzupełnienie

uniwersum

przestrzeń

A  – A =



A  – A = U

– ( – A ) =
A

– U = 

–  = U

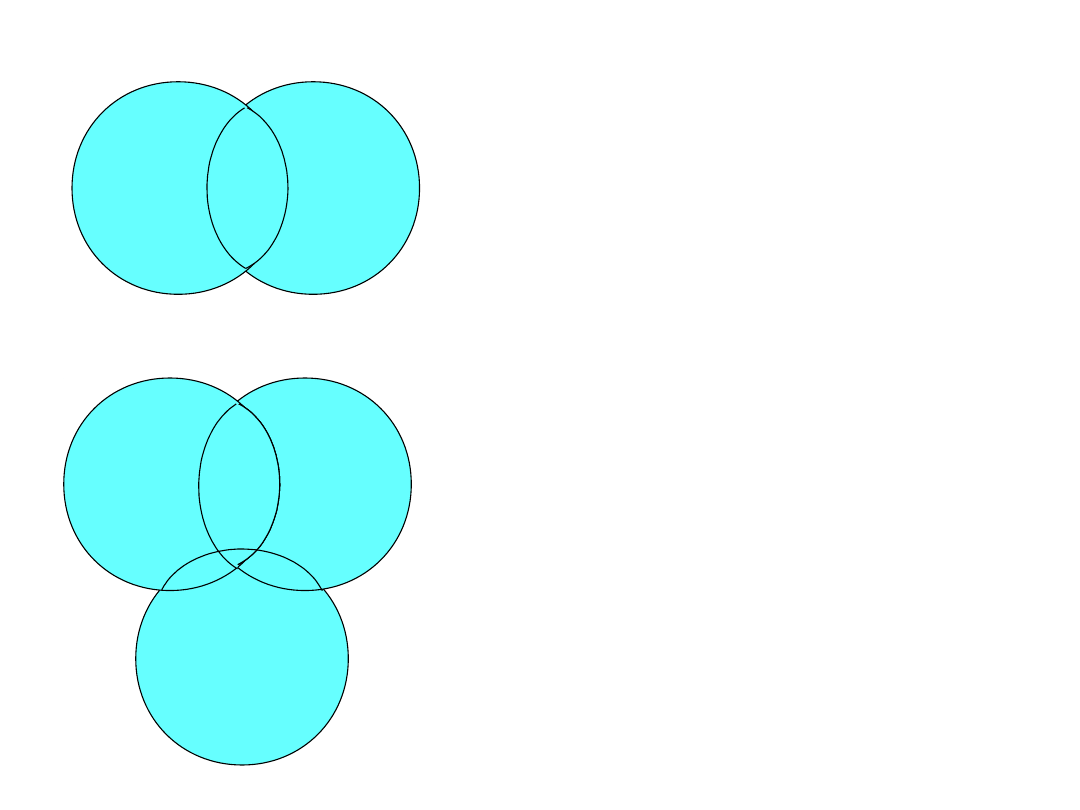
Suma zbiorów

A  B

A  B = B 

A

A  A = A

{ x 

A  B } 

{ x  A v x

 B

}

( A  B)  C = A  ( B 

C )

0  A = A

A

B

A

B

C

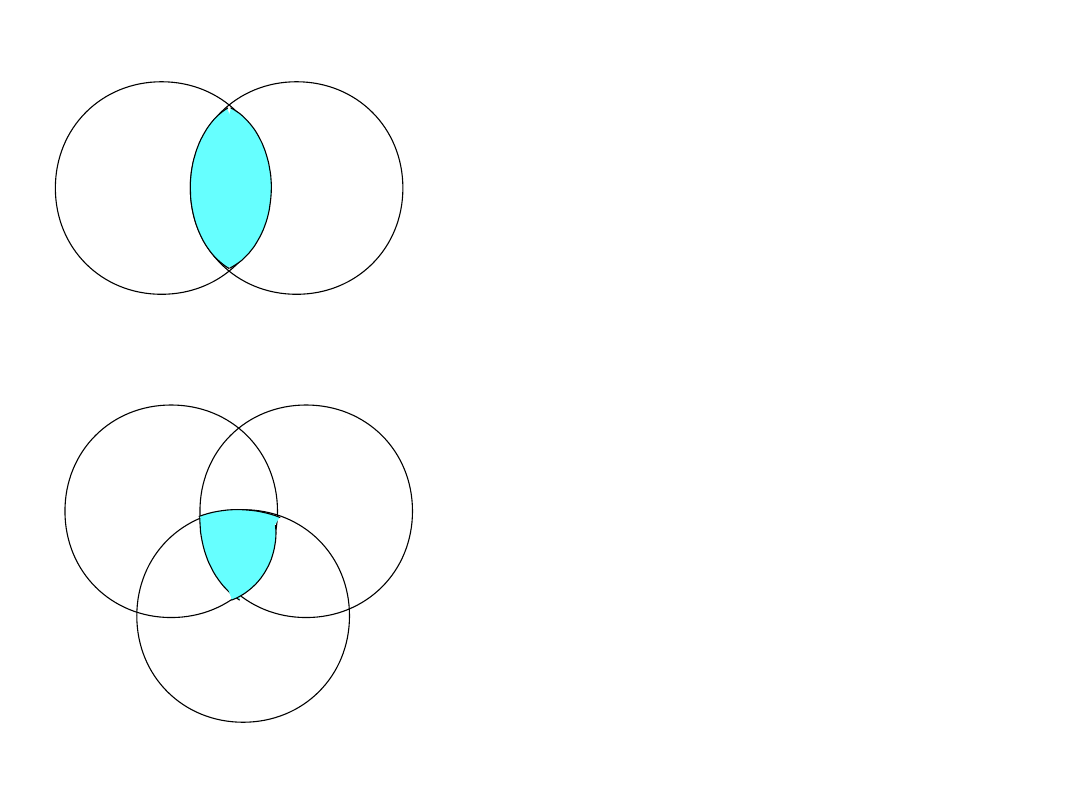
A  B = B  A przemienność

Iloczyn zbiorów

A  B

( A  B)  C = A  ( B 

C )

łączność

A



A = A

0



A = 0

{ x 

A  B } 

{ x  A  x

 B

}

B

A

B

A

C

A



B  B

A



B  A

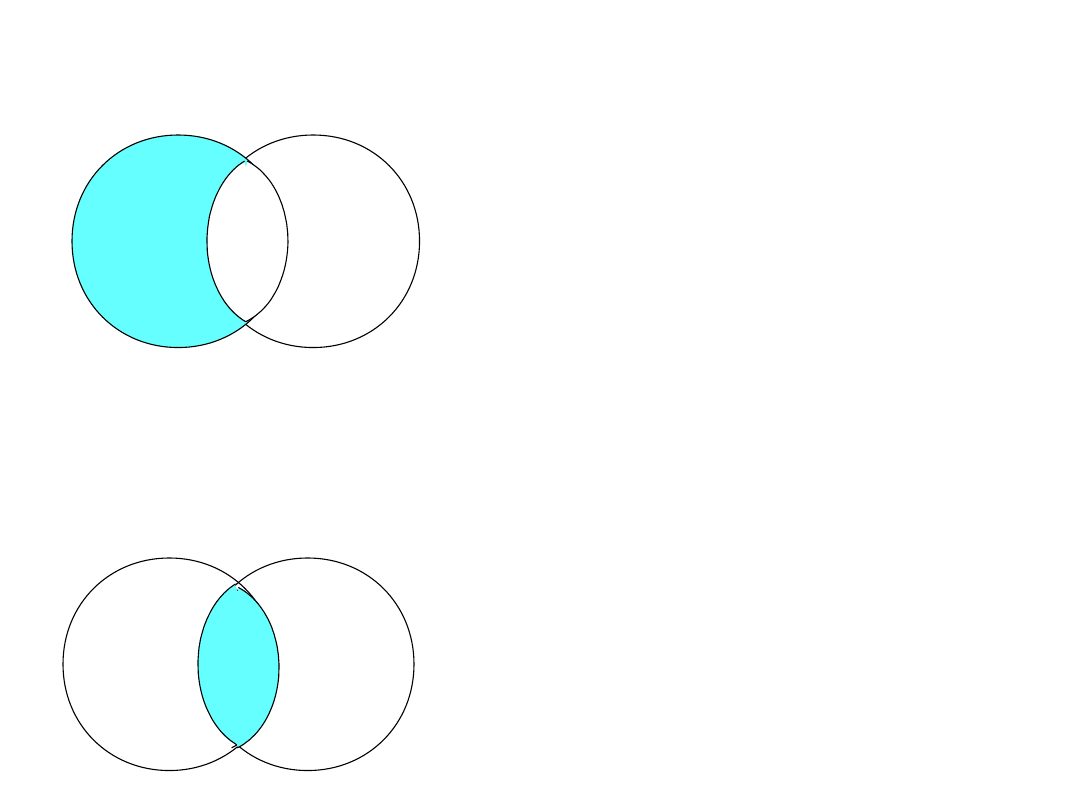
Różnica zbiorów A - B

A

B

{ x 

A - B } 

{ x  A  x 

B

}

A – B  A

A – ( B  C ) = ( A – B )  ( A –

C )

A – ( B  C ) = ( A – B )  ( A –

C )

A

B

A – ( A – B ) = A



B

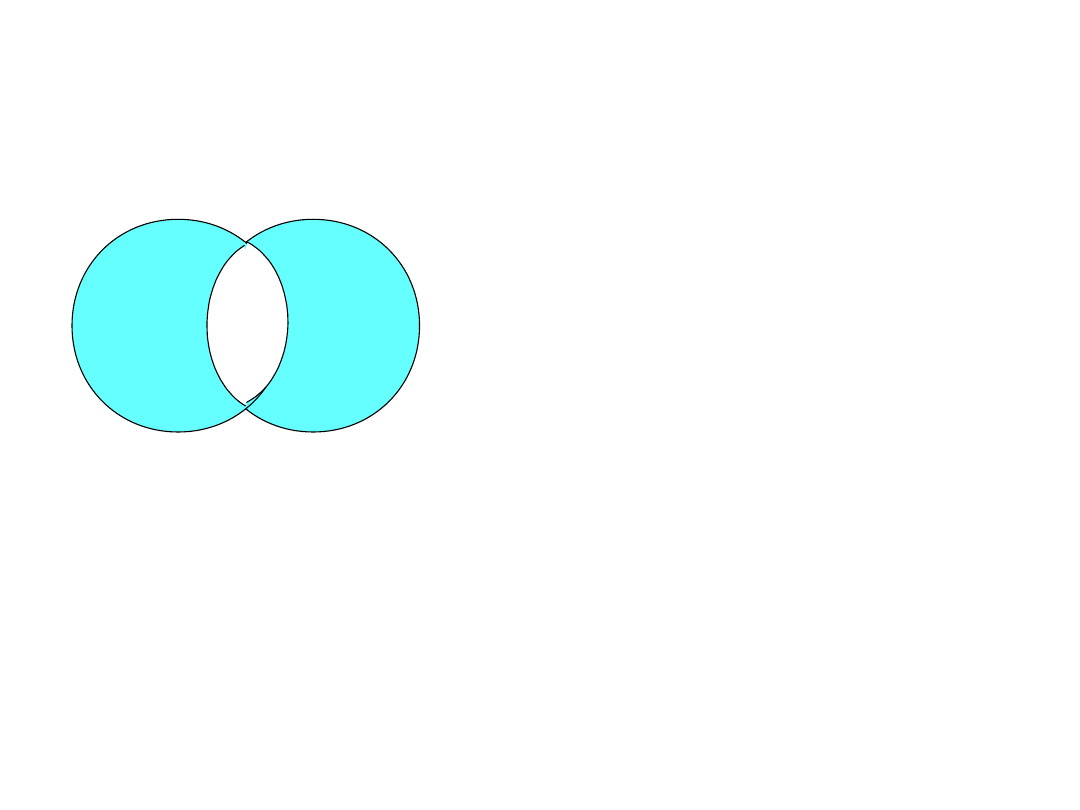
A ÷ B

= ( A - B )

 ( B - A )

B

A

Różnica symetryczna

zbiorów A ÷ B

A ÷ B

= ( A  B ) – (

B  A )

( A ÷ B ) ÷ C = A ÷ ( B ÷
C )

A  ( B ÷ C ) = ( A  B ) ÷ ( A 

C)

A ÷ 0

= A

A

B

A  B

Inkluzja zbiorów

A

 B

(A  B)  ( x  A  x 

B )



x

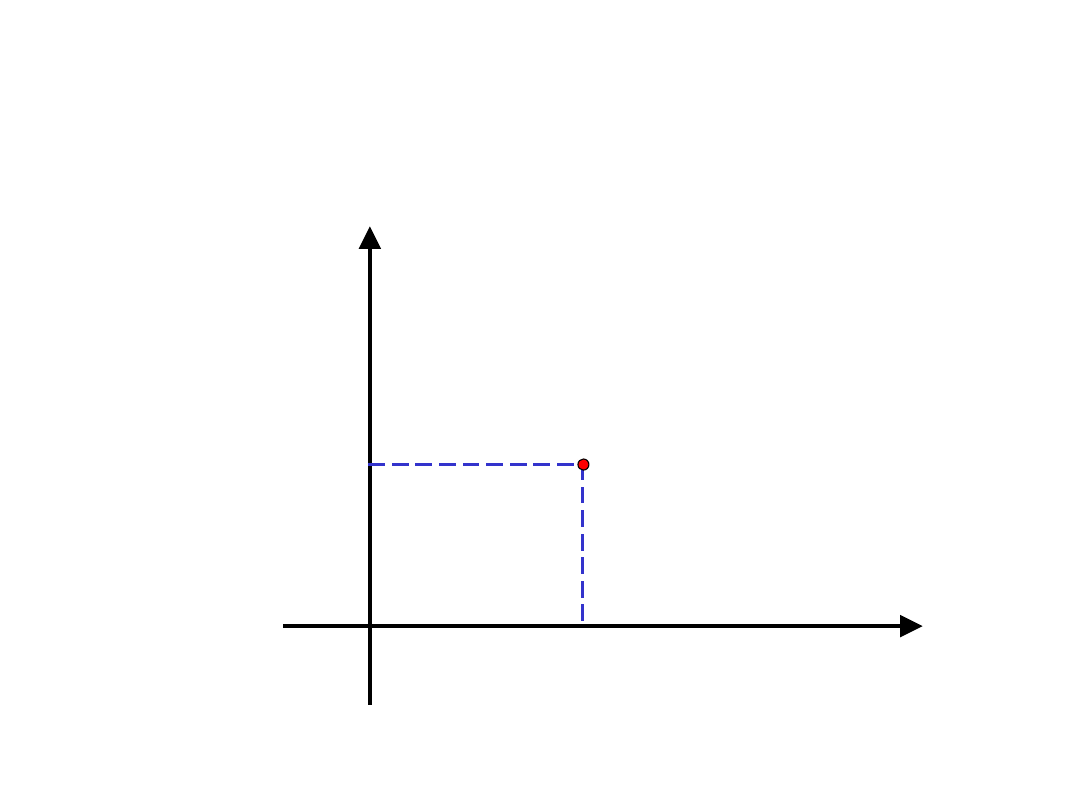
Iloczyn kartezjański zbiorów

A x B

A

B

(a,b)

– ( A  B ) = – A 

– B

– ( A  B ) = – B 

– A

Prawa

de’Morgan’a

- (

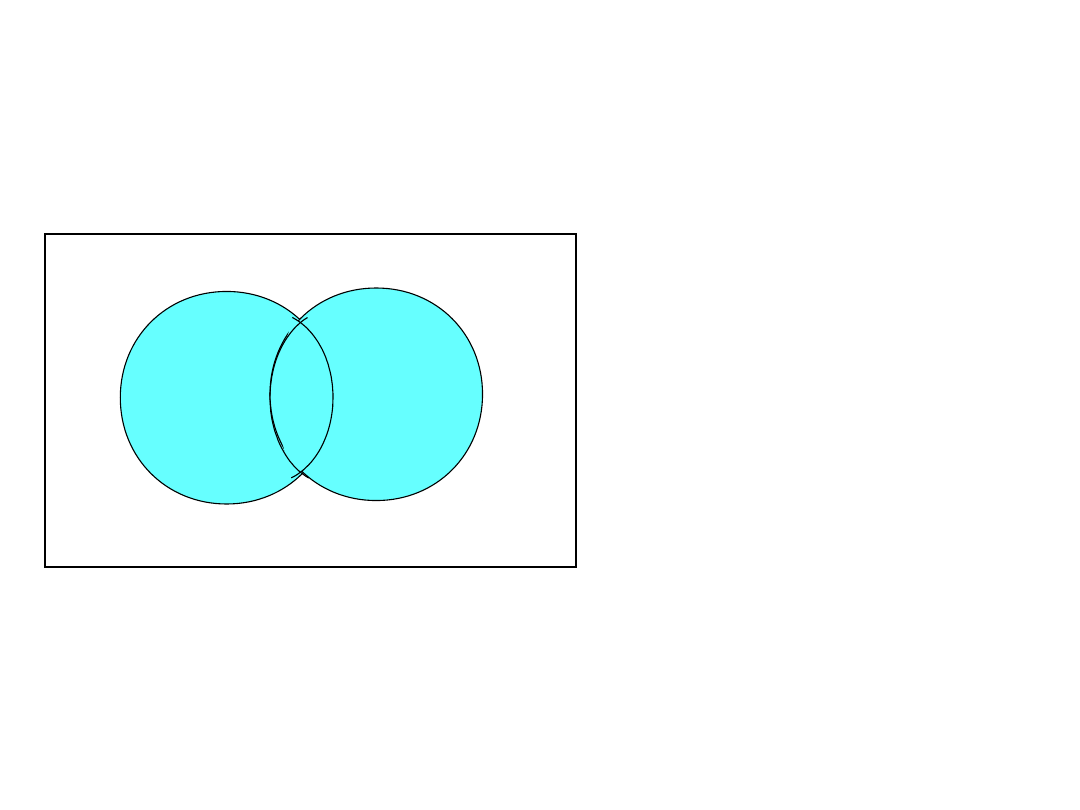
A



B )

=

- A

 -

B

(

A



B )

A

B

prawo de’Morgan’a

I

-(

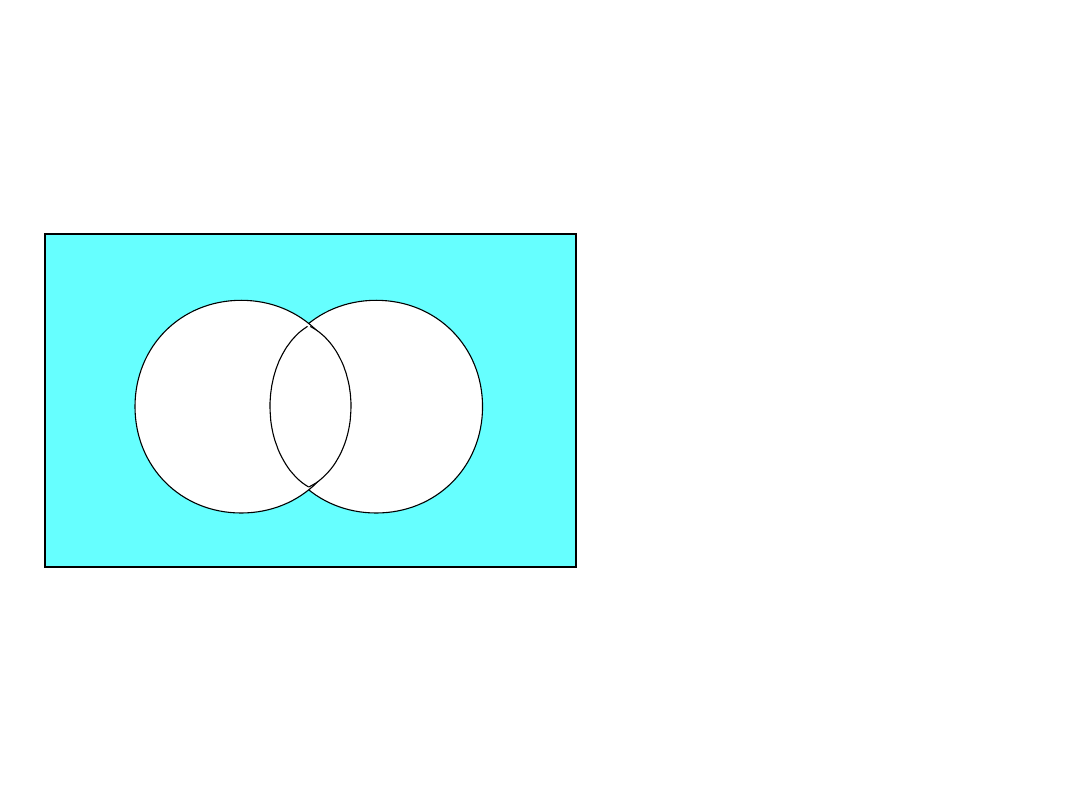
A



B )

A

B

prawo de’Morgan’a

I

- (

A



B )

=

- A

 -

B

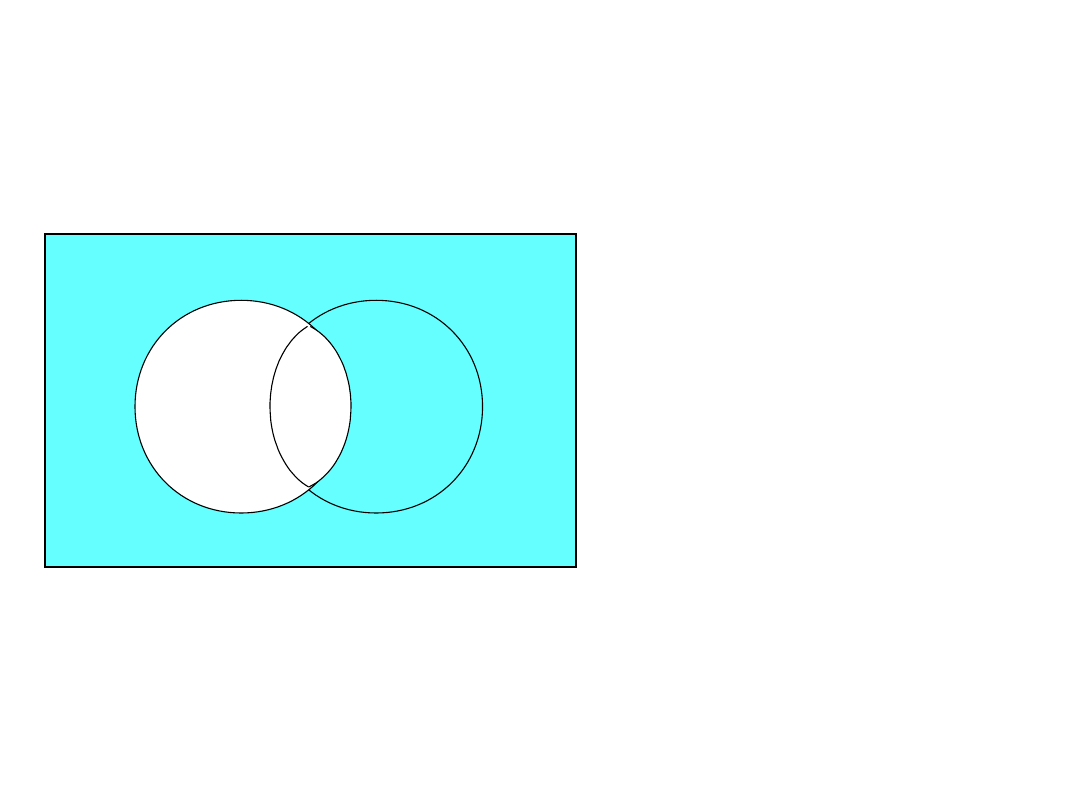
- A

A

B

prawo de’Morgan’a

I

- (

A



B )

=

- A

 -

B

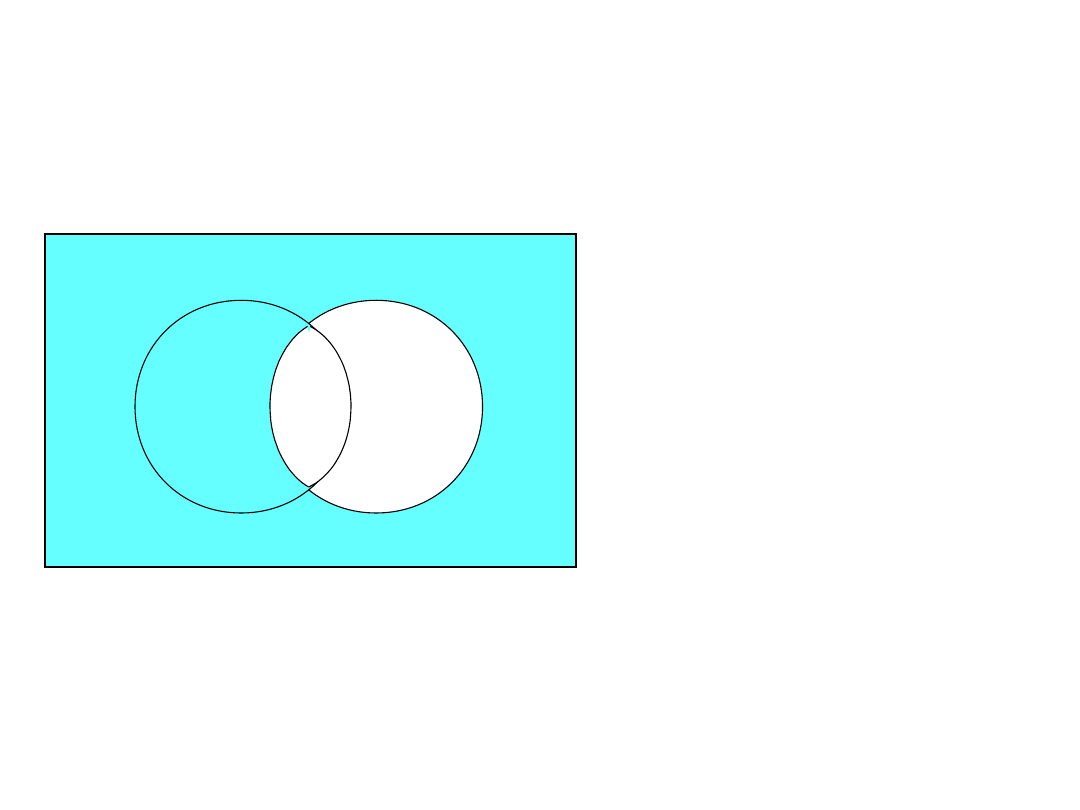
- B

A

B

prawo de’Morgan’a

I

- (

A



B )

=

- A

 -

B

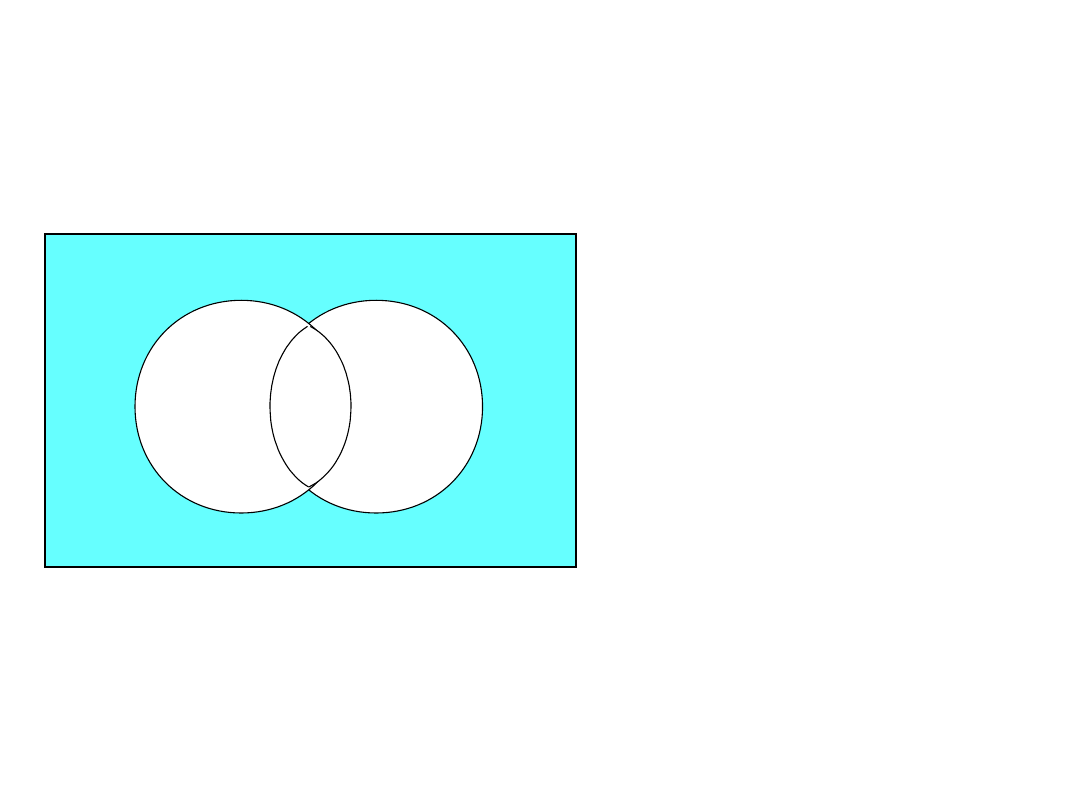
- A  - B

A

B

prawo de’Morgan’a

I

- (

A



B )

=

- A

 -

B

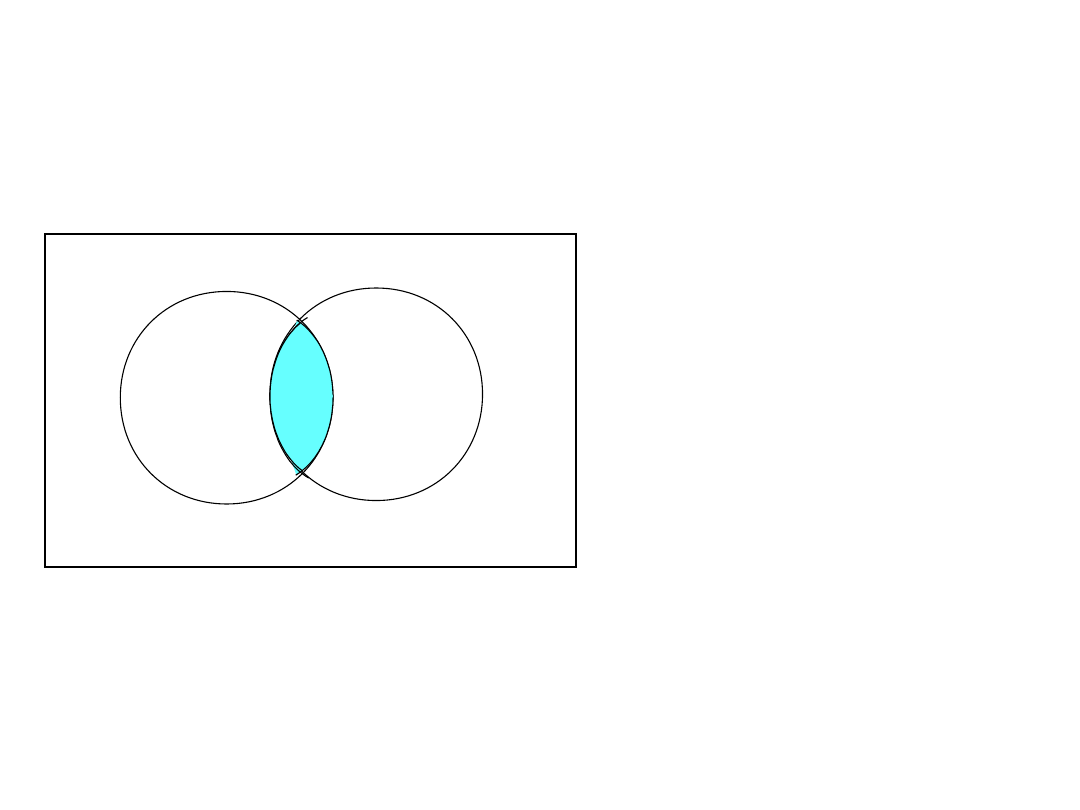
– ( A  B ) = – A  –

B

(

A



B )

A

B

prawo de’Morgan’a

II

– (

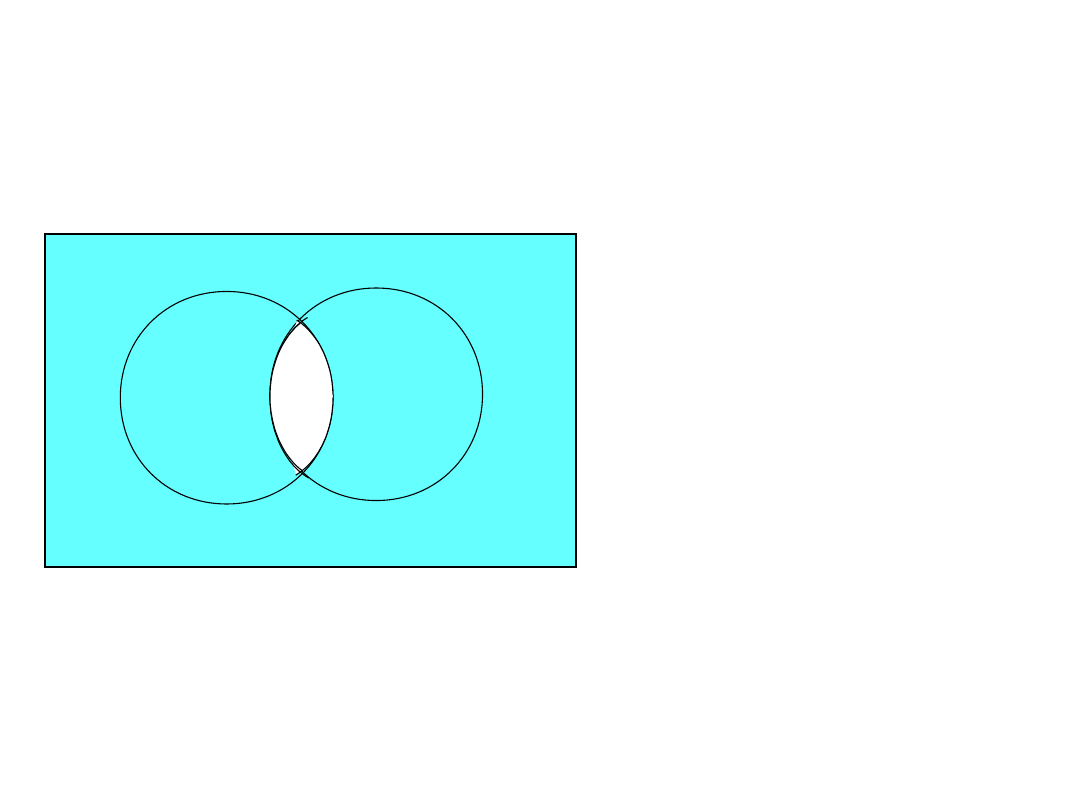
A



B

)

prawo de’Morgan’a

II

A

B

– ( A  B ) = – A  –

B

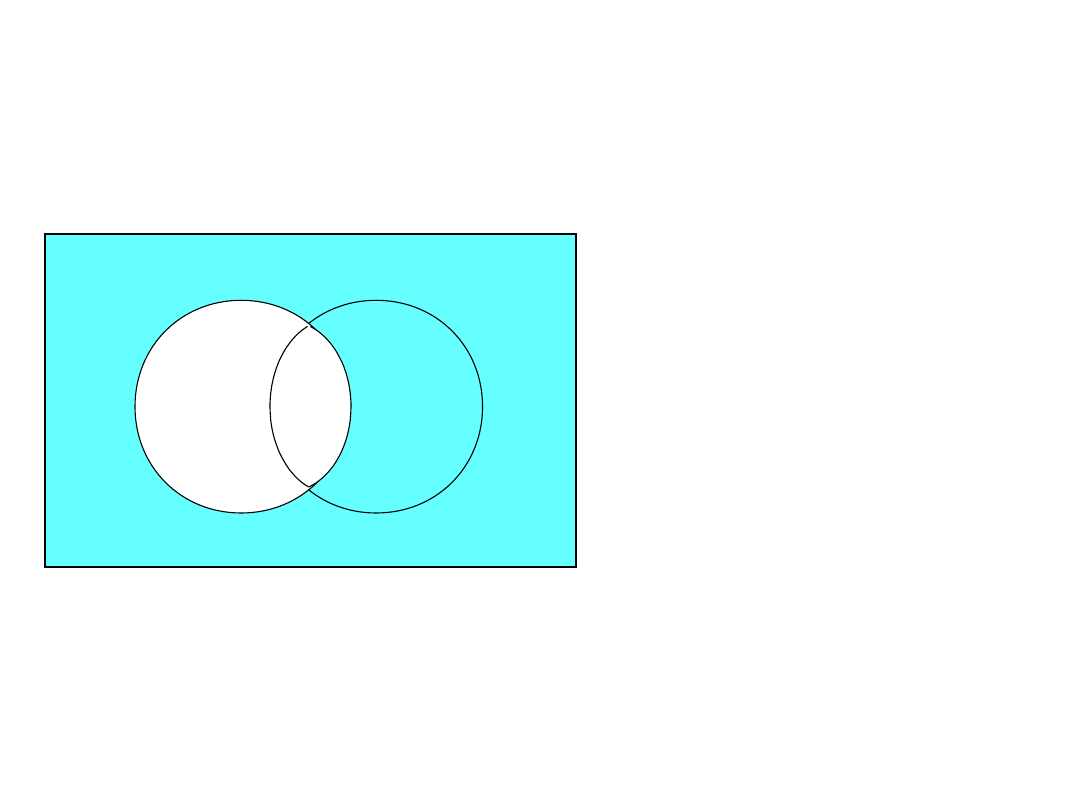
- A

A

B

prawo de’Morgan’a

II

– ( A  B ) = – A  –

B

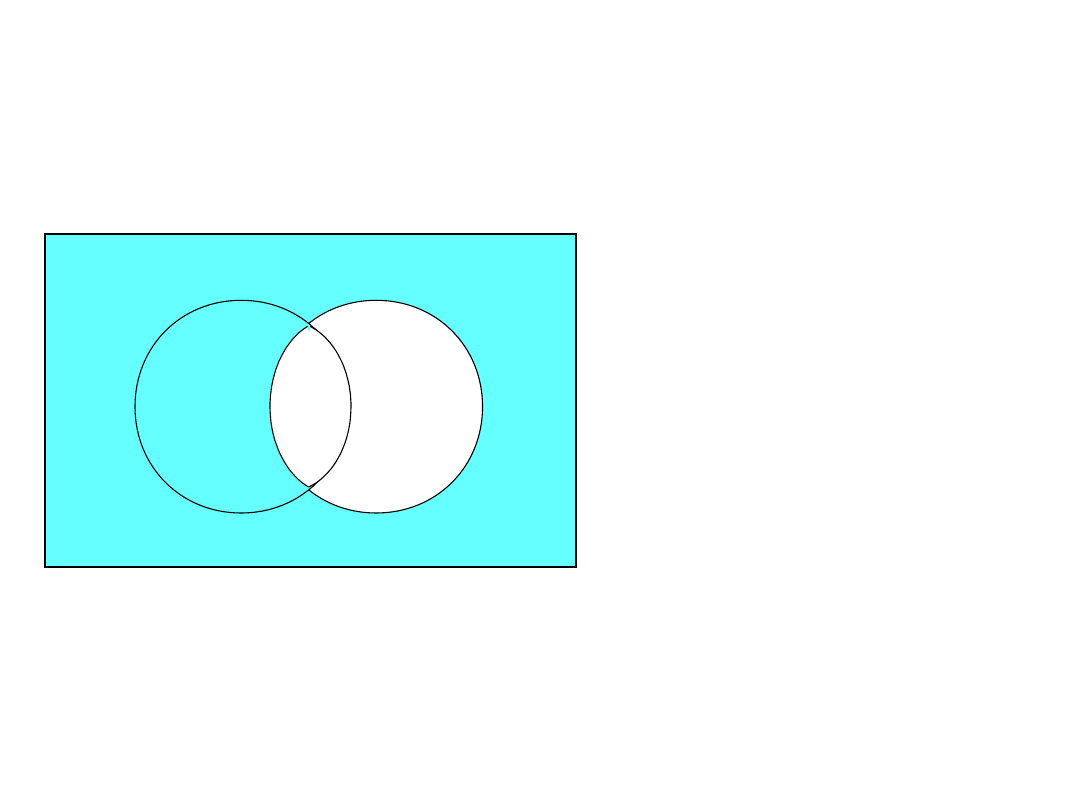
- B

A

B

prawo de’Morgan’a

II

– ( A  B ) = – A  –

B

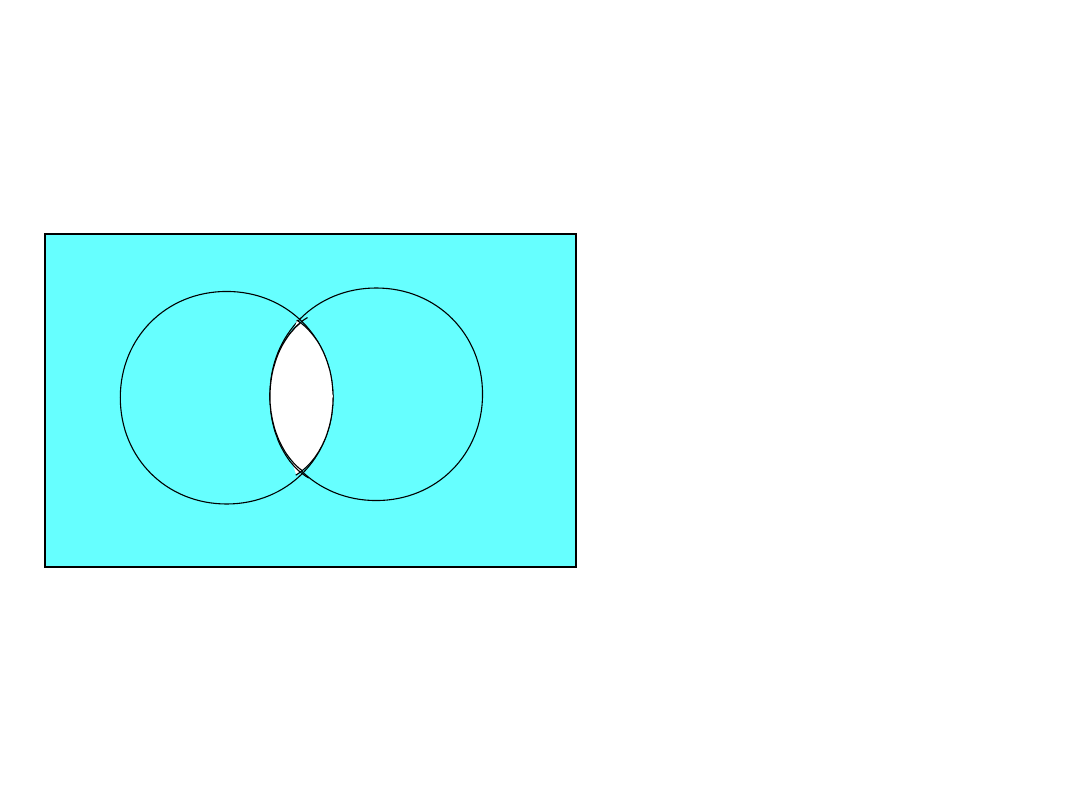
– A  – B

A

B

prawo de’Morgan’a

II

– ( A  B ) = – A  –

B

A  B = B  A

przemienność
A  B = B  A

( A  B)  C = A  ( B  C )

łączność

( A  B)  C = A  ( B  C )

A  ( B  C ) = ( A  B )  ( A  C )

rozdzielność

A  ( B  C ) = ( A  B )  ( A  C )

A



A = A

idempotentność

A  A = A

identyczność

A   =



A



 = A

A  U = A

A  U = U

– ( – A ) = A podwójna
negacja

A  – A =



dopełnienie

A  – A = U

– U = 

–  = U

Działania oznaczamy w następujący sposób:

, • ,  ,  ,  ,  , + ,  ,  itp..

Działaniem w zbiorze niepustym

A

nazywany odwzorowanie

f

iloczynu kartezjańskiego ( A  A ) zbioru A w zbiór A:

f : A  A  A

a b = c gdzie (a,b)  A  A c  A



A

b

,

a

Przykłady:

a  b = a + b + 1 a  b = a + b+ ab

Działania

wewnętrzne

oznaczamy

addytywnie

lub

multiplikatywnie

i

nazywamy

odpowiednio

dodawaniem

i

mnożeniem

.

Jeżeli określone jest

jedno

działanie, to oznaczamy

je na

ogół

multiplikatywnie

, a

addytywnie

jedynie

wtedy, gdy

jest to działanie

przemienne

.

.

Gdy określone są dwa działania, to jedno z
nich

(przemienne) oznaczamy addytywnie, a
drugie

(przemienne lub nie) multiplikatywnie.

Działanie zewnętrzne zawsze oznaczamy

multiplikatywnie stosując wyraźnie inne
oznaczenia

na elementy zbioru i operatory

.

Działanie określone w zbiorze A
nazywamy

przemiennym

jeśli

a b = b a



A

b

,

a

Działanie określone w zbiorze A
nazywamy

łącznym

jeśli

( a b ) c = b ( a

c )



A

c

,

b

,

a

Element e  A nazywa się

neutralnym

elementem działania jeśli

e a = a e = a



A

a

Element a’  A nazywa się

elementem

odwrotnym

do a jeśli

a a’ = a’ a = e



A

a

,



A

a

a’ = a

-

1

Relacją dwuargumentową jest każdy zbiór
par

uporządkowanych

( a,b )

.

Wyrażenie

aRb

czytamy:

•

elementy

a

i

b

pozostają w

relacji lub

•

relacja

R

przyporządkowuje

elementowi

a

element

b

,

•

a

i

b

spełniają relację

R

.

Relacje określamy jako zbiory par
uporządkowanych,

pary uporządkowane jako zbiory
dwuelementowe

( a,b )  { x,y: xRy }  aRb

Pojęcie relacji może być sprowadzone do pojęcia
zbioru.

xR

1

y  xy = x +

y

xR

2

y  x

2

- y

2

= 1

Przykłady

x  D

l

( R )  [ (x,y) 

R ]

y  D

p

( R )  [ (x,y) 

R ]

P( R ) = D

l

( R )  D

p

( R

)

x



y



Zbiory

D

l

( R ), D

p

( R ), P( R )

noszą nazwę

odpowiednio

lewą

i

prawą dziedziną

relacji R oraz

polem

tej relacji. Lewą i prawą dziedzinę

relacji

nazywane są często

dziedziną

i

przeciwdziedziną

.

Relacja równoważności

R  zwr(X)  xRx

relacja R jest

zwrotna

w zbiorze X

R  sym(X)  ( xRy  yRx )

relacja R jest

symetryczna

w zbiorze X

R  przech(X)  ( xRy  yRz 

xRz )

relacja R jest

przechodnia

w zbiorze X

A

x



A

y

,

x 



A

z

,

y

,

x





Funkcje

R  funkcji  ( xRy  xRz  y = z

)

R  funkcji  x  D

l

( f )  [ y = f(x)  x f y

]

A

z

,

y

,

x



