Modelowanie

Modelowanie

matematyczne

matematyczne

systemów

systemów

Modelowanie systemów

Modelowanie systemów

Po co tworzy się modele?..... Do czego służą modele?..

Po co tworzy się modele?..... Do czego służą modele?..

Służą:

Służą:



do lepszego poznawania istniejących lub projektowanych

do lepszego poznawania istniejących lub projektowanych

systemów empirycznych i z tego powodu mogą być modelami

systemów empirycznych i z tego powodu mogą być modelami

wiedzy naukowej,

wiedzy naukowej,



efektywnego (szybkiego i taniego) projektowania nowych

efektywnego (szybkiego i taniego) projektowania nowych

systemów empirycznych, spełniających zarazem wymagania ich

systemów empirycznych, spełniających zarazem wymagania ich

optymalizacji, które mogą być modelami wiedzy praktycznej,

optymalizacji, które mogą być modelami wiedzy praktycznej,



szybkiego i taniego doskonalenia już istniejących systemów

szybkiego i taniego doskonalenia już istniejących systemów

empirycznych.

empirycznych.



Posługiwanie się modelami systemów (procesów) empirycznych

ma tylko sens wtedy, gdy modele te wykazują ze względu na cel

modelowania wystarczające dobre podobieństwo do

modelowanych systemów.

Modelowanie systemów

Modelowanie systemów

Model

Model

jest pewnym przedstawieniem

jest pewnym przedstawieniem

oryginału

oryginału

, ściśle określonym

, ściśle określonym

przez cel modelowania.

przez cel modelowania.

Oryginał

Oryginał

istnieje wcześniej niż jego model, w procesie modelowania jest

istnieje wcześniej niż jego model, w procesie modelowania jest

wzorcem dla tworzonego modelu.

wzorcem dla tworzonego modelu.

Oryginałem może być:

Oryginałem może być:



istniejący już system empiryczny, który chcemy badać lub

istniejący już system empiryczny, który chcemy badać lub

doskonalić,

doskonalić,



pomysł (koncepcja) systemu materialnego lub abstrakcyjnego, o ile

pomysł (koncepcja) systemu materialnego lub abstrakcyjnego, o ile

jeszcze nie został w żaden sposób wyrażony przez jego twórcę,

jeszcze nie został w żaden sposób wyrażony przez jego twórcę,

istniejący tylko w zamyśle.

istniejący tylko w zamyśle.

Wyrażony może być:

Wyrażony może być:



opisowo – lingwistycznie,

opisowo – lingwistycznie,



formalnie jako opis matematyczny,

formalnie jako opis matematyczny,



graficznie – postaci szkicu,

graficznie – postaci szkicu,



schematu,

schematu,



w inny sposób, lecz zawsze za pomocą symboli, umownie kreujących dany

w inny sposób, lecz zawsze za pomocą symboli, umownie kreujących dany

system.

system.

Takie przedstawienie pomysłu jest jego pierwszym modelem abstrakcyjnym lub

Takie przedstawienie pomysłu jest jego pierwszym modelem abstrakcyjnym lub

materialnym (fizycznym0

materialnym (fizycznym0

Modelowanie systemów

Modelowanie systemów

Definicja modelu

Definicja modelu

Model to system materialny lub abstrakcyjny mogący

Model to system materialny lub abstrakcyjny mogący

zastępować oryginał w zakresie wyznaczonym przez cel

zastępować oryginał w zakresie wyznaczonym przez cel

modelowania.

modelowania.

Podobieństwo (a więc i zastępowalność) modeli do ich

Podobieństwo (a więc i zastępowalność) modeli do ich

oryginałów może odnosić się do:

oryginałów może odnosić się do:



struktur,

struktur,



struktur i działania,

struktur i działania,



tylko działania

tylko działania

.

.

Modelowanie systemów

Modelowanie systemów

Inne definicje modelu

Inne definicje modelu

Model (encykl.) – wzór, ideał, przedmiot do naśladowania

Model – układ fizyczny (model fizyczny) lub opis matematyczny
(model matematyczny) o własnościach zbliżonych do własności
modelowanego obiektu.

Model ekonomiczny – konstrukcja hipotetyczna obejmująca
układ założeń przyjętych w ekonomii politycznej dla uchwycenia
najistotniejszych cech i zależności występujących w danym
procesie ekonomicznym.

Model semantyczny (log.)- odwzorowanie, czyli interpretacja
danej teorii w postaci układu (dziedziny) przedmiotów
opisywanych prawdziwie przez tę teorię.

Model teoretyczny( metodol.) – konstrukcja hipotetyczna
odwzorowująca dany rodzaj rzeczywistości w sposób uproszczony,
sprowadzający jej cechy do związków najistotniejszych,
budowana w celach heurystycznych.

Modelowanie systemów

Modelowanie systemów



Modelowanie

Modelowanie

- doświadczalna metoda badania różnych układów,

- doświadczalna metoda badania różnych układów,

zjawisk i procesów na podstawie badania ich modeli, np. za

zjawisk i procesów na podstawie badania ich modeli, np. za

pomocą komputerów.

pomocą komputerów.



Modelowanie matematyczne

Modelowanie matematyczne

– działanie, którego celem jest

– działanie, którego celem jest

wyprowadzenie operacyjnego modelu matematycznego

wyprowadzenie operacyjnego modelu matematycznego

modelowanego systemy empirycznego

modelowanego systemy empirycznego

lub

lub



Modelowanie matematyczne –

Modelowanie matematyczne –

dziedzina, której zadaniem jest

dziedzina, której zadaniem jest

opis rzeczywistości w pewnym specyficznym języku matematyki i

opis rzeczywistości w pewnym specyficznym języku matematyki i

logiki formalnej.

logiki formalnej.

Modelowanie systemów

Modelowanie systemów



Model matematyczny –

Model matematyczny –

skończony zbiór symboli i relacji

skończony zbiór symboli i relacji

matematycznych oraz bezwzględnie ścisłych zasad

matematycznych oraz bezwzględnie ścisłych zasad

opisywania nimi, przy czym zawarte w modelu symbole i

opisywania nimi, przy czym zawarte w modelu symbole i

relacje mają interpretacje odnoszącą je do konkretnych

relacje mają interpretacje odnoszącą je do konkretnych

elementów modelowanego wycinka rzeczywistości. Zbiór

elementów modelowanego wycinka rzeczywistości. Zbiór

symboli i relacji matematycznych to twór abstrakcyjny;

symboli i relacji matematycznych to twór abstrakcyjny;

czynnikiem przekształcającym w model matematyczny jest

czynnikiem przekształcającym w model matematyczny jest

fizyczna interpretacja.

fizyczna interpretacja.

Modelowanie matematyczne jest to dziedzina interdyscyplinarna.

Modelowanie matematyczne jest to dziedzina interdyscyplinarna.

Zalety:

Zalety:



uniwersalizm języka matematyki,

uniwersalizm języka matematyki,



możliwość potwierdzenia przeprowadzonego rozumowania za

możliwość potwierdzenia przeprowadzonego rozumowania za

pomocą reguł i twierdzeń matematyki

pomocą reguł i twierdzeń matematyki

Modelowanie systemów

Modelowanie systemów

Ciąg logiczny obowiązujący dla modelowania

Ciąg logiczny obowiązujący dla modelowania

matematycznego, gdy wnioski końcowe będą zgodne

matematycznego, gdy wnioski końcowe będą zgodne

z rzeczywistością.

z rzeczywistością.

Aksjomaty

Przekształceni

a

logiczne

Twierdzenia

Modelowanie systemów

Modelowanie systemów

Proces tworzenia modelu matematycznego

Proces tworzenia modelu matematycznego



Sprecyzowanie koncepcji odnoszącego się do badanego wycinka

Sprecyzowanie koncepcji odnoszącego się do badanego wycinka

rzeczywistości.

rzeczywistości.



Zdefiniowanie zasad przyporządkowania cech zjawiska rzeczywistego

Zdefiniowanie zasad przyporządkowania cech zjawiska rzeczywistego

– obiektom matematycznym i sformułowanie relacji miedzy tymi

– obiektom matematycznym i sformułowanie relacji miedzy tymi

obiektami.

obiektami.



W wyniku otrzymujemy zbiór aksjomatów; w teorii naukowej nazywa

W wyniku otrzymujemy zbiór aksjomatów; w teorii naukowej nazywa

się to zbiorem hipotez teoretycznych.

się to zbiorem hipotez teoretycznych.



Wyciąganie wniosków na podstawie dedukcji logicznej. Wnioski te są

Wyciąganie wniosków na podstawie dedukcji logicznej. Wnioski te są

odpowiednikiem twierdzeń.

odpowiednikiem twierdzeń.



Uzasadnieniem poprawności takiego postępowanie jest to, że jak

Uzasadnieniem poprawności takiego postępowanie jest to, że jak

wynika z dotychczasowych doświadczeń , natura operuje taką sama

wynika z dotychczasowych doświadczeń , natura operuje taką sama

logika , jaka operuje umysł ludzki.

logika , jaka operuje umysł ludzki.

Modelowanie systemów

Modelowanie systemów

Zakres modelowania matematycznego

Zakres modelowania matematycznego



Geometria

Geometria



Fizyka

Fizyka



Ekonomia

Ekonomia



Nauki przyrodnicze: procesy biologiczne, ekologiczne,

Nauki przyrodnicze: procesy biologiczne, ekologiczne,

ewolucyjne, medyczne

ewolucyjne, medyczne



W ostatnich latach próby zastosowania w naukach

W ostatnich latach próby zastosowania w naukach

społecznych i humanistycznych.

społecznych i humanistycznych.



Modelowanie matematyczne ma zastosowanie tam, gdzie

Modelowanie matematyczne ma zastosowanie tam, gdzie

zjawiska mają charakter ilościowy i wówczas metody

zjawiska mają charakter ilościowy i wówczas metody

matematyczne umożliwiają uogólnienia i ścisłe

matematyczne umożliwiają uogólnienia i ścisłe

wnioskowanie.

wnioskowanie.

Modelowanie systemów

Modelowanie systemów

Etapy modelowania

•Sformułowanie celów
modelowania.

•Wybór kategorii modelu i
określenie jego struktury.

•Identyfikacja.

•Algorytmizacja obliczeń.

•Weryfikacja obliczeń.

Modelowanie systemów

Modelowanie systemów

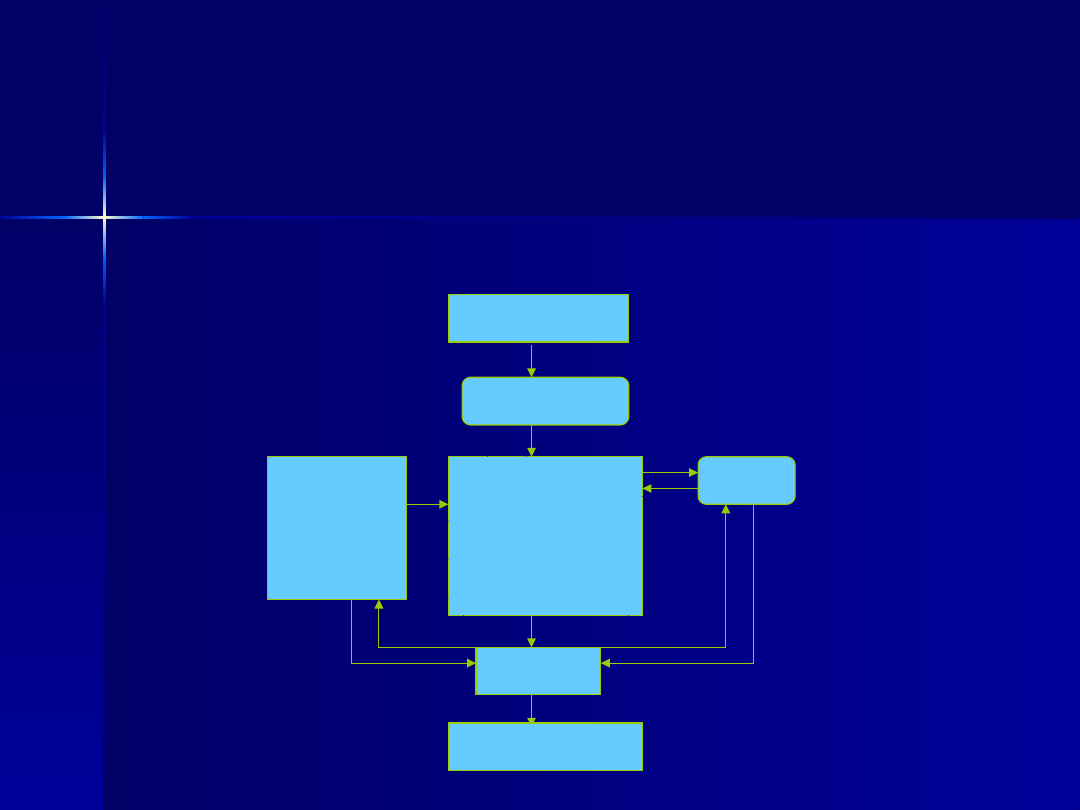
Schemat budowy modelu

Schemat budowy modelu

Cele
modelowania

Kategoria modelu

Struktura modelu

Identyfikacja

Algorytmy,

prognozy,

obliczenia

Dane

Weryfikacj
a

Hipotezy,
Teorie,
Prawa,
Wiedza
empiryczna

Problem
badawczy

Model
zweryfikowany

Modelowanie systemów

Modelowanie systemów



Modele matematyczne, struktury, metody modelowania

Modele matematyczne, struktury, metody modelowania

Modelowanie systemów

Modelowanie systemów

Def

Def

.

.

Abstrakcyjnym ogólnym modelem

Abstrakcyjnym ogólnym modelem

systemu empirycznego jest taki semantyczny

systemu empirycznego jest taki semantyczny

system abstrakcyjny , który ze względu na cel

system abstrakcyjny , który ze względu na cel

modelowania może zastępować dany system

modelowania może zastępować dany system

empiryczny.

empiryczny.

Model abstrakcyjny

Model abstrakcyjny

zastępując system (proces) może

zastępując system (proces) może

dostarczać informacji o:

dostarczać informacji o:



działaniu modelowanego systemu empirycznego (o

działaniu modelowanego systemu empirycznego (o

procesie empirycznym), nie wnosząc jednak informacji

procesie empirycznym), nie wnosząc jednak informacji

o jego strukturze,

o jego strukturze,



strukturze modelowanego systemu empirycznego

strukturze modelowanego systemu empirycznego

(systemu statystycznego),

(systemu statystycznego),



strukturze i działaniu systemu

strukturze i działaniu systemu

Modelowanie systemów

Modelowanie systemów



Def. Abstrakcyjnym, informacyjnym modelem

Def. Abstrakcyjnym, informacyjnym modelem

systemu empirycznego jest taka semantyczna

systemu empirycznego jest taka semantyczna

struktura abstrakcyjna, która może dostarczać

struktura abstrakcyjna, która może dostarczać

liczbowych informacji o działaniu modelowanego

liczbowych informacji o działaniu modelowanego

systemu empirycznego, natomiast nie musi być

systemu empirycznego, natomiast nie musi być

podobna do struktury systemu empirycznego

podobna do struktury systemu empirycznego



Matematycznymi modelami informacyjnymi są

Matematycznymi modelami informacyjnymi są

formuły empiryczne (regresje liniowe i nieliniowe,

formuły empiryczne (regresje liniowe i nieliniowe,

korelacje, rozkłady stochastyczne)

korelacje, rozkłady stochastyczne)



Modele takie to hipotezy istnienie.

Modele takie to hipotezy istnienie.



Modele te informują o systemie i oddziaływaniu

Modele te informują o systemie i oddziaływaniu

otoczenia tylko w takim zakresie i warunkach w jakich

otoczenia tylko w takim zakresie i warunkach w jakich

był wykonywany eksperyment. Należy dołączyć do

był wykonywany eksperyment. Należy dołączyć do

modelu zakres zmienności parametrów.

modelu zakres zmienności parametrów.

Modelowanie systemów

Modelowanie systemów

Def. Abstrakcyjnym, strukturalnym modelem

Def. Abstrakcyjnym, strukturalnym modelem

systemu

systemu

empirycznego jest semantyczna struktura podobna do

empirycznego jest semantyczna struktura podobna do

struktury modelowanego systemu ze względu na cel

struktury modelowanego systemu ze względu na cel

modelowania, której badanie może dostarczyć informacji

modelowania, której badanie może dostarczyć informacji

pozwalających na poznawanie działania i na doskonalenie

pozwalających na poznawanie działania i na doskonalenie

systemu.

systemu.

Strukturalnie podobne modele systemów empirycznych mogą być

Strukturalnie podobne modele systemów empirycznych mogą być

tworzone:

tworzone:

metodą dedukcyjną, gdy formalne (np. matematyczne)

metodą dedukcyjną, gdy formalne (np. matematyczne)

przedstawienie struktury modelu wynika z przesłanek pewnych,

przedstawienie struktury modelu wynika z przesłanek pewnych,

będących prawami lub twierdzeniami wiedzy naukowej,

będących prawami lub twierdzeniami wiedzy naukowej,



na podstawie przesłanek niekoniecznie pewnych, będących

na podstawie przesłanek niekoniecznie pewnych, będących

założeniami projektowymi, hipotezami istnienia lub hipotezami

założeniami projektowymi, hipotezami istnienia lub hipotezami

wyjaśniającymi, niekiedy formułowanymi wyłącznie w celu

wyjaśniającymi, niekiedy formułowanymi wyłącznie w celu

utworzenia modelu,

utworzenia modelu,



na podstawie wyników uzyskanych po przeprowadzeniu analizy

na podstawie wyników uzyskanych po przeprowadzeniu analizy

systemowej modelowanego systemu empirycznego.

systemowej modelowanego systemu empirycznego.

Modelowanie systemów

Modelowanie systemów

Def.1.

Def.1.

Modelem syntaktycznym

Modelem syntaktycznym

jest struktura

jest struktura

poprawnie zbudowana z nie zinterpretowanych

poprawnie zbudowana z nie zinterpretowanych

(pozbawionych znaczenia) symboli logiki lub

(pozbawionych znaczenia) symboli logiki lub

matematyki.

matematyki.

Przykładem takich modeli są struktury (modele)

Przykładem takich modeli są struktury (modele)

logiki formalnej, teorii mnogości, algebry,

logiki formalnej, teorii mnogości, algebry,

analizy matematycznej itp., jeżeli należą

analizy matematycznej itp., jeżeli należą

wyłącznie do tych dyscyplin naukowych.

wyłącznie do tych dyscyplin naukowych.

Modelowanie systemów

Modelowanie systemów

Def.2.

Def.2.

Modelem semantycznym

Modelem semantycznym

strukturalnym jest model

strukturalnym jest model

syntaktyczny zinterpretowany w pewnej klasie systemów

syntaktyczny zinterpretowany w pewnej klasie systemów

empirycznych, który spełnia warunki określone przez

empirycznych, który spełnia warunki określone przez

def. 1.

def. 1.

Przykład:

Przykład:

Równanie

Równanie

jest pewnym równaniem różniczkowym cząstkowym drugiego rzędu i

jest pewnym równaniem różniczkowym cząstkowym drugiego rzędu i

jednocześnie pewnym syntaktycznym modelem matematyki w

jednocześnie pewnym syntaktycznym modelem matematyki w

ortokartezjańskim układzie x, y, z. Jeżeli symbolowi f przypiszemy

ortokartezjańskim układzie x, y, z. Jeżeli symbolowi f przypiszemy

temperaturę, symbolowi τ - -czas, to ów model stanie się

temperaturę, symbolowi τ - -czas, to ów model stanie się

semantycznym modelem fizyki – modelem przewodzenia ciepła.w

semantycznym modelem fizyki – modelem przewodzenia ciepła.w

stanie niestacjonarnym w ciele stałym. Jeśli dalej określimy kształt

stanie niestacjonarnym w ciele stałym. Jeśli dalej określimy kształt

tego ciała, wartość współczynnika A, niekiedy konieczne jest

tego ciała, wartość współczynnika A, niekiedy konieczne jest

podanie właściwości tego ciała , zostaną podane warunki graniczne,

podanie właściwości tego ciała , zostaną podane warunki graniczne,

to po znalezieniu rozwiązania szczególnego tego równania

to po znalezieniu rozwiązania szczególnego tego równania

otrzymamy model operacyjny.

otrzymamy model operacyjny.









z

,

y

,

x

f

A

z

,

y

,

x

f

2











Modelowanie systemów

Modelowanie systemów

Def. 3

Def. 3

. Modelem operacyjnym

. Modelem operacyjnym

jest taki

jest taki

strukturalny model semantyczny, który

strukturalny model semantyczny, który

umożliwia przedstawienie wyników

umożliwia przedstawienie wyników

modelowanego systemu empirycznego za

modelowanego systemu empirycznego za

pomocą informacji liczbowych.

pomocą informacji liczbowych.

Modelowanie systemów

Modelowanie systemów

Kategorie modeli

Kategorie modeli

Modele funkcyjne i stochastyczne

Modele funkcyjne i stochastyczne

–

Modele w postaci zależności funkcyjnych (odwzorowań –

Modele w postaci zależności funkcyjnych (odwzorowań –

każdemu elementowi m zbioru wielkości wejściowych M

każdemu elementowi m zbioru wielkości wejściowych M

przyporządkowany jest jednoznacznie określony element

przyporządkowany jest jednoznacznie określony element

y zbioru wielkości wyjściowych Y.

y zbioru wielkości wyjściowych Y.

–

Modele o zależności stochastycznej – każdemu

Modele o zależności stochastycznej – każdemu

elementowi m zbioru wielkości wejściowych M

elementowi m zbioru wielkości wejściowych M

przyporządkowanych jest wiele elementów y1, y2,....,yn

przyporządkowanych jest wiele elementów y1, y2,....,yn

wielkości wyjściowych Y.

wielkości wyjściowych Y.

Modele o zależnościach stochastycznych: dystrybuanty, zależności

Modele o zależnościach stochastycznych: dystrybuanty, zależności

korelacyjne – przy zmianie jednej z wielkości zmienia się wartość

korelacyjne – przy zmianie jednej z wielkości zmienia się wartość

średnia drugiej ( zbiór punktów na płaszczyźnie), zależności

średnia drugiej ( zbiór punktów na płaszczyźnie), zależności

regresyjne – każdej wartości m przypisujemy średnią wartość y w

regresyjne – każdej wartości m przypisujemy średnią wartość y w

postaci zależności funkcyjnej.

postaci zależności funkcyjnej.

Modelowanie systemów

Modelowanie systemów

Rodzaje modeli

Rodzaje modeli



Model stochastyczny – model systemów w

Model stochastyczny – model systemów w

wbudowanym generatorem liczb losowych

wbudowanym generatorem liczb losowych



Modele korelacyjne i przyczynowe

Modele korelacyjne i przyczynowe



Model dynamiczny

Model dynamiczny



Modele statyczne

Modele statyczne



Modele o parametrach rozłożonych w

Modele o parametrach rozłożonych w

przestrzeni

przestrzeni



Modele całkowitoliczbowe i binarne

Modele całkowitoliczbowe i binarne

Modelowanie systemów

Modelowanie systemów

złożonych

złożonych

Etapy modelowania

Etapy modelowania

1.

1.

Analiza systemu i jego struktury, w tym opis działania

Analiza systemu i jego struktury, w tym opis działania

systemu i jego związków z otoczeniem. Utworzenie

systemu i jego związków z otoczeniem. Utworzenie

grafu odwzorowującego empiryczną strukturę systemu

grafu odwzorowującego empiryczną strukturę systemu

aktualnie istniejącego lub projektowanego. Wybór

aktualnie istniejącego lub projektowanego. Wybór

obiektów systemu i otoczenia oraz związków między

obiektów systemu i otoczenia oraz związków między

tymi obiektami, istotnych ze względu na cel

tymi obiektami, istotnych ze względu na cel

modelowania.

modelowania.

2.

2.

Odwzorowanie wybranych obiektów systemu w

Odwzorowanie wybranych obiektów systemu w

elementy modelu i określenie elementów przez

elementy modelu i określenie elementów przez

wybrane cechy obiektów.

wybrane cechy obiektów.

3.

3.

Utworzenie relacyjnego modelu i porównanie jego

Utworzenie relacyjnego modelu i porównanie jego

struktury ze strukturą relacyjną modelowanego sytemu.

struktury ze strukturą relacyjną modelowanego sytemu.

Modelowanie systemów

Modelowanie systemów

złożonych

złożonych

Etapy modelowania c.d.

Etapy modelowania c.d.

4.

4.

Jeżeli modelowany system jest procesem, analiza

Jeżeli modelowany system jest procesem, analiza

stanów każdego obiektu systemu i wybór stanów

stanów każdego obiektu systemu i wybór stanów

istotnych ze względu na cel modelowania. Utworzenie

istotnych ze względu na cel modelowania. Utworzenie

relacyjnego modelu stanów dla każdego elementów

relacyjnego modelu stanów dla każdego elementów

modelu i sformułowanie matematycznych modeli

modelu i sformułowanie matematycznych modeli

czasów przebywania elementów w wyróżnionych

czasów przebywania elementów w wyróżnionych

stanach. Pomocniczo określamy macierz lub graf

stanach. Pomocniczo określamy macierz lub graf

prawdopodobieństw zmian stanów każdego elementu.

prawdopodobieństw zmian stanów każdego elementu.

5.

5.

Sformułowanie matematycznych modeli pozostałych

Sformułowanie matematycznych modeli pozostałych

(innych niż czas) zmiennych zależnych, określonych w

(innych niż czas) zmiennych zależnych, określonych w

modelu relacyjnym.

modelu relacyjnym.

Modelowanie systemów

Modelowanie systemów

złożonych

złożonych

Etapy modelowania c. d.

Etapy modelowania c. d.

6.

6.

Utworzenie blokowego schematu działania relacyjnego

Utworzenie blokowego schematu działania relacyjnego

modelu, z uwzględnieniem języka oprogramowania

modelu, z uwzględnieniem języka oprogramowania

tego schematu dla symulacji komputerowej.

tego schematu dla symulacji komputerowej.

Przeprowadzenie oceny zgodności tego schematu z

Przeprowadzenie oceny zgodności tego schematu z

relacyjną strukturą modelu. Jeżeli taka zgodność jest

relacyjną strukturą modelu. Jeżeli taka zgodność jest

zachowana, to wówczas można uznać, że struktura

zachowana, to wówczas można uznać, że struktura

algebraiczna modelu będzie podobna do

algebraiczna modelu będzie podobna do

zaakceptowanej relacyjnej struktury modelowanego

zaakceptowanej relacyjnej struktury modelowanego

systemu empirycznego, a utworzony w taki sposób

systemu empirycznego, a utworzony w taki sposób

matematyczny model będzie strukturalnie podobny do

matematyczny model będzie strukturalnie podobny do

systemu empirycznego.

systemu empirycznego.

Modelowanie systemów

Modelowanie systemów

złożonych

złożonych

Etapy modelowania c. d.

Etapy modelowania c. d.

7.

7.

Zastąpienie poleceń bloków schematu funkcjami

Zastąpienie poleceń bloków schematu funkcjami

algebraicznymi lub zależnościami stochastycznymi,

algebraicznymi lub zależnościami stochastycznymi,

tzn. utworzenie modelu operacyjnego.

tzn. utworzenie modelu operacyjnego.

8.

8.

Oprogramowanie modelu operacyjnego w

Oprogramowanie modelu operacyjnego w

wybranym języku programowania; model dla jego

wybranym języku programowania; model dla jego

użytkownika ma postać programu komputerowego.

użytkownika ma postać programu komputerowego.

Opracowanie instrukcji dla ewentualnych

Opracowanie instrukcji dla ewentualnych

użytkowników modelu.

użytkowników modelu.

Modelowanie systemów

Modelowanie systemów

złożonych

złożonych



Zaprojektować czasowy model dystrybucji i zbioru kombajnowego

Zaprojektować czasowy model dystrybucji i zbioru kombajnowego

aronii.

aronii.



ROZWĄZANIE

ROZWĄZANIE



1. Określenie celu tworzenia modelu:

1. Określenie celu tworzenia modelu:



Celem stworzenia modelu jest sformułowanie matematycznego

Celem stworzenia modelu jest sformułowanie matematycznego

modelu czasu przygotowania owoców aronii do dystrybucji.

modelu czasu przygotowania owoców aronii do dystrybucji.



Rozpatrujemy zbiór obiektów, którego elementami jest aronia.

Rozpatrujemy zbiór obiektów, którego elementami jest aronia.



Zbiór owoców , przygotowanie do przechowywania, oraz ich

Zbiór owoców , przygotowanie do przechowywania, oraz ich

dystrybucja będzie składał się z następujących etapów:

dystrybucja będzie składał się z następujących etapów:



zbiór kombajnowy owoców,

zbiór kombajnowy owoców,



transport owoców do chłodni,

transport owoców do chłodni,



sortowanie i oddzielanie zanieczyszczeń,

sortowanie i oddzielanie zanieczyszczeń,



ważenie i pakowanie owoców,

ważenie i pakowanie owoców,



dystrybucja.

dystrybucja.





2.

2.

Wybór rodzaju modelu:

Wybór rodzaju modelu:



Model systemu złożonego - relacyjny

Model systemu złożonego - relacyjny

Modelowanie systemów

Modelowanie systemów

złożonych

złożonych



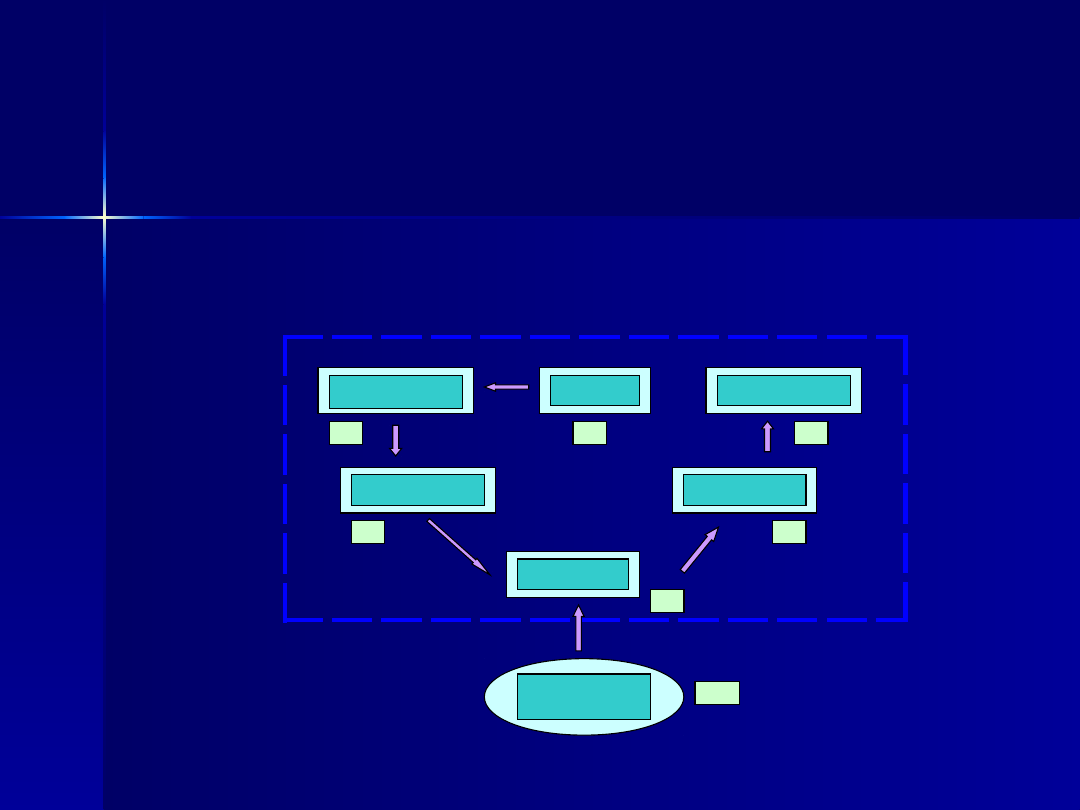
3. Określenie struktury modelu:

3. Określenie struktury modelu:



a) schemat systemu

a) schemat systemu

POLE

ZBIÓR

KOMBAJNOW

Y

TRANSPORT

ZBIORÓW

DYSTRYBUCJ

A

SORTOWNIA

CHŁODNIA

OTOCZENIE

A

B

F

C

E

D

O

Modelowanie systemów

Modelowanie systemów

złożonych

złożonych



b) obiekty główne modelu:

b) obiekty główne modelu:



A

A

– pole

– pole



B –

B –

zbiór kombajnowy

zbiór kombajnowy



C –

C –

transport zbiorów

transport zbiorów



D –

D –

chłodnia

chłodnia



E -

E -

sortownia

sortownia



F –

F –

dystrybucja

dystrybucja



O –

O –

otoczenie

otoczenie

Modelowanie systemów

Modelowanie systemów

złożonych

złożonych



4.Odwzorowanie izomorficzne głównych obiektów systemu:

4.Odwzorowanie izomorficzne głównych obiektów systemu:

O

O

biekt Obiekt Parametry charakteryzujące

biekt Obiekt Parametry charakteryzujące

empiryczny abstrakcyjny obiekt

empiryczny abstrakcyjny obiekt



A

A

a (wymiary pola, masa owoców),

a (wymiary pola, masa owoców),





B

B

b (wydajność, czas pracy, masa

b (wydajność, czas pracy, masa



przetrząsanych owoców, liczba

przetrząsanych owoców, liczba



awarii, czas napraw),

awarii, czas napraw),



C

C

c (liczba przyczep, ładowność, czas

c (liczba przyczep, ładowność, czas



rozładunku, liczba awarii, czas

rozładunku, liczba awarii, czas



napraw),

napraw),



D

D

d (pojemność chłodni),

d (pojemność chłodni),





E

E

e (wydajność, czas pracy, masa

e (wydajność, czas pracy, masa



sortowanych owoców, liczba

sortowanych owoców, liczba



awarii, czas napraw),

awarii, czas napraw),



F

F

f (liczba przyczep, ładowność, czas

f (liczba przyczep, ładowność, czas



rozładunku, liczba awarii, czas

rozładunku, liczba awarii, czas



napraw),

napraw),



O

O

o (warunki atmosferyczne: ilość

o (warunki atmosferyczne: ilość



opadów, czas opadów, czas

opadów, czas opadów, czas



czas dojazdu serwisu).

czas dojazdu serwisu).

Modelowanie systemów

Modelowanie systemów

złożonych

złożonych



Określenie modelu relacyjnego

Określenie modelu relacyjnego



Model relacyjny:

Model relacyjny:



MR = <E,SR>

MR = <E,SR>



E-

E-

elementy

elementy



SR- struktur modelu

SR- struktur modelu



E=

E=

{

{

a b c d e f o

a b c d e f o

}

}



SR c E2- zbiór par elementów należących do zbiorów

SR c E2- zbiór par elementów należących do zbiorów



SR c E2 = {

SR c E2 = {

a b c d e f o

a b c d e f o

}x {

}x {

a b c d e f o

a b c d e f o

} =

} =



{<aa> <ab> <ac> <ad> <ae> <af> <ao>

{<aa> <ab> <ac> <ad> <ae> <af> <ao>



<ba> <bb> <bc> <bd> <be> <bf> < <bo>

<ba> <bb> <bc> <bd> <be> <bf> < <bo>



<ca> <cb> <cc> <cd> <ce> <cf> <co>

<ca> <cb> <cc> <cd> <ce> <cf> <co>



<da> <db> <dc> <dd> <de> <df> <do>

<da> <db> <dc> <dd> <de> <df> <do>



<ea> <eb> <ec> <ed> <ee> <ef> <eo>

<ea> <eb> <ec> <ed> <ee> <ef> <eo>



<fa> <fb> <fc> <fd> <fe> <ff> <fo>

<fa> <fb> <fc> <fd> <fe> <ff> <fo>



<oa> <ob> <oc> <od> <oe> <of> <oo>}

<oa> <ob> <oc> <od> <oe> <of> <oo>}

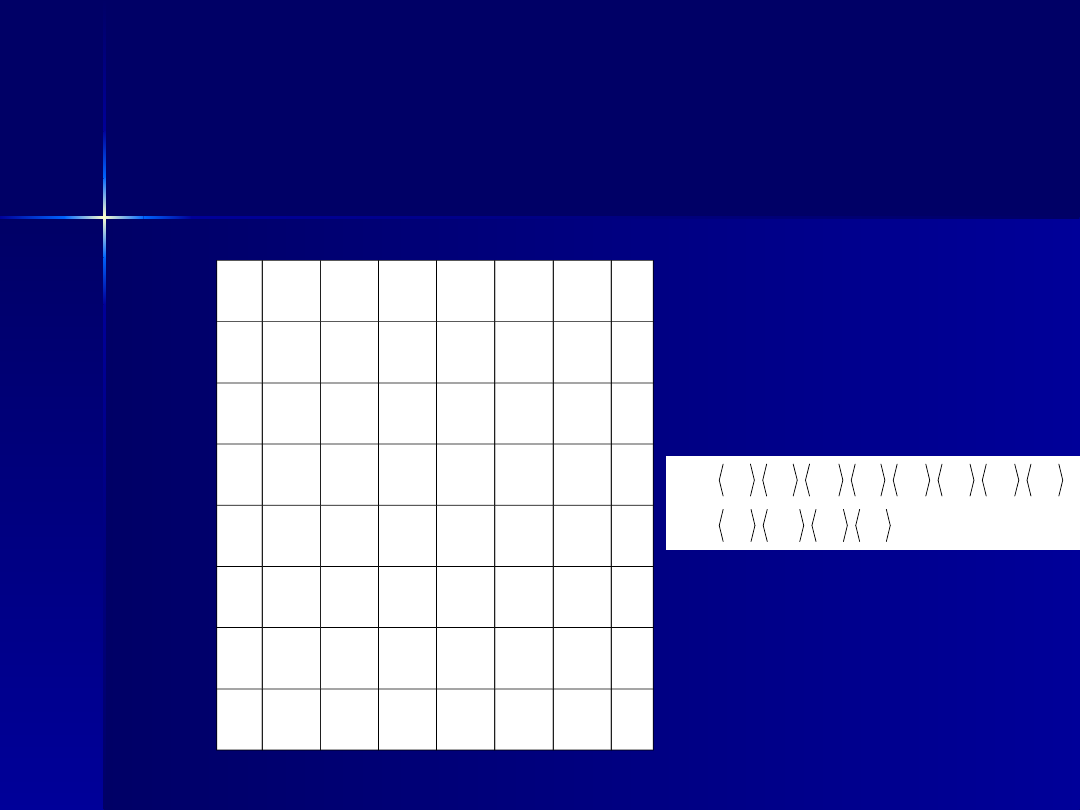
Modelowanie systemów

Modelowanie systemów

złożonych

złożonych

a

b

c

d

e

f

o

a

+

-

-

-

-

-

b

-

+

+

-

-

-

c

-

-

+

-

-

-

d

-

+

-

+

-

-

e

-

-

-

+

-

-

f

-

-

-

+

+

-

o

+

+

-

-

-

-

„-’’ oznacza brak relacji między
obiektami głównymi
„+’’oznacza istnienie relacji
między obiektami głównymi



















;

,

;

,

;

,

;

,

;

,

;

,

;

,

;

,

;

,

;

,

;

,

;

,

b

o

a

o

d

f

d

e

e

d

b

d

d

c

d

b

c

b

d

a

c

a

b

a

S

R

Modelowanie systemów

Modelowanie systemów

złożonych

złożonych

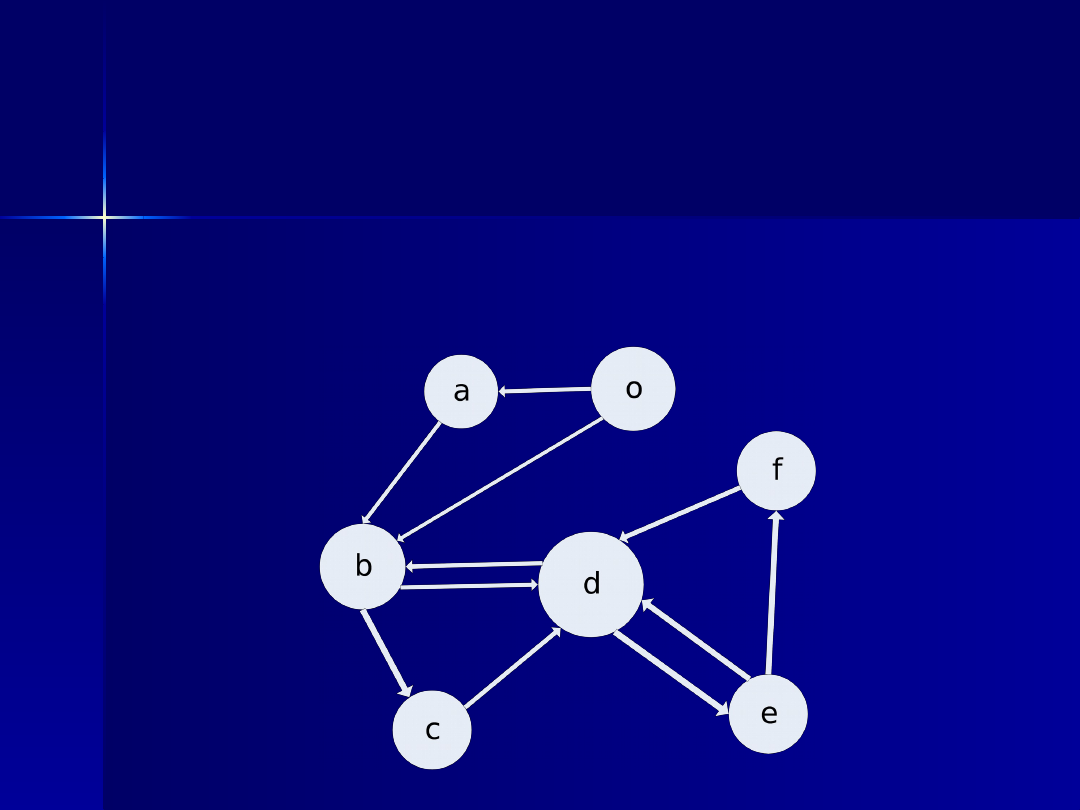
Graficzne przedstawienie relacji między

Graficzne przedstawienie relacji między

elementami modelu

elementami modelu

Modelowanie systemów

Modelowanie systemów

złożonych

złożonych

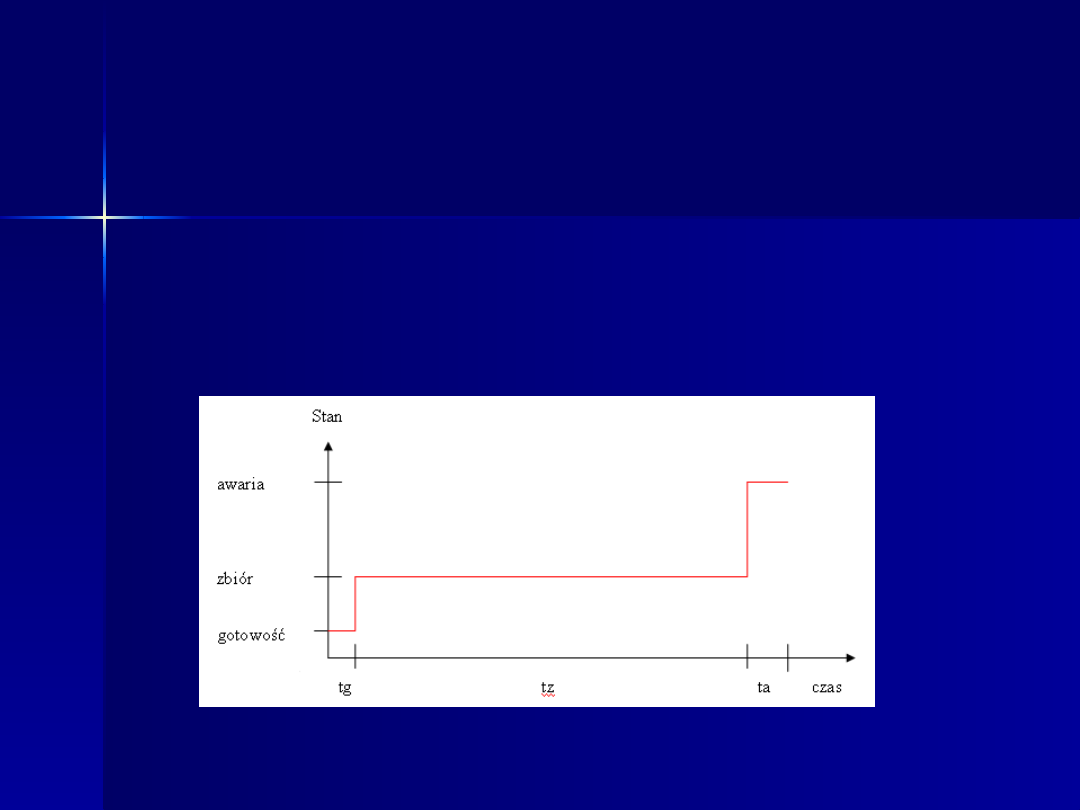
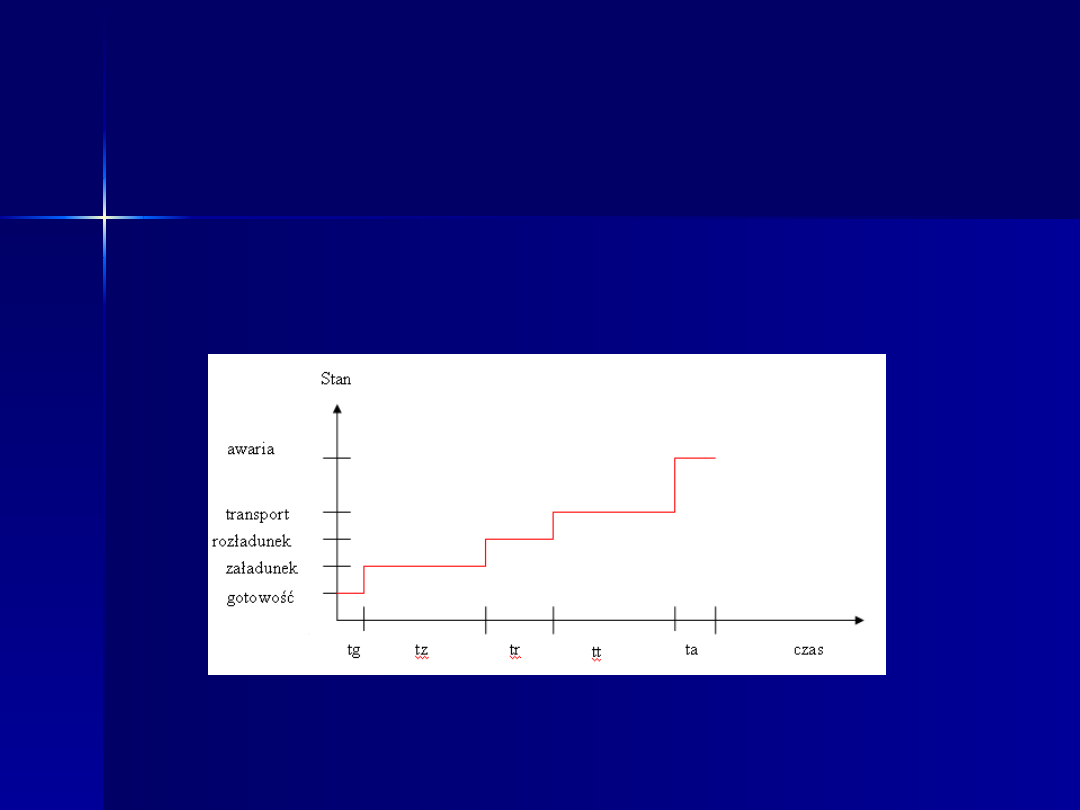
5.Trajektorie stanów elementów

5.Trajektorie stanów elementów

dynamicznych

dynamicznych

a) zbiór kombajnowy

Modelowanie systemów

Modelowanie systemów

złożonych

złożonych

Sformułowanie matematycznych modeli

Sformułowanie matematycznych modeli

czasów przebywania owoców aronii w

czasów przebywania owoców aronii w

wyróżnionych stanach

wyróżnionych stanach

zmienna losowa rozkładu równomiernego

zmienna losowa rozkładu równomiernego

zmienna losowa rozkładu równomiernego

zmienna losowa rozkładu równomiernego



gotowosci



kombajnu

wydajnosc

ha

aronii

plon

zbioru

_

_









awarii



Modelowanie systemów złożonych

Modelowanie systemów złożonych



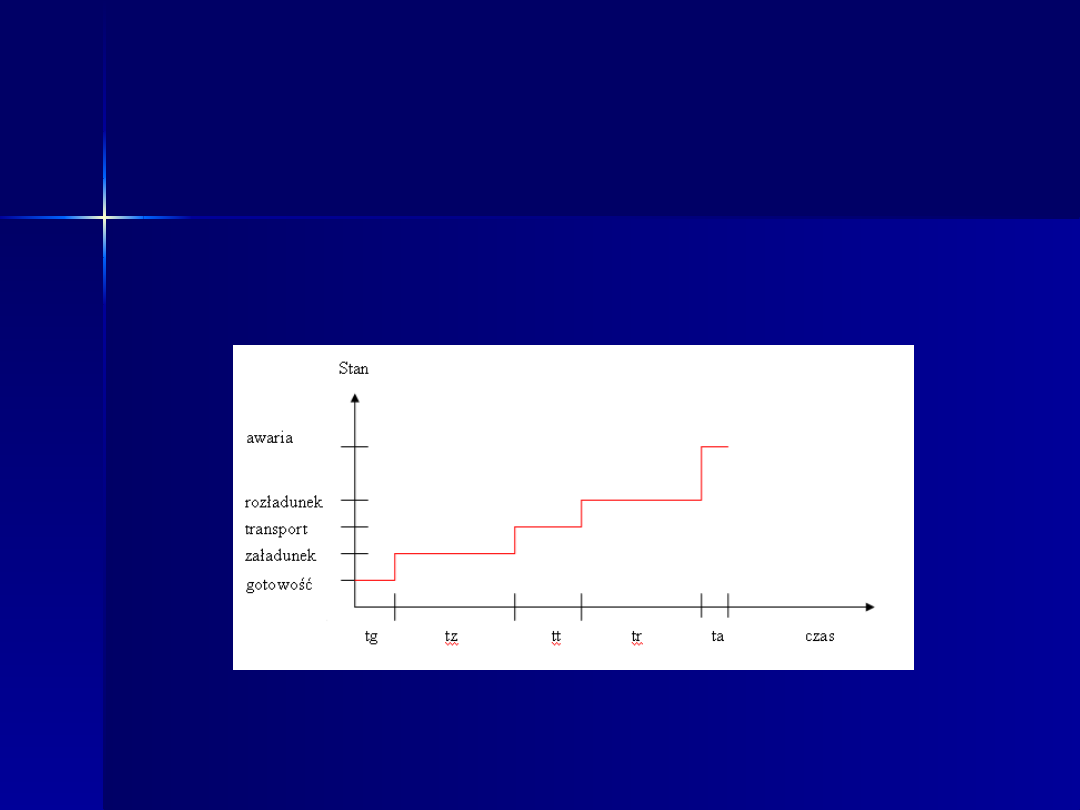
b) transport zbiorów do chłodni

b) transport zbiorów do chłodni

Modelowanie systemów złożonych

Modelowanie systemów złożonych

Sformułowanie matematycznych modeli

Sformułowanie matematycznych modeli

czasów przebywania owoców aronii w

czasów przebywania owoców aronii w

wyróżnionych stanach

wyróżnionych stanach

zmienna losowa rozkładu

zmienna losowa rozkładu

równomiernego

równomiernego

zmienna losowa rozkładu

zmienna losowa rozkładu

równomiernego

równomiernego

predkosc

droga

transportu







gotowosci





awarii



ladowania

wydajnosc

aronii

masa

załaładun

rozłozładu

_

_









Modelowanie systemów

Modelowanie systemów

złożonych

złożonych



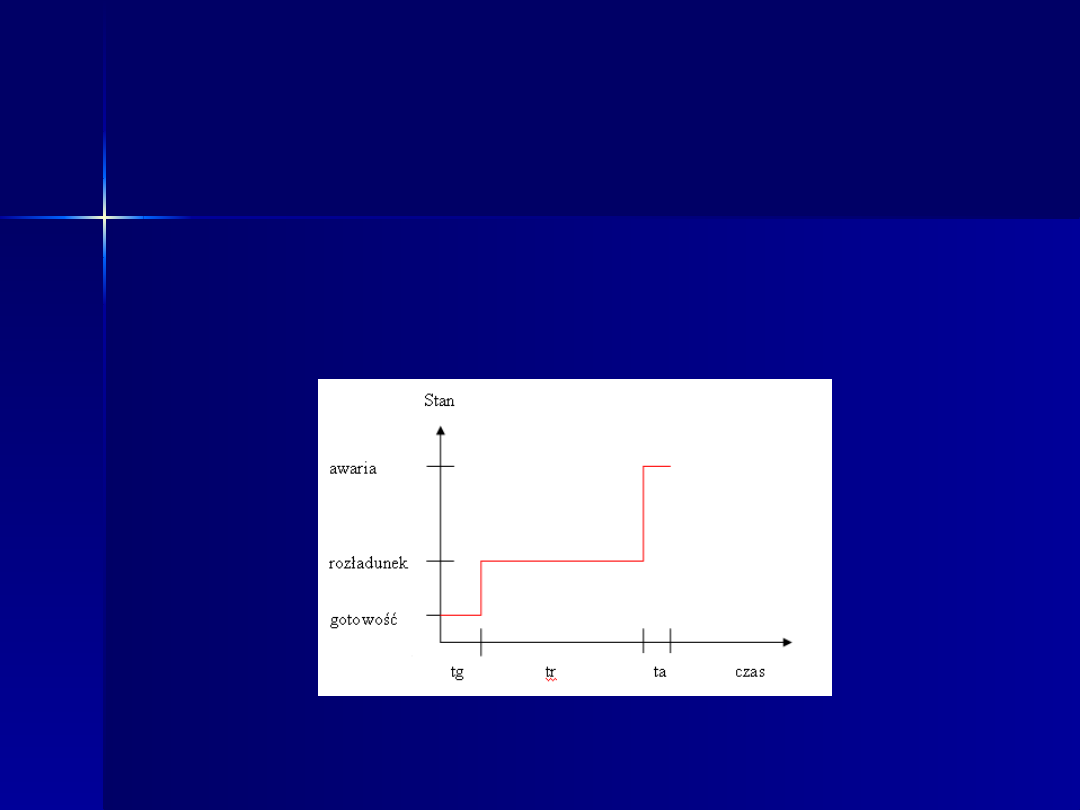
c) chłodnia

c) chłodnia

Modelowanie systemów

Modelowanie systemów

złożonych

złożonych

Sformułowanie matematycznych modeli czasów

Sformułowanie matematycznych modeli czasów

przebywania owoców aronii w wyróżnionych

przebywania owoców aronii w wyróżnionych

stanach

stanach

zmienna losowa rozkładu równomiernego

zmienna losowa rozkładu równomiernego

zmienna losowa rozkładu równomiernego

zmienna losowa rozkładu równomiernego



gotowosci





awarii



ladowania

wydajnosc

aronii

masa

załaładun

rozłozładu

_

_









Modelowanie systemów

Modelowanie systemów

złożonych

złożonych

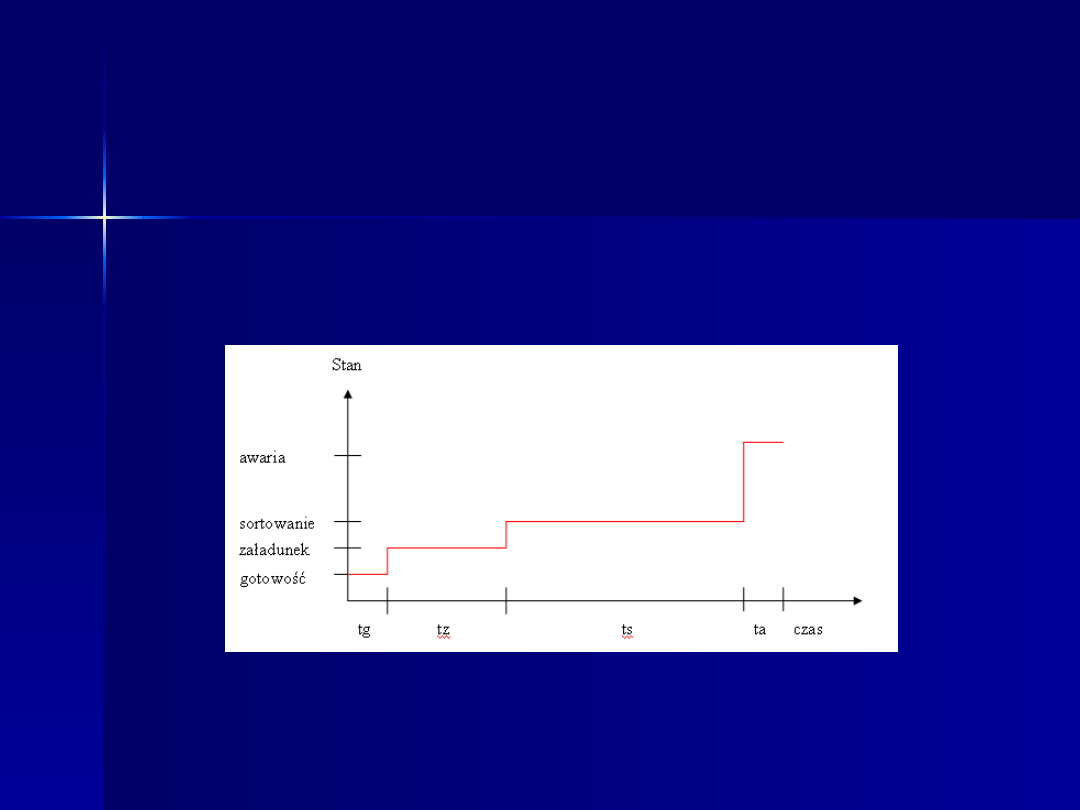
d) sortownia

d) sortownia

Modelowanie systemów

Modelowanie systemów

złożonych

złożonych

Sformułowanie matematycznych modeli czasów

Sformułowanie matematycznych modeli czasów

przebywania owoców aronii w wyróżnionych

przebywania owoców aronii w wyróżnionych

stanach

stanach

zmienna losowa rozkładu

zmienna losowa rozkładu

równomiernego

równomiernego

zmienna losowa rozkładu

zmienna losowa rozkładu

równomiernego

równomiernego



gotowosci





awarii



sortowni

wydajnosc

aronii

masa

sortowania

_

_





ladowania

wydajnosc

aronii

masa

załaładun

rozłozładu

_

_









Modelowanie systemów

Modelowanie systemów

złożonych

złożonych

e) dystrybucja

e) dystrybucja

Modelowanie systemów

Modelowanie systemów

złożonych

złożonych

Sformułowanie matematycznych modeli

Sformułowanie matematycznych modeli

czasów przebywania owoców aronii w

czasów przebywania owoców aronii w

wyróżnionych stanach

wyróżnionych stanach

zmienna losowa rozkładu

zmienna losowa rozkładu

równomiernego

równomiernego

zmienna losowa rozkładu

zmienna losowa rozkładu

równomiernego

równomiernego



gotowosci





awarii



predkosc

droga

transportu





sortowni

wydajnosc

aronii

masa

sortowania

_

_





ladowania

wydajnosc

aronii

masa

załaładun

rozłozładu

_

_









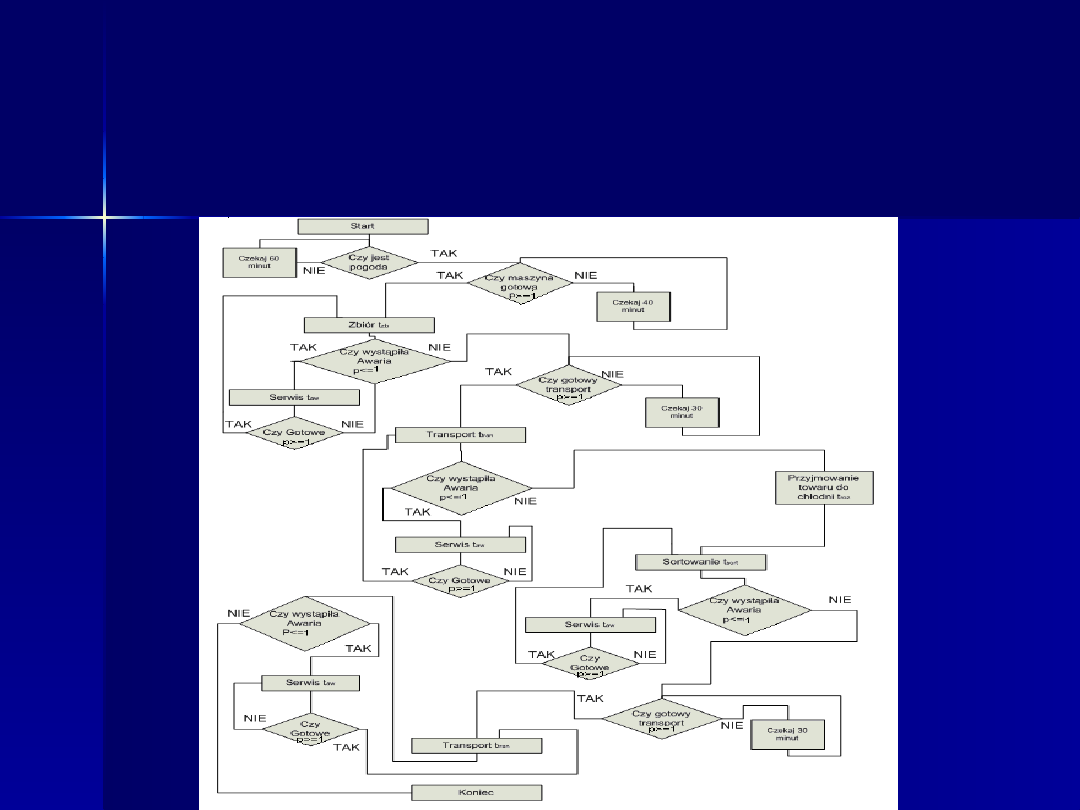
Modelowanie systemów złożonych

Modelowanie systemów złożonych

Schemat blokowy działania modelu dla symulacji komputerowej

Schemat blokowy działania modelu dla symulacji komputerowej