Systemy 

transportowe II

WYKŁAD 5

Odwzorowaniem

 

przemieszczania

 

ładunków 

i 

(lub) 

osób 

w 

systemie 

transportowym  jest 

POTOK  RUCHU

, 

który  przepływa  przez  węzły  i  łuki  w  sieci  o 
strukturze grafu G = <W, L>. 

Ładunki  i  (lub)  osoby  przewożone  są  w 
pojazdach,  wielkość  potoku  ruchu  wyrażamy 
zatem

liczbą pojazdów na jednostkę czasu
liczbą  jednostek  potoku  ruchu  na 
jednostkę czasu.

systemy transportowe II – W5 J. 

Żak

2

Potok ruchu można 
przedstawić w dwóch 
aspektach:

jako potok ruchu na 
drodze;

jako potok ruchu w sieci.

systemy transportowe II – W5 J. 

Żak

3

Potok ruchu na drodze

Analizując potok ruchu na drodze, na 
potrzeby modelowania ST, ograniczymy się 
do ustalenia wybranych charakterystyk: 
Intensywności potoku ruchu, 
Gęstości potoku ruchu, 
Prędkości  potoku ruchu, 
Czasu  przemieszczania się potoku ruchu, 
Równomierności  potoku ruchu, 
Struktury  potoku ruchu. 

systemy transportowe II – W5 J. 

Żak

4

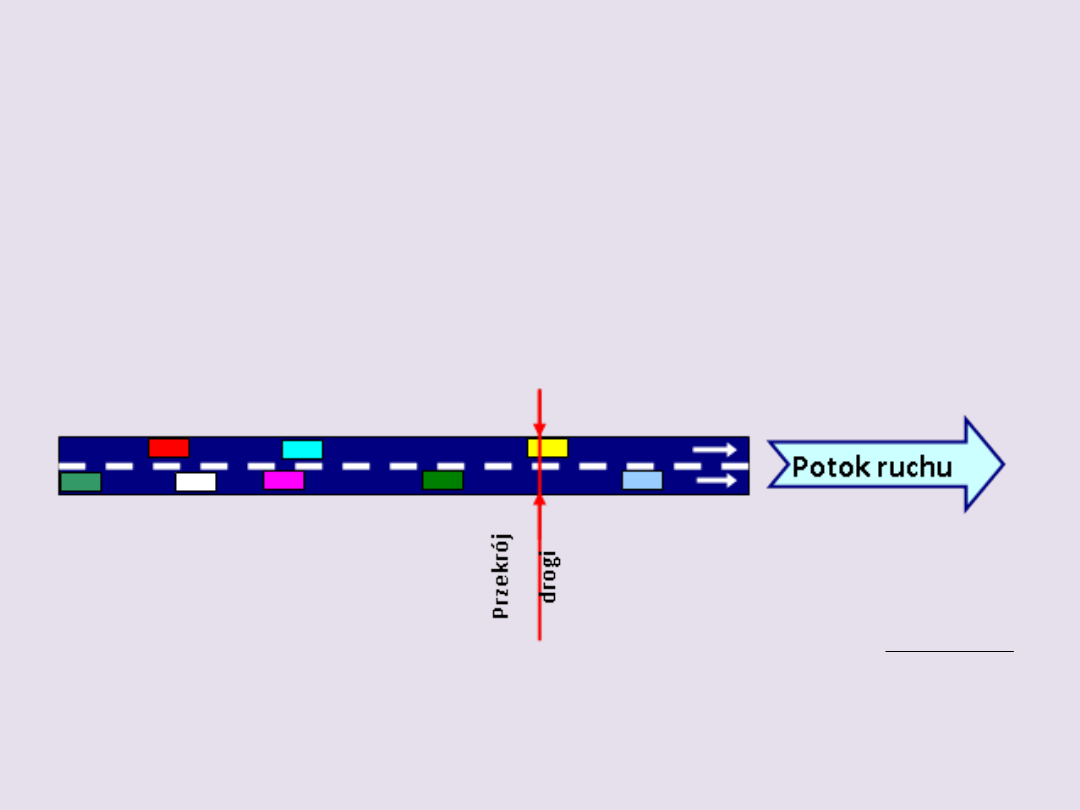
INTENSYWNOŚĆ 

(NATĘŻENIE) POTOKU 

RUCHU

Intensywność (natężenie) potoku ruchu 
- x 

, to liczba pojazdów przechodzących 

przez przekrój drogi w jednostce czasu. 

systemy transportowe II – W5 J. 

Żak

5

�

�

�

�

�

�

pojazdów

J EDNOSTKA -

godz.

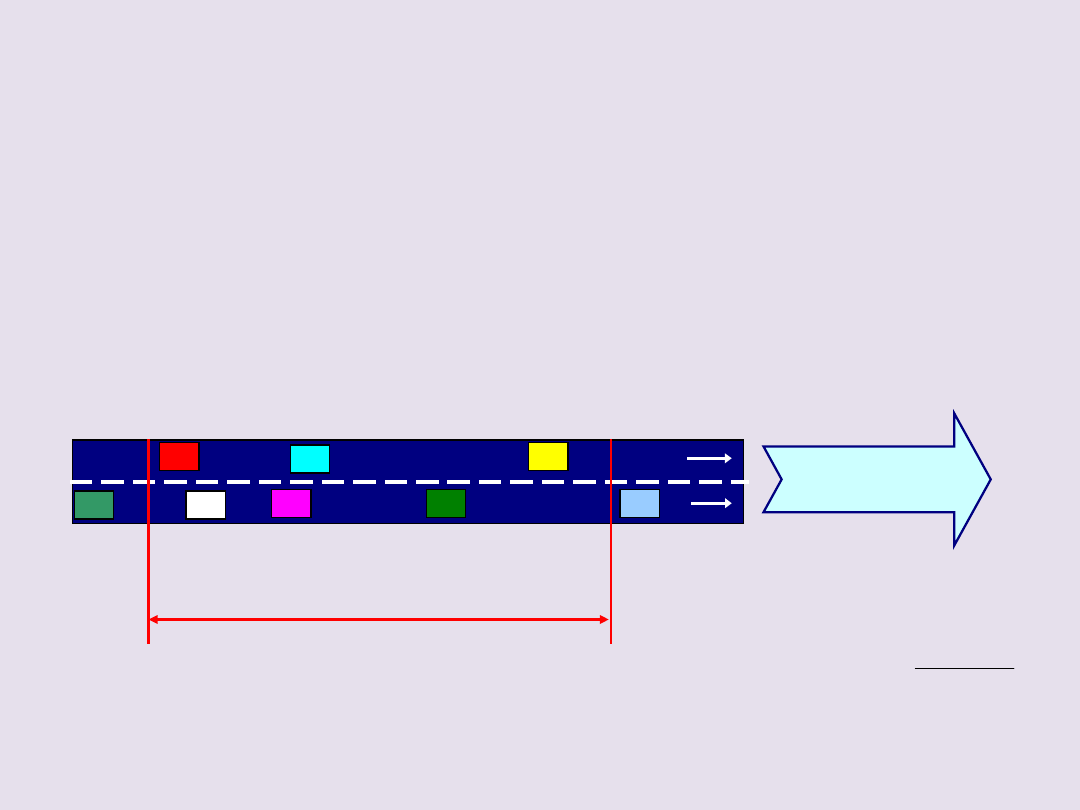
GĘSTOŚĆ POTOKU 

RUCHU 

Gęstość potoku ruchu - w

, to liczba pojazdów 

przypadająca na jednostkę długości drogi 
w określonej chwili. 

systemy transportowe II – W5 J. 

Żak

6

Odcinek drogi

Potok ruchu











km

pojazdów

JEDNOSTKA

PRĘDKOŚĆ RUCHU

prędkość ruchu - v:

systemy transportowe II – W5 J. 

Żak

7













km

pojazdów

JEDNOSTKA

w

x

v

 Omówione charakterystyki możemy 

rozpatrywać jako :
średnie,
minimalne,
maksymalne.

CZAS JAZDY

czas jazdy - �

systemy transportowe II – W5 J. 

Żak

8

 Czas jazdy może być rozpatrywany w 

układzie:

       a)  pojedynczy pojazd na drodze,

       b)  potok ruchu na drodze.

Zakładamy, że:

   

�

m

  

-  minimalny czas jazdy konieczny na 

pokonanie drogi;
 

 

�

s  

 

- średni czas  konieczny na pokonanie drogi 

przez przeciętny pojazd.

Zachodzi przy tym nierówność:

 

�

m 

  �  

s

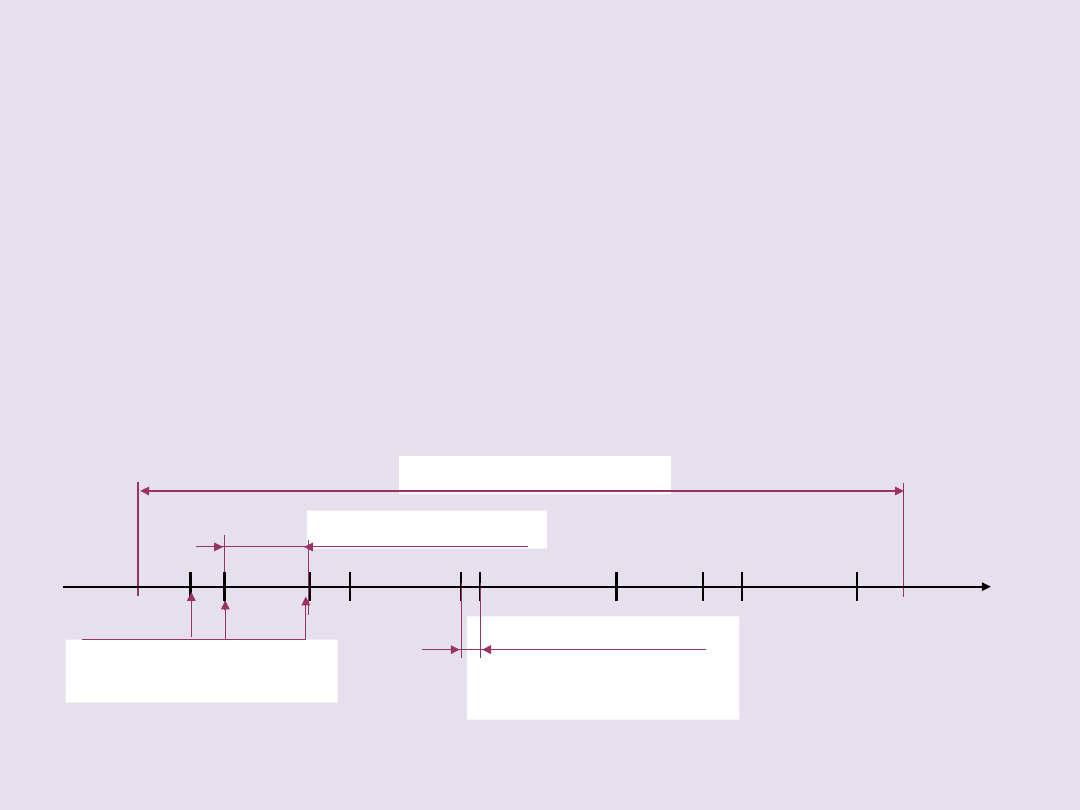
RÓWNOMIERNOŚĆ 

POTOKU RUCHU

Równomierność potoku ruchu - �: 

liczona 

jako iloraz minimalnego czasu następstwa 
pojazdów do średniego czasu ich następstwa 
w wybranym przedziale czasu obserwacji, tj.:
                           

systemy transportowe II – W5 J. 

Żak

9

czas następstwa

czas obserwacji

minimalny czas 

następstwa

chwile zgłoszeń 

pojazdów

STRUKTURA POTOKU 

RUCHU

Struktura potoku ruchu 

- to 

charakterystyka potoku ruchu 
wyrażona w % opisującą procentowy 
udział pojazdów określonego typu 
(klasy) w całym potoku ruchu, np.:
•

30%    -  jednoślady;

•

67%   -  samochody osobowe;

•

  3%   -  samochody ciężarowe

systemy transportowe II – W5 J. 

Żak

10

Najczęściej używanym opisem 
(modelem) potoku ruchu w układzie 

POJAZD - DROGA 

jest 

MODEL CZASU 

NASTĘPSTWA 

w postaci wartości 

ustalonej (

RÓWNOODSTĘPOWY 

POTOK

), zmiennej losowej, lub też 

rozkładu tej zmiennej losowej w postaci 
jej dystrybuanty.

 Dla 

POTOKU WIELOWYMIAROWEGO 

czas następstwa zgłoszeń może być 
wielowymiarową dystrybuantą.

systemy transportowe II – W5 J. 

Żak

11

POTOK RUCHU W SIECI 

TRANSPORTOWEJ

ST

 jest systemem 

otwartym

. Powiązanie 

systemu z otoczeniem dokonywane jest 
poprzez 

punkty styku systemu i otoczenia

. 

Zakładamy przy tym, że odwzorowaniem 

ODDZIAŁYWANIA OTOCZENIA 

na ST jest 

potok ruchu 

pojawiający się na 

WEJŚCIACH

 

do sieci, natomiast odwzorowaniem 
oddziaływania ST na 

OTOCZENIE

 jest potok 

ruchu pojawiający się na 

WYJŚCIACH

 z sieci.

systemy transportowe II – W5 J. 

Żak

12

Węzeł w którym powstaje 
zapotrzebowanie na potok ruchu 
będziemy nazywać 

ŹRÓDŁEM

 potoku 

ruchu. Natomiast węzeł, w którym 
zanika potok ruchu będziemy nazywać 

UJŚCIEM

 potoku ruchu. Źródła i ujścia 

opisują 

powiązania ST z otoczeniem

. 

Oznacza to, że:
źródła są wejściami  do ST,
ujścia są wyjściami  z ST

systemy transportowe II – W5 J. 

Żak

13

Wydajność

 źródeł i chłonność ujść 

będziemy interpretować jako 

ZAPOTRZEBOWANIE OTOCZENIA SYSTEMU 
TRANSPORTOWEGO NA PRZEWÓZ 

(

ZNP

). 

systemy transportowe II – W5 J. 

Żak

14

Zapotrzebowaniem na przewóz 
(ZNP) nazywamy potok ruchu, 
który należy przeprowadzić 
przez sieć transportową ze 
źródła do ujścia potoku. Para 
źródło - ujście jest relacją 
przewozu dla tego potoku 
ruchu.

Potok ruchu przepływający 
przez sieć transportową 
powiązany jest z:

a) punktami styku systemu 
transportowego z otoczeniem;

b) relacjami przewozu;
c) drogami przejścia potoku ruchu 
przez sieć transportową.

systemy transportowe II – W5 J. 

Żak

15

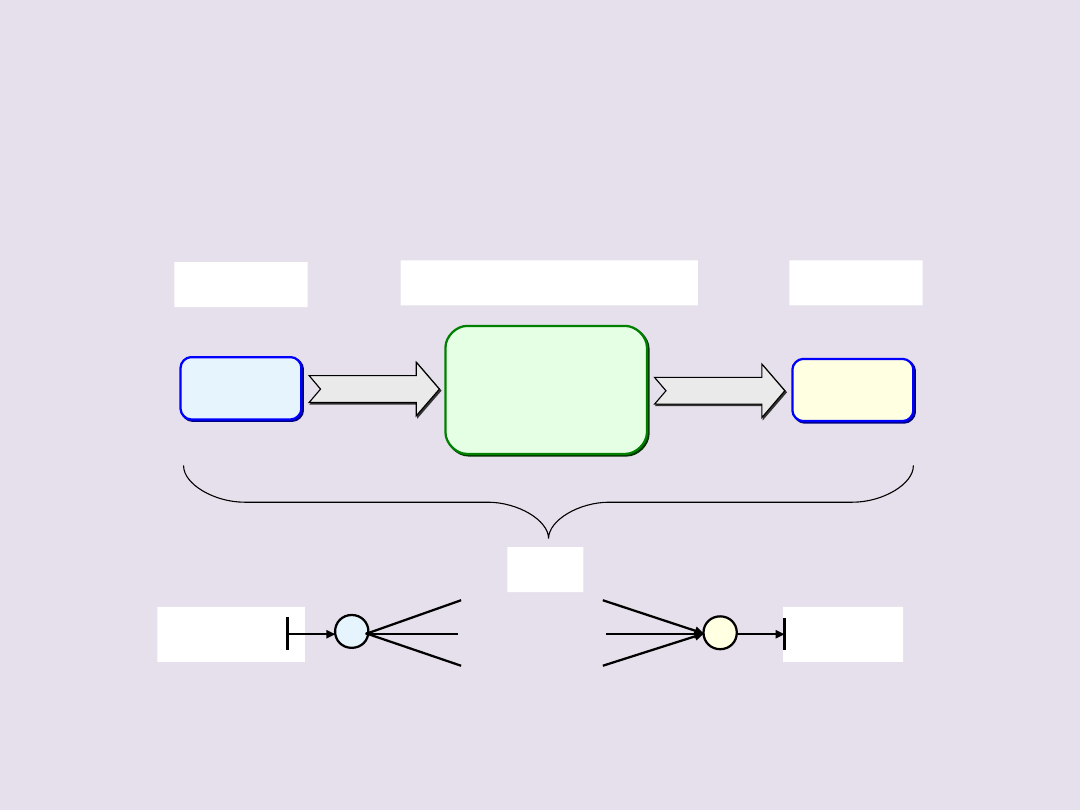
systemy transportowe II – W5 J. 

Żak

16

A

A

B

B

V

V

W

ŹRÓDŁ

A

UJŚCIA

WĘZŁY 

POŚREDNIE

POCZĄTEK 

PRZEWOZ

U

i=a

a-te 

źród

ło

j=b

b-te 

ujści

e

KONIEC 

PRZEW

OZU

Dekompozycja zbioru węzłów struktury 
ST

RELACJA PRZEWOZU

Relacją przewozu nazywamy parę (a, b), 
w której pierwszy element nazywamy 
początkiem  relacji, a drugi element – jej 
końcem ; a∈A, b ∈ A; 
(a,b - numer (nazwa) węzła)
Relacja przewozu jest podzbiorem iloczynu 
kartezjańskiego. Stąd, jeśli przez E 
oznaczymy zbiór relacji przewozu w badanej 
sieci transportowej

EAB={(a ,b): aA, bB}

systemy transportowe II – W5 J. 

Żak

17

systemy transportowe II – W5 J. 

Żak

18

W  przypadku  sieci  transportowych 
wymaga 

się, 

aby 

węzeł 

b 

był 

OSIĄGALNY

  z  węzła  a.  Zakładamy, 

zatem, 

że 

graf 

G, 

będący 

odwzorowaniem 

struktury 

sieci 

transportowej ma własność spójności w 
sensie  dróg.  Wymaga  się  zatem  aby 
sieć transportowa była spójna w sensie 
relacji przewozu. 

Struktura  G  jest  spójna  dla  zbioru 
relacji przewozu E, gdy dla każdej pary 
(a,b)∈E  zbiór  P

ab

  ≠Ø,  tzn.  istnieje  co 

najmniej jedna droga łącząca węzeł a z 
węzłem b. 

 







ab

a,b

P

E

)

(

Ø

systemy transportowe II – W5 J. 

Żak

19

p,ab

ij

x

Rozszerzając 

wcześniej 

przyjęte 

oznaczenia 

na 

sieć 

transportową, przyjmujemy następującą notację oznaczeń:

•[x

ij

]  –  macierz  potoku  ruchu  przemieszczanego  po  łukach  (i, 

j),  (i,  j)∈L  należących  do  sieci  transportowej,  czyli  macierz 
rozłożenia potoku ruchu w sieci transportowej o strukturze  G 
=  <W,  L>;  w  modelu  rozłożenia            potoku  ruchu  jest  to 
macierz zmiennych decyzyjnych modelu;

•[        ]  –  macierz  wartości  liczbowych  opisujących  ustalone 
rozłożenie potoku ruchu w sieci transportowej; są to wartości 
otrzymane  w  wyniku  rozwiązania  zadania  rozłożenia  potoku 
ruchu w sieci transportowej;

•[x

ab

]    –  macierz  zapotrzebowania  na  przewóz  (ZNP), 

określająca  wymaganą  wielkość  potoku  do  przeprowadzenia 
przez  sieć  transportową  dla  zbioru  relacji  przewozu  –  E,  z 
węzła a do węzła b (a∈A, b∈B);

•    

  –  składowa  potoku  ruchu  w  relacji  (a,  b), 
przemieszczanego p-tą drogą po łuku   (i,j)∈L (a∈A, 
b∈B; p∈P

ab

).

ij

x

Warunki nakładane na potok ruchu 

przemieszczany po elementach 

struktury sieci transportowej

Zbiór dróg łączących źródło a z ujściem b 
i zawierających  łuk (i,j)

systemy transportowe II – W5 J. 

Żak

20

L

L 







p

a,b

 

 

 

i,j

 

: 

p

 = 

E,

p

L

ab

P

 

ab

ij

P

)

}

)

(

(

{

Wielkość

 potoku ruchu przemieszczanego łukiem (i, j) 

będzie sumą potoku ruchu przemieszczanego po drogach p 
należących do różnych relacji (a, b) i zawierających łuk (i, j), 
co zapisujemy:

ab

p

p

b

a

,

)

,

(









ab

ij

P

E

x

ij

x =

=

 

WARUNEK NIEUJEMNOŚCI 

POTOKU RUCHU (NP.)

a) dla łuków sieci transportowej:

b) dla dróg w sieci transportowej:

    

c) dla składowych potoku ruchu:

systemy transportowe II – W5 J. 

Żak

21

0

L

)

(







ij

x

i,j

0

)

(

,

ab











x

P

E

ab

p

p

a,b

0

)

,

(

)

(

,

ab















ab

p

j

i

p

a,b

ij

x

L

P

E

WARUNEK 

ADDYTYWNOŚCI POTOKU 

RUCHU (AP)

systemy transportowe II – W5 J. 

Żak

22

 











E

P

x

x

)

,

(

,

)

,

(

b

a

p

ij

ab

p

ij

ab

j

i

L

Wykonalność operacji dodawania 
na składowych potoku ruchu 
nazywamy warunkiem 
addytywności 

WARUNEK ZACHOWANIA 

POTOKU RUCHU (ZP)

dla węzłów pośrednich:

systemy transportowe II – W5 J. 

Żak

23



















)

(

i

1

i

Γ

Γ

k

ik

j

ji

i

x

x

V

0

dla źródeł potoku 
ruchu



















)

(

i

1

i

Γ

Γ

k

ik

j

ji

i

x

x

A

- x

ab

i

ab

ik

k

i

x

x

�G

�

=-

"

�

A

1

i

Γ

-

=�

systemy transportowe II – W5 J. 

Żak

24

dla ujść potoku 
ruchu



















)

(

i

1

i

Γ

Γ

k

ik

j

ji

i

x

x

B

x

ab 

ab

j

ji

x

i













1

i

Γ

x

B





































B

V

A

i

dla

x

i

dla

i

dla

x

i

ab

ab

k

ik

j

ji

0

)

x

x

(

i

1

i

Γ

Γ

W

Uogólniając dla danej relacji przewozu (a,b) równanie 
zachowania potoku ruchu w sieci transportowej ma postać

systemy transportowe II – W5 J. 

Żak

25

systemy transportowe II – W5 J. 

Żak

26