Rachunek
prawdopodobieństwa 2
uczelnia: PJWSTK
przedmiot: Matematyka Dyskretna 2
wykładowca: dr Magdalena Kacprzak
data: styczeń 2009
Materiały pomocnicze do wykładu

Zmienna losowa

Definicja
Niech będzie przestrzenią zdarzeń
elementarnych. Każdą funkcję określoną
na zbiorze i o wartościach w zbiorze liczb
rzeczywistych nazywać będziemy
zmienną
losową
.
Jeśli zmienna przyjmuje co najwyżej przeliczalną
liczbę wartości, to będziemy ją nazywali
zmienną
losową dyskretną
.

Przykład
(a) Rozpatrzymy doświadczenie polegające na
rzucie monetą. Wówczas możemy przyjąć
następującą zmienną losową:
X(orzeł)=0, X(reszka)=1
(b) Rozpatrzmy doświadczenie polegające na
rzucie kostką do gry. Wówczas mamy
następującą zmienna losową:
X(1)=1, X(2)=2, X(3)=3,...,X(6)=6

Definicja
Powiemy, że dwie zmienne losowe X i Y są
niezależne
wttw dla dowolnych przedziałów I, J
zbioru liczb rzeczywistych
P(XI i YJ) = P(XI)P(YJ)
Jeśli zmienne X i Y są zmiennymi dyskretnymi, to
niezależność zmiennych wyraża się warunkiem:
P(X=x i Y=y)=P(X=x)P(Y=y)
dla dowolnych x,y R.

Rozkład prawdopodobieństwa

Definicja
Funkcję f
X
określoną na zbiorze liczb
rzeczywistych R i o wartościach w zbiorze
[0,1] taką, że f
X
(x)=P(X=x) dla xR
nazywamy
rozkładem prawdopodobieństwa
zmiennej losowej X.

Przykład
Rzucamy dwiema symetrycznymi kostkami do gry. Każdemu
z rzutów przypisujemy wartość bezwzględną różnicy liczby
oczek wyrzuconej na jednej i drugiej kostce. Podaj rozkład
zmiennej losowej.
UWAGA! p
0
+p
1
+
p
2
+... + p
5
=1
x
i
0
1
2
3
4
5
p
i
6/36 10/3
6
8/36 6/36 4/36 2/36
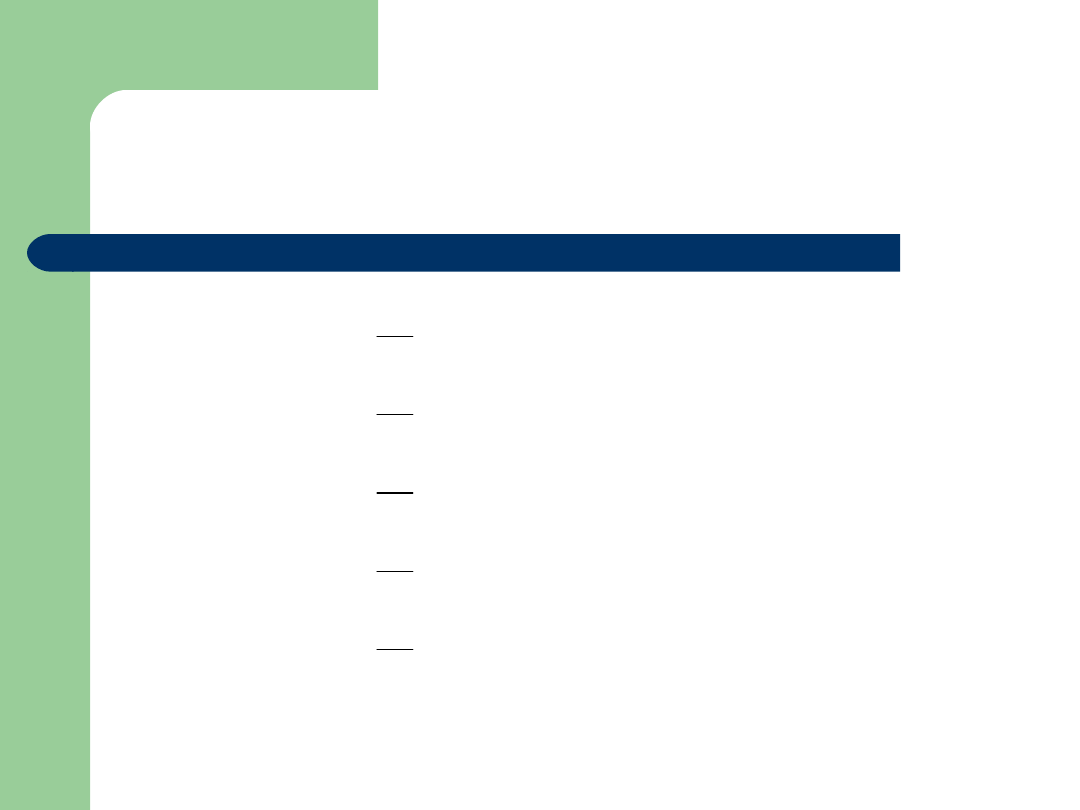
Przykład
x
innych
dla
0
5
x
dla
36
2
4
x
dla
36
4
2
x
dla
36
8
1
x
dla
36
10
3
x
i
0
x
dla
36
6
)
x
(
f
X
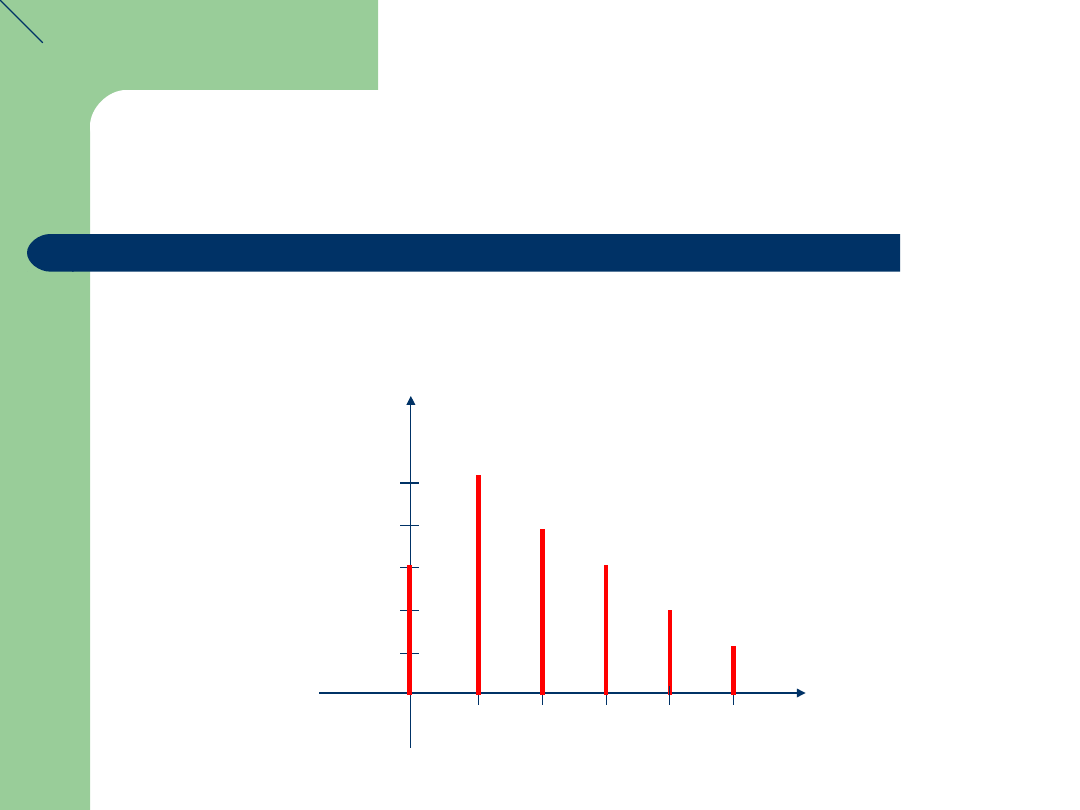
Przykład
{(0,6/36), (1,10/36), (2,8/36), (3,6/36), (4,4/36), (5,2/36)}
0 1 2 3 4
5
10/36
8/36
6/36
4/36
2/36

Definicja
Rozkładem dwumianowym
(Bernoulliego)
Nazywamy rozkład prawdopodobieństwa
określony wzorem
0
p)
(1
p
k
n
f(k)
k
n
k
dla k=0,1,...,n
dla pozostałych wartości k

Przykład
Wiadomo, że szansa poprawnego oznaczenia próbki
w jednokrotnym badaniu mikroskopijnym wynosi 3:4.
Poddano badaniu 3 próbki. Niech X oznacza liczbę próbek,
które zostały poprawnie oznaczone. Wyznaczyć te
prawdopodobieństwa.

Przykład
64
27
4
1
4
3
3
3
p
64
27
4
1
4
3
2
3
p
64
9
4
1
4
3
1
3
p
64
1
4
1
4
3
0
3
p
0
3
3
1
2
2
2
1
1
3
0
0
x
i
0
1
2
3
p
i
1/64 9/64 27/6
4
27/6
4
p
0
+p
1
+
p
2
+p
3
=
1/64+9/64+27/64+27/64=1

Definicja
Rozkład prawdopodobieństwa określony
wzorem f(k) = p(1-p)
k-1
nazywamy
rozkładem geometrycznym
.

Przykład
Rozważmy doświadczenie polegające na serii niezależnych
rzutów
symetryczną monetą powtarzanych dopóty dopóki nie
wypadnie
orzeł. Niech X będzie zmienną losową, której wartością jest
liczba
wykonanych prób do chwili uzyskania orła. Wyznacz rozkład
prawdopodobieństwa.
p=1/2, (1-p)=1/2,
p(1-p)
i-1
=(1/2)(1/2)
i-1
=(1/2)
i
x
i
1
2
3
....
i
....
p
i
1/2
(1/2)
2
(1/2)
3
....
(1/2)
i
....

Definicja
Rozkład prawdopodobieństwa dyskretnej
zmiennej losowej nazywamy
jednostajnym (jednorodnym)
,
jeśli przybiera ona wszystkie swoje
wartości z takim samym
prawdopodobieństwem.
Przykład
Dwaj gracze grają w orła i reszkę. Jeśli wypadnie orzeł gracz
G
1
płaci graczowi G
2
złotówkę. Jeśli wypadnie reszka, to gracz
G
2
płaci
graczowi G
1
złotówkę. Niech X będzie zmienną losową
opisującą
wygraną gracza G
1
. Wyznacz rozkład prawdopodobieństwa.
x
i
-1
1
p
i
1/2
1/2

Dystrybuanta
zmiennej losowej

Definicja
Niech X będzie zmienną losową określoną na
dowolnej przestrzeni zdarzeń losowych .
Dystrybuantą
zmiennej X nazywamy
funkcję F:R [0,1] taką, że
F
X
(x) = P(X x) dla xR.

Definicja
W przypadku zmiennej losowej dyskretnej
powyższy wzór przyjmuje postać
F
X
(x) =
yx
f
X
(y)
gdzie f
X
jest rozkładem
prawdopodobieństwa zmiennej X.
Przykład
Do tarczy oddaje się w sposób niezależny 3 strzały. P-d trafienia
do tarczy wynosi ½ dla każdego strzału. Niech zmienna losowa
X oznacza liczbę trafień w tarczę. Wyznaczyć dystrybuantę
zmiennej losowej.
X
(-,0) [0,1)
(1,2]
(2,3]
(3,+
)
F(x)
0
1/8
4/8
7/8
1
x
i
0
1
2
3
p
i
1/8
3/8
3/8
1/8
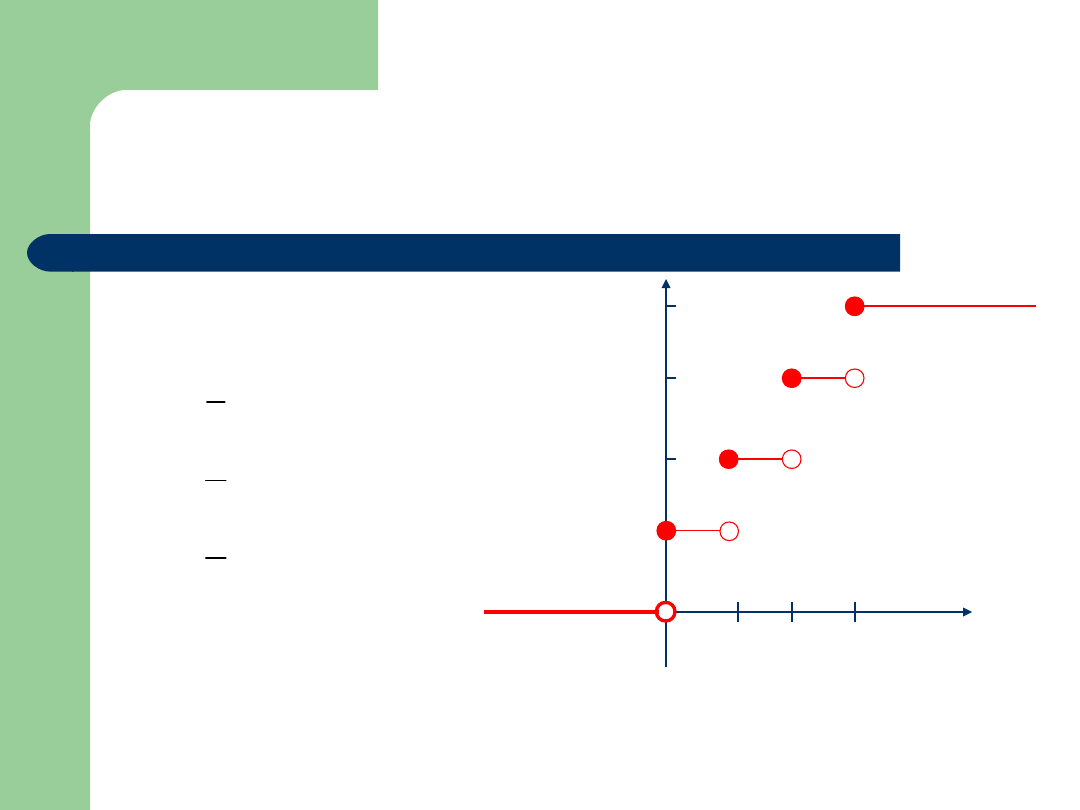
Przykład
3
x
dla
1
3
x
2
dla
8
7
2
x
1
dla
2
1
1
x
0
dla
8
1
0
x
dla
0
)
x
(
F
F(2)=P(X2)=P(X=2)+P(X=1)+P(X=0)=3/8+3/8+1/8=7/8
1 2 3
1
7/8
1/2
1/8

Lemat
Dystrybuanta zmiennej losowej dyskretnej
jest funkcją niemalejącą. Co więcej,
dystrybuanta zmiennej losowej rośnie
skokowo w punktach należących do zbioru
wartości tej zmiennej.

PARAMETRY ROZKŁADU

Wartość oczekiwana
zmiennej losowej

Definicja
Niech będzie przestrzenią zdarzeń
elementarnych, a X zmienną losową
określoną w .
Wartością oczekiwaną
zmiennej X nazywamy liczbę
E(X) =
w
X(w) P({w})
Stwierdzenie
Jeśli wszystkie zdarzenia elementarne są
jednakowo prawdopodobne, a przestrzeń
jest skończona, to P({w}) = 1/||, a
wtedy
Ω
X(w)
E(X)
Ω
w

Lemat
Niech X będzie zmienną losową dyskretną
określoną w pewnej przestrzeni zdarzeń
elementarnych oraz niech (x
i
)
iI
będzie
ciągiem wszystkich różnych wartości jakie
przyjmuje ta zmienna. Jeżeli suma
i
(x
i
P(X=x
i
))
jest określona, to
I
i
i
X
i
))
(x
f
(x
E(X)

Przykład
Zakładając, że liczba wezwań górskiego pogotowia
ratunkowego w ciągu doby ma następujący rozkład
(a) Obliczyć p-d, że w ciągu doby liczba wezwań będzie wynosić od 2 do
4
P(2X4)=P(X=2)+P(X=3)+P(X=4)=0,18+0,15+0,12=0,45
(b) Obliczyć oczekiwaną liczbę wezwań w ciągu doby
E(X)=00,12+10,32+20,18+30,15+40,12+50,08+60,003=2,19
X=x
i
0
1
2
3
4
5
6
P(X=x
i
)
0,12
0,32
0,18
0,15
0,12
0,08
0,003

Suma zmiennych losowych
Niech będzie ustaloną przestrzenią zdarzeń,
w której mamy określone dwie zmienne losowe
dyskretne X i Y.
Suma zmiennych losowych
X i Y jest zmienną losową Z, określoną dla
dowolnego zdarzenia elementarnego w tej
przestrzeni jako
Z(w) = X(w)+Y(w).
Jeśli zmienna X przyjmuje wartości x
i
dla iI, a
zmienna Y przyjmuje wartości y
j
dla jJ, to
zmienna Z przyjmuje jako swoje wartości liczby
(x
i
+y
j
) dla dowolnych iI i jJ.

Twierdzenie
Niech będzie przestrzenią zdarzeń,
w której określone są zmienne losowe X i Y.
Jeśli wartości oczekiwane zmiennych X i Y istnieją,
to dla dowolnego c zachodzą równości
(1) E(cX) = cE(X),
(2) E(X+Y) = E(X)+E(Y),
(3) E(X - E(X)) = 0.

Iloczyn zmiennych losowych
Analogicznie jak sumę zmiennych, można
zdefiniować
iloczyn zmiennych losowych
X i Y
określonych w tej samej przestrzeni .
Przyjmujemy
Z(w) = X(w) Y(w) dla w.
Zmienna Z przyjmuje jako swoje wartości iloczyny
x
i
y
j
dla i I i j J, jeśli x
i
i y
j
są wartościami
zmiennych X i Y odpowiednio.

Twierdzenie
Jeśli X i Y są niezależnymi zmiennymi
losowymi, to
E(XY) = E(X)E(Y).

Wariancja
zmiennej losowej

Definicja
Wariancją
zmiennej losowej X, oznaczaną przez
V(X), nazywamy wartość oczekiwaną zmiennej
losowej (X-EX)
2
, tzn.
V(X) = E((X-EX)
2
)
Jeśli X jest zmienną dyskretną o rozkładzie
prawdopodobieństwa {(x
i
,p
i
)}
i=1,...n
, oraz
E(X) = m, to
V(X) = (x
1
- m)
2
p
1
+...+ (x
n
- m)
2
p
n

Twierdzenie
Dla dowolnej zmiennej losowej dyskretnej
(1)
V(X) = E(X
2
) - (E(X))
2
(2) dla dowolnego cE(X), V(X)<E((X-c)
2
)

Twierdzenie
Jeżeli V(X) jest wariancją zmiennej losowej
dyskretnej X, a V(Y) jest wariancją
zmiennej losowej dyskretnej Y, to dla
dowolnej stałej rzeczywistej c,
(1) V(cX) = c
2
V(X),
(2) Jeśli zmienne losowe X i Y są
niezależne, to V(X+Y)= V(X) + V(Y).
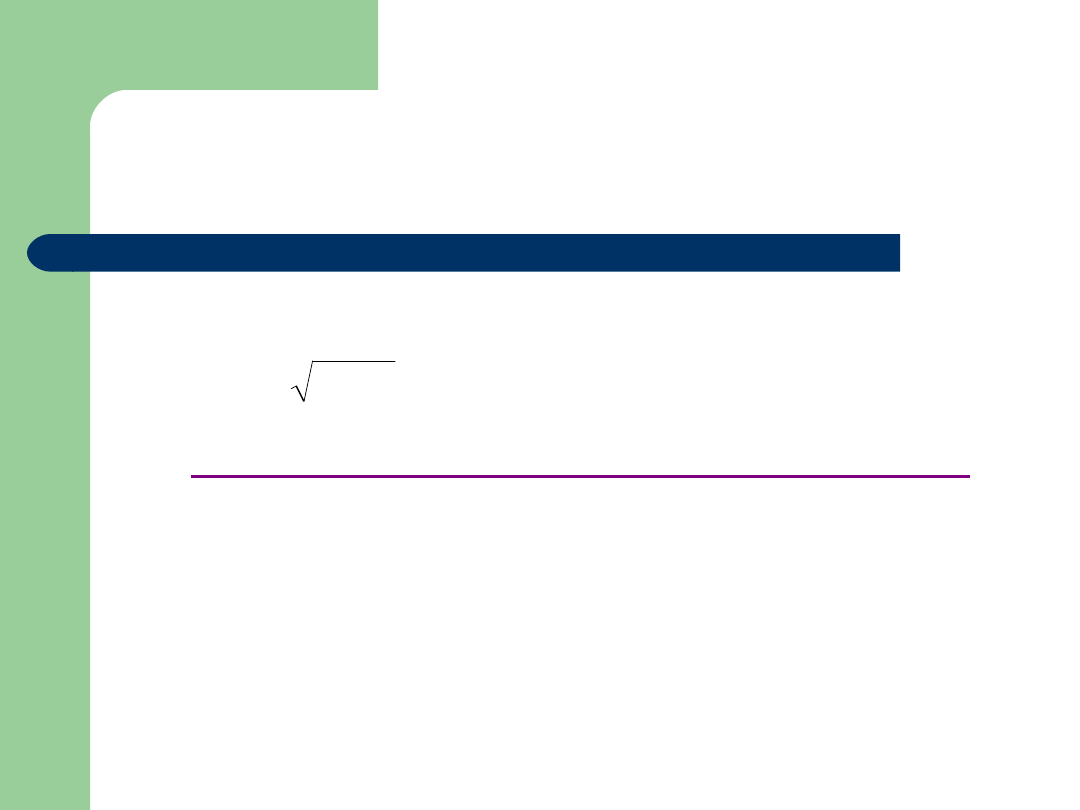
Definicja
Liczbę nazywamy
odchyleniem standardowym
zmiennej X.
V(X)
Przykład
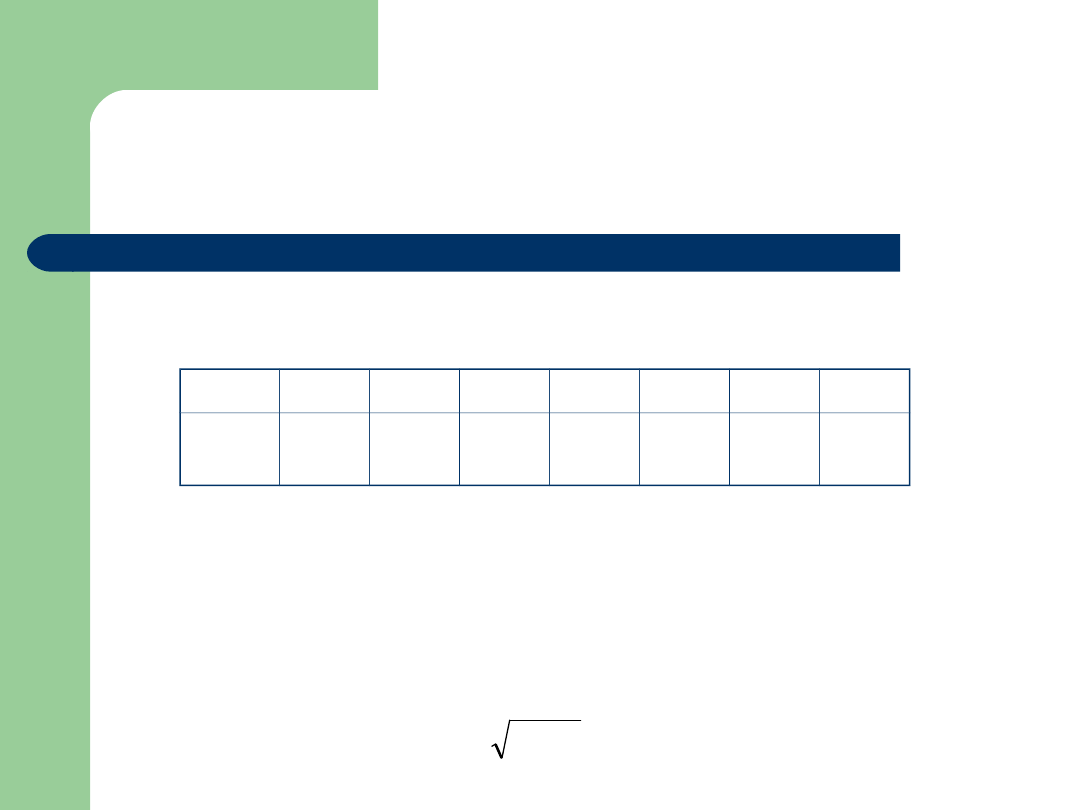
Zakładając, że liczba wezwań górskiego pogotowia
ratunkowego w ciągu doby ma następujący rozkład
Obliczyć wariancje i odchylenie standardowe.
Wiemy, że E(X)=2,19,
E(X
2
)=00,12+10,32+40,18+90,15+160,12+250,08+360,003=
6,418.
Stąd V(X)=6,418-(2,19)
2
=1,6219 oraz
27
,
1
)
X
(
V
X=x
i
0
1
2
3
4
5
6
P(X=x
i
)
0,12
0,32
0,18
0,15
0,12
0,08
0,003

Parametry
znanych rozkładów
prawdopodobieństwa

Lemat
Niech X będzie zmienną losową o
rozkładzie zerojedynkowym
P(X=1) = p i P(X=0) = 1-p.
Wtedy
E(X)=p
oraz
V(X)=p(1-p)
.

Przykład
Rozważmy następującą grę. Gracz rzuca monetą, jeśli
wypadnie reszka otrzymuje 1 zł jeśli wypadnie orzeł o
trzymuje 0 zł. Niech X będzie zmienną losową, której
wartością jest otrzymana kwota pieniędzy. Wyznacz wartość
oczekiwaną, wariancję i odchylenie standardowe.
Przykład
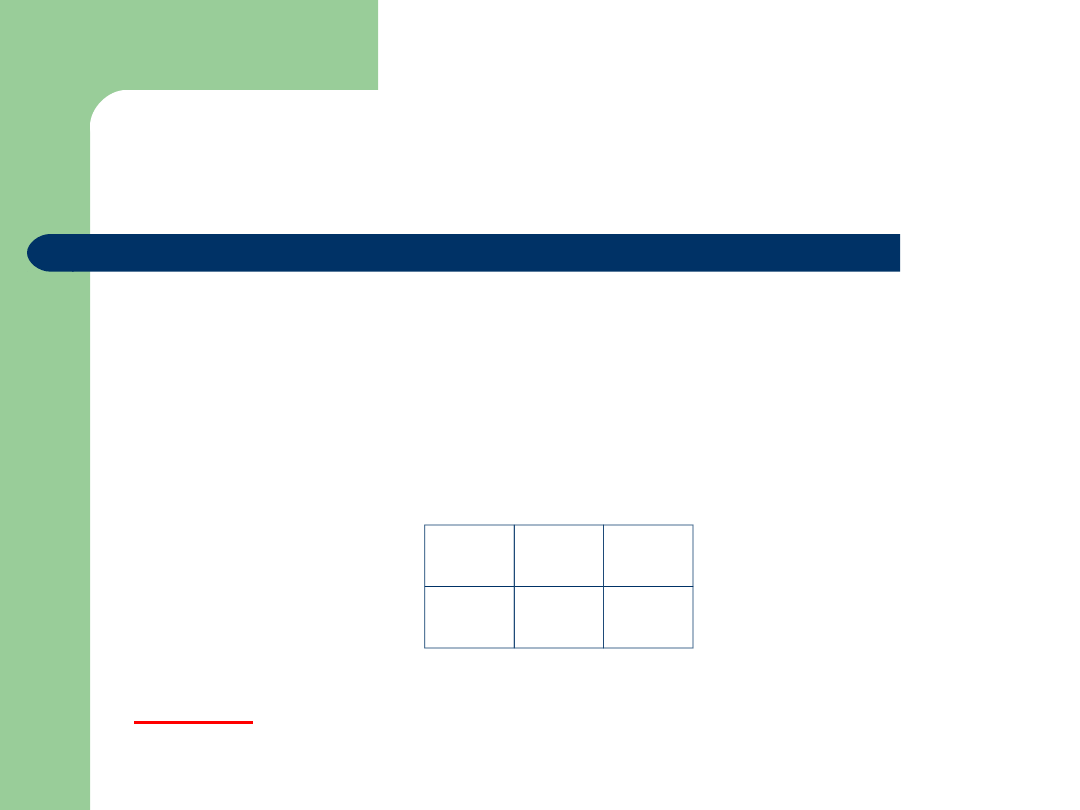
Rozważmy następującą grę. Gracz rzuca monetą, jeśli
wypadnie reszka otrzymuje 1 zł jeśli wypadnie orzeł o
trzymuje 0 zł. Niech X będzie zmienną losową, której
wartością jest otrzymana kwota pieniędzy. Wyznacz wartość
oczekiwaną, wariancję i odchylenie standardowe.
x
i
0
1
p
i
1/2
1/2
E(X)=p=1/2
V(X)=p(1-p)=1/21/2=1/4
(V(X))=1/2
p=1/2

Lemat
Niech zmienna losowa X opisuje liczbę
sukcesów w
schemacie Bernoulliego
z
parametrami n i p (n – ilość prób,
p- prawdopodobieństwo sukcesu).
Wtedy
E(X)=np
oraz
V(X)=np(1-p)
.

Przykład
Wiadomo, że szansa poprawnego oznaczenia próbki
w jednokrotnym badaniu mikroskopijnym wynosi 3:4.
Poddano badaniu 3 próbki. Niech X oznacza liczbę próbek,
które zostały poprawnie oznaczone. Wyznaczyć wartość
oczekiwaną, wariancję i odchylenie standardowe.

Przykład
Wiadomo, że szansa poprawnego oznaczenia próbki
w jednokrotnym badaniu mikroskopijnym wynosi 3:4.
Poddano badaniu 3 próbki. Niech X oznacza liczbę próbek,
które zostały poprawnie oznaczone. Wyznaczyć wartość
oczekiwaną, wariancję i odchylenie standardowe.
x
i
0
1
2
3
p
i
1/64 9/64 27/6
4
27/6
4
E(X)=np=33/4=9/4=2,25
V(X)=np(1-p)= 33/41/4=9/16
(V(X))=3/4=0,75
n=3, p=3/4

Lemat
Niech zmienna X ma
rozkład
geometryczny
, tzn. rozkład określony
następująco:
f
X
(k)=P(X=k)=p(1-p)
k-1
dla k=1,2,3,...
Wtedy wartość oczekiwana zmiennej X,
EX=1/p
.

Przykład
Rozważmy doświadczenie polegające na serii niezależnych
rzutów
symetryczną monetą powtarzanych dopóty dopóki nie
wypadnie
orzeł. Niech X będzie zmienną losową, której wartością jest
liczba
wykonanych prób do chwili uzyskania orła. Wyznacz wartość
oczekiwaną.
Przykład
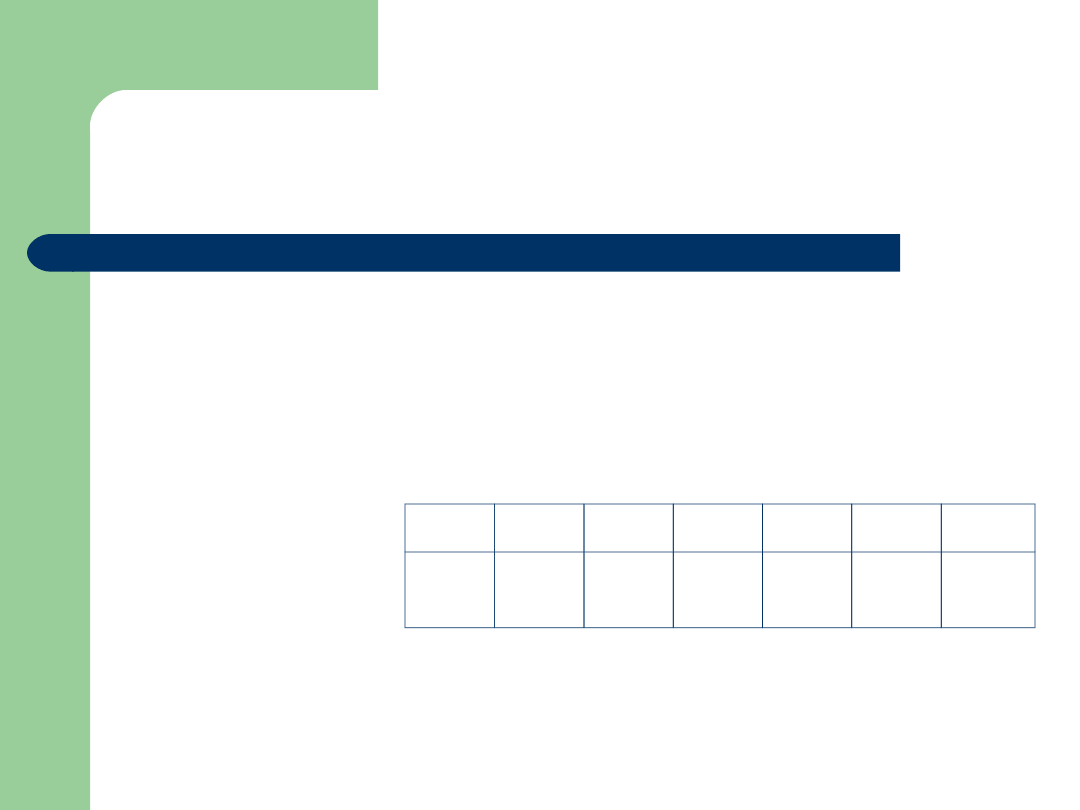
Rozważmy doświadczenie polegające na serii niezależnych
rzutów
symetryczną monetą powtarzanych dopóty dopóki nie
wypadnie
orzeł. Niech X będzie zmienną losową, której wartością jest
liczba
wykonanych prób do chwili uzyskania orła. Wyznacz wartość
oczekiwaną.
p=1/2, (1-p)=1/2,
x
i
1
2
3
....
i
....
p
i
1/2
(1/2)
2
(1/2)
3
....
(1/2)
i
....
EX=1/p=1/(1/2)=2
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
- Slide 38
- Slide 39
- Slide 40
- Slide 41
- Slide 42
- Slide 43
- Slide 44
- Slide 45
- Slide 46
- Slide 47
- Slide 48
- Slide 49
Wyszukiwarka
Podobne podstrony:
MAD2 VII Rachunek prawdopodobienstwa 1
Kordecki W, Jasiulewicz H Rachunek prawdopodobieństwa i statystyka matematyczna Przykłady i zadania
Matematyka - rachunek prawdopodbieństwa - ściąga, szkoła
09 Rachunek prawdopodobie ästwaid 7992
7 ELEMENTY RACHUNKU PRAWDOPODOBIEŃSTWA
MATEMATYKA Rachunek prawdopodobieństwa, str tytułowa, Marcin Nowicki
ćwiczenia rachunek prawdopodobieństwa i statystyka, Z Ćwiczenia 01.06.2008
Statystyka dzienne wyklad1, Rachunek prawdopodobie˙stwa
1 zadania z rachunku prawdopodobieństwa, Zad
Zestaw10 rachunek prawdopodobie Nieznany
ćwiczenia rachunek prawdopodobieństwa i statystyka, Z Ćwiczenia 18.05.2008
więcej podobnych podstron