OBLICZANIE ROZPŁYWÓW 

PRĄDÓW

W SIECIACH OTWARTYCH

- Metoda liczb 
zespolonych

- Pierwsze prawo 
Kirchhoffa

 

 

N

a

p

ię

c

ie

 

i 

p

r

ą

d

 

w

 

w

ę

ź

le

 

o

d

b

io

r

c

z

y

m

 

w

y

r

a

ż

a

ją

 

s

ię

 

w

z

o

r

a

m

i:

u

j

f

f

e

U

U





i

j

Ie

I





Podstawowe zależności i 

określenia

 

 

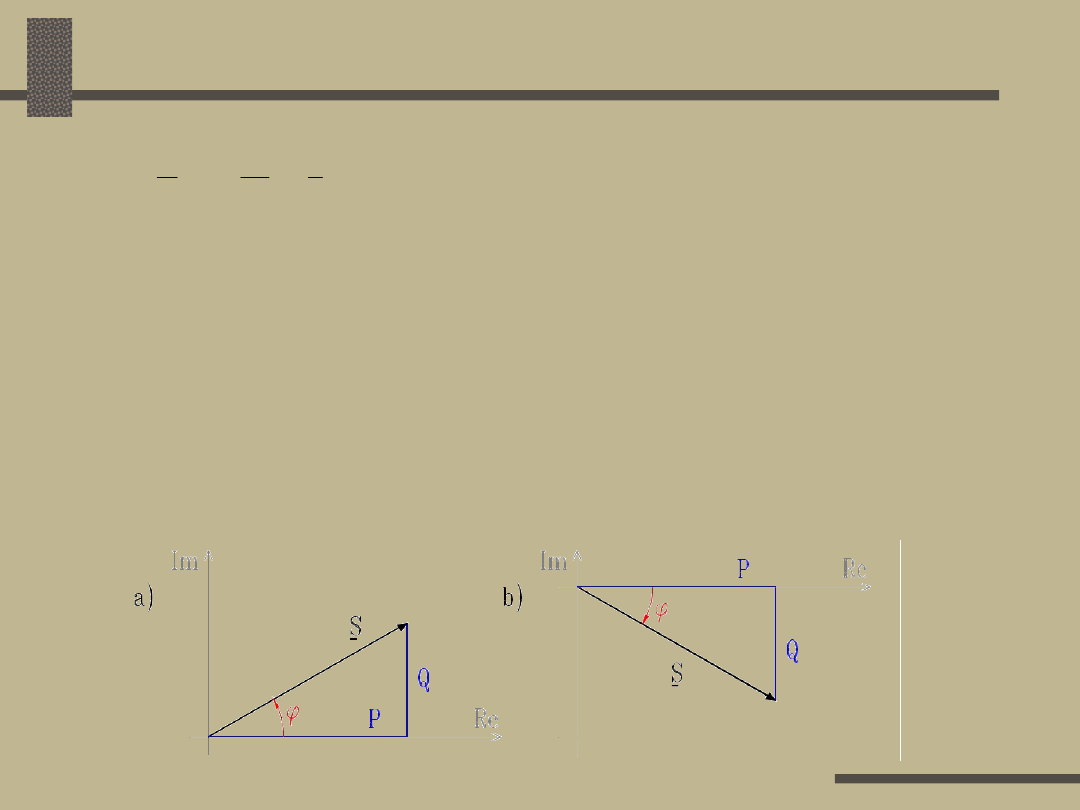
jQ

P

sin

I

U

3

j

cos

I

U

3

Ie

U

3

Ie

U

3

Ie

e

U

3

I

U

3

S

f

f

j

f

)

(

j

f

j

j

f

f

i

u

i

u













































Przy obciążeniu indukcyjnym kąt  jest 
dodatni i moc bierna jest również dodatnia, 
przy obciążeniu pojemnościowym kąt  i moc 
Q są ujemne.

Podstawowe zależności i 

określenia

 

 

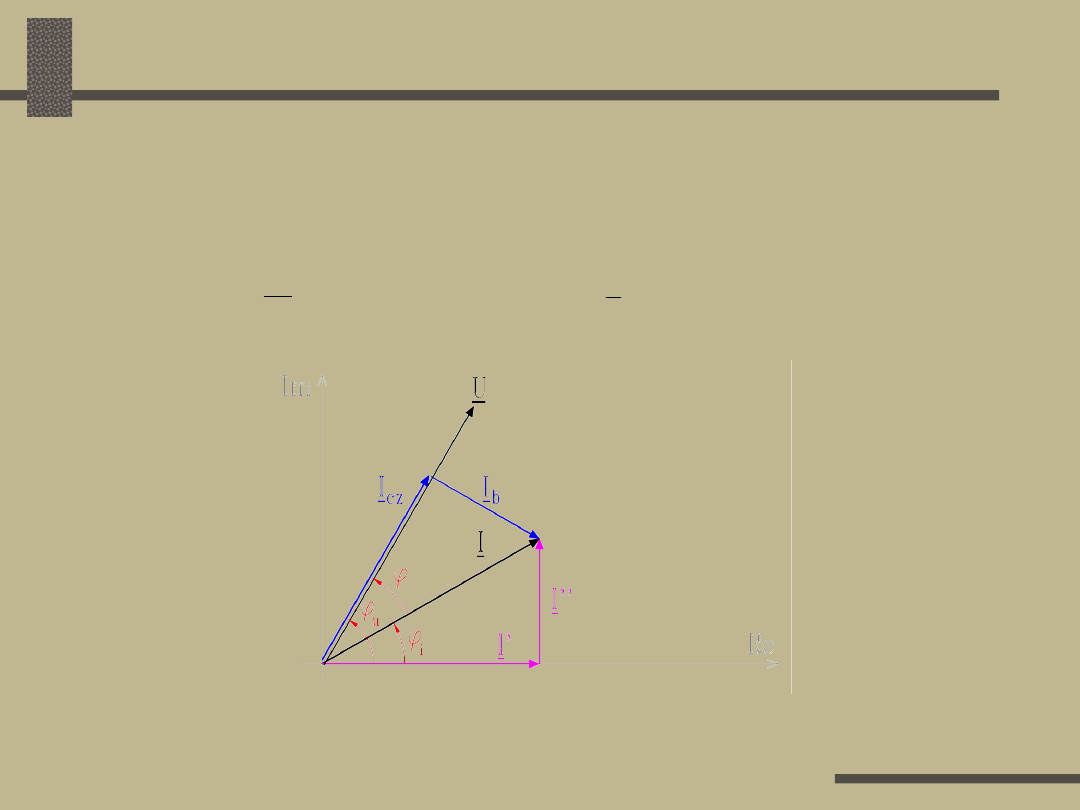
Prąd

 

czynny

 I

cz

 jest to rzut wektora prądu na kierunek, w 

którym położony jest wektor napięcia:

I

cz

 = I cos

Prąd

 

bierny

 I

b

 jest to rzut wektora prądu na kierunek 

prostopadły do wektora napięcia:

I

b

 = I sin

Składowa

 

rzeczywista

 prądu I’ jest to rzut wektora prądu 

na kierunek osi rzeczywistych:

I’ = I cos

i

Składowa

 

urojona

 prądu I” jest to rzut wektora prądu na 

kierunek osi urojonych

I” = I sin

i

Podstawowe zależności i 

określenia

 

 

Podstawowe zależności i 

określenia

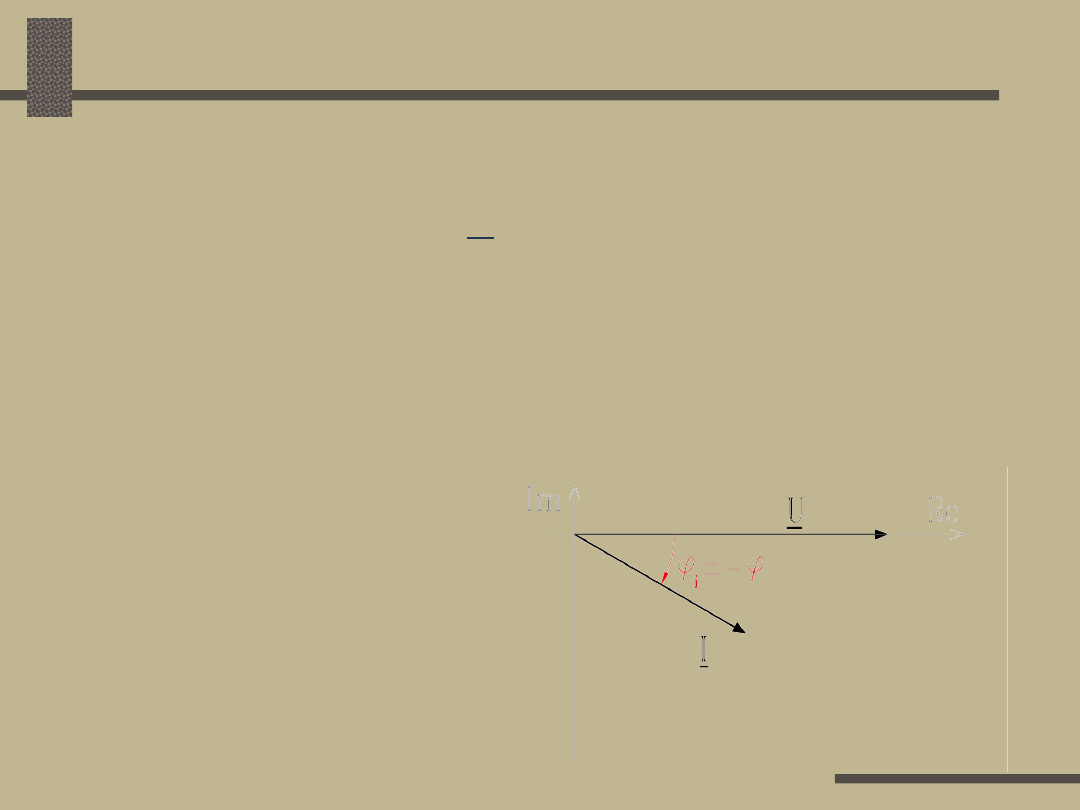
Jeżeli wektor napięcia położony jest w osi 
rzeczywistych, czyli U = U i  = -  

i 

, wówczas 

składowa urojona prądu równa jest składowej 
biernej z przeciwnym znakiem:

I = I’ - j I” = I cos 

 i 

– j I sin 

 i 

= I cos(- ) - j I sin 

(-)

I’ = I cos 

 i  

= I cos  = I

cz

- I” = - I sin 

 i  

= I sin  = I

b 

 

 

Podstawowe zależności i 

określenia

Podsumowując:

Przy obciążeniu indukcyjnym

 > 0,

Q > 0,

I” < 0

Przy obciążeniu 

pojemnościowym

 < 0,

Q < 0,

I” > 0

 

 

α

n

α

α

φ

cos

U

3

P

=

I

Założenia do obliczeń

Obliczenia rozpływu prądów rozpoczyna się od 
wyznaczenia prądów odbiorów.

Dla węzła  znane są wartości mocy 
odbieranej, najczęściej w postaci par: P

 

, Q

 

 

lub  P

 

, cos

  

 Prąd odbioru określony jest wzorem ogólnym:

I 

 

= I 

  

(cos  

i 

+ j sin  

i

)

Gdzie: 

 

 

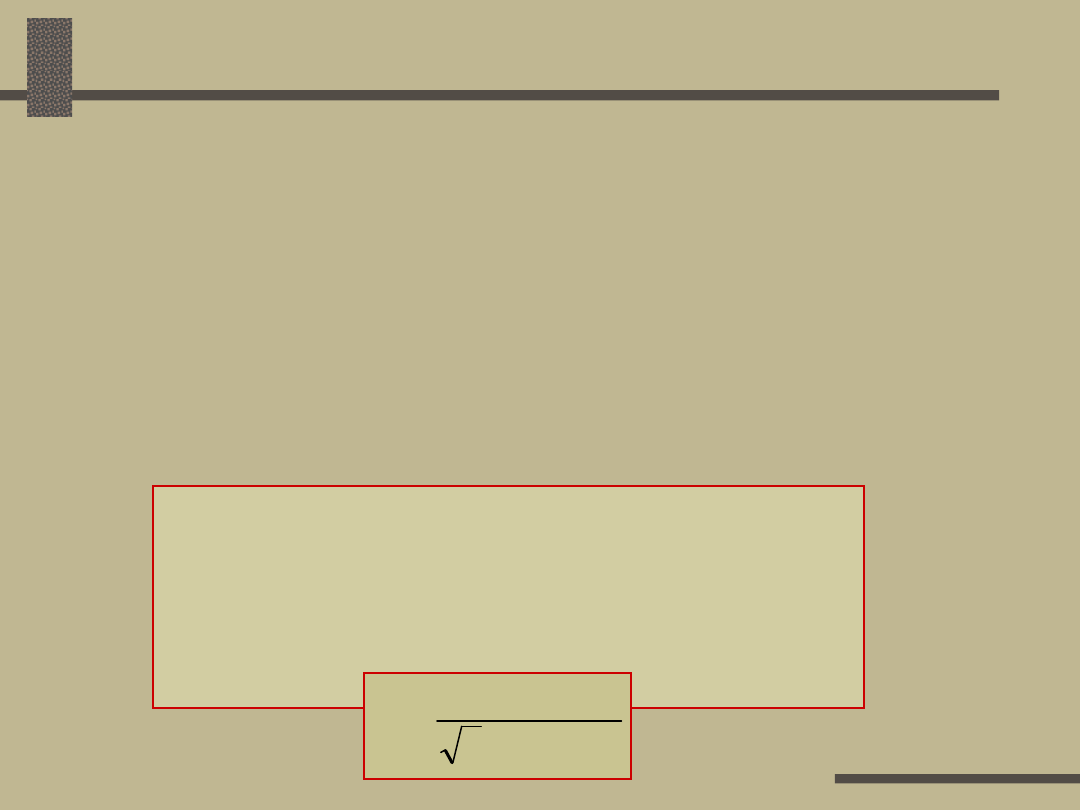
Założenia do obliczeń

Przyjmuje się następujące założenia:

1. W każdym węźle panuje napięcie 

znamionowe:

U



 = U

n

2. Wektor napięcia położony jest w osi 

rzeczywistych:

U



 = U



Przy takich założeniach:

I 



 = I 



  (cos  



 - j sin  



)

Gdzie:

α

n

α

α

φ

cos

U

3

P

=

I

 

 

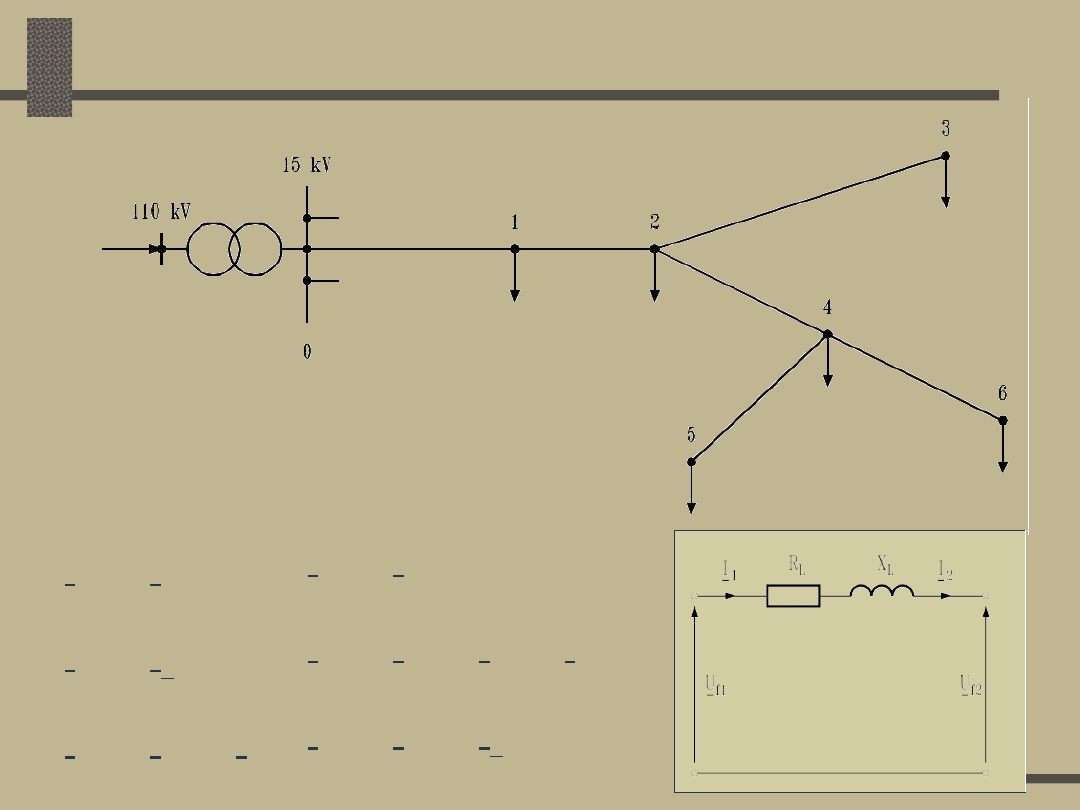
Sieci I i II rodzaju

1. Obliczenie prądów odbiorów
2. Obliczenie prądów w 

gałęziach sieci

I

46 

= I

6

 

I

54 

= I

5

I

24 

= I

46 

+ I

54 

+ I

4

I

23 

= I

3

I

12 

= I

23 

+ I

24 

+ I

2

I

01 

= I

12 

+ I

1

 

 

 

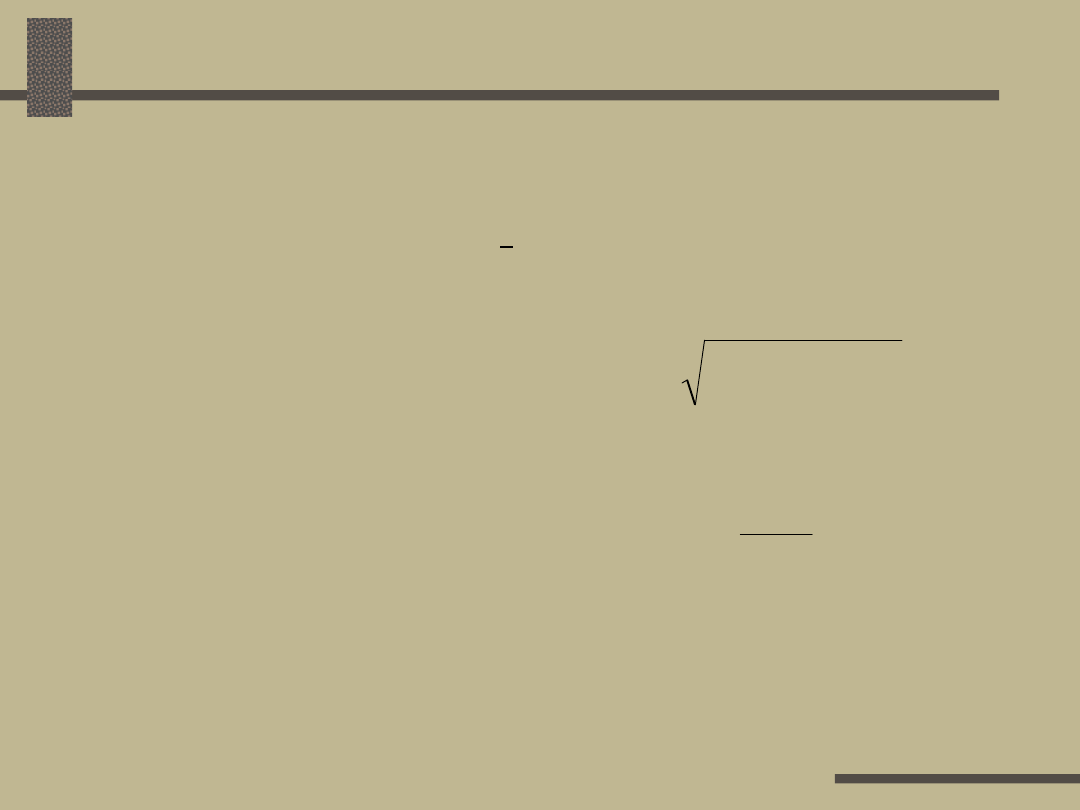
O gó lnie:   

 

 

 

 I

jk

 = I

jk

’

 –  jI

jk

”

 

 

 

M o duł p rądu gałęz io w eg o :   

   

2

"

jk

2

'

jk

jk

I

I

I





 

 

K ąt im pedancji linii:   

 













 





'

jk

"

jk

jk

I

I

ctg

ar

 

Sieci I i II rodzaju

 

 

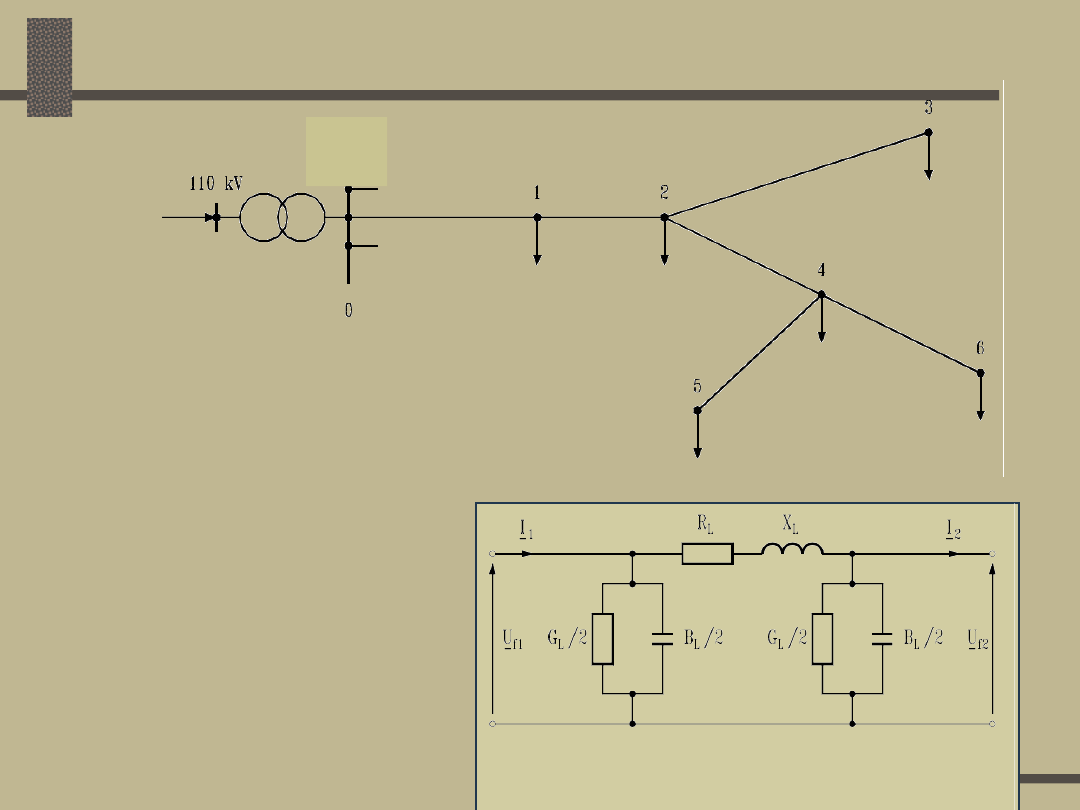
Sieci III rodzaju

30 
kV

1. Obliczenie prądów 

odbiorów

2. Obliczenie prądów 

pojemnościowych

3. Obliczenie prądów w 

gałęziach sieci

 

 

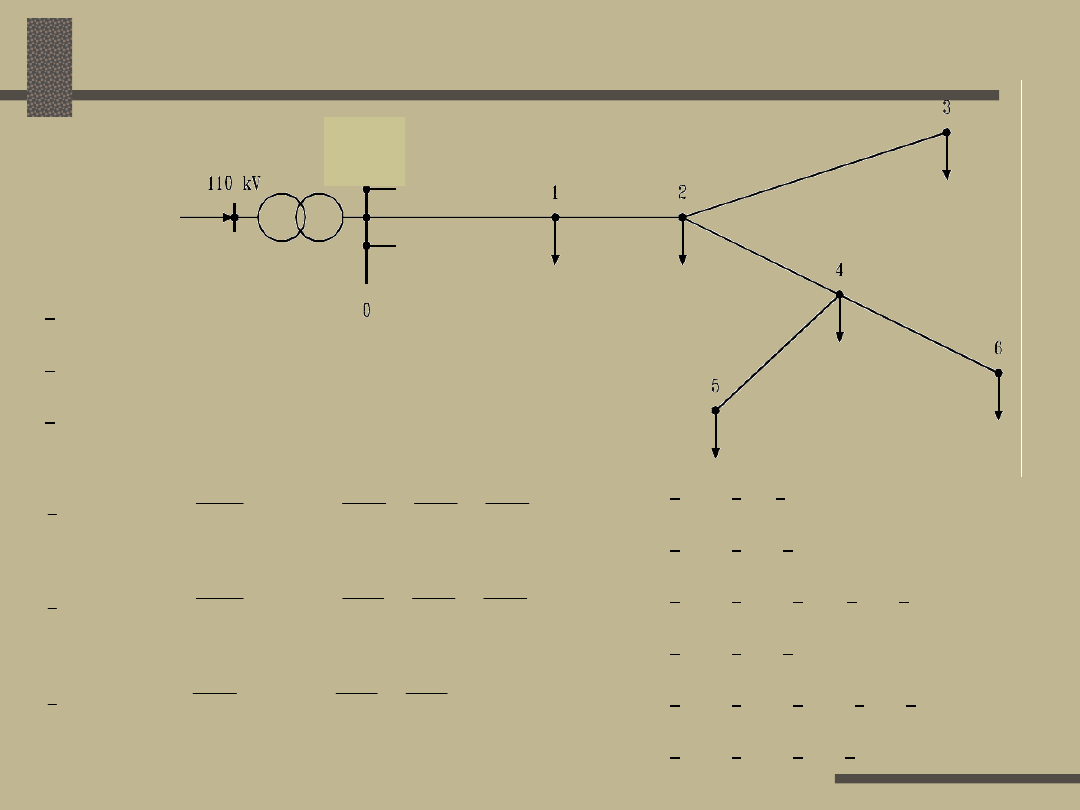
Sieci III rodzaju

30 
kV

I

c6

 = jU

fn

B

46

/2

I

c5

 = jU

fn

B

45

/2

I

c3

 = jU

fn

B

23

/2

























2

B

2

B

2

B

jU

2

B

jU

I

46

45

24

fn

4

fn

4

c

























2

B

2

B

2

B

jU

2

B

jU

I

24

23

12

fn

2

fn

2

c























2

B

2

B

jU

2

B

jU

I

12

01

fn

1

fn

1

c

I

46

 = I

6

 +I

c6

I

54

 = I

5

 + I

c5

I

24

 = I

46

 + I

54

 +I

4

 + I

c4

I

23

 = I

3

 + I

c3

I

12

 = I

23

 + I

24

 + I

2

 + I

c2

I

01

 = I

12

 + I

1

 + I

c1

 

 

OBLICZANIE SPADKÓW I 

STRAT NAPIĘCIA

W SIECIACH OTWARTYCH

 

 

2

f

1

f

12

U

U

U







2

f

1

f

12

U

U

U







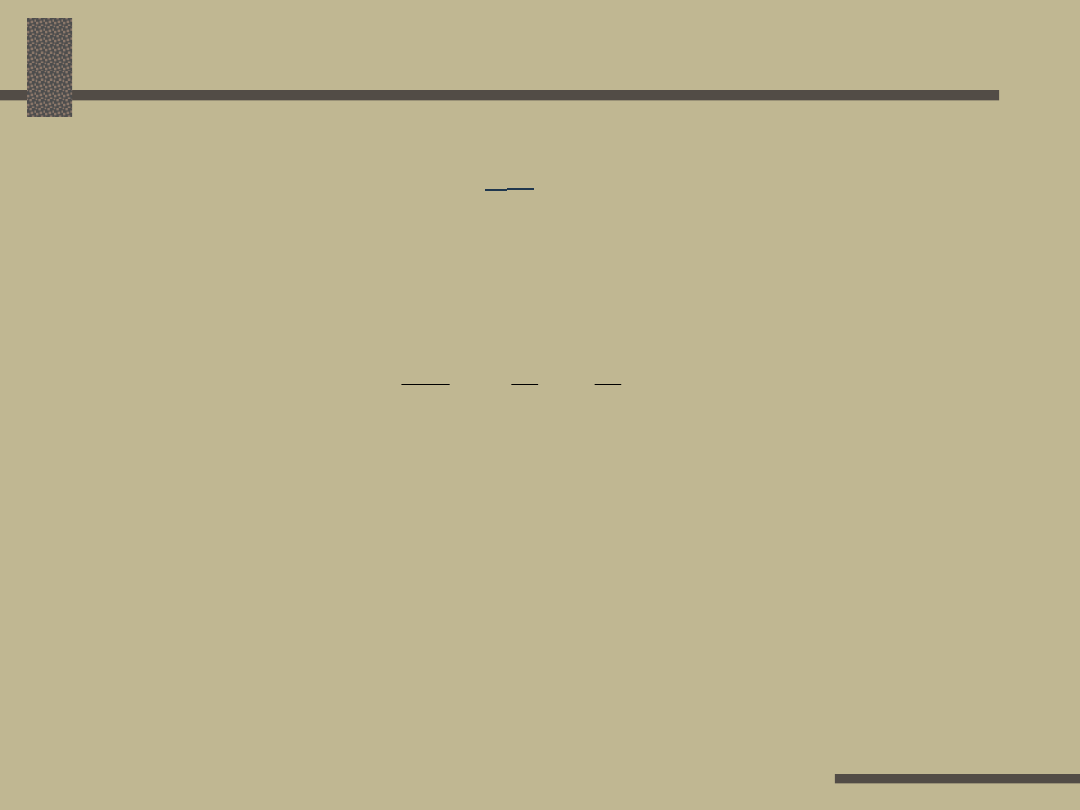
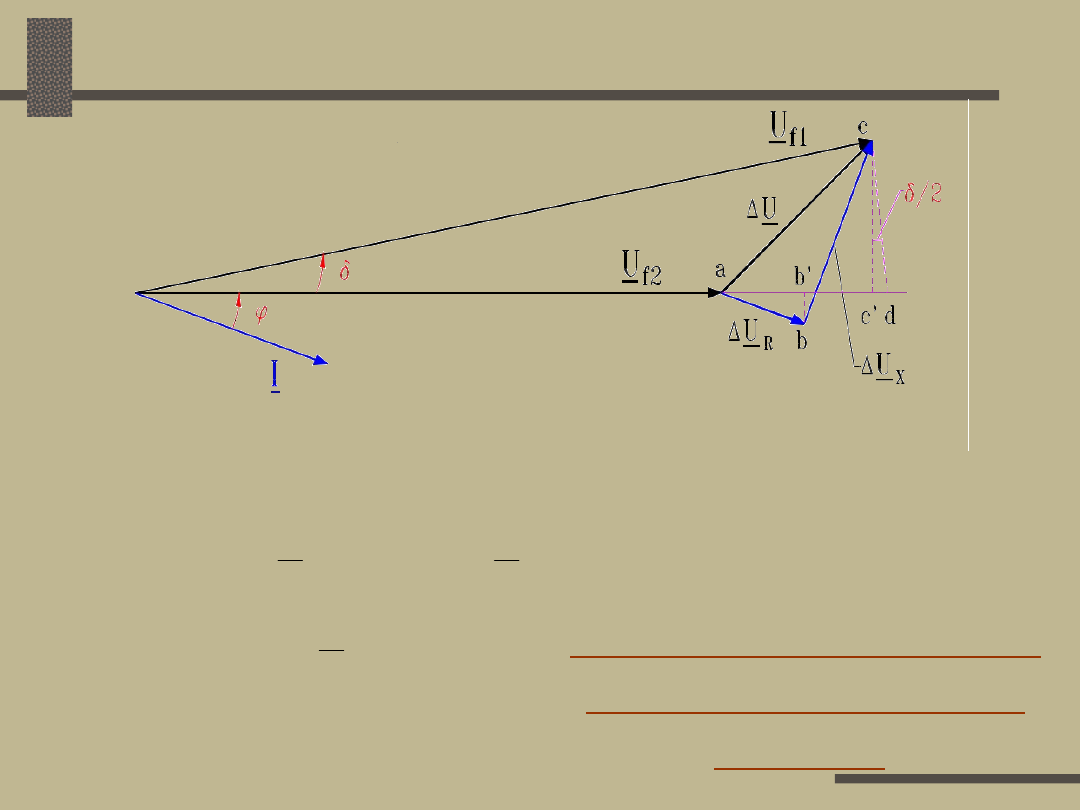
Definicje

Stratą  napięcia

  U

12

  nazywa  się  różnicę 

geometryczną  napięć  w  dwóch  punktach 
(węzłach) sieci 1 i 2:

Spadkiem napięcia

 nazywa się algebraiczną 

różnicę napięć w dwóch punktach sieci

 

 

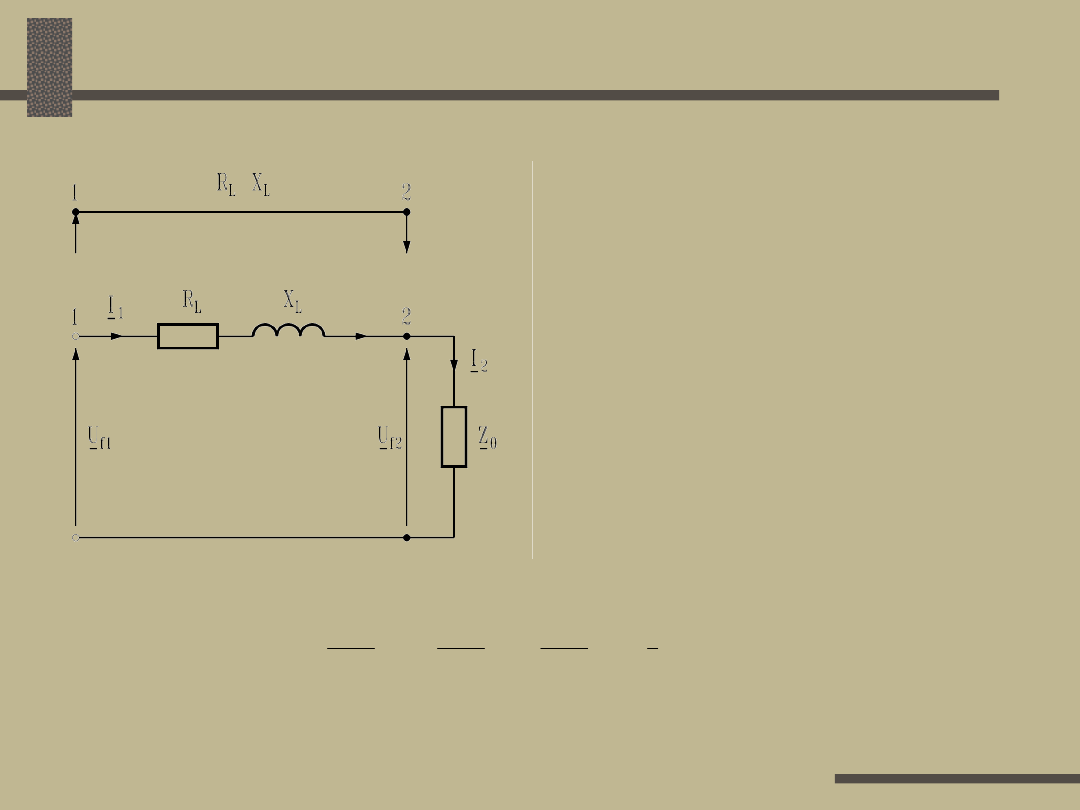
Składowe wektora straty

Strata  napięcia  w 
linii jest równa sumie 
geometrycznej 
czynnej 

i 

biernej 

straty napięcia:

)

X

j

R

(

I

U

U

U

L

L

X

R

12















 

 

Podłużną  stratą  napięcia

  U’  w  linii  przesyłowej 

nazywa  się  rzut  wektora  całkowitej  straty  napięcia 
U  na  kierunek  osi  rzeczywistych  (kierunek 
odniesienia).

Poprzeczną  stratą  napięcia

  U”  nazywa  się  rzut 

wektora  całkowitej  straty  napięcia  na  kierunek  osi 
urojonych (prostopadły do kierunku odniesienia).

Czynną  stratą  napięcia

  nazywa  się  stratę 

napięcia na rezystancji linii:

L

R

R

I

U







Bierną  stratą  napięcia

  nazywa  się  stratę 

napięcia na reaktancji linii:

L

X

jX

I

U







Składowe wektora straty

 

 

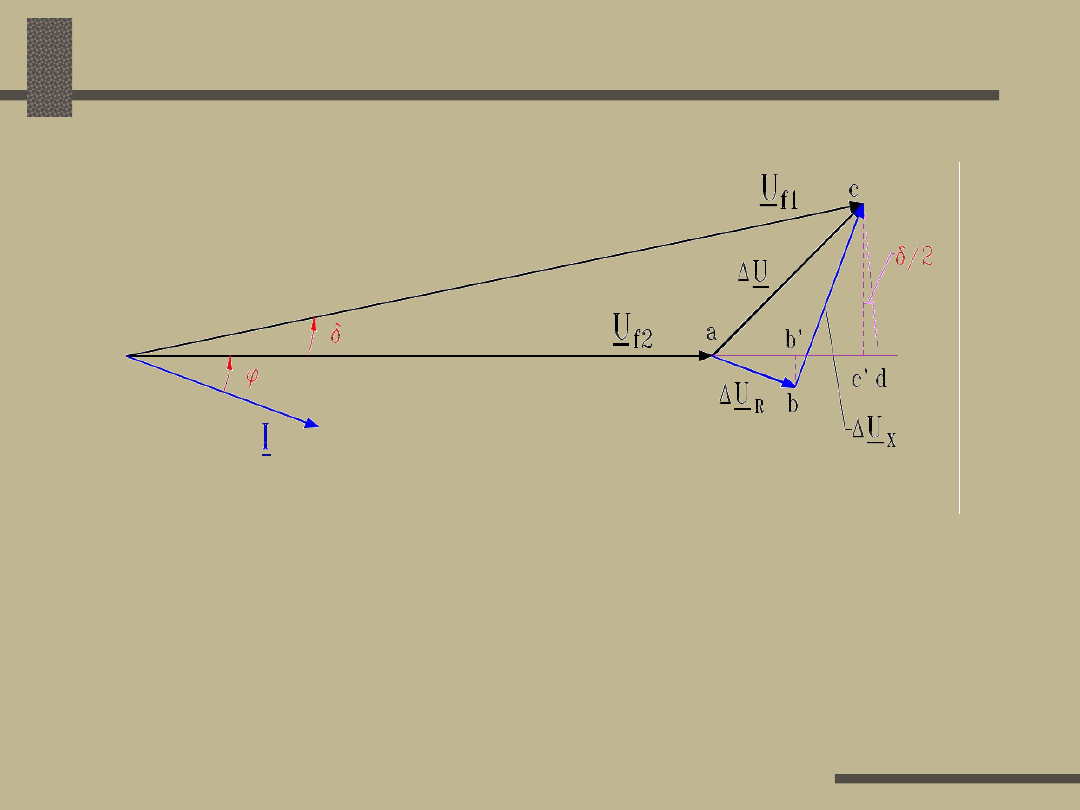
Strata a spadek

Podłużna strata napięcia równa się odcinkowi ac’: 
U’ = ac’

Poprzeczna  strata  napięcia  równa  się  odcinkowi 
c’c: U” = c’c

 

 

Sieci I i II rodzaju

Podany zostanie sposób obliczania 
spadku napięcia przy dowolnym 
obciążeniu dla linii:

 zasilającej

 rozdzielczej

Jako przypadek ogólniejszy zostanie 
rozważona linia II-go rodzaju. Linię I-go 
rodzaju można traktować jako przypadek 
szczególny, przyjmując Z

L

 = R

L

 

 

 

d

'

c

+

'

ac

=

ad

U

U

=

ad

=

U

δ

f

f

2

1

-

2

δ

*tg

δ

tg

'

oc

=

2

δ

tg

*

c

'

c

=

d

'

c

δ

tg

,

=

δ

tg

5

0

2

δ

tg

'

oc

,

=

d

'

c

2

5

0

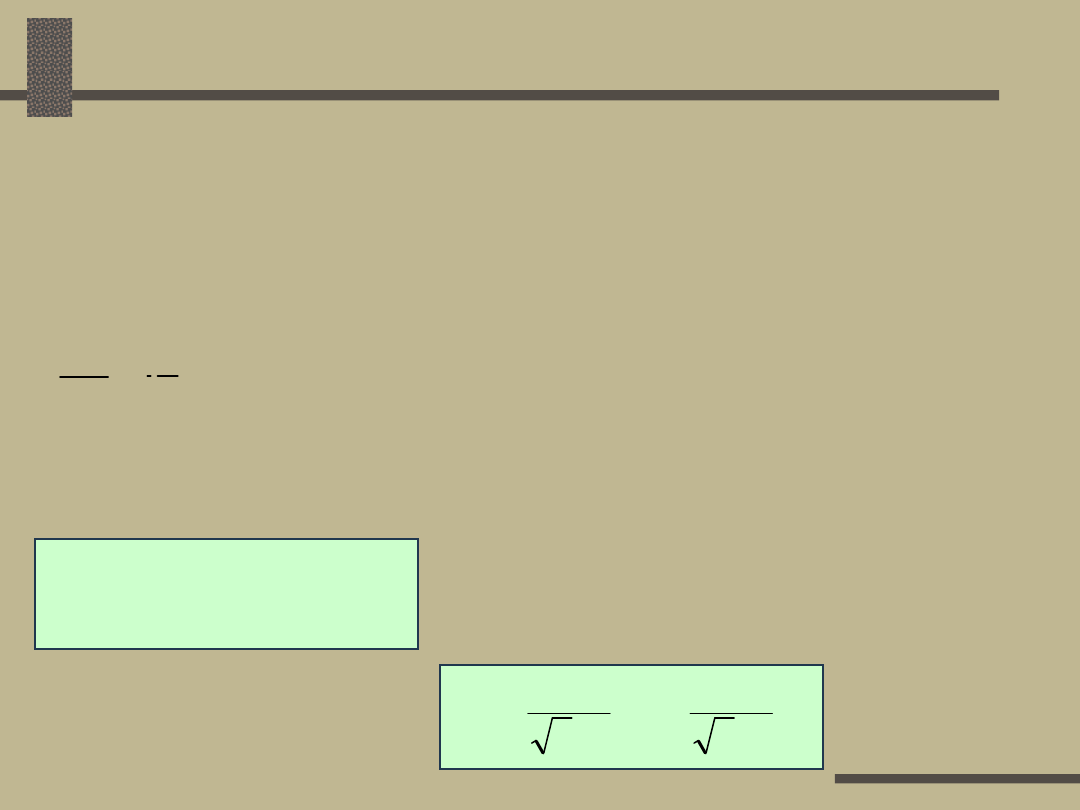
Spadek napięcia w linii 

zasilającej

dla 
małych : 

więc 

U = ac’ = U’

Przy 

założeniu 

c’d = 0:

Spadek napięcia równy 

jest podłużnej stracie 

napięcia

 

Obciążenie 
indukcyjne

 

 

(

)(

)

(

)

"

'

L

L

L

L

L

L

L

U

Δ

j

+

U

Δ

=

=

R

"

I

+

X

'I

j

+

X

"

I

R

'I

=

X

j

+

R

"

Ij

+

'I

=

Z

I

=

U

Δ

-

L

b

L

cz

L

L

'

X

I

+

R

I

=

=

X

"

I

R

'I

=

U

Δ

=

U

δ

-

Obliczanie spadku napięcia

Wykorzystując  powyższe  założenie  można 
określić praktyczny wzór na spadek napięcia. 

Ponieważ całkowita strata 
napięcia:

Stąd:

Jeżeli odbiornik określony jest 
wartościami mocy czynnej i 
biernej, wówczas wzór na 
spadek napięcia można zapisać 
w postaci:

L

n

L

n

X

U

Q

+

R

U

P

=

U

δ

3

3

 

 

Obliczanie spadku napięcia

Jeżeli  obciążenie  ma  charakter  indukcyjny  to 
składowa urojona prądu jest ujemna, a prąd bierny i 
moc bierna są dodatnie. Wówczas:

U

f1 

 > U

f2

   i   U > 0

Jeżeli  obciążenie  ma  charakter  pojemnościowy  to 
składowa urojona prądu jest dodatnia, a prąd bierny 
i moc bierna są ujemne. Stąd:

U

f1 

 U

f2

   i   U  0

Możliwy jest przypadek, że:

U

f1 

= U

f2

   i   U = 0

 

 

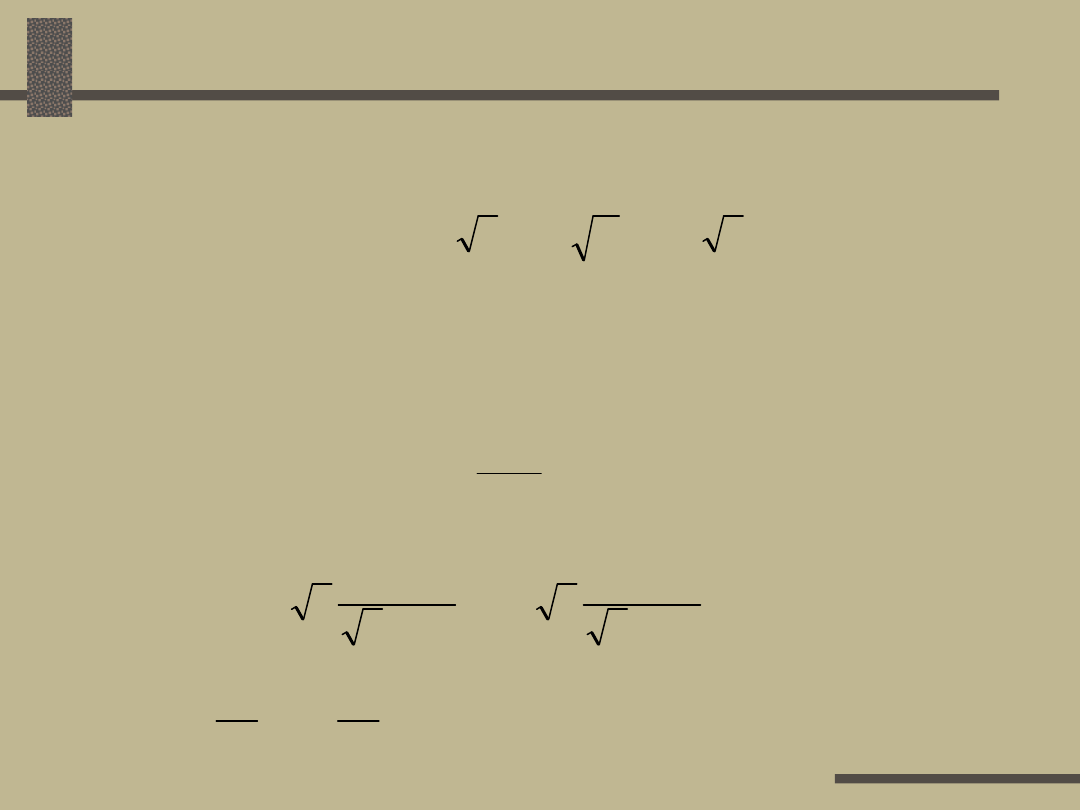
U

δ

=

U

U

=

U

U

=

U

δ

f

f

p

3

3

-

3

-

2

1

2

1

100

n

p

%

U

U

δ

=

U

δ

100

100

3

3

3

3

2

2

*

X

U

Q

+

R

U

P

=

=

*

X

U

U

Q

+

R

U

U

P

=

U

δ

L

n

L

n

L

n

n

L

n

n

%

W obliczeniach praktycznych operuje się 
procentowym spadkiem napięcia, odniesionym 
do napięcia znamionowego 

Spadek przewodowy:

lub:

Obliczanie spadku napięcia

 

 

(

)

(

)

∑

∑

n

=

α

α

,

1

-

α

α

,

1

-

α

b

α

,

1

-

α

α

,

1

-

α

cz

n

1

=

α

α

,

1

-

α

α

,

1

-

α

α

,

1

-

α

α

,

1

-

α

0n

0n

X

I

+

R

I

=

=

X

''

I

-

R

'I

=

'

U

Δ

=

U

δ

1

 

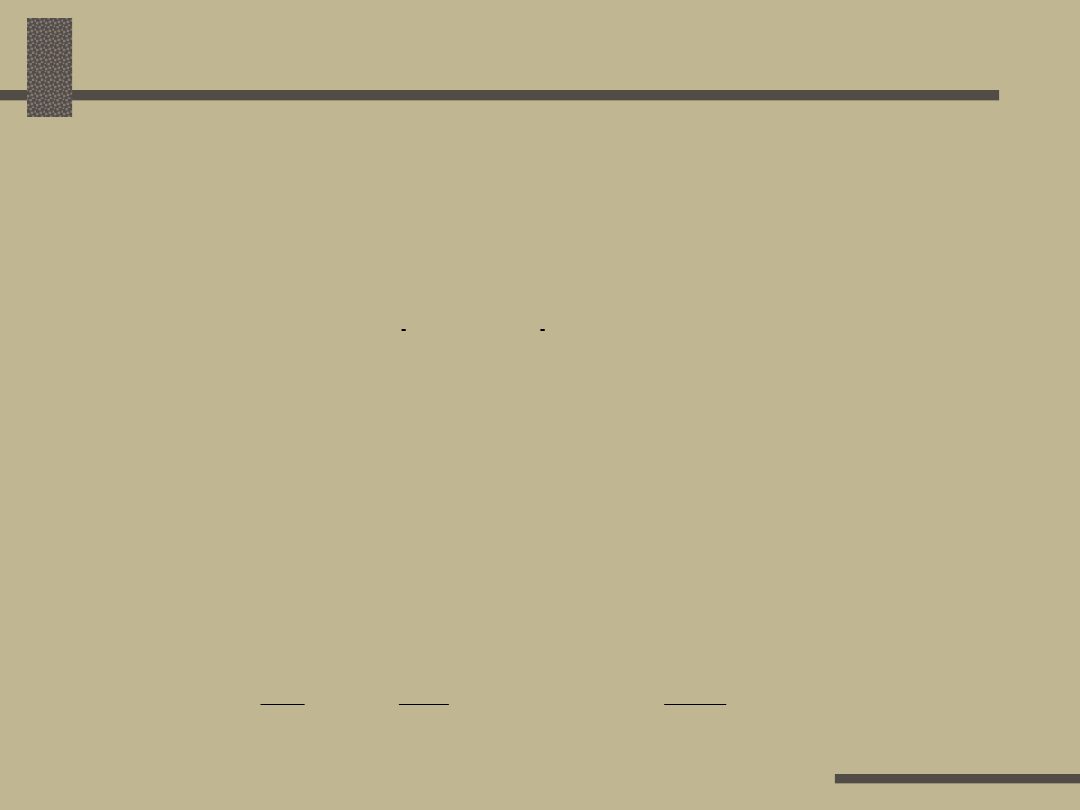
Spadek napięcia w linii 

rozdzielczej

Spadek  napięcia  w  całej  linii  równa  się 
sumie spadków napięcia na poszczególnych 
jej odcinkach:

Metoda

 „sumowania odcinkami”

 

 

 

(

)

∑

∑

n

=

α

n

1

=

α

α

0

α

α

0

α

2

n

α

0

2

n

α

α

0

2

n

α

%

0n

X

Q

+

R

P

U

100

=

100

*

X

U

Q

+

R

U

P

=

U

δ

1

Pamiętając, że prądy w gałęziach wynikają z 
sumowania prądów odbiorów 

∑

n

α

=

j

j

α

,

1

α

I

=

I

-

można wyrazić spadek napięcia w zależności od 
prądów odbiorów, a nie linii:

(

)

(

)

∑

∑

n

=

α

α

0

α

b

α

0

α

cz

n

1

=

α

α

0

α

α

0

α

0n

X

I

+

R

I

=

X

''

I

R

'I

=

U

δ

1

-

Metoda

 „sumowania momentami”

lub w zależności od mocy odbiorów:

Obliczanie spadku napięcia

 

 

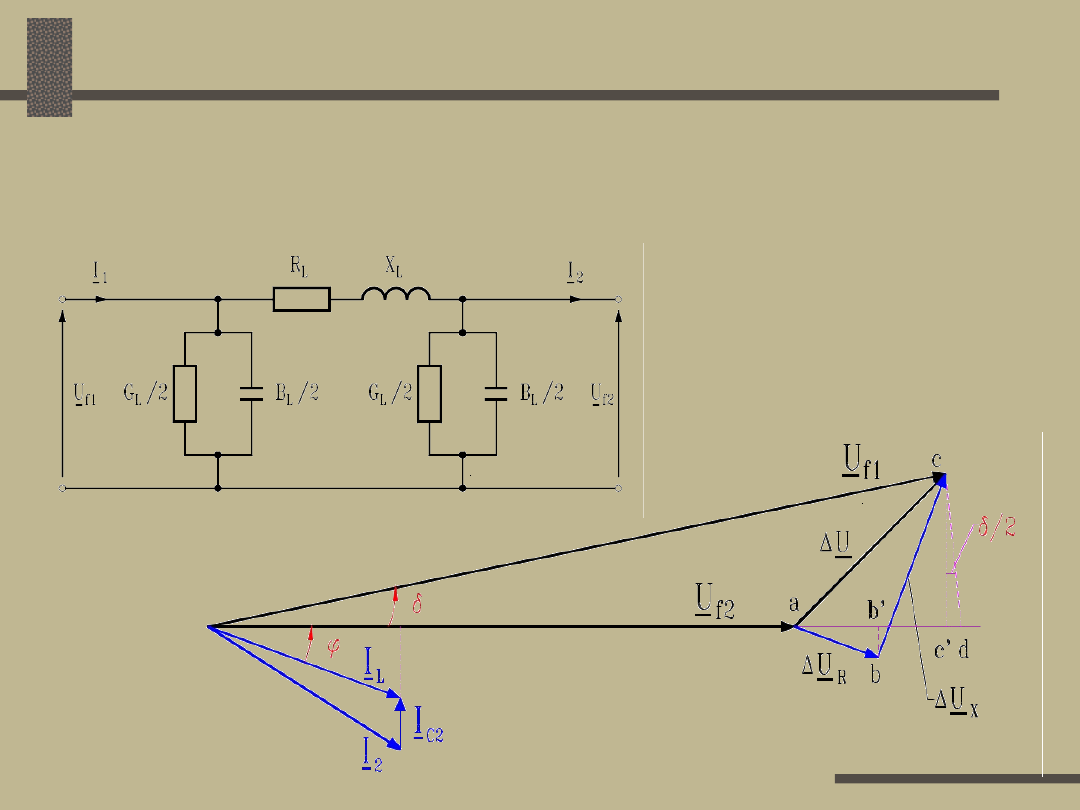
Sieci III rodzaju

Linia zasilająca, obciążona mocą 

czynną i bierną indukcyjną

 

 

L

L

L

L

X

''

I

-

R

'I

=

'

c

a

≠

U

δ

f2

f1

U

-

U

=

U

δ

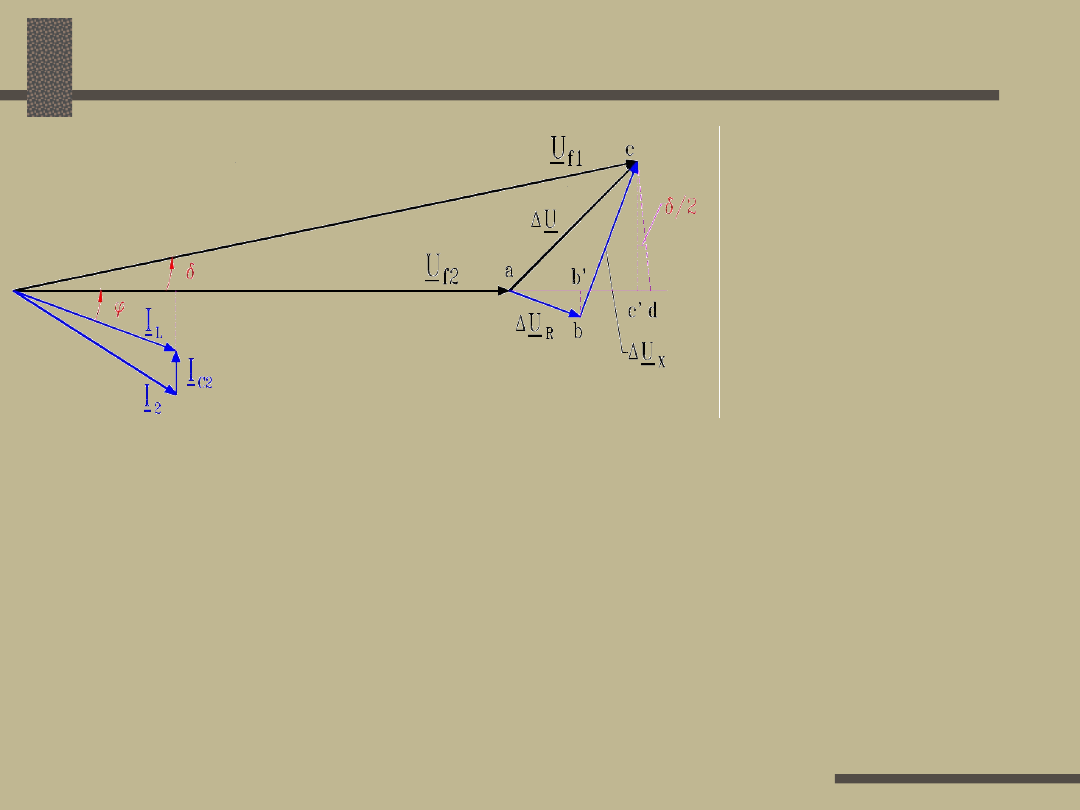
Obliczanie spadku napięcia

Dla linii III-go rodzaju 

kąt  jest na tyle 

duży, że nie można 

pominąć odcinka c’d, 

a zatem:

Najłatwiej  obliczyć  spadek  napięcia  w  linii  III 
rodzaju  określając  dowolną  metodą  moduł 
wektora  napięcia  na  początku  linii  U

f1

,  a 

następnie  obliczając  spadek  napięcia  z  jego 
definicji:

 

 

(

)

X

U

Q

+

R

U

P

2

=

X

I

+

R

I

2

=

U

δ

L

n

L

n

L

b

L

cz

X

U

Q

+

R

U

P

2

=

U

δ

L

2

n

L

2

n

%

Linia

 

jednofazowa

Obliczenia spadków, jak również strat napięcia w 
linii jednofazowej przeprowadza się tak samo jak 
w linii trójfazowej, należy jednak pamiętać, że 
prąd obciążenia I płynie w tym przypadku 

dwoma 

przewodami

 linii. Wobec tego jeżeli R

L

 i X

L

 są 

odpowiednio rezystancją i reaktancją jednego 
przewodu linii i oba przewody są jednakowe, to 
dla linii II rodzaju spadek napięcia obliczymy ze 
wzoru:

 

 

T

b

2

T

cz

2

T

"

2

T

'

2

T

X

I

+

R

I

=

X

I

-

R

I

=

U

δ

3

2

1

I

+

I

=

I

T2

"
2

T2

'
2

T1

"

1

T1

'

1

T12

X

I

-

R

I

+

X

I

-

R

I

=

U

δ

T3

"
3

T3

'
3

T1

"

1

T1

'

1

T13

X

I

-

R

I

+

X

I

-

R

I

=

U

δ

Transformator

Przy 

obliczaniu 

spadków 

napięcia 

w 

transformatorze  pomija  się  gałąź  magnesującą 
schematu  zastępczego.  Wówczas  schemat  ten 
ma  taką  samą  postać  jak  schemat  zastępczy 
linii II rodzaju. Wobec tego:

Dla transformatora 
dwuuzwojeniowego:

Dla transformatora 3-
uzwojeniowego: