Adam Gałuszka, p.936
Metody Obliczeniowe Optymalizacji – wykład 1

http://www.zsir.ia.polsl.pl/~dydaktyka/mo_gliwice/index.html

Organizacja przedmiotu:

15 h wykładu, podzielone na 1 wykład 1h wprowadzający

i 7 wykładów 2h.

Zaliczenie wykładu: kolokwium zaliczające 1 h zegarowa

(4 zagadnienia: 2 teoretyczne i 2 praktyczne), po

ostatnim wykładzie (w godz. wykładu)

15 h laboratorium, podzielone na 4 ćwiczenia 3h i termin

odrobieniowy 3h – regulamin i warunki zaliczenia na

stronie lab.

literatura

• Bryson A., Y.C. Ho: Applied optimal control, Blaisdell, 1969

• Findeisen W., J. Szymanowski, A. Wierzbicki: Metody

optymalizacji, PWN, 1977

• Helmke U., J. Moore: Optimization and dynamical systems,

Springer, 1994

• Luenberger D.: Optimization by vector space methods, John

Wiley, 1969 (Polish translation-Teoria optymalizacji, PWN,

1974)

• Luenberger D.: Introduction to linear and nonlinear

programming, Adison-Wesley, 1973

• Ogonowski Z., J. Smieja: Optimization Methods and Decision

Making, Art&Kolor, Gliwice, 2001

• MATLAB Optimization Toolbox

optymalizacja

• Wyznaczanie przy użyciu metod

matematycznych optymalnego (najlepszego)

ze względu na dane kryteria, rozwiązania

danego problemu.

• Łac.: „optimus” – najlepszy

• Rozwiązać problem optymalizacyjny =

znaleźć minimum (lub maksimum) funkcji

kosztów uwzględniając ograniczenia dane

przez model procesu, który mamy

optymalizować.

Optymalizacja statyczna

• Tzw. Programowanie matematyczne

• Programowanie liniowe

• Programowanie kwadratowe

• Programowanie nieliniowe

• Programowanie całkowito-liczbowe

(całkowito-liczbowe binarne)

• Model procesu i rozwiązania nie zależą od

czasu

Optymalizacja dynamiczna

• Tzw. Sterowanie optymalne

• Programowanie dynamiczne

• Model procesu, rozwiązania problemu

są funkcjami czasu

Przykład 1 – alokacja zasobów

(resource allocation)

Consider the problem of allocation of m resources for production of n

commodities. Denote:

n – number of products (j = 1,2 ... n)
m – number of resources (i = 1,2 ... m)
xj - amount of the product j (to be produced)
aij - amount of the i-th resource needed for a unit of the j-th product
bi – available amount of the i-th resource
cj - price (per unit) of the j-th product constraints
We have the following constraints:

and the profit (cost functional) is given as:

In a vector form the problem may be described as:

This problem is an example of Linear Programming Problem.







n

j

i

j

ij

b

x

a

1

n

j

m

i

x

j

,...,

2

,

1

;

,...,

2

,

1

;

0













n

j

j

j

x

c

Max

1

x

c

Max

x

b

Ax

T







0

,

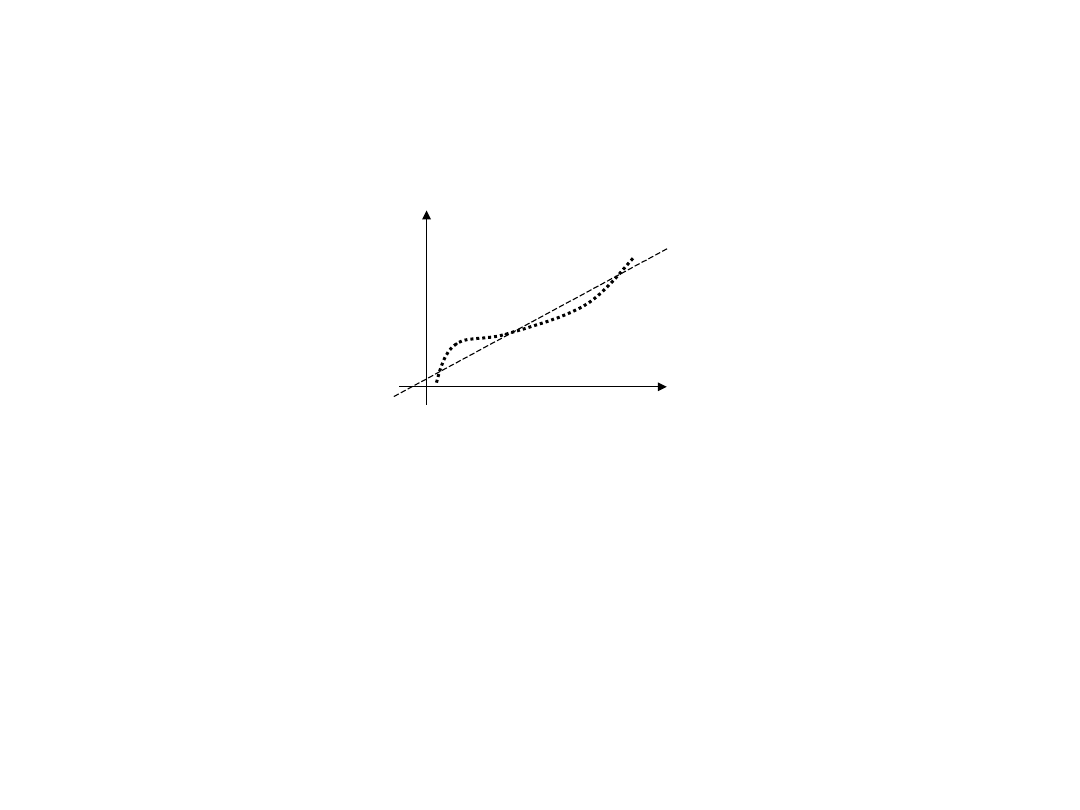
Przykład 2 - Approximation

(e.g. linear regression)

y

We want to approximate our data by the ‘’best’’ fitted straight line,
so the objective is to find:





i

i

i

a

ax

y

Min

2

)

(

Przykład 3 – problem

rakietowy











T

dt

u

Min

h

T

x

x

x

0

)

(

0

)

0

(

0

)

0

(



g

u

x







h

Here the problem is how to change the trust of the rocket
to elevate it to the given altitude while minimizing
fuel consumption which is instantenously proportional
to the absolute value of the trust.

Fuel

consumption

Trust (per mass unit) can be described by:

Przykład 4 – problem

farmera

0

)

0

(

x

x

ux

x







1

0



u







T

xdt

u

Max

0

)

1

(

Prof
t

A farmer wants to maximize his profit by optimization of
the reinvestment ratio.

If x – amount of the farmer’s production then

where u is a investment fraction:

The optimization problem is to maximize the profit:

Wspólne cechy problemu

optymalizacji

• Funkcja celu (minimalizacja strat lub maksymalizacja zysków)

• Ograniczenia w postaci modelu procesu

• Dodatkowe ograniczenia

• W postaci matematycznej: (oznaczamy F – funkcja celu, g – ograniczenia):

R

X

J

Max

Min





:

)

(

0

)

( 

x

g

0

)

( 

x

g

0

)

( 

x

g





X

g:

1)

2)

Program wykładu

1. Ekstremum funkcji bez ograniczeń, przykłady

2. Ekstremum funkcji z ograniczeniami równościowymi,

przykłady

3. Ekstremum funkcji z ograniczeniami

nierównościowymi - tzw. Warunki Kuhna-Tuckera,

przykłady

4 i 5. Zadanie Programowania Liniowego – metoda

Sympleksów, dualność w ZPL, przykłady

6 i 7. Zadanie Programowania Kwadratowego – metoda

Wolfa, przykłady

Program laboratorium

Prowadzący:

Ćw. 1: Dr inż. Adam Gałuszka, pok. 936, [e-mail]
Ćw. 2: Dr inż. Rafał Grygiel,

pok. 929, [e-mail]

Ćw. 3: Dr inż. Robert Bieda,

pok. 627, [e-mail]

Ćw. 4: Mgr inż. Aneta Bal,

pok. 627, [e-mail] 

1. Programowanie liniowe
2. Minimalizacja na kierunku i metody prostych kierunków poprawy
3. Metody kierunków sprzężonych
4. Metody newtonowskie i metody funkcji kary

Zajęcia wg harmonogramu na stronie:

•

http://www.zsir.ia.polsl.pl/~dydaktyka/mo_gliwice/index.html