Wykład 15
Indukcja elektromagnetyczna

1. Prawo Faradaya
2. Reguła Lenza
3. Indukcyjność

A. Transformator
B. Indukcyjność własna
C. Indukcja wzajemna

4. Obwody RC i RL, stałe czasowe

A. Obwód RC
B. Obwód RL

5. Energia a pole magnetyczne
6. Gęstość energii a pole
magnetyczne

1. Prawo Faradaya

Zjawisko indukcji elektromagnetycznej

- powstawanie prądów

elektrycznych w zamkniętym obwodzie, podczas przemieszczania się
względem siebie źródła pola magnetycznego i zamkniętego obwodu.

Wtedy w obwodzie jest

indukowana siła elektromotoryczna (SEM

indukcji),

która wywołuje przepływ

prądu indukcyjnego

.

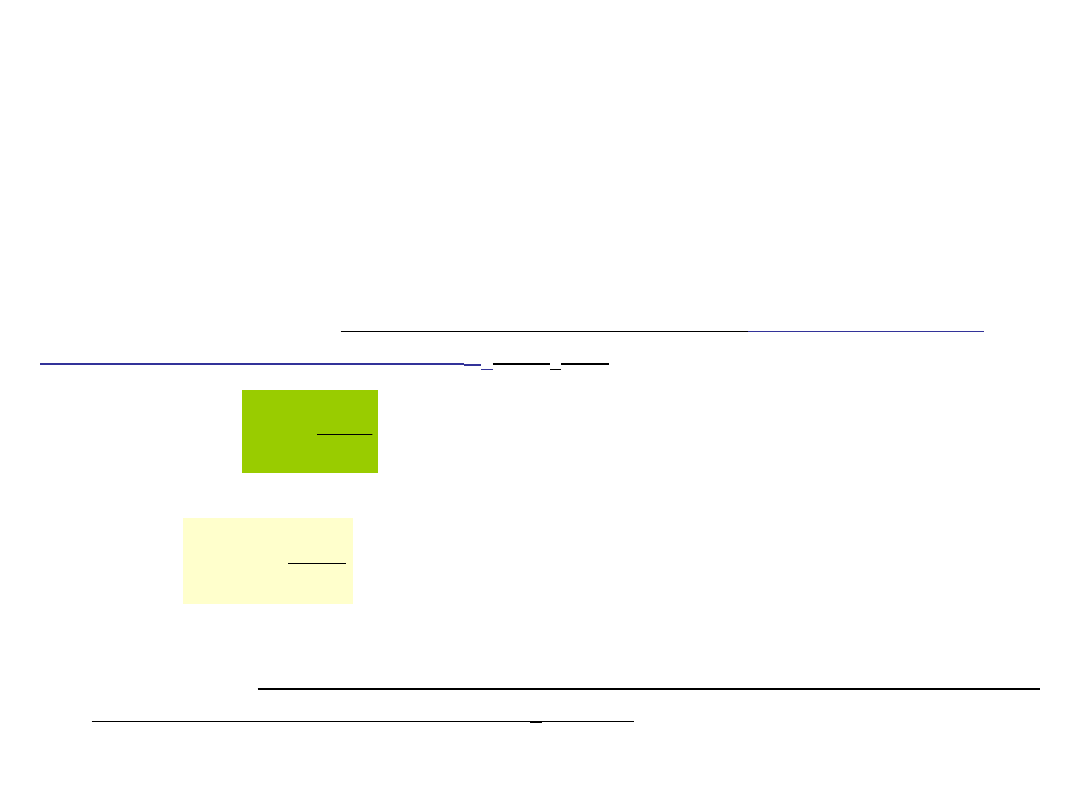
t

B

d

d









Prawo Faradaya

Jeżeli mamy obwód złożony z N zwojów to

t

N

B

d

d









gdzie

 - SEM jest pracą na jednostkę ładunku wykonaną przy przeniesieniu
ładunku wokół zamkniętej pętli ( = W/q),

 – strumień magnetyczny przechodzący przez tę pętlę.

Faraday stwierdził, że czynnikiem decydującym jest

szybkość zmian

strumienia magnetycznego



B

(dΦ

B

/dt), czyli

Prawo indukcji Faradaya stosuje się do trzech różnych sytuacji fizycznych:

• Nieruchoma pętla, względem której porusza się źródło pola

magnetycznego (tzw. elektryczną SEM).

• Przewód w kształcie pętli porusza się w obszarze pola magnetycznego

(tzw. magnetyczna SEM).

• Nieruchoma pętla i nieruchome źródło pola magnetycznego, lecz

zmienia się prąd, który jest źródłem pola magnetycznego (także tzw.
elektryczna SEM).

2. Reguła Lenza

Prąd indukowany ma taki kierunek, że przeciwstawia się zmianie,

która go wywołała. Kierunek prądu indukowanego w pętli (rysunek)
zależy od tego czy strumień rośnie czy maleje (zbliżamy czy oddalamy
magnes). Ta reguła dotyczy prądów indukowanych.

Rys. 1:

Magnes sztabkowy porusza się

na

prawo,

zwiększając

strumień

przechodzący przez zamkniętą pętlę
przewodu.

Indukowany

prąd

I

wytwarza pole B (pętla). Pole to
przeciwdziała wzrostowi strumienia,
związanego z magnesem.

Rys.

2:

Magnes

sztabkowy

(początkowo nieruchomy) przesuwa
się na lewo, co zmniejsza strumień
przez pętlę. Powstanie indukowany
prąd I (w pętli) przeciwdziałający
zmianie, tzn. pole B będzie starało
się utrzymać początkową wartość
strumienia przechodzącego przez
pętlę.

W przypadku (1), wypadkowa siła działająca na cewkę jest skierowana
w prawo, a w przypadku (2) w lewo.

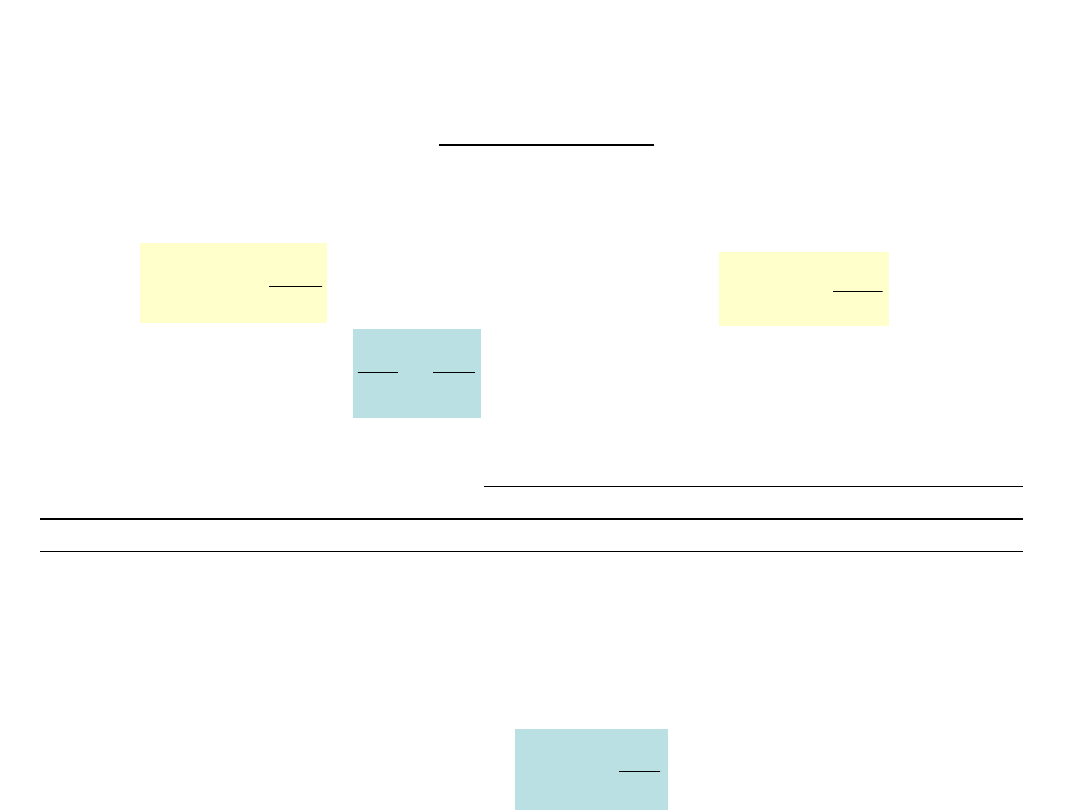
oraz SEM dla cewki (1)

t

N

U

B

d

d

1

1







Stosunek napięć

1

2

1

2

N

N

U

U



Widać, że regulując ilość zwojów w cewkach możemy zamieniać małe
napięcia na duże i odwrotnie. Ta wygodna metoda zamiany małych
napięć na duże i odwrotnie jest jedną z przyczyn, dla których używanie
prądów zmiennych jest wygodniejsze niż używanie prądów stałych
(ekonomiczne generatory wytwarzają prąd o raczej niskim napięciu).

B. Indukcyjność własna
Gdy natężenie prądu przepływającego przez cewkę zmienia się, to

zmienia się też strumień przechodząc przez każdy zwój tej cewki.
Zgodnie z prawem indukcji Faradaya - w każdym zwoju indukuje się
SEM -

siła elektromotoryczna samoindukcji.

t

N

d

d









3. Indukcyjność

A. Transformator
Gdy dwie cewki są nawinięte na tym samym rdzeniu (często jedna na

drugiej) - prąd zmienny w jednej, wywołuje SEM indukcji w drugiej. Można
tę SEM obliczyć korzystając z prawa Faradaya.

N

1

- liczba zwojów w cewce pierwotnej, N

2

- liczba zwojów w cewce

wtórnej

SEM () lub napięcie U

2

indukowane w cewce (2)

t

N

U

B

d

d

2

2







Wielkość N

 jest całkowitym strumieniem zawartym w obwodzie –

strumień skojarzony

.

Strumień skojarzony jest proporcjonalny do prądu płynącego przez
cewkę.

N

 = LI

Stała proporcjonalności

nazywana jest

indukcyjnością

.

Zróżniczkowanie (po czasie) równania N

 = LI, daje

t

I

L

t

N

d

d

d

d





stąd

t

I

L

d

d







Jednostką L jest henr. [1H] = [1Vs/A] lub [1H] = [1s].

Jako przykład obliczmy indukcyjność cewki o długości l

0

i N zwojach.

Strumień przez każdy zwój wynosi

 = BS

gdzie B dla cewki wynosi

B =



0

nI =



0

I(N/l

0

)

Zatem

I

l

NS

0

0







Indukcyjność L otrzymujemy mnożąc strumień przez N/I, bo L = N/I

0

2

0

l

S

N

L





Zauważmy, że L zależy tylko od czynników geometrycznych.

Indukcyjność cewki

L = N

/I

C. Indukcja wzajemna

Omawiając transformator pokazywaliśmy, że dwie cewki mogą

oddziaływać na siebie. Prąd zmienny w jednej wywoływał SEM w
drugiej. Tym razem strumień przechodzący przez cewkę 2 jest
proporcjonalny do prądu płynącego przez cewkę 1.

N

2



21

= M

21

I

1

Stałą proporcjonalności M

21

nazywamy

indukcją wzajemną

.

Różniczkując to równanie otrzymujemy

t

I

M

t

N

d

d

d

d

1

21

21

2





Stąd

t

I

M

d

d

1

21

2







Jeżeli zmieniamy prąd I

2

to analogicznie

t

I

M

d

d

2

12

1







Można pokazać (ale w skomplikowany sposób), że

M

12

= M

21

= M

Podobnie jak L tak samo M zależy tylko od geometrii układu.

4. Obwody RC i RL, stałe czasowe

Zaczniemy teraz zajmować się prądami zmieniającymi się w czasie.

Gdy do obwodu zawierającego opornik i kondensator (lub opornik i
cewkę indukcyjną) nagle zostanie przyłożone napięcie - pojawi się

prąd

zmieniający się wykładniczo w czasie -

prąd tłumiony

.

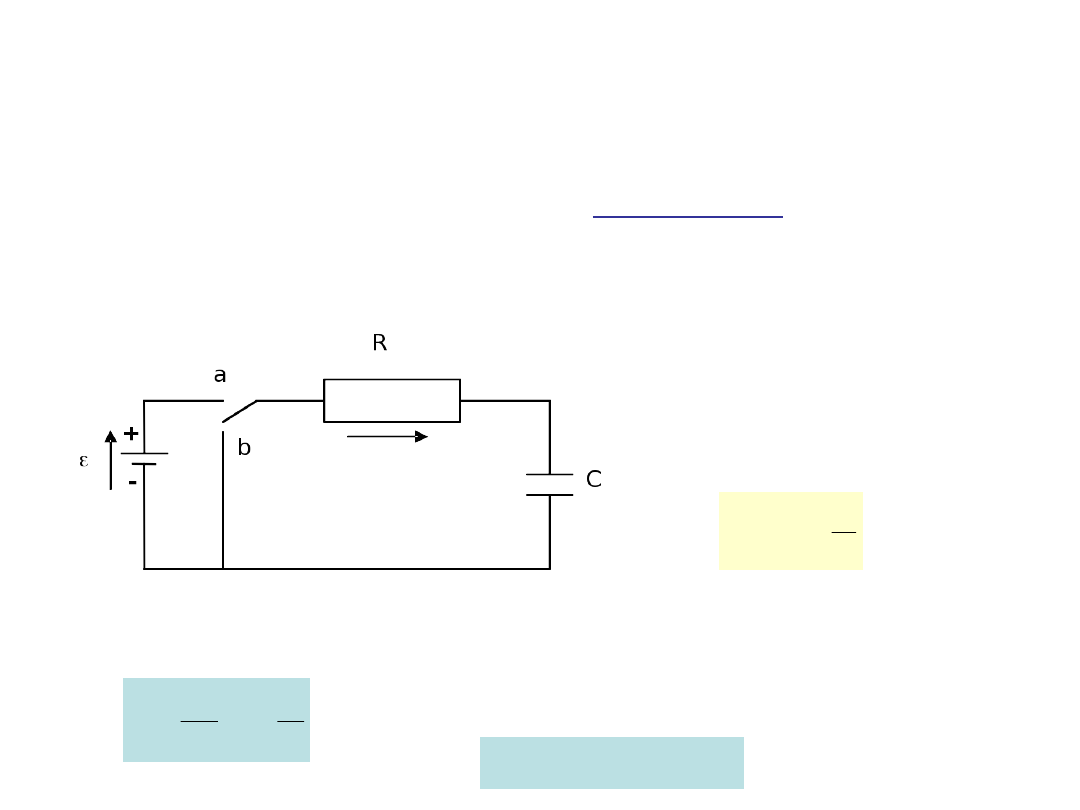
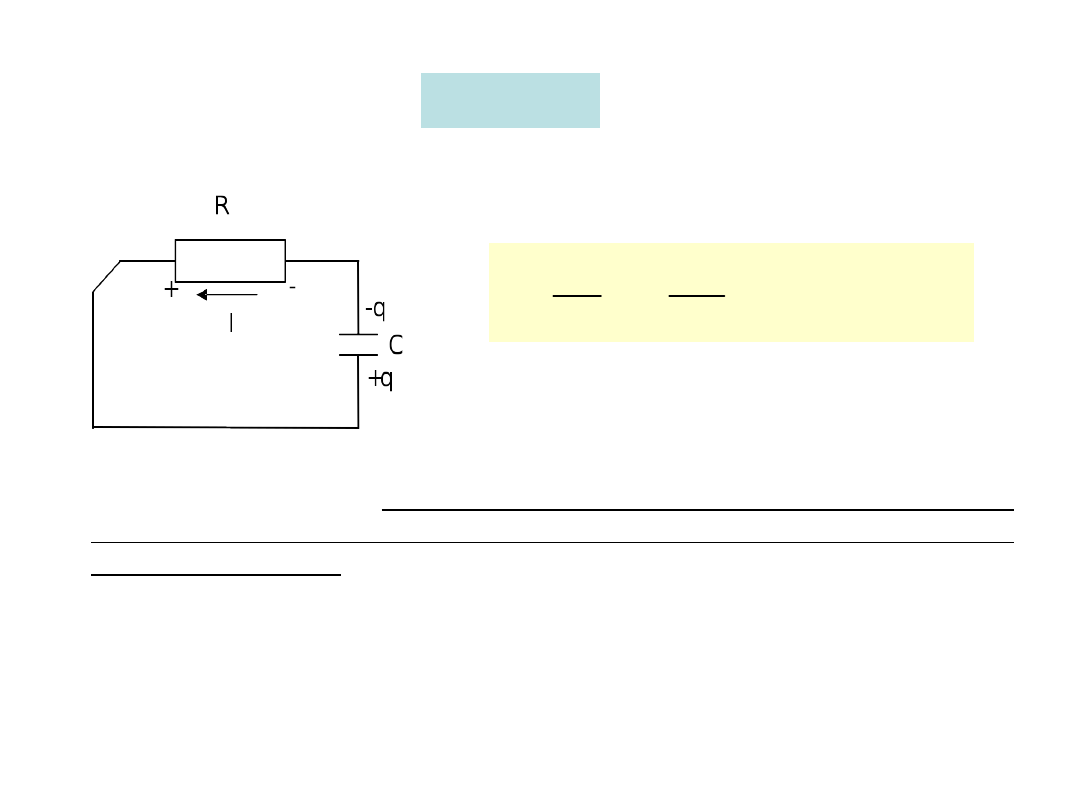
A. Obwód RC

Rozpatrzmy, jaki prąd popłynie w obwodzie po zamknięciu

wyłącznika do pozycji (a).

Korzystamy

z

prawa

Kirchoffa (do szeregowo
podłączonych
kondensatora i opornika
podłączona jest bateria).

C

q

IR





W równaniu tym są dwie niewiadome I oraz q. Ale możemy skorzystać
ze związku I = dq/dt. Otrzymujemy równanie różniczkowe

C

q

R

t

q





d

d



Szukamy rozwiązania q(t). Ma ono postać

)

1

(

/ RC

t

e

C

q









Sprawdzamy, czy funkcja ta jest rozwiązaniem równania różniczkowego
poprzez jej podstawienie do równania.
Prąd obliczamy różniczkując dq/dt

RC

t

RC

t

e

I

e

R

t

q

I

/

0

/

d

d













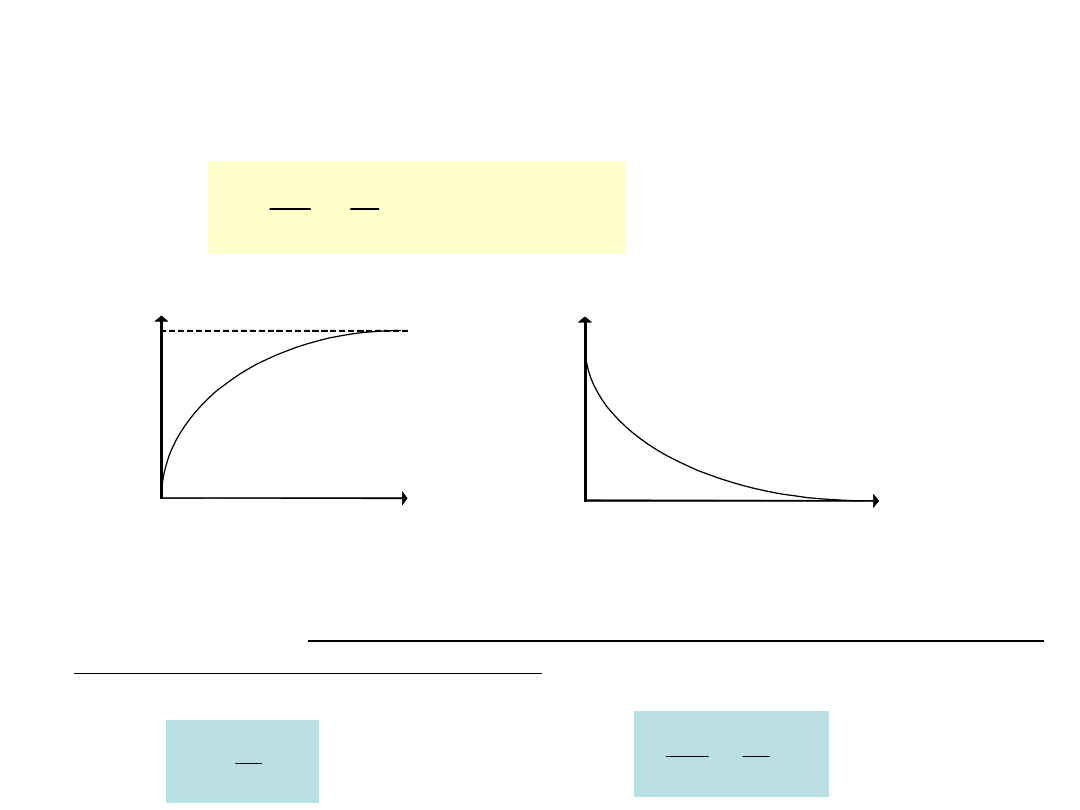
Rysunki przedstawiają zależność q(t) oraz I(t).

q

t

C



I



/R

t

Jeżeli teraz przełączymy wyłącznik do pozycji (b) - rozładowujemy
kondensator przez opornik R.
W każdej chwili napięcie na kondensatorze q/C jest równe spadkowi
napięcia na oporniku IR (q/C = IR).
Stąd prawo Kirchoffa przyjmuje postać (w obwodzie nie ma

)i

0





C

q

IR

czyli

0

d

d





C

q

t

q

R

Rozwiązanie ma postać

W równaniach opisujących ładowanie i
rozładowanie kondensatora wielkość RC
ma wymiar czasu i jest nazywana

stałą

czasową obwodu (

C

= RC).

RC

t

e

q

q

/

0





gdzie q

0

jest ładunkiem początkowym na kondensatorze.

Natężenie prądu przy rozładowaniu wynosi

C

t

RC

t

e

I

e

RC

q

t

q

I



/

0

/

0

d

d













Opisuje ona fakt, że ładunek na kondensatorze nie osiąga od razu
wartości końcowej, lecz zbliża się do niej wykładniczo. Podobnie
przy rozładowaniu (po czasie  = RC ładunek zmniejsza się do 1/e

początkowej wartości).

B. Obwód RL
Analogicznie opóźnienie w narastaniu i zanikaniu prądu pojawia się

w obwodzie RL (cewka indukcyjna L podłączona do opornika R) przy
włączaniu lub wyłączaniu źródła SEM.

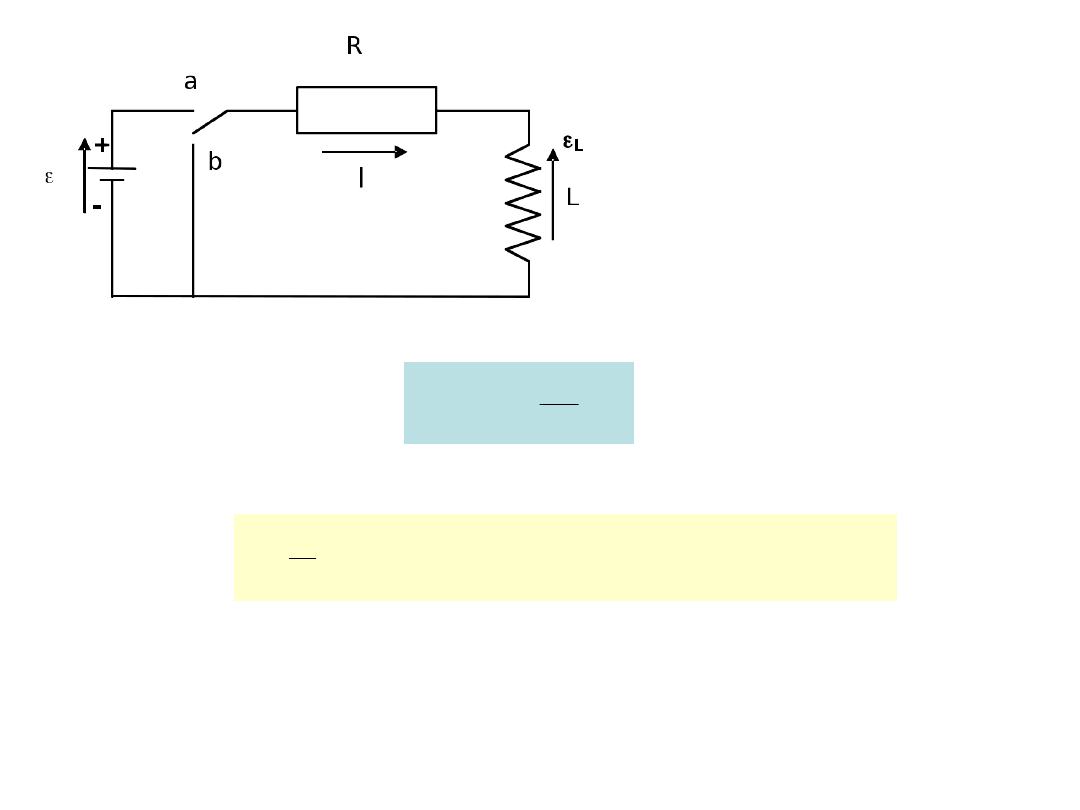
Gdyby nie było cewki prąd
osiągnąłby

natychmiast

wartość

/R. Dzięki cewce w

obwodzie

pojawia

się

dodatkowo SEM samoindukcji
L, która zgodnie z regułą

Lenza przeciwdziała wzrostowi
prądu

(po

włączeniu),

co

oznacza, że jej zwrot jest
przeciwny do

.

Z prawa Kirchoffa otrzymujemy

0

d

d







t

I

L

IR



Poszukujemy rozwiązania tego równania różniczkowego w postaci I(t).
Ma ono postać

)

1

(

)

1

(

)

1

(

/

0

/

0

/

L

t

L

Rt

L

Rt

e

I

e

I

e

R

I























Sprawdzamy je poprzez podstawienie do równania.

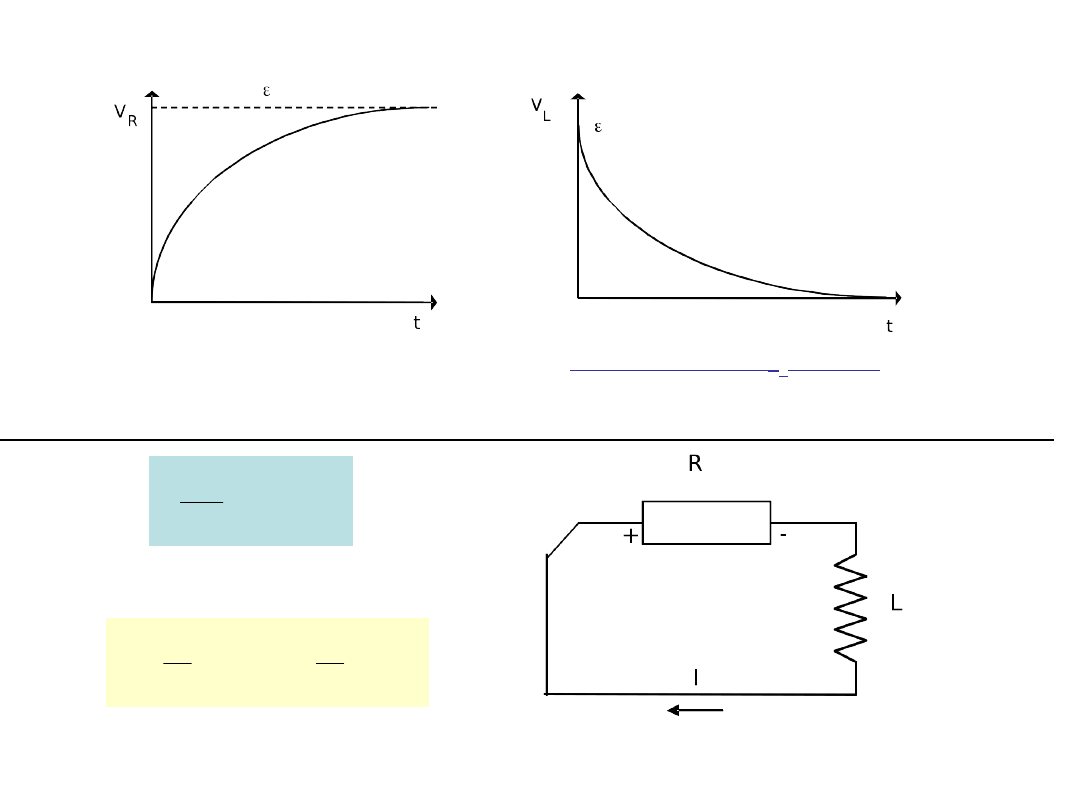
Napięcie na oporniku i cewce pokazane jest na rysunkach poniżej.

Narastanie prądu w obwodzie jest opisane

stałą czasową



L

 = L/R.

Jeżeli przełącznik ustawimy w pozycji (b) to wyłączmy źródło SEM i otrzymamy

0

d

d



 IR

t

I

L

z rozwiązaniem

L

t

L

Rt

e

R

e

R

I







/

/









5. Energia a pole magnetyczne

Pozostańmy przy obwodzie RL. Z prawa Kirchoffa otrzymaliśmy

t

I

L

IR

d

d







Mnożąc to równanie przez I dostajemy

t

I

LI

R

I

I

d

d

2







Interpretacja tego równania z punktu widzenia pracy i energii jest

następująca:

1. lewa strona równania - szybkość (moc =

I = dq/dt = dW/dt) z jaką

źródło przekazuje do obwodu energię

q.

2. pierwszy wyraz po prawej stronie - szybkość (moc) wydzielania

ciepła na oporze R.

3. drugi wyraz po prawej stronie - szybkość (moc) z jaką energia

gromadzi się w polu magnetycznym.

Ten ostatni wyraz możemy zapisać jako

t

I

LI

t

W

B

d

d

d

d



czyli

I

LI

dW

B

d



Po scałkowaniu otrzymujemy

2

2

1

d

d

LI

I

LI

W

W

W

B

B

L













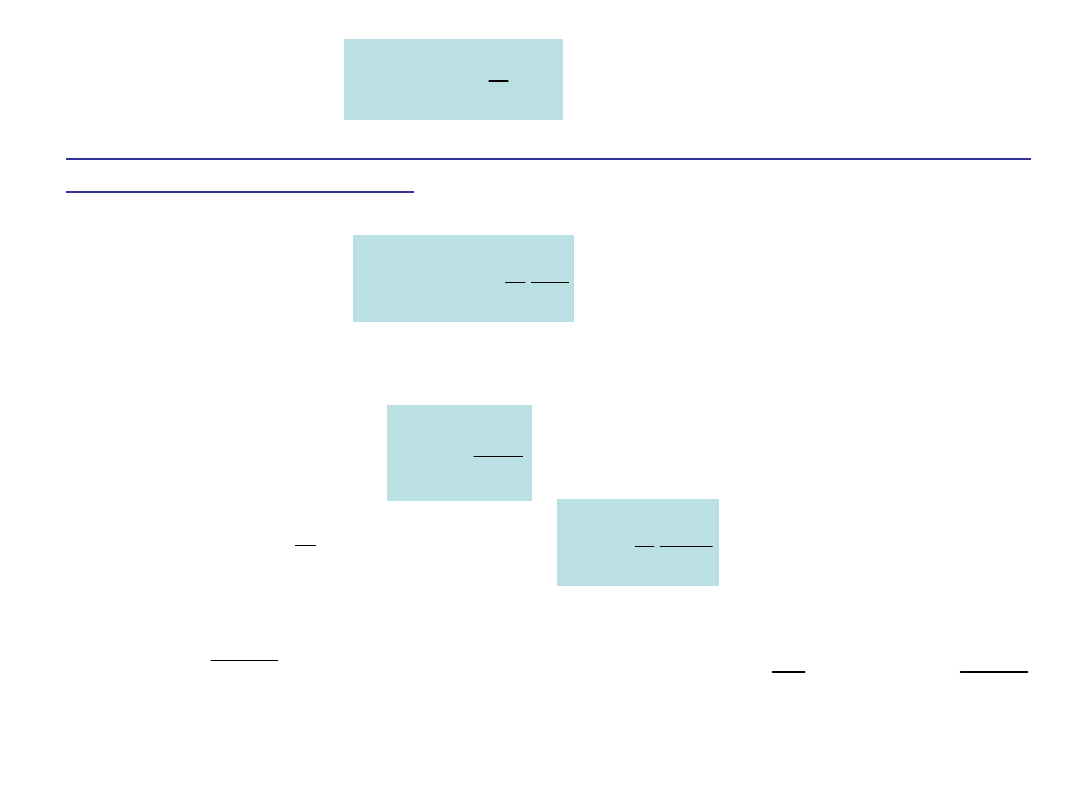
całkowitą energię magnetyczną zawartą w cewce o indukcyjności L
przez, którą płynie prąd I.

Można to porównać to z energią naładowanego kondensatora

C

q

W

W

C

E

2

2

1





Równanie określa

2

2

1

LI

W

W

B

L





6. Gęstość energii a pole magnetyczne

Rozpatrzmy solenoid o długości l i powierzchni przekroju S, czyli o objętości lS.
Tak, więc gęstość energii

lS

W

w

B

B



Ponieważ

2

2

1

LI

W

B



lS

LI

w

B

2

2

1



więc

Przypomnijmy, że

l

S

N

L

2

0





0

0

0







N

Bl

I

l

N

I

In

B









oraz

co w połączeniu daje wyrażenie

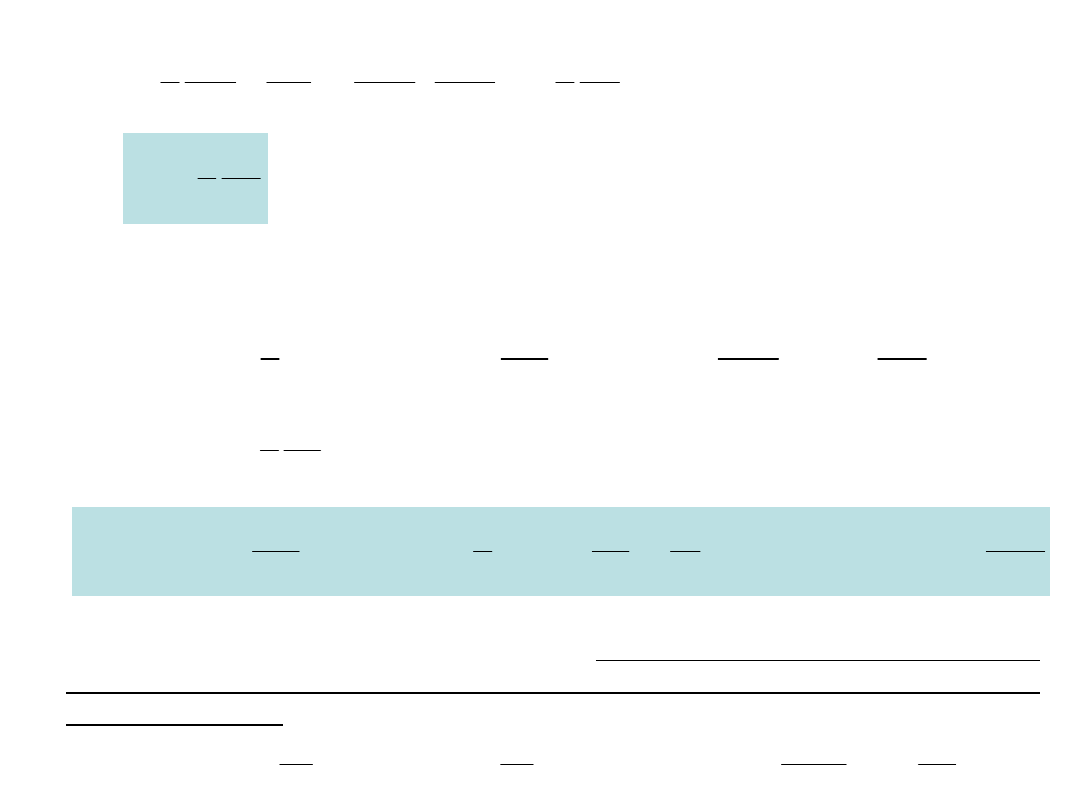
0

2

2

0

2

0

2

2

1

2

1

2

1







B

N

Bl

l

S

N

lS

lS

LI

w

B



















0

2

2

1



B

w

B



opisuje

gęstość energii pola magnetycznego

zawartej w każdym punkcie przestrzeni w której jest
indukcja magnetyczna B.

W ogólności w przestrzeni może istnieć zarówno pole elektryczne, jak
i

magnetyczne,

a

całkowita

gęstość

energii

pola

elektromagnetycznego wynosi

0

2

0

0

2

2

0

2

1

4

1

4

1

8

1

lub

2

1













B

w

k

k

bo

E

k

w

E

w

B

E

E













Zobaczymy później, że fala elektromagnetyczna wypromieniowana
przez zmieniający się prąd ma

E = cB

. Energia promieniowania zawarta

w polu elektrycznym jest, więc równa energii zawartej w polu
magnetycznym.

2

0

2

0

0

0

2

2

2

2

0

2

2

2

0

1

1

)

(

2

)

(

2

B

B

B

c

B

c

B

c

E

w

w

w

B

E





























0

0

2

2

2

2

0

0

2

2

0

2

2

2

1

)

(

2

)

(

2

1

)

(

8

1































c

bo

B

c

E

B

E

B

c

E

k

w

w

w

B

E