Dynamika

-

zasady dynamiki

-

zasady zachowania

-

układy inercjalne

-

układy nieinercjalne

Wykład - KURS 3 -

Dynamika



badanie przyczyn ruchu



badanie związków między ruchem
ciała a siłami działającymi na ciało



określenie ruchu ciała pod działaniem
znanych sił



wyznaczenie sił działających na ciało,
gdy znany jest jego ruch

2

Dynamika – badanie przyczyn
ruchu (Newton, XVIII w.)

Oddziaływania fundamentalne

Oddziaływania

Źródło

Intensywność

względna

Promień

działania

Grawitacyjne

Masa

10

-39

Daleko-

zasięgowe

Słabe

Cząstki elementarne

10

-15

Krótko-

zasięgowe

(10

-15

m)

Elektro-

magnetyczne

Ładunki elektryczne

10

-2

Daleko-

zasięgowe

Jądrowe (silne)

Hadrony (protony,

neutrony, mezony)

1

Krótko-

zasięgowe

(10

-15

m)

3

a

m

F







Masa, pęd, siła



masa – wielkość skalarna



charakteryzuje właściwości inercjalne ciała, czyli jego

uległość wobec oddziaływań na niego innych ciał



mechanika klasyczna  masa ciała nie zależy od prędkości



określenie masy poprzez porównanie z masą innego ciała

wzorca



pęd – wielkość wektorowa



wielkość dynamiczna charakteryzująca ruch ciała



pęd p – iloczyn masy i prędkości ciała



siła – wielkość wektorowa



będąca miarą oddziaływań prowadzących do zmiany

prędkości – jeśli ciało o masie m porusza się z

przyspieszeniem a, to pozostaje ono pod działaniem siły F

definiowanej jako

v

m

p







4

Siły wewnętrzne i zewnętrzne
w układzie ciał



układ ciał – zbiór dwóch lub większej liczby ciał



układ zamknięty – masa układu podczas ruchu
nie ulega zmianie



siła wewnętrzna – siła działająca między
ciałami składowymi układu



siła zewnętrzna – siła pochodząca ze strony
ciał nie należących do układu



układ odosobniony(izolowany) – wypadkowa
sił zewnętrznych na układ jest równa zeru

5

Ciało



pozostaje w spoczynku



porusza się ruchem jednostajnym prostoliniowym

dopóki wypadkowa sił zewnętrznych nie zmieni tego

stanu, czyli jest równa zeru

I zasada dynamiki Newtona –
przyczyna zachowania stałej
prędkości ciała



prędkość ciała pozostaje stała (w szczególności równa zero,
czyli ciało pozostaje w spoczynku), dopóki oddziaływania ze
strony innych ciał (zewnętrzne siły) jej nie zmienią, czyli
wypadkowa siła działająca na to ciało jest równa zero

lub

a= 0

Z doświadczenia:

6

7

Pierwsza zasada dynamiki nosi nazwę
zasady bezwładności.
Przez bezwładność rozumiemy właściwość ciała
decydującą o tym, że ciało bez działania sił nie
może zmienić ani wartości, ani kierunku swej
prędkości. Czyli bez działania sił pozostaje w
takim stanie jak było wcześniej: spoczywa jeśli
spoczywało, lub porusza się ruchem jedno-
stajnym jeśli było w jakimkolwiek ruchu.

Pośrednim wnioskiem z pierwszej

zasady jest fakt, że wszelkie zmiany
prędkości mogą zachodzić jedynie pod
działaniem sił. Musi więc istnieć związek między
siłą a zmianami prędkości. Ta zależność jest
treścią drugiej zasady dynamiki.

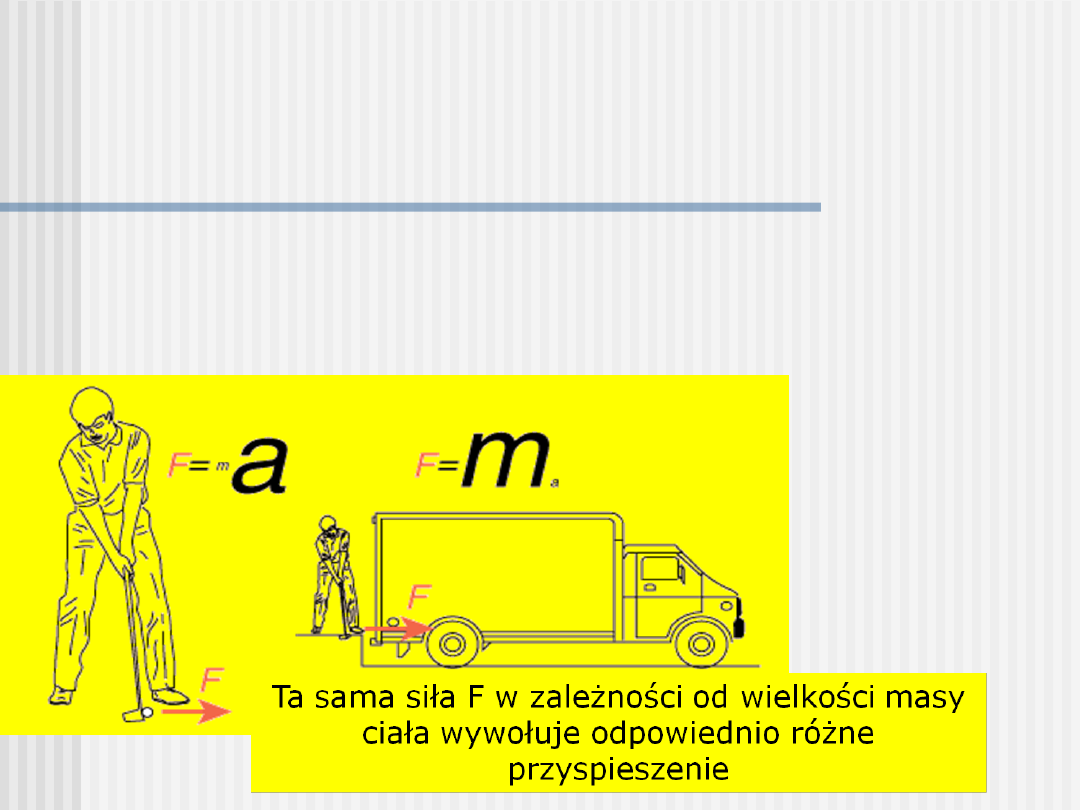
II zasada dynamiki Newtona –
przyczyna zmiany prędkości ciała

F

wyp

- wypadkowa siła (suma wektorowa wszystkich sił ) działa-

jąca na ciało o masie m zmienia jego prędkość, czyli nadaje mu
przyspieszenie a

8

a

m

F

wyp







9

II zasada dynamiki nie jest fundamentalnym
prawem fizyki



nie ma zastosowania dla ciał o bardzo małej
masie rzędu mas atomowych – mechanika
kwantowa



w podanej postaci ma zastosowanie tylko dla
ciał o stałej masie

10

Ogólne ujęcie drugiej zasady dynamiki

Do wyrażenia

podstawiamy znane wyraże-

nie:

i otrzymujemy

Iloczyn siły i czasu jej działania nazywamy

popędem siły

. Jest to wektor o kierunku

zgodnym z kierunkiem wektora .

Iloczyn masy i prędkości nosi nazwę

pędu

. Jest

to również wektor.
Kierunek wektora pędu jest zgodny z kierunkiem
prędkości . Równanie ostatnie wyraża, że

wektor

popędu siły jest równy wektorowemu przyrostowi
pędu wywołanemu przez tę siły.

czyli

a

m

F







1

2

1

2

t

t

a





















.

m

m

t

t

F

1

2

1

2





















p

t

t

F

1

2











.

t

p

F











II zasady dynamiki Newtona
- ogólna postać



zmiana masy występuje w przypadku:



straty lub przyrostu materii



dla ciał poruszających się z prędkościami bliskimi

prędkości światła c - efekty relatywistyczne

Szybkość zmiany pędu ciała jest równa sile

wypadkowej działającej na to ciało



ogólniejsza postać II zasady dynamiki Newtona



słuszna także dla ciał o zmieniającej się masie

a

m

dt

v

d

m

F

wyp











dla



11

wyp

F

dt

p

d







dt

dm

v

dt

v

d

m

dt

v

dm

dt

p

d

F

wyp



















0



dt

dm

12

Gdy prędkość ciała jest porównywalna z prędkością
światła, należy uwzględniać zmienność masy podczas
ruchu co opisuje szczególna teoria względności.
Zmienność masy wynikająca z ruchu ciała jest
określona równaniem Einsteina:

(3.4)

gdzie m oznacza masę ciała będącego w ruchu,

m

0

– masę tegoż ciała w spoczynku,

c – prędkość światła w próżni (ok. 3000 000 km/s).

Ze wzoru wynika, że nawet wtedy, gdy prędkość ciała równa
się 30 000 km/s, zmiana masy jest niewielka, mniejsza od
1%. Gdy prędkości zbliżają się do prędkości świata (co może
występować np. w przypadku mikrocząsteczek), masa coraz
szybciej rośnie. W tych warunkach zamiast mechaniki
niutonowskiej należy stosować mechanikę relatywistyczną.

2

2

0

c

/

1

m

m







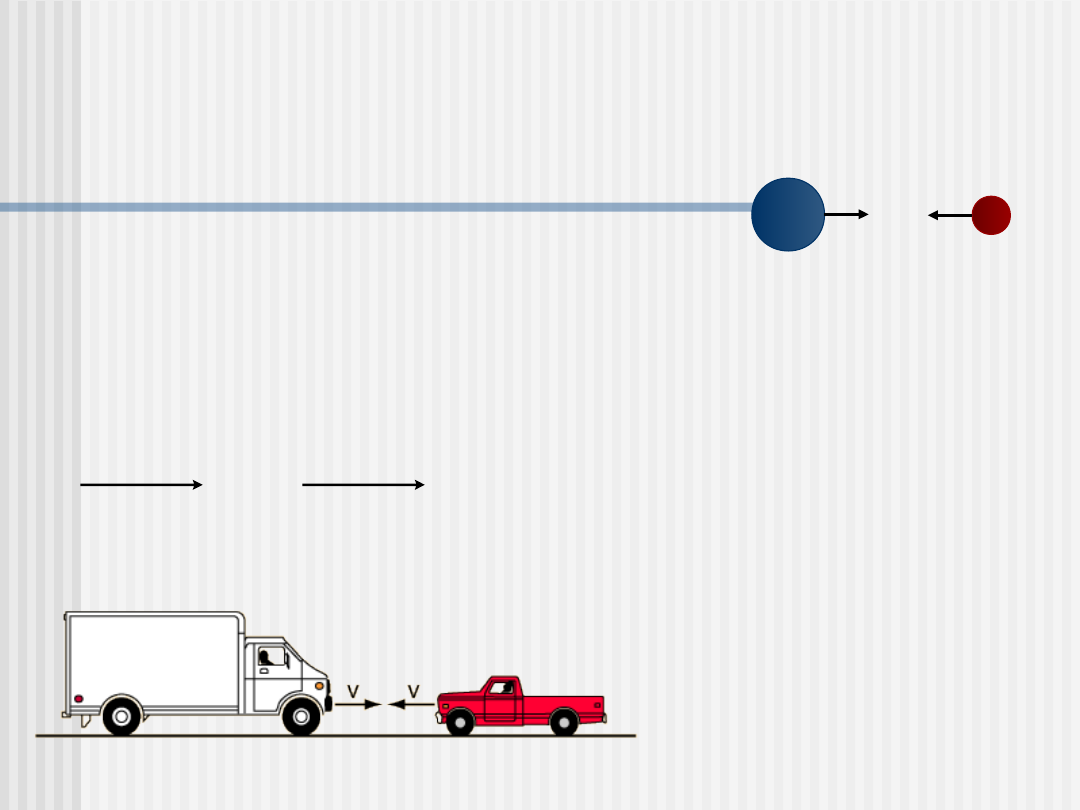
III zasada dynamiki Newtona –
wzajemne oddziaływanie dwóch ciał



dla każdej zewnętrznej siły
działającej na ciało występuje
siła równa co do wartości, ale
przeciwnie skierowana, którą
dane ciało wywiera na ciało,
będące źródłem siły zewnętrznej

A

B

F

AB

F

BA



dla sił wewnętrznych, sile jednej
części układu przeciwdziała siła
reakcji innej części układu 

wypadkowa siła w izolowanym z
układzie jest równa zeru. Tylko
siły zewnętrzne mogą być przy-
czyną ruchu układu.

W przyrodzie nie ma izolowanych sił

III zasada dynamiki

Newtona – przykład

uniwersalnej zasady

symetrii, nie ma od niej

odstępstw

Podczas zderzenia siła z jaka mały samochód działa na duży jest takiej samej wartości

13

A

B

B

A

F

F









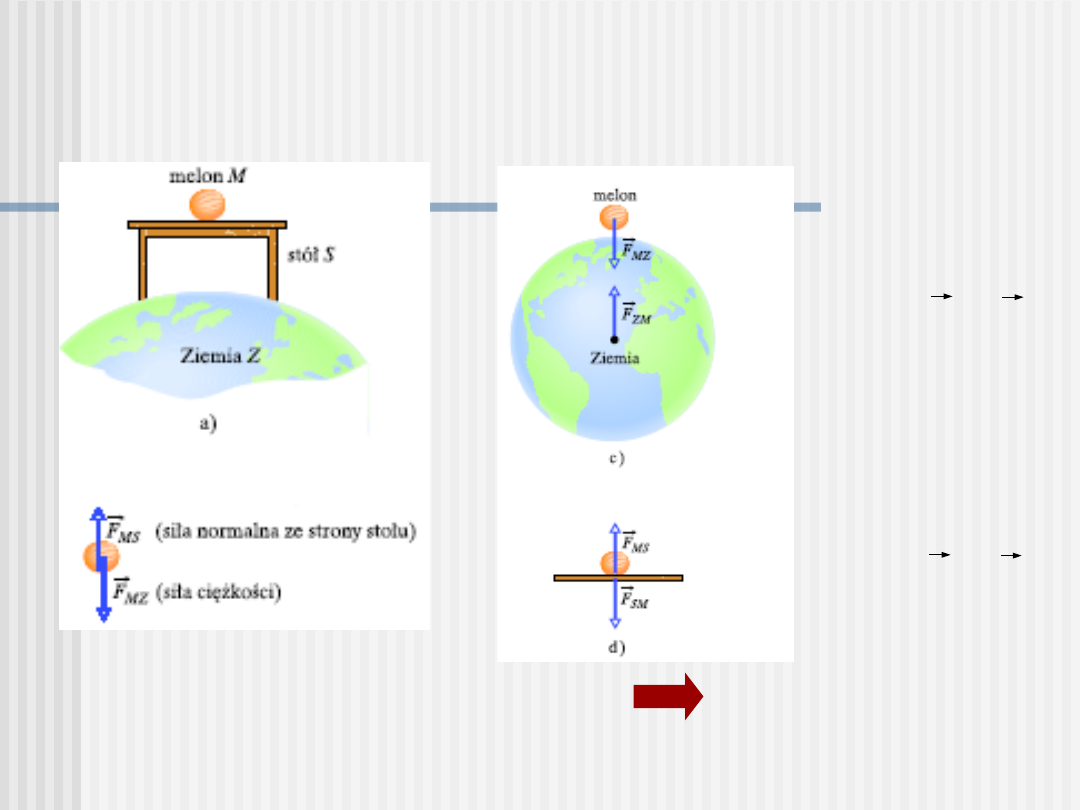
III zasada dynamiki Newtona –
siły akcji i reakcji działają na różne ciała

siły działające na melon:

F

MS

i F

MZ

- nie są siłami akcji i

reakcji (działają na to samo

ciało)

- są siłami akcji i

reakcji

pary sił F

MS

i F

SM

pary sił F

MZ

i F

ZM

14

Zasady dynamiki Newtona



Ciało pozostaje w spoczynku lub porusza się

ruchem jednostajnym prostoliniowym dopóki nie

zostanie zmuszone za pomocą odpowiednich sił do

zmiany tego stanu (zasada bezwładności)



Szybkość zmiany pędu ciała jest równa sile
wypadkowej działającej na to ciało



Gdy dwa ciała oddziaływają wzajemnie to siła
wywierana przez ciało drugie na ciało pierwsze jest
równa i przeciwnie skierowana do siły z jaką ciało
pierwsze działa na ciało drugie

A

B

B

A

F

F













wyp

F

dt

p

d







wyp

F

a

m

dt

v

d

m

dt

v

dm















15

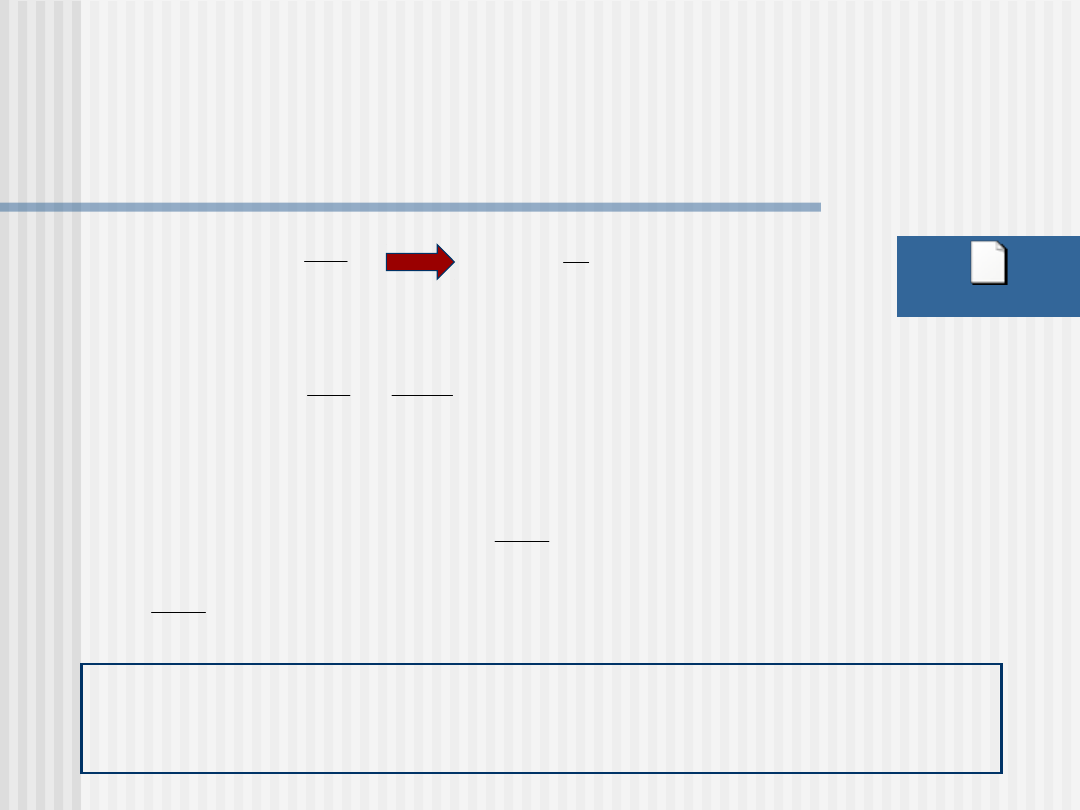
Równanie ruchu





t

v

r

F

F

,

,











dt

v

d

m

a

m

F











dt

m

F

v









x

0

, v

0

– położenie i prędkość w

początkowej chwili czasu t

0

=0

Z równania ruchu można otrzymać prędkość i tor ciała w dowolnej
chwili czasu , odtworzyć ruch przeszły i przewidzieć poruszanie
się w przyszłości  charakter deterministyczny

Jeżeli znamy masę i siłę działającą na ciało to II
zasada dynamiki Newtona określa tzw. równanie
ruchu

dt

v

r









Przykład: Rozpatrzmy ruch jednowymiarowy o a=const.





0

0,

,

x

r 



2

2

dt

x

d

dt

dv

a





1

C

at

dt

a

v









 

1

0

0

C

v

v





0

v

at

v









2

0

2

0

2

C

t

v

at

dt

v

at

dt

v

x

















 

2

0

0

C

x

x





0

0

2

2

x

t

v

at

x







ConstantAccel.swf

16

Zasady zachowania –

najbardziej

fundamentalne prawa

„zewnętrzne” – pędu,
momentu pędu, energii
„wewnętrzne” – ładunku,
liczby nukleonów, liczby
leptonowej

Energia



Energia to wielkość fizyczna charakteryzująca stan ciała

(układu ciał) pod względem jego zdolności do wykonywania

pracy (ruchu ciała)



zależnie od różnych rodzajów procesów fizycznych mówimy

o różnych formach energii:



wewnętrznej



mechanicznej



elektromagnetycznej



jądrowej



chemicznej



zasadniczo rozróżnia się energię:



E

k

kinetyczną – związaną z ruchem ciała



U potencjalną – związaną z siłami działającymi na ciało i

jego położeniem

18

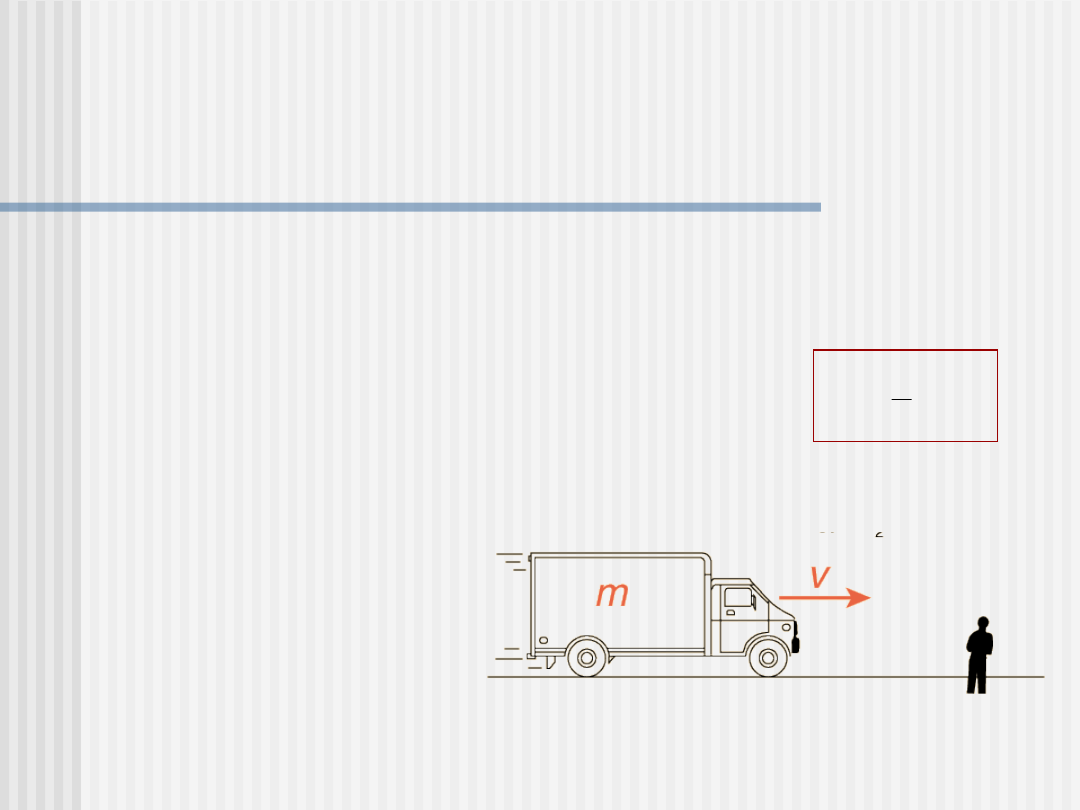
Energia kinetyczna
punktu materialnego

Energia kinetyczna K punktu materialnego

o masie m poruszającego się z prędkością v,

dużo mniejszą od prędkości światła c (v<<c)

2

2

1

v

m

K





Energia kinetyczna jest związana z ruchem ciała,
ciało posiada energię kinetyczną ponieważ porusza się

Energia kinetyczna
wyraża fakt, że
poruszające się ciało jest
zdolne go wykonania
pracy nad ciałem, w
które uderzy

19

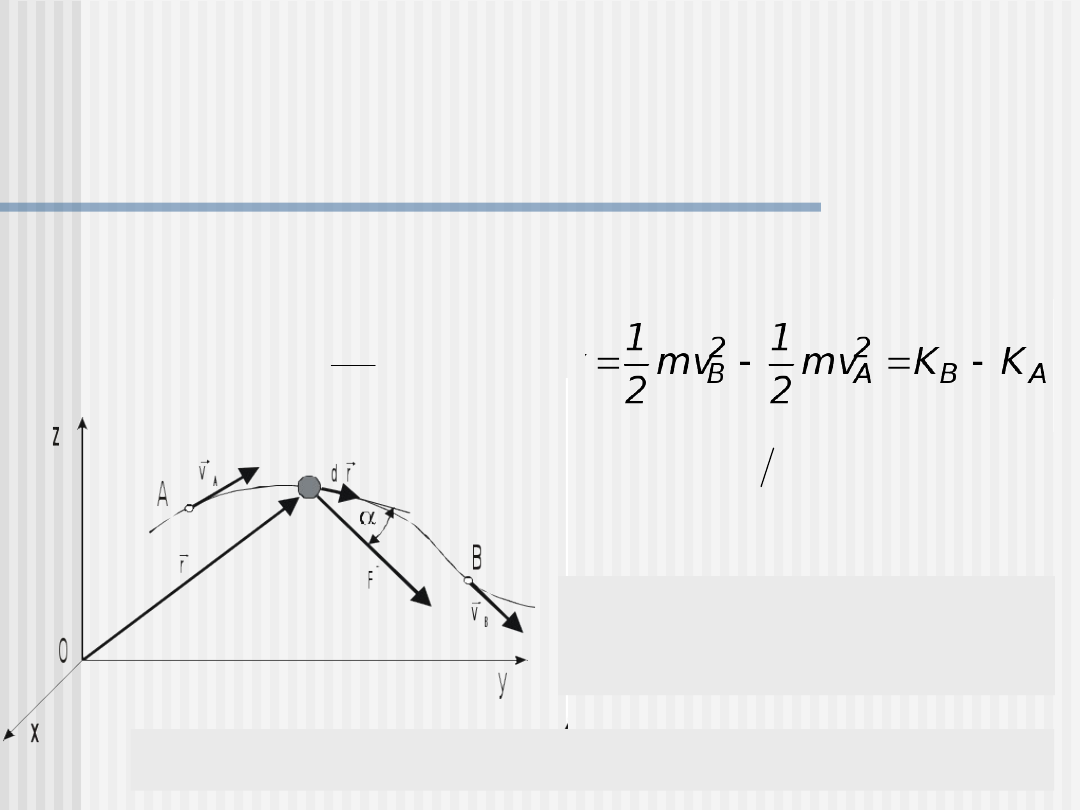
Energia kinetyczna



Wyznaczmy całkowitą pracę siły F wzdłuż toru AB











B

A

B

A

B

A

AB

v

d

v

m

r

d

dt

v

d

m

=

r

d

F

=

W













to energia kinetyczna

 

2

mv

2

1

K 

gdzie

Zasada równoważności pracy i energii

Zmiana energii kinetycznej
cząstki jest równa całkowitej
pracy wykonanej nad cząstką

20

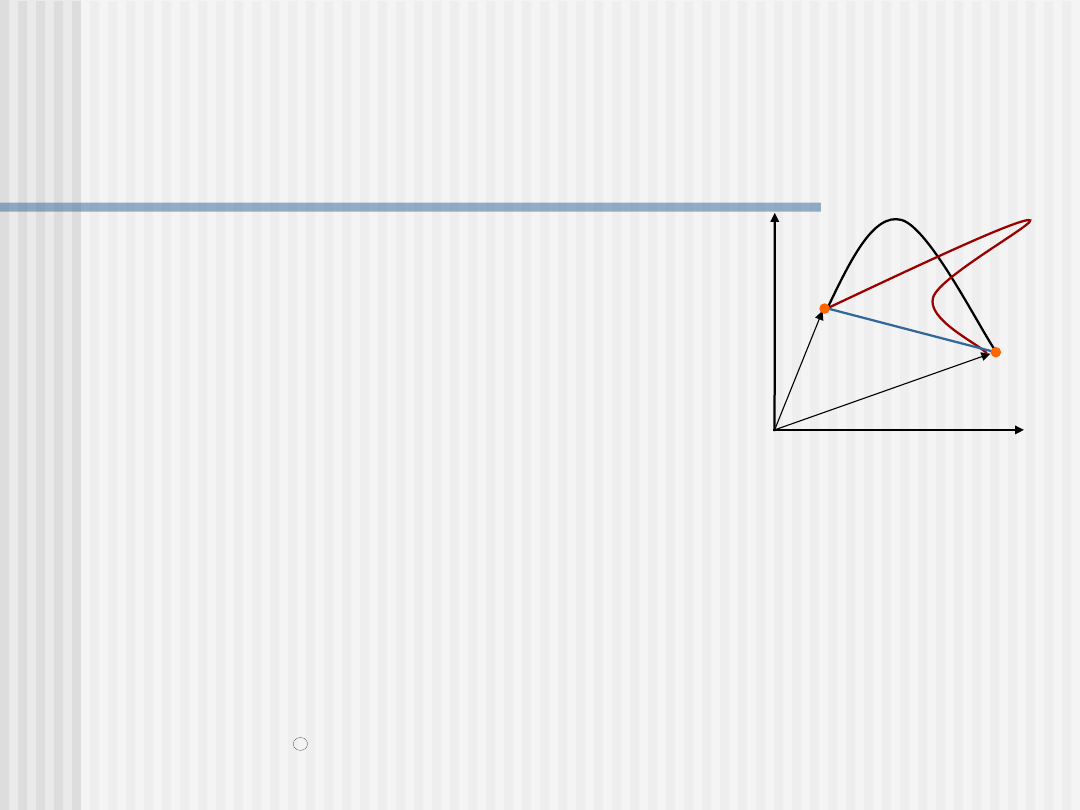
Grupy i rodzaje sił

Dla sił zachowawczych



praca sił pomiędzy dwoma punktami

nie zależy

od

wyboru drogi, a tylko od położenia końcowego i
początkowego punktu



praca po drodze zamkniętej jest równa zero

x

r

d

r

F

r

d

r

F

r

d

r

F

W

L

L

L

AB































3

1

2

)

(

)

(

)

(

Z punktu widzenia zasady zachowania
energii w mechanice:



siły zachowawcze (grawitacyjne,
sprężystości)



siły rozpraszające (tarcie)

0







r

d

r

F

W

ABA







)

(

B

A

L

1

L

3

L

2

0

y

21

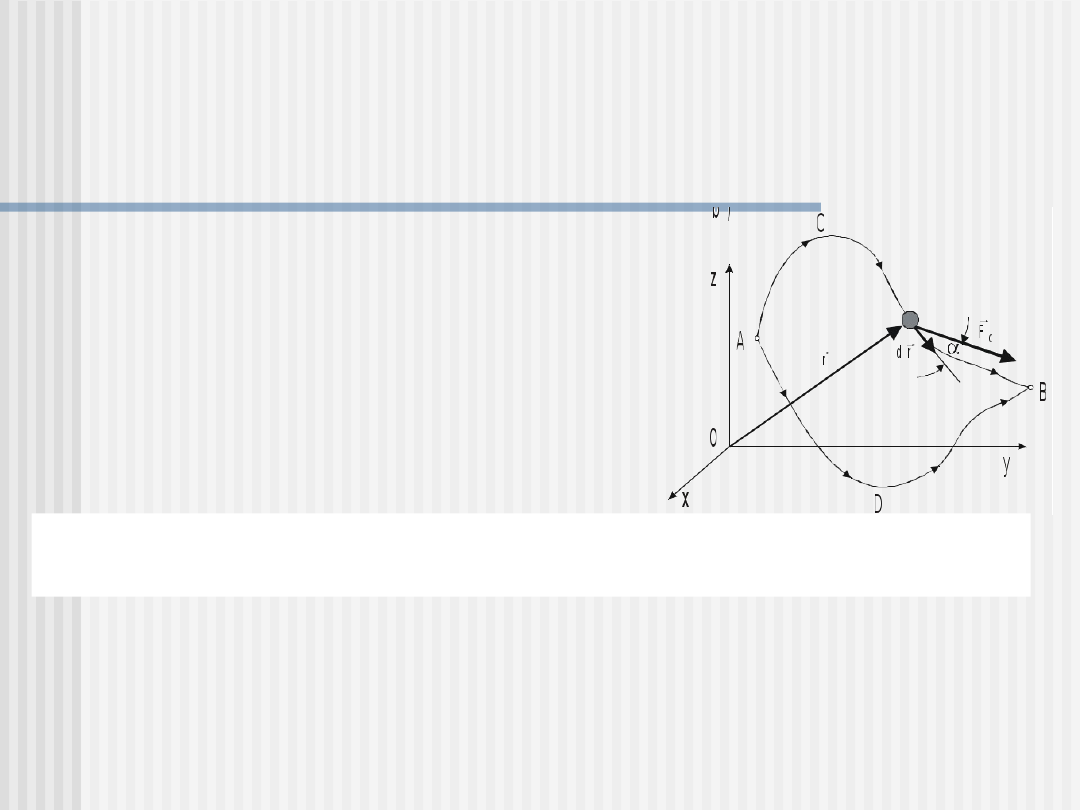
Siły zachowawcze – energia
potencjalna

const

r

d

F

r

d

F

W

ADB

ACB

AB























Jeżeli praca wykonana przez siłę
przemieszczająca cząstkę z punktu A
do B jest niezależna od toru
łączącego punkty A i B, to siła jest
siłą zachowawczą.

Zmiana energii potencjalnej to praca wykonana nad ciałem
przez siłę zachowawczą, wzięta z przeciwnym znakiem















B

A

A

B

AB

AB

U

=U

r

d

F

W

=

U





Zwykle A wybiera się w nieskoń-
czoności i przyjmuje

0



A

U









B

B

r

d

F

-

U





czyli określa energię potencjalną w punkcie B

22

Energia potencjalna
punktu materialnego

Energia potencjalna – energia wynikająca z położenia lub

konfiguracji układu ciał względem siebie

Jeśli siły działające na ciało zależą tylko od położenia F(r)
tzw.

siły zachowawcze

, to mogą być reprezentowane

przez funkcję energii potencjalnej U

)

(r

F

dr

dU





punkt odniesienia r

odn

o zerowej energii

potencjalnej może być dowolnie wybrany

Energia potencjalna = praca wykonana przez siły zewnętrzne
przy przesunięciu ciała z punktu odniesienia o zerowej energii
potencjalnej do danego punktu o położeniu r









r

r

odn

r

d

F

r

U





)

(

znając energię potencjalną można wyznaczyć
siłę działającą na ciało

23

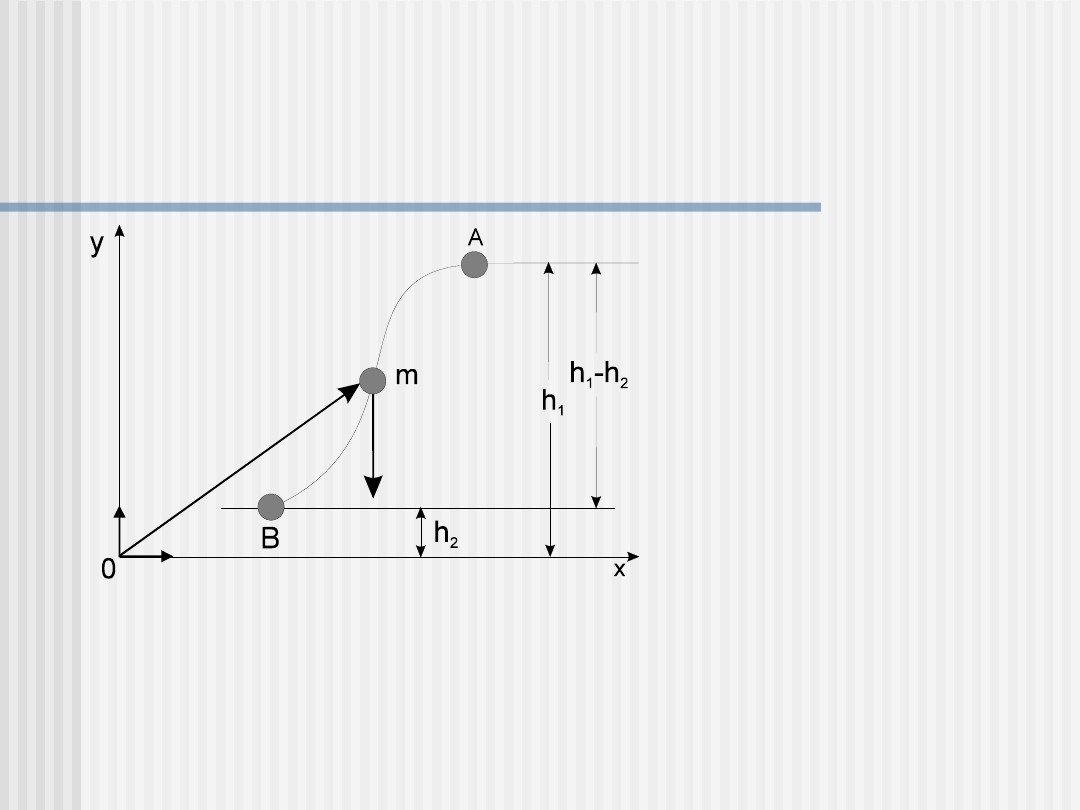
PRZYKŁAD

Praca wykonana przez siłę grawitacyjną

r

j

r

i

r

r





F

mg

g





 











=mgh

h

h

=mg

dy

mg

dy

j

dx+

i

mg

j

W

2

1

h

h

h

h

AB

2

1

2

1

=





















Ponieważ praca
wykonana przez siłę
grawitacyjną jest
niezależna od tego po
jakim torze porusza się
cząstka między punktami
A i B, więc jest to siła
zachowawcza

r

d

F

W

AB

g

AB











mgh

W

U

AB











24

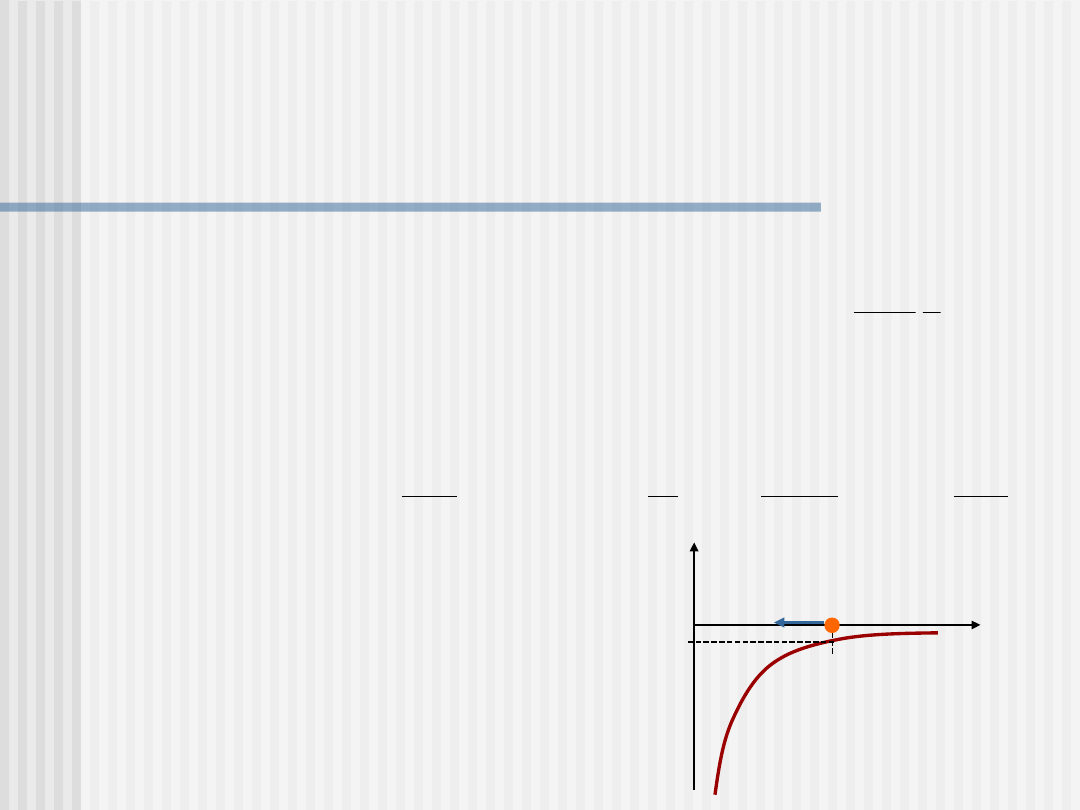
Grawitacyjna energia
potencjalna

r

Mm

G

r

GMm

dr

r

GMm

dr

r

Mm

G

r

d

F

r

d

F

U

R

R

R

R

R















































2

2

1









Energia potencjalna to praca jaką należy wykonać przenosząc
daną masę z nieskończoności do danego punktu pola

Energia potencjalna masy m w polu
grawitacyjnym ma zawsze wartość
ujemną i rośnie do zera w miarę
oddalania się do nieskończoności

r

r

r

M

m

G

F





2





W polu grawitacyjnym zgodnie z prawem powszechnego
ciążenia na masę m działa siła grawitacyjna

U

r

0

F m

25

Prawo zachowania energii
mechanicznej



jeżeli wszystkie siły działające na cząstkę są zachowawcze, to

całkowita energia cząstki w każdym jej położeniu jest wielkością

stałą, zwaną całkowitą energią mechaniczną



siła niezachowawcza np. siła tarcia, ciepło, promieniowanie



energia układu izolowanego może przekształcać się z jednej

postaci w inną, jednak energia całkowita w jej różnorodnych

formach nie może być ani stworzona z niczego, ani też

unicestwiona

A

B

AB

K

K

W





B

A

AB

U

U

)

e

zachowawcz

(

W





const

=

U

+

K

=

U

+

K

B

B

A

A

)

U

K

(

)

U

K

(

)

wcze

niezachowa

(

W

A

A

B

B

AB









A

B

AB

AB

K

K

wcze

niezachowa

W

e

zachowawcz

W







)

(

)

(

26

Zasada zachowania pędu



pęd cząstki o masie bezwładnej m i prędkości jest wektorem



całkowity pęd izolowanego i zamkniętego układu cząstek pozostaje stały

(jeśli na układ cząstek nie działają siły zewnętrzne lub ich wypadkowa jest równa zeru, to całkowity

pęd układu nie ulga zmianie)



pęd początkowy jest równy pędowi końcowemu



jeśli wypadkowa sił zewnętrznych jest wzdłuż pewnej osi równa zeru, to składowa pędu w tym kierunku

nie ulega zmianie

v

m

p







z

y

x

mv

k

mv

j

mv

i

p















v



const

v

m

v

m

v

m

v

m

N

i

i

i

N

N

B

B

A

A













1











konc

pocz

p

p







27

Zderzenie sprężyste

m

1

v

1

+ m

2

v

2

= m

1

u

1

+ m

2

u

2

2

2

2

2

2

2

2

2

1

1

2

2

2

2

1

1

u

m

u

m

m

m







v

v

Zasada zachowania pędu Zasada zachowania energii

przed

po

Zderzeniem nazywamy krótkotrwały proces, w którym jakieś
ciała zbliżają się do siebie, a następnie w wyniku wzajemnego
oddziaływania ich ruch ulega zmianie.

28

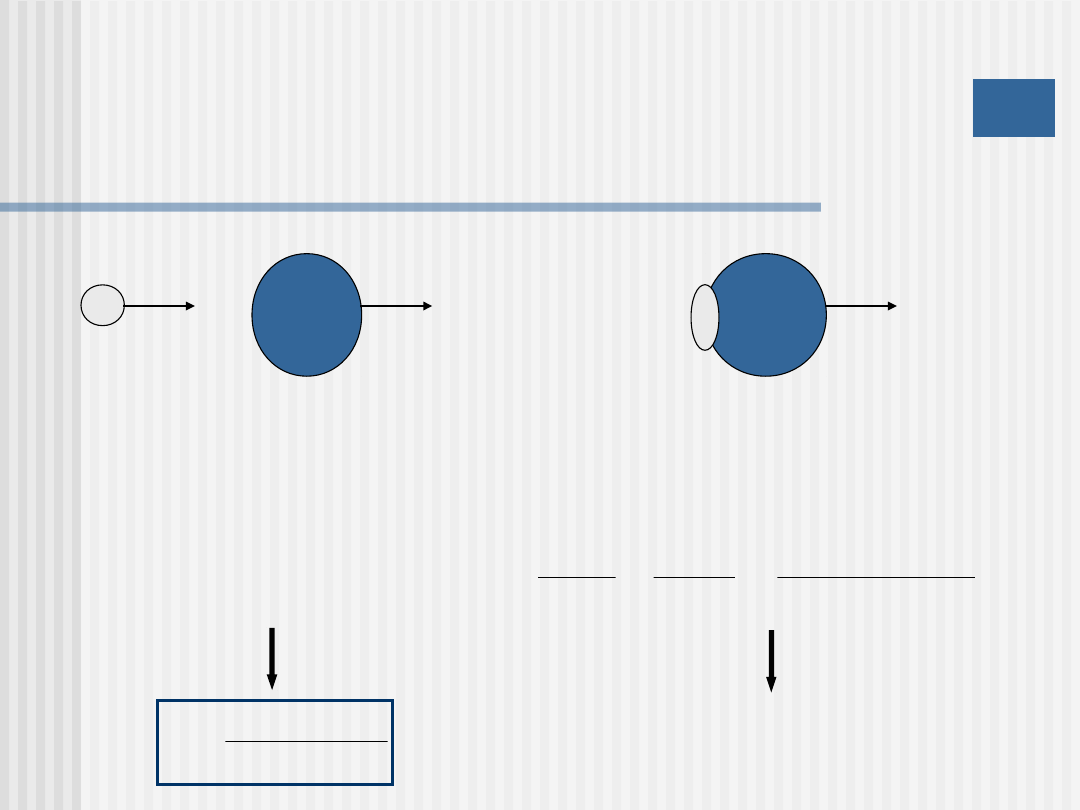
Zderzenie niesprężyste (idealne)

1

1

V

m

2

2

V

m

1

2

1

u

m

m 

Zasada zachowania pędu

Zasada zachowania energii





1

2

1

2

2

1

1

u

m

m

V

m

V

m













E

u

m

m

V

m

V

m













2

2

2

2

1

2

1

2

2

2

2

1

1

E



2

1

2

2

1

1

1

m

m

v

m

v

m

u







strata energii

Airtrack.s wf

29

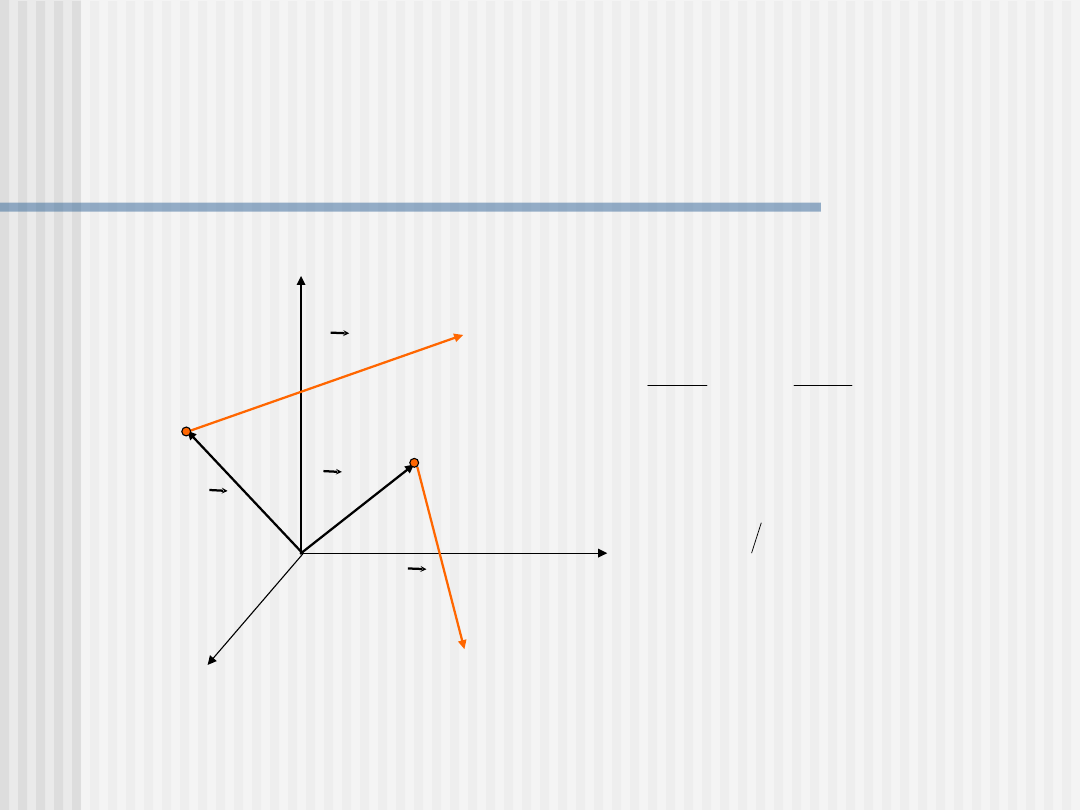
Prawa ruchu Newtona konsekwencją
zasady zachowania pędu

const

v

m

v

m

B

B

A

A









a

m

F







B

B

A

A

a

m

a

m









B

A

F

F









const

v =



0



F



II P.N.

III P.N.

I P.N.

x

y

z

m

A

m

B

v

B

r

A

v

A

r

B

Rozpatrzmy dwie masy m

A

i m

B

poruszające się z prędkościami

0





dt

v

d

m

dt

v

d

m

B

B

A

A









m

F

a

1



B

A

v

v





,

30

Równorzędność zasady zachowania
pędu i praw Newtona



z zasady zachowania pędu można wyprowadzić
prawa Newtona



z II i III zasady dynamiki Newtona można
wyprowadzić zasadę zachowania pędu

const

p

p

dt

p

p

d

dt

p

d

dt

p

d

dt

v

dm

dt

v

dm

dt

v

d

m

dt

v

d

m

F

F

B

A

B

A

B

A

B

B

A

A

B

B

A

A

A

B

B

A





















































0

)

(

III zasada dynamiki Newtona

II zasada dynamiki Newtona

w układzie odosobnionym pęd
całkowity układu jest stały w
czasie

31

32

Dynamika ruchu punktu materialnego po okręgu.

Siła dośrodkowa.

Rozważmy ruch jednostajny po okręgu z punktu widze-
nia dynamiki. Zgodnie z I zasadą dynamiki tylko ruch
jednostajny prostoliniowy może istnieć bez działania
sił.

Ruch jednostajny po okręgu wymaga już istnienia

siły.

Według II zasady dynamiki wartość liczbowa tej siły wyraża
się zależnością

F=ma.

(3.6)

Pamiętamy, że przyspieszenie a w ruchu jednostajnym po
okręgu możemy zapisać

(3.7)

 

Uwzględniając wyrażenie (3.6) i (3.7) otrzymujemy

lub

(3.8)

Kierunek tej siły jest zgodny z kierunkiem przyspie-
szenia a, tak więc siła ta działa wzdłuż promienia r do
środka koła. Stąd pochodzi nazwa siły dośrodkowej.

r

r

a

2

2









r

m

F

2





r

m

F

2





33

Można

wymienić

wiele

przykładów

siły

dośrodkowej.

 Gdy kamień przymocowany do sznurka wprawiamy
w ruch po okręgu, to siłę dośrodkową wywiera nasza
ręka za pośrednictwem napiętego sznurka.

 Gdy pociąg posuwa się po zakrzywionym torze, to
sprężyste oddziaływanie zewnętrznej szyny stanowi
siłę dośrodkową.

 Jeśli przyjmiemy, że Księżyc krąży dokoła Ziemi po
torze

kołowym,

to

siłę

dośrodkową

stanowi

przyciąganie grawitacyjne Ziemi.

 Podczas krążenia elektronu po kołowej orbicie dokoła
jądra atomu siłę dośrodkową stanowi elektryczne
przyciąganie ujemnie naładowanego elektronu przez
dodatnio naładowane jądro atomowe.

34

Inercjalne układy
odniesienia

Z pierwszej zasady dynamiki wynika, że jeśli na ciało
nie działają żadne siły lub działają siły zrównoważone
(F=0), to ciało jest nieruchome lub porusza się ru-
chem jednostajnym prostoliniowym. >Ponieważ ruch
jest zmianą położenia ciała względem układu odnie-
sienia, możemy zapytać,

czy w każdym układzie

odniesienia będzie spełniona I zasada dynamiki
Newtona.

Otóż okazuje się, że zasada ta obowiązuje tylko

w inercjalnych układach odniesienia.

Układy odniesie-

nia, w których I zasada dynamiki nie jest spełniona,
noszą nazwę układów nieinercjalnych

. Pierwsza

zasada dynamiki jest w istocie postulatem, że
układ inercjalny istnieje.

Inercjalne układy

odniesienia



Jeżeli ciało, na które nie działają żadne siły,

pozostaje w spoczynku lub porusza się ruchem

jednostajnym prostoliniowym to układ odniesienia

nazywamy inercjalnym



Pierwsza zasada dynamiki Newtona nie jest

prawem przyrody, lecz postulatem układu

inercjalnego w przyrodzie



Układ związany z Ziemią jest przybliżeniem układu

inercjalnego

35

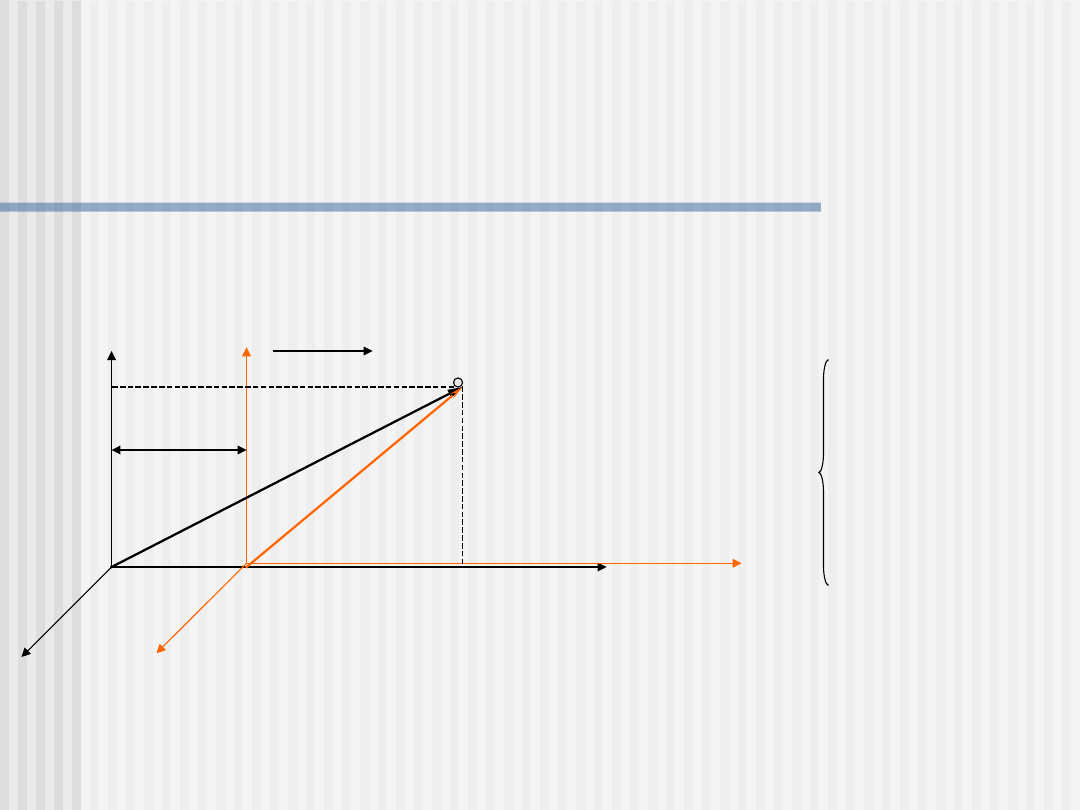
Transformacje Galileusza

Punkt P nieruchomy w stacjonarnym układzie 0

1

obserwowany jest

z układu 0

2

poruszającego się z prędkością względem układu 0

1

v



vt

-

x

x

1

2



1

2

y

=

y

1

2

z

=

z

1

2

t

=

t

y

1

x

1

z

1

0

1

y

2

x

2

z

2

0

2

v

P

vt

Transformacje Galileusza to układ równań wiążący współrzędne
i czas dwóch układów inercjalnych (słuszny gdy v << c)

const

v

v





)

,

,

(

0

0



36

Niezmienniczość Galileusza



Czas we wszystkich układach inercjalnych jest taki sam,
biegnie jednakowo



Galileuszowskie dodawanie prędkości



Przyspieszenie jest niezmiennikiem transformacji Galileusza



Zasada względności Galileusza: istnieje nieskończenie wiele
układów inercjalnych w których spełniona jest pierwsza i
druga zasada dynamiki Newtona. Wszystkie te układy są
równoważne i żaden z nich nie jest wyróżniony

v

v

v

2

1











1

2

=t

t

1

2

a

a







v

dt

dx

dt

dx





1

2

37

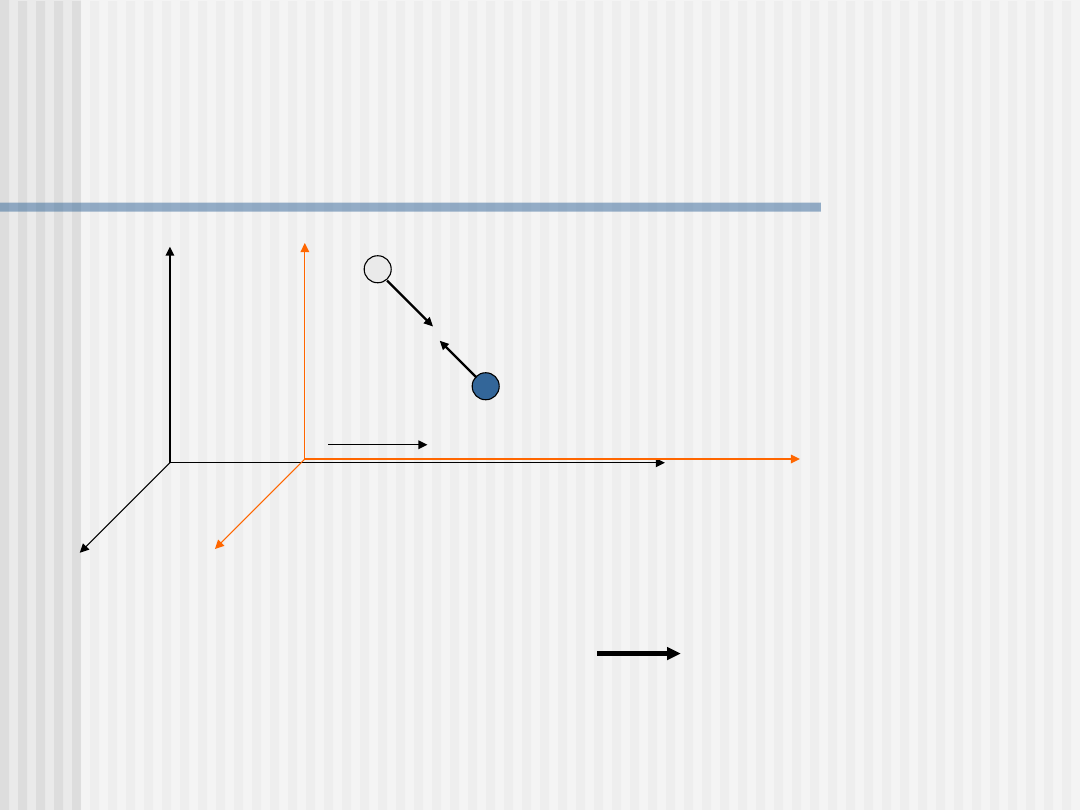
Prawo zachowania pędu jest niezmiennikiem
transformacji Galileusza

const

v

m

v

m





'

'

1

1





w układzie
0

1

const

v

m'

v

m

'

2

2









w układzie
0

2

Prawo zachowania pędu pozostaje niezmiennicze we

wszystkich układach inercjalnych

y

1

x

1

z

1

0

1

y

2

x

2

z

2

0

2

m

v



m’

1

v



'

1

v



v

v

v

2

1











v

v

v











'

'

2

1





v

m

m

const

v

m'

v

m

'

2

2







'









38

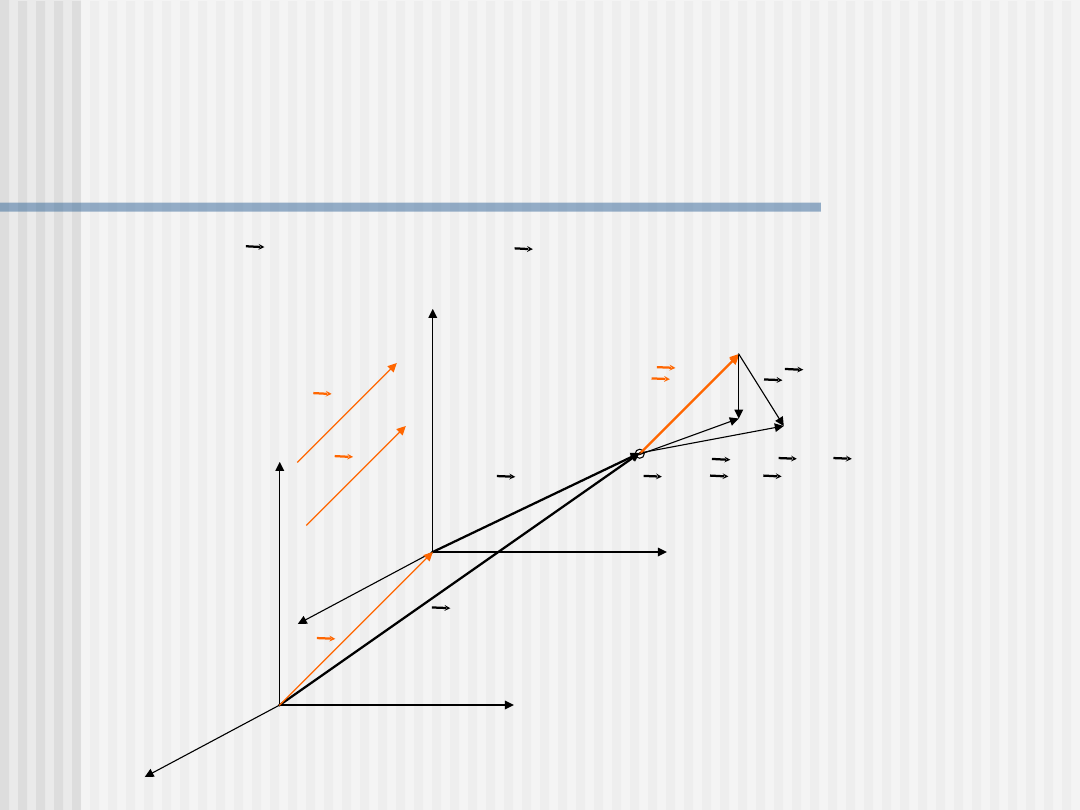
z

1

x

1

y

1

z

2

y

2

x

2

P

Układy nieinercjalne

a

v

v

v

2

v

1

=v

2

+v

r

2

r

1

a

a

2

a

1

=a

2

+a

r

Układ 0

2

porusza się ruchem niejednostajnym prostoliniowym

z prędkością v i przyspieszeniem a

39

Układy nieinercjalne



Przyspieszenie (siła) nie są niezmiennicze

przy przejściu z jednego układu do drugiego



W układzie nieinercjalnym do sił rzeczywiście

działających trzeba dodać siły bezwładności –

zmodyfikowane drugie prawo Newtona

a

m

a

m

a

m

1

2











b

2

F

F

a

m











gdzie

a

m

F

b









siła bezwładności

40

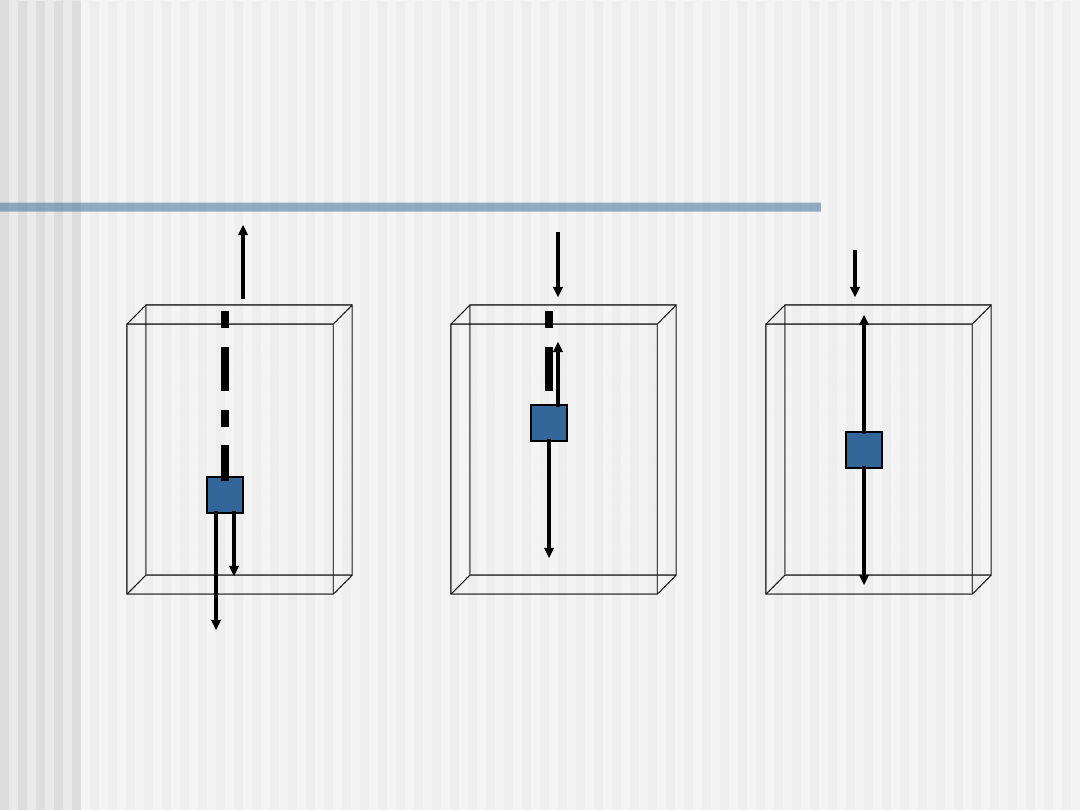
PRZYKŁAD

Winda poruszająca się ruchem niejednostajnym

a

b

F



g

m

b

F

F

F











2

a

b

F



g

m

b

F

F

F











2

g

a 

 

b

F



g

m

0

2



F



41

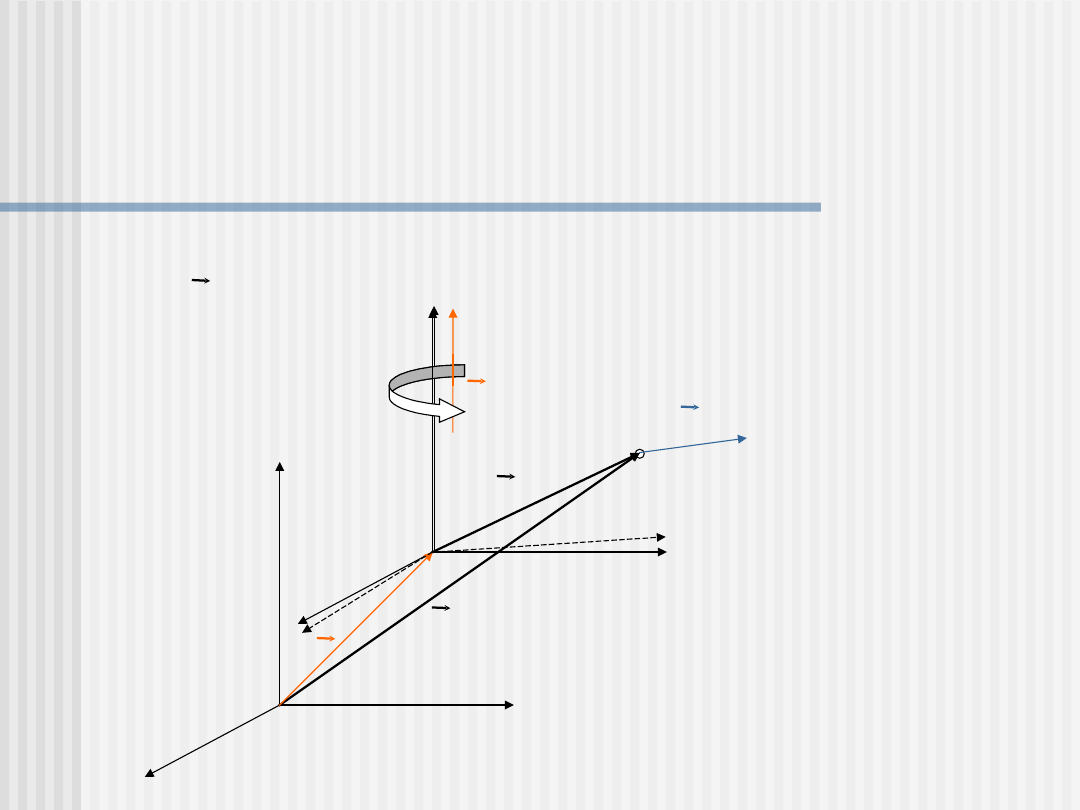
Wirujący układ odniesienia

Układ O

2

wiruje wokół dowolnej osi ze stała prędkością

kątową 

z

1

x

1

y

1

z

2

y

2

x

2

P

r

2

r

1

r

z

2



v

2

42

Siły bezwładności w ruchu obrotowym



Układ 0

2

wiruje wokół osi ze stałą prędkością kątową 

2

2

1

2

2

v

m

r

m

a

m

a

m





























siła odśrodkowa



skierowana jest w kierunku promienia obrotu



siła Coriolisa



jeżeli prędkość ciała względem 0

2

jest zerowa – siła Coriolisa nie

występuje



jeżeli prędkość ciała w układzie 0

2

jest skierowana w kierunku osi

obrotu- siła Coriolisa nie występuje

Układy nieinercjalne

siła odśrodkowa

siła Coriolisa

43

Pole grawitacyjne

>> Ruch satelitów

44

Pole grawitacyjne

45

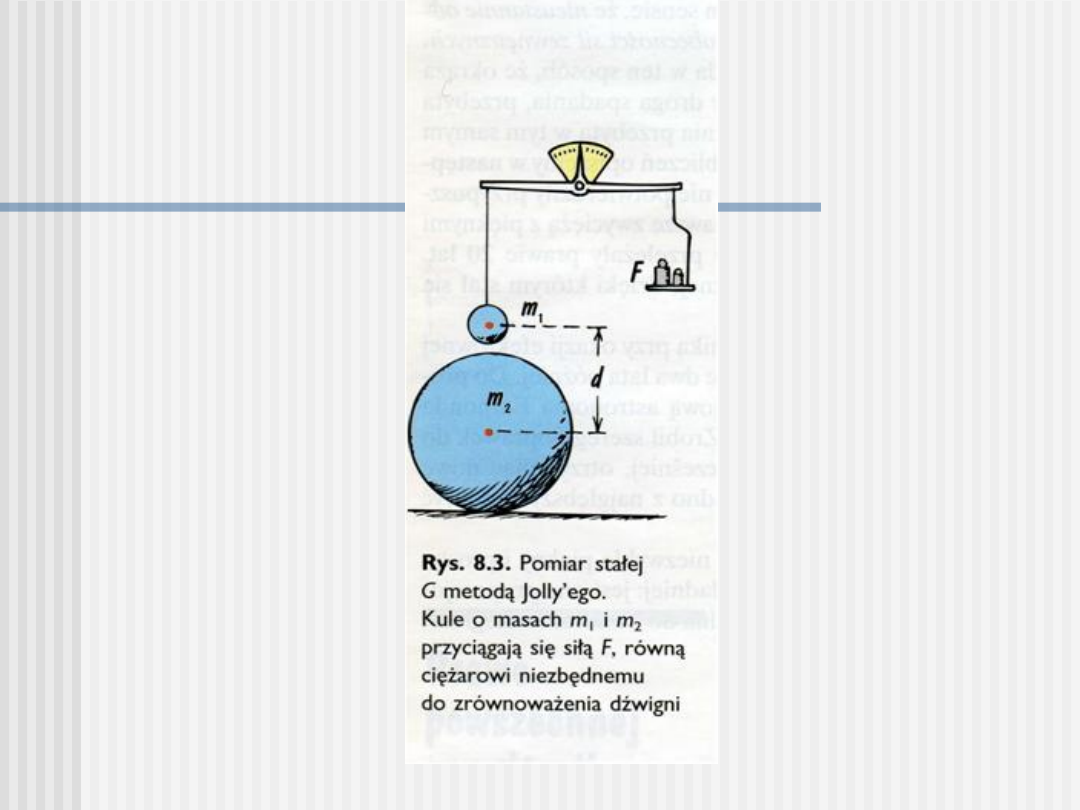
Prawo powszechnego ciążenia:

Dwa punkty materialne o masach m

1

i m

2

przyciągają się

wzajemnie siłą proporcjonalną do iloczynu ich mas i odwrotnie
proporcjonalną do kwadratu ich odległości r

Kule oddziałują ze sobą tak, jak

punkty materialne umieszczone

w środkach tych kul.

Na powierzchni Ziemi m

1

= m, m

2

= M, r = R

gdzie R = 6400km, M = 6·10

24

kg

r

r

r

m

m

G

F





2

2

1









2

2

11

10

67

,

6

kg

m

N

G







s

m

R

M

g

mg

F

81

,

9

,

2









46

Natężenie pola grawitacyjnego

47

Oddziaływanie grawitacyjne realizuje się za pośredni-
ctwem pola grawitacyjnego. O „intensywności” takiego pola
świadczy wartość siły grawitacji działającej na umieszczone w
danym punkcje pola ciało o jednostkowej masie m

Natężenie pola w pobliżu powierzchni Ziemi jest równe

przyspieszeniu ziemskiemu g

Wartość g nie jest wszędzie na powierzchni
Ziemi jednakowa, gdyż:

•Ziemia nie jest jednorodna
•Ziemia nie jest kulista
•Ziemia się obraca

r

r

r

M

G

m

F

a

g







2







g

a

g







Energia potencjalna i potencjał
grawitacyjny

48

Energia potencjalna to praca jaką należy wykonać przenosząc

daną masę z nieskończoności do danego punktu pola

Potencjał pola grawitacyjnego przedstawia energię potencjalną

przypadającą na jednostkę masy ciała umieszczonego w

danym punkcie pola

r

Mm

G

r

GMm

dr

r

GMm

dr

r

Mm

G

r

d

F

r

d

F

U

R

R

R

R

R















































2

2

1























kg

J

r

GM

m

E

V

p

49

I prawo Keplera
Ruch planety wokół Słońca odbywa
się po elipsie. Słońce znajduje się
w jednym z dwóch ognisk elipsy.
II prawo Keplera (prawo pól)
Podczas obiegu orbitalnego plane-
ty wokół Słońca jej promień wo-
dzący - łączący planetę ze Słoń-
cem - zakreśla jednakowe pola w
jednakowych odstępach czasu.
Innymi słowy, prędkość polowa
planety jest stała.
III prawo Keplera
Drugie potęgi okresów obiegu
planet wokół Słońca (T

1

, T

2

) są

wprost proporcjonalne do trzecich
potęg wielkich półosi (a

1

, a

2

) ich

orbit: T

1

2

:a

1

3

=T

2

2

:a

2

3

.

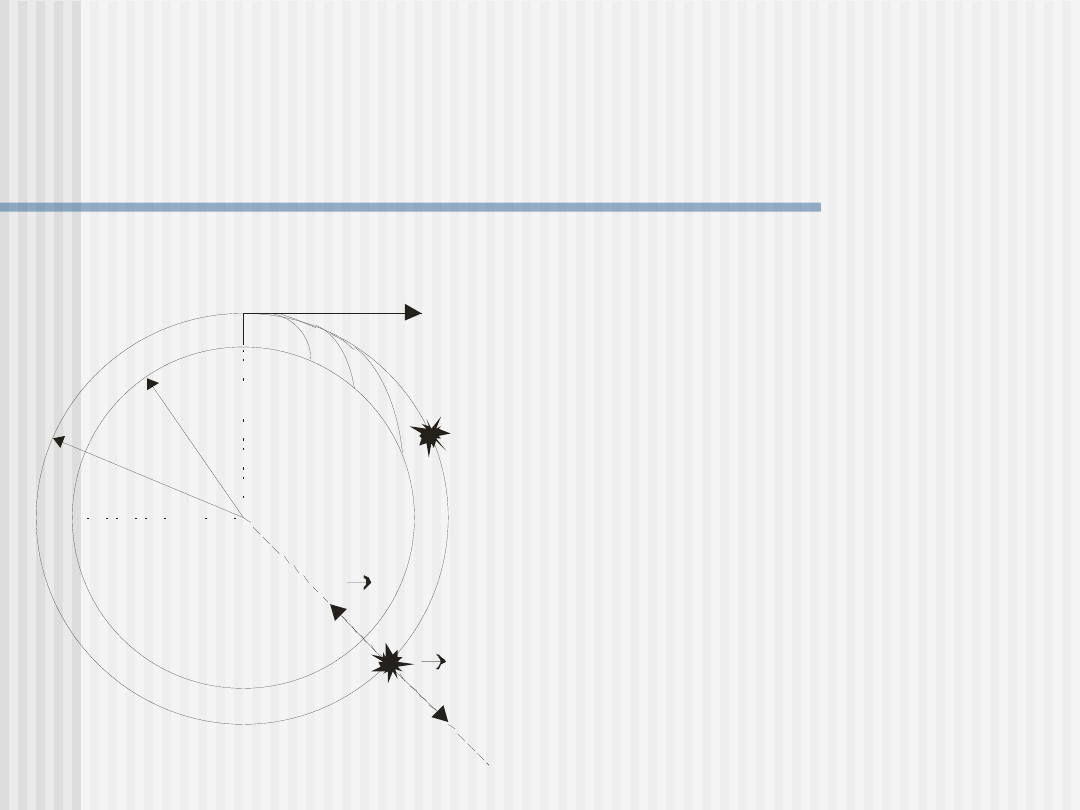
Zaczniemy od policzenia I i II prędkości kosmicznej

Wyznaczyć pierwszą prędkość kosmiczną, czyli najmniejszą
możliwą prędkość , jaką musi mieć punkt materialny (satelita)
swobodnie krążący po orbicie wokół Ziemi. Promień Ziemi
R=6400 km.

R

r

F

1

F

2

h



Ziemia

Wyobraźmy sobie pocisk wy-
strzelony poziomo na wys. h
nad Ziemią, któremu nadano
pewną prędkość początkową .

Po przebyciu pewnej drogi pocisk
spadnie na Ziemię. Jeżeli będzie-
my zwiększać prędkość początko-
wą pocisku, to jego droga będzie
coraz dłuższa i przy pewnej
prędkości początkowej pocisk
zacznie obiegać Ziemię dookoła i
nie spadnie na jej powierzchnię.
Nastąpi to wtedy, gdy prędkość
początkowa pocisku

osiągnie

pierwszą

prędkość

kosmi-

czną.

50

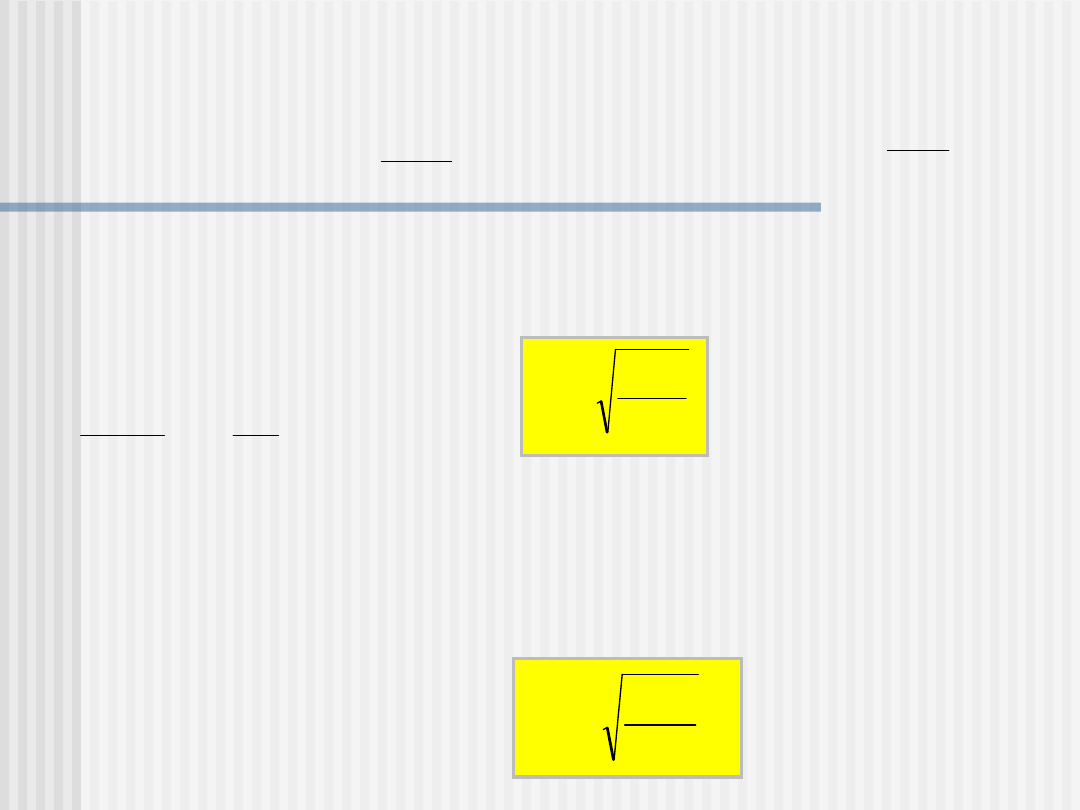
Na poruszający się po orbicie pocisk o masie m działają dwie siły
F

1

i F

2

o przeciwnych zwrotach:

siła odśrodkowa

i siła grawitacji

Warunkiem, aby orbita, po której porusza się pocisk, była stabil-
na jest równowaga tych sił

r

m

F

2

2





2

g

1

r

Mm

k

F 

2

1

F

F 

r

m

r

m

M

k

2

2

g







r

M

k

g





stąd

Promień r orbity satelity wynosi:

Ponieważ h<<R to pierwsza prędkość kosmiczna 

I

wyraża się wzorem

h

R

r





R

M

k

g

I





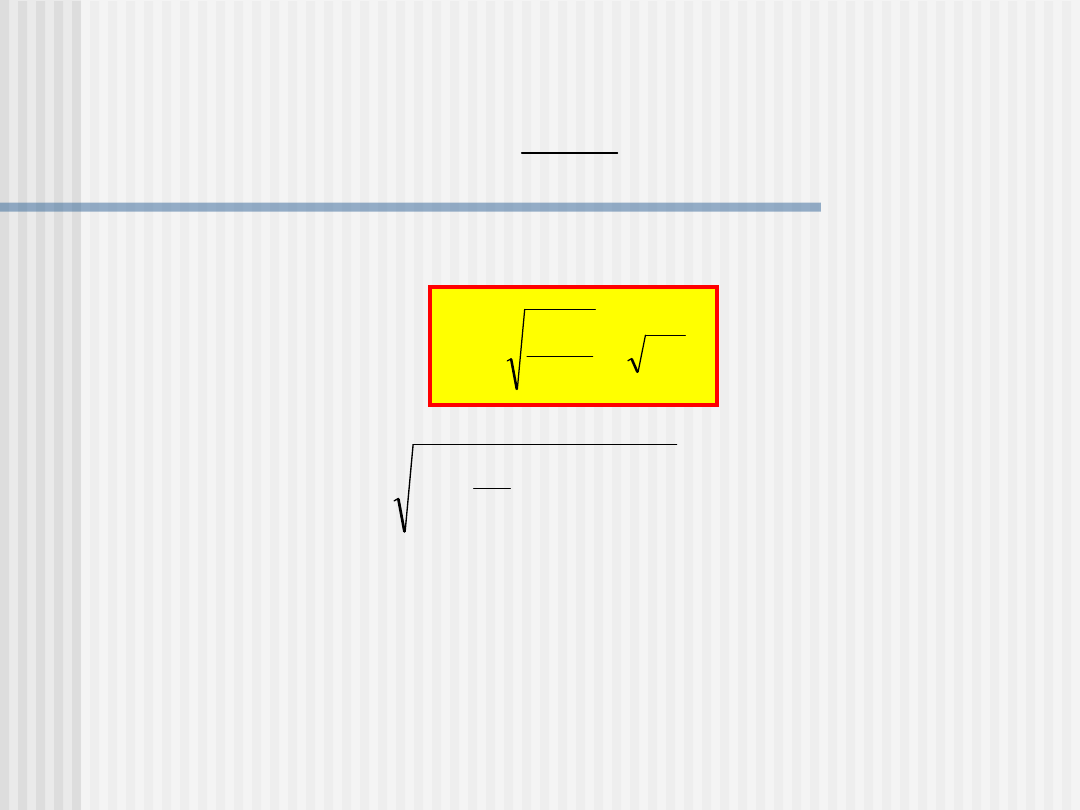
Ale wiemy, że na powierzchni Ziemi spełnione jest równanie:

2

g

R

M

m

k

mg





2

g

R

g

M

k







gR

R

M

k

g

I







ostatecznie

m

6400000

s

m

81

.

9

2

I







s

/

km

9

.

7

s

/

m

7924

I







= 29 000 km/h

Wyobraźmy sobie ruch z taką prędkością w

atmosferze ziemskiej

52

A teraz kilka słów o tym jak naprawdę wyglądają

tory satelitów

.

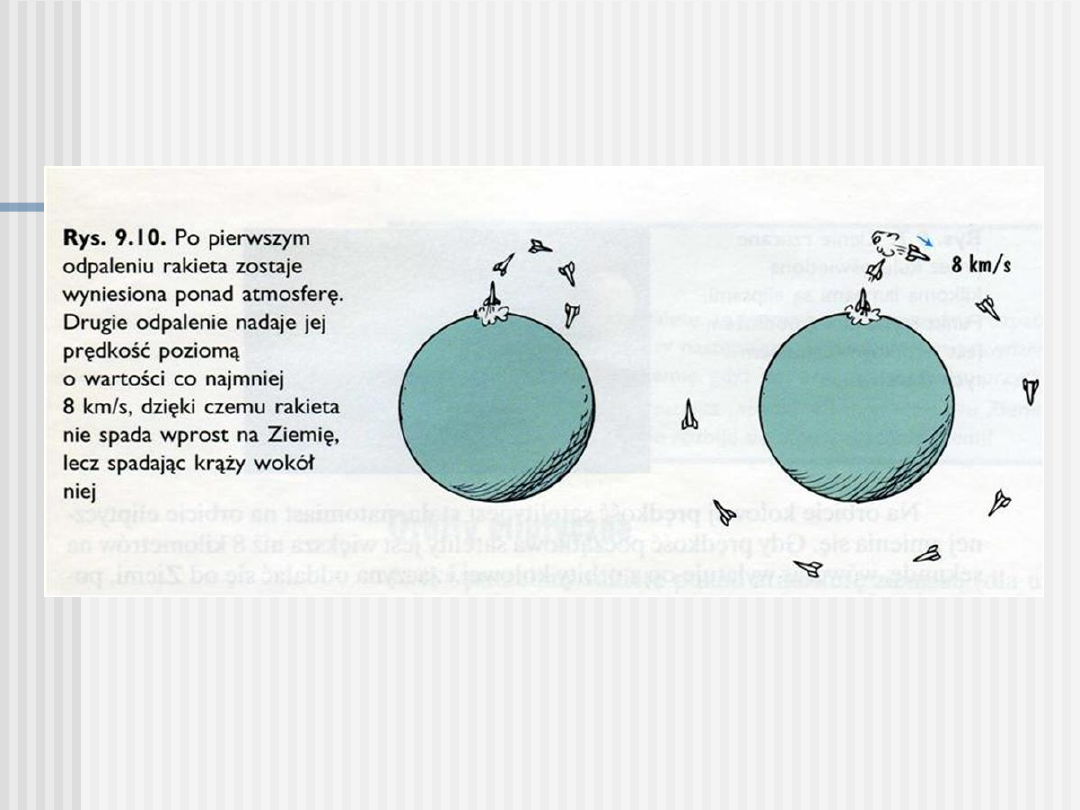
Jeśli wystrzelimy rakietę z prędkością 8 km/s > to zajmie
ona orbitę kołową blisko powierzchni Ziemi. W każdej
sekundzie przebywa ona 8 km w kierunku poziomym
(stycznym) i 4,9 m w kierunku pionowym (radialnym) =
zakrzywienie Ziemi.

Wartość prędkości na orbicie kołowej pozostaje

stała, zmienia się tylko jej kierunek. Ruch satelity odbywa
się w kierunku prostopadłym do pola grawitacyjnego
Ziemi. Nie wykonuje on ruchu w kierunku pola co
powodowałoby wzrost prędkości, ani w kierunku
przeciwnym.

Przy ruchu prostopadłym do kierunku pola

prędkość satelity nie zmienia się co do wartości – zmienia
się jedynie jej kierunek

> satelita leci równolegle do

powierzchni Ziemi, spadając na nią w specyficzny
sposób.

53

54

W przypadku satelity krążącego blisko powierzchni
Ziemi okres jednego obiegu wynosi około 90 min.

Na większych wysokościach prędkość satelity

jest mniejsza i okres wzrasta >> satelity
telekomunikacyjne krążą na wysokości 5,5 razy
większej niż promień Ziemi >>> ich okres obiegu
wynosi 24 godziny. Tak więc satelita „wisi” nad
ustalonym punktem na powierzchni Ziemi.

Księżyc jest dalej i jego okres wynosi 27,3 dni

55

56

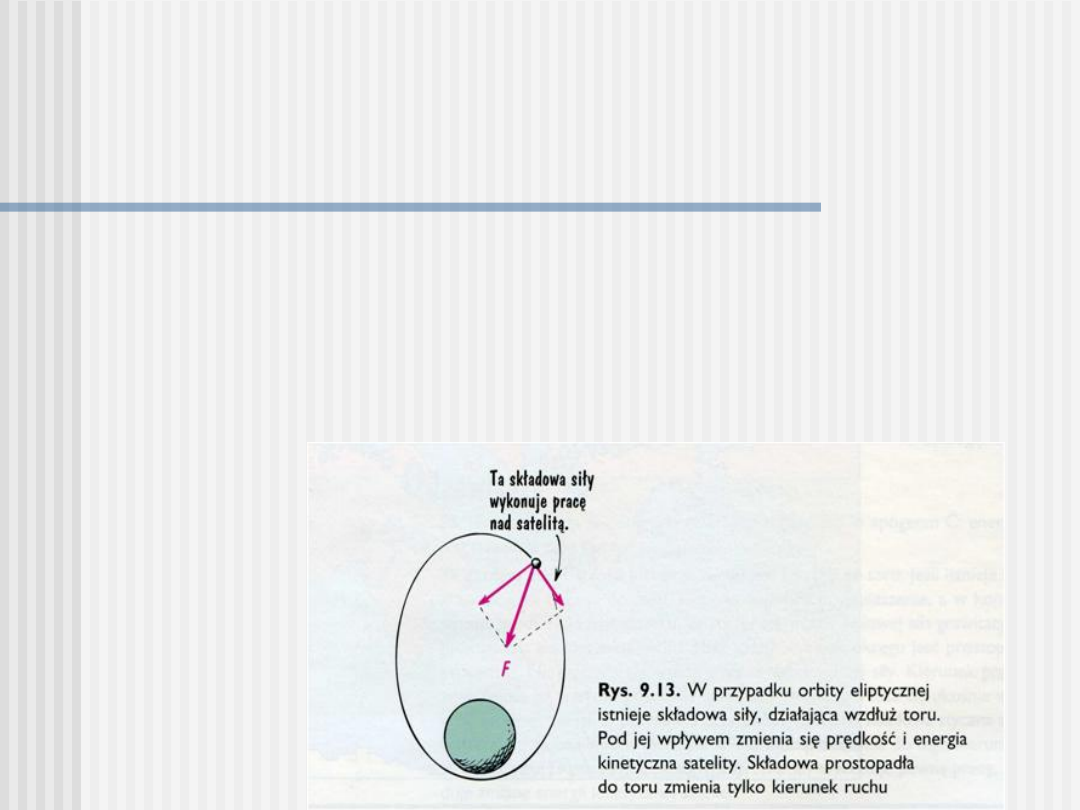
Orbity eliptyczne

Jeśli wystrzelimy rakietę ponad atmosferę ziemską (dla
uniknięcia oporu powietrza) z prędkością większą od 8
km/s to wyleci ona z orbity kołowej i jej tor stanie się
owalny = eliptyczny.

Na orbicie eliptycznej prędkość rakiety zmienia się.

Gdy prędkość jest większa od 8 km/s satelita wylatuje z
orbity kołowej i zaczyna się oddalać od Ziemi > porusza
się przeciwnie do siły grawitacji > dlatego jego prędkość
stopniowo się zmniejsza. …

57

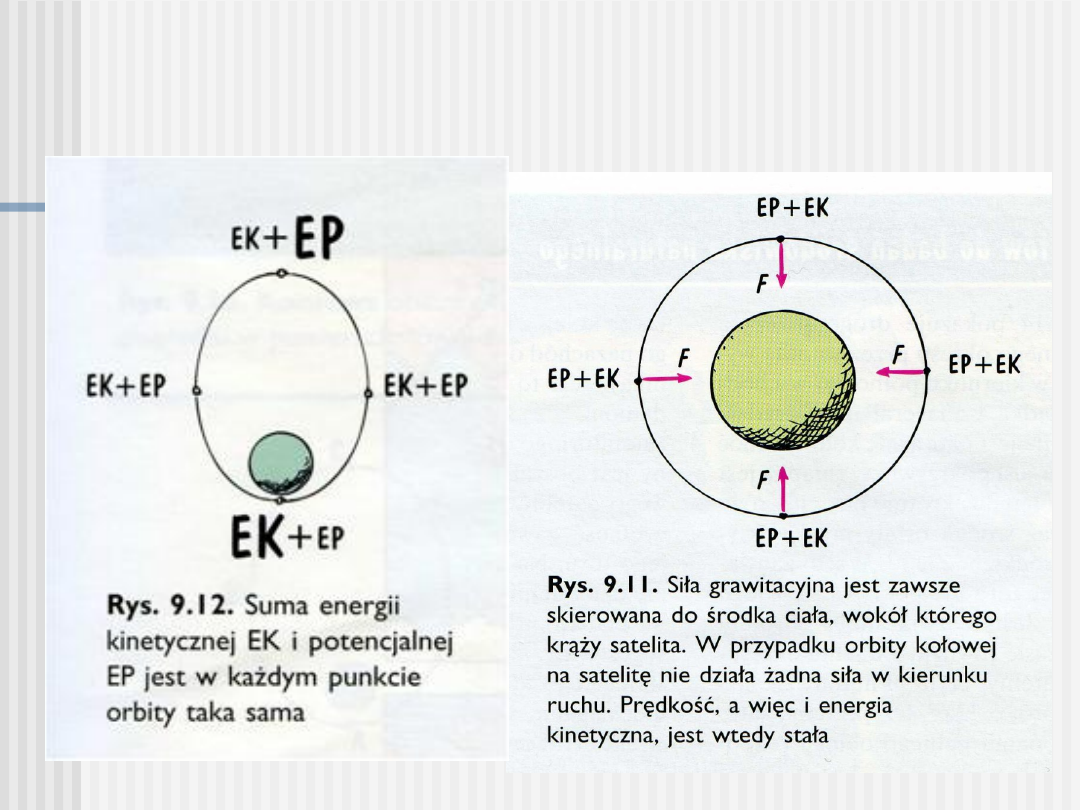
Zasada zachowania energii w ruchu

satelitarnym

58

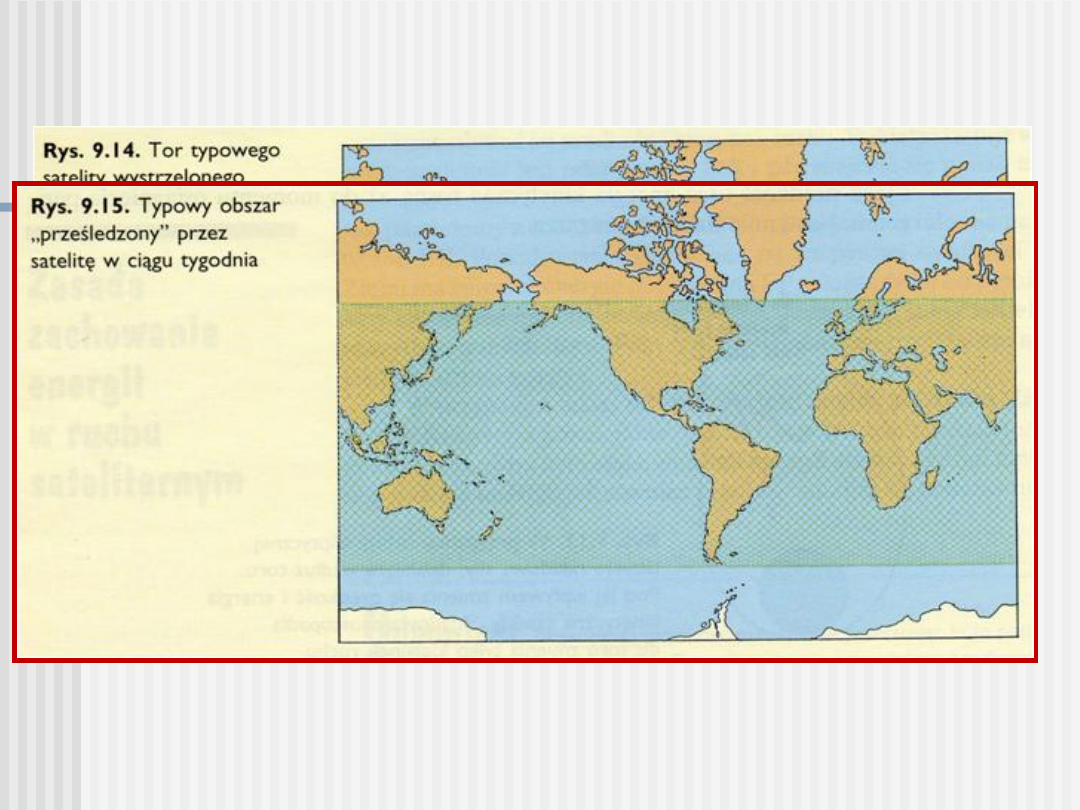
Tor typowego satelity

S 174

59

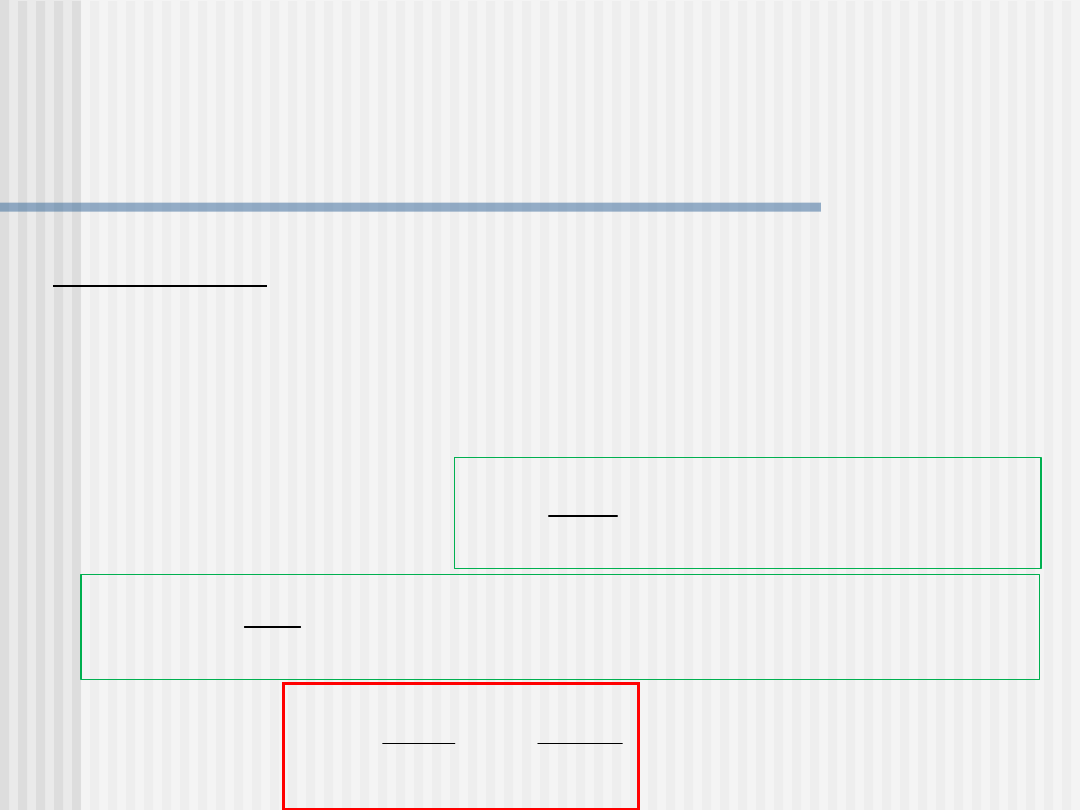
Wyznaczyć

drugą

prędkość

kosmiczną

tzw.

prędkość ucieczki

, czyli najmniejszą możliwą prędkość



II

jaką musi mieć punkt materialny (satelita) przy

powierzchni Ziemi, aby mógł się oddalić od Ziemi w
nieskończoność. Promień Ziemi R=6400 km.
Rozwiązanie:
Obliczmy najpierw, z jaką prędkością  trzeba rzucić ciało

pionowo do góry, aby wzniosło się ono na wysokość h.
Zastosujemy w tym celu zasadę zachowania energii.
Całkowita energia mechaniczna E

1

na powierzchni Ziemi

wynosi:

gdzie

to energia kinetyczna

to grawitacyjna energia potencjalna

 

R

E

E

E

p

k

1





2

m

E

2

k





R

Mm

k

E

g

p





R

m

M

k

2

m

E

g

2

1









60

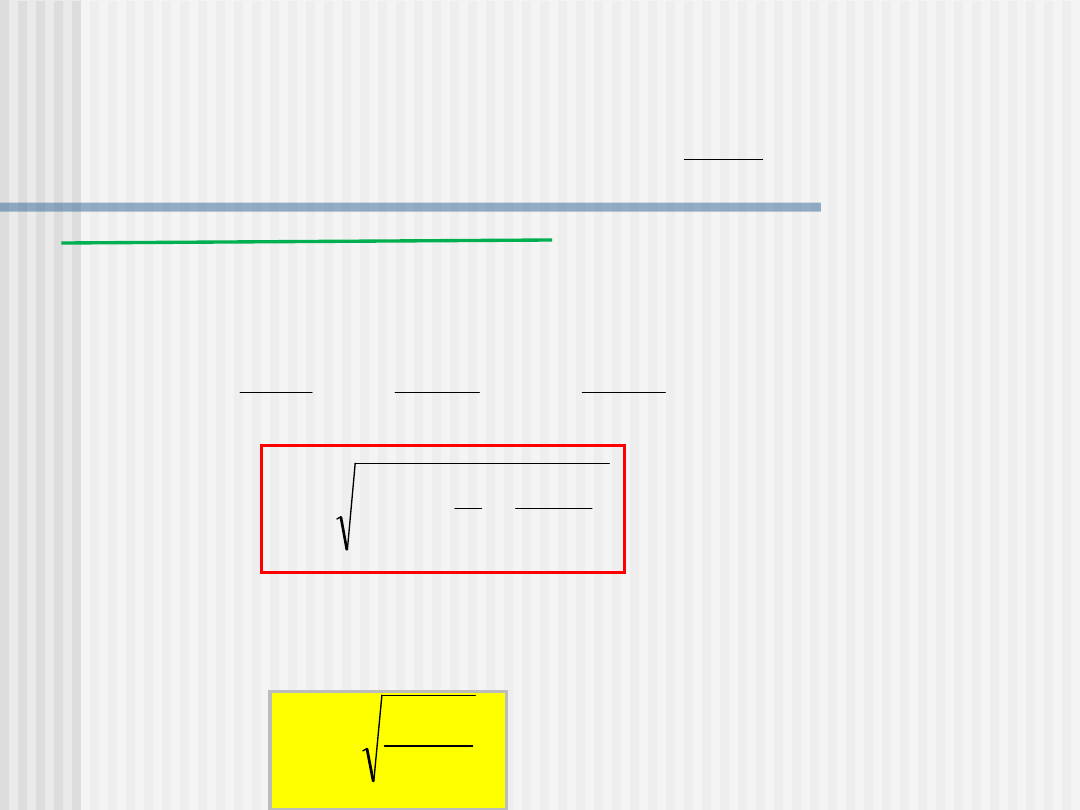
Całkowita energia mechaniczna E

2

ciała na

wysokości h ma postać:

bo na wysokości h; E

k

=0

Z prawa zachowania energii

h

R

Mm

k

E

g

2







2

1

E

E 

h

R

Mm

k

R

m

M

k

2

m

g

g

2

































h

R

1

R

1

M

k

2

g

Podstawiając

, otrzymujemy prędkość

ucieczki





h

R

M

k

2

g

II





61

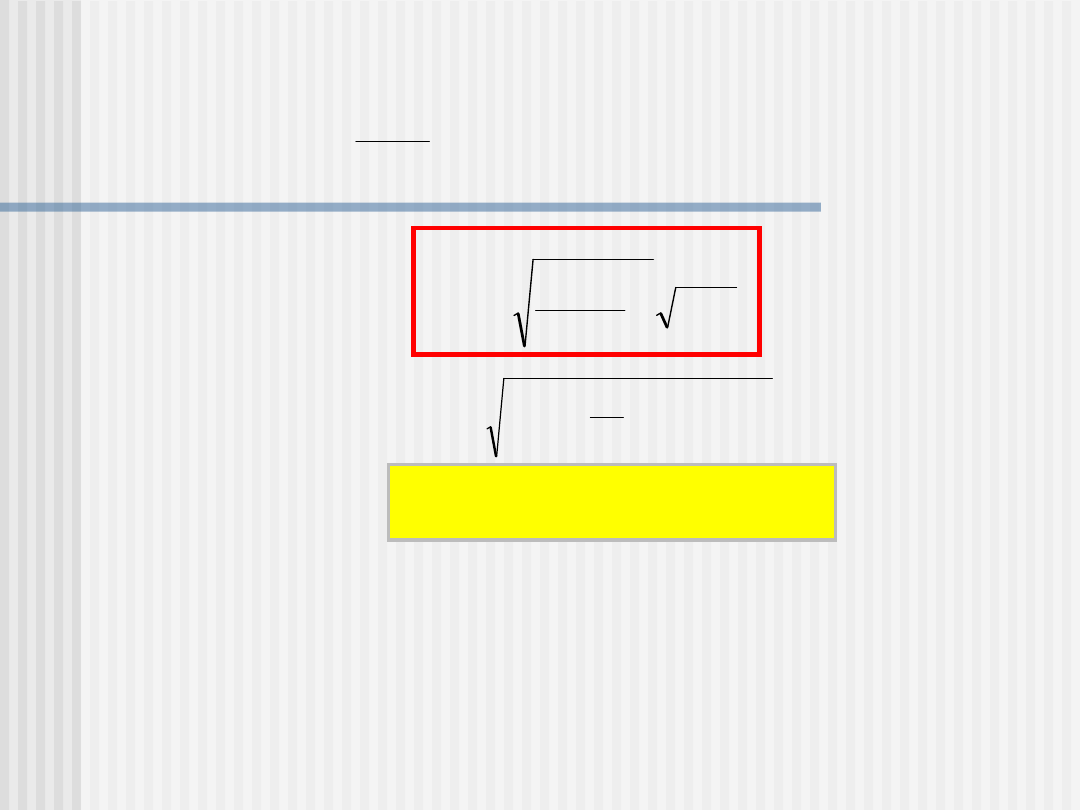
Ale wiedząc, że na powierzchni Ziemi spełniona jest
równość

2

g

R

m

M

k

mg





2

g

R

g

M

k





gR

2

R

M

k

2

g

II







ostatecznie

m

6400000

s

m

81

.

9

2

2

II









s

/

km

2

.

11

s

/

m

11206

II







=40 320 km/h

Odpowiada to energii 62MJ /kg masy

Prędkość opuszczenia Układu Słonecznego =
42,5 km/s

62

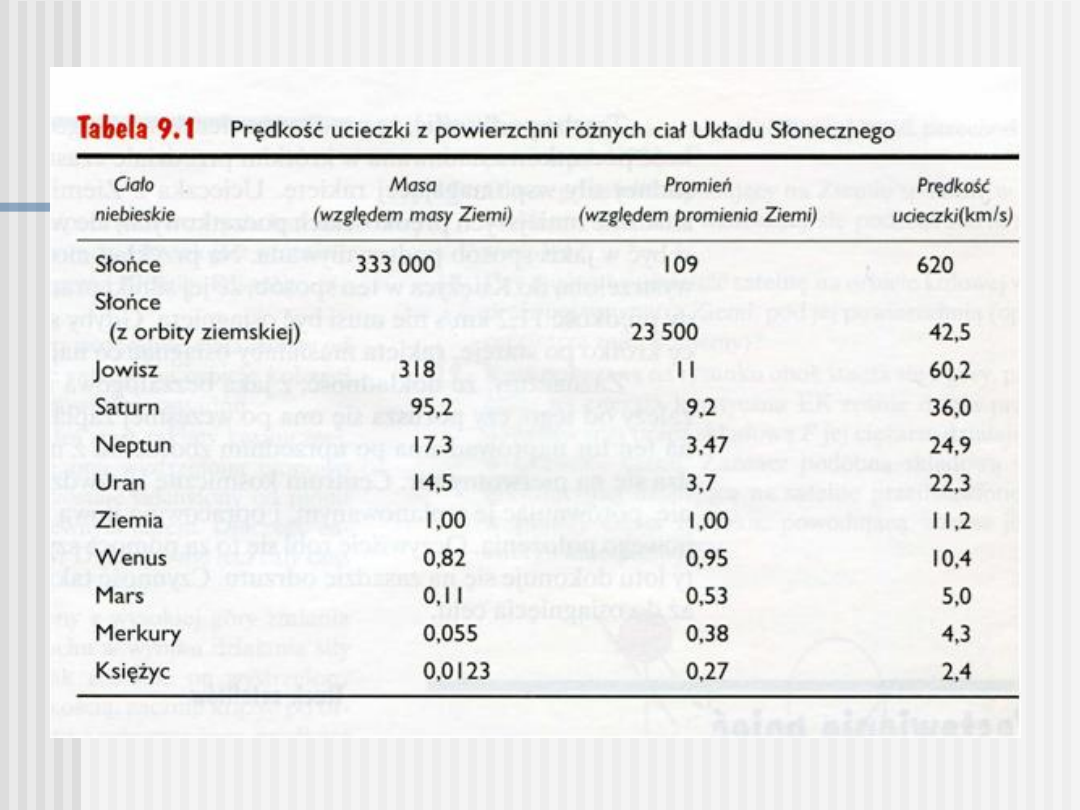
Tab 9.1 177

63

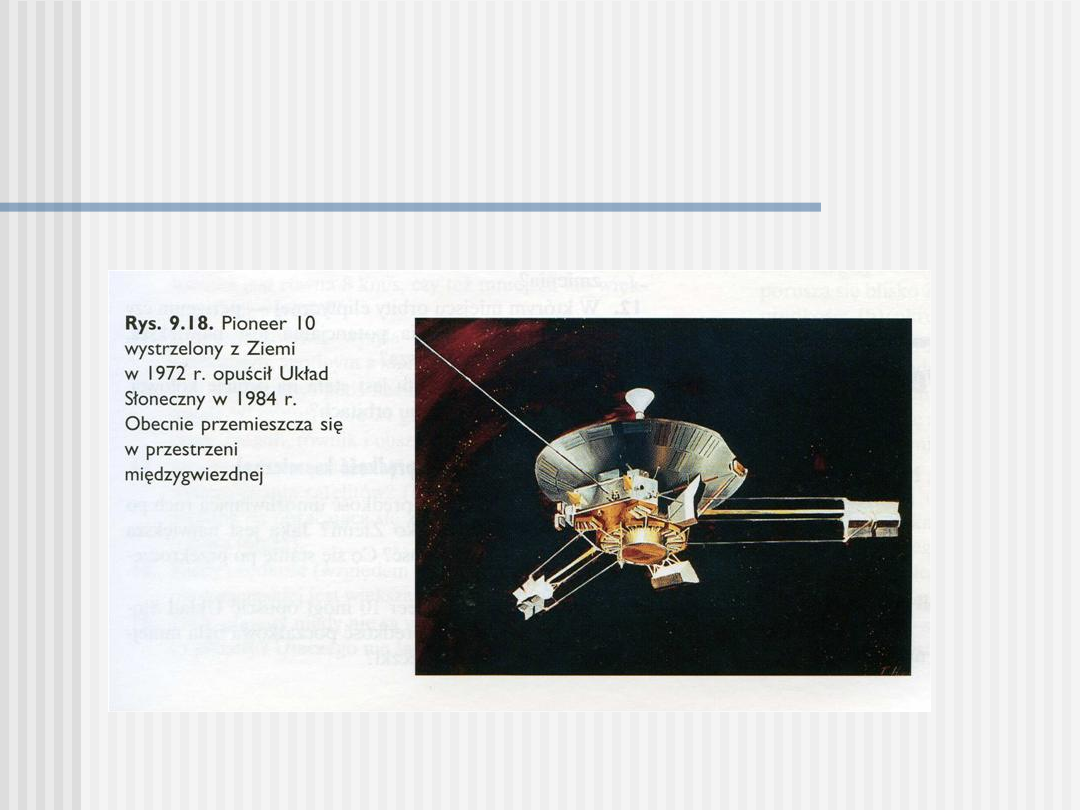
Pierwszą próbę wysłania rakiety poza Układ
Słoneczny podjęto w1972 roku kiedy to wystrzelono
Pioniera 10 z prędkością 15km/s.

Rakietę naprowadzono na orbitę Jowisza dzięki

czemu została ona dodatkowo przyspieszona. Tak
zwiększona prędkość wystarczyła żeby Pionier
opuścił obszar przyciągania słonecznego. W roku
1984 przeciął on orbitę Plutona.

Nasza ziemska butelka powędrowała w

kosmos

Na koniec jedna uwaga – wszystkie

podane prędkości dotyczą przypadku gdy
silnik przestaje pracować krótko po starcie –
gdyby silnik pracował przez dłuższy czas
prędkość mogłaby być mniejsza.

64

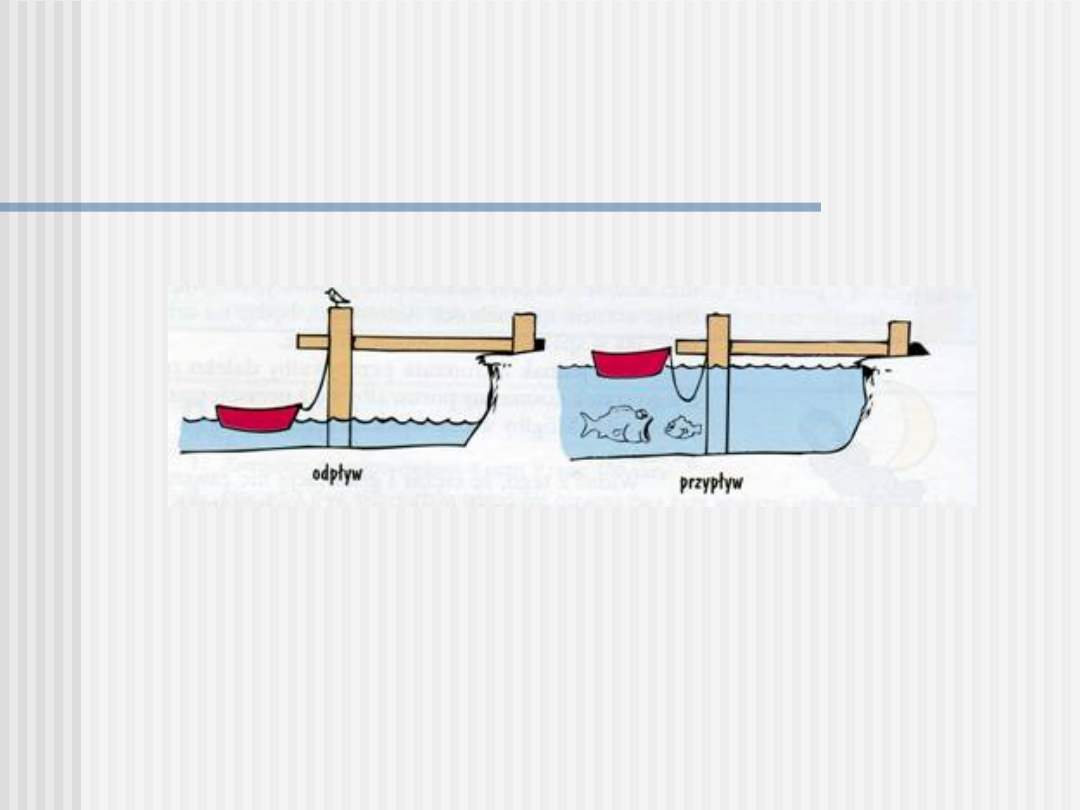
Kolejne „drobiazgi”

65

będące skutkiem grawitacji … >>>

66

67

68