Prof. dr hab. Jerzy Ginter

dla Studium Podyplomowego

Fizyki z Astronomią na Wydziale Fizyki

Uniwersytetu Warszawskiego

Wykład pt.: „Funkcje i ich

pochodne”

Opracował mgr Mirosław Maciejczyk

2

x

Pojęcie pochodnej

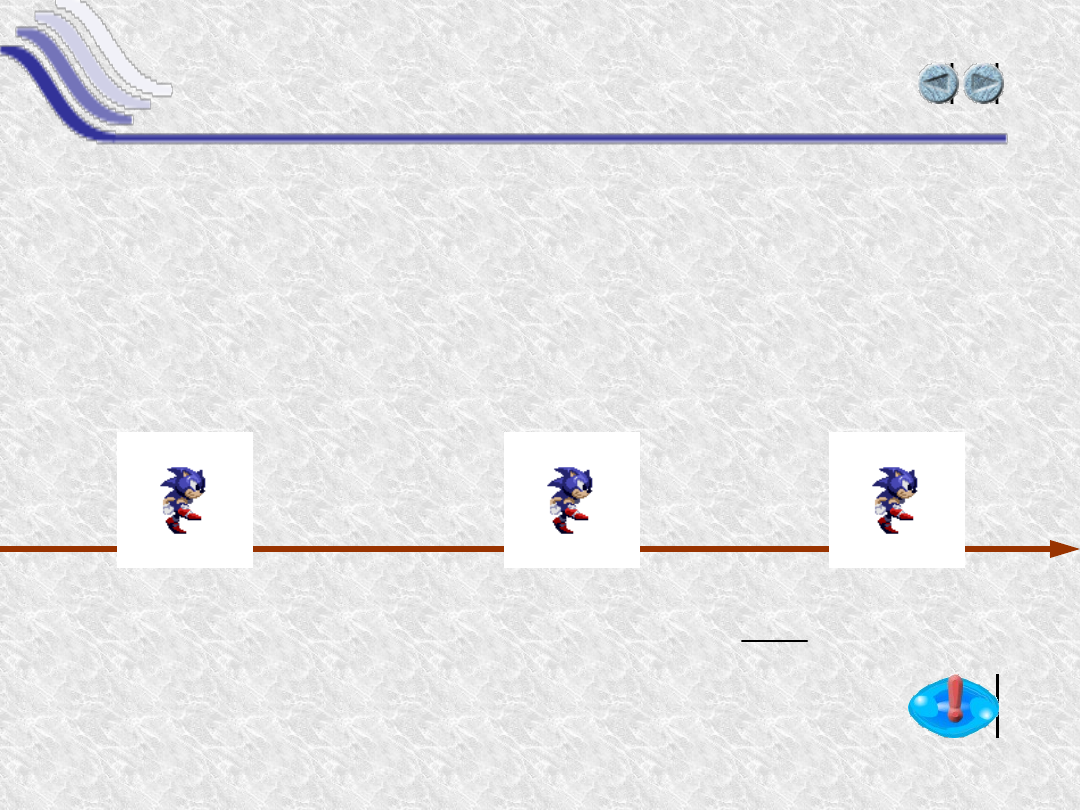
Gdy ciało porusza się po linii prostej, współrzędna
jego
położenia x zmienia się wraz z upływem czasu t.

Przypuśćmy, że w pewnym przedziale czasu t

położenie zmieniło się o x. Powiemy, że w

przedziale czasu
t ciało miało prędkość średnią:

t

x

v

sr







X

3

Pojęcie pochodnej

Jednak w czasie t ciało mogło zwalniać i

przyspieszać. Można zatem zadać pytanie: jaka była

prędkość chwilowa

na początku omawianego

przedziału czasu?

Aby uzyskać odpowiedź na tak postawione pytanie,

należałoby zmierzyć zmianę położenia ciała w

krótszym przedziale czasu.

x

Interesuje nas więc granica

t

x

v

t











lim

0

zwana

pochodną położenia x względem

czasu t.

x

x

x

4

x

x

y

x

x

y

x

y

x

y

x

x



























)

(

)

(

)

(

0

0

0

0

0

lim

lim

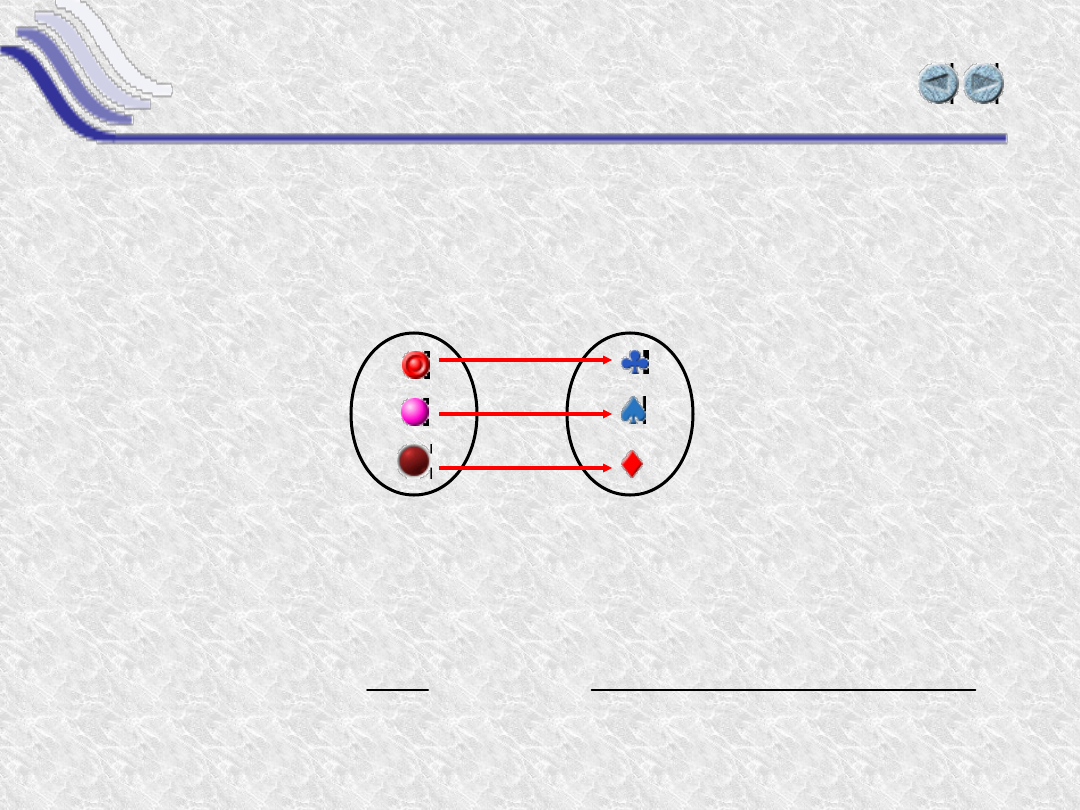
Definicja pochodnej

Przypuśćmy, że określona jest funkcja y(x), która
przyporządkowuje wielkości x (

zmiennej niezależnej

)

pewną inną wielkość y (

zmienną zależną

).

Pochodną funkcji y(x) w punkcie x

o

nazywamy

granicę
„ilorazu różnicowego”:

X

Y

5

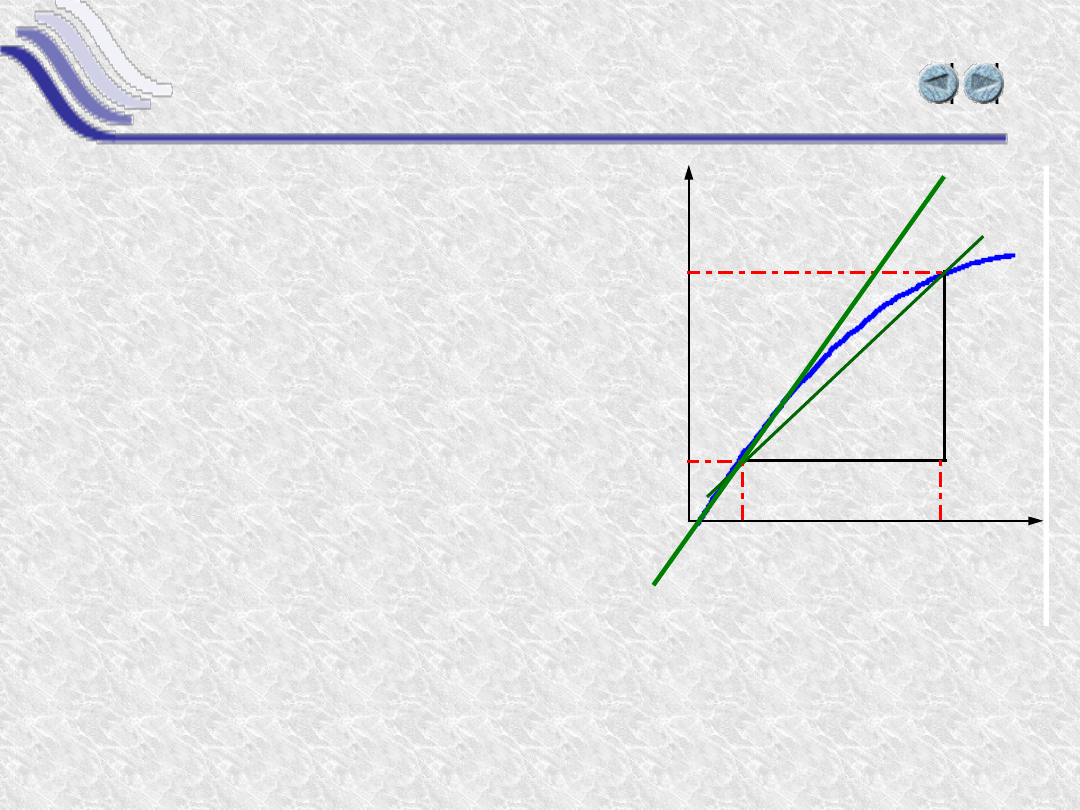
Interpretacja geometryczna

x





y

y

x

x

x+

x

y(x)

y(x+x)

Pochodna równa jest tangensowi kąta nachylenia
stycznej do osi OX.

Wartość ilorazu różnicowego
y/x jest tangensem kąta,

określającego

nachylenie

siecznej

, czyli linii, która

przecina krzywą w punktach
(x, y(x)) i (x+x, y(x+x)).

Kiedy x0, sieczna dąży

do stycznej do krzywej
w punkcie (x,y(x)).

6

0

0,5

1

1,5

2

0

0,5

1

1,5

2

x

0

x

1

x

2

x

3

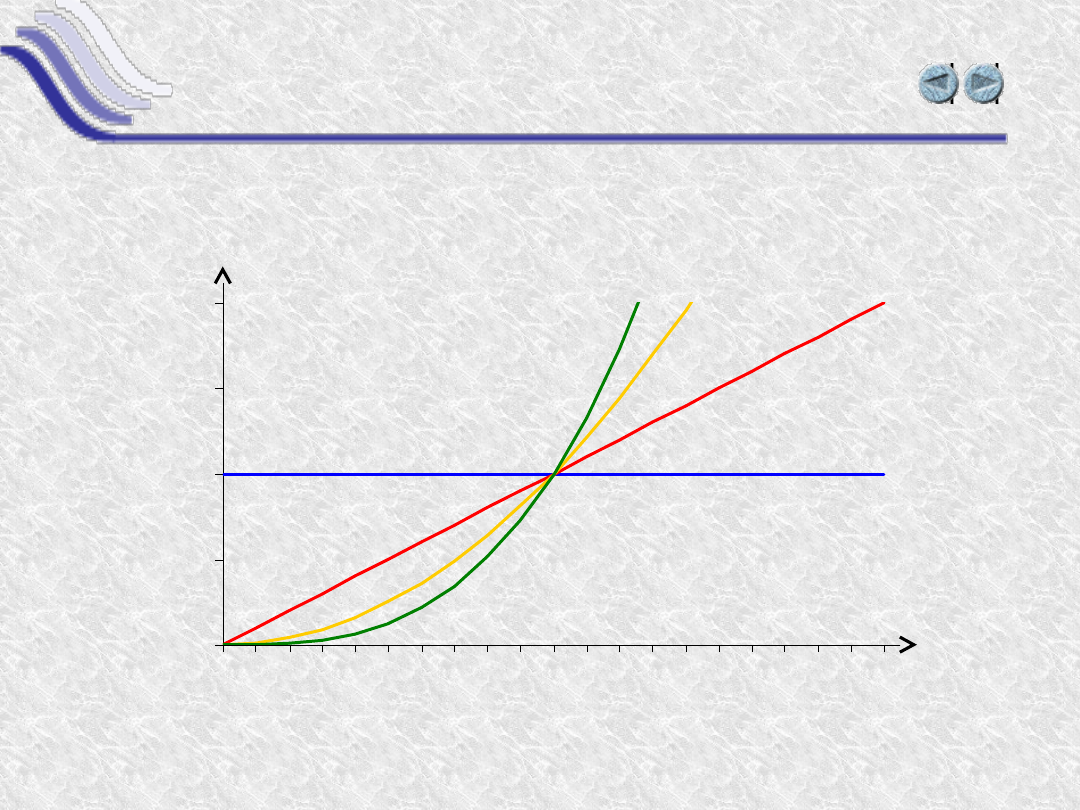
Funkcje potęgowe

Funkcje potęgowe mają postać y(x) = x

n

.

7

Pochodne funkcji potęgowych

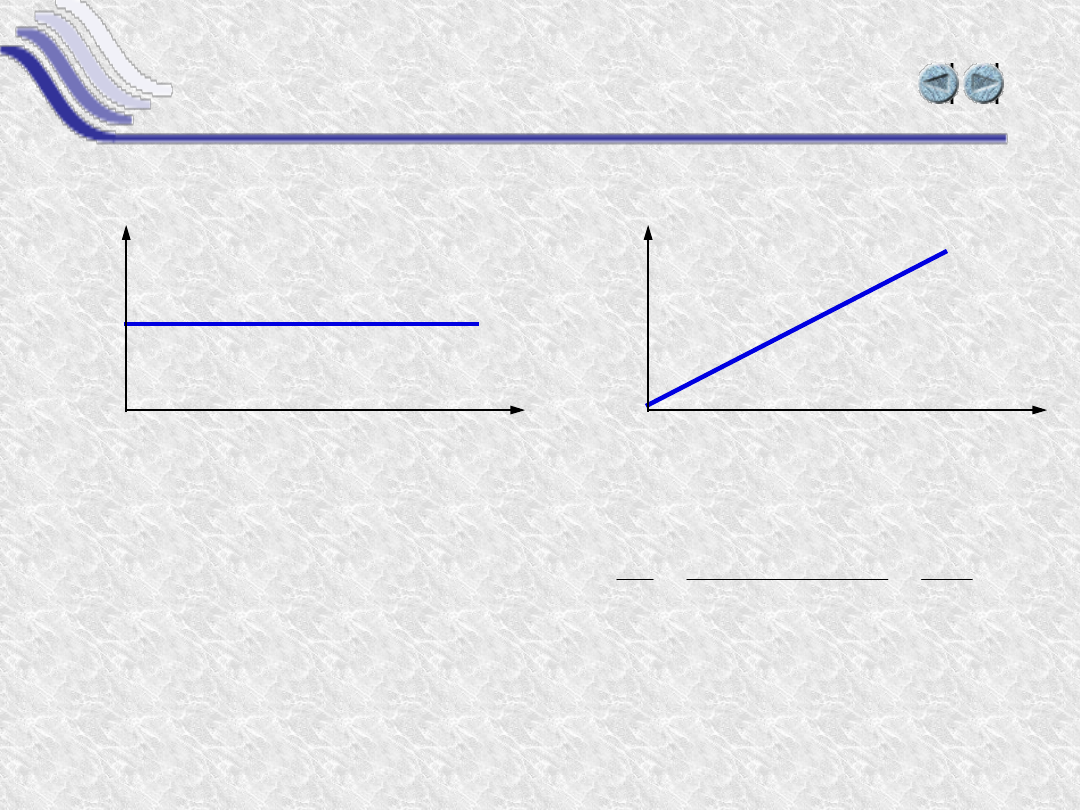
Funkcja stała y(x) = c

Licznik ilorazu
różnicowego jest równy:

y = y(x+ x) - y(x) = c-c

= 0

Pochodna funkcji stałej
jest równa zero.

y

x

Funkcja liniowa
y(x)=a·x

y

x

Iloraz różnicowy wynosi:

a

x

x

a

x

x

y

x

x

y

x

y























)

(

)

(

Pochodna funkcji liniowej
jest stała i wynosi a.

8

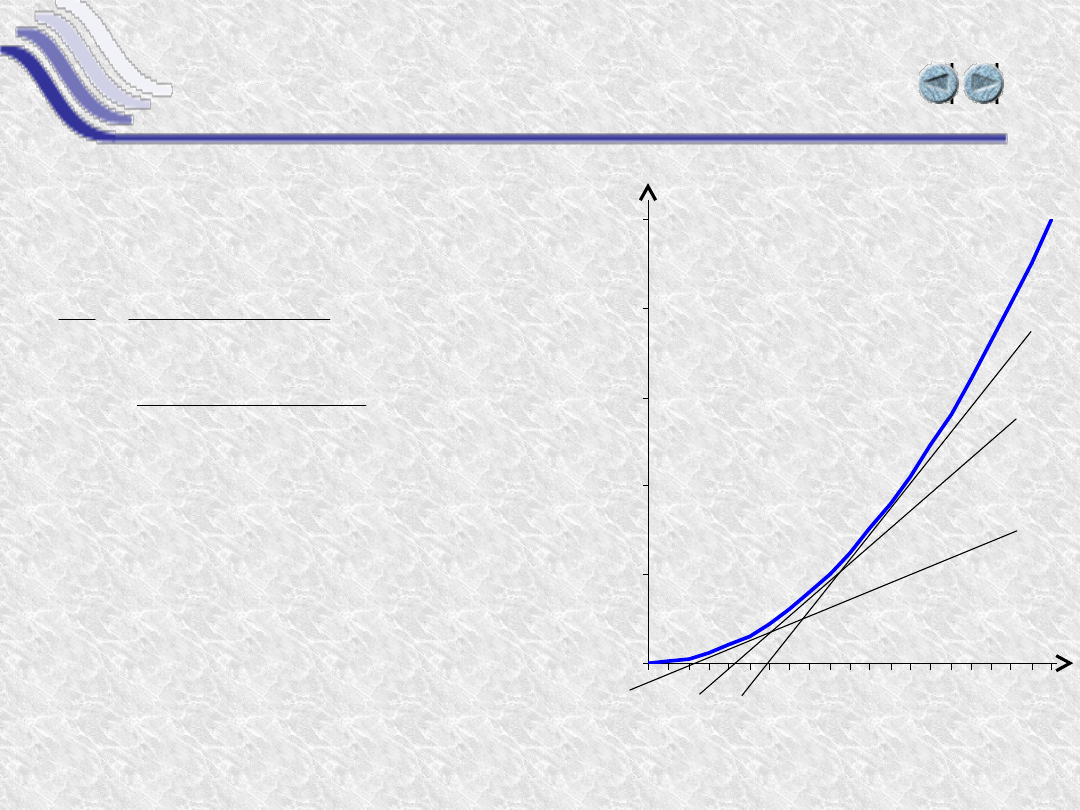
Funkcja kwadratowa y=a·x

2

Pochodne funkcji potęgowych

Iloraz różnicowy wynosi:

Pochodna jest granicą tego
ilorazu dla x0 i wynosi

y’(x)=2ax

Kąt nachylenia stycznej do
wykresu funkcji rośnie wraz ze
wzrostem x.

















x

x

y

x

x

y

x

y

)

(

)

(

x

a

ax

x

x

a

x

x

a

















2

)

(

)

(

2

2

0

0,2

0,4

0,6

0,8

1

0

0,2

0,4

0,6

0,8

1

y(x)=x

2

9

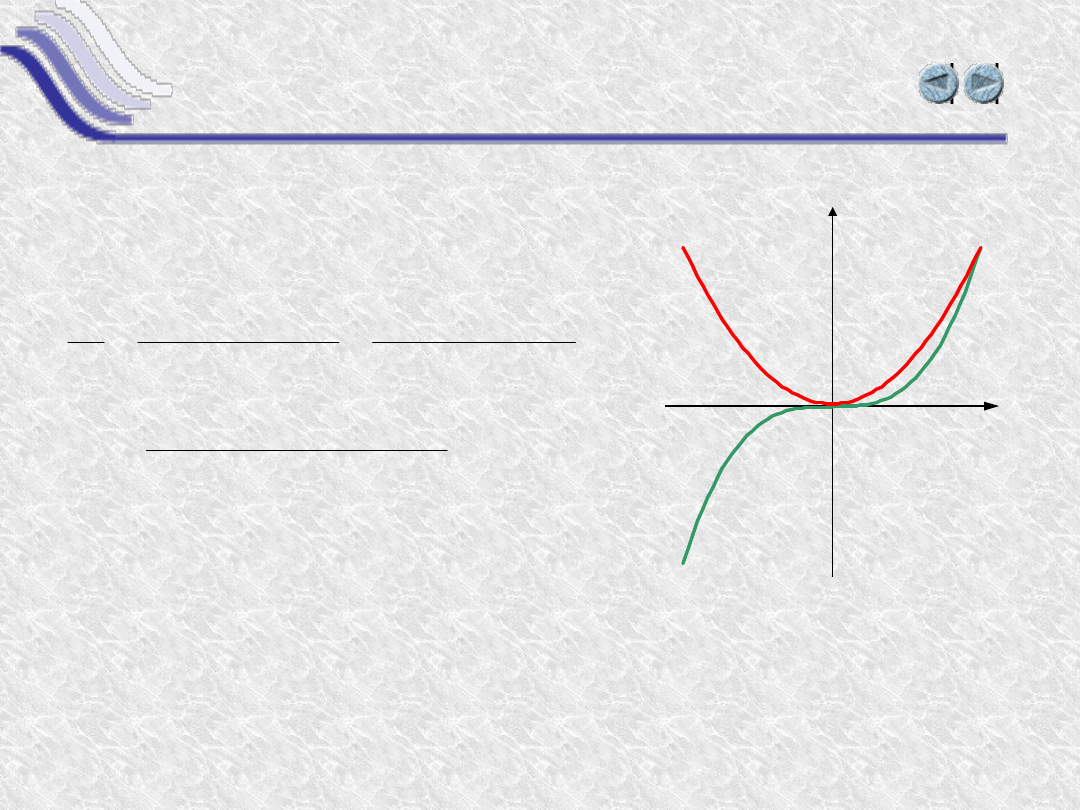
Pochodne funkcji potęgowych

Funkcja trzeciego stopnia y(x) = a·x

3

Pochodna , czyli granica tego ilorazu dla x

dążącego do zera, wynosi

y’(x)=3ax

2



























x

ax

x

x

a

x

x

y

x

x

y

x

y

3

3

)

(

)

(

)

(

Iloraz różnicowy jest równy:

x

x

a

x

ax

x

ax















3

2

2

3

3

2

2

3

3

x

a

x

ax

ax











x

y

y(x)=x

3

y’(x)=x

2

10

Pochodne funkcji potęgowych

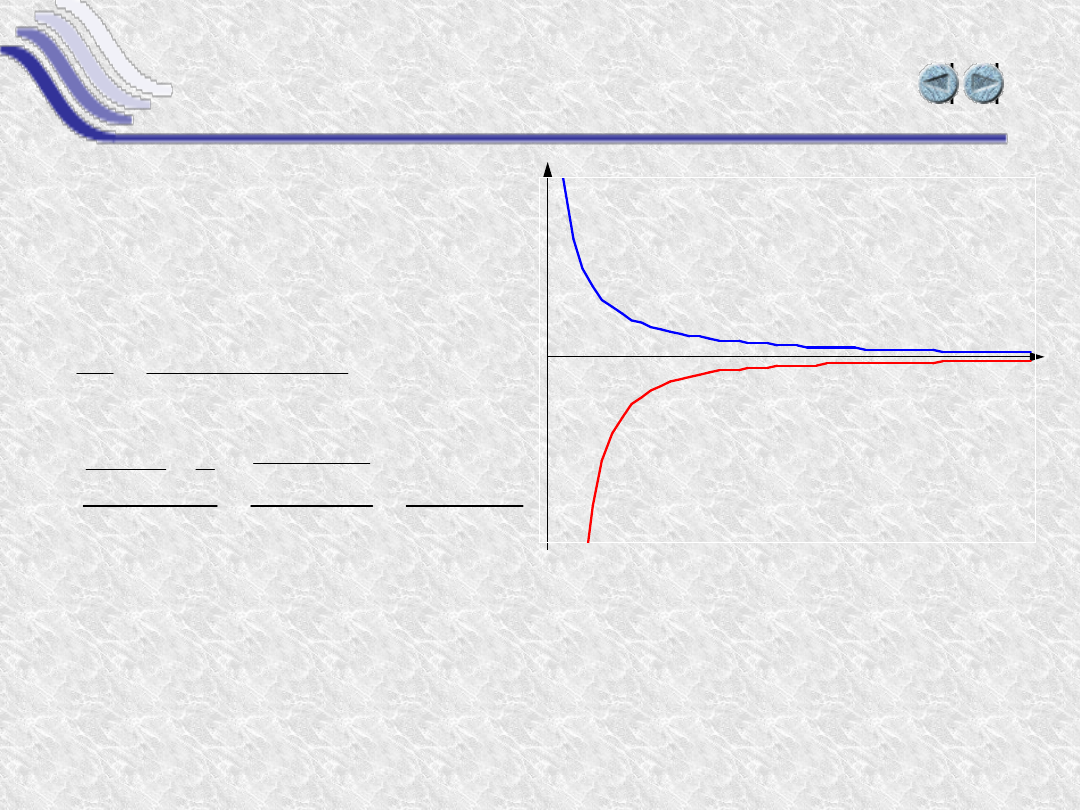
Funkcja stopnia -1
y(x) = x

-1

Iloraz różnicowy wynosi:

Pochodna jest granicą tego ilorazu dla x dążącego

do zera i wynosi

y’(x) = (-1)·x

-2

Funkcja jest malejąca, więc jej pochodna jest ujemna.

















x

x

y

x

x

y

x

y

)

(

)

(

)

(

1

)

(

1

1

x

x

x

x

x

x

x

x

x

x

x

x































x

y

y(x)=1/x

y’(x)=-1/x

2

11

Pochodne funkcji potęgowych

12

Iloraz różnicowy wynosi:

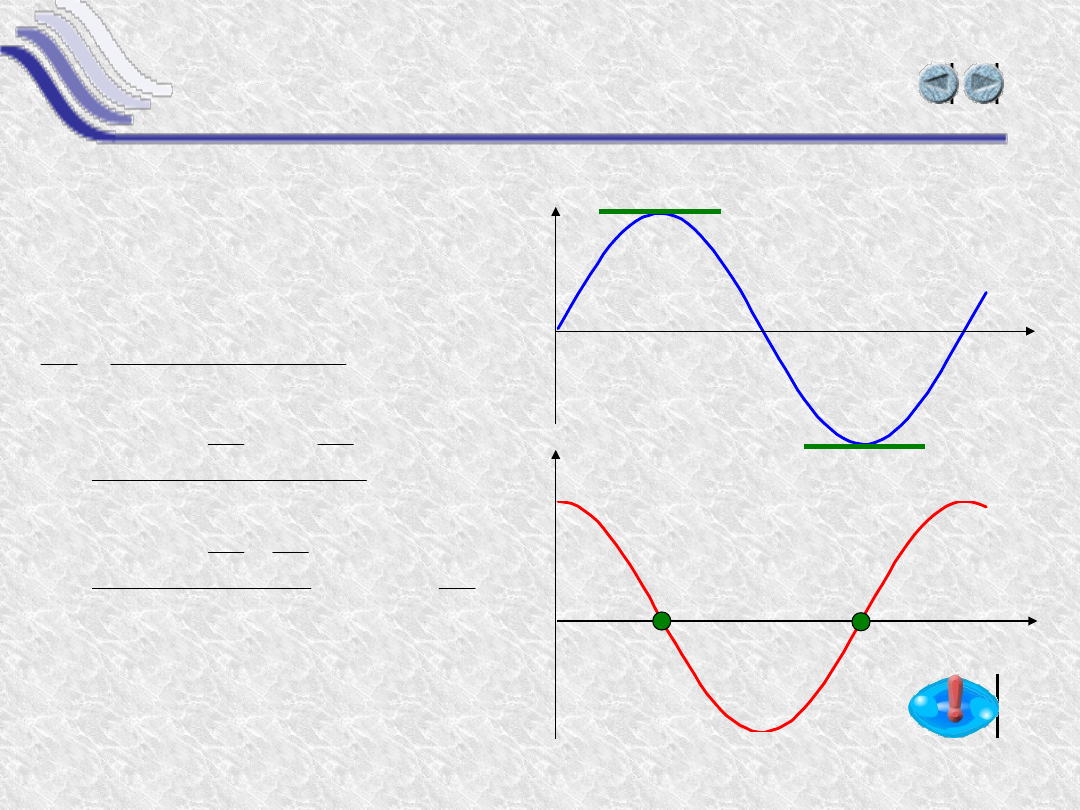
Pochodna funkcji sinus

Funkcja y(x) = sin(x)

Czyli

sin’(x) = cos(x)

















x

x

x

x

x

y

)

sin(

)

sin(















x

x

x

x

)

2

sin(

)

2

cos(

2

)

2

cos(

2

)

2

cos(

2

x

x

x

x

x

x



















y

x



2

0

y(x)=sin(x)

y

x



2

1

0

y’(x)=cos(x)

13

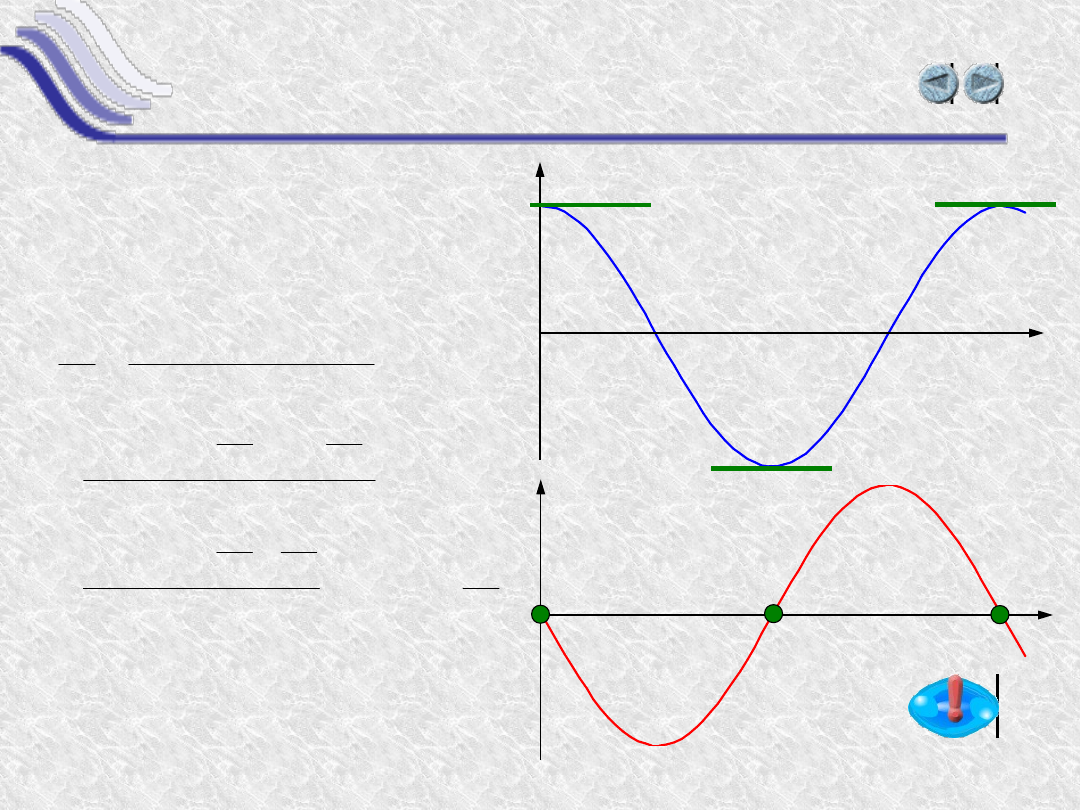
Pochodna funkcji cosinus

Funkcja y(x) = cos(x)

Iloraz różnicowy wynosi:

















x

x

x

x

x

y

)

cos(

)

cos(

Pochodną funkcji cosinus
jest -sinus

















x

x

x

x

)

2

sin(

)

2

sin(

2

)

2

sin(

2

)

2

sin(

2

x

x

x

x

x

x























y(x)=cos(x)

x

y



2



0

y’(x)=-sin(x)

y

x



2



0

14

Pochodna funkcji wykładniczej

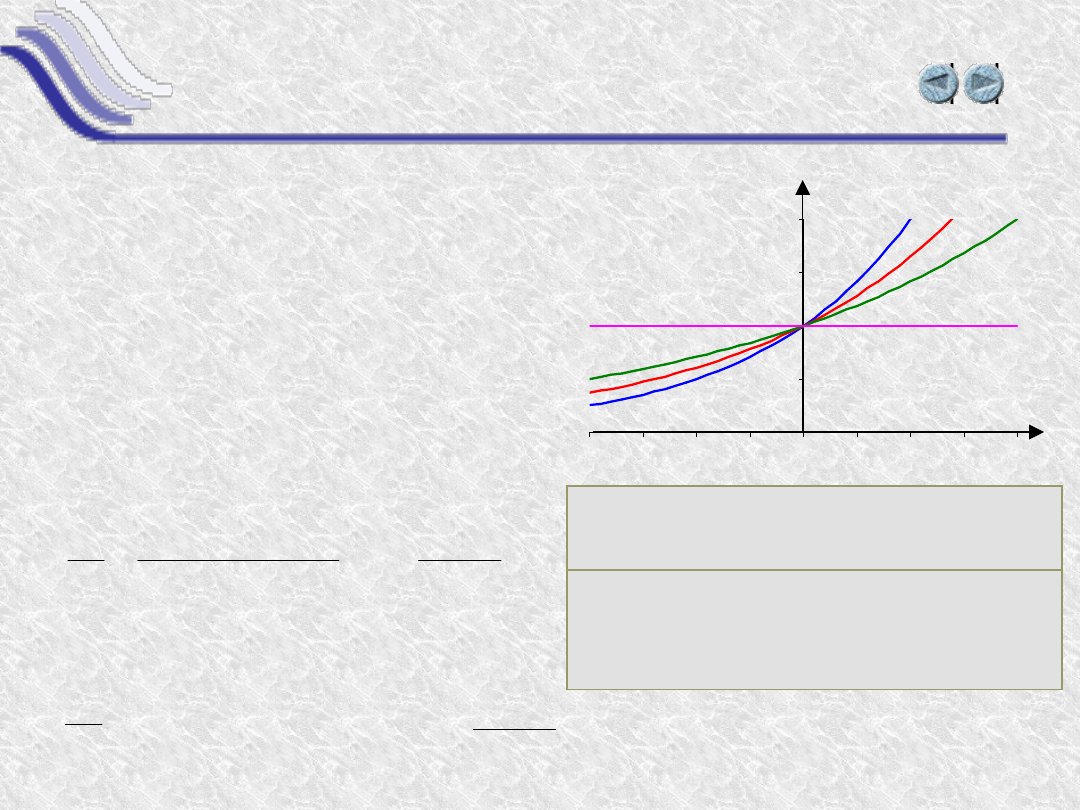
Funkcja y(x) = a

x

Licznik ilorazu różnicowego:





















x

x

x

a

a

x

y

x

x

y

y

)

(

)

(

)

1

(













x

x

x

x

x

a

a

a

a

a

4

x

e

x

2

x

1

x

Iloraz różnicowy ma postać:



































x

a

a

x

x

y

x

x

y

x

y

x

x

1

)

(

)

(

0,0

0,5

1,0

1,5

2,0

-1,0

-0,5

0,0

0,5

1,0

x

y

Pochodna a

x

jest więc do samej

funkcji proporcjonalna.

,

)

(

x

a

a

C

x

y









Można więc napisać:

x

a

a

C

x









1

)

(

gdzie

Ułamek od x nie zależy, nie
zależy więc od x i jego granica
dla x0.

15

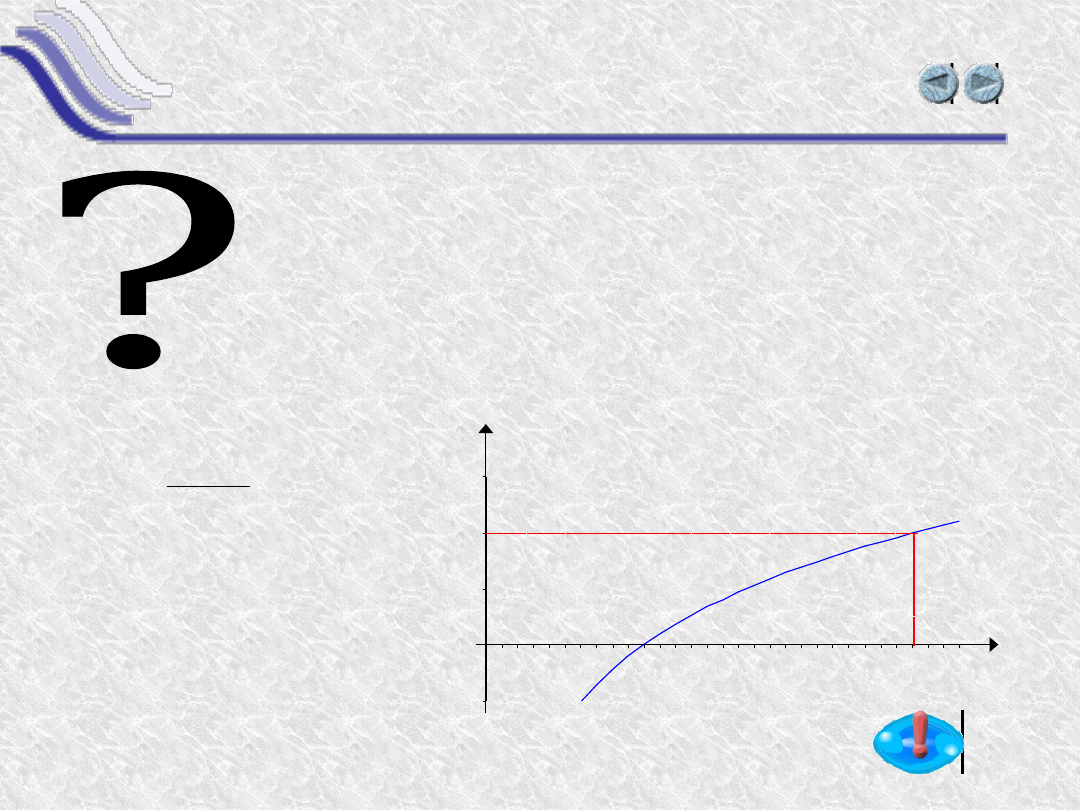
Wprowadzenie liczby e

Nasuwa się więc pytanie: czy można tak
dobrać a, aby granica ułamka była
równa jedności. Dla takiego a pochodna
byłaby po prostu równa samej funkcji (a
nie tylko proporcjonalna do niej).

1

)

(



e

a

C

...

71828

,

2



e

x

a

a

C

x









1

)

(

-0,5

0,0

0,5

1,0

1,5

0,0

0,5

1,0

1,5

2,0

2,5

3,0

x = 0,001

a

C(a)

e

16

Pochodna funkcji wykładniczej

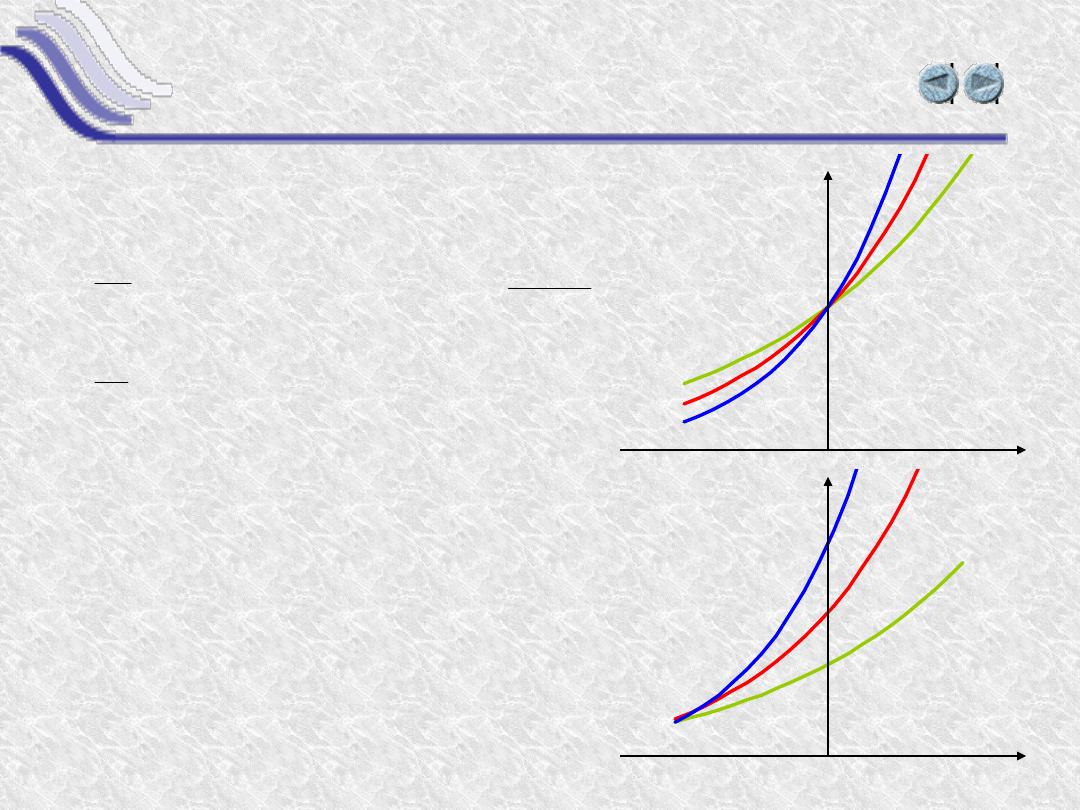
Po obliczeniu granicy ułamka
dla x0 otrzymamy wzór

pochodnej:

1

x

y

2

x

4

x

e

x

1

x

y

2

x

ln2

e

x

4

x

ln4

Funkcja y(x) = a

x

(a

x

)’= a

x

lna

)

(

lim

0

a

C

a

dx

dy

x

x









x

a

a

C

x









1

)

(

gdzie

,

)

(

x

a

a

C

x

y









17

Pochodna funkcji wykładniczej

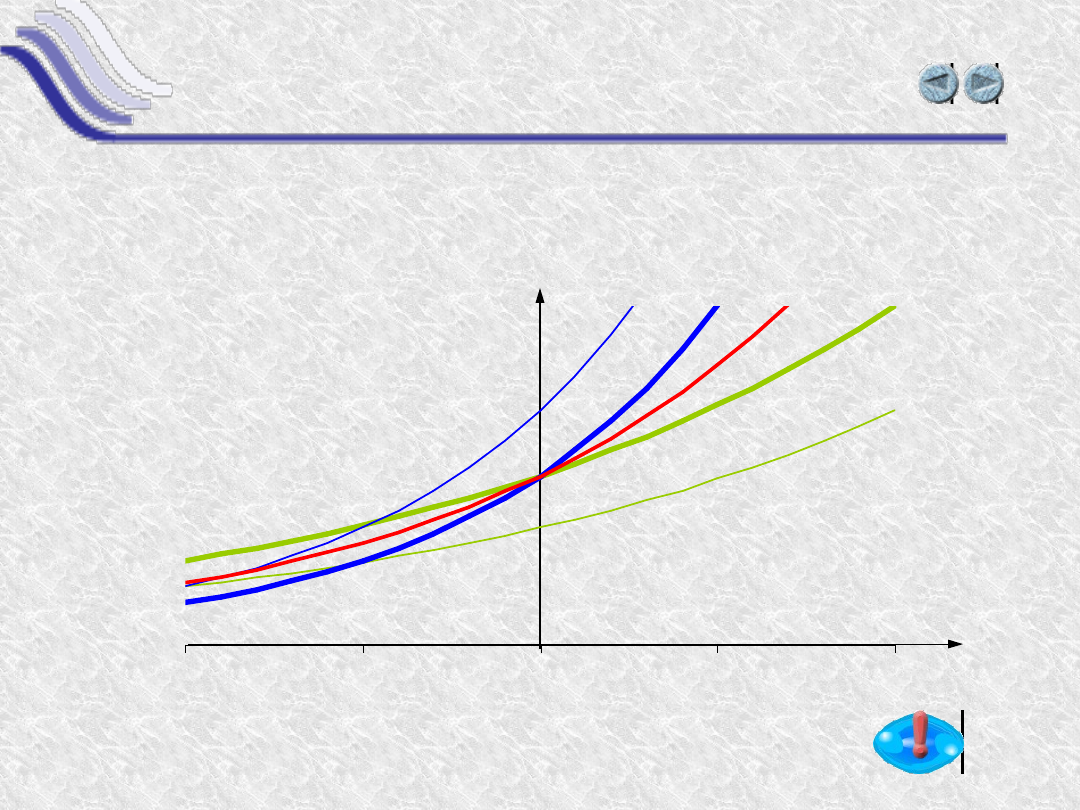
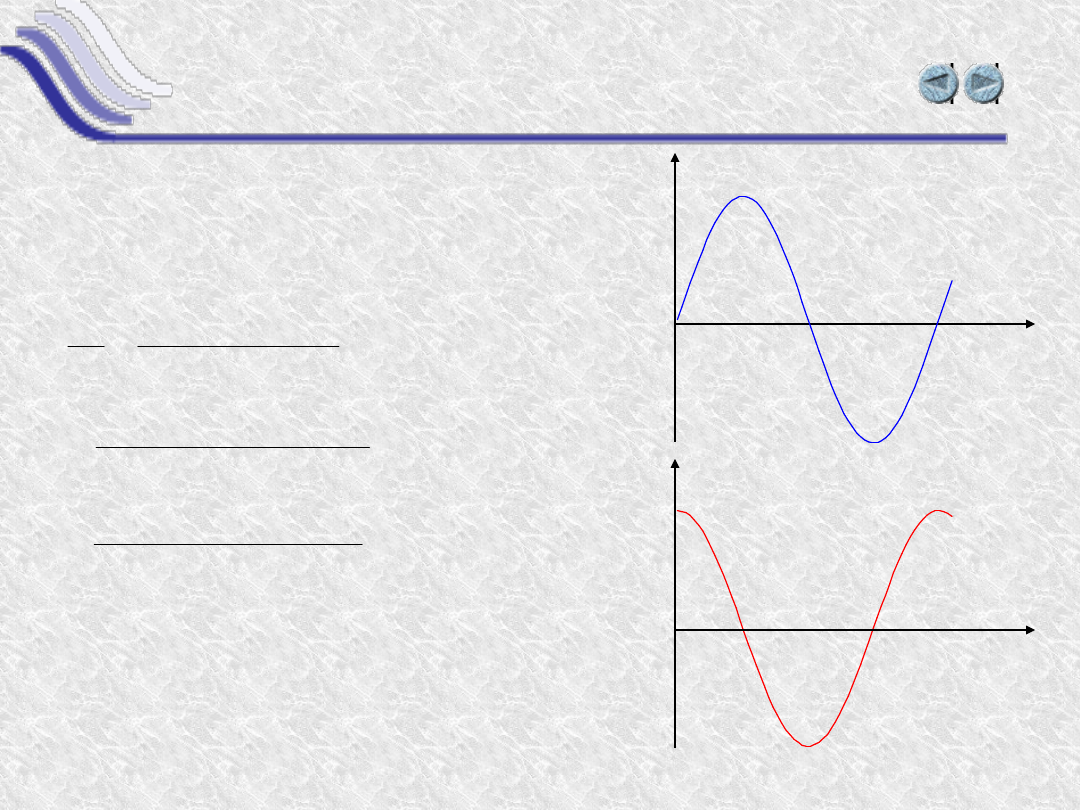
Pochodna funkcji wykładniczej jest proporcjonalna
do samej funkcji.

x

y

1

2

x

2

x

ln2

-1

-0,5

0

0,5

1

4

x

4

x

ln4

-1

-0,5

0

0,5

1

e

x

-1

-0,5

0

0,5

1

18

Pochodna funkcji y(x)=a·f(x)

Pochodna funkcji
pomnożonej przez stałą
y(x) = af(x)

Iloraz różnicowy ma
postać:

Jeśli obliczymy granicę tego
ilorazu, otrzymamy wzór:

y’(x) = a  f’ (x)

















x

x

y

x

x

y

x

y

)

(

)

(

















x

x

f

a

x

x

f

a

)

(

)

(















x

x

f

x

x

f

a

)]

(

)

(

[(

2

1

x

y

2sin(x)



2

0

2

1

x

y

2cos(x)



2

0

19

Pochodna sumy funkcji

Licznik ilorazu różnicowego jest równy:

Pochodna sumy funkcji jest równa sumie ich
pochodnych:

y’(x) = f’(x) + g’(x)

x

x

g

x

x

g

x

x

f

x

x

f





















)

(

)

(

)

(

)

(

Δx

Δy

Cały iloraz różnicowy ma więc postać sumy
dwóch
ilorazów różnicowych:

Pochodna sumy funkcji y(x) = f(x)

+

g(x)

y = y (x+



x) - y(x) =

= (f(x+



x) + g(x+



x)) - (f(x) + g(x)) =

= (f(x+



x)-f(x)) + (g(x+



x)–g(x))

20

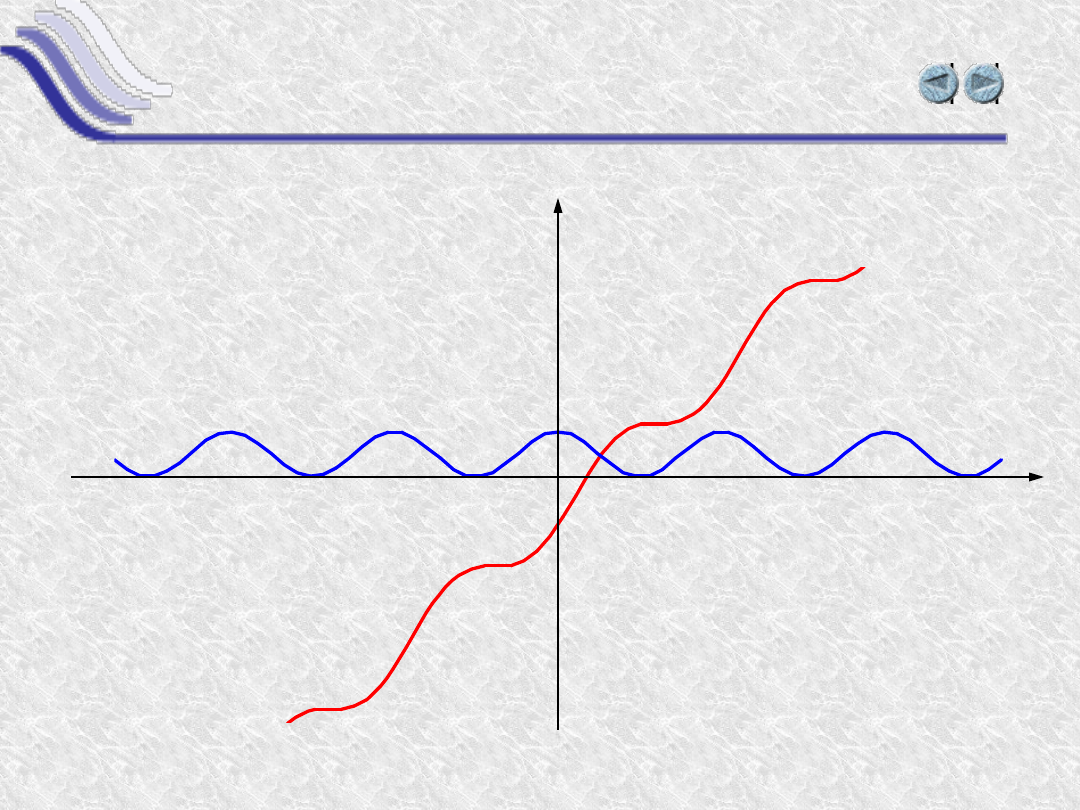
y(x) = x+sin(x)

Pochodna sumy funkcji

y’(x) = 1+cos(x)

Funkcja y(x) = x +
sin(x)

i jej pochodna

y

2

5

1
0

-5

-

10

2

-

-4

x



-3

-2

3

4

5

-5

0

21

Pochodna iloczynu funkcji

Pochodna iloczynu funkcji y(x) =
f(x)•g(x)

x

x

g

x

x

g

x

f

x

x

g

x

x

f

x

x

f

























)

(

)

(

)

(

)

(

)

(

)

(

Δx

Δy

Iloraz różnicowy ma postać:

y’(x) = f’(x)•g(x)+f(x) •g’(x)

Licznik ilorazu różnicowego jest równy:

y = f(x+x)g (x+x) -f(x)g (x) =

= (f(x+x) – f(x))g(x+x) – f(x)(g(x+x)–g(x))

Dla x0 otrzymujemy:

22

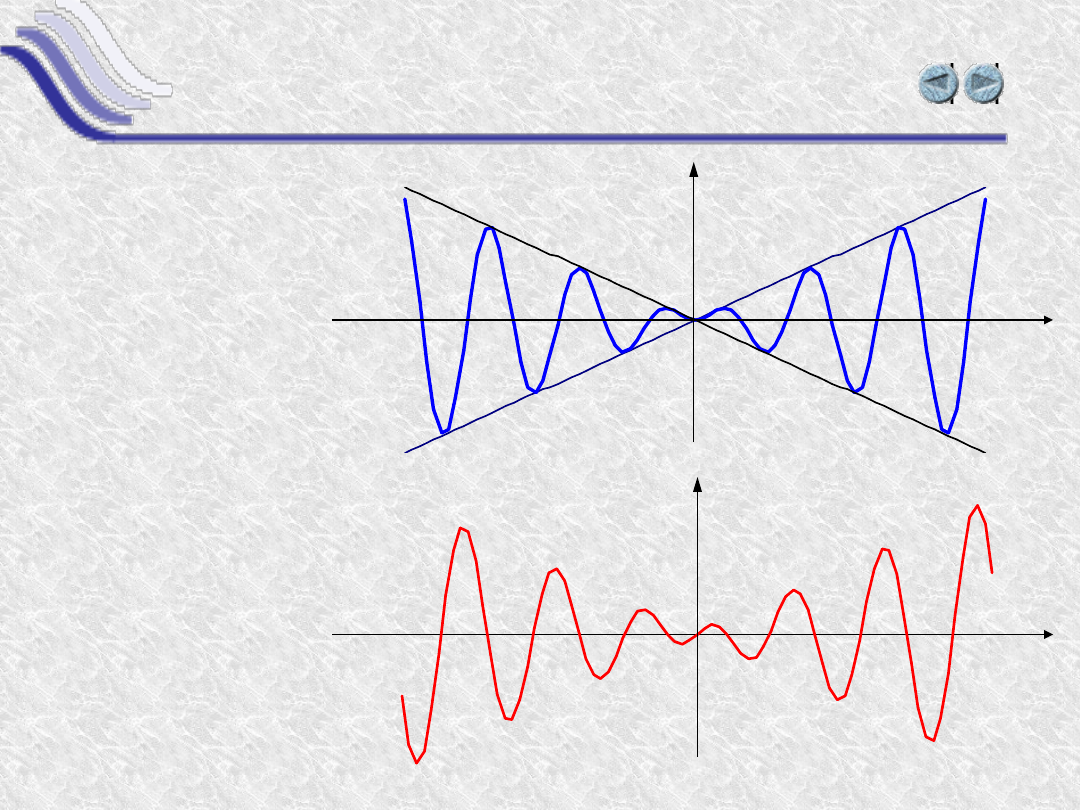
Pochodna iloczynu funkcji

y=x·sin(x
)

y’=sin(x)
+x·cos(x)

y

x

 2 3 4 5 6

-

-2

-3

-4

-5

-6

 2 3 4 5 6

-

-2

-3

-4

-5

-6

y

x

23

Pochodna ilorazu funkcji

x

x

g

x

x

g

x

g

x

x

g

x

f

x

g

x

f

x

x

f

x

y

































)

(

)

(

))]

(

)

(

)(

(

)

(

))

(

)

(

[(

Iloraz różnicowy można zapisać
następująco:

Pochodna ilorazu funkcji y(x) =
f(x)/g(x)

Dla x0 mamy:

Pochodna ilorazu funkcji f(x) przez g(x) jest równa
stosunkowi iloczynu pochodnej pierwszej funkcji przez
drugą, pomniejszonemu o iloczyn pierwszej funkcji
przez pochodną drugiej, do kwadratu drugiej funkcji.

y’(x) =

f’(x)· g(x) - f(x)· g’(x)

g(x)

2

24

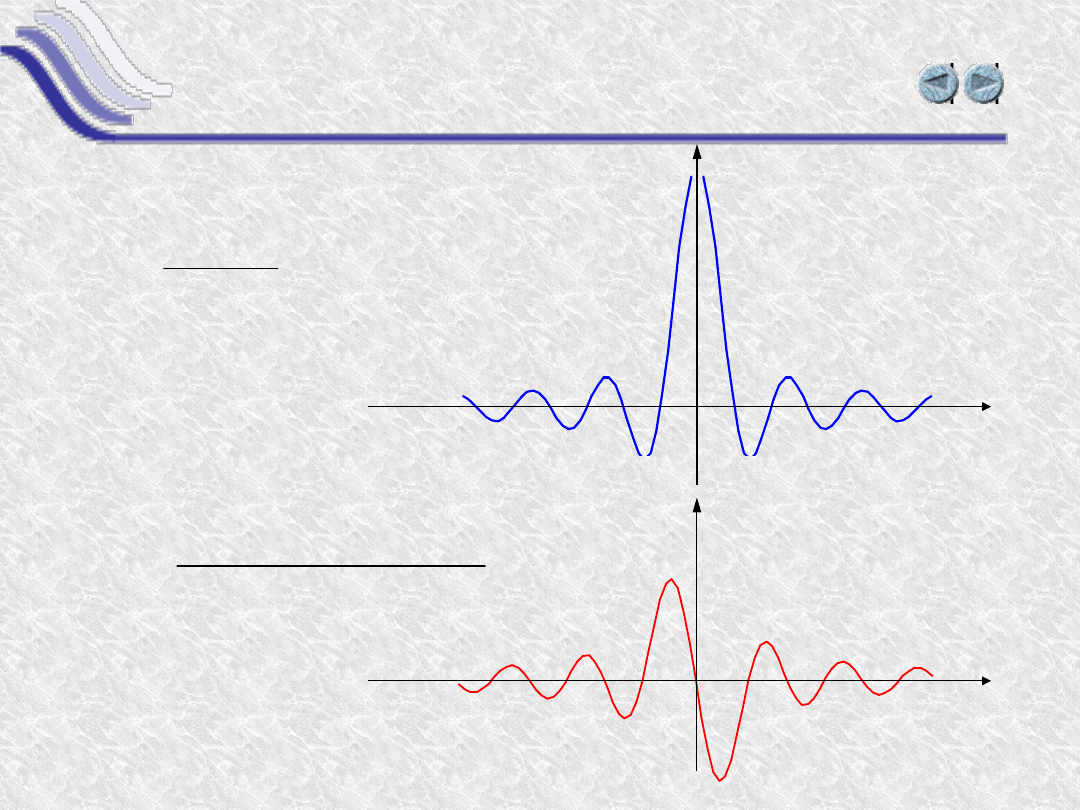
Pochodna ilorazu funkcji

2

)

sin(

)

cos(

x

x

x

x

y







x

x

y

)

sin(





3



5



-

-3

-5

x



3



5



-

-3

-5

x

25

Pochodną funkcji y(x) = cos(x) jest
funkcja:

-sin(x)

-tg(x)·cos(x)

Obie odpowiedzi są poprawne

Pochodną funkcji y(x) = tg(x) jest
funkcja:

ctg(x)

1/cos

2

(x)

1/x

2

Pochodną funkcji y(x) = 2x

3

+ 4 jest

funkcja:

3x

2

+4

6x

2

+4

6x

2

Pochodną funkcji y(x) = 1/x jest funkcja:

-1/x/x

-1/x

2

Obie odpowiedzi są poprawne

30

Pochodną funkcji y(x) = e

x

jest funkcja:

x·e

x

e

x

e

x

/x

32

1.

Wielka internetowa encyklopedia multimedialna

http://www.encyklopedia.pl

2.

Dydaktyka w Internecie

http://www.szkoly.edu.pl/dydaktyka.html

4.

H. Łubowicz, B. Wieprzkowicz: Matematyka. Podstawowe

wiadomości teoretyczne i ćwiczenia dla studentów
studiów
inżynierskich.

5.

K. Litewska, J. Muszyński: Analiza matematyczna, cz.1.

6.

W. Żakowski: Matematyka, cz. 1.

3.

J. Ginter: Mechanika.

Neto- i bibliografia