Metoda Clarke’a

dla małych trójkątów

1. Obliczenie M

1

i N

1

w punkcie P

1

dla danej szerokości

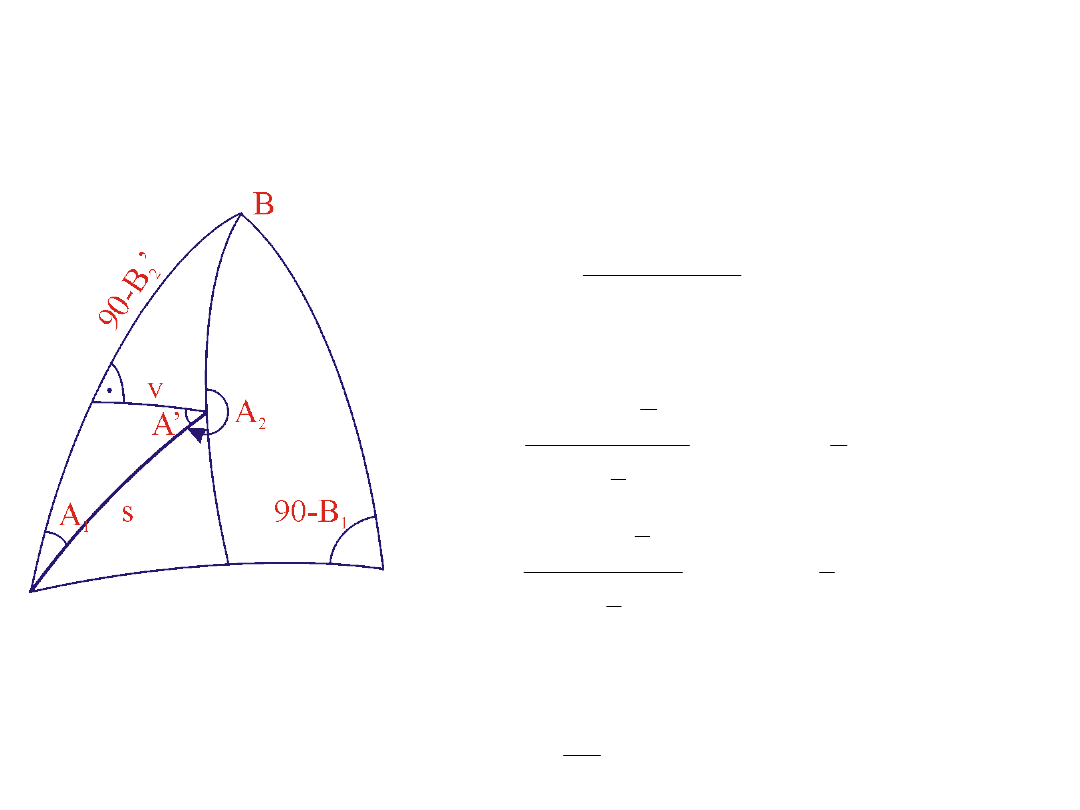
2. Obliczenie nadmiaru sferycznego dla trójkąta P

1

P

2

’P

2

1

1

1

1

2

2

cos

sin

"

N

M

A

A

s





3. Obliczenie boków u i v











 













 









3

2

cos

3

1

cos

3

2

cos

1

1

A

s

A

s

u











 













 









3

1

sin

3

1

cos

3

1

sin

1

1

A

s

A

s

v

4. Obliczenie przybliżonej różnicy B

0

między

punktami P

1

i P

2

’

1

0

M

u

B 



Obliczenie szerokości średniej między punktami
P

1

i P

2

’

2

0

1

B

B

B

S







5. Obliczenie promienia M

S

dla argumentu B

S









3

2

2

sin

1

1

S

S

B

e

e

a

M







6. Obliczenie szerokości punktu P

2

’

S

M

u

B

B





1

2

'

7. Obliczenie B

2

na podstawie rozwiązania trójkąta prostokątnego P

2

BP

2

’









v

B

B

cos

'

90

cos

90

cos

2

2







v

B

B

cos

'

sin

sin

2

2







2

sin

2

'

sin

cos

1

'

sin

sin

'

sin

2

2

2

2

2

v

B

v

B

B

B











2

sin

'

sin

2

2

'

cos

2

'

sin

2

2

2

2

2

2

2

v

B

B

B

B

B







'

sin

4

'

cos

2

'

2

2

2

2

2

B

v

B

B

B





'

tan

2

'

2

2

2

2

B

v

B

B





'

tan

'

'

2

'

2

2

2

2

B

N

M

v

B

B





M’, N’ dla argumentu B

2

’

'

tan

'

'

2

2

2

1

2

B

N

M

v

M

u

B

B

S







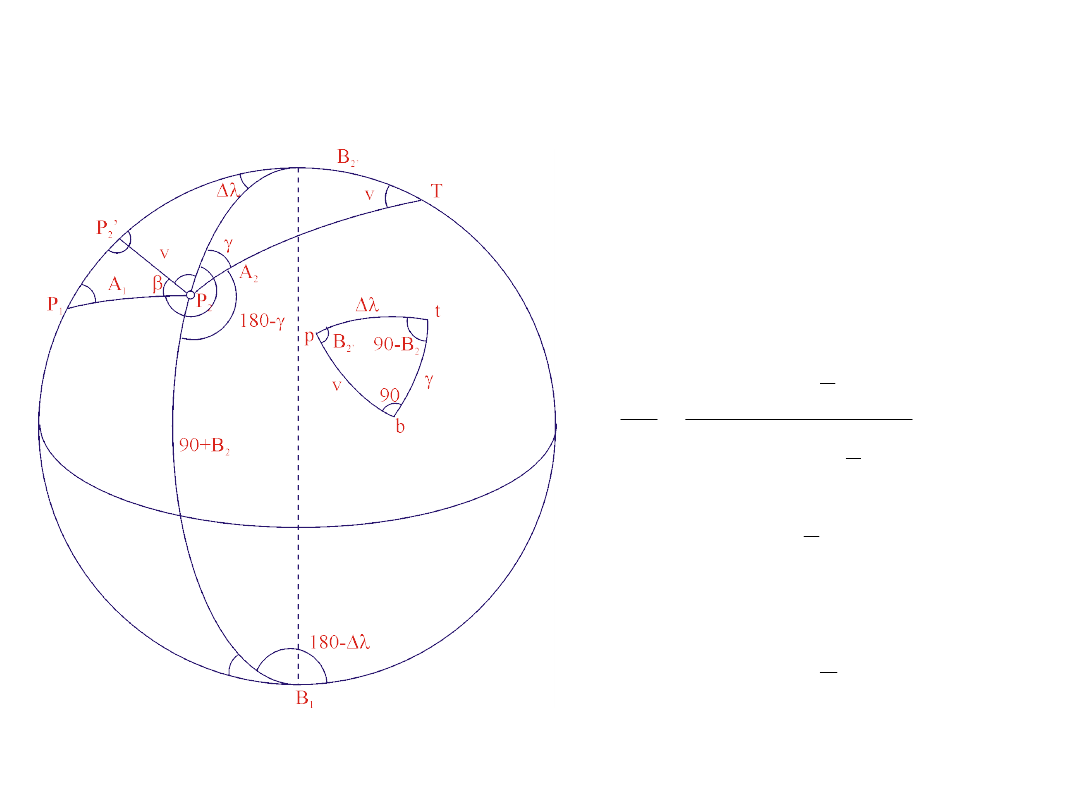
Tworzymy trójkąt biegunowy do dużego trójkąta P

2

TB

1

(ptb) zakreślając

z wierzchołków łuki o promieniu 90°. W myśl twierdzenia że boki i kąty
odpowiednich trójkątów dopełniają się do 180° otrzymamy odpowiednie
elementy trójkąta biegunowego.

8. Obliczenie nadmiaru sferycznego w

trójkącie biegunowym ptb

2

2

1

' B

B 





9. Obliczenie boku  w trójkącie

sferycznym ptb z twierdzenia
sinusowego















































1

2

1

3

1

90

sin

3

1

90

sin







B

v



















1

2

3

1

sec





B

v

10. Obliczenie zbieżności południków z

tego samego trójkąta



















1

2

3

2

sin





B

L

11. Obliczenie azymutu A

2



180

1

2













A

A