Idea ADT

Twierdzenie (Church)

Rachunek predykatów jest częściowo rozstrzygalny.
Tzn. istnieje algorytm, który dla dowolnej formuły  będącej tautologią, potrafi

to stwierdzić

UWAGA: Dzięki twierdzeniu Posta (i odpowiadającemu mu twierdzeniu
dla rachunku predykatów), sprawdzenie prawdziwości formuły 

na podstawie prawdziwości formuł zawartych w zbiorze X ( X|=  )

można sprowadzić do zagadnienia poszukiwania wnioskowania
(dowodu)  ze zbioru X. Wnioskowanie jako operacja czysto

syntaktyczna dobrze poddaje się automatyzacji.

ADT - RP

W przypadku rachunku predykatów opracowano wiele metod
ADT, np. procedura Herbranda (postać normalna, standardowa
postać Skolema, sprzeczny zbiór formuł, Uniwersum Herbranda-
Skolema).

W naszych rozważaniach ograniczymy się do pokazania, jak
realizować ADT
w pewnym ograniczonym języku reprezentacji wiedzy
nazywanym językiem
klauzul (w szczególności klauzul Horna).
Rozważać będziemy dwa sposoby dowodzenia: wstępujące i
zstępujące.
W przypadku dowodów zstępujących wnioskować będziemy
zgodnie z regułą
wnioskowania znaną jako „zasada rezolucji” („modus tollens”).

Klauzule definicje
Atom P(t

1

, t

2

, .., t

n

) P-predykat t

i

– termy

Klauzula B

1

, B

2

, .., B

m

 A

1

, A

2

,.., A

n

gdzie dowolne A

i

, B

j

są

atomami

Dokładniej
A

1

, A

2

,.., A

n

– koniunkcja atomów

B

1

, B

2

, .., B

m

– alternatywa atomów

Klauzule Horna

Klauzulę postaci

B  A

1

, A

2

,.., A

n

nazywamy klauzulą Horna

Jeśli klauzula B  A

1

, A

2

,.., A

n

zawiera zmienne x

1

, x

2

, .., x

k

, to

należy ją interpretować jako stwierdzenie, że:

dla wszystkich x

1

, x

2

, .., x

k

zachodzi B jeśli A

1

, A

2

,.., A

n

Jeśli n=0, czyli mamy postać B, to zapis ten oznacza
stwierdzenie faktu B

Jeśli w konkluzji nie występuje żaden atom, to mamy postać:

A

1

, A

2

,.., A

n

którą interpretujemy jako – dla wszystkich x

1

, x

2

, .., x

k

nieprawda, że A

1

, A

2

,.., A

n

(pamiętając, że z prawej strony klauzuli mamy koniunkcję)

Przykłady

Baza związków rodzinnych:
Ojciec(zeus. ares).
Ojciec(ares, harmonia).
Ojciec(kadmos, semele).
Ojciec(zeus, dionizos).
Matka(afrodyta, harmonia).
Matka(hera, ares).
Matka(harmonia, semele).
Bog(zeus).
Bog(hera).
Bog(ares).
Bog(afrodyta).
Krolowa(harmonia).
Plec-zenska(X) <- Matka(X, Y).
Plec-meska(X) <- Ojciec(X, Y).
Dziecko(Y, X) <- Matka(X, Y).
Dziecko(Y, X) <- Ojciec(X, Y).
Wnuk(X, Y) <- Dziecko(X, Z), Dziecko(Z, Y).
Plec-meska(X), Plec-zenska(X) <- Czlowiek(X).

Sprzeczność zbioru

klauzul

Zbiór klauzul S jest sprzeczny wttw nie jest niesprzeczny 
Sprzeczność zbioru klauzul można wykazać drogą:

-

semantyczną

-

syntaktyczną (już wiemy, że ta lepiej nadaje się do
algorytmizacji)

Metoda semantyczna

Zbiór klauzul S jest niesprzeczny, jeśli w pewnej Interpretacji

wszystkie

klauzule tego zbioru są prawdziwe.

Uniwersum Herbranda-Skolema

Uniwersum zbioru klauzul

S – zbiór klauzul

H

0

={ stałe występujące w S} lub H

0

={a} jeśli w S nie ma

stałych (stała Skolema)

H

k+1

=H

k

{ f(t

1

, t

2

,..,t

n

) : t

i

H

k

}

H=



N

k

k

H



Uniwersum Herbranda-Skolema

Uniwersum zbioru klauzul S – zbiór wszystkich termów

ustalonych, które daje się

zbudować ze stałych i symboli funkcyjnych występujących w

klauzulach zbioru S

UWAGA !!: Jeśli chcemy wykazać, że w języku klauzul zbiór założeń S
implikuje pewną konkluzję  , to zakładamy, że konkluzja ta nie jest

prawdziwa i pokazujemy, że negacja konkluzji jest sprzeczna z założeniami.

Czyli, że zbiór klauzul S{}

jest sprzeczny

dotyczy metody semantycznej i syntaktycznej

Interpretacja (dopuszczalna) zbioru

klauzul

Za interpretację zbioru klauzul S będziemy uważać przypisanie

każdemu

n-argumentowemy symbolowi predykatowemu występującemu w

klauzulach

pewnej relacji między indywiduami należącymi do Uniwersum.

Wykazanie sprzeczności zbioru klauzul metodą semantyczną

sprowadza się do

pokazania, że w żadnej interpretacji nie są one (te klauzule)

wszystkie

jednocześnie prawdziwe.

Przykład – Omylnego Greka

Przykład (Omylny Grek):
1. Czlowiek(kowalski).
2. Czlowiek(sokrates).
3. Grek(sokrates).
4. Omylny(X) <- Czlowiek(X).

Pytam, czy na podstawie tych założeń mogę

wyciągnąć konkluzję, że istnieje omylny Grek.

Dołączam klauzulę
5. <- Omylny(X), Grek(X).
Sprawdzam czy zbiór klauzul 1-5 jest sprzeczny

Uniwersum {kowalski, sokrates} - nie ma symboli funkcyjnych, więc jest prosto

Ile tutaj jest możliwych różnych Interpretacji ?
3 – symbole predykatowe, 2 – stałe, 2 – wartości logiczne
Zatem każdemu z trzech symboli predykatowych może być przypisana jedna
z czterech różnych interpretacji, zatem:

4*4*4=64 - tyle jest Interpretacji

Przykład cd.

Przykład (Omylny Grek):
1. Czlowiek(kowalski).
2. Czlowiek(sokrates).
3. Grek(sokrates).
4. Omylny(X) <- Czlowiek(X).
5. <- Omylny(X), Grek(X).

Rozpatrzmy najpierw tylko pierwsze cztery klauzule.
Istnieją tylko dwie interpretacje, w których klauzule 1-4 są wszystkie jednocześnie
prawdziwe.

pierwsza
Czlowiek(sokrates)

prawda

Omylny(sokrates)

prawda

Grek(sokrates)

prawda

Czlowiek(kowalski) prawda
Omylny(kowalski)

prawda

Grek(kowalski)

prawda

druga
Czlowiek(sokrates)

prawda

Omylny(sokrates)

prawda

Grek(sokrates)

prawda

Czlowiek(kowalski) prawda
Omylny(kowalski)

prawda

Grek(kowalski)

fałsz

Przykład - koniec

Przykład (Omylny Grek):
1. Czlowiek(kowalski).
2. Czlowiek(sokrates).
3. Grek(sokrates).
4. Omylny(X) <- Czlowiek(X).
5. <- Omylny(X), Grek(X).

Dla zbioru klauzul 1-5 Uniwersum oraz liczba interpretacji są identyczne jak dla
1-4.
Ale w żadnej z owych dwóch interesujących nas Interpretacji klauzule 1-5 nie są
wszystkie jednocześnie prawdziwe. W szczególności X=sokrates czyni fałszywą
klauzulę 5 w obu interesujących nas interpretacjach

Zatem stwierdzenie, że istnieje omylny grek jest logiczną

konsekwencją zbioru

klauzul 1-4

Taki sposób dowodzenia daje się automatyzować

-

Algorytm Gilmore`a - nieefektywny obliczeniowo

-

Reguły Davisa i Putmana – pozwalają zmniejszyć liczbę
klauzul w zbiorze S
np. poprzez usunięcie z niego wszystkich tautologii

Metoda syntaktyczna

Dowodzenie (wnioskowanie) metodą syntaktyczną

przeprowadzać będziemy

za pomocą reguły wnioskowania, znanej jako modus tollens (lub

ogólniej zasady

rezolucji)

Zasada rezolucji dla KRZ: p , q

i

, r

j

- zdania

p  q

1

..q

n

, p  r

1

.. r

m

q

1

 q

n

 r

1

 .. r

m

W szczególnym przypadku zasada rezolucji redukuje się do

reguły odrywania

rezolwenta

,   



Modus tollens

, 

 



Modus ponens

UWAGA: Zasada rezolucji stanowi zatem uogólnienie reguły odrywania.

Metoda syntaktyczna

Twierdzenie
Rezolwenta  formuł ,  jest ich logiczną konsekwencją

W systemach dowodzących opartych na zasadzie rezolucji gra

ona (klauzula pusta)

niebagatelną rolę, ponieważ jej wyprowadzenie ze zbioru formuł

S oznacza

sprzeczność zbioru klauzul S.

Jeśli przesłankami rezolucji są dwie pojedyncze klauzule (atomy),

to ich

rezolwenta jest klauzulą pustą (ozn.  ).

Klauzula pusta jest fałszywa przy każdej interpretacji.

, 



Metoda syntaktyczna –

dowód wstępujący

Dowodzenie sprzeczności metodą wstępującą rozpoczyna się od

początkowego

zbioru klauzul, kończy z chwilą wyprowadzenia takich wniosków,

które

bezpośrednio zaprzeczają negacji dowodzonej tezy.

Przy czym krok wnioskowania polega na dopasowaniu (w

możliwie ogólny

sposób) odpowiedniej liczby predykatów – konkluzji klauzuli – do

warunków

klauzuli i wyprowadzenia nowej konkluzji.

Dowód wstępujący to dowód w sensie dowodu formalnego,

którego definicja dla

KRZ podawana była na trzecim wykładzie.

Startujemy z aksjomatów (którymi są klauzule znajdujące się w

zbiorze S)

i stosując dopuszczalne reguły wnioskowania postępujemy tak,

aby otrzymać

klauzulę, której prawdziwość chcemy dowieść (lub klauzulę

pustą, jeśli do zbioru S dołączyliśmy zaprzeczenie klauzuli,
której prawdziwość chcemy dowieść).

Przykład dowodu wstępującego

Zakładamy, że dostępna jest baza wiedzy nt. związków rodzinnych (slajd nr 9)
to jest nasz zbiór S.

Mamy wykazać, że harmonia jest wnuczką zeusa.

Czyli, że ze zbioru S{ <-Wnuk(harmonia, zeus) } da się wyprowadzić klauzulę

pustą.

Ojciec(zeus,ar
es)

Ojciec(ares,harmon
ia)

Dziecko(ares,
zeus)

Dziecko(harmonia, ares)

Wnuk(harmonia,zeus
)

<-
Wnuk(harmonia,zeus
)



Efektywność metody wstępującej

W poprzednim drzewie dowodowym tak dobieraliśmy

początkowe fakty i

reguły wnioskowania (tutaj klauzule w postaci implikacji), aby

owe drzewo było

jak najmniejsze.
Metoda algorytmiczna musiałaby rozważać wszystkie drogi,

również te nie-

prowadzące do celu.
Klauzule rozpatrywane byłyby po kolei (tak jak występują w

zbiorze S).

Wniosek, iż taka metoda byłaby złożona obliczeniowo, jest jak

najbardziej

uprawniony.

Efektywniejsza jest metoda zstępująca.

Metoda syntaktyczna – dowód

zstępujący

Dowodzenie sprzeczności metodą zstępującą, polega na

rozpoczęciu dowodu od

negacji należącej do początkowego zbioru klauzul (tej negacji,

którą dołączyliśmy

do zbioru S).
Następnie implikacji i asercji (czyli po prostu faktów) używa się

do

wyprowadzenia nowych negacji z negacji już istniejących

(stosujemy zasadę

rezolucji).
Dowód kończy się z chwilą wyprowadzenia klauzuli pustej.

Dokładniej – wnioskowanie zstępujące polega na dopasowaniu

wybranego

warunku negacji do konkluzji pewnej implikacji, wyprowadzeniu

nowej negacji

przez zastąpienie wybranego warunku, warunkami tej

(dopasowanej) implikacji

i zastosowaniu do niej podstawienia dopasowującego.

Jeśli implikacja jest asercją (faktem), to w wybrany warunek jest

usuwany, a

podstawienie dopasowujące stosuje się do pozostałej części

negacji.

Jeśli wybrany warunek jest jedynym warunkiem negacji,

wówczas nowo

wyprowadzana negacja jest klauzulą pustą.

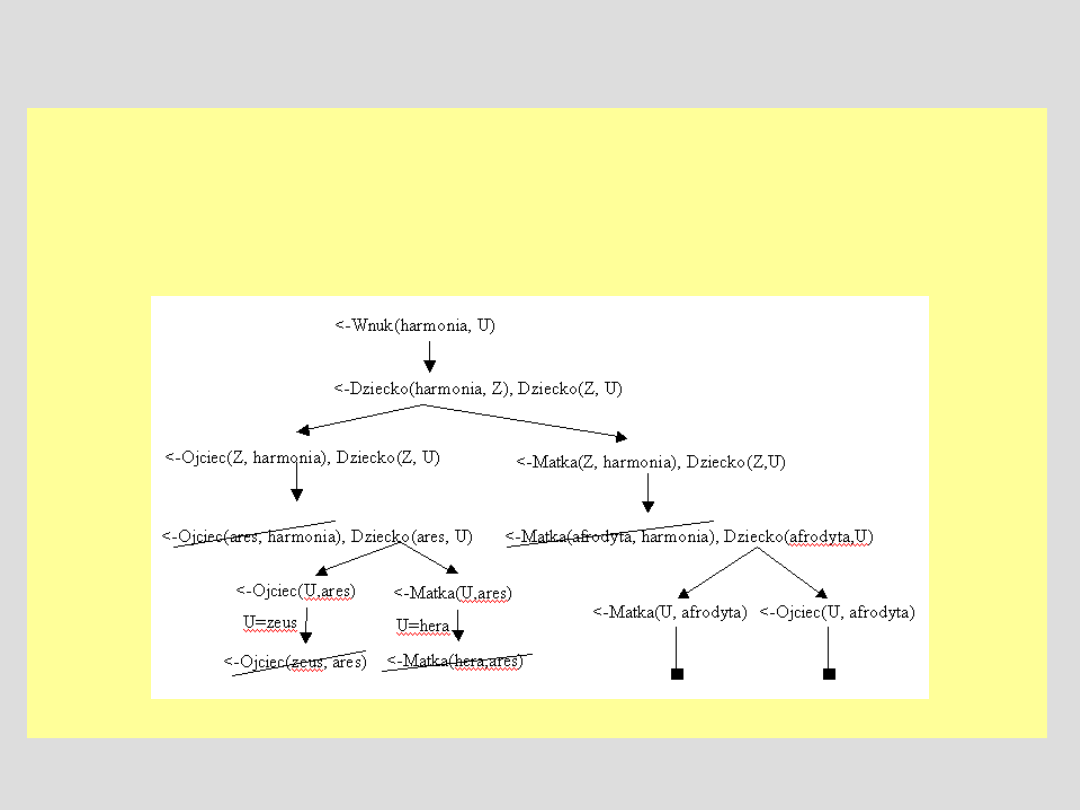
Przykład

Baza wiedzy ta sama (ten sam zbiór S), zadanie :
Szukamy wszystkich dziadków harmonii.
Czyli, że ze zbioru S{ <-Wnuk(harmonia, U) } da się wyprowadzić klauzulę

pustą. Dokładnie dla jakich U da się to zrobić

Efektywność metody

zstępującej

Przedstawione na poprzednim slajdzie drzewo dowodowe

również może wyglądać

inaczej.
Postać drzewa przeszukiwania zależeć będzie od strategii

dopasowywania

implikacji

Drzewa dowodowe możemy zbudować stosując strategie

przeszukiwania:

„w głąb” i „wszerz”.
Z punktu widzenia szybkości znalezienia odpowiedzi, strategia

„w głąb” jest

bardziej efektywna.

W punktach oznaczonych okręgami (tam, gdzie ścieżka się

rozgałęzia) wykonano tzw. nawroty. Znaczy to, że w danym
węźle udało się dopasować więcej niż jedną implikację.

Na czerwono zaznaczono ścieżkę, która zostanie zbadana
w pierwszej kolejności.

Rodzaje twierdzeń

Przeprowadzając dowód pokazujący, że klauzula  jest logiczną

konsekwencją

zbioru formuł S, formuła  pełni rolę tezy twierdzenia, a zbiór

formuł S jest

zbiorem założeń owego twierdzenia – stąd tytuł wykładu

Automatyczne

Dowodzenie Twierdzeń.

UWAGA: Możemy formułować twierdzenia dwojakiego rodzaju:
i) wynikiem dowodu jest odpowiedź TAK/NIE (teza nie zawiera

zmiennych)
ii) wynikiem są te wartości zmiennej (zmiennych) występujących w tezie,

które czynią twierdzenie prawdziwym (przy spełnionych założeniach)

Przykład:
i)

Wnuk(harmonia, zeus) - czy harmonia jest wnuczką zeusa

ii) Wnuk(harmonia, U) - czyją harmonia jest wnuczką

UWAGA: Odpowiedź w obu przypadkach zależy jedynie od postaci zbioru
założeń S !!! Czyli bez odpowiedniej informacji w tym zbiorze wynikiem
dla pkt. i) może być odpowiedź NIE.

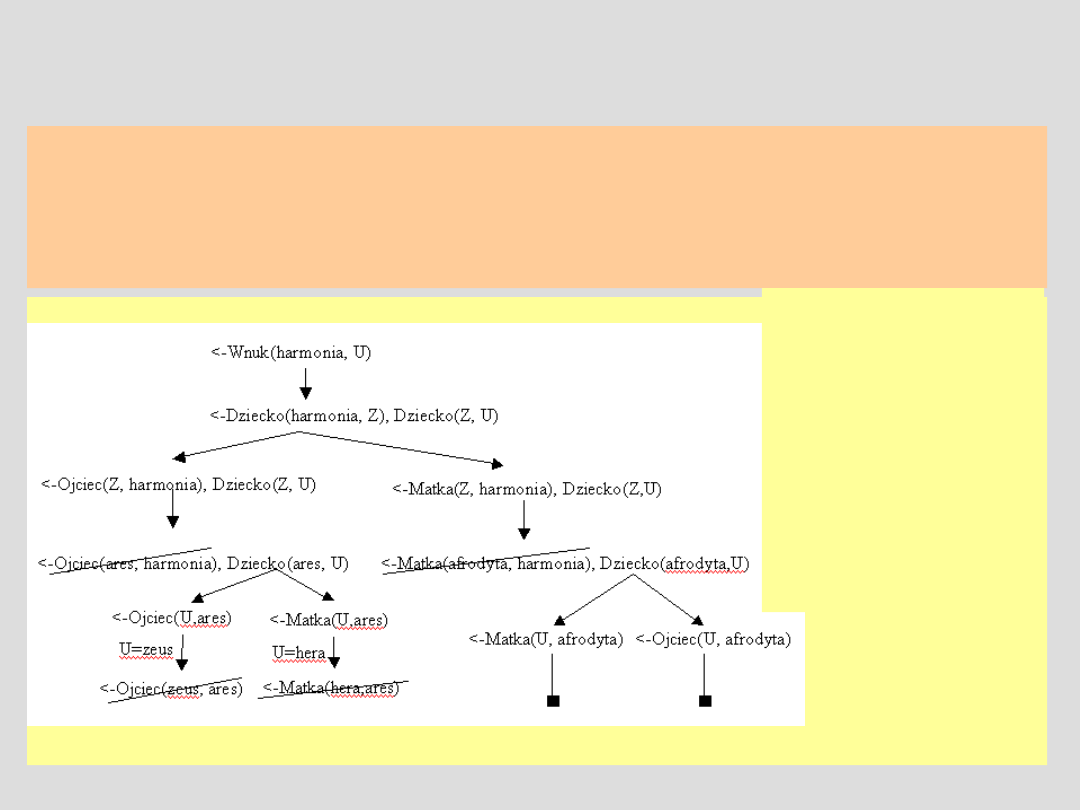
Strategia tworzenia bazy

wiedzy

UWAGA: We wnioskowaniu zstępującym przyjmuje się następującą strategię
tworzenia drzewa dowodowego:

i) pierwsza klauzula z procedury, którą można dopasować

ii) pierwszy podcel w przesłankach nowej negacji

Baza związków rodzinnych:
Ojciec(kadmos, semele).
Ojciec(zeus, dionizos).
Ojciec(ares, harmonia).
Ojciec(zeus.ares).
Matka(afrodyta, harmonia).
Matka(harmonia, semele).
Matka(hera, ares).
Dziecko(Y, X) <- Matka(X, Y).
Dziecko(Y, X) <- Ojciec(X, Y).
Wnuk(X, Y) <- Dziecko(X, Z),
Dziecko(Z, Y).

Formalizacja pojęć

Załóżmy, że dany jest zbiór klauzul Hornowskich S oraz

dana jest strategia

wyboru jednego z warunków negacji (strategia tworzenia

drzewa

dowodowego).

Definicja
Ciąg negacji C

1

, C

2

, ..,C

n

jest zstępującym dowodem klauzuli C

1

ze zbioru

klauzul S jeśli:
i)

C

1

należy do zbioru S.

ii) Dla każdego i=2,..,n, klauzula C

i

otrzymywana jest z C

i-1

przez zastosowanie

wnioskowania zstępującego (zasady rezolucji) z użyciem

jednej z klauzul

zbioru S.
i)

Ze zbioru C

1

, C

2

, ..,C

n

da się już wywieść klauzulę pustą.

Formalizacja pojęć cd.

W kwestii dowodów
Gdy dana jest negacja  A

1

,...,A

i-1

, A

i

, A

i+1

,.., A

m

oraz implikacja

B  B

1

,..,B

n

, która nie ma z negacją wspólnych zmiennych (jeśli

są, to

przemianować).

Nową negację możemy otrzymać, jeśli A

i

pasuje do konkluzji B.

Nowa negacja jest postaci:
 ( B

1

,..,B

n

,...,A

i-1

, A

i

, A

i+1

,.., A

m

) 

gdzie  jest podstawieniem dopasowującym A

1

do B

Definicja
Podstawienie : X T to funkcja przypisująca zmiennym termy

UWAGA: W przypadku konkretnego zbioru S rozpatrujemy oczywiście tylko
zmienne i termy występujące w S

.

Formalizacja pojęć cd.

Przykład
Jeśli E jest wyrażeniem (termem, atomem, klauzulą), to wynikiem podstawienia
={ X

1

=t

1

,..., X

m

=t

m

} jest wyrażenie E identyczne z E, poza tym, że

( X

i

=t

i

 ) wszędzie tam, gdzie w E występuje X

i

, w E występuje t

i

.

O wyrażeniu E mówimy, że jest konkretyzacją wyrażenia E
Definicja
Podstawienie  uzgadnia dwa wyrażenia E i E`, jeśli czyni je (te

wyrażenia)

identycznymi

Przykład
Wnuk(harmonia, U). Wnuk(harmonia, X). U:=Z, X:=Z
Wnuk(harmonia, U) . Wnuk(harmonia, zeus). U:=zeus
Wnuk(harmonia, U) . Wnuk(achilles, U). nie da się uzgodnić

Formalizacja pojęć cd.

Definicja
Podstawienie  dopasowuje wyrażenia E i E` (tzn. jest

najbardziej ogólnym

podstawieniem uzgadniającym (ozn. MGU)), jeśli spełnia dwa

następujące

warunki:
i)

 uzgadnia E i E`

ii) Jeśli  E=E`, to istnieje pewne  takie, że

E=(E`)

Stwierdzenie
Każde dwa wyrażenia, które można uzgodnić, można również

dopasować.

UWAGA: W języku prolog w czasie wnioskowania szukamy MGU.
Istnieje algorytm znajdowania (jeśli istnieje) MGU.

Przykład

Ojciec(zeus, U).

Ojciec(X, Y)

<- Dziecko(Y,X),Plec-meska(X).

Można dopasować
Ojciec(zeus, ares). X:=zeus, U:=ares, Y:=ares
Ojciec(zeus, V). X:=zeus, U:=V, Y:=V <- to jest MGU