Fizyka ciała stałego

SIEĆ KRYSTALICZNA CIAŁ

STAŁYCH

Wykład – 9 -

2

 

Terminy zaliczeń poprawkowych w semestrze letnim
2010/11
o 28 marzec

o 18 kwiecień

o 16 maj

o 13 czerwiec

Przypominam, że

Przypominam, że

 na wszystkie kolejne terminy poprawkowe
obowiązują karty zie-lone.

 Do zaliczenia można podejść po zaliczeniu ćwiczeń
rachunko-wych

 zaliczona w terminie zerowym teoria a nie wpisana

zaliczona w terminie zerowym teoria a nie wpisana

do indeksu została skreślona

do indeksu została skreślona

Zaliczenia zaczynają się o
godz. 15
sala 2 bud 5

W tym semestrze

Zaliczenie przedmiotu jest w formie egzaminu

> Aby móc przystąpić do egzaminu trzeba mieć
zaliczone ćwicze-nia i laboratoria. Pozytywne oceny
muszą być wpisane do karty o-cen i do indeksu.

Egzamin składa się z dwóch części:

- Pisemnej student pisze odpowiedź na 3 pytania z
zestawu 4-ech

- Ustnej odpowiedzi uzupełniające na pytania z
zestawu pisemne-go + inne pytania.

Wszyscy znamy budowę powłok elektronowych

atomu. Atomy, dzięki występującym między nimi siłom
przyciągania, mogą łączyć się w cząsteczki chemiczne
(molekuły) albo w ze-społy zawierające olbrzymie
ilości atomów, które w zależności od stanu skupienia
zaliczamy do

ciał stałych lub cieczy

. Przedmiotem

aktualnych naszych rozważań będą właściwości
elektronowe

ciał

stałych,

a

w

szczególności

półprzewodników, dlatego najpierw zaznajomimy się z
budową tych ciał.

Ciało stałe definiuje się jako ciało

odznaczające się stabilnością kryształu

. W

zależności od stopnia uporzą-dkowania struktury
wewnętrznej ciała stałe dzielimy na krysta-liczne i
amorficzne, czyli bezpostaciowe.

Jeśli położenia atomów wykazują okresowe
uporządko-wanie w przestrzeni (uporządkowanie
dalekiego zasię-gu) to takie ciało stałe nazywamy
ciałem krystalicznym lub kryształem

.

W przypadku gdy uporządkowanie występuje w

całej objętości kryształu, to taki kryształ nazywamy
monokryszta-łem.

Jeżeli natomiast prawidłowe uporządkowanie

występuje tylko wewnątrz pewnych obszarów zwanych
ziarnami

krystali-cznymi,

wówczas

mówimy

o

polikryształach. Zwykle wię-kszość występujących w
przyrodzie i otrzymanych sztucznie ciał krystalicznych
stanowią polikryształy.

Jedną z cech charakterystycznych kryształu jest

anizo-tropia jego właściwości polegająca na tym, że
kryształ wyka-zuje w różnych kierunkach różne
właściwości fizyczne.

W odróżnieniu od kryształów, ciecze i ciała

amorficzne (których typowym przykładem jest szkło)
nie mają prawidłowej struktury krystalicznej i nie
wykazują anizotropii właściwości. W ciałach tych
występuje tzw. uporządkowanie bliskiego zasięgu.

Ciała krystaliczne charakteryzują się ponadto

skokową zmianą właściwości przy przejściach z jednej
fazy do drugiej

. W ciałach amorficznych właściwie nie

istnieje granica między fazami (ciekłą i stałą). Z tego
powodu ciała amorficzne są często traktowane jako
przechłodzone ciecze.

W tym miejscu należy zaznaczyć, że niektóre

ciecze również charakteryzują się uporządkowaniem
cząsteczek. Związana z tym jest anizotropia ich
różnych właściwości fizycznych, mechanicznych,
optycznych, elektrycznych, magnetycznych i wielu
innych. Takie ciecze nazywamy ciekłymi kryształami.

Ciała stałe



to substancje o regularnej, przestrzennej budowie
krystali-cznej, czyli regularnym uporządkowaniu w
przestrzeni elementów tworzących ciało (atomów,
jonów, cząsteczek)



w zależności od stopnia uporządkowania struktury
wewnętrznej wyróżniamy ciała



krystaliczne (kryształ) gdy elementy uporządkowane są w
sposób okresowy tzw. uporządkowanie dalekiego zasięgu,
anizotropia



polikryształy – uporządkowanie wewnątrz obszarów (ziaren)



amorficzne (bezpostaciowe) – uporządkowanie bliskiego zasięgu



ciekłe kryształy – ciecze anizotropowe, charakteryzują
się uporządkowanym ułożeniem cząsteczek

SIEĆ KRYSTALICZNA I
UKŁADY
KRYSTALOGRAFICZNE

Idealny nieskończony kryształ jest strukturą
utworzoną

przez

regularne

powtarzanie

w

przestrzeni

identycznych

elementów.

Ten

charakterystyczny dla danego ciała układ
atomów nazywamy jego siecią krystaliczną

.

Najmniejszy

pojedynczy

element

sieci,

powtarzający się periodycznie w trzech wymiarach
przestrzeni,

nazywamy

bazą

tej

sieci

.

W

najprostszym przypadku baza jest utwo-rzona z
jednego atomu danego pierwiastka. Na ogół zawie-
ra ona 2 lub więcej atomów, przy czym mogą to być
atomy tego samego lub różnych pierwiastków.

Grupy atomów stanowiące bazę są ustawione

w kry-sztale wg określonej sieci przestrzennej, którą
nazywamy siecią translacyjną lub siecią punktową.

Jest ona utworzona z punktów nazywanych węzłami
sieci.

Na rysunku w celu ułatwienia zobrazowania

pokazano sieć dwuwymiarową. Można jednak z
łatwością

rozszerzyć

rozważania

na

sieć

trójwymiarową.

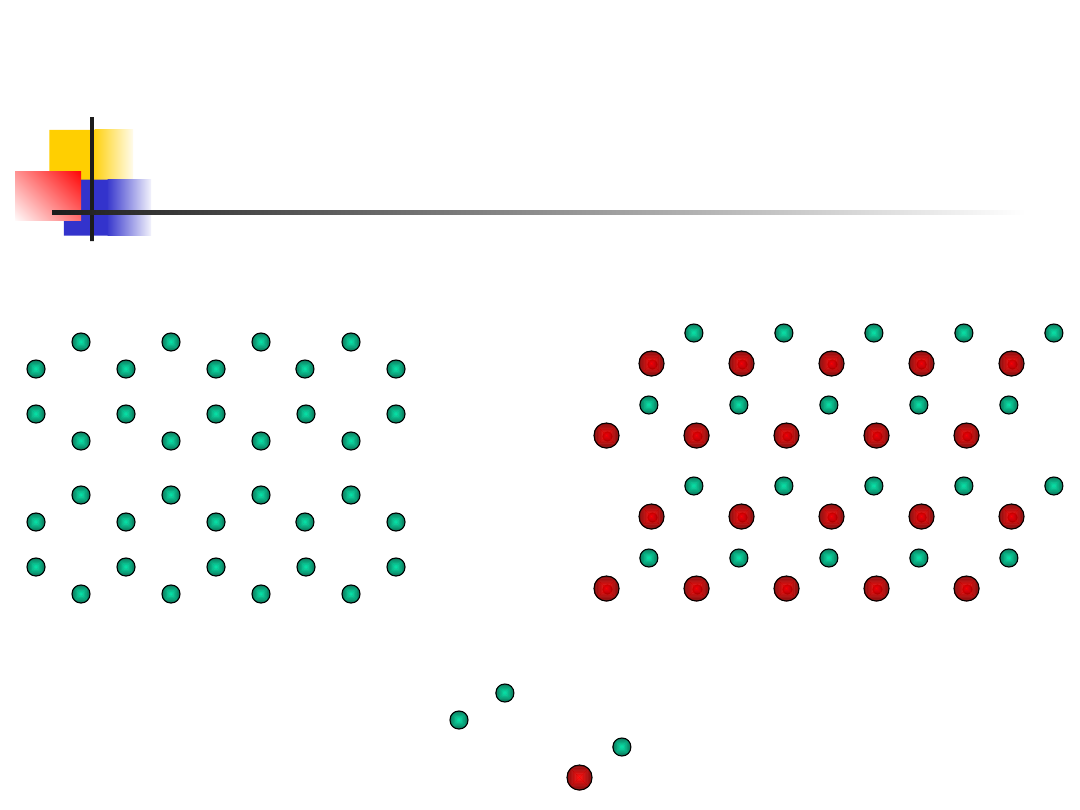
Przykład sieci
dwuwymiarowej

sieć krystaliczna

sieć translacyjna

baza

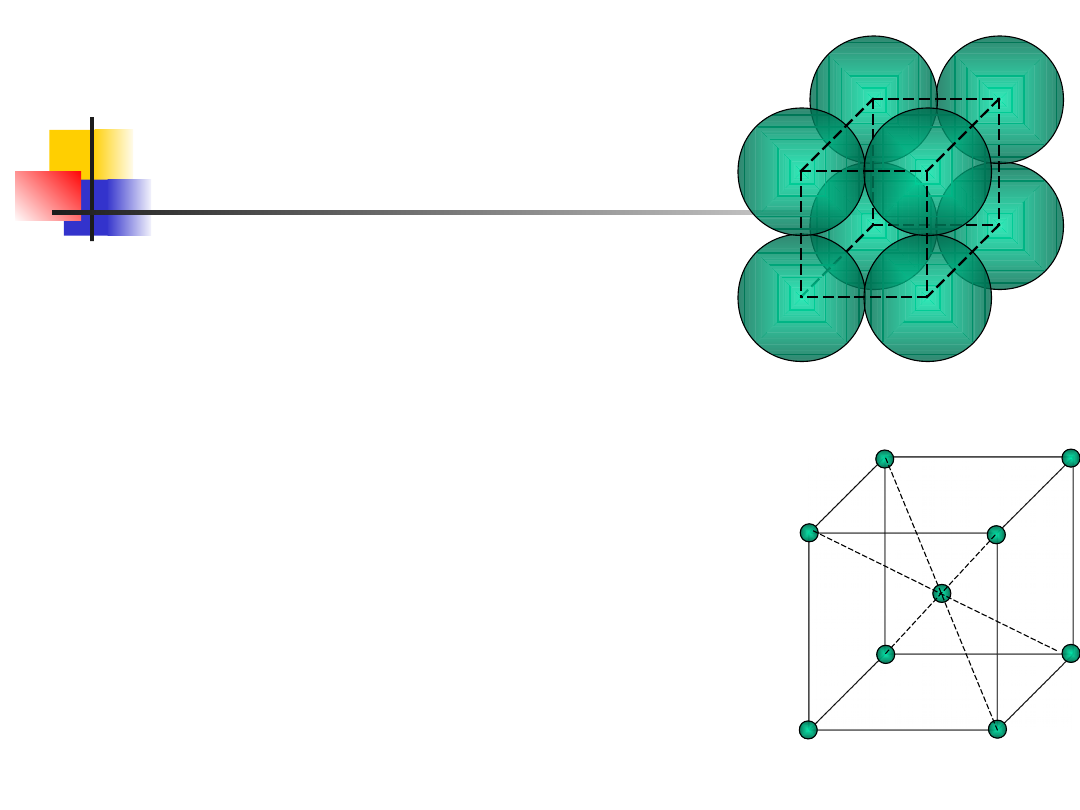
Sieć krystaliczna



sieć krystaliczna określa charakter okresowego

uporządkowania w przestrzeni powtarzających

się elementów strukturalnych kryształu



baza sieci to najmniejszy powtarzający się

element strukturalny:



pojedynczy atom



grupy atomów



jon



molekuła



sieć

translacyjna

to

sieć

przestrzenna

utworzona przez punkty bazy – węzły sieci

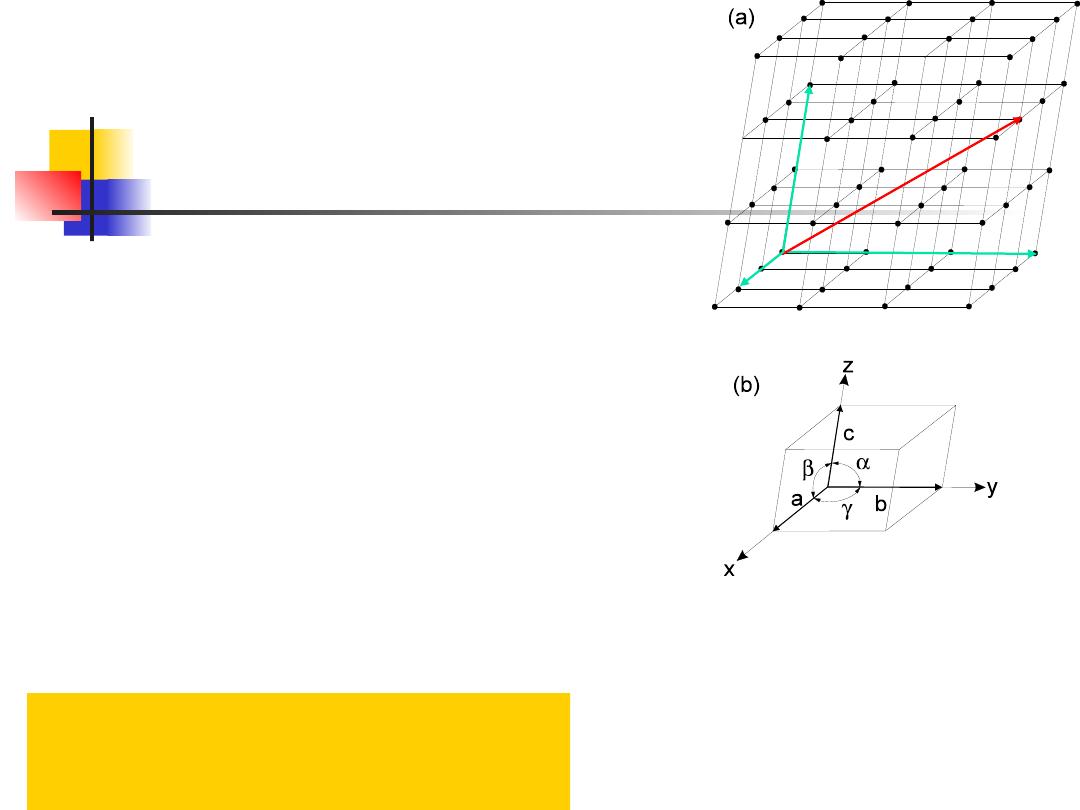
Symetria translacyjna sieci wyraża się tym, że
położenie dowolnego węzła w stosunku do węzła
przyjętego za punkt odniesienia, może być
określone za pomocą wektora translacji

gdzie: m, n, p – liczby całkowite, zaś

–

odpowiednio

dobrane

wektory,

nazywane

elementarnymi wektorami translacji.

Długości tych

wektorów, tzn. liczby a, b, c nazywamy stałymi
sieci.

Równoległościan zbudowany na elementarnych
wektorach

translacji

nazywamy

komórką

elementarną prostą lub pry-mitywną. Jak widać z
rys.,

sieć

przestrzenną

kryształu

sta-nowi

nieskończony

zbiór

jednakowych

komórek

ułożonych

równolegle

względem

siebie

i

wypełniających całą przestrzeń.

c

p

b

n

a

m

R















c

,

b

,

a







Sieć Bravais’go

Trójwymiarowa sieć translacyjna Bravais’go
jest zbiorem wszystkich tych punktów
przestrzeni, których wektory wodzące
mają postać:

c

p

b

n

a

m

R















gdzie m, n, p dowolne liczby całkowite

dowolna trójka wektorów nie
leżących w jednej płaszczyźnie,
wektory te generują sieć (sieć jest
rozpięta na tych wektorach)

c

b

a





 ,

,

długości tych wektorów tzn.
liczby a, b i c nazywamy
stałymi sieci

Równoległościan
zbudowany na
elementarnych wektorach
translacji nazywamy
komórką elementarną

c

b

a

R









2

3

2







Równoległościan zbudowany na elementarnych
wektorach

translacji

nazywamy

komórką

elementarną prostą lub pry-mitywną. Jak widać z
rys.,

sieć

przestrzenną

kryształu

sta-nowi

nieskończony zbiór jednakowych komórek ułożonych
równolegle względem siebie i wypełniających całą
prze-strzeń.

W komórce prostej węzły sieci przestrzennej

znajdują się tylko w narożach, a zatem na jedną
komórkę przypada jeden węzeł. W niektórych
rodzajach sieci wygodniej jest posługiwać się
komórkami o większych rozmiarach, ale za to o
niższym stopniu symetrii niż komórka prosta. Są to
tzw. komórki złożone, które oprócz węzłów w
narożach zawierają dodatkowe węzły. Sieci takie
nazywamy sieciami centrowanymi.

Komórka elementarna jest scharakteryzowana

przez tzw. parametry sieci, tzn. długości jej krawędzi
a, b, c oraz kąty α, β, γ, zawarte między tymi
krawędziami. Kierunki wyznaczone przez wektory

nazywamy osiami kry-stalograficznymi.

c

,

b

,







a

Właściwości sieci
krystalicznej



komórka prosta – węzły tylko

w narożach (jeden węzeł na komórkę)



komórki złożone – sieci centrowane



komórka elementarna – odzwierciedla symetrię

sieci



stałe sieci i kąty to tzw. parametry sieci



liczba atomów w komórce elementarnej



liczba koordynacyjna – liczba punktów

sieci leżących najbliżej danego węzła



współczynnik upakowania k



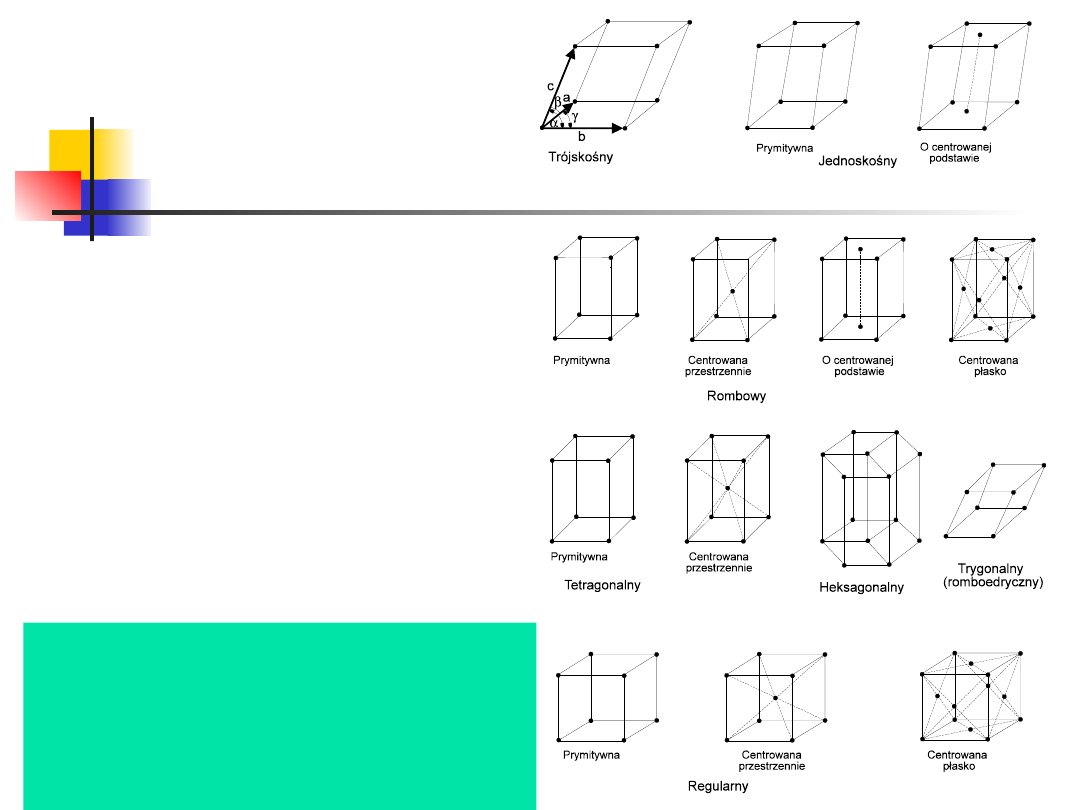
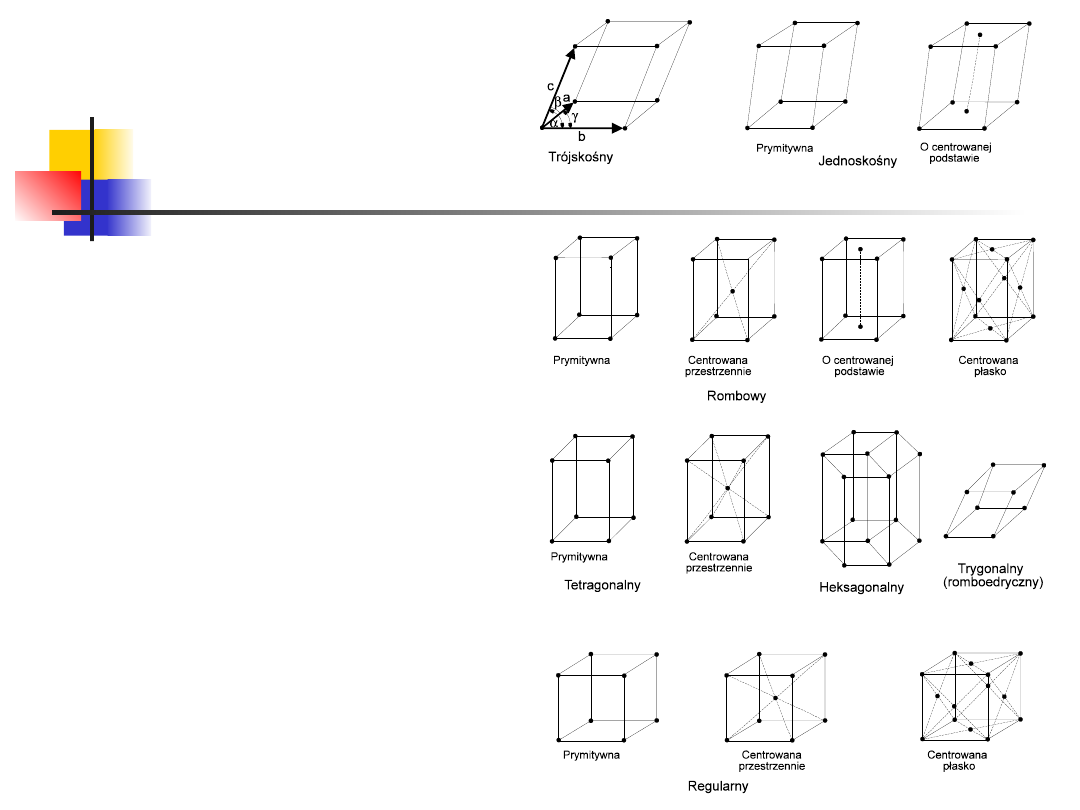
7 układów krystalograficznych:

regularny,

tetragonalny, rombowy, jednoskośny, trójskośny,

heksagonalny i trygonalny

a=b=c, ===90

  

 

 

a b c

 



 


 

90

90

o

o

a b c

  

  

 

90

o

a b c

  

  

 

90

o

a b c

  

  

 

90

o

a b c

  

  

 

90

o

a b c

krystalograficzne
układy

W zależności od stopnia symetrii,

sieci Bravais’go dzieli się na

siedem układów

krystalograficznych:

regularny,

tetragonalny,

rombowy,

jednoskośny,

trójskośny,

heksagonalny i trygonalny

Wśród nich wyróżnia się 14
typów sieci krystalograficznych
o różnym centrowaniu:
przestrzennym,
powierzchniowym i w
podstawach.

W zależności od stosunku długości i

wzaje-mnej orientacji krawędzi komórki
elementarnej, istnieje 14 typów sieci
krystalograficznych, tzw. sieci Bravais’go.

W zależności od stopnia symetrii, sieci

Bravais’go dzieli się na siedem układów
krystalograficznych: regu-larny, heksagonalny,
tetragonalny,

trygonalny

(rombo-edryczny),

rombowy, jednoskośny i trójskośny

W

układzie

regularnym,

komórką

elementarną jest sześcian. Występują trzy rodzaje
sieci:

prosta,

centrowa-na

przestrzennie

i

centrowana powierzchniowo.

Elementarna

komórka

układu

heksagonalnego

ma

postać

prostego

graniastosłupa, którego podstawą jest romb o
kątach 60 i 120. Trzy takie komórki tworzą gra-

niastosłup heksagonalny, który bardziej oddaje
symetrię układu niż komórka prosta.

W

układzie

tetragonalnym

komórką

elementarną jest prostopadłościan o podstawie
kwadratowej. Występują dwa rodzaje sieci: prosta i
centrowana przestrzennie.

W

układzie

trygonalnym

komórka

elementarna ma postać romboedru (w związku z
tym układ ten nazywa się romboedrycznym). Kąty
α, β, γ, są jednakowe, różne od 90 i mniejsze od

120.

W

układzie

jednoskośnym

komórka

elementarna

ma

postać

pochyłego

równoległościanu, którego dwie pary ścian są
prostokątami, a dwie ściany są równoległobokami.
W układzie tym występują dwie sieci: prosta i z
centro-waną podstawą.

Komórka elementarna układu trójskośnego

jest równoległościanem, którego krawędzie a, b i c i
kąty α, β, γ są różne.

  

 

 

a b c

 



 


 

90

90

o

o

a b c

  

  

 

90

o

a b c

  

  

 

90

o

a b c

  

  

 

90

o

a b c

  

  

 

90

o

a b c

krystalograficzne
układy

W zależności od stopnia symetrii,

sieci Bravais’go dzieli się na

siedem układów

krystalograficznych:

regularny,

tetragonalny,

rombowy,

jednoskośny,

trójskośny,

heksagonalny i trygonalny

OZNACZENIE WĘZŁÓW,
KIERUNKÓW I PŁASZCZYZN W
KRYSZTALE

Wskaźniki węzłów

Położenie dowolnego węzła sieci, względem obranego
począ-tku układu współrzędnych, jest określane
poprzez podanie trzech jego współrzędnych x, y, z,
które można wyrazić nastę-pująco

x =

ma, y = nb,

z = pc,

gdzie a, b, c – długości krawędzi komórki elementarnej;
m, n, p – liczby całkowite.

Jeśli za jednostkę

długości przyjąć stałe a, b, c to współrzędnymi węzła
będą liczby m, n, p. Liczby te nazywają się
wskaźnikami węzła i są zapisane następująco: mnp
Dla wskaźników ujemnych

znak minus umieszcza się

nad wskaźnikiem

.

Jeżeli węzeł znajduje się wewnątrz

komórki, to liczby m, n i p będą liczbami ułamkowymi

.

Wskaźniki kierunków

Wskaźniki kierunków w krysztale stanowią zbiór

najmniejszych liczb u, v, w, które mają się do siebie
tak, jak rzuty wektora równoległego do danego
kierunku na osie krystalograficzne. Wskaźniki zapisuje
się w nawiasach kwadratowych [u,v,w]. Symbol prostej
przechodzącej przez dwa punkty leżące na tej prostej
otrzymujemy w ten sposób, że odejmujemy od siebie
współrzędne tych punktów i otrzymane liczby
sprowadzamy

do

liczb

całkowitych.

Kierunki

równoległe mają wskaźniki identyczne.

Wskaźniki płaszczyzn

Położenie płaszczyzn jest określone przez podanie
trzech odcin-ków A, B, C, które płaszczyzna odcina na
osiach sieci. Wskaźniki płaszczyzn znajdujemy w
następujący sposób. Odcinki A, B, C wyrażamy w
jednostkach osiowych i piszemy odwrotności tych
odcinków 1/A, 1/B, 1/C. Otrzymane ułamki sprowadzamy
do najmniejszego wspólnego mianownika D. Liczby
całkowite

A

D

h

B

D

k 

C

D

l 

są wskaźnikami płaszczyzny i zapisujemy je w postaci
(hkl).

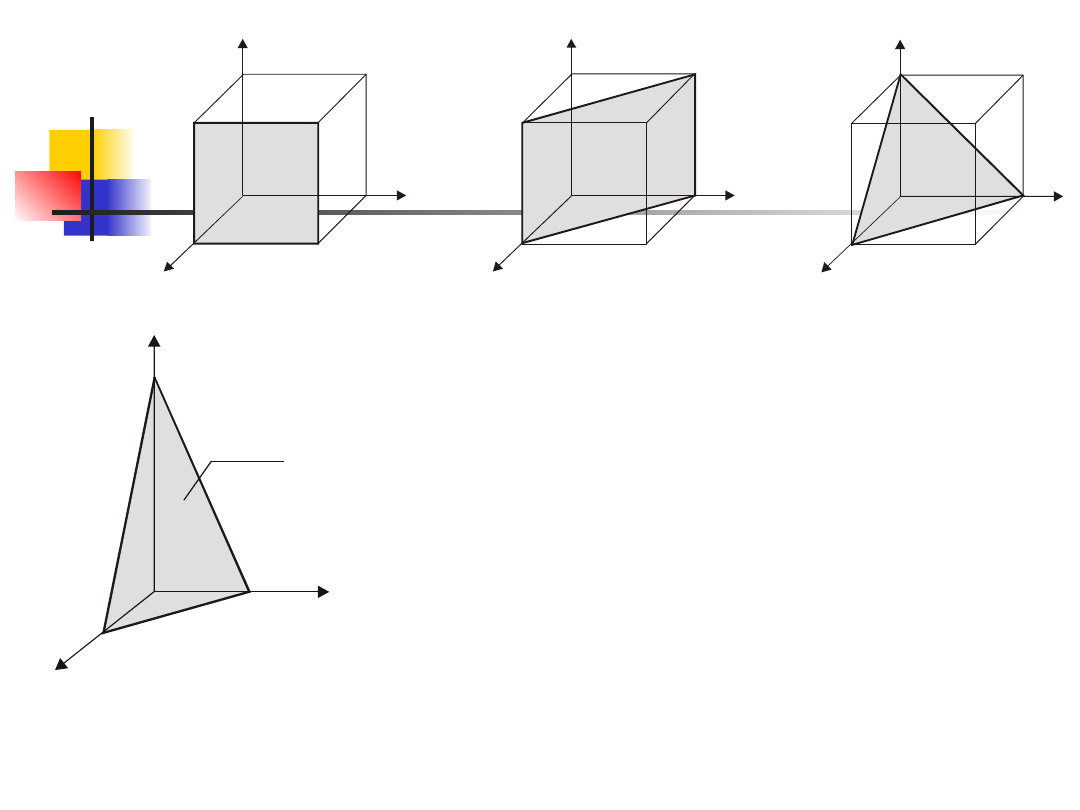
y

x

z

6 a

( 3 2 1 )

2 a

3 a

A

B

C

O

Płaszczyzna (321).

y

y

y

z

z

z

x

x

x

( 1 0 0 ) ( 1 1 0 ) ( 1 1 1 )

Przykłady symboli płaszczyzn
sieciowych w sieci regularnej.
 

PROSTE STRUKTURY
KRYSTALICZNE

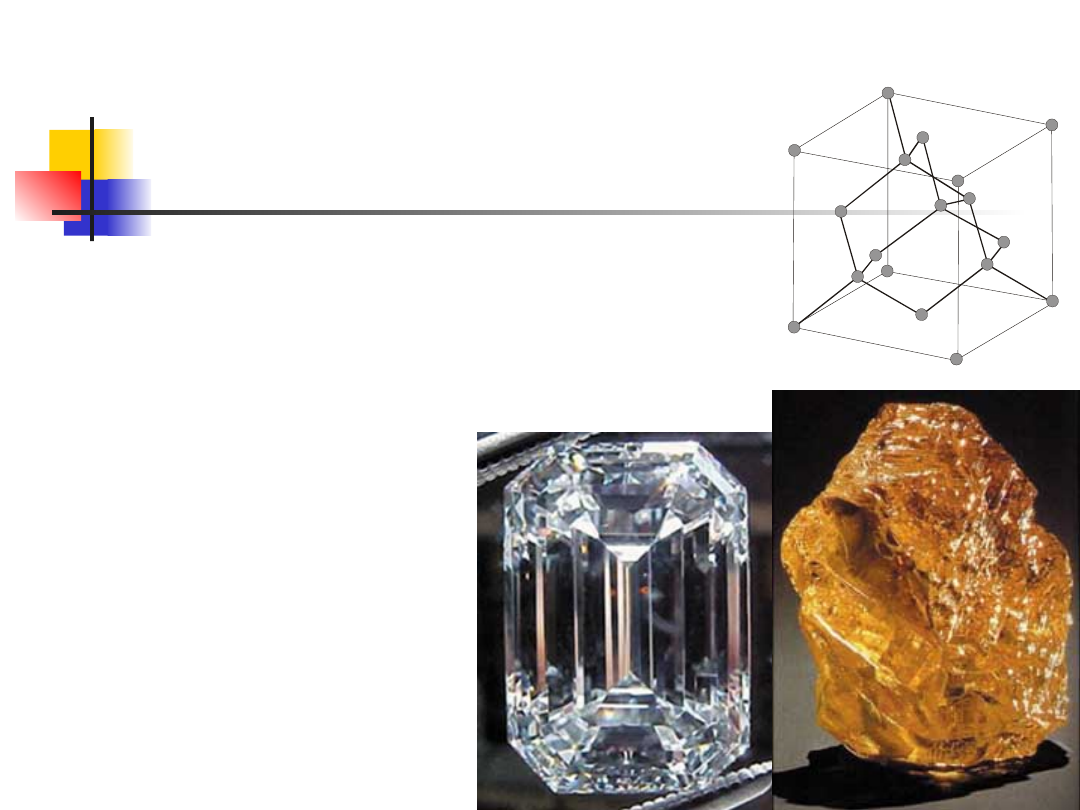
Typowe struktury krystaliczne

struktura diamentu

płasko centrowana sieć
regularna
z dwupunktową bazą (dwa
atomy węgla przesunięte
wzdłuż głównej przekątnej o ¼
długości),
liczba koordynacyjna 4

pierwiastki C (diament),
Si (krzem), Ge (german)

C

Struktura diamentu jest strukturą regularną,
będącą kombinacją dwóch sieci regularnych
powierzchniowo

centrowanych,

przesuniętych

względem siebie o jedną czwartą głównej
przekątnej.

Rys. przedstawia strukturę diamentu.

Każdy atom ma czterech najbliższych sąsiadów. W
komórce elementarnej znajduje się osiem atomów,
a odległość między nimi wynosi
gdzie a jest długością krawędzi komórki
elementarnej. We wszystkich węzłach sieci
znajdują się atomy tego samego rodzaju. W
strukturze tej krystalizuje między innymi diament,
krzem i german.

4

3/

a

Jeżeli dwie przecinające się sieci regularne centrowane
powierz-chniowo obsadzone są przez atomy różnych
pierwiastków, po-wstaje nowa struktura zwana strukturą
siarczku cynku. W stru-kturze tej krystalizują między
innymi GaAs, CuCl oraz ZnS od którego pochodzi nazwa
struktury.

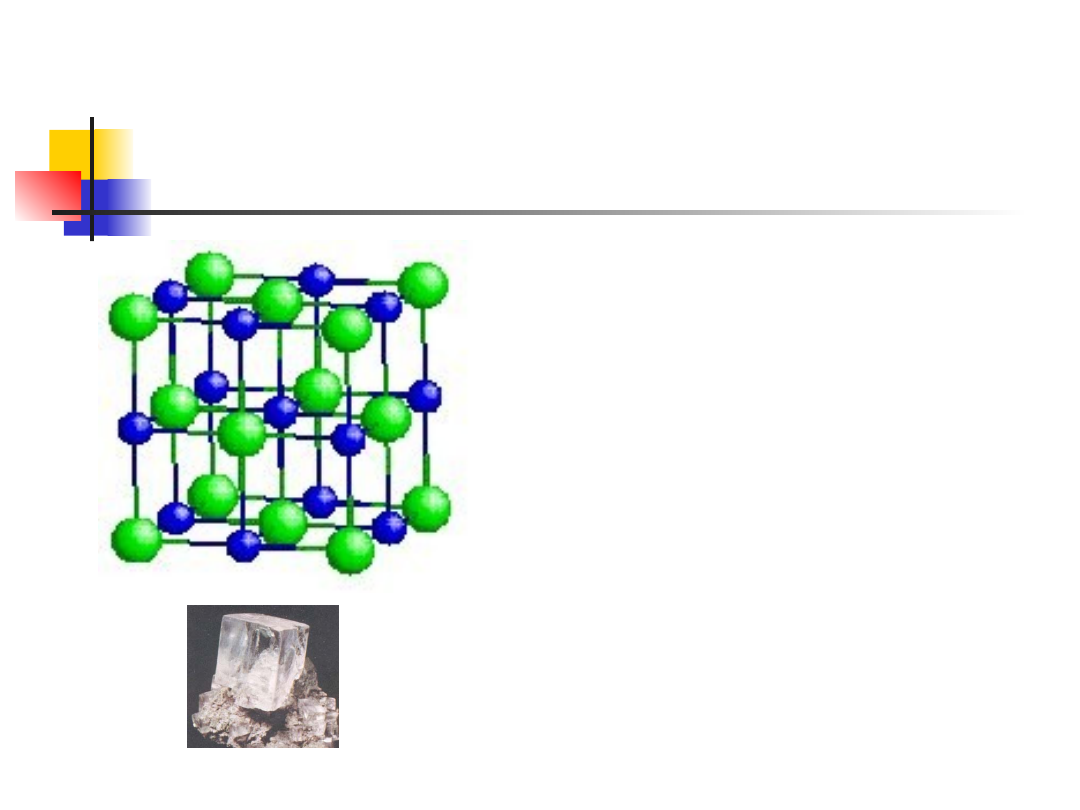
Typowe struktury krystaliczne

struktura chlorku sodu

Chlorek sodu (NaCl) –
struktura jonowa – sieć
regularna, centrowana
powierzchniowo, z bazą
dwupunktową z jonu Na i
jonu Cl przesuniętego o ½
głównej przekątnej (dwie
podsieci: sodu i chloru)

liczba koordynacyjna 6

inne związki: LiF, KCl, PbS

Na

+

Cl

-

Na rys. przedstawiono strukturę chlorku sodu. W
elementar-nej komórce znajdują się cztery jony Na i
cztery jony Cl, czyli cztery cząsteczki NaCl. Każdy jon
jednego rodzaju jest oto-czony sześcioma jonami
drugiego rodzaju, a w związku z czym liczba
koordynacyjna równa się 6.

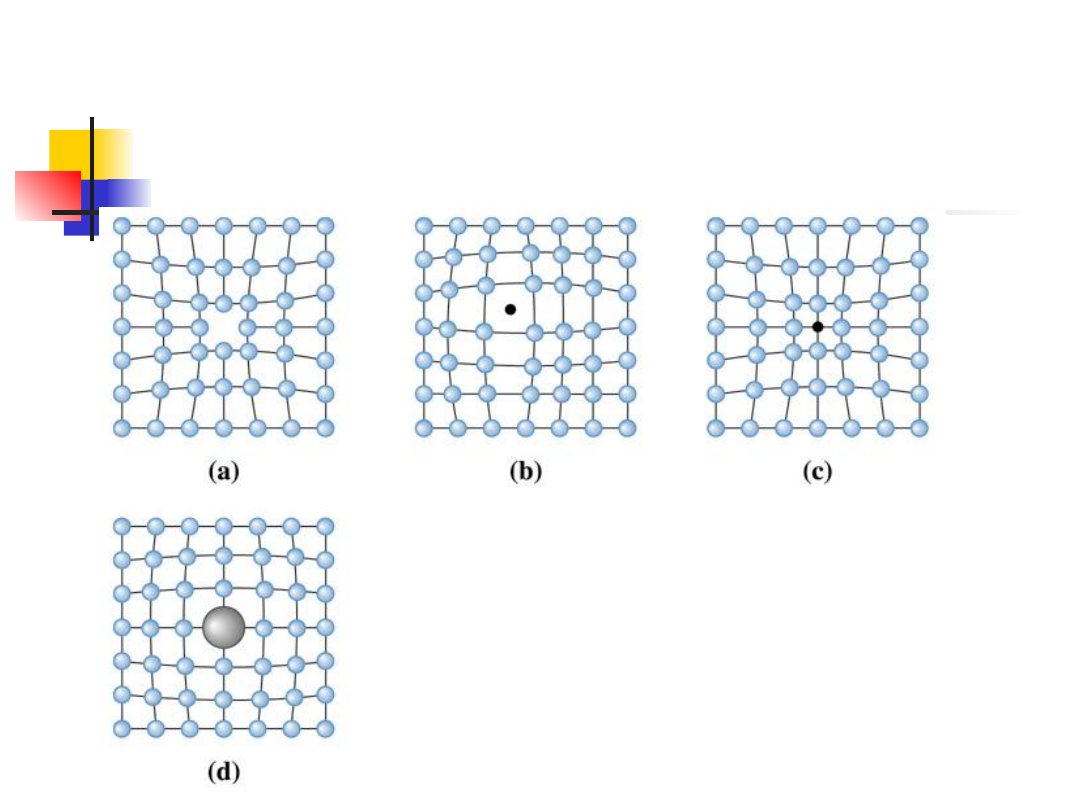
DEFEKTY SIECI
KRYSTALICZNEJ

W rzeczywistych kryształach występują odstępstwa
od ide-alnej struktury krystalicznej. Oznacza to, że
prawidłowość rozmieszczenia atomów jest w pewien
sposób zaburzona. Odchylenia od idealnej struktury
nazywamy niedoskonało-ściami lub defektami.

Spośród różnych defektów sieci, najważniejsze

są tzw. defekty punktowe. Defektami punktowymi
mogą być: puste węzły sieci (luki), atomy
międzywęzłowe oraz domie-szki chemiczne.

Najprostszym defektem jest
lu-ka w sieci, zwana też
defektem

Schottky'ego,

która

jest

wywo-łana

brakiem atomu lub jonu w
węźle sieci

Luki występują we wszystkich kryształach. Energia Ev
potrzebna do wytworzenia luki wynosi zwykle około 1 eV.
Ponieważ energia ta jest znacznie większa od średniej
energii drgań cieplnych atomów, wnioskujemy, że tylko
niewielka ilość atomów na skutek drgań będzie mogła
wyrwać się z sieci i zająć miejsce na powierzchni
kryształu. Można wykazać, że w temperaturze T
koncentracja luk wyraża się wzorem





kT

/

E

exp

n

n

v

v





Defekt Schottky'ego można sobie wyobrazić jako
prze-mieszczenie atomu z węzła sieci leżącego w
głębi kry-ształu do węzła leżącego na jego
powierzchni. Istnienie defektów Schottky'ego
powoduje

zmniejszenie

gęstości

kryształu

(wzrasta objętość przy niezmienionej masie).

gdzie n jest koncentracją atomów, Ev – energią aktywacji
potrze-bną

do

wytworzenia

luki.

Ze

wzrostem

temperatury liczba luk sil-nie wzrasta i w pobliżu
temperatury topnienia wynosi około 0.1% W temp.
pokojowej ilość luk wynosi zaledwie 10

–10

%.

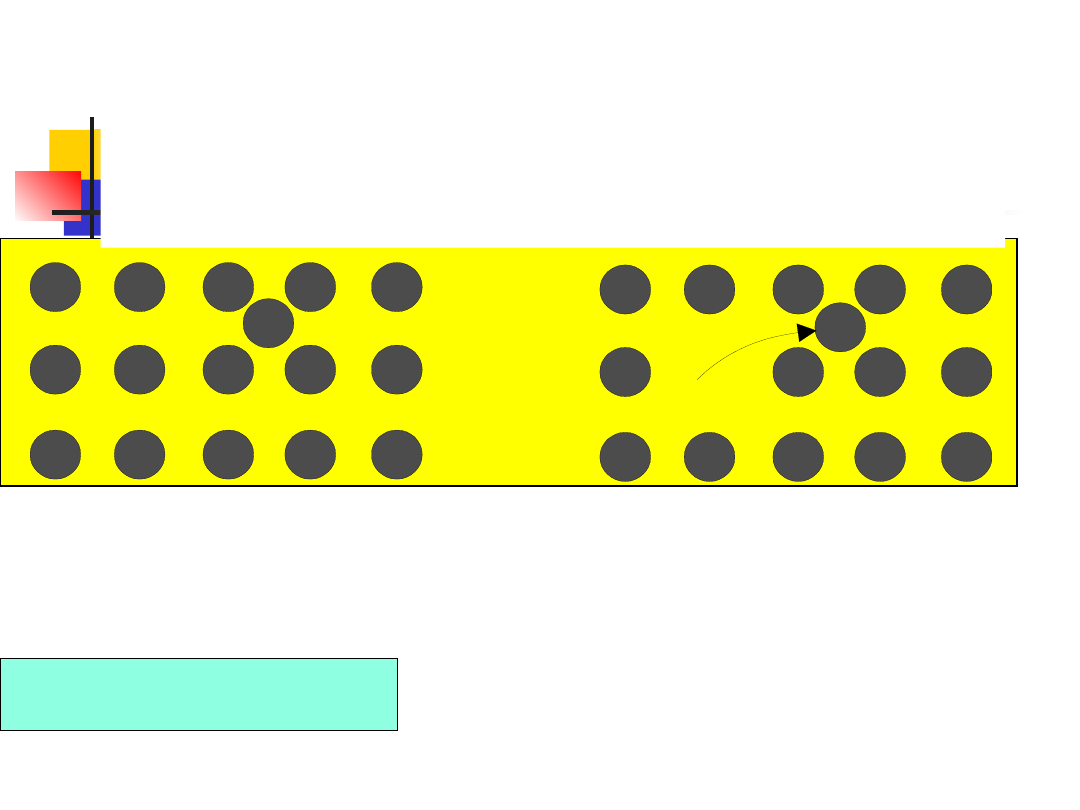
Innym rodzajem defektów punktowych są atomy
między-węzłowe, czyli dodatkowe atomy nie
zajmujące węzłów sieci. Atom może też zająć
położenie międzywęzłowe przeskakując z węzła
sieci i pozostawiając za sobą lukę. Oba rodzaje
tych defektów przedstawiono na rys.

Obliczenia wskazują, że równowagowa koncentracja
atomów międzywęzłowych może być określona za
pomocą następu-jącej zależności





kT

/

E

exp

kn

n

i

i





gdzie jest energią aktywacji potrzebną
do

wy-tworzenia

atomu

międzywęzłowego, n – liczbą węzłów w
jednostce objętości, k – liczbą całko-witą
(na ogół bliską 1) określającą liczbę rów-
noważnych położeń międzywęzłowych
wokół atomu w węźle.

Energia E

i

jest większa od energii E

v

, dlatego

zwy-kle koncentracja atomów międzywęzłowych
jest znacznie mniejsza niż koncentracja luk.

Luki i atomy międzywęzłowe nie pozostają trwale
w miej-scach gdzie zostały wytworzone, lecz
przemieszczają się w krysztale na skutek dyfuzji.

Dyfuzja

jest

procesem

samorzutnym

prowadzącym do wyrównania rozkładu koncentracji
defektów

punktowych

wsku-tek

ich

nieuporządkowanych ruchów cieplnych. Ruchliwość ato-
mów międzywęzłowych jest na ogół większa niż
ruchliwość luk.

Oprócz drgań mogą istnieć jeszcze inne powody

występowania defektów w kryształach. Wówczas ich
ilość przewyższa wartości równowagowe dla danej
temperatury określone powyższymi wzorami.

Inne

sposoby

wytwarzania

defektów

to:

gwałtowne

ochłodzenie

kryształu,

obróbka

plastyczna,

bombardowanie

kryształu

wysokoenergetycznymi

naładowanymi cząstkami.

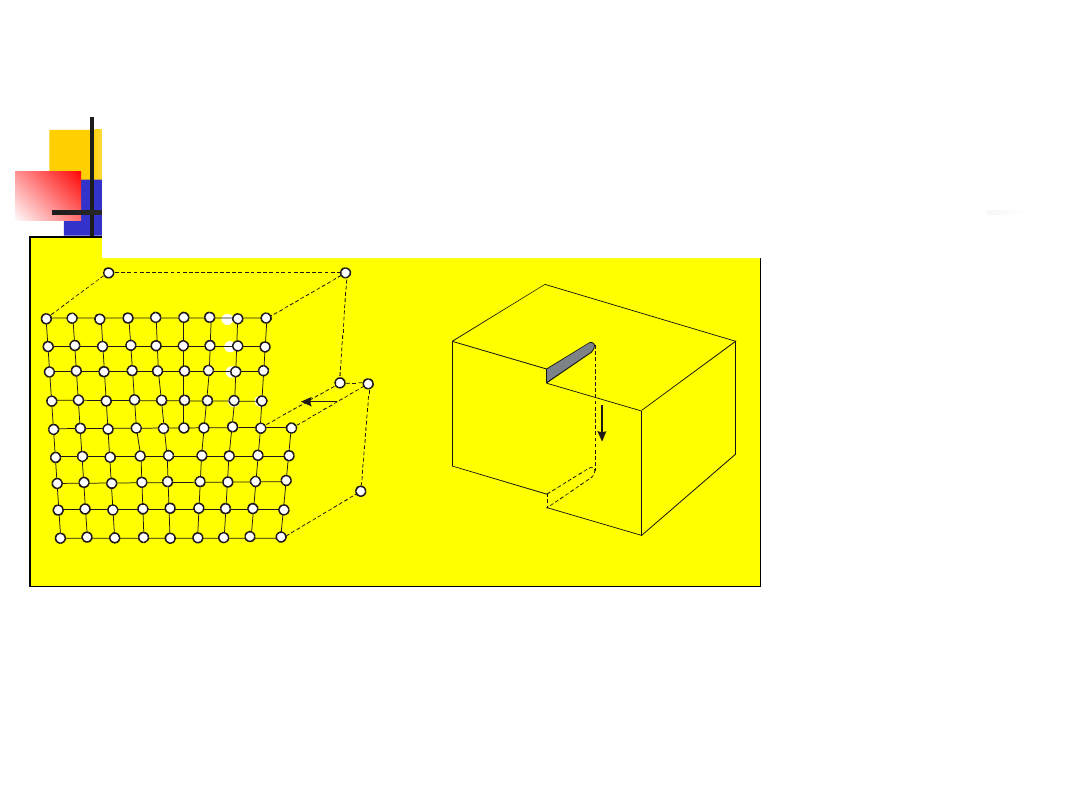
Oprócz defektów punktowych dużą rolę w fizyce
ciała stałego (szczególnie półprzewodników)
odgrywają

defekty liniowe, zwane dyslokacjami.

Wśród

nich

wyróżniamy

dyslokacje

krawędziowe i śrubowe.

( a ) ( b )

c

Dyslokacja

krawędziowa

jest

najprostszym

rodzajem dys-lokacjom polegającym na tym, że w
pewnej płaszczyźnie sieciowej ciągłość sieci urywa
się wzdłuż linii (krawędzi) oznaczonej na rys. a
symbolem c. To zaburzenie struktury można sobie
wyobrazić jako wynik ”wsunięcia” półpłaszczyzny
sieciowej do jednej części kryształu. Strzałka
wskazuje kierunek, w którym górna część sieci
krystalicznej została przesunięta w stosunku do
dolnej.

Dyslokacja

śrubowa

oznacza

granicę

między

przesuniętą a nie-przesuniętą częścią kryształu.
Granica ta biegnie równolegle do kierunku poślizgu; a
nie prostopadle, jak to zachodzi w przypa-dku dyslokacji
krawędziowej. Można sobie wyobrazić, że dyslo-kacja
śrubowa powstaje przy częściowym nacięciu kryształu
no-żem i przesunięciu części naciętej o jeden odstęp
atomowy równolegle do krawędzi cięcia. Dyslokacja
śrubowa przekształca kolejne płaszczyzny atomowe w
powierzchnie śrubowe, z czego wywodzi się nazwa tej
dyslokacji.

Bardzo poważnym defektem strukturalnym jest
powie-rzchnia kryształu

na której raptownie

urywa się periodyczna struktura sieci krystalicznej.
Ponadto powierzchnia kryształu jest narażona na
oddziaływanie

zewnętrznego

otoczenia.

Na

powierzchni gromadzi się (zostają zaabsorbowane)
znaczne ilości obcych atomów.

Defekty sieci krystalicznej, a szczególnie obce
atomy, w zasadniczy sposób wpływają na
właściwości fizyczne, zwłaszcza elektryczne i
optyczne ciał stałych. Występują one w każdym,
nawet najbardziej czystym krysztale. Współczesne
sposoby oczyszczania nie pozwalają na uzy-skanie
substancji zawierających mniej niż 10

–9

% domie-

szek, tzn. około 10

17

atomów domieszkowych w 1

m

3

.

Najbardziej czułe na obce domieszki są półprzewodniki

,

w któ-rych wprowadzenie nawet bardzo małych ilości
pewnych pier-wiastków (np. 1 atom na miliard atomów
własnych) może spo-wodować wzrost przewodności
elektrycznej o kilka rzędów wielkości. W celu więc
osiągnięcia

określonych

właściwości

fizycznych

półprzewodników

stosuje

się

domieszkowanie

kryształów.

(c

) 2

0

0

3

B

ro

o

k

s/

C

o

le

P

u

b

lis

h

in

g

/

T

h

o

m

so

n

L

e

a

rn

in

g

Defekty punktowe

DRGANIA SIECI
KRYSTALICZNEJ

Rozpatrując sieć krystaliczną zakładaliśmy, że
atomy są nieruchome, utrzymywane przez
oddziaływania międzya-tomowe. W rzeczywistości
atomy wykonują drgania wokół swoich położeń
równowagi. Drgania te występują w każ-dej
temperaturze, nawet w temperaturze zera
bezwzglę-dnego jako tzw. drgania zerowe.
Amplituda drgań ciepl-nych nie przekracza 10

–11

m.

Z drganiami atomów związanych jest wiele

ważnych zaga-dnień, jak np. rozszerzalność cieplna i
przewodnictwo cieplne ciał stałych. Drgania cieplne
atomów są najważniejszą przyczyną występowania
oporu elektrycznego.

Ponieważ amplituda drgań cieplnych jest znacznie

mniej-sza od odległości międzyatomowych można w
pewnym przybli-żeniu przyjąć, że oddziaływanie między
atomami jest harmoni-czne, tzn. że siła oddziaływania
jest proporcjonalna do wychyle-nia.

Drgania każdego atomu naruszają równowagę
sąsie-dnich atomów, w wyniku czego rozciągają
się one na całą sieć w postaci fal sprężystych
rozchodzących się w krysztale we wszystkich
możliwych kierunkach. Taki ruch atomów w
postaci fali sprężystej nosi nazwę drgań nor-
malnych.

Fale

te

nazywamy

też

falami

sieciowymi.

Widmo częstotliwości drgań sieci obejmuje zakres od
zera do ponad 10

13

Hz. Fale sieciowe o najmniejszych

częstotliwościach są to dobrze nam znane fale
akustyczne.

Zamiast rozpatrywać drgania 3-wymiarowej sieci

krystali-cznej,

posłużymy

się

prostym

jednowymiarowym modelem w postaci periodycznego
łańcucha złożonego z oddziaływujących na siebie
atomów.

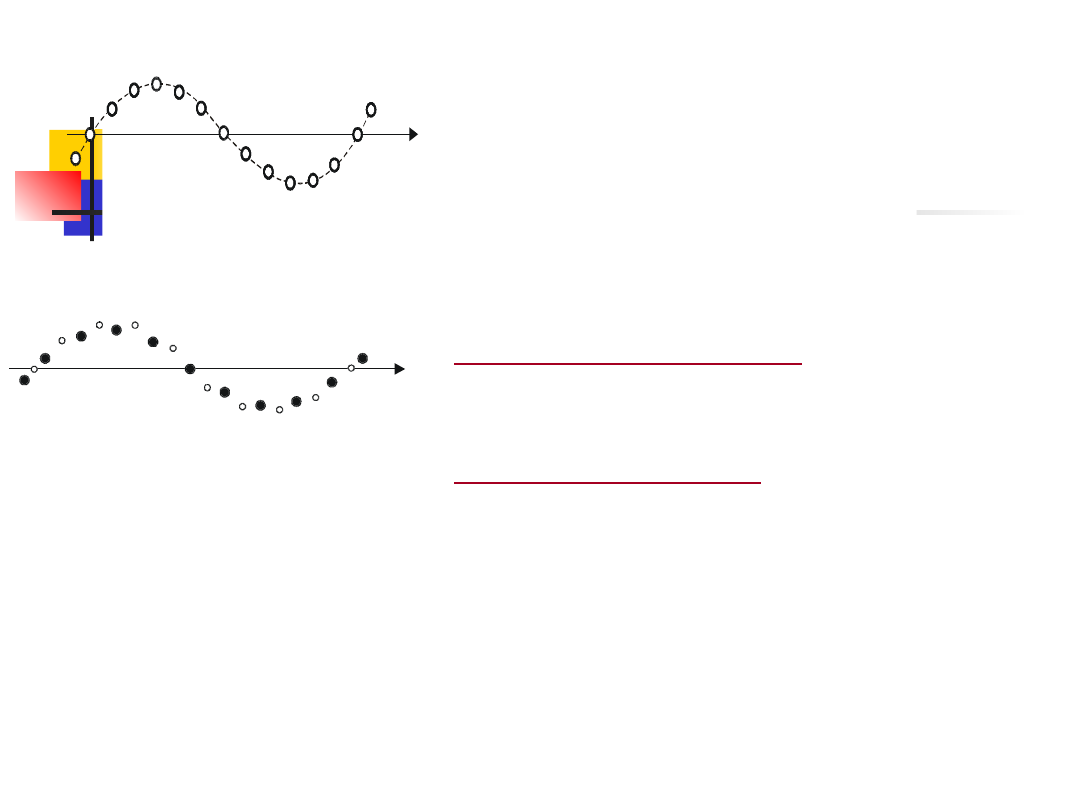
Jeden z możliwych sposobów
drgań

takiego

łańcucha

przedstawiono na rys. 14.12.
W łańcuchu zbudowanym nie z
jedne-go, lecz z dwóch rodzajów
atomów,

mogą

występować

następujące dwa typy drgań:

drgania akustyczne

(rys. 14.13a),

w których oba rodzaje atomów
drgają w tych samych fazach, oraz

drgania optyczne

(rys. 14.13b), w

któ-rych atomy różnych rodzajów
drgają w przeciwnych fazach.
Drgania tego typu mogą być
wywołane

zmiennym

polem

elektrycznym,

np.

falą

elektromagnety-czną

o

częstotliwości

zwykle

zakresu

podczerwieni – tym tłumaczy się
nazwa ”drgania

optyczne”.

x

x

x

( a )

( b )

Drgania akustyczne obejmują zakres mniejszych
częstotli-wości (od zera do pewnej częstotliwości
granicznej)

i

mniejszych

wartości

energii,

natomiast drgania optyczne obejmują zakres tylko
największych częstotliwości i są związane ze
stosunkowo wysokoenergetycznymi zjawiska-mi
elektro-magnetycznymi.

Rozważmy bliżej drgania akustyczne. Ponieważ

drgania każdego atomu można rozłożyć na dwa drgania
poprzeczne i je-dno podłużne, liczba drgań które mają
powstać w krysztale wy-nosi 3N, gdzie N jest całkowitą
liczbą atomów.

Mówiąc inaczej, w ciele stałym

propagują się trzy fale akustyczne: jedna
podłużna i dwie poprzeczne.

Fale te dochodzą do

powierzchni kryształu, odbijają się od niej i interferują z
falami nadbiegającymi tworząc układ fal stojących.
Oznacza to, że na całej długości kryształu L musi odłożyć
się całkowita liczba połówek długości fal

2



n

L 

Drgania sieci krystalicznej



atomy sieci krystalicznej wykonują drgania wokół swoich położeń

równowagi



drgania te występują nawet w T=0K



amplituda drgań (10

-11

m) jest dużo mniejsza od odległości

międzysieciowych, tak że można je traktować jako drgania

harmoniczne



rozszerzalność cieplna i przewodnictwo cieplne związane są z

drganiami atomów



drgania cieplne są przyczyną występowania oporu elektrycznego



drgania rozchodzą się w krysztale w postaci fal sprężystych

zwanych sieciowymi



ze względu na ograniczoność sieci krystalicznej energia tych

drgań jest skwantowana w postaci porcji zwanych fononami

WIĄZANIA ATOMÓW W
KRYSZTALE

Zrozumienie wielu procesów zachodzących w ciałach stałych
wyma-ga znajomości charakteru wiązań między atomami
występujących w tych ciałach.
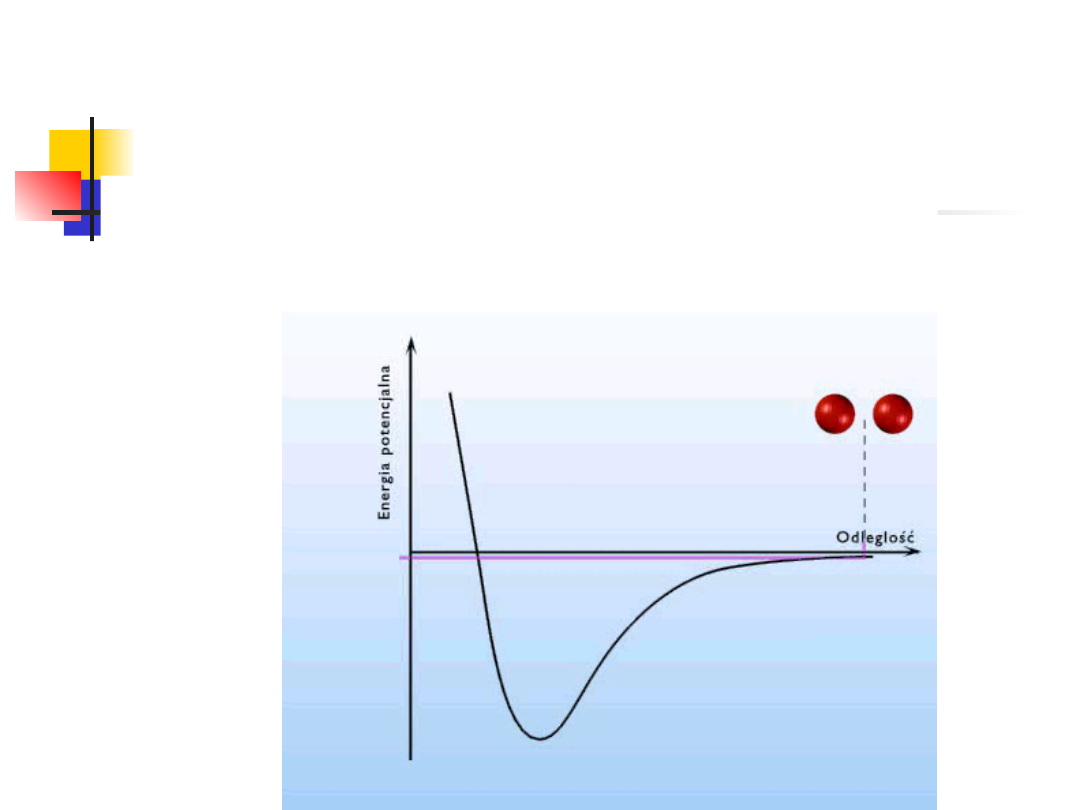
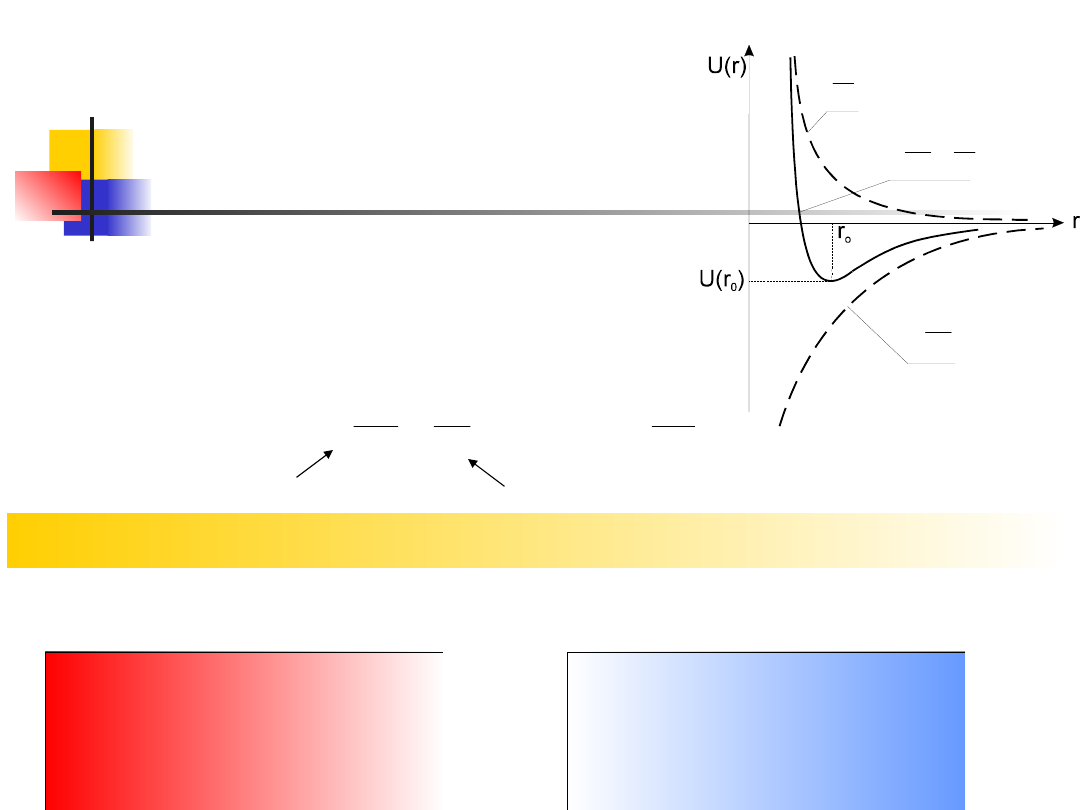
Istnienie ciał stałych świadczy o występowaniu sił
międzyatomowych, które dla dużych odległości są siłami
przyciągania, a dla małych odle-głości – siłami odpychania.
Przy odległościach międzyatomowych rzę-du 10

–10

m siły te

równoważą się

Charakter wiązań

B

r

n



A

r

m





A

r

B

r

m

n

 

n

m

r

B

r

A

r

U







Niezależnie od natury sił
międzyatomowych, przebieg energii
potencjalnej w funkcji odległości między
atomami ma podobną postać:

siły przyciągania

siły odpychania

Siły przyciągania są bardziej dalekozasięgowe więc n>m

W stanie równowagi trwałej dla r=r

o

energia osiąga

minimum

dr

dU

F





Siły odpychania
wynikają z
nakładania się jąder
atomowych

Siły przyciągania
mają charakter sił
elektromagnetyczny
ch

Rodzaje wiązań



wiązania jonowe



elektrostatyczne przyciąganie się ładunków



wiązania kowalencyjne



nakładanie się powłok elektronowych



wiązania metaliczne



oddziaływanie chmury elektronów z jądrami



wiązania molekularne



wiązania między cząsteczkowe siłami van der
Walsa

Natura sił działających między atomami i jonami jest
często podstawą klasyfikacji kryształów. Mamy więc
kryształy jono-we, kowalencyjne, metaliczne i
molekularne. Wymienione wyżej rodzaje wiązań
rzadko występują w czystej postaci.

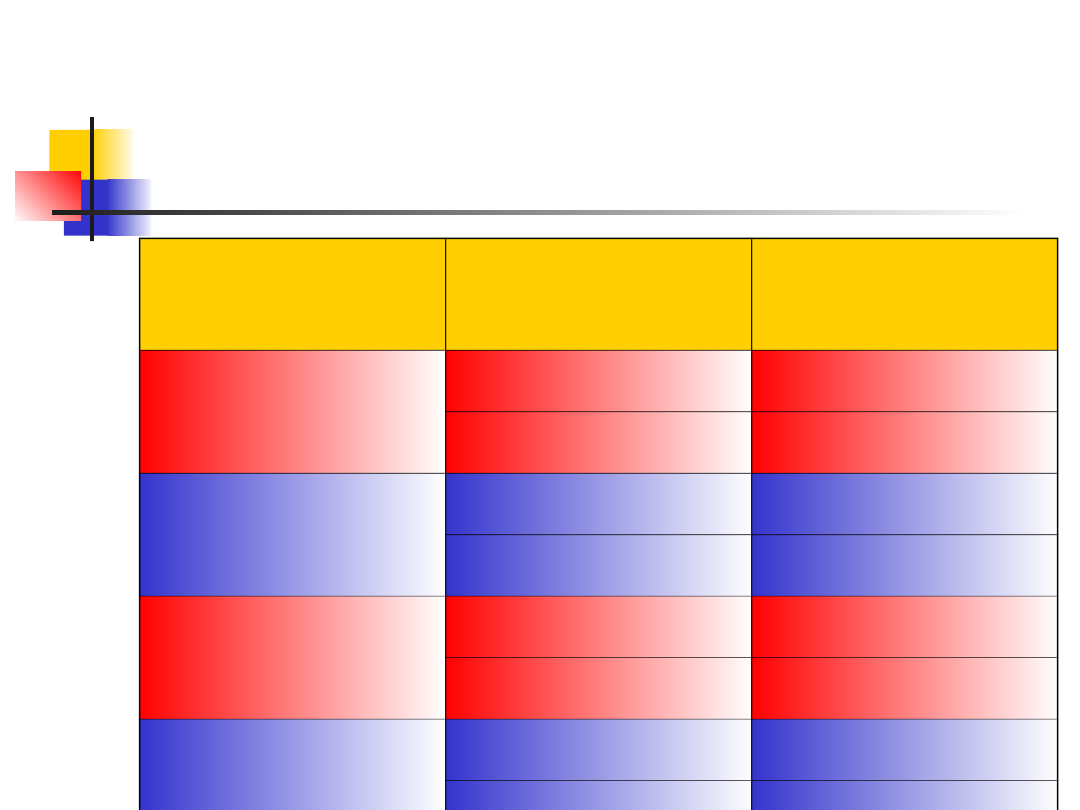
Miarą wielkości sił wiążących atomy w

krysztale jest energia wiązania, czyli minimalna
energia potrze-bna do rozdzielenia kryształu na
swobodne atomy

. Wyraża się ją w elektronowoltach

na atom lub w dżulach na mol. Energia ta zawiera się
w bardzo szerokich granicach od 0,02 eV/atom dla
neonu (temperatura topnienia –249C) do 8,9 eV/atom

dla wolframu (temperatura topnienia + 3370C). Dla

kryształów jonowych może być większa

Energia wiązania atomów

Typ wiązania

Przykłady

Energia

kJ/mol

jonowe

LiF

1014

NaCl

765

kowalencyjne

Ge

374

Si

448

metaliczne

Cu

338

Fe

393

molekularne

Ne

1,9

Kr

3,2

100kJ/mol =
1eV/atom

Wiązanie jonowe



występuje w kryształach utworzonych z silnie
elektrododatnich atomów metali i silnie elektroujemnych
atomów chlorowców (NaCl, CsCl, KJ)



wzajemne oddziaływanie jonów Na

+

i Cl

-



kryształy jonowe są twarde, o wysokiej temperaturze
topnienia, złe przewodniki ciepła i prądu

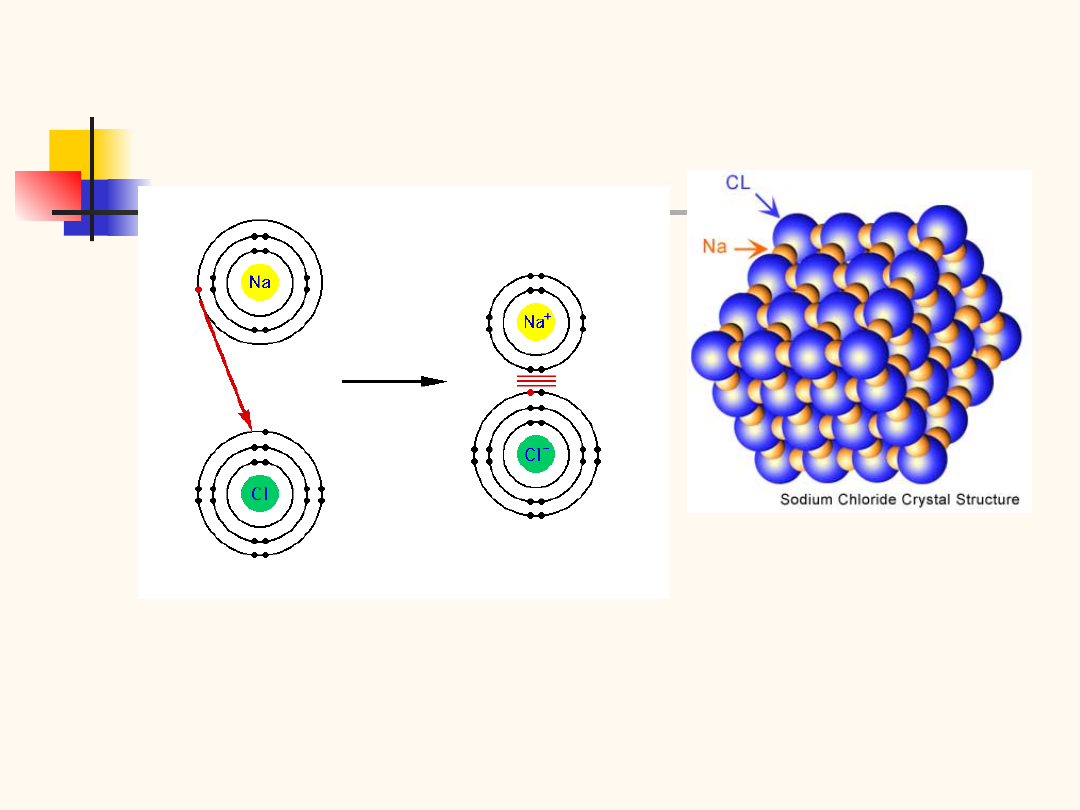
Wiązanie jonowe w czystej postaci występuje w
kryszta-łach typu NaCl, CsCl, KJ itp, a więc w
kryształach utwo-rzonych z silnie elektrododatnich
atomów metali i silnie elektroujemnych atomów
chlorowców.

Wiązania te omówimy na przykładzie

kryształu NaCl, którego strukturę przedstawiono na
rys. W węzłach sieci znajdują się przemiennie jony
Na+ i Cl–. Powstanie jonów możemy wytłumaczyć
w sposób następujący. Ener-gia jonizacji atomu Na
wynosi około 5,2 eV, przyłączenie elektronu od
atomu chloru jest związane z wydzieleniem energii
3,8 eV. Do przemieszczenia elektronu z atomu
sodu do atomu chloru potrzebna jest zatem
energia 1,4 eV. Jeżeli więc atomy (jony) znajdują
się od siebie w tak dużej odległości, że można
zaniedbać ich wzajemne oddziaływanie, to układ
Na

+

+ Cl– posiada energię o 1,4 eV wyższą od

energii układu Na + Cl.

Przy zmniejszeniu odległości r między jonami
coraz

wię-kszą

rolę

zaczyna

odgrywać

oddziaływanie kulombowskie. Wartość energii 1,4
eV

jest osiągana przy odległości r =

10

–9

m.

Przy mniejszych odległościach układ jonów jest
bardziej stabilny niż układ atomów. Przy jeszcze
większym zbliże-niu się jonów pojawiają się siły
odpychające, o których mówiliśmy poprzednio. W
wyniku

otrzymujemy

przebieg

energii

przedstawiony na rys.

r

/

e

=

o



4

2

Energia oddziaływania dwóch jonów sieci krystalicznej
może być przedstawiona w postaci wzoru

Parametr n wynosi około 10, tzn. że siły odpychania
maleją bar-dzo szybko ze wzrostem odległości i można
ograniczyć się do oddziaływania najbliższych sąsiadów.

 

n

o

r

B

r

e

r

U









4

2

Natomiast w przypadku bardziej długo zasięgowych
oddziały-wań

kulombowskich

należy

uwzględnić

oddziaływanie z dalszy-mi sąsiadami. W rezultacie
energia potencjalna jonu w kryszta-le wynosi

gdzie α

M

nosi nazwę stałej Madelunga i uwzględnia

oddziały-wanie

kulombowskie

jonu

z

dalszymi

sąsiadami.

 

n

o

M

r

B

r

e

r

U











4

2

Wiązanie kowalencyjne
(atomowe)

występuje w atomach leżących blisko siebie w układzie
okresowym, o tej samej lub zbliżonej elektroujemności

U ( r )

r

orbital wiążący
siły przyciągania

orbital antywiążący
siły odpychania

Oddziaływanie uwarunkowane wymianą elektronów między
atomami ma kwantowy charakter i nosi nazwę oddziaływania
wymiennego

W przypadku jodowodoru HJ po utworzeniu wspólnej pary
elektronowej wodór ma dublet charakterystyczny dla He, a jod
oktet taki jak ksenon

H· + ·Ï: = H:Ï:

..

..

wodór H

2

, azot

N

2

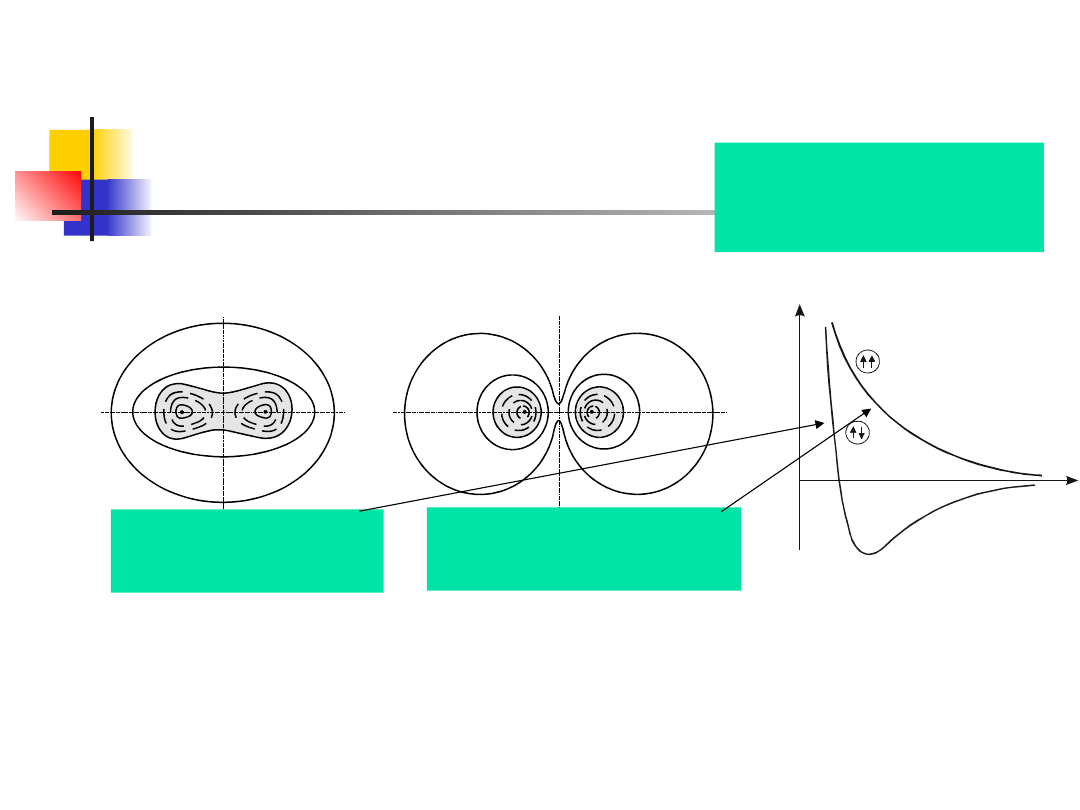
Przy zbliżaniu się dwóch atomów nakrywają się ich chmury
elektrono-we

i

rośnie

prawdopodobieństwo

przejścia

elektronu z jednego atomu do drugiego. Przy odpowiednio
małej odległości stopień pokrywania się chmur jest tak duży,
że można powiedzieć, iż elektrony należą do obu jąder.
Mówimy wówczas, że są skolektywizowane lub uwspólnio-ne.
Okazuje się ponadto, że nakrywaniu chmur elektronowych
towa-rzyszy przegrupowanie gęstości elektronowej i zmiana
energii układu.

Jeżeli spiny elektronów są ustawione przeciwnie, to gęstość chmury
elektrono-wej w przestrzeni między jądrami będzie większa niż ta,
którą otrzymalibyśmy w wyniku dodania chmur elektronowych
dwóch odosobnionych atomów. Jednocześnie poza tym obszarem
gęstość chmury jest mniejsza niż w odoso-bnionych atomach.
Funkcję falową opisującą gęstość chmury elektronowej utworzonej w
ten sposób nazywamy orbitalem wiążącym. Pojawienie się stanu o
większej

gęstości

chmury

elektronowej

(przy

przeciwnie

ustawionych spi-nach) powoduje zmniejszenie energii układu i
prowadzi do pojawienia się sił przyciągania. Jeżeli natomiast spiny
elektronów są skierowane zgodnie, mię-dzy atomami pojawiają się
siły odpychania. Układ taki może więc znaleźć się w stanie
równowagi, a przypisany temu stanowi orbital nazywamy antywią-
żącym. Oddziaływanie uwarunkowane wymianą elektronów
między atomami ma kwantowy charakter i nosi nazwę
oddziaływania wymiennego. Siły takiego oddziaływania
nazywamy siłami wymiany, a ich energię - energią wymiany.

Wyżej omówione wiązanie, które powstaje za
pośredni-ctwem

oddziaływania

elektronów

walencyjnych

nazywamy

wiązaniem

kowalencyjnym.
W kryształach typowe wiązanie kowalencyjne
występuje w pierwiastkach czwartej grupy (węgiel
o

strukturze

dia-mentu,

krzem,

german).

Wszystkie te kryształy posiadają strukturę
diamentu.

Atomy IV grupy mają na orbicie walencyjnej cztery
elektrony (np. o konfiguracji 2s

2

2p

6

dla węgla): dwa w

stanie s (o spinach przeciwnych) i dwa w stanie p (o
spinach zgodnych). Na skutek oddziaływania między
atomami w krysztale, konfiguracja elektro-nów w atomie
zmienia się w ten sposób, że w stanie s jest jeden
elektron, a w stanie p trzy elektrony, przy czym
wszystkie cztery elektrony mają spiny równoległe. Każdy
elektron może uczestni-czyć w czterech wiązaniach i
będzie tworzył pary elektronowe z czterema sąsiednimi
atomami.

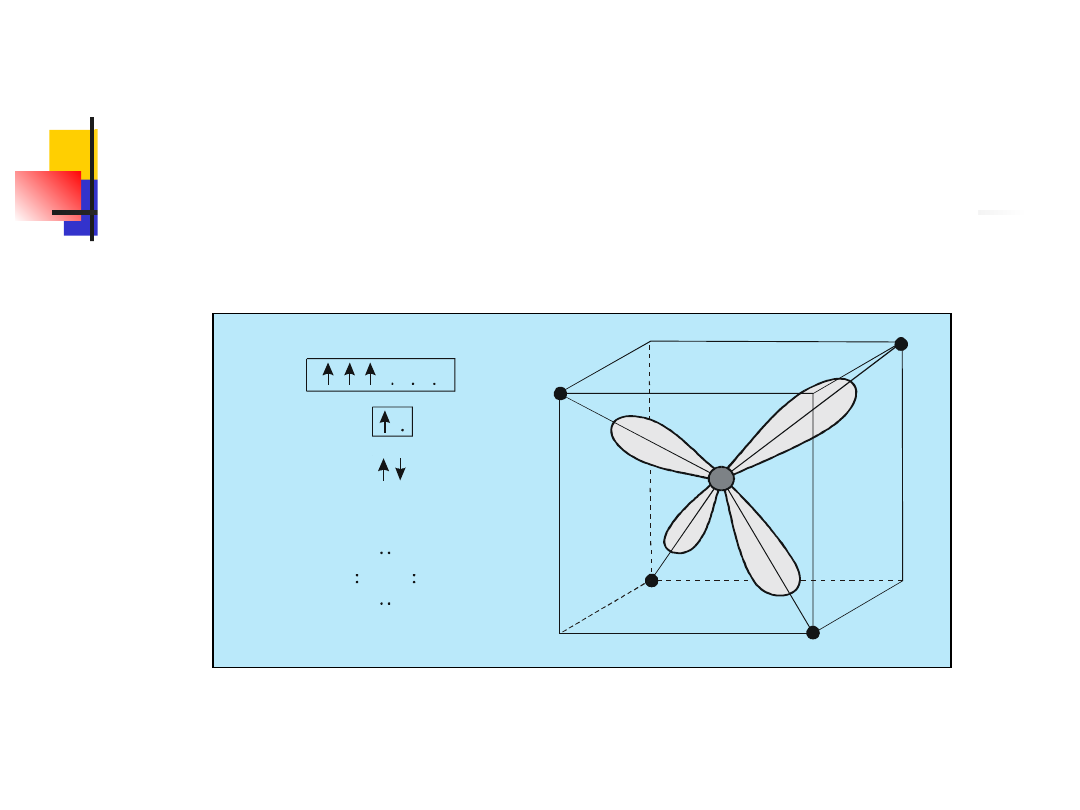
W cząsteczce CH

4

orbitale 2s i 2p atomu węgla nie

zacho-wują swego normalnego kształtu, lecz
ulegają zmieszaniu (czyli tzw. hybrydyzacji), w
wyniku czego powstaje orbital będący kombinacją
liniową jednej funkcji falowej 2s oraz trzech funkcji
falowych 2p. Nosi on nazwę orbitalu zhy-
brydyzowanego sp

3

. Jego kształt przedstawiono w

sposób poglądowy na rys.

Chmura elektronowa otaczająca rdzeń atomowy węgla
ma czte-ry równoważne ”ramiona” skierowane wzdłuż
osi

łączących

śro-dek

czworościanu

foremnego

(tetraedru) z narożami.

C

C

H

H

H

H

H

H

H

H

( a ) ( b )

( c )

2 p

2 s

1 s

Wiązanie

kowalencyjne

jest

wiązaniem

silnym

. Ma charakter wysoce kierunkowy,

ponieważ powstaje w tym kierunku, w którym
skupiona

jest

największa

część

chmu-ry

elektronowej skolektywizowanych elektronów.

Sztywność struktury elektronowej powoduje, że
kryształy są twarde i niepodatne na odkształcanie.

W temperaturach bardzo niskich kryształy kowalencyjne
są izola-torami,

gdyż każdy elektron walencyjny jest

związany z atomem. Ponieważ jednak powłoka
walencyjna nie jest zamknięta, siły wiążące na tej
powłoce nie są zbyt duże. W wysokiej temperatu-rze
energia drgań cieplnych jest wystarczająco duża do
zerwania niektórych wiązań i uwolnienia pewnej liczby
elektronów. Kryształ staje się przewodnikiem prądu.
Wiązanie kowalen-cyjne jest typowym wiązaniem
kryształów półprzewo-dnikowych.

Wiązanie metaliczne



występuje dla atomów o małej liczbie elektronów

wa-lencyjnych



przy zbliżaniu atomów następuje przekrywanie

funkcji falowych tych elektronów tak, że gęstość

prawdopo-dobieństwa ich znalezienia jest stała



delokalizacja

elektronów

i

łatwość

ich

przemieszcza-nia pod wpływem pola elektrycznego



wiązanie ma charakter kolektywny i objętościowy

do-datnio naładowane jądra oddziaływają z chmurą

oderwanych elektronów swobodnych



wiązanie metaliczne nie jest skierowane, więc

metale są plastyczne. Koncentracja elektronów

10

23

cm

-3

miedź, żelazo

Wiązanie metaliczne

Wiązanie molekularne

W przypadku kryształów molekularnych w węzłach sieci
krysta-licznej znajdują się molekuły połączone ze sobą
siłami moleku-larnymi, zwanymi inaczej siłami van der
Walsa.

Oddziaływanie tego typu występuje w każdej

substancji, jest jednak zdominowane przez inne
(omówione wcześniej) oddziaływania. Jeżeli jednak
powłoki elektronowe w atomach są całkowicie
wypełnione, to siły van der Walsa są głównymi siłami
jakie występują między atomami i cząstkami. Sytuacja
taka występuje np. w gazach szlachetnych. Wiązania
moleku-larne

mają

charakter

wiązań

elektrostatycznych. Wyróżniamy trzy rodzaje sił:
orientacyjne, indukcyjne i dyspersyjne.

Siły orientacyjne występują w przypadku, gdy
cząstki mają trwałe elektryczne momenty dipolowe.
Siły oddzia-ływania elektrostatycznego starają się
ułożyć je w okre-ślonym porządku, któremu
odpowiadać będzie minimum energii. Ruchy
termiczne cząstek burzą to uporządkowa-nie,
dlatego energia tych oddziaływań zmniejsza się ze
wzrostem temperatury.

Siły indukcyjne występują w przypadku, kiedy tylko część
mo-lekuł ośrodka ma trwałe momenty dipolowe. Pole
elektryczne wytworzone przez te dipole indukuje momenty
dipolowe w pozo-stałych niepolarnych cząstkach i
powoduje ich przyciąganie.
Oddziaływanie

dyspersyjne

występuje

między

molekułami, które nie mają trwałych elektrycznych
momentów dipolowych. Ponieważ molekuła jest układem
dynamicznym, to w poszczegól-nych chwilach występuje
pewne rozsunięcie środków ciężkości ładunków dodatnich i
ujemnych. Kierunki tych momentów są w każdej chwili
różne. Jednak w wyniku ich oddziaływania zmiany
kierunków oddziaływania mogą odbywać się w sposób
skoordy-nowany, co prowadzi do pojawienia się trwałej siły
przyciągania

.

Na ogół w kryształach występują wszystkie rodzaje
oddziały-wań, przy czym największa część energii
przypada

na

od-działywanie

orientacyjne

i

dyspersyjne.

Warto

również

zapa-miętać,

że

wymienione oddziaływania są oddziaływaniami
krótkiego zasięgu. Niewielka wartość tych sił
powoduje, że wiązania międzycząsteczkowe łatwo
ulegają zniszczeniu na skutek ruchów termicznych.
Na skutek tego kryształy cząste-czkowe (hel, azot,
wodór) topią się w niskich temperaturach i łatwo
parują. Słabe wiązania sprawiają także, że kryształy
molekularne są podatne na odkształcenia, a brak
swobo-dnych elektronów powoduje, że są one bardzo
złymi prze-wodnikami ciepła i prądu elektrycznego.

Wiązanie molekularne



Wiązania molekularne mają charakter wiązań

elektrostatycznych (siły van der Walsa) i

dzielimy na:



oddziaływanie trwałych lub indukowanych

momentów dipolowych cząsteczek



oddziaływania te są krótkiego zasięgu i łatwo

ni-szczone na skutek ruchów termicznych –

istotne w procesach biologicznych



kryształy molekularne są podatne na

odkształce-nia,

topią

się

w

niskich

temperaturach, źle prze-wodzą ciepło i prąd

argon, krypton,
naftalen