ROLA STATYSTYKI

W SŁUŻBIE ZDROWIA

Opracował:

dr n. med. Marian Jędrych

Motto:

"Dotychczasowa historia nauki

potwierdza jednoznacznie, że
prawdziwy postęp w jakiejkolwiek
dziedzinie wiedzy i działalności
nie jest możliwy bez świadomego
i celowego odwoływania się do
ściśle określonych metod
badawczych."

Statystyka jako dziedzina wiedzy jest
metodą badania zjawisk i procesów
masowych i wyciąganiem wniosków z tych
zjawisk. Znajduje zastosowanie wszędzie
tam, gdzie takie zjawiska występują i
gdzie takie racjonalne postępowanie
wymaga znajomości statystycznych,
charakterystycznych dla tych zjawisk.

W dziedzinie medycyny występuje taki

właśnie rodzaj prawidłowości Chorowanie,
leczenie, zapobieganie, zachorowania
pacjentów- to wszystko zjawiska masowe

.

W zjawiskach tych występują

prawidłowości statystyczne, a coraz
szersze i gruntowniejsze poznanie
tych prawidłowości jest istotnym
elementem postępu medycyny.
Statystyka pełni więc w medycynie
rolę jednej z podstawowych metod
badawczych. Stosowanie tej metody
umożliwia wykrywanie prawidłowości
wiążących się ze zdrowiem całego
społeczeństwa, jak i jego
poszczególnych członków.

Znajomość tych prawidłowości jest

nieodzowna dla codziennej praktyki lekarza
klinicysty, stomatologa, pielęgniarki,
profilaktyka, epidemiologa, organizatora
ochrony zdrowia oraz dla działalności
naukowej i odkrywczej twórców nowoczesnej
medycyny. Wynalezienie, wypróbowanie i
ocena skuteczności każdego nowego
sposobu leczenia wymagała, wymaga i
zawsze będzie wymagać odpowiednio dużej
liczby obserwacji. Narodziny nowoczesnej
statystyki przypadają na XVII wiek. Burzliwy
rozwój statystyki datuje się dopiero od końca
XIX wieku. Od tego czasu obserwuje się
ściślejszy związek z medycyną.

Przed XVII- XVIII wiekiem lekarze sami w
swojej długoletniej praktyce obserwowali
prawidłowości dotyczące przebiegu
choroby i leczenia. Uogólnione wyniki tych
obserwacji wchodziły do skarbnicy wiedzy
lekarskiej i były przekazywane uczniom i
następcom, bądź w późniejszych czasach
publikowane. Robiono więc to samo, co
leży u podstawy nowoczesnych badań
statystycznych, a mianowicie dokonywano
dużej liczby obserwacji i po analizie ich
wyników formułowano odpowiednie
prawidłowości

.

Różnica przed czasami
„przedstatystycznymi”, a współczesnością
polega na tym, że kiedyś decydującą rolę
w badaniach i formułowaniu wniosków z
nich płynących odgrywała wyłącznie
intuicja badacza, a dziś może on
korzystać z bogatej skarbnicy dokładnie
opracowanych metod wnioskowania
statystycznego, których znajomość i
właściwe stosowanie zapewnia pełną
poprawność przeprowadzenia procesu
badawczego, począwszy od jego fazy
przygotowawczej, a skończywszy na
wyciągnięciu właściwych wniosków.

Osiągnięcia nowoczesnej diagnostyki są wynikiem
licznych badań, w których metody statystyczne
odgrywają ważną rolę. Wybór właściwej metody
leczenia powinien opierać się na znajomości
skuteczności rozmaitych metod, a ocena tej
skuteczności może być dokonana najczęściej w
rezultacie badań statystycznych. W epidemiologii
badanie dużych populacji wymaga bezwzględnie
stosowania metod statystycznych. Medycyna
zapobiegawcza w pełni wykorzystuje statystykę
dla oceny skuteczności różnych metod
zapobiegawczych. Jedną z podstaw kierowania i
zarządzania całą służbą zdrowia i poszczególnymi
jej odcinkami jest sprawozdawczość, a
uogólnienie wniosków z tej sprawozdawczości jest
niemożliwe bez statystyki.

Szczególnie doniosłe znaczenie mają

metody statystyczne w doświadczalnych
badaniach naukowych we wszystkich
działach medycyny. Znajomość
statystyki pozwala ustalić z góry liczbę
koniecznych powtórzeń doświadczenia
bądź liczbę pomiarów, które trzeba
wykonać, aby wnioski dały się uogólnić w
sposób naukowy. Statystyka określa
warunki, w jakich doświadczenia
powinny się odbywać, aby unikać błędów
systematycznych. Statystyka pozwala w
końcu zweryfikować słuszność wniosków
płynących z doświadczeń.

Celem uzyskiwania danych statystycznych w

ochronie zdrowia jest dostarczanie

informacji dla podejmowania decyzji, a więc

wyboru najlepszych kierunków działania w

celu zaspokojenia potrzeb zdrowotnych

społeczeństwa. Podejmowanie decyzji, a

więc dokonywanie nielosowego wyboru

odpowiedniego działania, jest istotą

zarządzania. Zarządzanie w ochronie

zdrowia nie stanowi pod tym względem

wyjątku. Decydent, czyli osoba podejmująca

decyzję, musi znać sytuację decyzyjną, aby

działać celowo, ponieważ od takiej wiedzy

zależy skuteczność i ekonomiczność działań

zdrowotnych. Wiedzę tę otrzymuje się przez

informację statystyczną.

Do metod roboczych, którymi

najczęściej posługuje się badacz
zaliczamy:

• metody obserwacji,
• metody eksperymentalne,
• metody testów,
• wywiady,
• ankiety - kwestionariusze,
• metodę analizy dokumentów,
• metody statystyczne

W celu podjęcia racjonalnych działań
zdrowotnych koniecznym etapem wstępnym
jest analiza sytuacji, która powinna
obejmować rozpoznanie stanu zdrowia
ludności, zasobów ludzkich i materialnych
bieżącej działalności służby zdrowia, a w tym –
natężenia działań zdrowotnych, intensywności
pracy personelu służby zdrowia jakości
udzielanych świadczeń. Informacje te
otrzymujemy ze sprawozdawczości
medycznej. Po analizie sytuacji opracowuje się
zbiór wszystkich alternatywnych sposobów
działania dla osiągnięcia wyznaczonego celu

Wynika z tego jednoznacznie, że uzyskanie pełnego

zbioru ścisłych informacji dotyczących sytuacji

zdrowotnej i organizacyjnej jest niezbędnym

warunkiem podejmowania racjonalnych decyzji

kierowniczych. Po opracowaniu wszystkich możliwych

alternatyw działania dokonuje się wyboru wariantu

optymalnego i przystępuje się do realizacji

wyznaczonych zadań. Z realizacją zadań jest

nieodłącznie związana ich ocena.
Ocena działań zdrowotnych obejmuje te same

elementy, które wymieniono w analizie sytuacji, a więc:

• zmianę stanu zdrowia ludności,
• zmiany w zasobach ludzkich i materialnych,
• zmiany w działalności służby zdrowia,
• natężeniu działań,
• intensywności pracy personelu i jakości udzielanych

świadczeń

Mimo tak dużej różnorodności problematyki,

jednolita jest metoda wnioskowania

statystycznego. Konieczność stosowania metod

statystycznych w planowaniu badań oraz w

analizie i interpretacji wyników spowodowana jest

w dużym stopniu coraz szerszym wprowadzaniem

ilościowych metod pomiaru wyników badań.

Podejmujący badania musi zrozumieć cel

zastosowania metod statystycznych, ich miejsce

w całokształcie prowadzonych badań, a także

poznać możliwe zastosowania i sposoby

interpretacji wyników.
Doceniając w pełni rolę i znaczenie metod

statystycznych w badaniach naukowych, nie

można zapominać, że statystyka nie spełnia w

nich roli nadrzędnej, ale jest jednym z cennych

narzędzi. Podstawowe znaczenie przy analizie

statystycznej ma plan badania. Składa się on z

następujących, scharakteryzowanych poniżej

elementów.

1. Cel badania

• Powinien być określony w sposób

zwięzły i precyzyjny, np. ustalenie
wpływu określonego leku na
skuteczność leczenia określonej
choroby.

• Przy planowaniu analizy

statystycznej należy sformułować
hipotezę badawczą, np. lek zwiększa
skuteczność leczenia.

2. Badane obiekty

• Aby badana próba dobrze reprezentowała całą

populację, każdy element populacji powinien mieć

szanse trafienia do próby zgodnie z

prawdopodobieństwem występowania. Oczywiste jest,

że zwykle im większa jest wybrana do badań próba

(losowanie próby było zgodne z rozkładem cechy), tym

bardziej jest ona reprezentatywna dla całej populacji.

• Istnieją 4 sposoby pobierania próby: dobór losowy -

polega na wybieraniu obiektów do analizy drogą

losowania z określonymi rozkładami; dobór konieczny -

ma miejsce wtedy, gdy warunki prowadzenia badania

ograniczają a priori analizowane jednostki; dobór

celowy - badacz sam wybiera jednostki do analizy,

uwzględniając własny pogląd na najlepszy dobór próby

do reprezentacji populacji; dobór dobrowolny -

jednostki do badania zgłaszają się dobrowolnie.

• Przy pobieraniu próby w badaniach biologicznych i

medycznych należy w maksymalnie możliwym stopniu

stosować dobór losowy.

3. Badane cechy

• Po dokonaniu wyboru cech do badania

należy je podzielić na jakościowe i ilościowe
(skokowe i ciągłe). Ma to istotne znaczenie,
ponieważ dla każdego w podanych
rodzajów cech stosuje się do analizy inne
metody statystyczne.

4. Metody pomiaru cech badanych

• Przy określaniu metod pomiaru należy

uwzględnić, że dla cech ilościowych
otrzymuje się wartości w określonych
jednostkach, natomiast dla cech
jakościowych prowadzona jest klasyfikacja
do jednej z kategorii.

5. Analiza statystyczna

W najprostszym przypadku analizowane są

oddzielnie poszczególne cechy. Takie podejście
nazywane jest analizą jednowymiarową.
Obejmuje ona wyznaczanie rozkładu, czyli
wskaźników częstości występowania wartości
(struktury, natężenia i poglądowości), bądź
parametrów rozkładu (m.in. wartości średniej
arytmetycznej, geometrycznej, harmonicznej,
mediany, modalnej, błędu wartości średniej,
odchylenia standardowego, wariancji,
współczynnika zmienności, elementu
maksymalnego, elementu minimalnego,
rozstępu, oceny normalności rozkładu, oceny
losowości pobrania próby)

6. Opracowywanie wyników

Podczas opracowywania wyników

powinno się zwracać uwagę m.in.: czy
materiał i metody są jasno opisane, czy
materiał jest ujednolicony, czy
zastosowane do analizy narzędzia
spełniały warunki ich stosowalności, czy
wyniki są poprawnie zinterpretowane, czy
wyniki są uzasadnione w świetle
znajomości przedmiotu, czy wnioski
znajdują zastosowanie w odniesieniu do
całej populacji, czy wnioski uzasadniono
wynikami analizy statystycznej.

Statystyka

jest więc nauką zajmującą się

metodami badania przedmiotów i zjawisk w ich

masowych przejawach oraz ich ilościową lub

jakościową analizą z punktu widzenia dyscypliny

naukowej, w której zakres wchodzą:

• - statystyka opisowa
• - statystyka matematyczna.

- rodzaje zmiennych i stałych wykorzystywanych

w opisie przedmiotów i zjawisk:

• -liczba przedmiotów lub zjawisk (klasyfikacja –

zliczenie )

• - nasilenie właściwości (cechy), którą wykazuje

przedmiot lub zjawisko (porównanie z wzorcem

-porządkowanie lub przypisanie nasileniu

właściwości / cechy liczby)

• - mierzenie.

Dwa zasadnicze rodzaje właściwości

(rodzaje cech):

• - właściwości (cechy) jakościowe, to
n p. płeć miejsce pobytu (województwo,

powiat lub gmina), wykonywany zawód,
kierunek wykształcenia, obywatelstwo,
narażenie na zakażenie.

• - właściwości (cechy) ilościowe
n p. wiek, okres wylęgania choroby, czas

trwania choroby, temperatura ciała,
poziom przeciwciał i t d.

Mierniki epidemiologiczne

M

iary częstości występowania chorób

najczęściej stosowane w
epidemiologii to:

• współczynnik zapadalności
• współczynnik chorobowości.
Ważne mierniki, chociaż rzadziej

stosowane to:

• współczynnik umieralności
• współczynnik śmiertelności.

Zapadalność

Współczynnik zapadalności skumulowanej (zbiorczej):
określa liczbę nowych zachorowań, które wystąpiły w

określonym czasie (w liczniku) w stosunku do liczby

osób w populacji (w mianowniku)

• z reguły jest standaryzowany, tj. przeliczany na

zapadalność w populacji o określonej wielkości (100

tys. ludności, 10 tys.,1 tysiąc)

• W praktyce współczynnik zapadalności określa

zapadalność-na chorobę ogółem lub (przypadek)

-osób na chorobę (osoba).

• Współczynnik zapadalności zwany gęstością

zachorowań określa rzeczywiste

prawdopodobieństwo zachorowania odnosząc liczbę

nowych zachorowań (w liczniku) do sumarycznego

osobo-czasu (w mianowniku).

• –Jednostkami osobo-czasu mogą być osobo-lata,

osobo-miesiące, osobo-dni.

Specyficzną formą zapadalności jest zapadalność

epidemiczna będąca:

• -kumulacyjną zapadalnością,
• - w specyficznej grupie ryzyka,
• -obserwowaną w określonym czasie,
• -(często) spowodowaną specyficzną przyczyną.
Przykład.
• W mieście liczącym 80 000 mieszkańców w ciągu

roku zarejestrowano 72 nowych przypadków

gruźlicy.

• Współczynnik zachorowalności wynosi, więc:

Wz = 72 / 80000 * 10 000 = 9,0 / 10 000

• Oznacza to, że przeciętnie na każdych 10 000

mieszkańców przypadało 9 zachorowań na

gruźlicę.

 

 

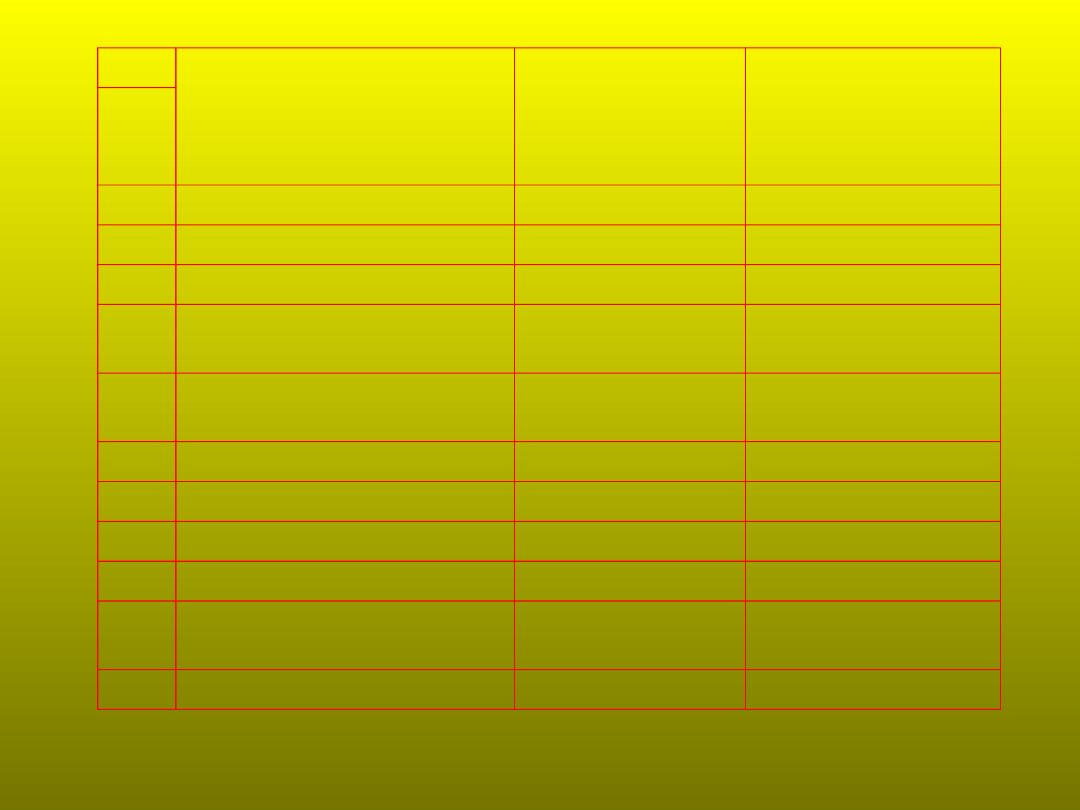
W liczbach

bezwzględny

ch

Na 10000 ludności

Lp.

1 grypa

3 768 054

11 075,5

2 biegunka u dzieci do lat 2

32 953

2 714,4

3 odra

146 664

431,1

4 zapalenie przyusznic

nagminne

138 118

406

5 wirusowe zapalenie

wątroby

74 559

219,2

6 rzeżączka

37 134

109,2

7 czerwonka

9 220

27,1

8 kiła

8 149

24

9 dur brzuszny

276

0,8

10 porażenie dziecięce

nagminne

9

0

11 błonica

-

-

Zachorowania na niektóre choroby zakaźne w Polsce 1975

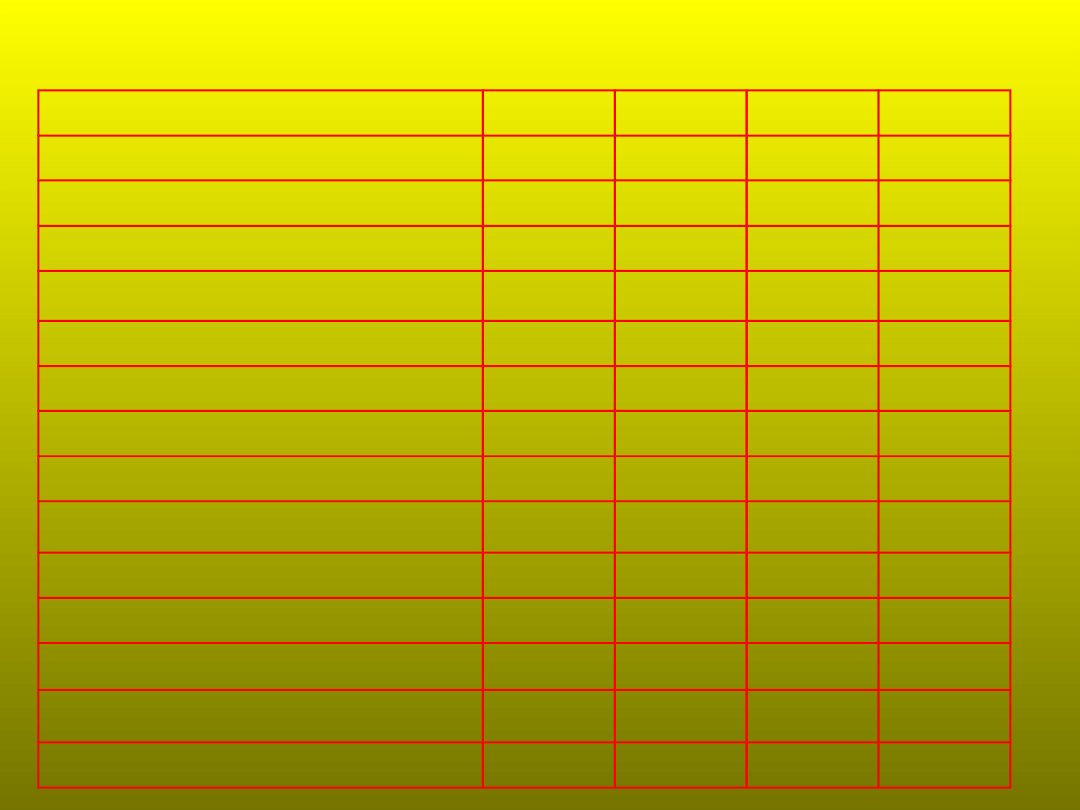
Nowo zarejestrowane zachorowania na niektóre choroby w Polsce

Choroby

1995

2000

2002

2003

Gruźlica

15959

11477

10475

10124

W tym gruźlica płuc

15311

10960

9438

9207

Choroby weneryczne

3135

1713

1759

1630

W tym kiła

1576

975

1165

984

Choroby zakaźne i zatrucia

 

 

 

 

Odra

752

77

34

48

Różyczka

57351

46181

40518

10588

Krztusiec

549

2269

1788

2034

Wirusowe zapalenie wątroby

30276

5360

4449

4228

AIDS

115

120

116

130

Salmonellozy

30093

22799

20689

16612

Czerwonka bakteryjna

815

121

220

75

Inne bakteryjne zatrucia pokarmowe

3868

3990

6159

3725

Biegunki u dzieci do lat 2

19525

17538

17769

16470

Nowo zarejestrowane zachorowania na niektóre choroby w Polsce cd.

Choroby

1995

2000

2002

2003

Szkarlatyna (płonica)

26466

8345

4053

3872

Zapalenie opon mózgowych

6688

2110

1974

1904

Zapalenie mózgu

575

570

503

761

Świnka (zapalenie przyusznicy nagminne)

82337

17548

39978

87336

Świerzb

22880

16914

15831

13741

Grypa

1122916

1596920

228055

1216285

Nowotwory złośliwe

105186

114432

114440

 

Zaburzenia psychiczne i zaburzenia

zachowania

176065

232975

304233

318000

Podczas gdy zachorowalność mierzy natężenie nowych

zachorowań w populacji, to miarą

rozpowszechnienia zarówno nowych, jak uprzednio

istniejących przypadków choroby, jest chorobowość.

Wyróżniamy chorobowość:
• - punktową,
• - okresową,
Chorobowość punktowa określa rozpowszechnienie

choroby w populacji w danym momencie

Chorobowość okresowa przedstawia ogólną liczbę

przypadków choroby, które stwierdzono w

analizowanym okresie na danym terenie, w

populacji podlegającej ryzyku choroby. Jest to suma

chorobowości punktowej stwierdzonej na początku

danego okresu i zachorowalności osób w

analizowanym okresie.

UMIERALNOŚĆ

• Jedną z tradycyjnych metod w badaniach

stanu zdrowia jest analiza umieralności.

Obliczamy następujące współczynniki

umieralności:

• - współczynnik umieralności ogólnej,
• - współczynnik specyficzny umieralności.
• Współczynnik umieralności ogólnej należy

interpretować z zachowaniem ostrożności,

ponieważ na ich wartość wpływa struktura

badanej zbiorowości. Dlatego obliczamy

specyficzne współczynniki umieralności, które

najczęściej uwzględniają strukturę populacji

wg płci, wieku, przyczyny zgonu itp.

• Tak, więc, obliczając współczynnik umieralności z

powodu określonej przyczyny bierzemy pod

uwagę wyłącznie zgony z powodu tej przyczyny.

Szczególny aspekt w analizie zgonów stanowi

umieralność niemowląt. Współczynnik

umieralności niemowląt jest to stosunek liczby

zgonów niemowląt ( dzieci przed ukończeniem

pierwszego roku życia) do liczby urodzeń żywych.

W obliczeniu tego współczynnika należy

uwzględnić fakt, że część zmarłych w danym roku

niemowląt urodziła się w roku poprzednim. Stąd

też w mianowniku sumujemy ¼ liczby urodzeń z

roku poprzedniego i ¾ liczby urodzeń z roku

bieżącego.

• Wśród przyczyn umieralności niemowląt wyróżnia

się tzw. przyczyny endogeniczne i egzogeniczne.

• Różna umieralność niemowląt jest spowodowana

głównie tzw. przyczynami egzogenicznymi, czyli

takimi, które są wynikiem niekorzystnego

oddziaływania środowiska zewnętrznego. Należą

tu głównie choroby infekcyjne ( zapalenia płuc,

biegunki), których niekorzystnym skutkom można

łatwiej zapobiec niż zaburzeniom zdrowia

spowodowanym czynnikami dziedzicznymi lub

wrodzonymi ( przyczyny endogeniczne).

• Pojęcie "wnioskowania statystycznego w

medycynie" często jest traktowane w sposób

zróżnicowany. Dla klinicysty jest to narzędzie do

oceny stosowanych metod diagnostycznych i

terapeutycznych. Epidemiolog oczekuje zasad

uzyskiwania wyników dotyczących m.in.

rozprzestrzeniania się chorób zakaźnych oraz

skuteczności szczepień ochronnych.

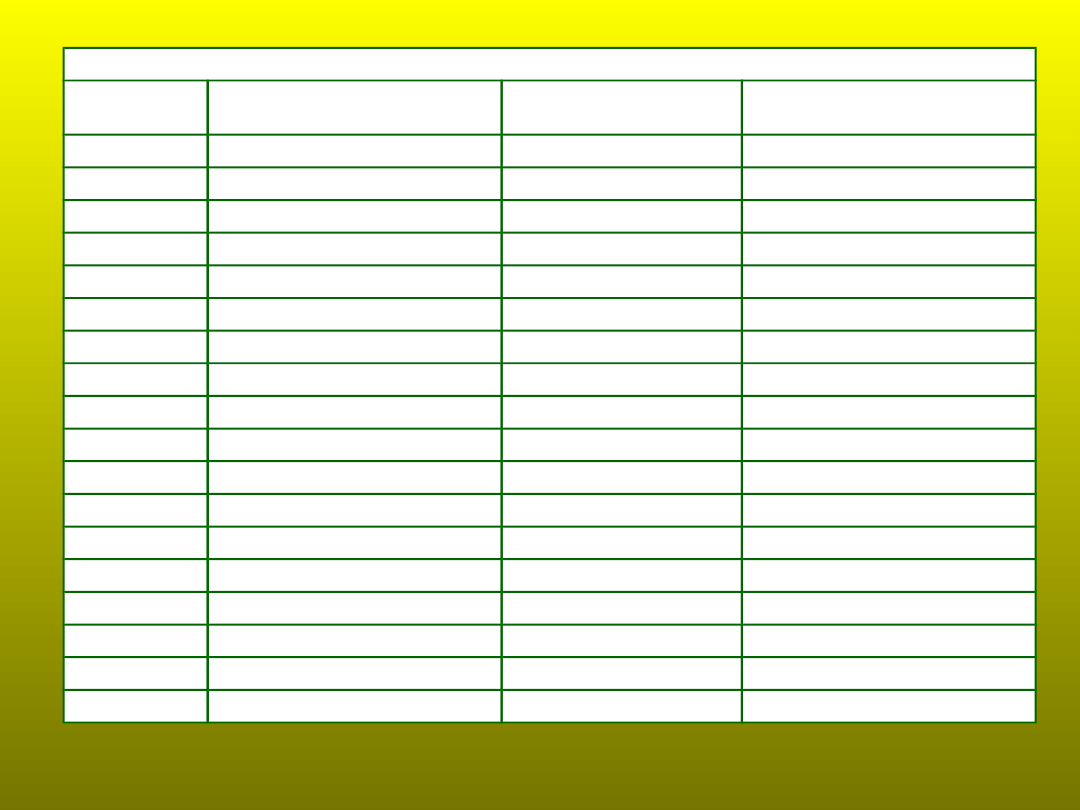
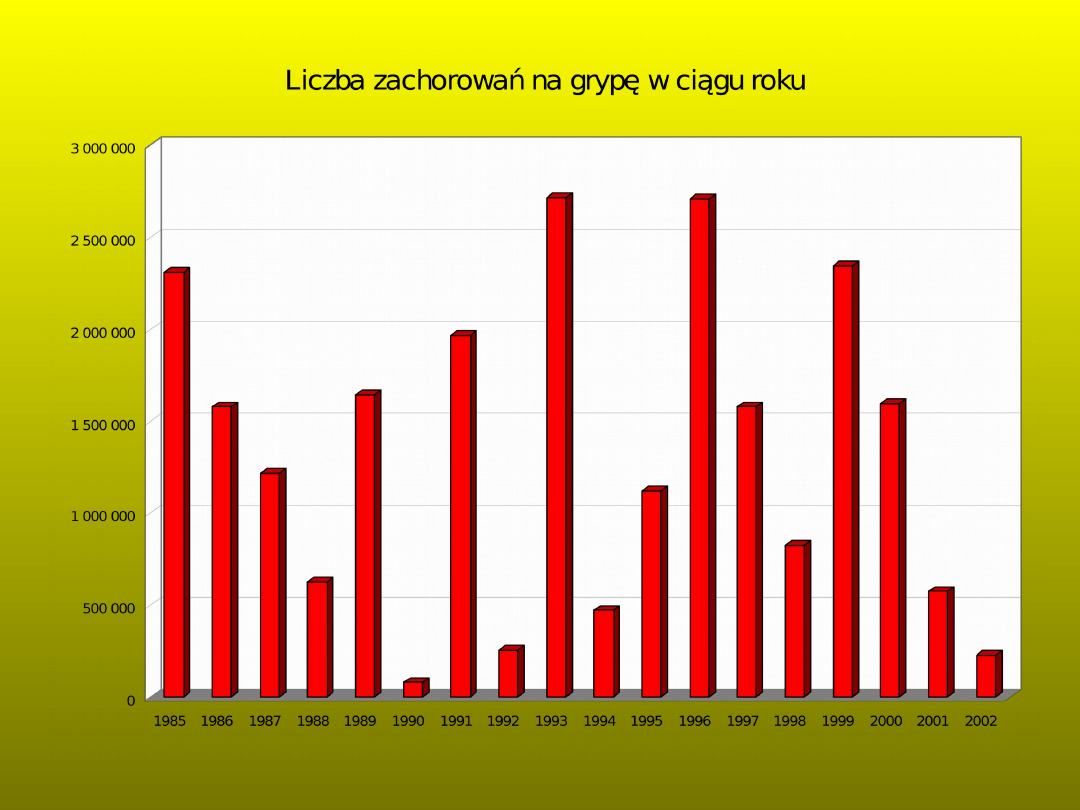
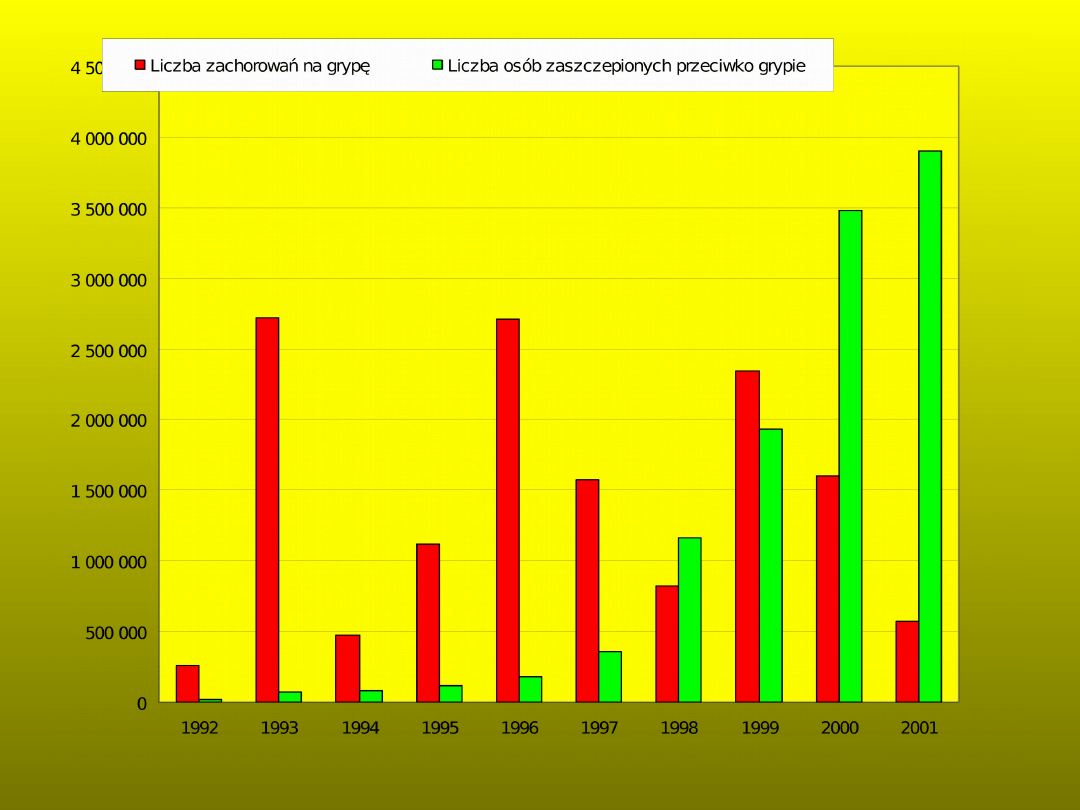
Zachorowania na grypę w Polsce

Rok

Liczba zachorowań w ciągu

roku

Zapadalność na 100

000 ludności

Odsetek osób

hospitalizowanych

1985

2 309 875

6 208,80

0,04%

1986

1 578 975

4 215,60

0,06%

1987

1 218 292

3 234,70

0,03%

1988

628 690

1 660,50

0,03%

1989

1 642 126

4 325,60

0,02%

1990

80 161

210,3

0,07%

1991

1 968 463

5 147,00

0,02%

1992

256 692

669,1

0,06%

1993

2 717 585

7 066,20

0,01%

1994

471 524

1 223,40

0,02%

1995

1 122 916

2 910,00

0,03%

1996

2 711 174

7 020,50

0,12%

1997

1 578 494

4 084,10

0,11%

1998

825 345

2 134,50

0,06%

1999

2 344 773

6 066,10

0,17%

2000

1 596 920

4 132,20

0,44%

2001

576 449

1 491,80

0,12%

2002

228 055

590,3

0,10%

Rok

Liczba

zachorowań

Liczba zgonów

Umieralność na 100

000

Śmiertelność

(%)

1988

628 690

35

0,09

0,006

1989

1 642 126

65

0,17

0,004

1990

80 161

43

0,11

0,053

1991

1 968 463

43

0,11

0,053

1992

256 692

43

0,11

0,002

1993

2 717 585

88

0,23

0,016

1994

471 524

30

0,08

0,006

1995

1 115 237

66

0,17

0,006

1996

2 711 174

212

0,54

0,007

1997

1 573 046

207

0,53

0,013

1998

825 345

63

0,16

0,007

1999

2 341 924

402

1,04

0,017

2000

1 596 920

358

0,92

0,022

2001

576 449

26

0,067

0,0045

Grypa w Polsce w latach 1988-2001

Rok

Liczba osób zaszczepionych przeciwko

grypie

Odsetek zaszczepionej

populacji

1992

20 000

0,05%

1993

70 000

0,17%

1994

80 000

0,20%

1995

115 000

0,28%

1996

180 000

0,45%

1997

360 000

0,90%

1998

1 160 000

3%

1999

1 932 000

5%

2000

3 478 000

7%

2001

3 900 000

10%

2002

4 200 000

10,50%

.

liczba osób zaszczepionych przeciw grypie w latach 1992-2002 w Polsce

Grupy

wiekow

e

1997

1998

1999

2000

2001

1-19

4

 

2

1

2

20-39

4

1

10

4

 

40-64

25

10

34

37

1

65 +

174

52

356

316

23

Razem

207

63

402

358

26

.

Liczba zgonów w Polsce z powodu grypy, uwzględniająca podział na

grupy wiekowe.

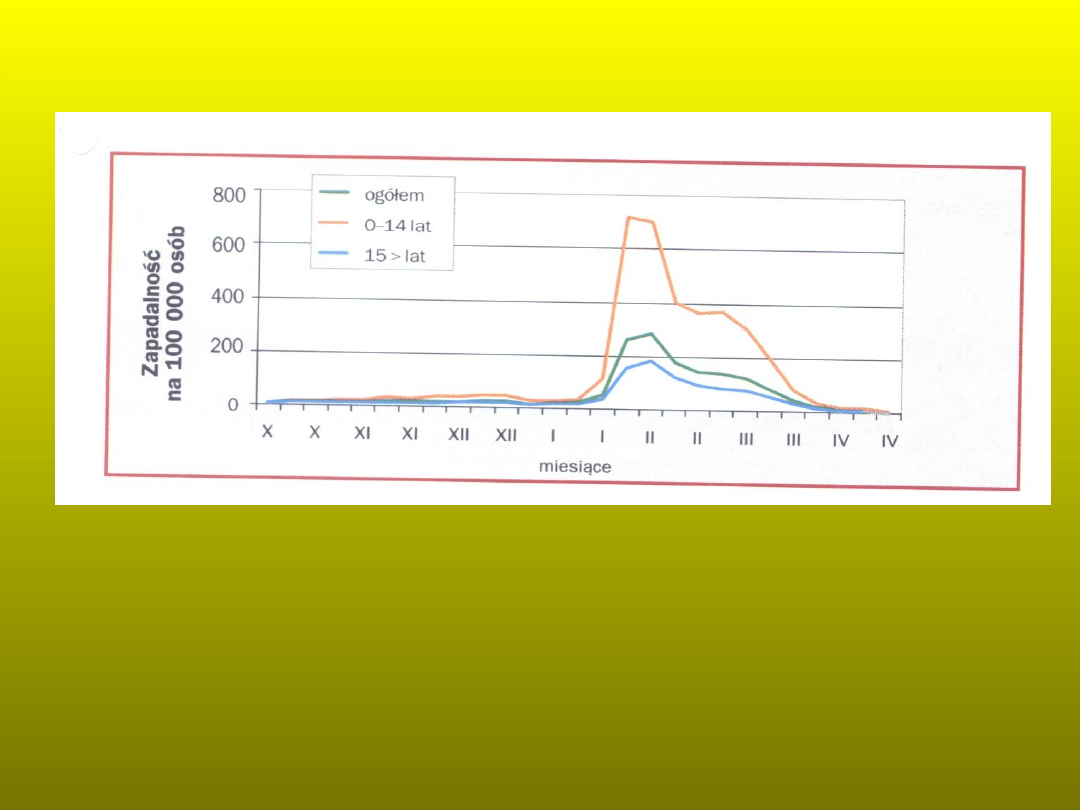
Zapadalność na grypę w Polsce w poszczególnych sezonach
grypowych

• Dla organizatora służby zdrowia ważne jest

ocenienie jej organizacji i skuteczności działania.

Najbardziej typowe miary:
• - średnia arytmetyczna (oznaczana przez M)
• - średnia geometryczna (oznaczana przez M

g

)

• - mediana (oznaczana przez Me)
• - modalna. (oznaczana przez Mo)
W trakcie opisu danych oprócz opisania wartości

przeciętnej istnieje również potrzeba opisania

rozrzutu wyników:

• - wariancja (oznaczana przez SD

2

)

• - odchylenie standardowe (oznaczana przez SD)
• - współczynnik zmienności (oznaczana przez M)
• - odchylenie przeciętne (oznaczana przez d)
• - rozstęp (oznaczana przez R).

• Statystyka stanowi nie tylko

podstawę funkcjonowania opieki
zdrowotnej w każdym rozwiniętym
państwie. Znajomość jej
podstawowych prawideł i zasad jest
również niezbędna w pracy każdego
z lekarzy i to niezależnie od rodzaju
wykonywanej specjalizacji. Ma ona
również bardzo duże znaczenie w
ekonomicznej ocenie funkcjonowania
placówek opieki zdrowotnej.

• W XXI wieku możemy bardzo dokładnie

przeanalizować dane statystyczne niemal z

każdej dziedzinie życia. W medycynie

odgrywają one bardzo ważną rolę. Statystyka

pomaga decydować o otwieraniu nowych

oddziałów szpitalnych tam, gdzie wskazują na

to między innymi wyniki jej badań.

• Malejący przyrost naturalny sprawia, że

oddziały położnictwa i patologii ciąży nie są w

pełni wykorzystane w istniejących już

placówkach. Z danych statystycznych

wynika, że zarówno obecnie jak i w

najbliższym czasie potrzebne będą łóżka na

oddziałach np: onkologicznych,

kardiologicznych, ratownictwa medycznego i

geriatrii.

PRACOWNICY MEDYCZNI Stan w dniu 31 XII

Wyszczególnienie

2000

2002

2003

Lekarze

85031

88070

87617

Lekarze stomatolodzy

11758

10775

10737

Farmaceuci

22161

24421

25217

Felczerzy

374

294

197

Pielęgniarki

189632

185892

181291

W tym magistrzy
pielęgniarstwa

 

4437

4866

Położne

21997

21743

21129

WIRUSOWE ZAPALENIE WĄTROBY: TYPU B OGÓŁEM

Liczba zachorowań (w kwartałach i ogółem), zapadalność oraz liczba i procent hospitalizowanych wg
województw

Województwo

Liczba zachorowań w
kwartałach

Liczba zachorowań
w roku

Zapadalność na
100 tys.

Hospitalizacja

I

II

III

IV

Liczba

%

POLSKA

2003 r

503

399

406

504

1812

4,74

1686

93

2004 r

416

403

363

388

1570

4,11

1401

89,2

1

Dolnośląskie

62

67

52

52

233

8,05

226

97

2

Kujawsko-Pomorskie

40

21

33

31

125

6,05

96

76,8

3

Lubelskie

28

16

12

14

70

3,2

63

90

4

Lubuskie

6

9

9

12

36

3,57

36

100

5

Łódzkie

43

67

61

60

231

8,91

229

99,1

6

Małopolskie

43

27

23

21

114

3,5

74

64,9

7

Mazowieckie

50

50

41

42

183

3,56

162

88,5

8

Opolskie

6

7

13

8

34

3,23

34

100

9

Podkarpackie

15

8

8

16

47

2,24

46

97,9

10

Podlaskie

11

14

7

6

38

3,16

38

100

11

Pomorskie

16

12

9

20

57

2,6

54

94,7

12

Śląskie

29

35

38

43

145

3,08

145

100

Opierając się na badaniach

statystycznych warto mieć na
uwadze stwierdzenie, które
przypisuje się Newtonowi:
„Celem obliczeń nie są
liczby, ale zrozumienie
prawdy…”