Geodezja Wyższa i

Astronomia

Geodezyjna

Mgr inż. Marta
Krywanis



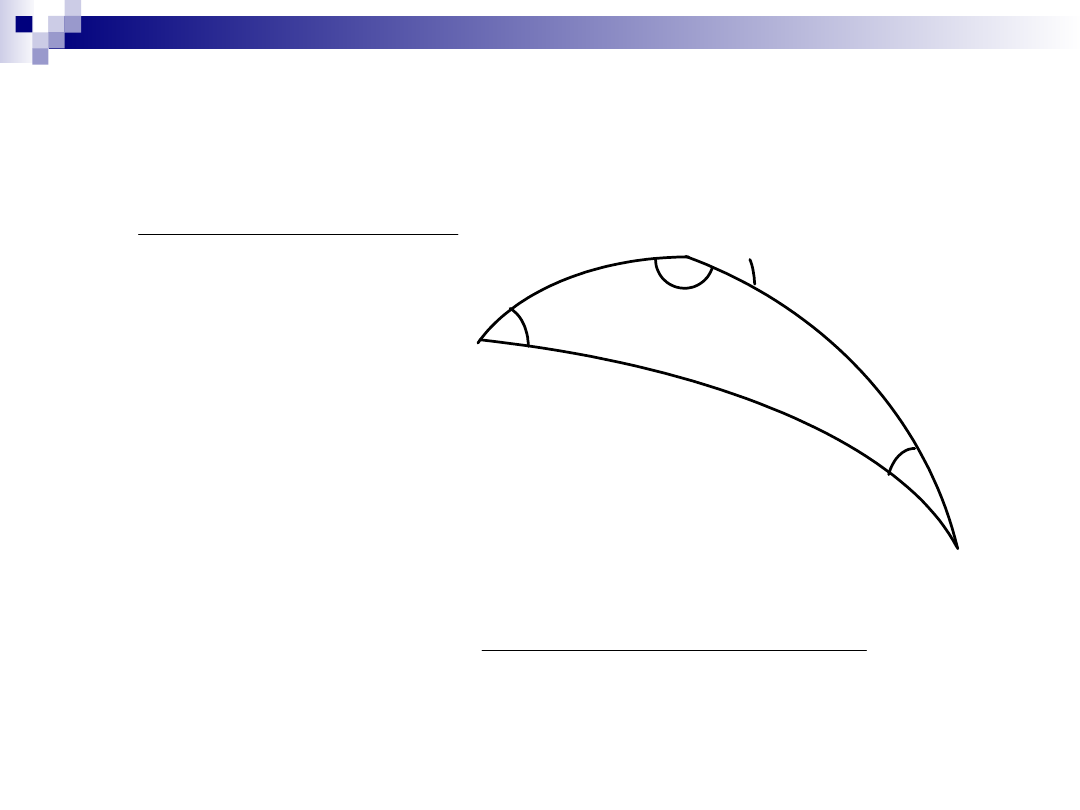
sin  = sin   cos z - cos   sin z  cos A



cos   sin t = sin z  sin A



cos   cos t = cos   cos z + sin   sin z  cos A

A

180-A

t



90-h=z







BPn

Z

BPn

G

A

cos

z

sin

sin

+

z

cos

cos

A

sin

z

sin















t

tg

sin z  sin A = cos   sin t

sin z  cos A = -cos   sin  + sin   cos   cos t

cos z = sin   sin  + cos   cos   cos t

tg A 









cos sin t

-cos sin + sin cos cos t











Ćwiczenie

1. Obliczyć deklinację i kąt godzinny gwiazdy, mając

dane :



 = 52° 05’=



A = 30° 10’=



z = 54° 30’ =

2. Obliczyć azymut i odległość zenitalną gwiazdy,

mając dane :



 = 52° 05’=



t = 2h 20m =





= 41° 20’ =

W domu 

Imię i nazwisko . . . . . . . . . . . . . . . . . . . . . . . .

N= . .

. . .

M= .

. . . .

N - numer kolejny
M – numer grupy
1. Obliczyć deklinację i kąt godzinny gwiazdy, mając dane :

 = 52° 05’

A = [10+N]° 10’ =
z = [55-M]° 30’ =

2. Obliczyć azymut i odległość zenitalną gwiazdy, mając dane :

 = 52° 05’

t = 2

h

N

m

=

 = [40+M]° 20’ =

WYNIKI :

 = °

‘

t =

h

m

A = °

‘

z = °

‘

Ćwiczenie 2

Rozwiązywanie trójkątów

sferycznych: metoda Legendre’a

i Soldnera.

Trójkąty sferyczne i
paralaktyczne



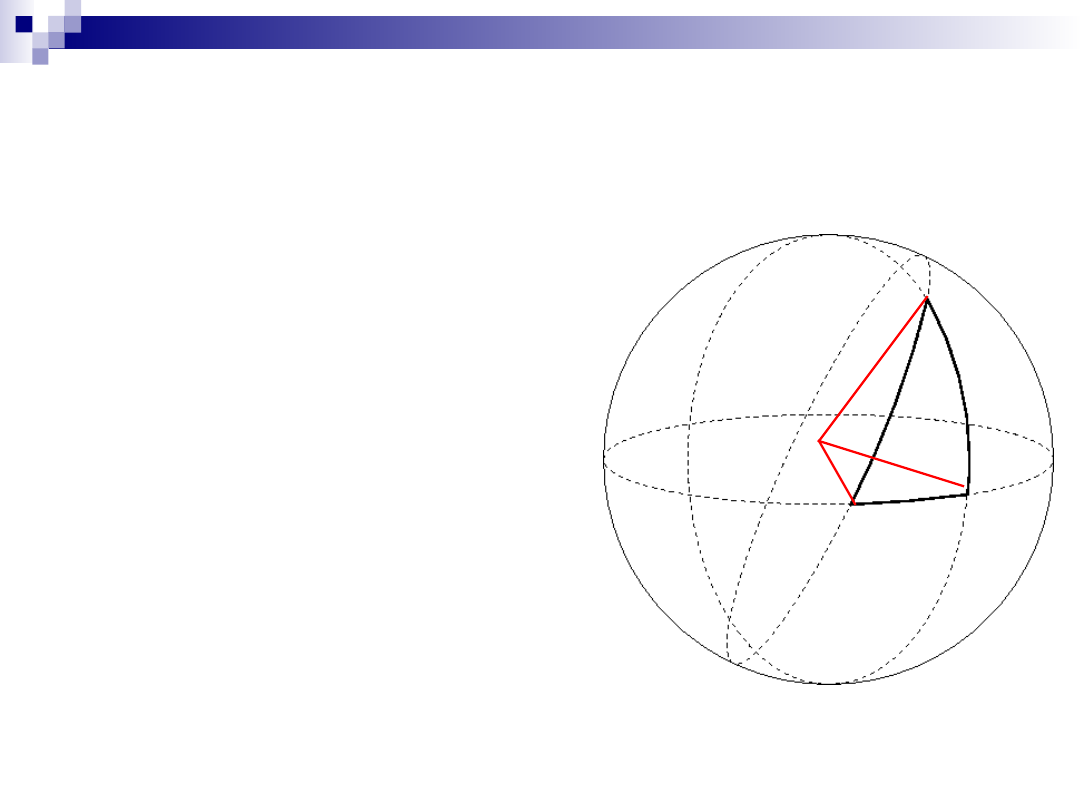
Trójkąt sferyczny

Trójkąt leżący na

powierzchni kuli

Boki są fragmentami

kół wielkich

Boki opisujemy jako

kąty z wierzchołkami
w środku sfery

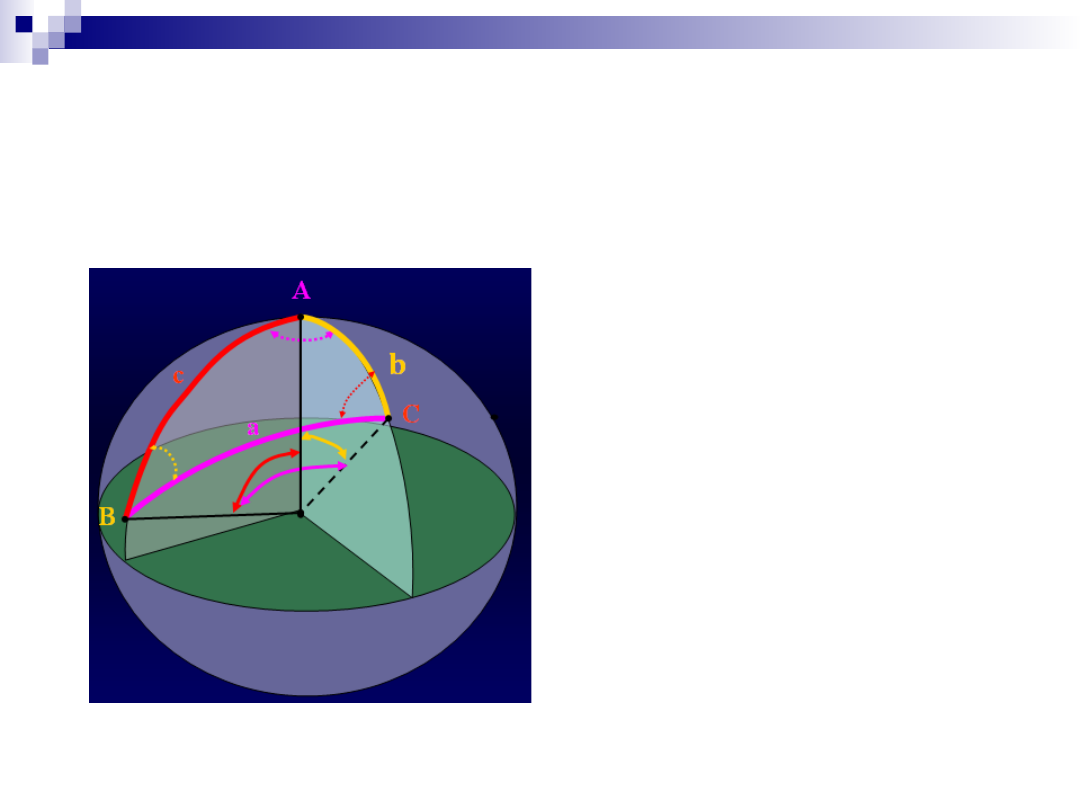
Jednym z głównych zadań geodezji wyższej jest rozwiązywanie
trójkątów geodezyjnych. Jeżeli boki trójkątów triangulacyjnych są
małe w stosunku do promieni krzywizny elipsoidy, to zadanie
rozwiązywania trójkątów elipsoidalnych sprowadza się do rozwiązania
trójkątów sferycznych na kuli o odpowiednio dobranym promieniu.

Znane: A, B, C, a
Szukane: b,c

R=6370 km
a<60 km

Metoda Legendre’a

W celu rozwiązania trójkąta sferycznego możemy posłużyć

się tzw. twierdzeniem Legendre’a, które mówi, że mały

trójkąt sferyczny można rozwiązać zamieniając go na

trójkąt płaski, w którym długości boków pozostają

niezmienione w stosunku do odpowiednich długosci na

sferze, natomiast każdy kąt jest zmniejszony o 1/3

nadmiaru sferycznego.

Wzór na nadmiar sferyczny (eksces sferyczny):

e=(P/R^2)*ro”=((a*b*sinC)/2*R^2)*ro”

b=(a*sinB)

(prawdziwe dla małych trójkątów sferycznych, których boki

mają do 90km, gdyż obliczamy P jak dla trójkata płaskiego)

Gdy mamy wiekszy trójkąt sferyczny korzystamy z

rozszerzonego tw. Legendre’a:

e1=e(1+(m^2/8*R^2))

Gdzie: m^2=(a^2+b^2+c^2)/3

a,b – boki trójkąta płaskiego
C – kąt między nimi zawarty
R – promień kuli, na którym położony jest trójkąt

A’=A-e/3
B’=B-e/3 b=(a*sinB’)/sinA’
C’=C-e/3 c=(a*sinC’)/sinA’

Metoda additamentów (Soldnera)

Metodę tą stosuje się do trójkątów o
małych bokach w stosunku do promienia
kuli, przy czym wyrazy małe wyższych
rzędów zostają opuszczone. Myślą
przewodnią tej metody jest rozwiązanie
trójkątów sferycznych, przy
zastosowaniu wzoru sinusów
trygonometrii płaskiej, po uprzedniej
zmianie boków (a nie kątów jak w
metodzie Legendre’a)

Sin(b/R)= sin(a/R)*(sinB/sinA)

Rozwinięcie w szereg:

ZADANIE



DANE:



B1 = 53° 33’ 01,7594”



L1 = 20° 33’ 52,3613”



h1 = 145,243m



A12 = 8° 07’ 37,11”



s12 = c= 22 858,907m =22,858 907km



kąt 1 = A = 36° 12’ 43,42”



kąt 2 = B = 89° 54’ 51,17”

kąt 1 = A = 0,632019695 rad
kąt 2 = B = 1,569299077 rad

OBLICZENIA Z WYKORZYSTANIEM WZORÓW TRYGONOMETRII

SFERYCZNEJ

1)

zamiana jednostek długości boku na jednostki kątowe

<s12 = (s12/R)*P”
Gdzie:
R = 6370km
Ρ”= 206 264,80624 7096355
<s12 = (22,858 907km /6370km)* P”

<s12 = 0° 12’ 20,19” = 0,003588542386 rad

2) Określenie wartości kąta 3

cos3 = - cos1 cos2 + sin1 sin2 cos s12
cos3 = -cos 0,632019695 rad*cos 1,569299077 rad +
+sin 0,632019695 rad*sin 1,569299077 rad*
cos 0,003588542386 rad

3 = arcos 0,589563023

A+B+C= 36° 12’ 43,42” + 89° 54’ 51,17” + 53° 52’

26,38”

= 180° 00’ 00,97”

cos3 = 0,589563023

3 = 0,940278591
rad
3 = 53° 52’ 26,38”

3) Określenie wartości boku s23

sin s23/sin 1 = sin s12/sin 3
sin s23 = (sin s12*sin 1)/sin 3

s23 = 0,0026246870rad = 0° 09’ 01,38” = 541,38”

4) Określenie wartości boku s13

sin s13/sin 2 = sin s12/sin 3
sin s13 = (sin s12*sin 2)/sin 3

s13 = 0,004442777316rad = 0° 15’ 16,39” = 916,39”

5) zamiana jednostek kątowych na jednostki

długości boku s23

s23 = (<s23/ P”)*R
Gdzie:
R = 6370km
Ρ”= 206 264,80624 7096355

s23 = 16,719239km = 16 719,239m

6) zamiana jednostek kątowych na jednostki długości boku s13
s13 = (<s13/ P”)*R
Gdzie:
R = 6370km
Ρ”= 206 264,80624 7096355

s13 = 28,300535km = 28 300,535m

1) wyznaczanie ekscesu – ε
ε=[(a*b*sinC)/2R2]* P”
ε=[(a*c*sinB)/2R2]* P”
ε =[( 16,719239km*22,858 907km *sin89° 54’

51,17”)/ 2R2]* P”

ε = 0,9714”

2) wyznaczenie odchyłki kątowej
ω = 1’+2’+3’ – (180°+ ε)
ω = 36° 12’ 43,42” + 89° 54’ 51,17” + 53° 52’ 26,38”-
(180°+0,9714”)

ω = 180° 00’ 00,97”– (180°+0,9714”)
ω = -0,0014”

n= c/sinC°
c = n*sinC°
a = n*sinA°
b = n*sinB°

n= c/sinC° = 22 858,907/ 0,807721450= 28 300,483 m
c = n*sinC° = 28 300,483*0,807721450= 22 858,907m
a = n*sinA° = 28 300,483*0,590774260= 16 719,197m
b = n*sinB° = 28 300,483*0,999998876= 28 300,451m

Metoda Additamentów

c’ = c – (c3/6R2)
c = c’+c3 / 6R2c’

= 22,858 858km

= 22,858 907km

a) zmniejszenie boku a:

b) obliczenie pozostałych zmniejszonych boków:

a’ = c’ (sin Awyr/ sin Cwyr )
a’ = 22,858 858km *(sin 36° 12’ 43,4205” / sin 53° 52’ 26,3805” )
a’ = 16,719 178km
a = a’+a’3 / 6R2
a = 16,719 178+0,000 019 = 16,719 197km

b’ = c’ (sin Bwyr/ sin Cwyr )
b’ = 22,858 858km*(sin 89° 54’

51,1705”/ sin 53° 52’ 26,3805” )

b’ = 28,300 358km
b = b’+b’3 / 6R2
b = 28,300 358km +0,000 093 =

28,300451km

W domu 

ROZWIĄZYWANIE TRÓJKĄTÓW SFERYCZNYCH

Wzory trygonometrii sferycznej

Metoda Legendre’a

Metoda additamentów (Soldnera)

Dane:



B1 = 53° 33’ 01,7573” + n*0,0001” = 53° 33’ 01,7594”



L1 = 20° 33’ 52,3634” - n*0,0001” = 20° 33’ 52,3613”



h1 = 145,243m



A12 = 8° 07’ 35,01” + n*0,10” = 8° 07’ 37,11”



s12 = c= 22 856,807m +n*0,10m = 22 858,907m =22,858

907km



kąt 1 = A = 36° 12’ 41,32” + n*0,10” = 36° 12’ 43,42” =

0,632019695 rad



kąt 2 = B = 89° 54’ 51,17” = 1,569299077 rad