Modele nieliniowe

sprowadzane do

liniowych

przykład

Model nieliniowy

– często

wykorzystywany do opisu wielu zjawisk
ekonomicznych. Występuje tutaj
ograniczona możliwość estymacji,
jednak można ją przezwyciężyć poprzez
przekształcanie modelu nieliniowego na
liniowy, wówczas powstaje

model

linearyzowany

. Będzie to pomocniczy

model, który pomoże opisać zjawiska
ekonomiczne, a występujące w nim
zmienne to

zmienne pomocnicze

.

Model hiperboliczny

teoria

Przykładowe zastosowanie
modelu hiperbolicznego

• Szacowanie jednostkowego kosztu

całkowitego jako funkcji wielkości
produkcji

ZADANIE

• X

– średni koszt jednostkowy w tys zł

• Y

– średnia wielkość produkcji w tys

szt

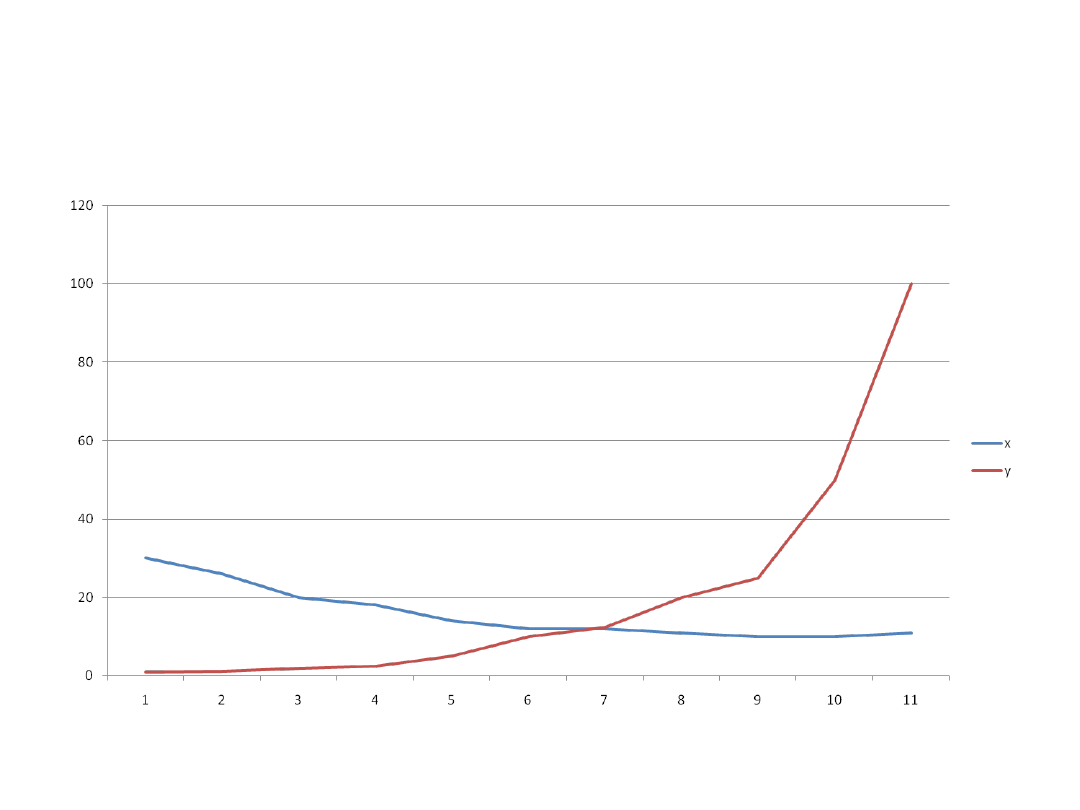
Analiza zależności średniej wielkości
produkcji od średnich kosztów
całkowitych w pewnym
przedsiębiorstwie w latach 2000-
2010

lata

X

Y

2000

30

1

2001

26

1,25

2002

20

2

2003

18

2,5

2004

14

5

2005

12

10

2006

12

12,5

2007

11

20

2008

10

25

2009

10

50

2010

11

100

Ponieważ zebrane dane mają postać

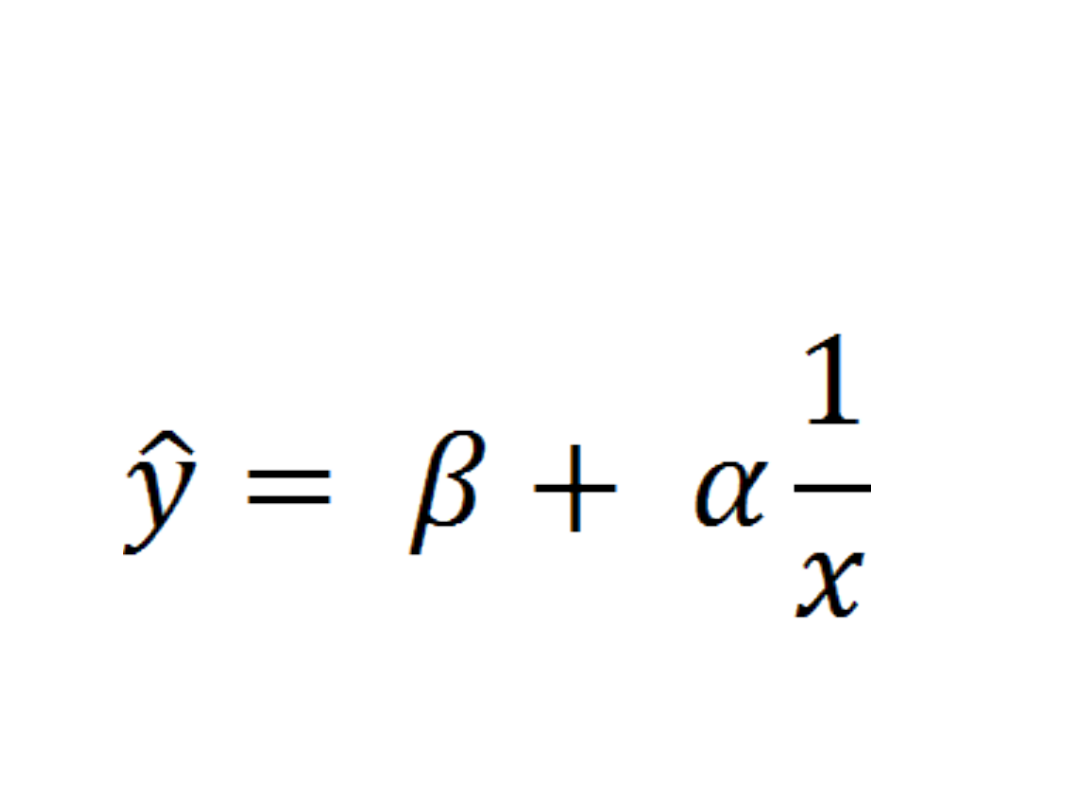
Z wykresu wynika, że jest to model
nieliniowy, w tym przypadku hiperboliczny,
którego postać ogólna jest dana
równaniem:

Aby oszacować
parametry równania,
sprowadzamy
dotychczasowe
równanie do równania
liniowego…

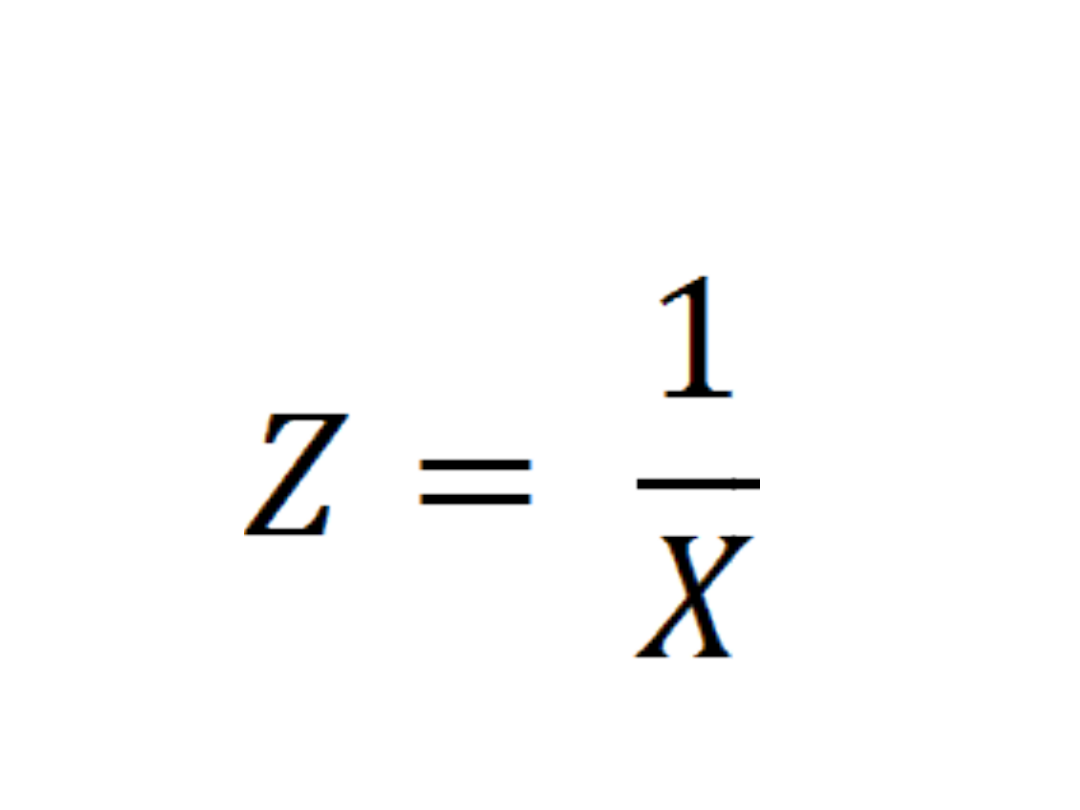
Podstawiamy więc…

I otrzymujemy…

lata

y

x

Z

2000

1

30

0,0333

2001

1,25

26

0,0385

2002

2

20

0,0500

2003

2,5

18

0,0556

2004

5

14

0,0714

2005

10

12

0,0833

2006

12,5

12

0,0833

2007

20

11

0,0909

2008

25

10

0,1000

2009

50

10

0,1000

2010

100

11

0,0909

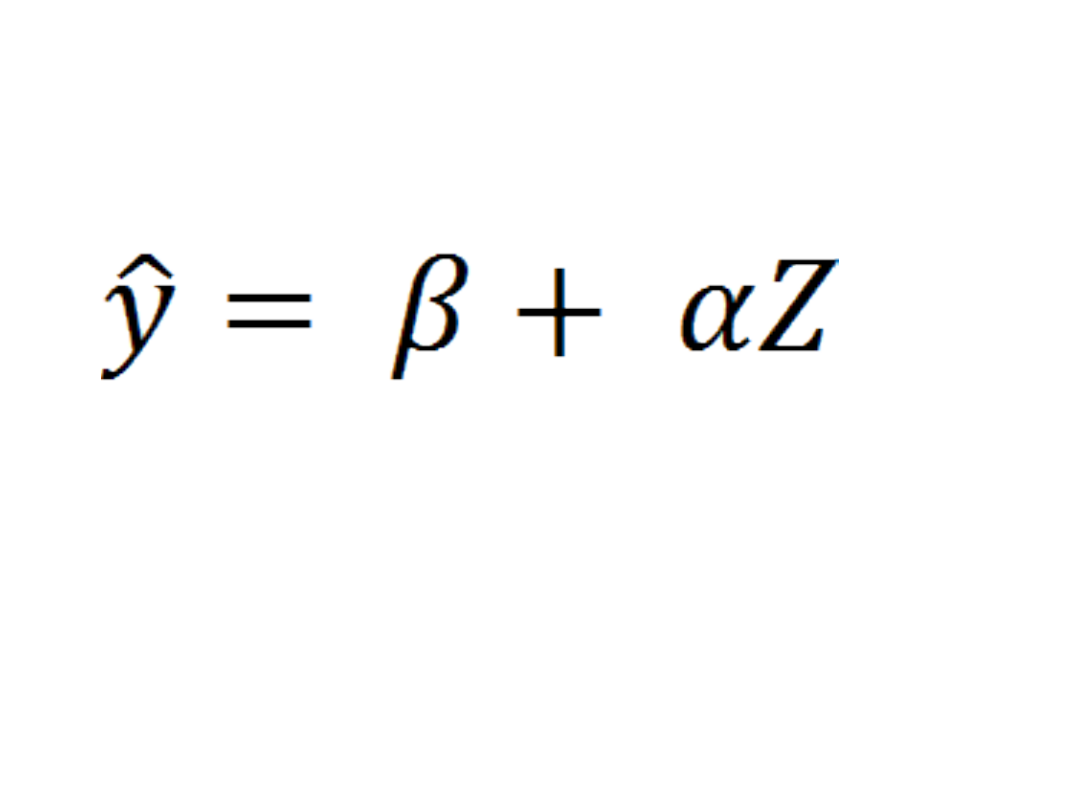
Po podstawieniu nowe
równanie ma postać…

Model ten jest liniowy względem nowej zmiennej
objaśniającej Z

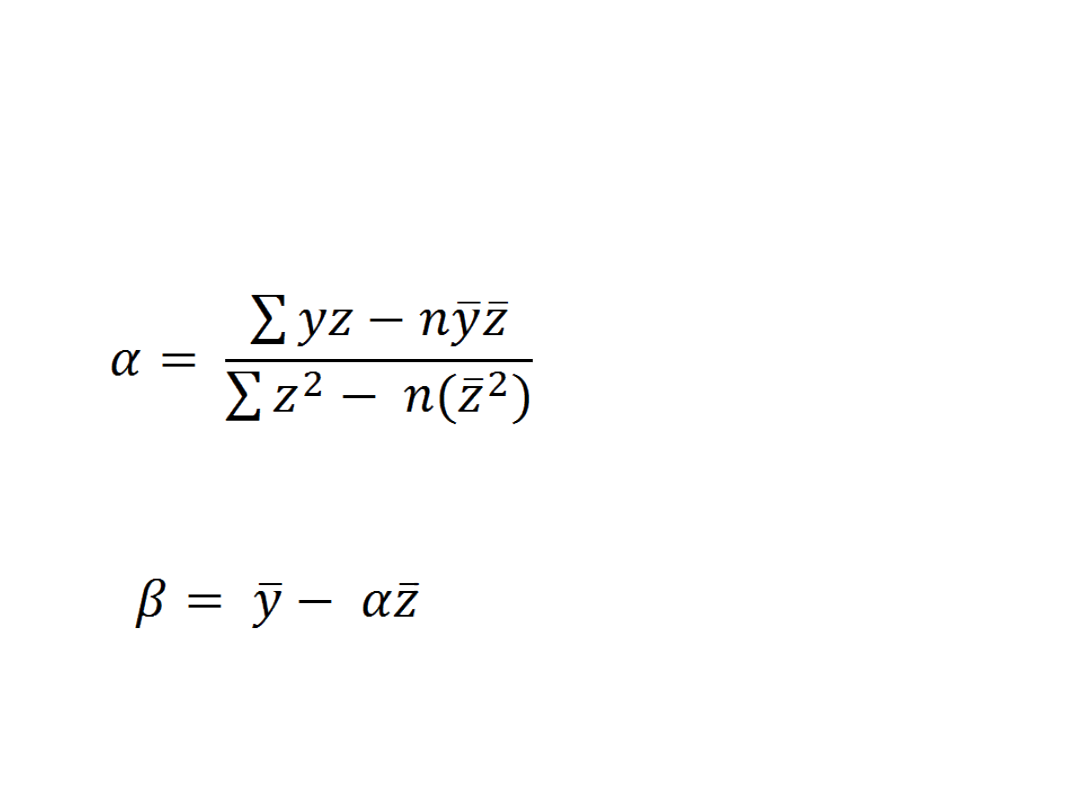
Wyznaczanie parametrów
równania za pomocą metody
najmniejszych kwadratów

n = 11

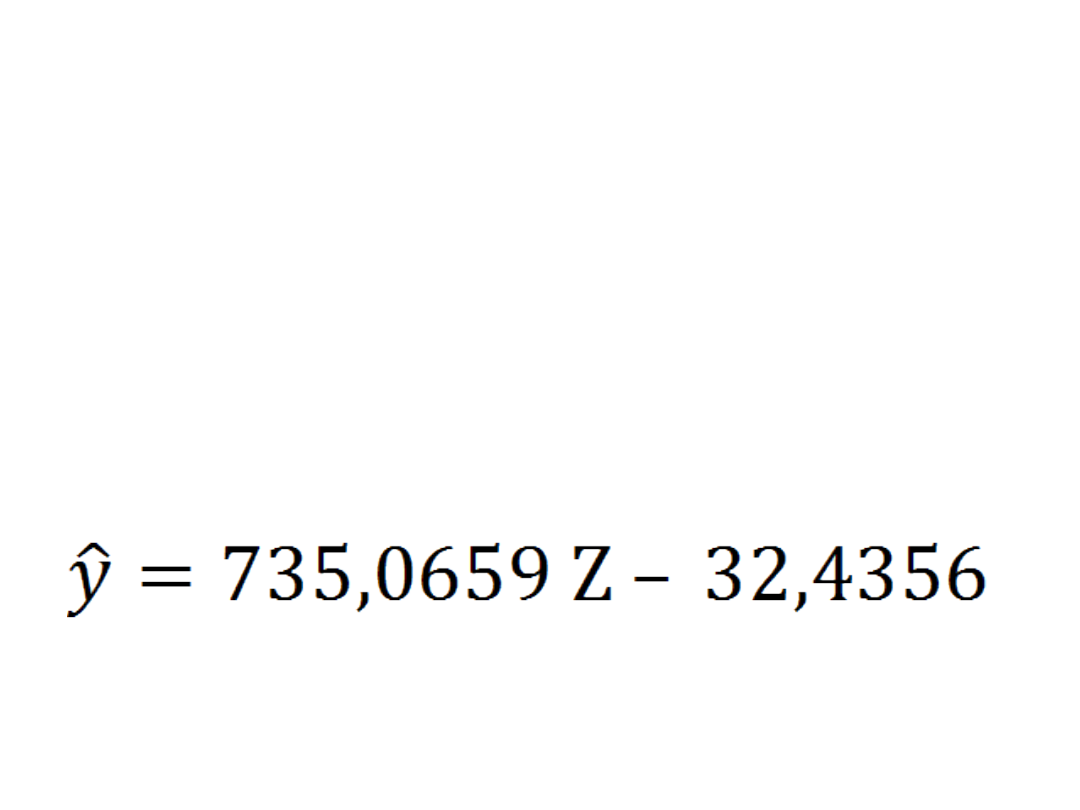
Po podstawieniu do wzoru
otrzymujemy parametry
równania

a = 735,0659
b = -32,4356

Więc model ma postać

•-32,4356

– wartość teoretycznego,

średniego poziomu produkcji w tys. zł. przy
założeniu że średni koszt jednostkowy
produkcji w tys. zł. jest równy zero.

•735,0659

– jeśli średni koszt

produkcji zwiększy się o 1 tys. zł. to
wartość średniego poziomu produkcji
wzrośnie o 735,0659 tys. zł.

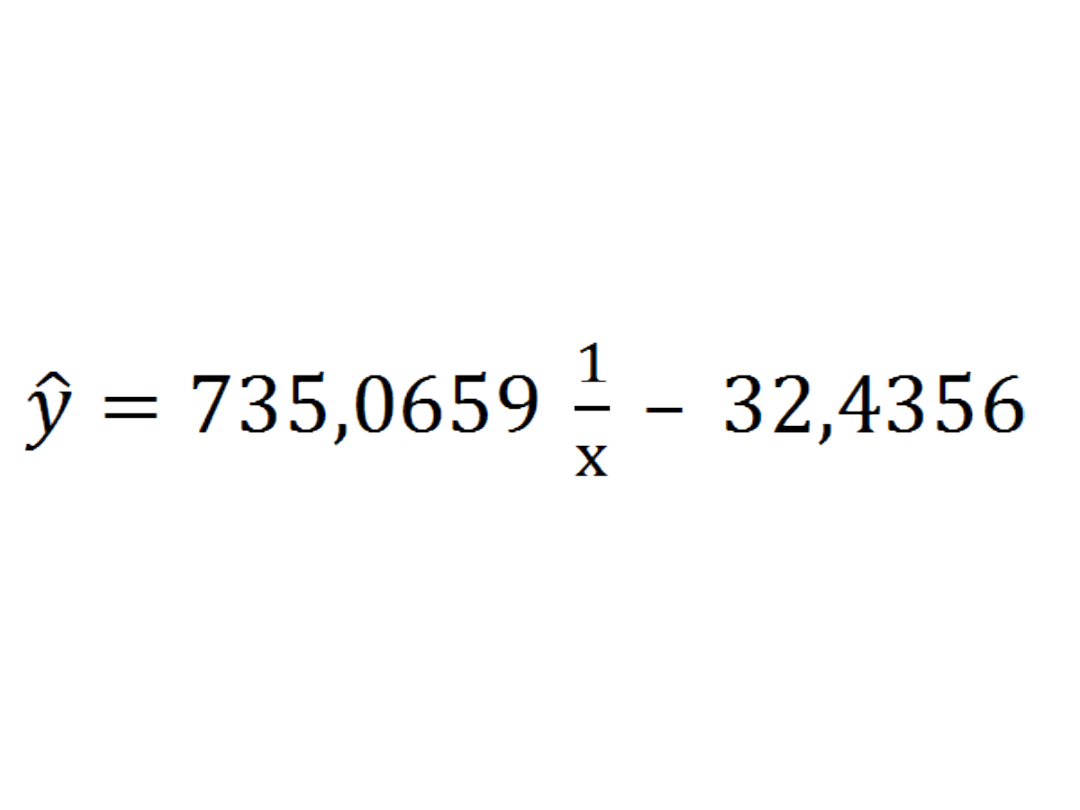
Model pierwotny

•-32,4356

– wartość teoretycznego,

średniego poziomu produkcji w tys. zł. przy
założeniu że średni koszt jednostkowy
produkcji w tys. zł. jest równy zero.

•735,0659

– jeśli średni koszt

produkcji zwiększy się o 1 tys. zł. to
wartość średniego poziomu produkcji
wzrośnie z odwrotnością o 735,0659 tys. zł.

Weryfikacja

modelu

Weryfikacja modelu

Cel:

badanie czy zbudowany model

dobrze opisuje badane zależności

Weryfikacja sprowadza się do zbadania
trzech właściwości:



Stopnia zgodności modelu z danymi
empirycznymi



Jakości ocen parametrów strukturalnych



Rozkładu odchyleń losowych

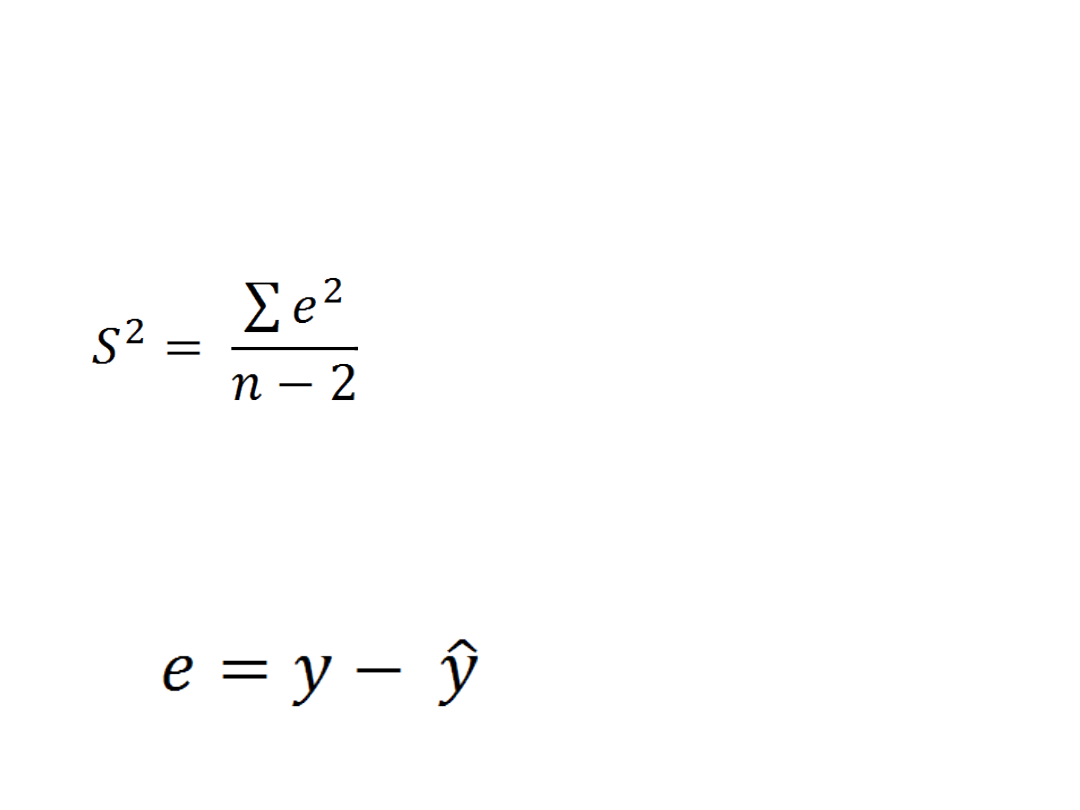
Ocena zgodności modelu
z danymi empirycznymi

• Wariancja odchyleń losowych

Gdzie e jest różnicą wartości empirycznej i

teoretycznej wynikającej z modelu

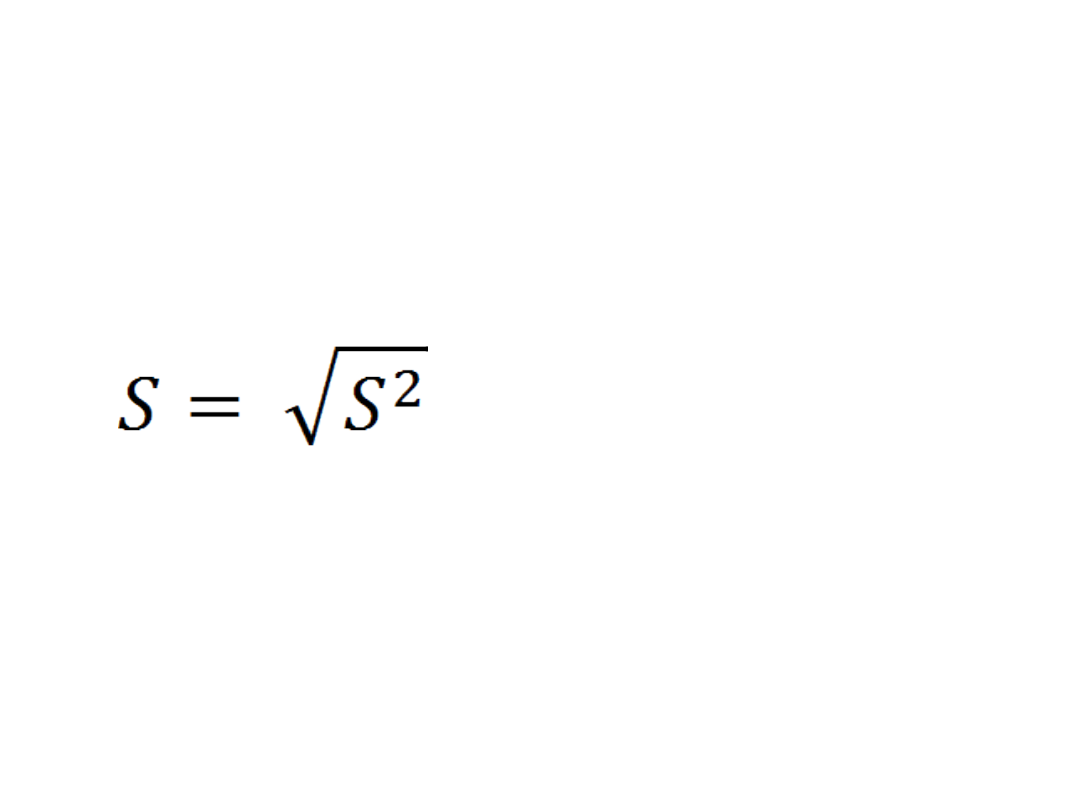
• Odchylenie standardowe

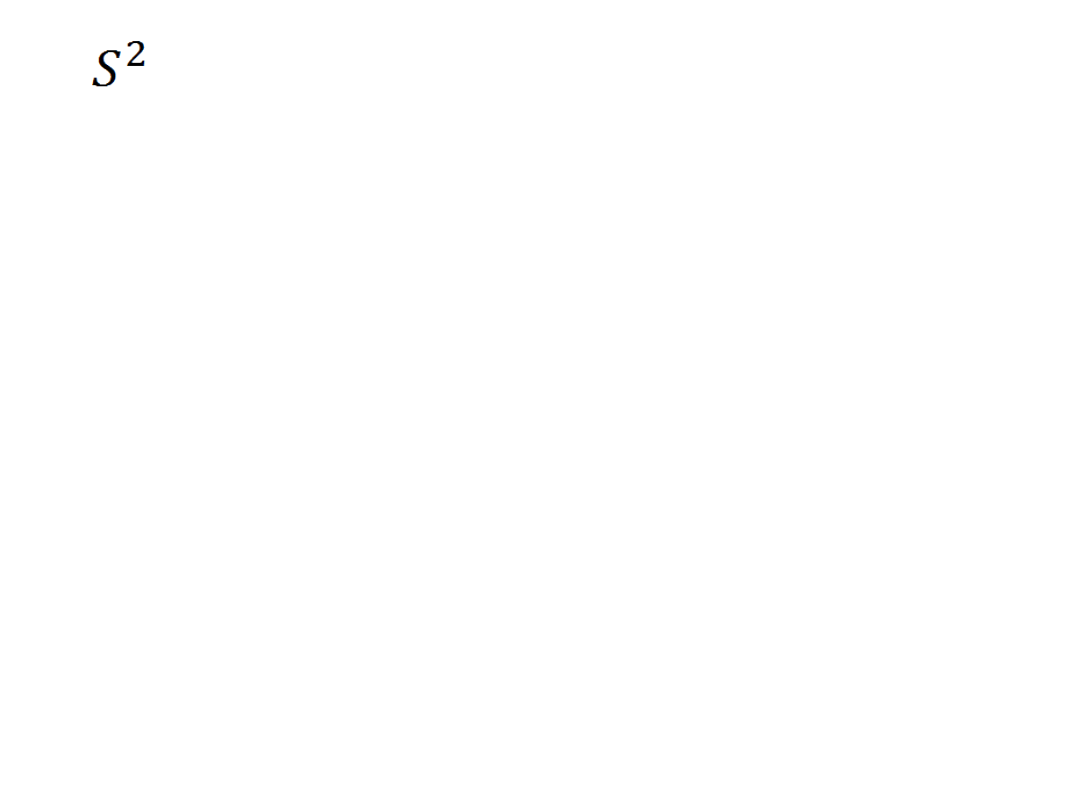
• = 649,6459

• S = 25,48815

– zaobserwowane

wartości zmiennej objaśnianej
(średniej wielkości produkcji)
przeciętnie różnią się od
teoretycznych wartości tych
zmiennych o 25,49 tys. zł. Taka
wartość świadczy o stosunkowo
dobrym dopasowaniu modelu do
danych empirycznych.

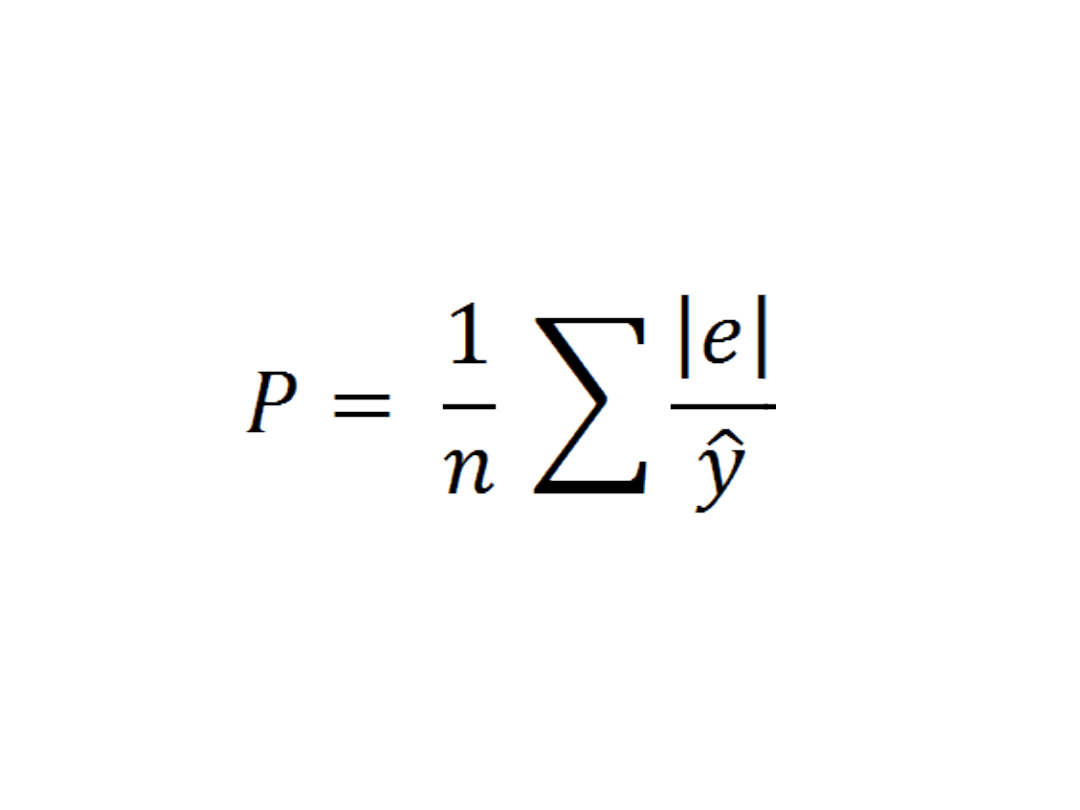
• Wskaźnik średniego względnego

poziomu reszt

P = 0,338

– reszty modelu

stanowią 0,338 teoretycznych
wartości zmiennej objaśnianej. W
związku z tym można uznać, że
dopasowanie modelu do danych
jest stosunkowo dobre

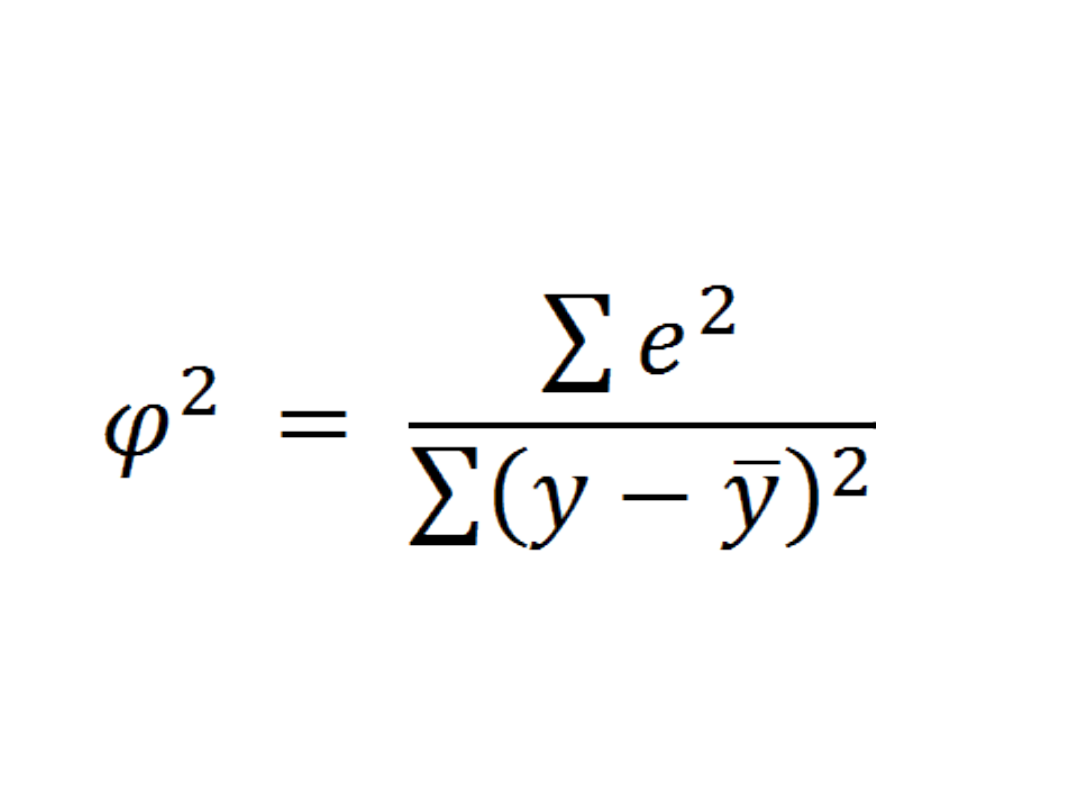
•Współczynnik zbieżności

=

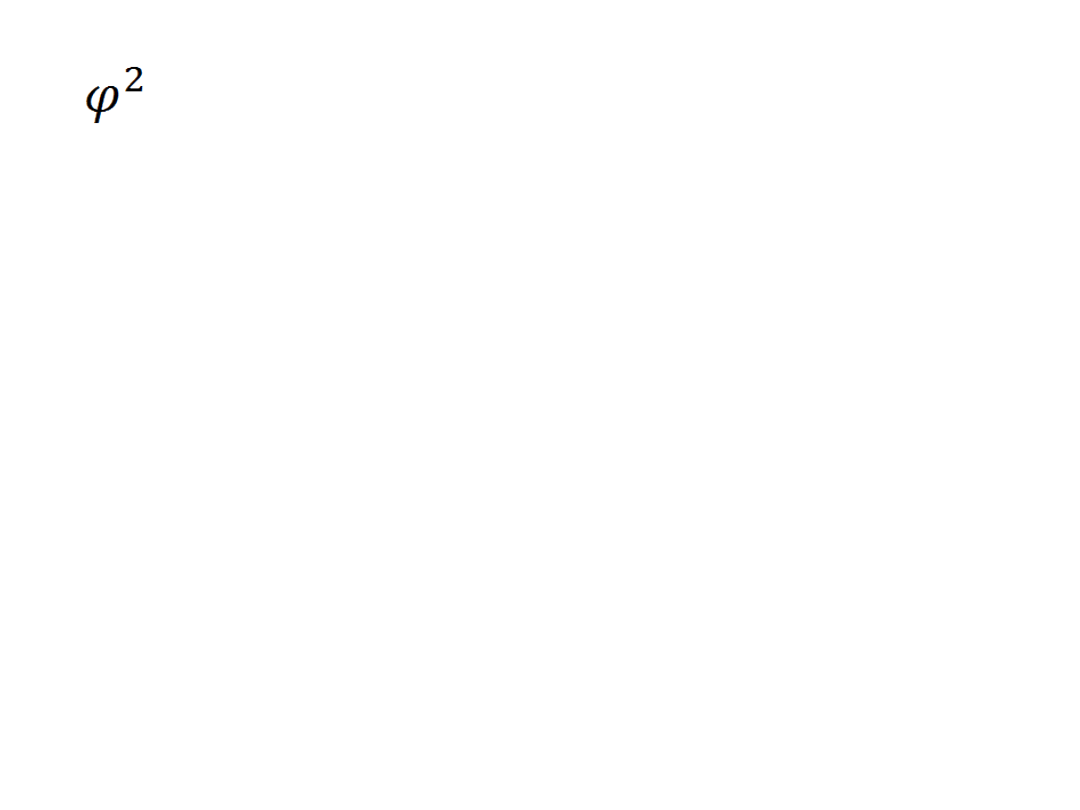
0,6467

– oznacza to że

ok.

64,67%

całkowitej zmienności

zmiennej objaśnianej nie jest
wyjaśniona przez model, oznacza to
że

64,67%

zmienności całkowitego

średniego poziomu wielkości produkcji
nie jest wyjaśniana przez zmienne
średnich kosztów. Wysoka wartość
tego wskaźnika świadczy o tym że
model nie jest dobrze dopasowany do
danych.

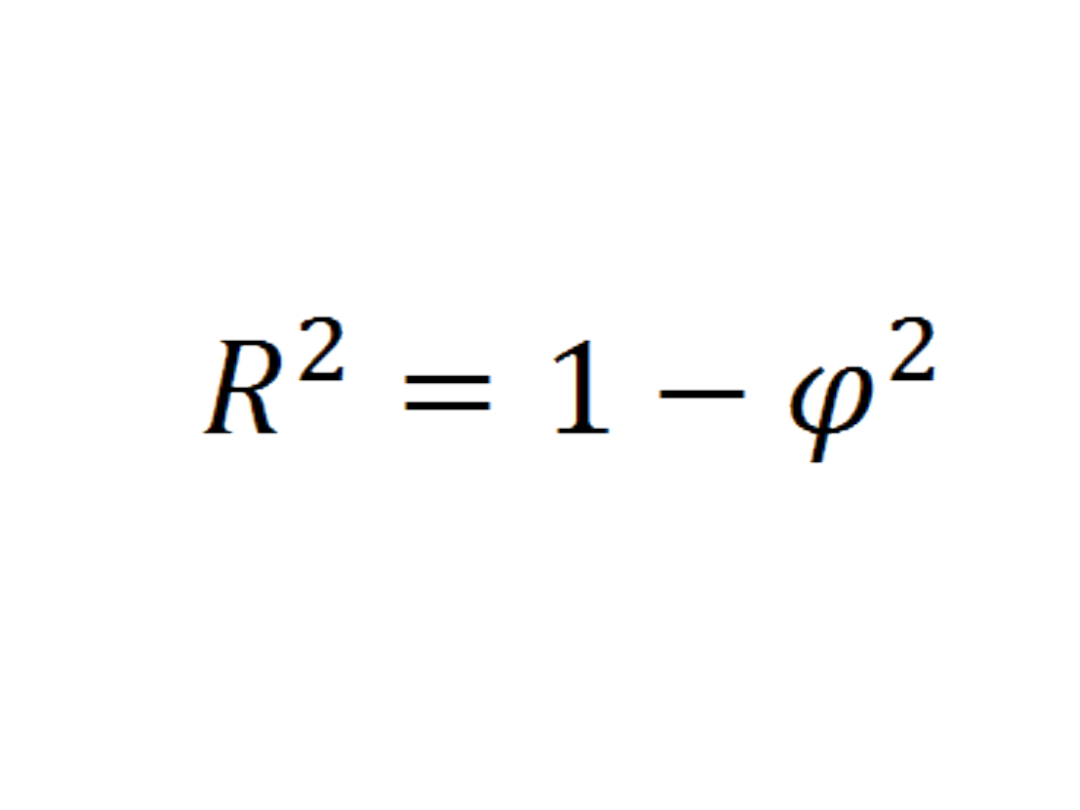
•Współczynnik

determinacji

=

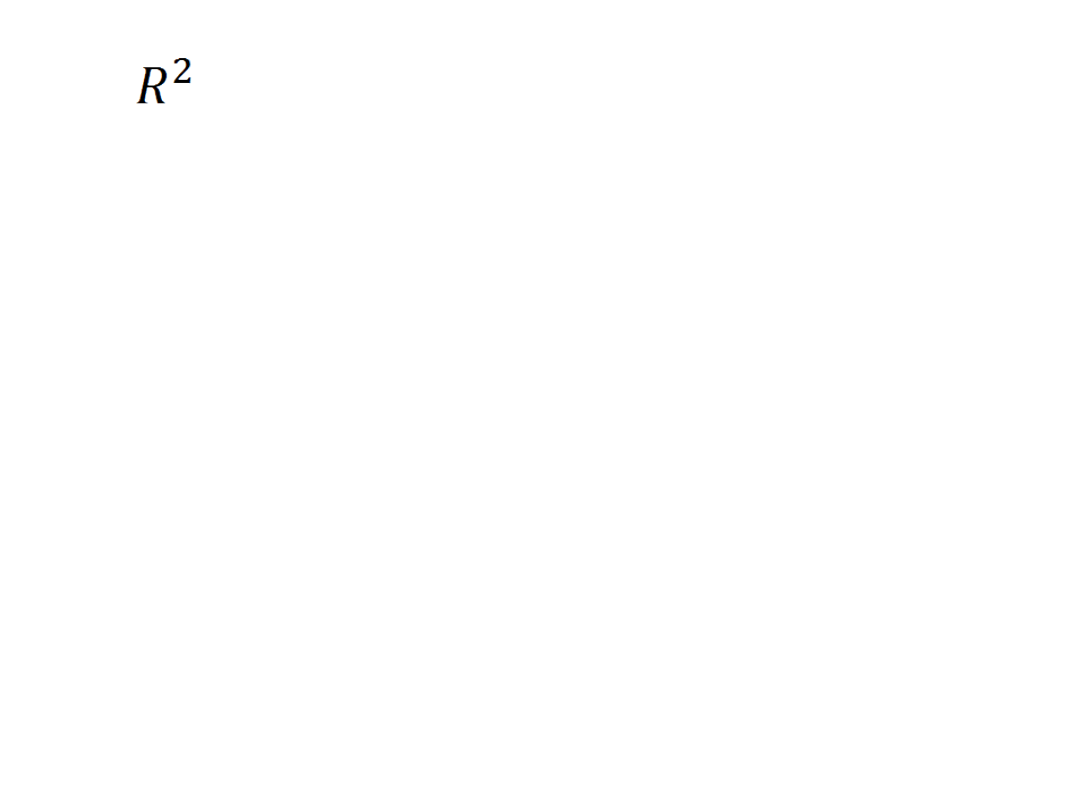
0,3533

– oznacza to że

wartości teoretyczne zmiennej
objaśniającej stanowią

35,33%

całkowitej zmienności zmiennej
objaśnianej. Jest to część
zdeterminowana przez zmienne
objaśniające. Wynika stąd, że

35,33%

zmienności całkowitego średniego
poziomu produkcji jest wyjaśniana przez
zmienne średnich kosztów. Niska
wartość tego wskaźnika wskazuje na złe
dopasowanie modelu do danych.

Badanie istotności
parametrów
strukturalnych

• Standardowe błędy szacunku

parametrów modelu –

wartość

względna

• Standardowe błędy szacunku

parametrów modelu –

wartość

bezwzględna

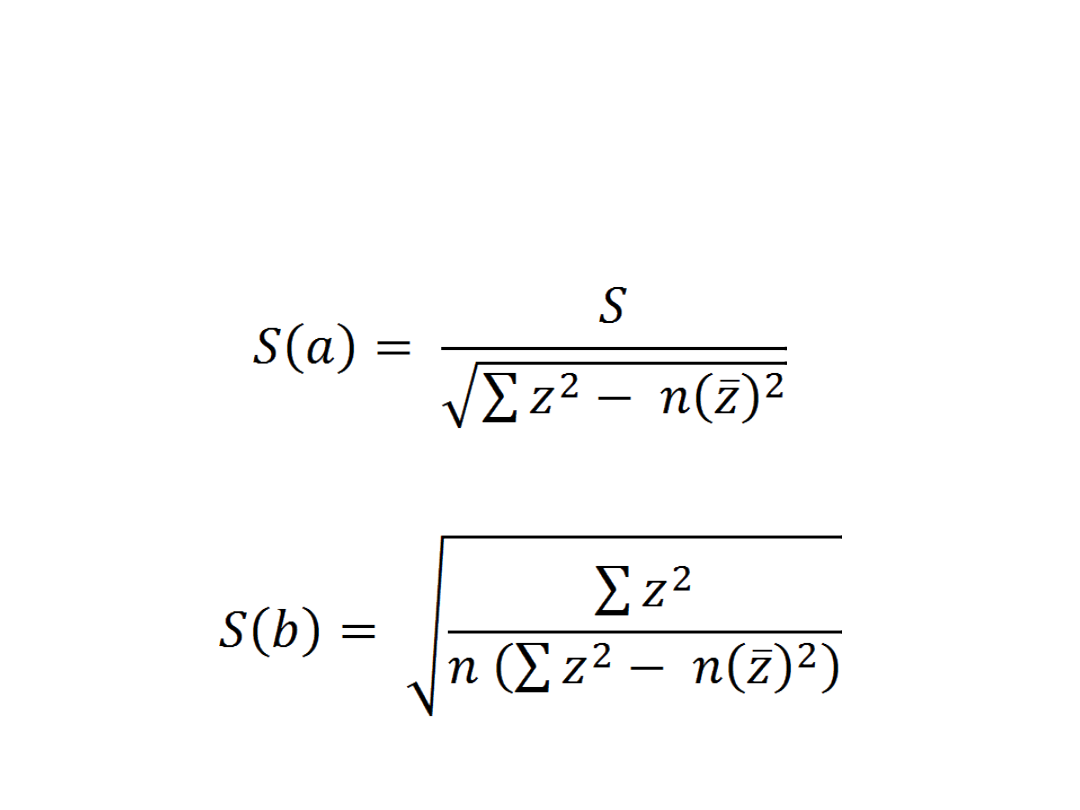
Standardowe błędy szacunku

parametrów modelu – wartość

względna

• Dla parametru a

• Dla parametru b

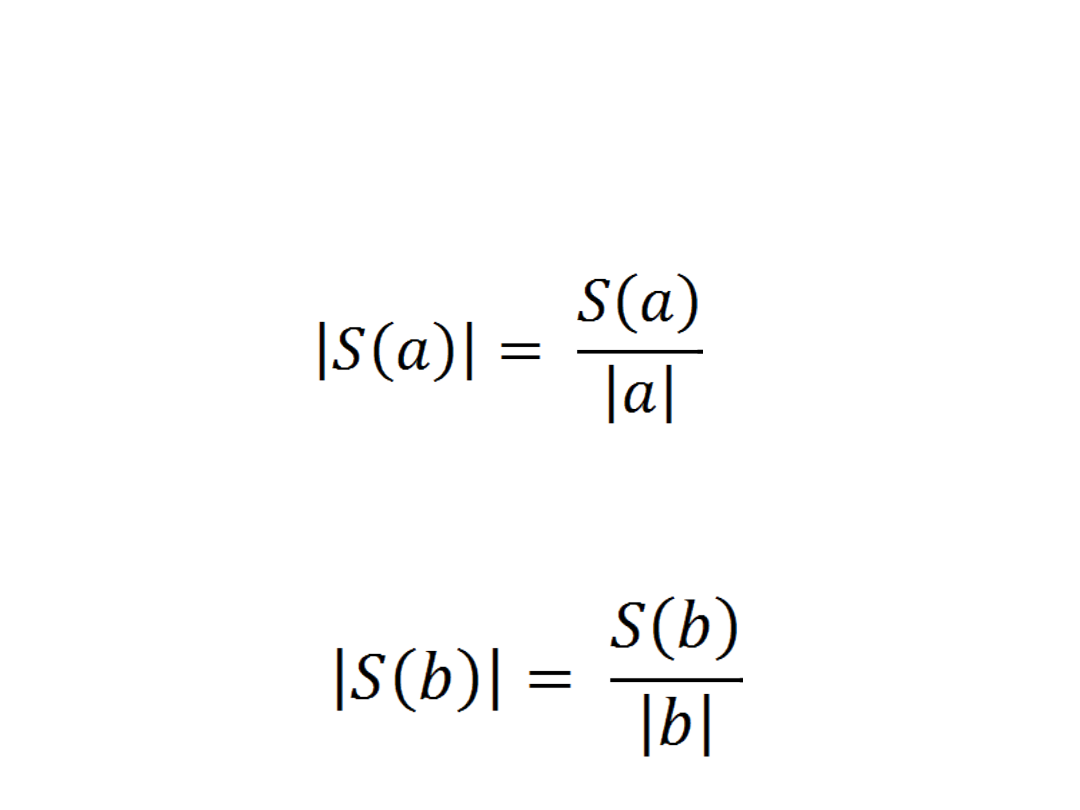
Standardowe błędy szacunku

parametrów modelu – wartość

bezwzględna

• Dla parametru a

• Dla parametru b

•

S(a) = 331,486

– szacując

parametr a na poziomie 735,0659,
popełniamy średni błąd

331,486

, co

stanowi

45,1%.

Błąd w tym przypadku

jest stosunkowo mały.

•

S(b) = 25,2248

– szanując

parametr b na poziomie -32,4356,
popełniamy średni błąd

25,2248

, co

stanowi

77,77%

. Błąd w tym przypadku

jest stosunkowo duży.

Określenie relatywnego wpływu
zmiennych objaśniających na
zmienną objaśnianą

• Współczynnik ważności

b = 2,5563

– taka wartość tego

wskaźnika świadczy o tym, że
zmienna objaśniająca ma relatywnie
większy wpływ na wartość zmiennej
objaśnianej. Oznacza to że wartość
średnich kosztów produkcji ma
większy wpływ na średnią wielkość
produkcji.

Prognozowani

e

Predykcja

ekonometryczna

Cel:

oszacowanie wartości

nieznanej zmiennej w określonym
czasie w przyszłości na podstawie
danego modelu ekonometrycznego.

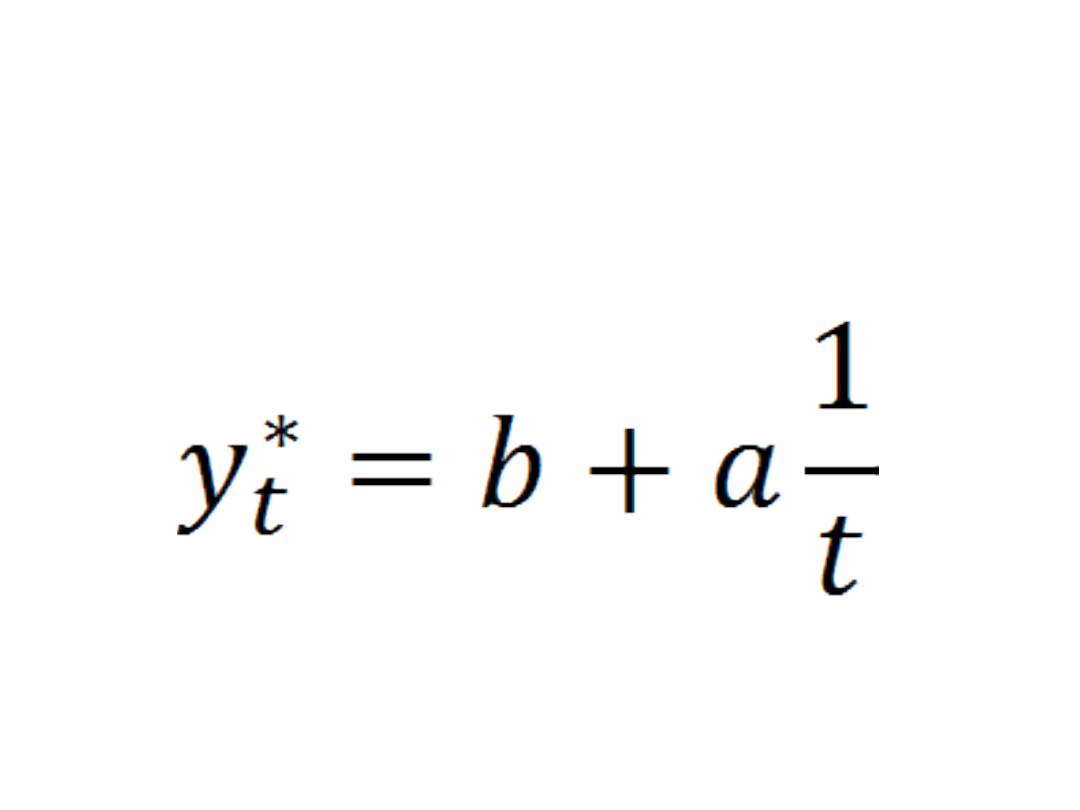
Ponieważ model jest nieliniowy, a jego
posrać sprowadza się do funkcji
hiperbolicznej, to model trendu będzie
miał postać…

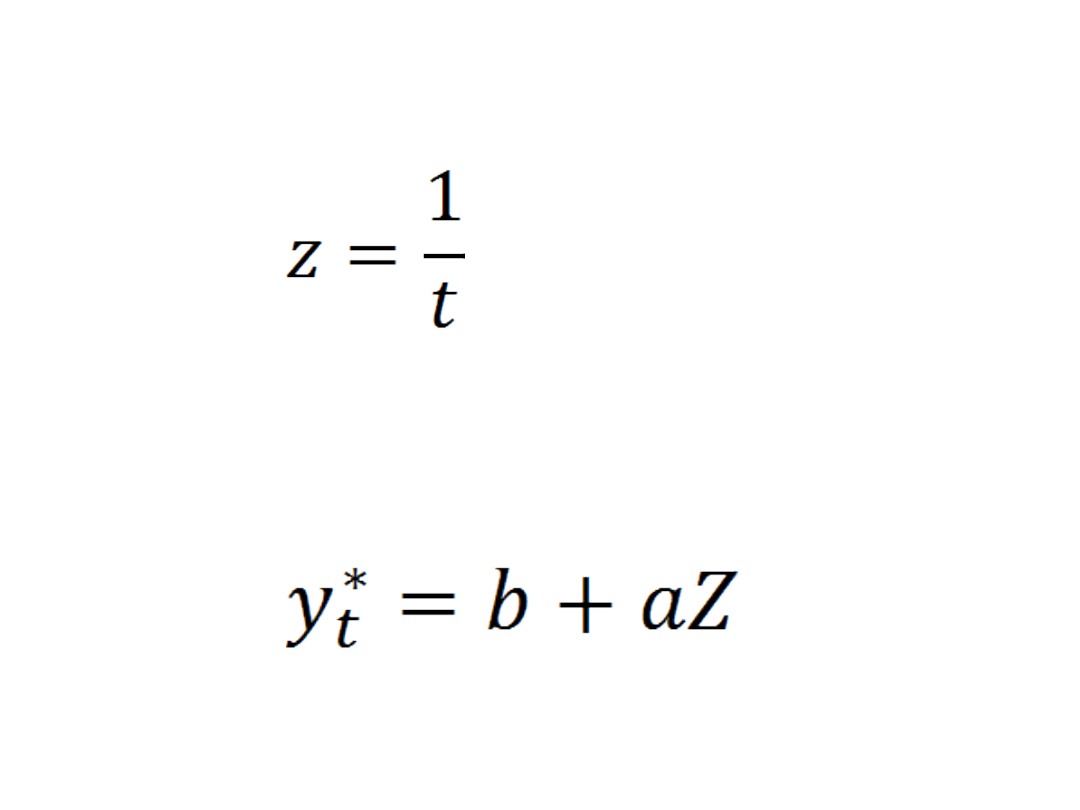
Po sprowadzeniu modelu do postaci
liniowej, czyli

to model będzie miał postać

lata

t

y

2000

1

1

2001

2

1,25

2002

3

2

2003

4

2,5

2004

5

5

2005

6

10

2006

7

12,5

2007

8

20

2008

9

25

2009

10

50

2010

11

100

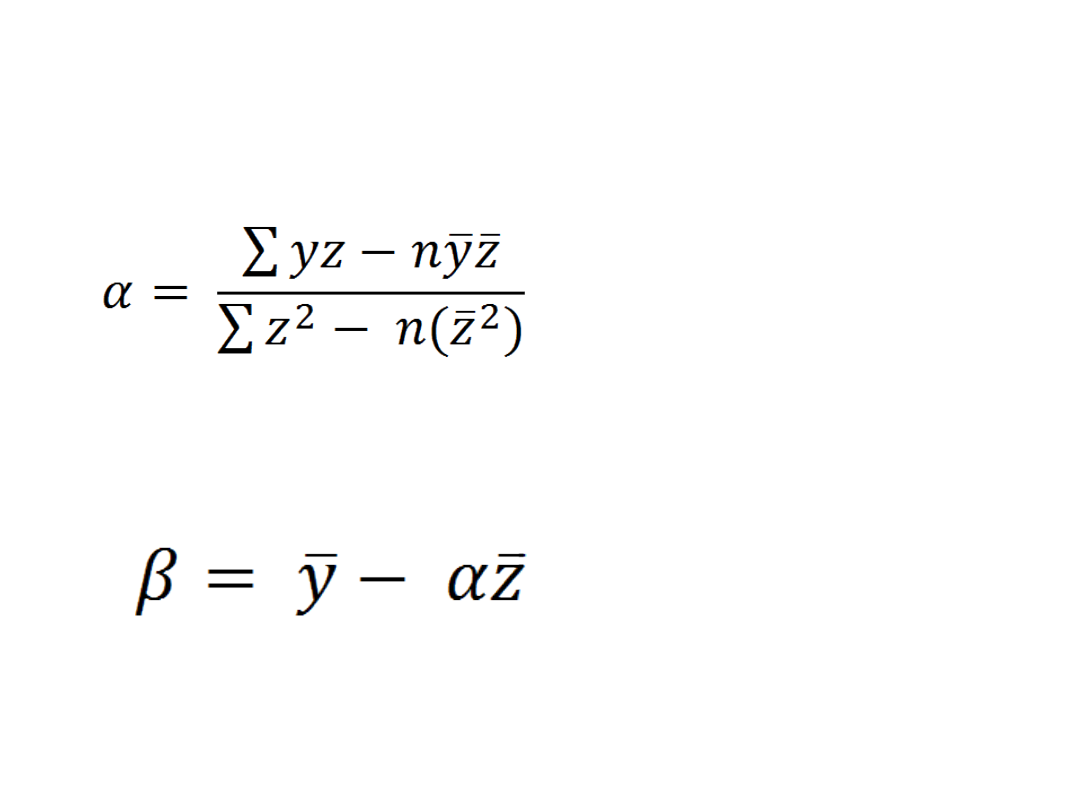
Do oszacowania parametrów funkcji
trendu posługujemy się wzorami

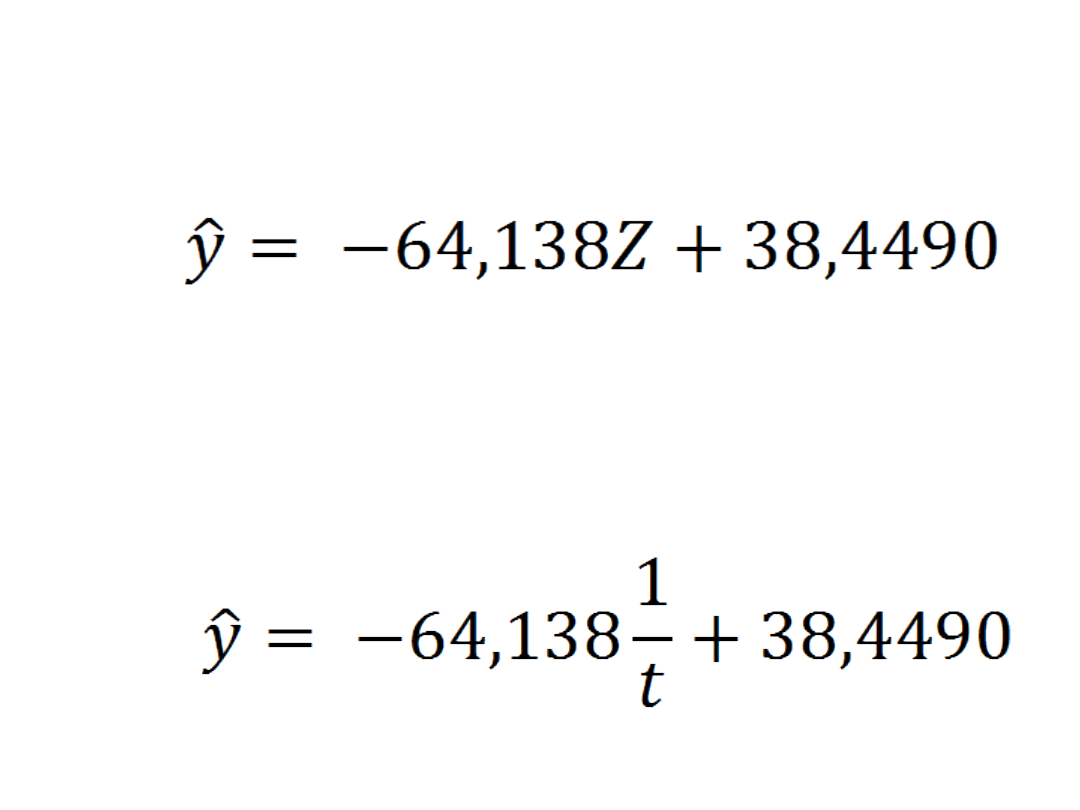
Po oszacowaniu parametrów model
ma postać

a pierwotna postać modelu

a=-64,138

– z każdym

rokiem w latach 2000-2010 średnia
wielkość produkcji malała z roku na
rok przeciętnie o 64,138 tys. szt.

b= 38,449

– teoretyczna

wielkość produkcji w okresie t=0 czyli
w 1999r wynosiła 38,449 tys. szt.

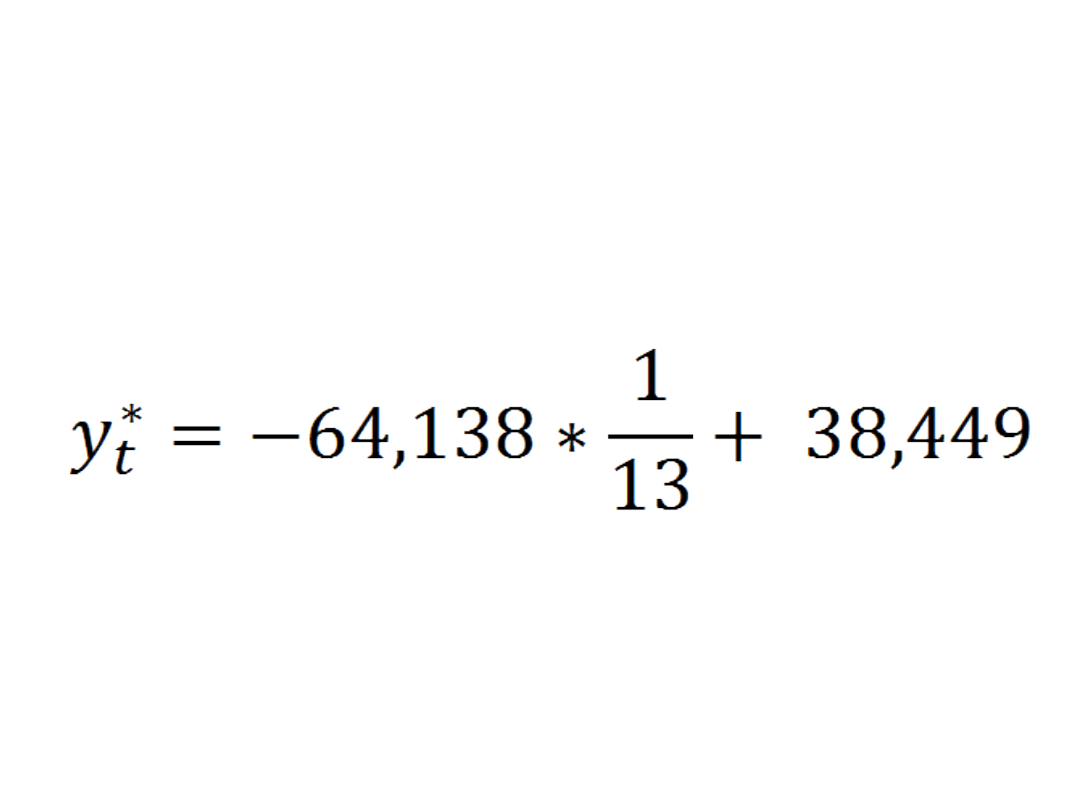
Na podstawie modelu trendu możemy
wyznaczyć jaka będzie prognozowana
wielkość produkcji w roku 2012 czyli
w okresie T=13

= 33,5153

–

prognozowana wielkość produkcji w
roku 2012 czyli w okresie T=13
wynosi 33,5153 tys. szt.

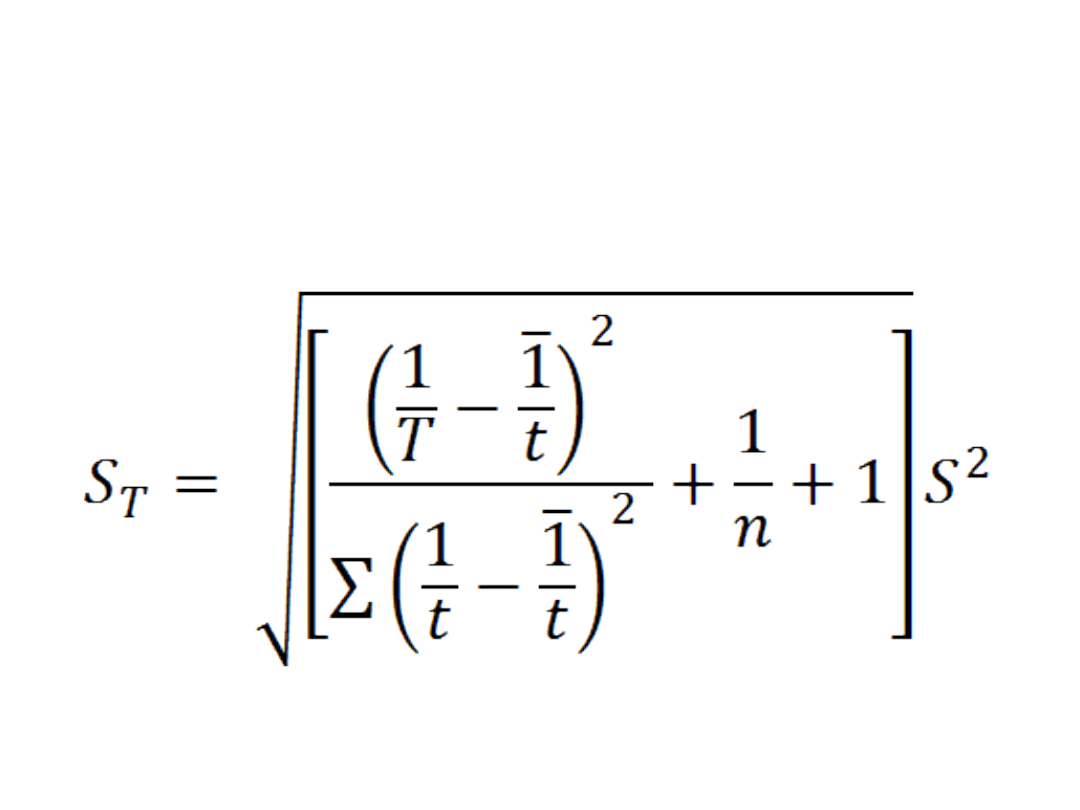
Średni błąd prognozy

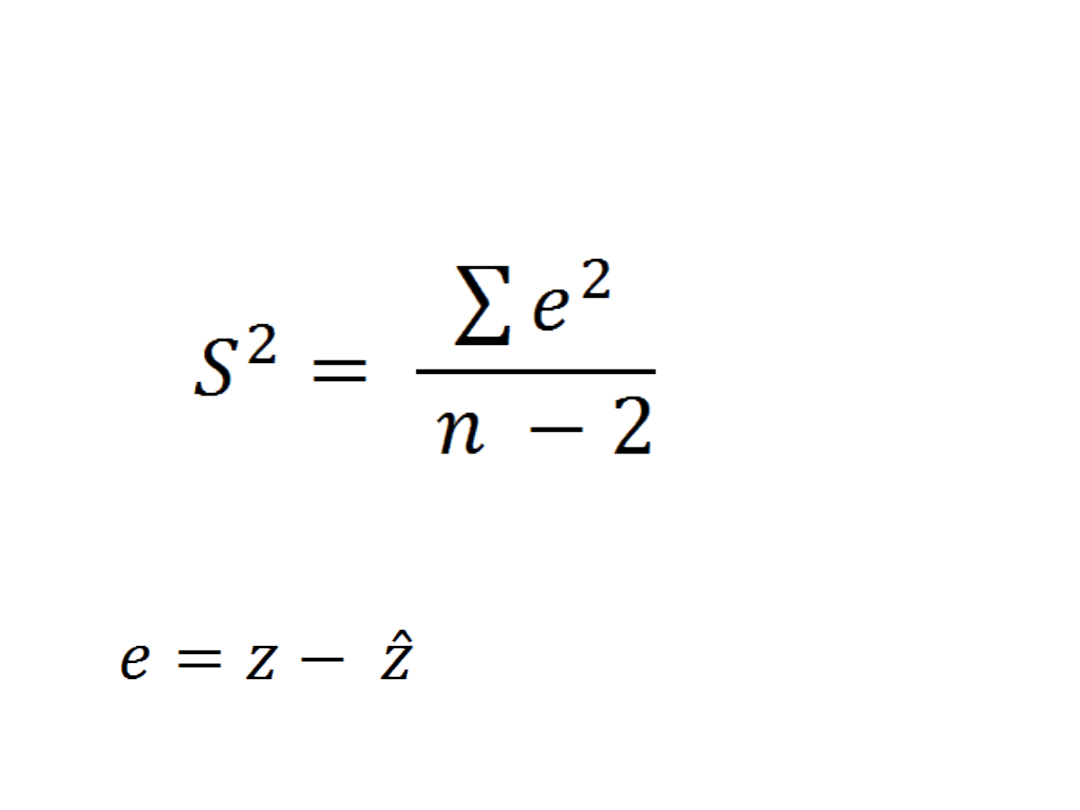
Wariancja resztowa

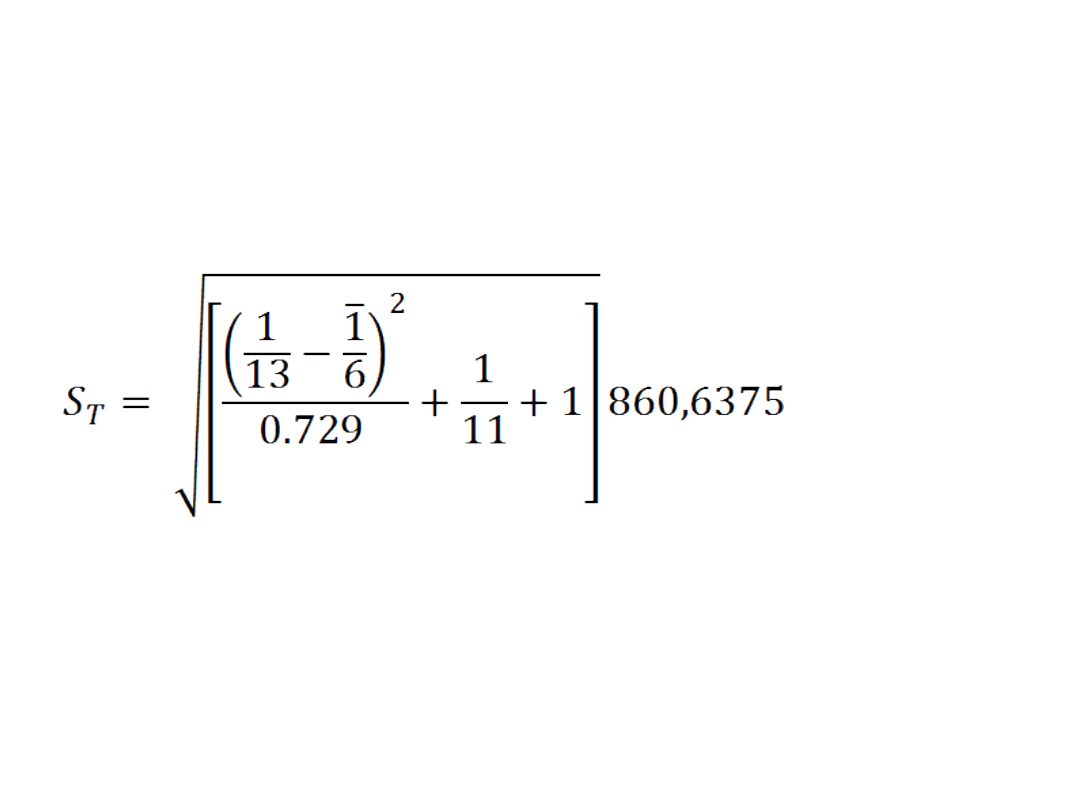
Po podstawieniu…

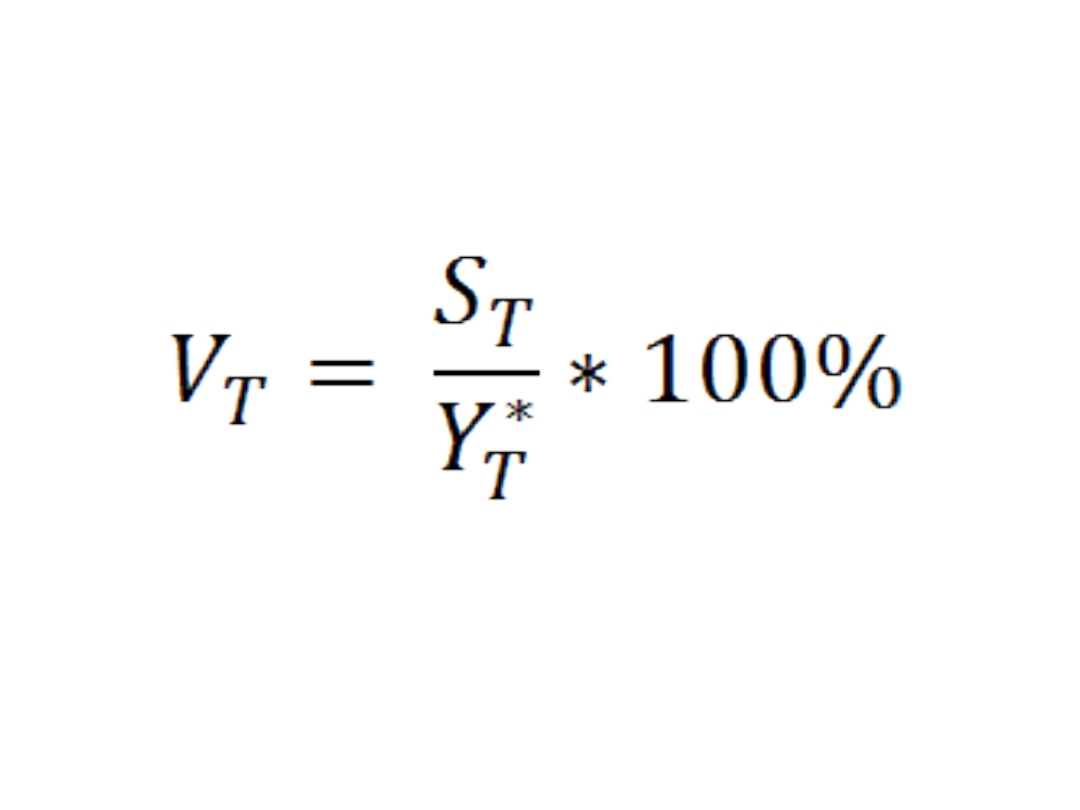
Względny błąd prognozy

St=31,3844

– szacując

wielkość produkcji w okresie T=13 na
poziomie 33,5153 tys. Szt. Mylimy się
średnio o 31,3844 tys. Szt, co stanowi
ok. 93,64%. Ponieważ błąd ten jest
stosunkowo duży możemy prognozę
tą odrzucić.