
RÓWNANIA
SPROWADZALNE
DO RÓWNAŃ
KWADRATOWYCH
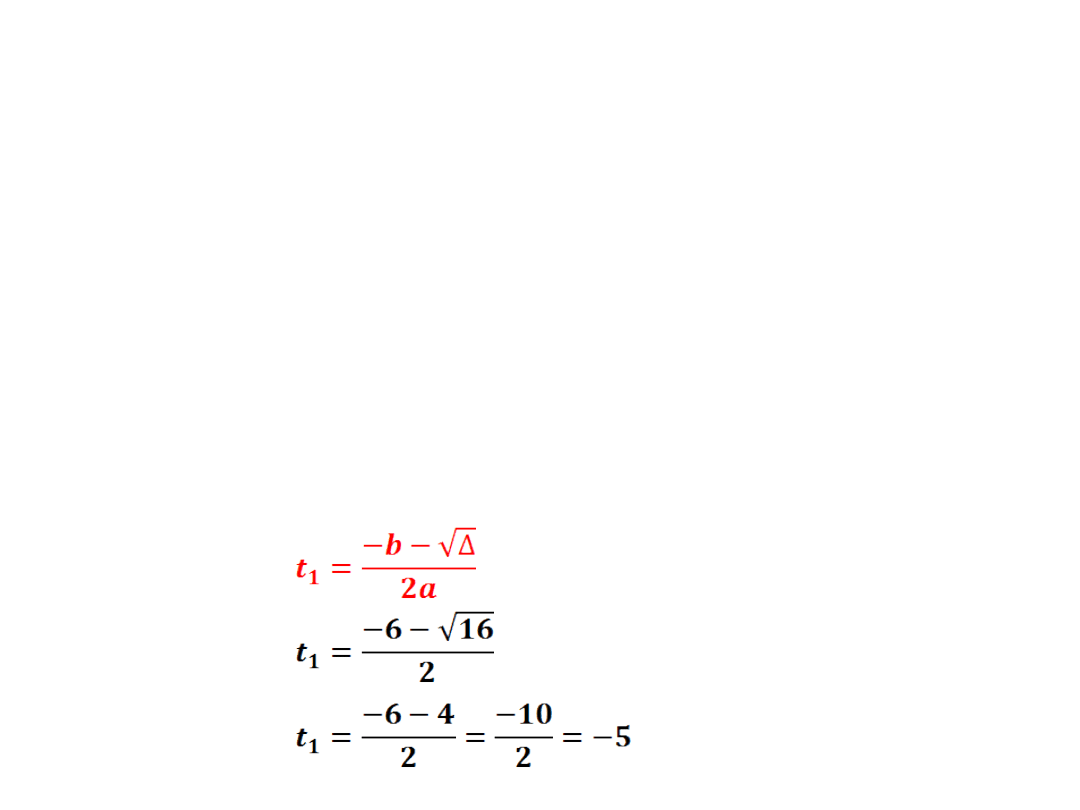
ROZWIĄŻ RÓWNANIA:
1) x
4
+6x
2
+5=0
(x
2
)
2
+6x
2
+5=0
podstawiam x
2
=t
t
2
+6t+5=0
a=1 b=6 c=5
Δ = b
2
-4ac
Δ = 6
2
-4·1·5=36-20=16
Δ
>
0
- wyznaczamy dwa miejsca zerowe
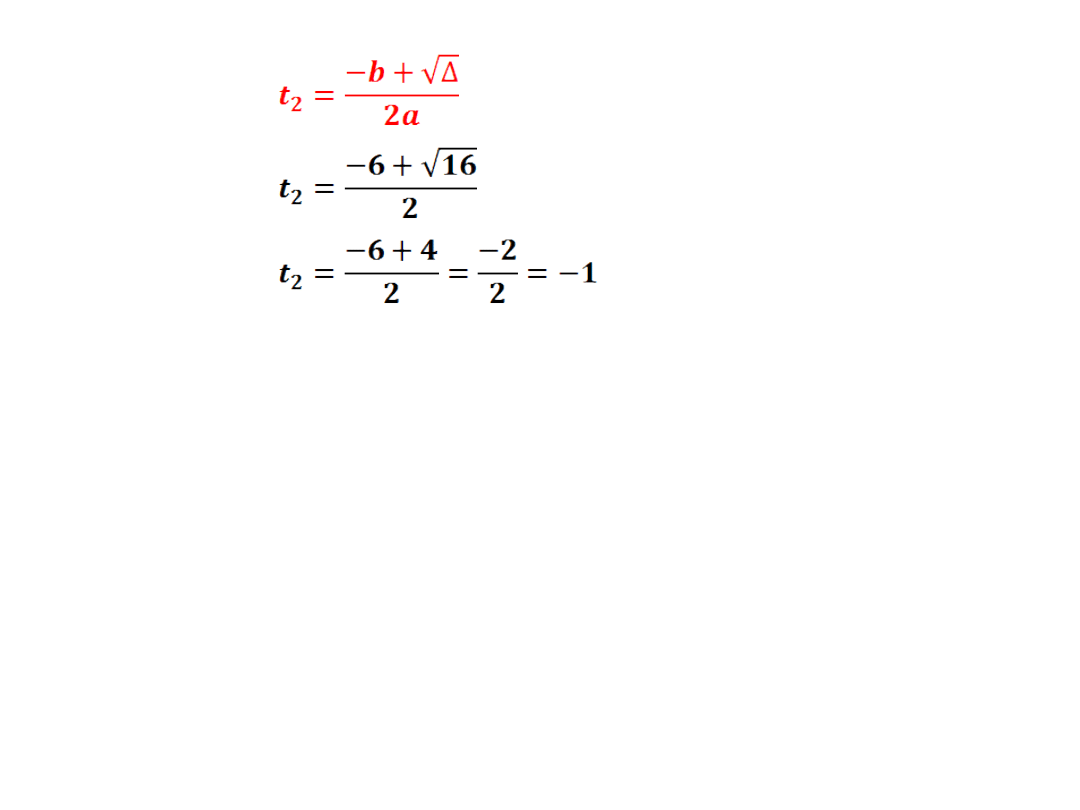
wracamy do podstawienia x
2
=t
x
2
=-5 ∨ x
2
=-1
xØ xØ
Rozwiązaniem równania jest zbiór pusty.
Z
R
=Ø
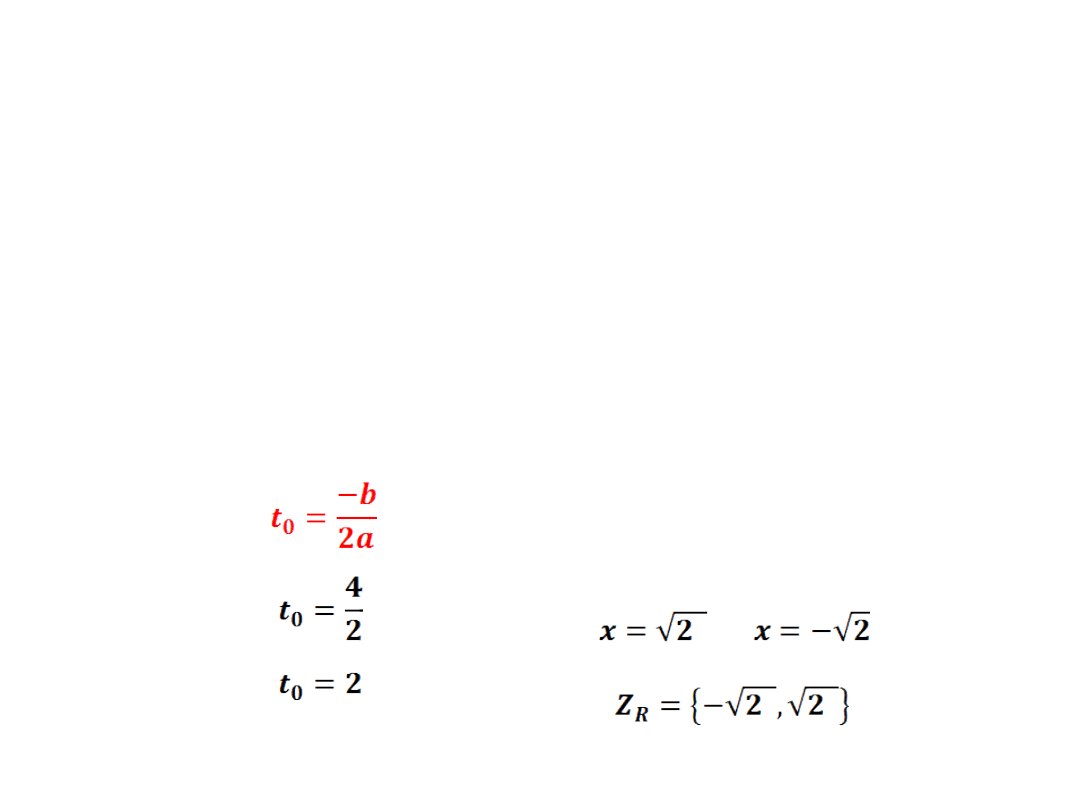
2) x
4
-4x
2
+4=0
(x
2
)
2
-4x
2
+4=0
podstawiam x
2
=t
t
2
-4t+4=0
a=1 b=-4 c=4
Δ = b
2
-4ac
Δ = (-4)
2
-4·1·4=16-16=0
Δ =
0
- wyznaczamy jedno miejsce zerowe
wracamy do podstawienia
x
2
=t
x
2
=2
∨
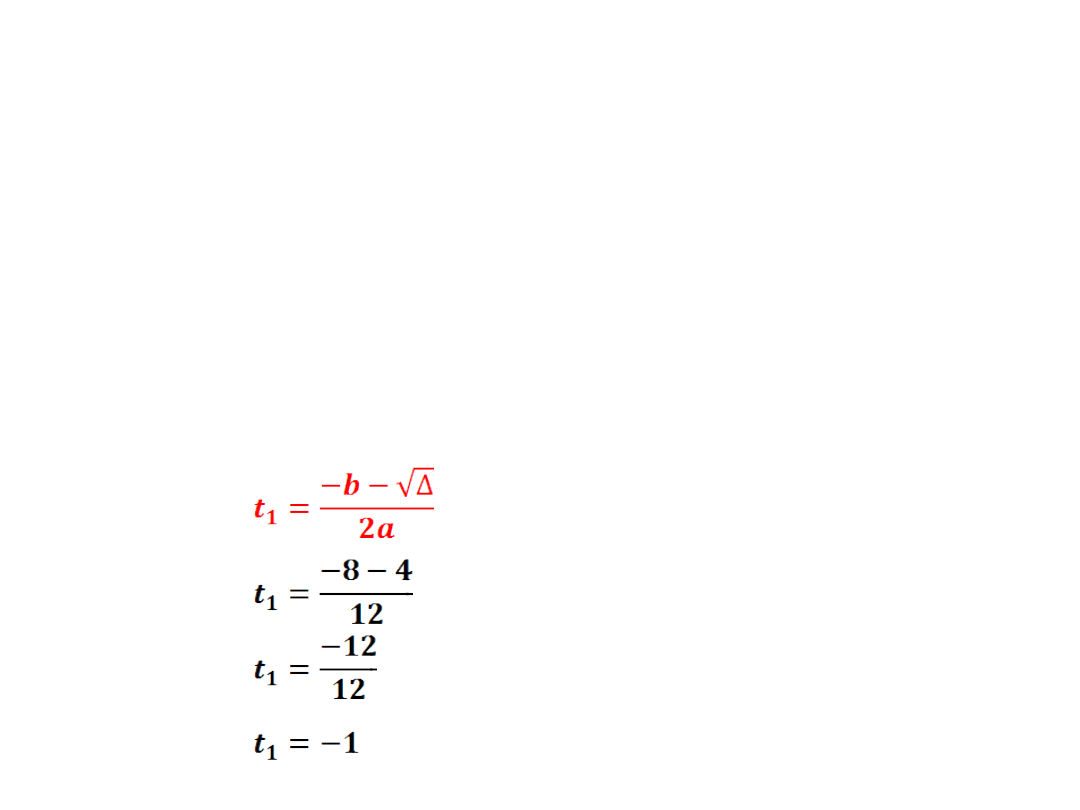
3) 6x
6
+8x
3
+2=0
6(x
3
)
2
+8x
3
+2=0
podstawiam x
3
=t
6t
2
+8t+2=0
a=6 b=8 c=2
Δ = b
2
-4ac
Δ = 8
2
-4·6·2=64-48=16
Δ
>
0
- wyznaczamy dwa miejsca zerowe
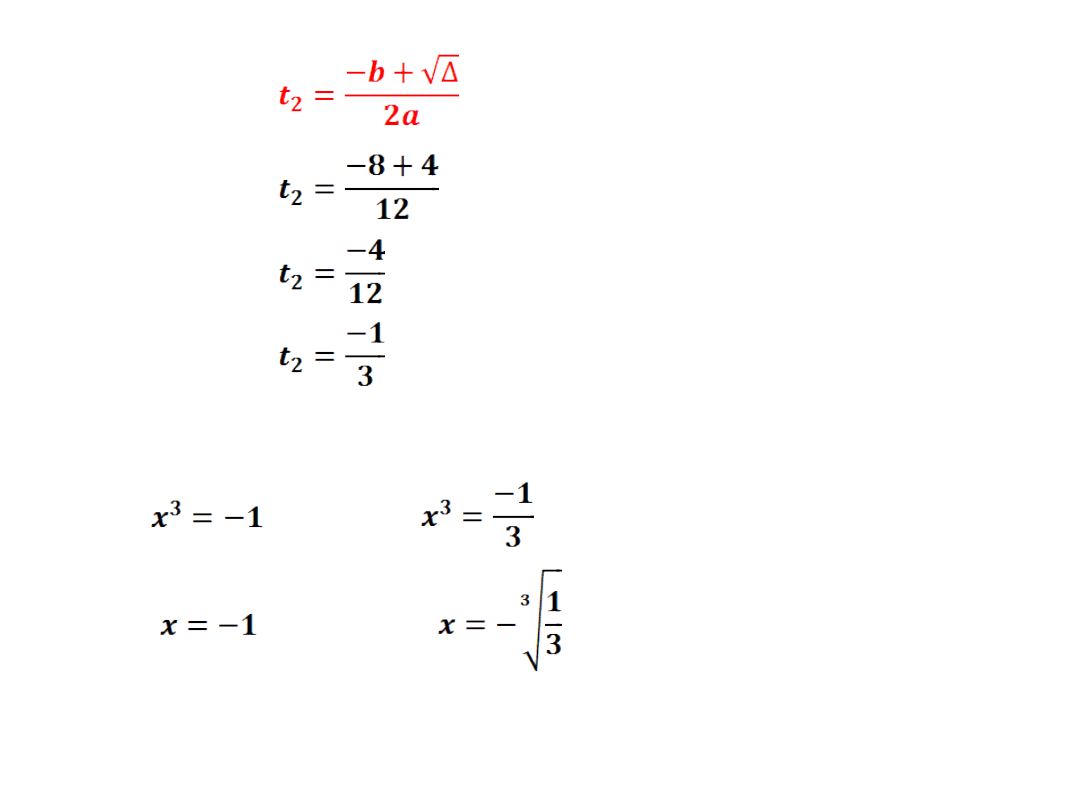
wracamy do podstawienia x
3
=t
∨
∨
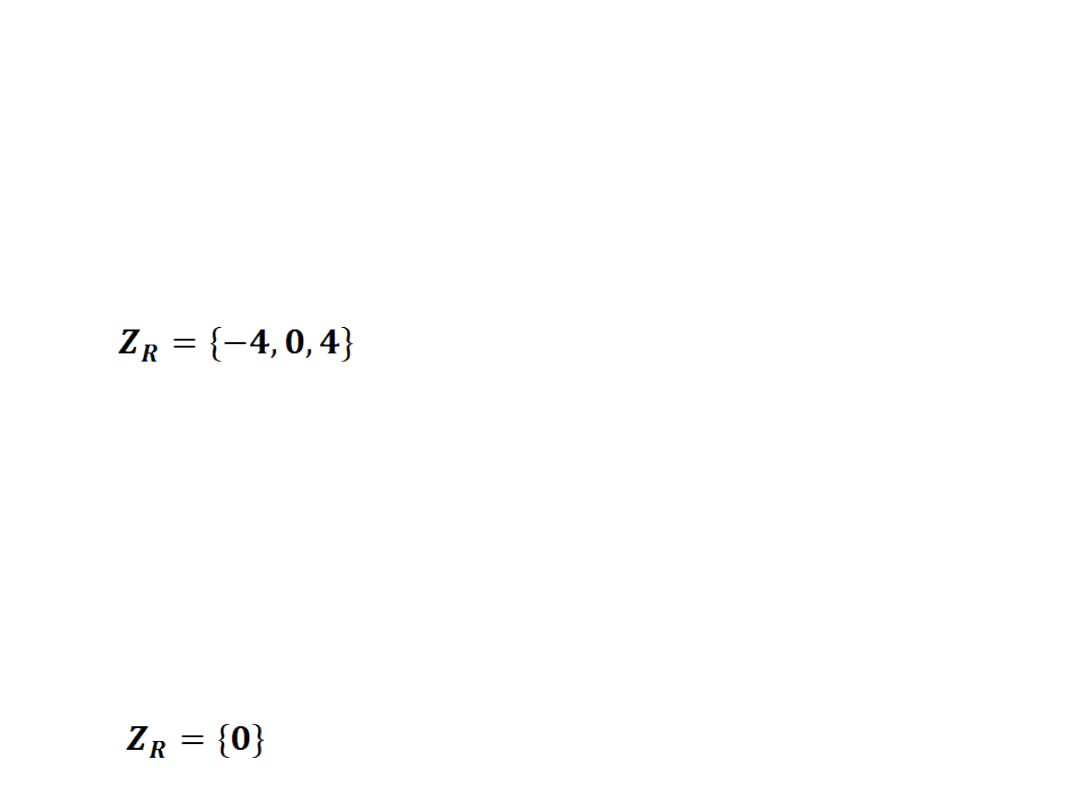
4) x
4
-16x
2
=0
x
2
(x
2
-16)=0
x
2
(x-4)(x+4)=0
x
2
=0 x-4=0 x+4=0
x=0 x=4 x=-4
5) x
6
+x
4
=0
x
4
(x
2
+1)=0
x
4
=0
x
2
+1=0
x=0
x
2
=-1
xØ
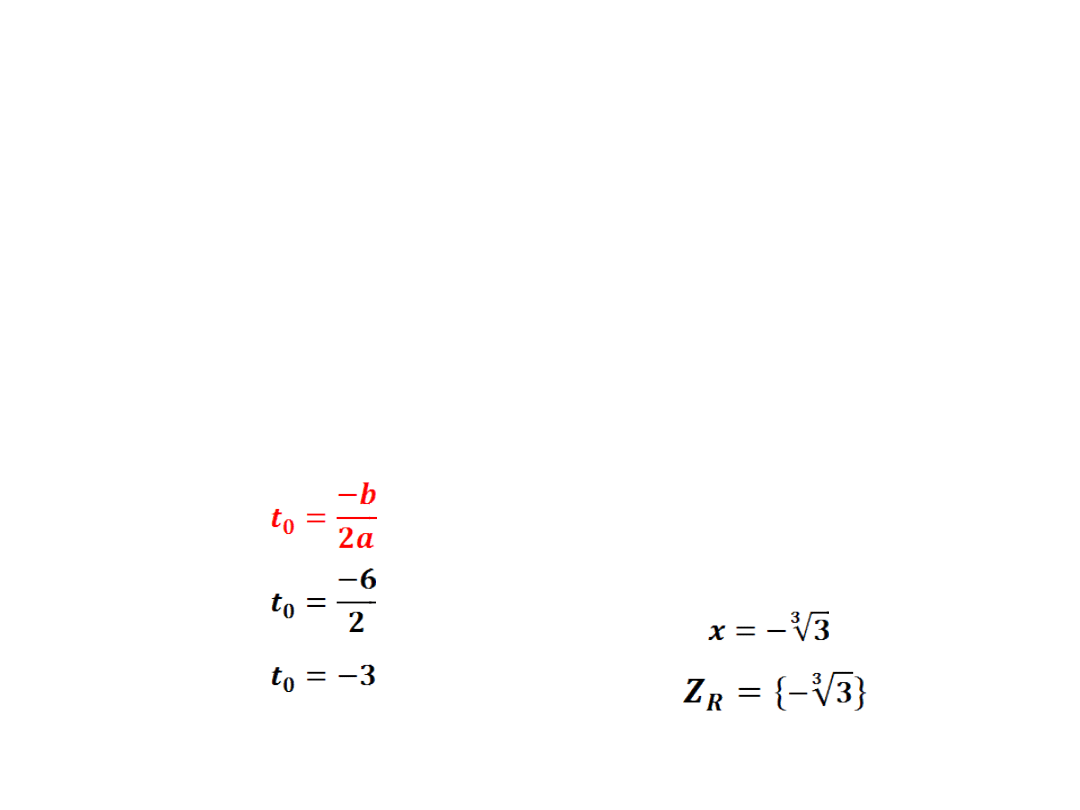
6) x
6
+6x
3
+9=0
(x
3
)
2
+6x
3
+9=0
podstawiam x
3
=t
t
2
+6t+9=0
a=1 b=6 c=9
Δ = b
2
-4ac
Δ = 6
2
-4·1·9=36-36=0
Δ = 0
- wyznaczamy jedno miejsce zerowe
wracamy do podstawienia
x
3
=t
x
3
=-3
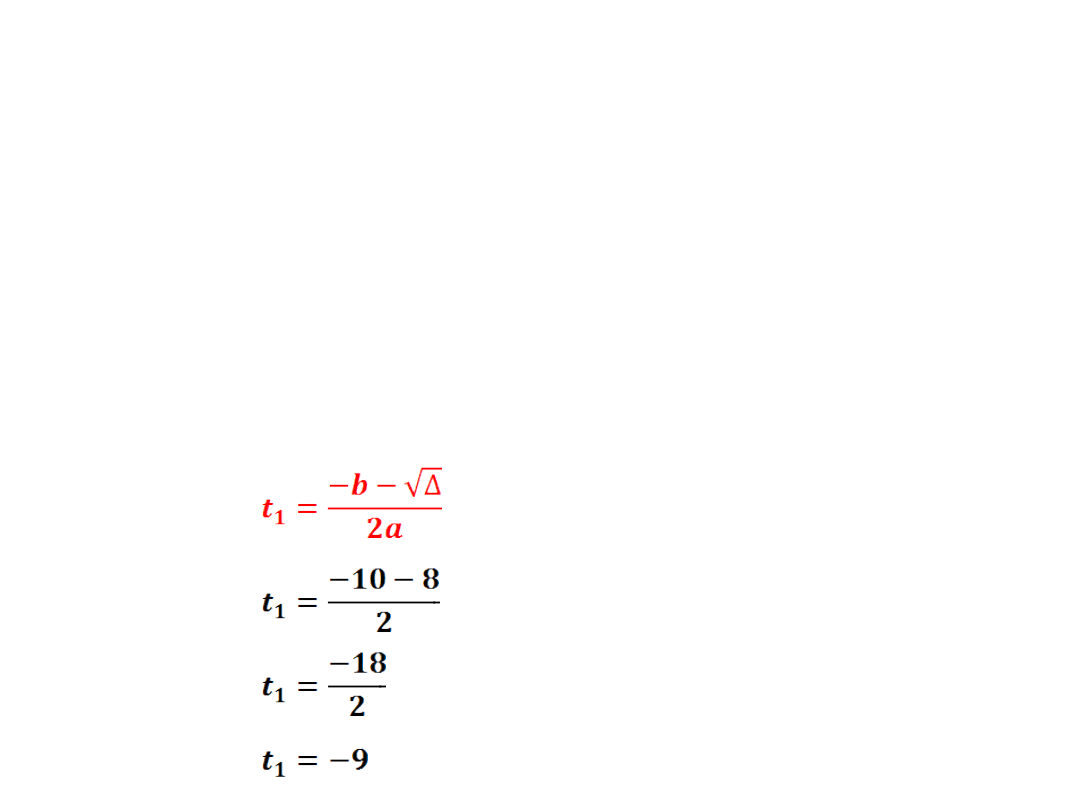
7) x
4
+10x
2
+9=0
(x
2
)
2
+10x
2
+9=0
podstawiam x
2
=t
t
2
+10t+9=0
a=1 b=10 c=9
Δ = b
2
-4ac
Δ = 10
2
-4·1·9=100-36=64
Δ
>
0
- wyznaczamy dwa miejsca zerowe
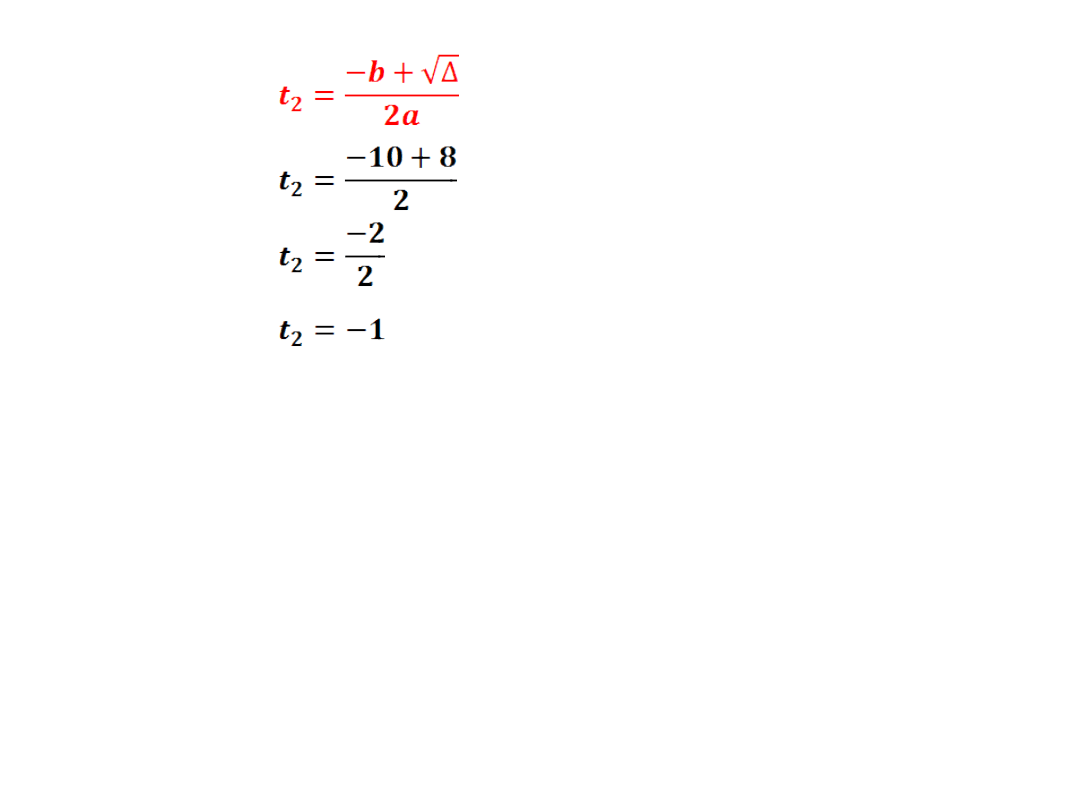
wracamy do podstawienia x
2
=t
x
2
=-9 ∨ x
2
=-1
xØ xØ
Rozwiązaniem równania jest zbiór pusty.
Z
R
=Ø
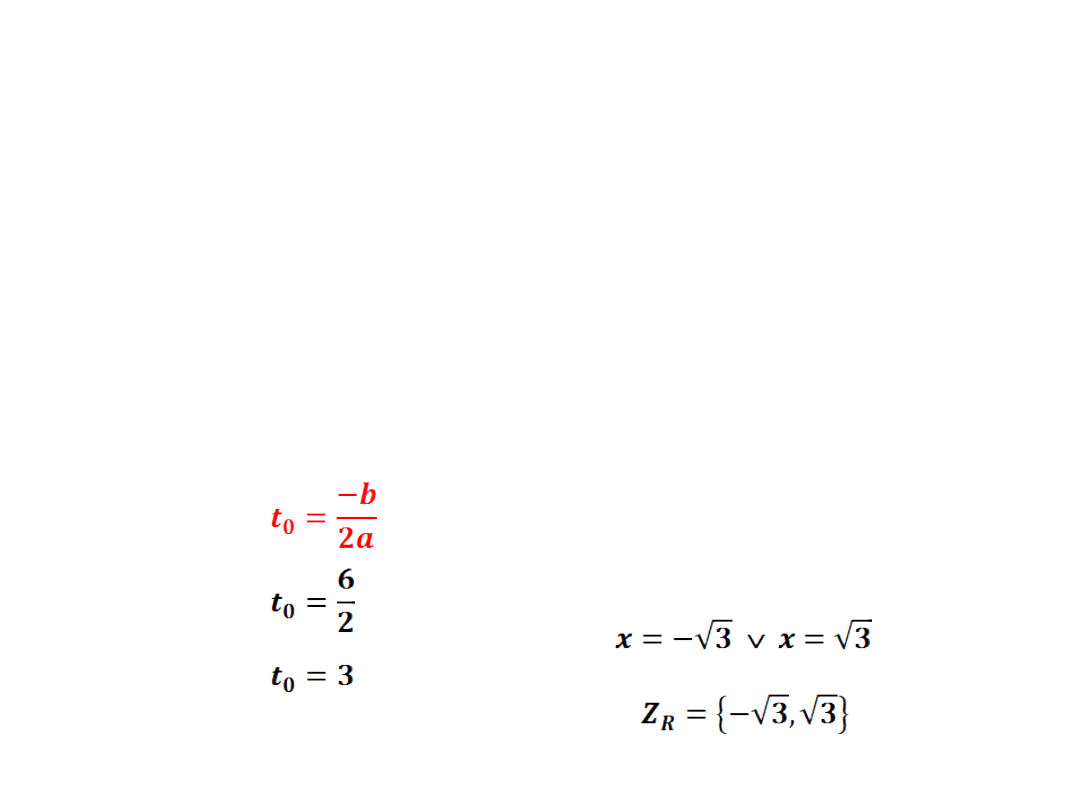
8) x
4
-6x
2
+9=0
(x
2
)
2
-6x
2
+9=0
podstawiam x
2
=t
t
2
-6t+9=0
a=1 b=-6 c=9
Δ = b
2
-4ac
Δ = (-6)
2
-4·1·9=36-36=0
Δ =
0
- wyznaczamy jedno miejsce zerowe
wracamy do podstawienia
x
2
=t
x
2
=3
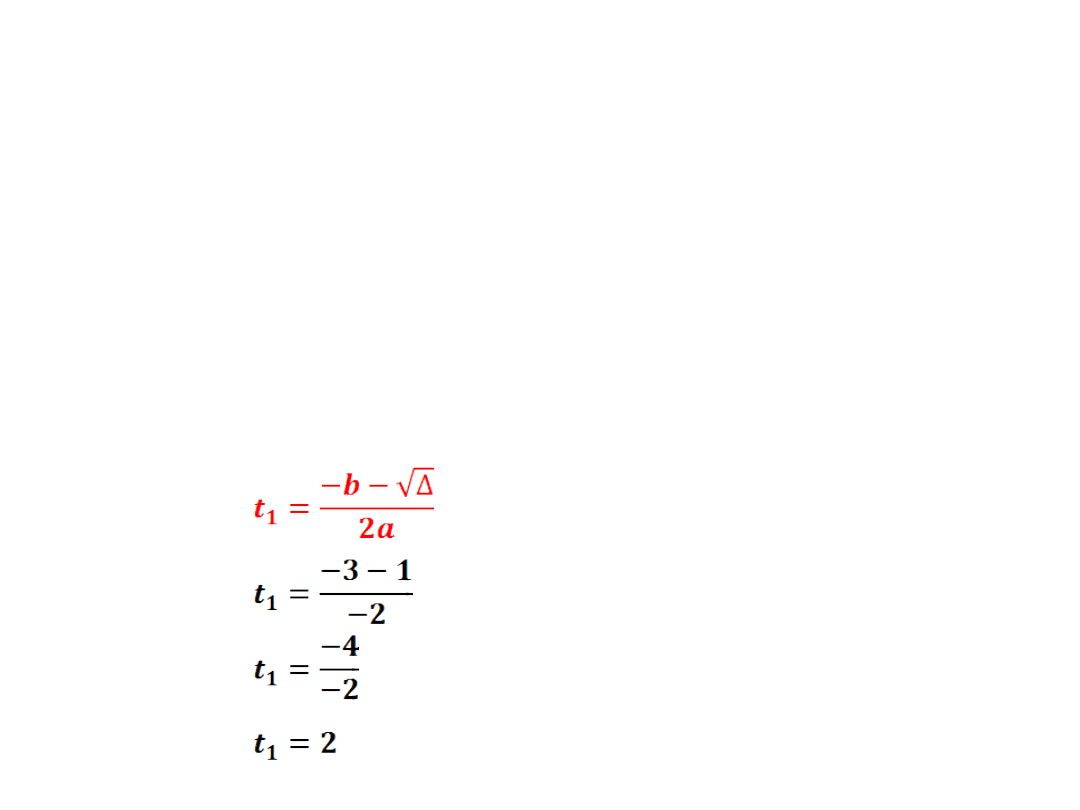
9) –x
4
+3x
2
-2=0
-(x
2
)
2
+3x
2
-2=0
podstawiam x
2
=t
-t
2
+3t-2=0
a=-1 b=3 c=-2
Δ = b
2
-4ac
Δ = 3
2
-4·(-1)·(-2)=9-8=1
Δ
>
0
- wyznaczamy dwa miejsca zerowe
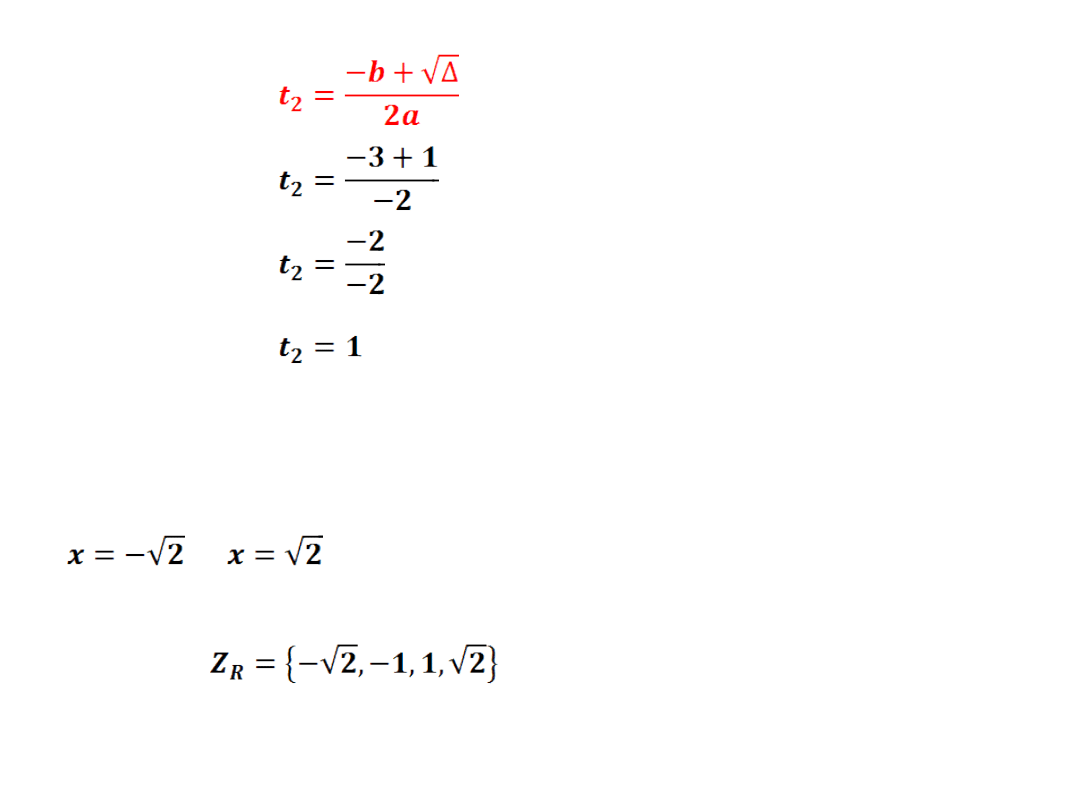
wracamy do podstawienia x
2
=t
x
2
=2
∨
x
2
=1
∨ ∨
x=-1
∨
x=1
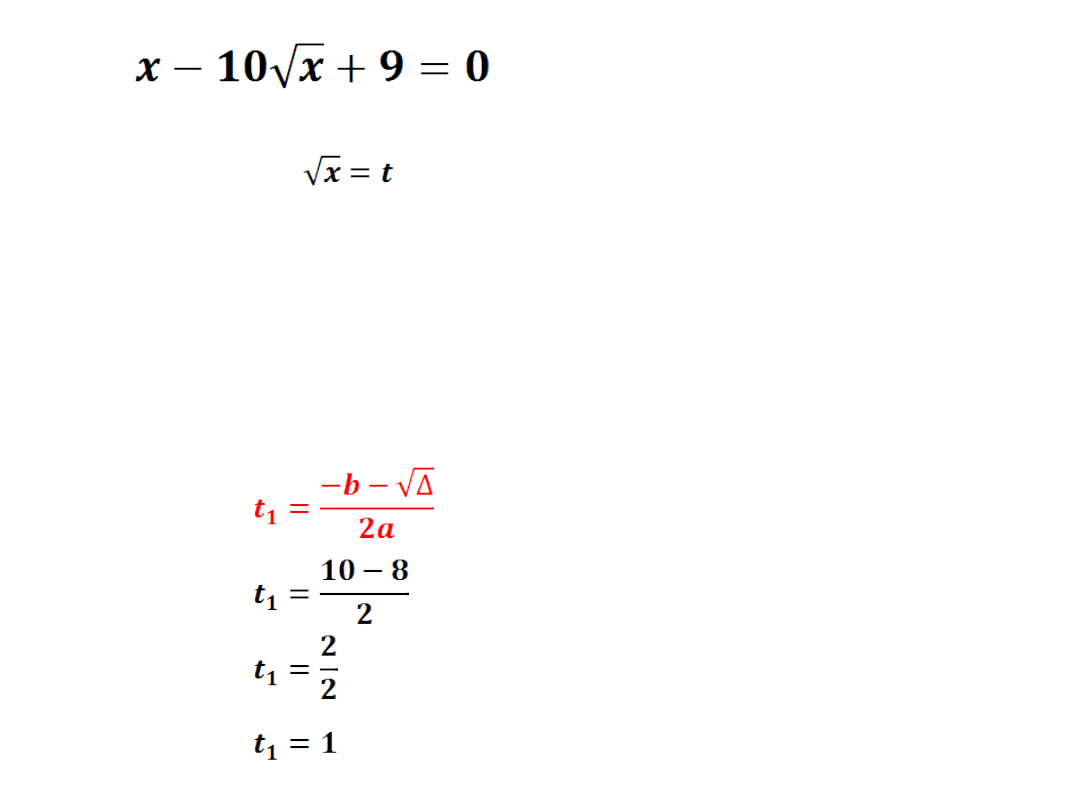
10)
podstawiam
t
2
-10t+9=0
a=1 b=-10 c=9
Δ = b
2
-4ac
Δ = (-10)
2
-4·1·9=100-36=64
Δ
>
0
- wyznaczamy dwa miejsca zerowe
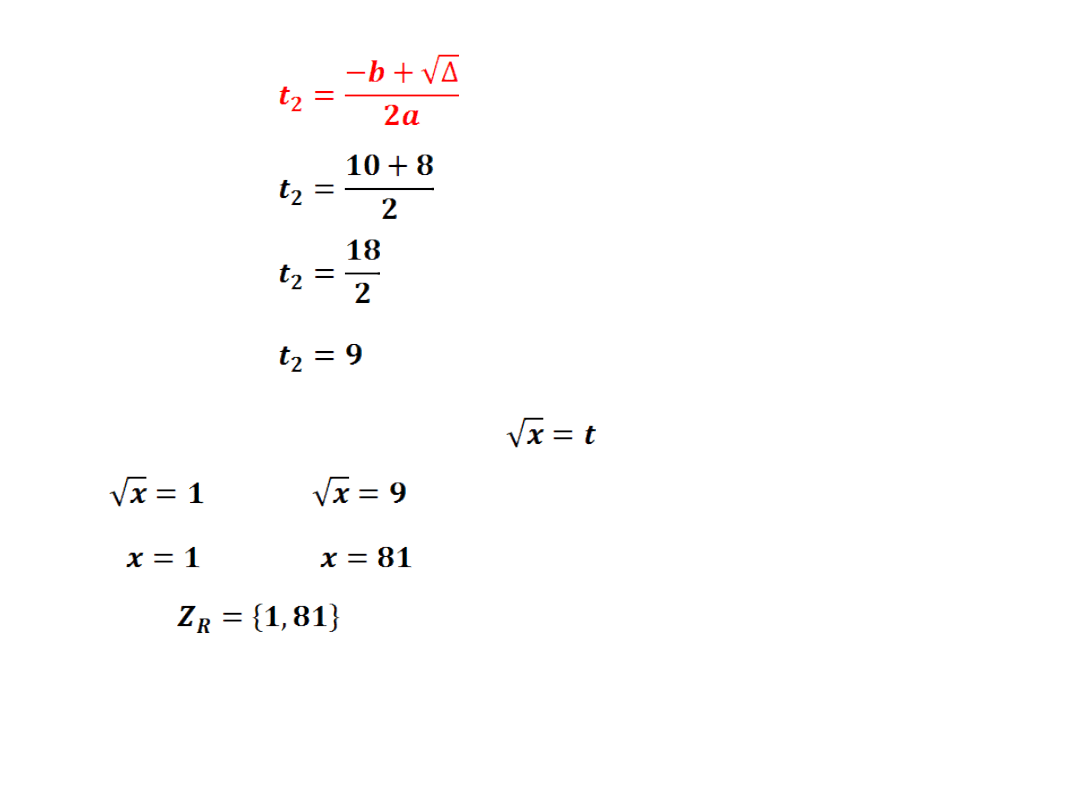
wracamy do podstawienia
∨
∨
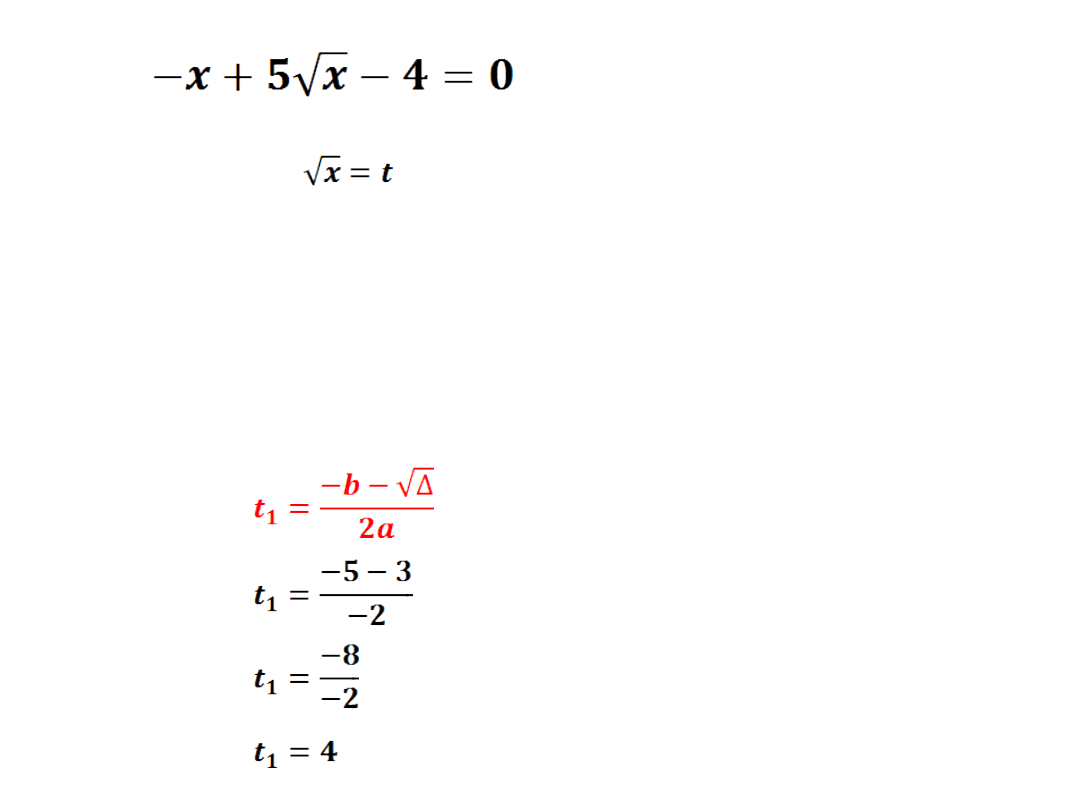
11)
podstawiam
-t
2
+5t-4=0
a=-1 b=5 c=-4
Δ = b
2
-4ac
Δ = 5
2
-4·(-1)·(-4)=25-16=9
Δ
>
0
- wyznaczamy dwa miejsca zerowe
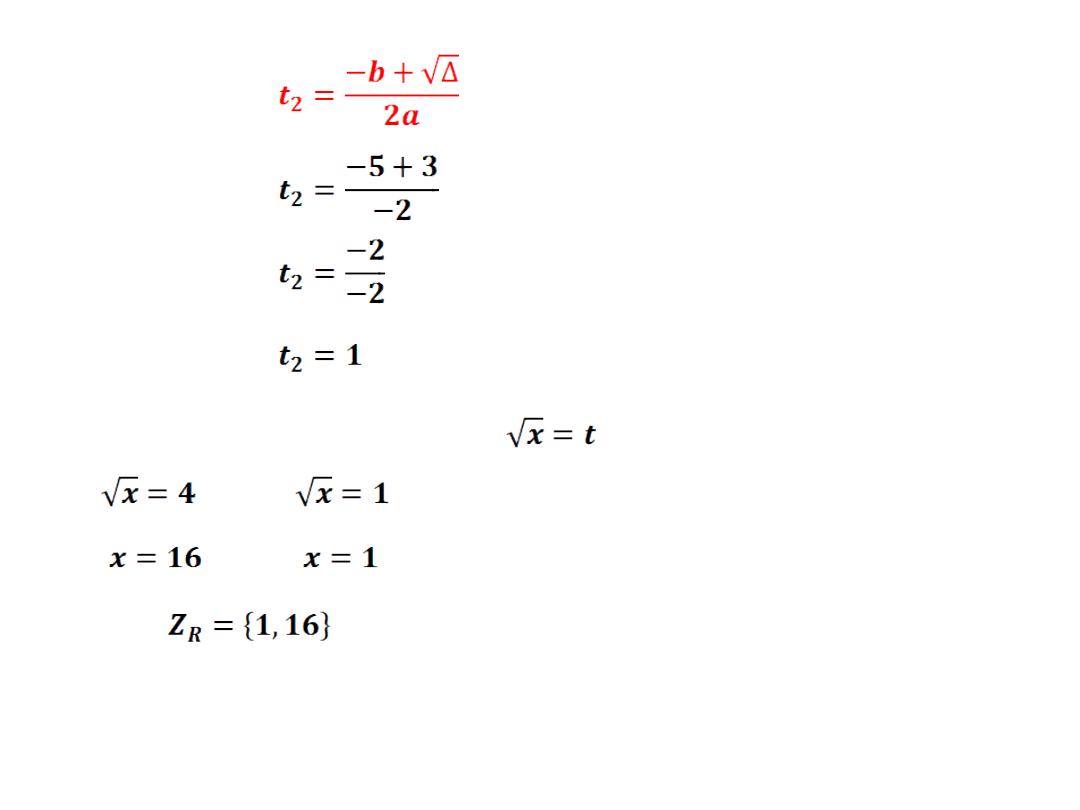
wracamy do podstawienia
∨
∨
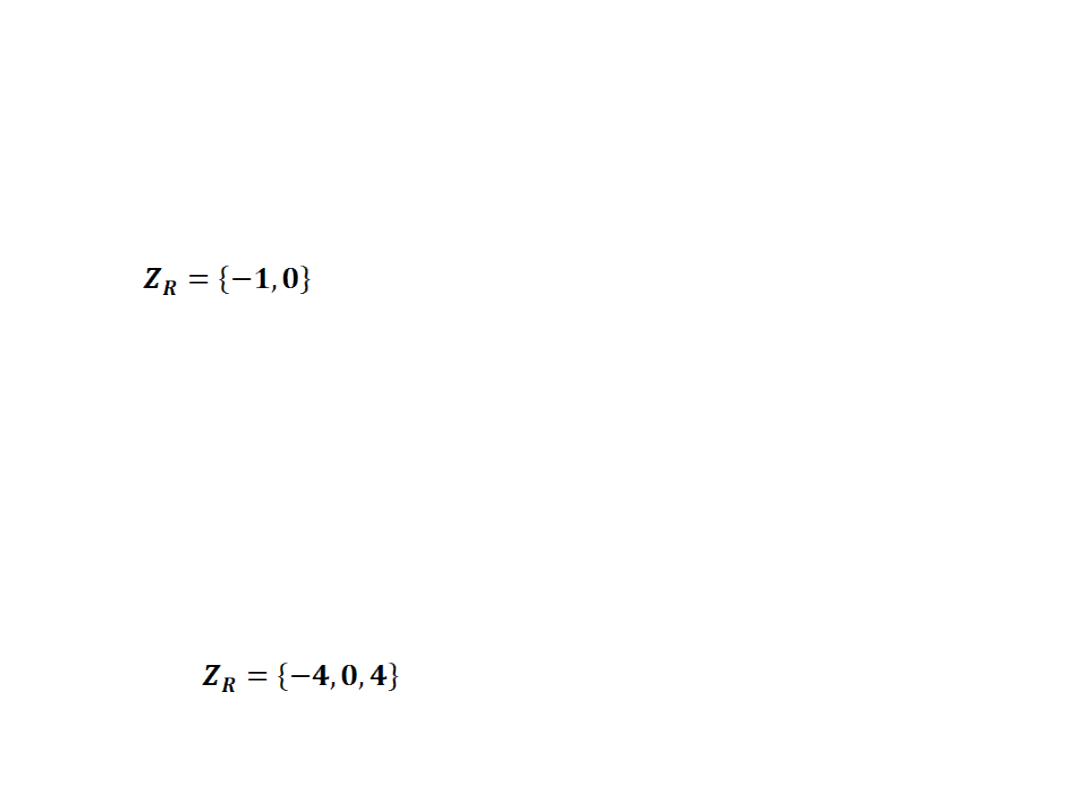
12) x
4
+x
3
=0
x
3
(x+1)=0
x
3
=0 x+1=0
x=0 x=-1
13) x
4
-16x
2
=0
x
2
(x
2
-16)=0
x
2
=0
x
2
-16=0
x=0
x
2
=16
x=0 x=-4 x=4
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
Wyszukiwarka
Podobne podstrony:
11Rownania rozniczkowe, 3.Równania różniczkowe rzędu pierwszego sprowadzone do równań różniczkowych
Matematyka III (Ćw) Lista 03 Równania rzędu drugiego sprowadzalne do równań rzędu pierwszego Zada
Równania różniczkowe, RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE RZĘDU DRUGIEGO SPROWADZALNE DO RÓWNAŃ RZĘDU PIE
Inne materiały, Mat-równania kwadratowe, 1 rozwiązanie: a0, =0 lub a=0, b0
matematyka, równania kwadratowe, Wyrażenia algebraiczne(+-*/)
Inne materiały, mat-równania kwadratowe2
równanie kwadratowe
Równania kwadratowe- wzory, POLITECHNIKA LUBELSKA, ROK 1, SEMESTR 1, Ćwiczenia, Matematyka
równania kwadratowe, Matematyka
Równanie kwadratowe
równania kwadratowe, Matematyka, Liceum
1 rownania kwadratowe zad+odp, matematyka srednia
alg blokowy rownanie kwadratowe
Równania kwadratowe
Równania kwadratowe z parametrem, Matematyka. Zadania i rozwiązania
Wyznaczanie pierwiastków równania kwadratowego ax2
zapisywanie, wczytywanie, grafika rownanie kwadratowe
więcej podobnych podstron