OGÓLNE PODSTAWY MATEMATYCZNE POMIARÓW

I OBLICZEŃ GEODEZYJNYCH NA MAŁYCH

OBSZARACH

Definicja obszaru małego

Obszarem małym (lub niedużym) z geodezyjnego

punktu widzenia nazywamy obszar nie przekraczający 750

km

2

.

Na obszarze do 750 km

2

(o promieniu nie większym niż

15,5km) można wykonać pomiary liniowe i kątowe z

zaniedbaniem wpływu zakrzywienia powierzchni ziemskiej.

W geodezji na płaszczyźnie do wyznaczania położenia

punktów stosujemy najczęściej układ współrzędnych

prostokątnych. Ze względu na stosowanie w geodezji jako

kąta kierunkowego azymutu, liczonego od kierunku

północnego (dodatniego kierunku osi x) zgodnie z ruchem

wskazówek zegara, układ współrzędnych w geodezji różni się

od układu przyjętego w matematyce.

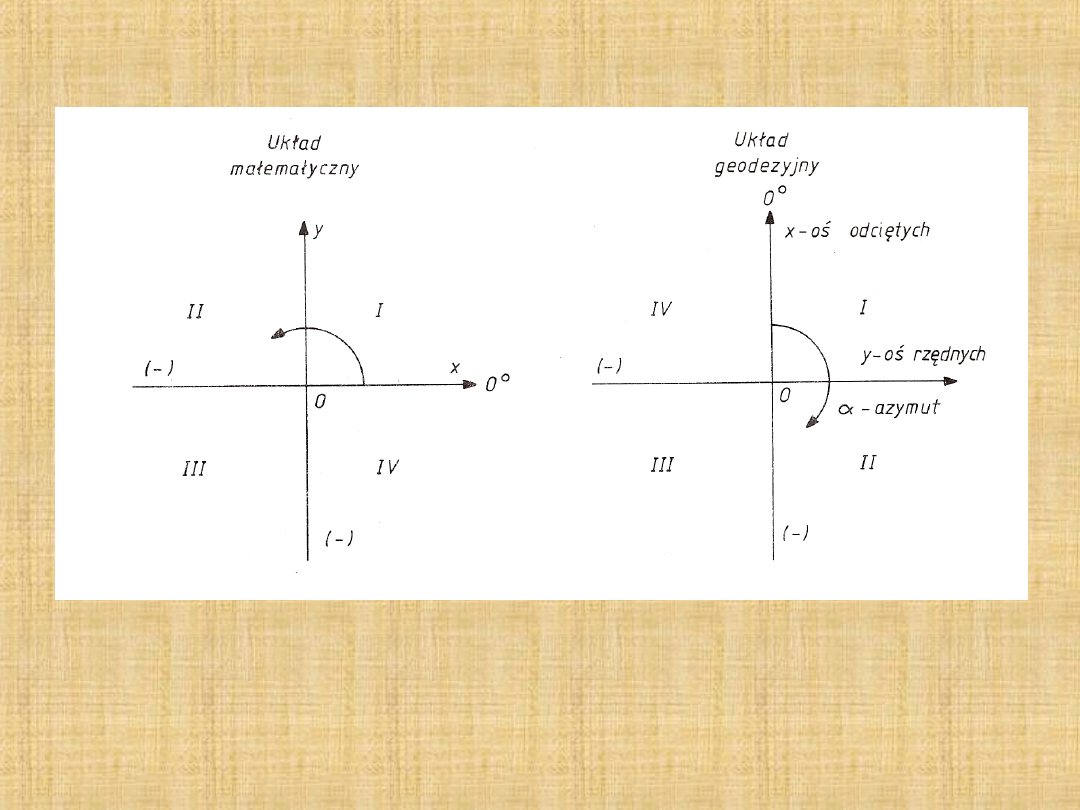
UKŁAD MATEMATYCZNY A UKŁAD GEODEZYJNY

Układ geodezyjny w stosunku do układu

matematycznego ma zamienione oznaczenie osi, a także
kierunek liczenia ćwiartek.

A

B

A

B

AB

AB

AB

x

x

y

y

x

y

tg















2

2

AB

AB

AB

y

x

d









AB

AB

AB

AB

AB

x

y

d





cos

sin









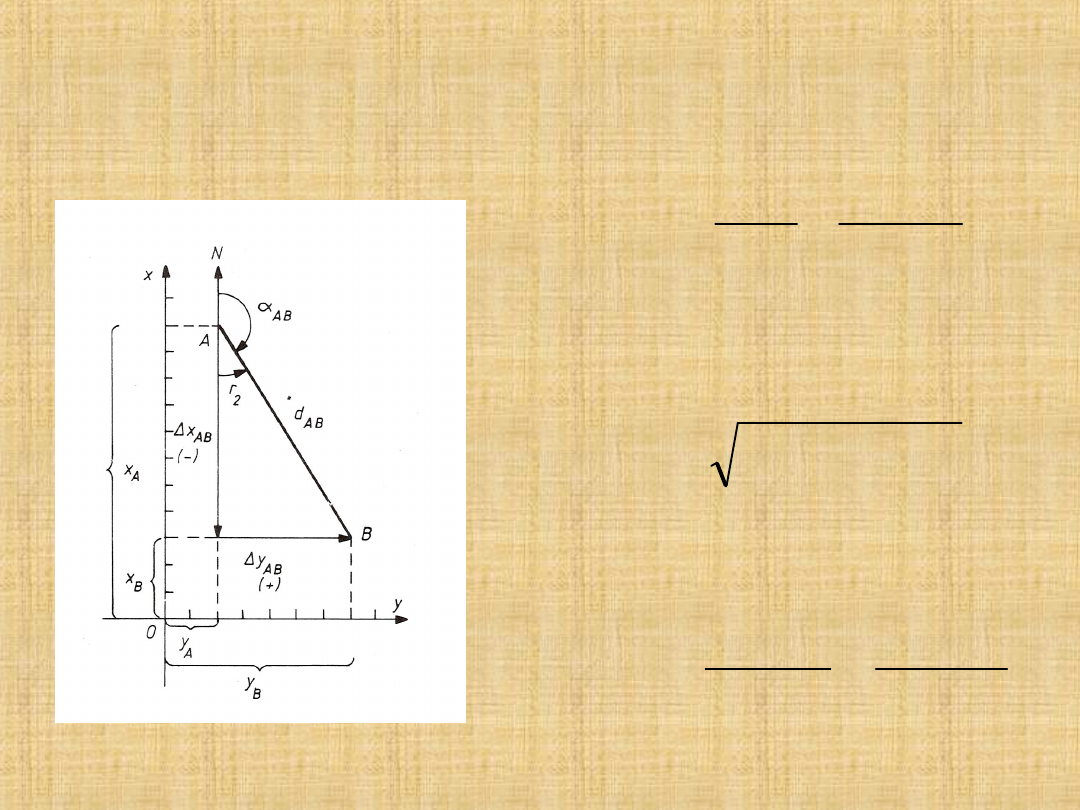
OBLICZENIE AZYMUTU I DŁUGOŚCI LINII

Azymut α

AB

obliczamy ze wzoru:

Długość linii AB:

lub

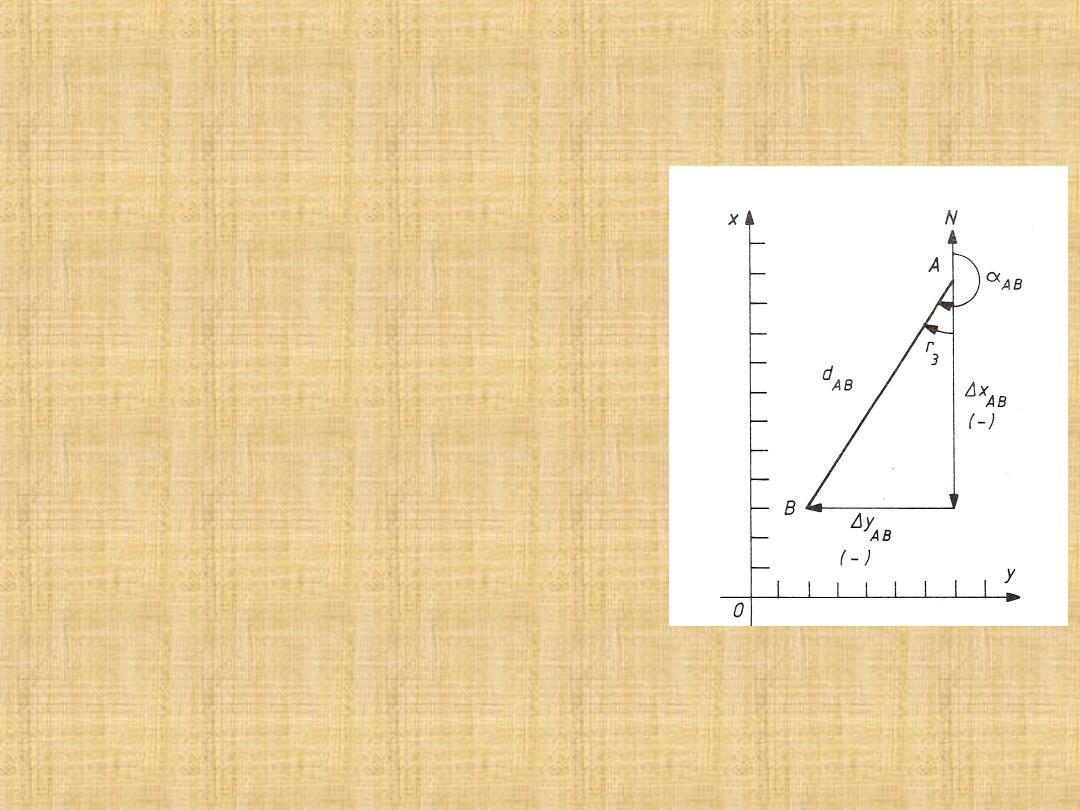
Dane: współrzędne punktu A(x

A

,y

A

), azymut linii 

AB

oraz jej długość d

AB

.

Szukane: współrzędne punktu B(x

B

, y

B

).

Współrzędne obliczamy ze wzorów:

AB

AB

A

AB

A

B

d

x

x

x

x



cos











AB

AB

A

AB

A

B

d

y

y

y

y



sin











OBLICZENIE WSPÓŁRZĘDNYCH PUNKTU

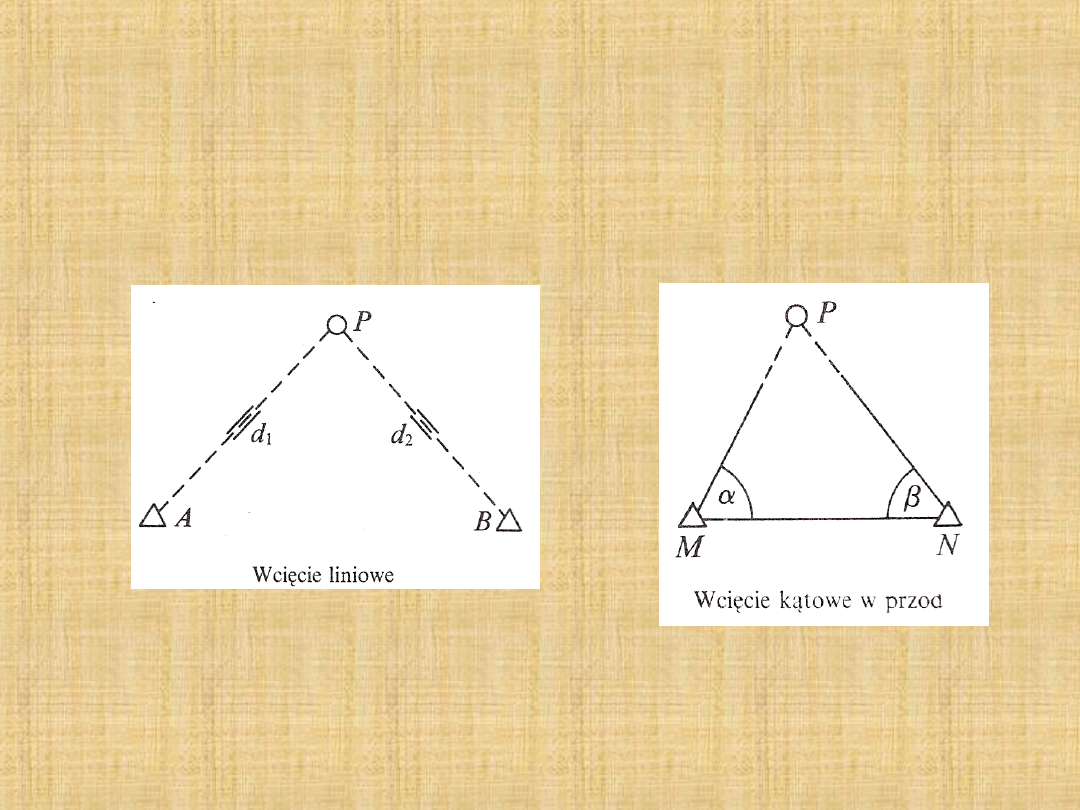
W praktyce geodezyjnej bardzo często wyznacza się współrzędne

punktów za pomocą specjalnych konstrukcji, takich jak:

a)wcięcie kątowe w przód;
b)wcięcie liniowe w przód;

KONSTRUKCJE GEODEZYJNE - WCIĘCIA

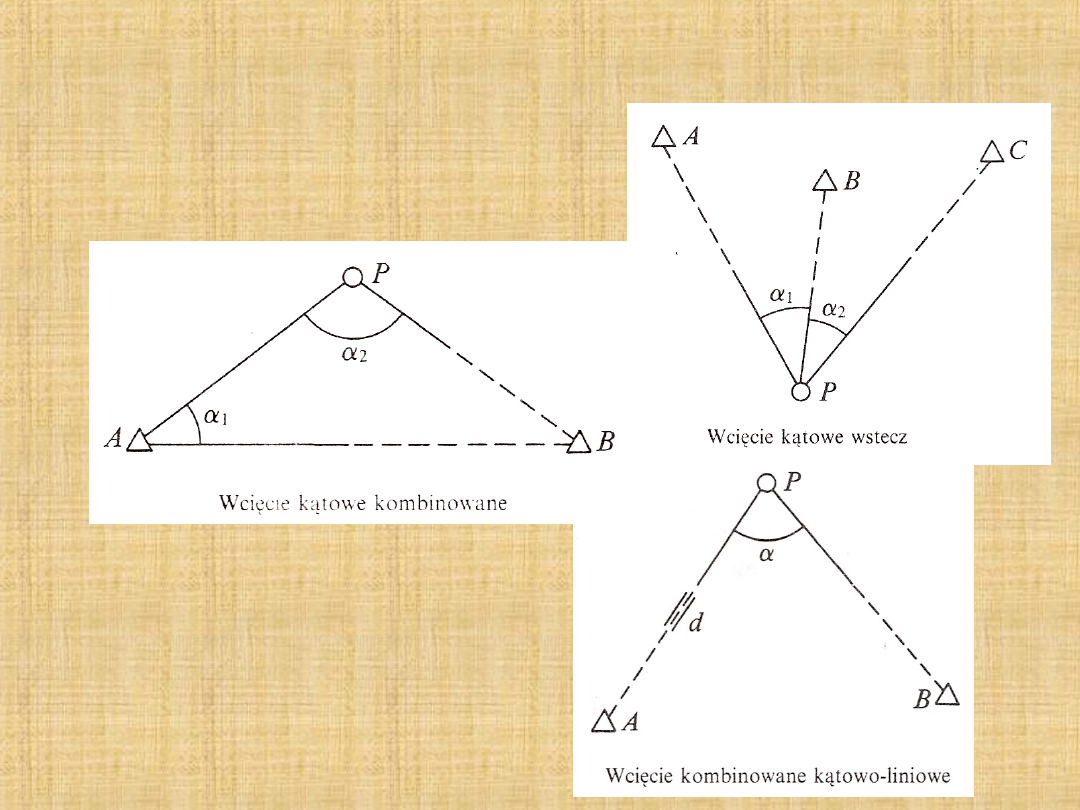
c) wcięcie kątowe wstecz;
d) wcięcie kątowe kombinowane;
e) wcięcie kombinowane kątowo-liniowe.

KONSTRUKCJE GEODEZYJNE - WCIĘCIA

Azymut linii następnej w ciągu poligonowym, gdy

znany jest azymut linii poprzedniej i kąt zawarty między

danymi liniami, wyznaczamy na podstawie następujących

wzorów:

- dla kąta prawego

- dla kąta lewego

Wzór na określenie azymutu końcowego ostatniej linii

w ciągu o n kątach:

- dla kątów prawych

- dla kątów lewych

CIĄG POLIGONOWY OTWARTY OBUSTRONNIE

NAWIĄZANY

pr















180

1

2

l















180

1

2

 

pr

p

k

n

















180

 

l

p

k

n

















180

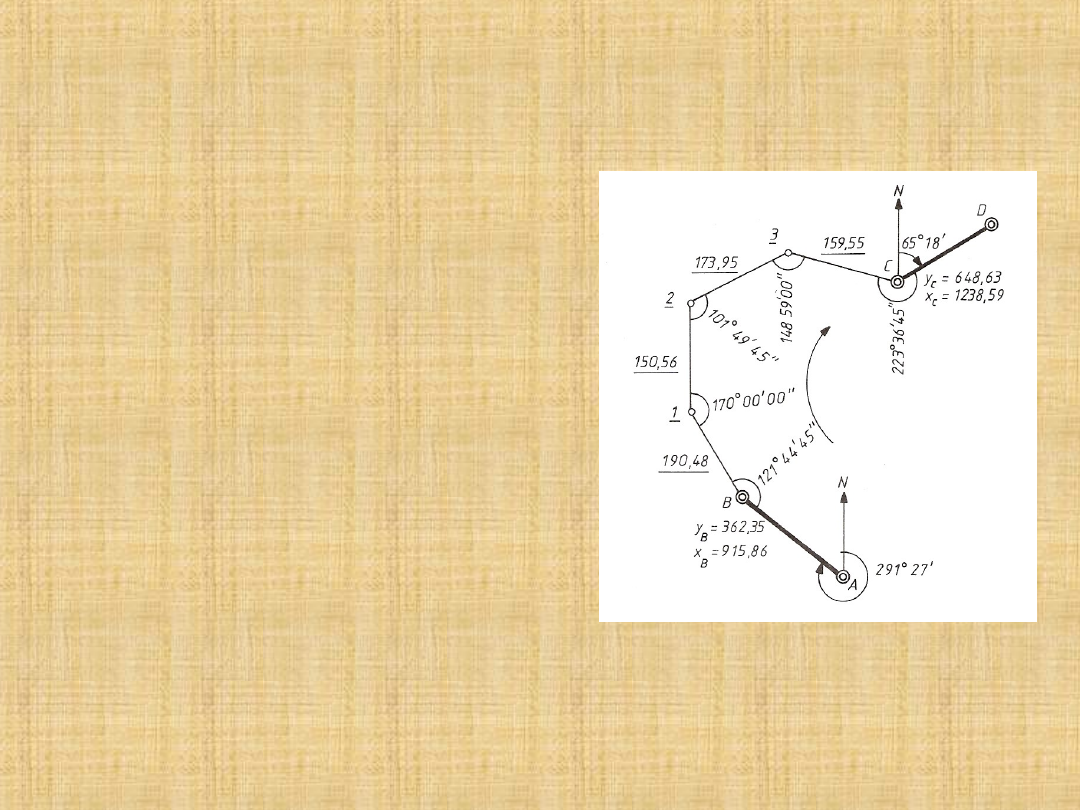
CIĄG POLIGONOWY OTWARTY OBUSTRONNIE

NAWIĄZANY

suma pomierzonych kątów
wewnętrznych ciągu:

sumy obliczonych przyrostów
Δx i Δy:

 













180

)

(

n

A

A

k

p

p

l



 

p

k

x

x

x







 

p

k

y

y

y







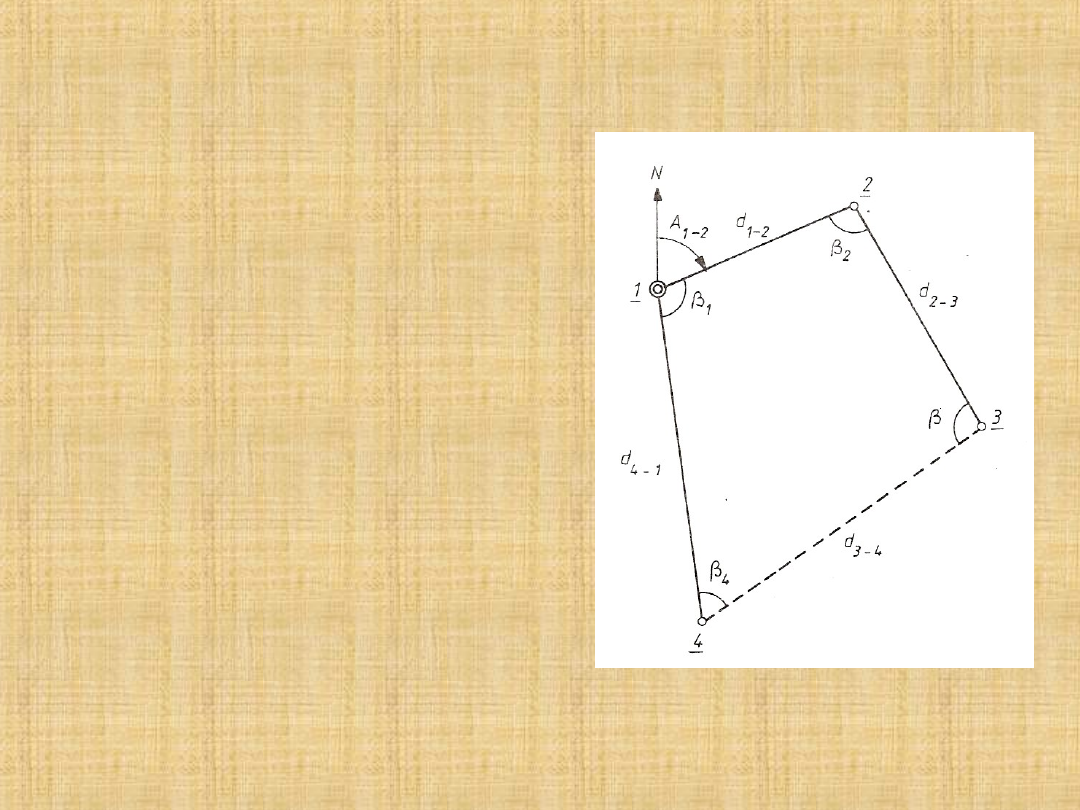
CIĄG POLIGONOWY ZAMKNIĘTY

suma pomierzonych kątów
wewnętrznych wieloboku:

sumy obliczonych
przyrostów
Δx i Δy:

 

)

2

(

180 





n

w



 

0



x

 

0



y