Kodowanie

Kodowanie

UTK

mgr inż. Robert Szczepaniak

Kodowanie liczb i tekstów



Kody binarne

Kody binarne



kod naturalny NKB

kod naturalny NKB



kod BCD

kod BCD



kod Gray’a

kod Gray’a



inne kody

inne kody



Kodowanie znaków (tekstów)

Kodowanie znaków (tekstów)

Kodowanie

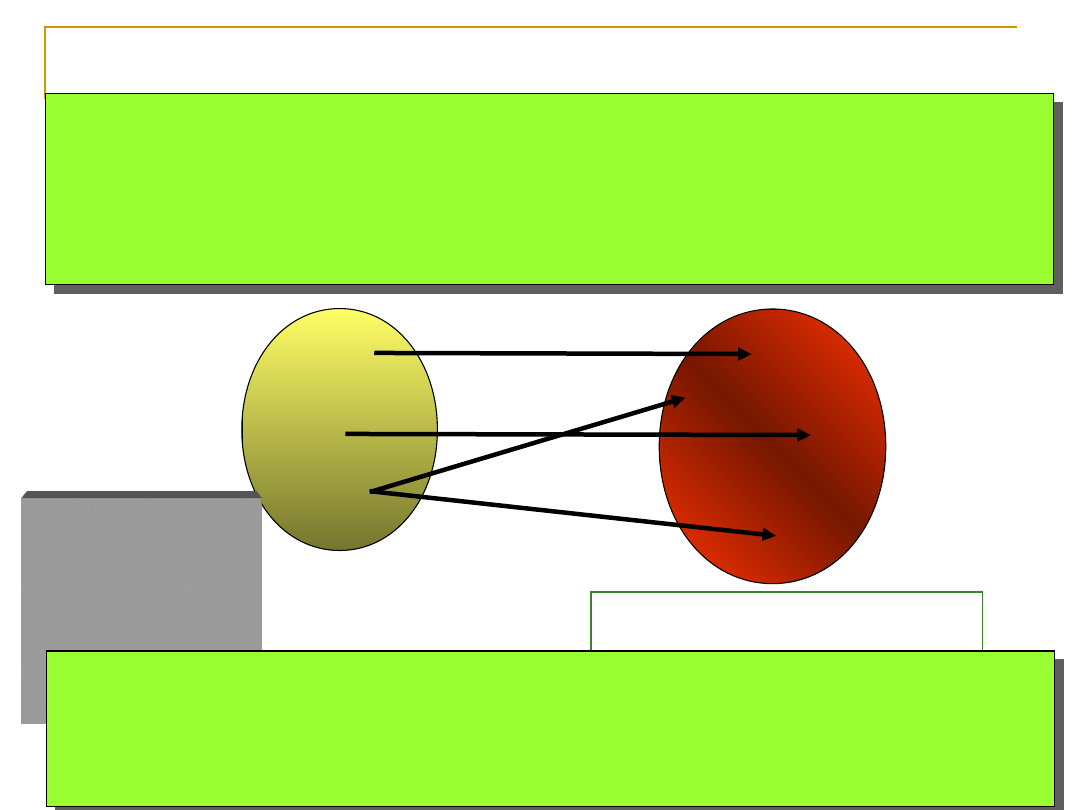
Def.1. Kodowaniem nazywamy przyporządkowanie

Def.1. Kodowaniem nazywamy przyporządkowanie

poszczególnym obiektom zbioru kodowanego

poszczególnym obiektom zbioru kodowanego

odpowiadających im elementów zwanych słowami

odpowiadających im elementów zwanych słowami

kodowymi, przy czym każdemu słowu kodowemu musi

kodowymi, przy czym każdemu słowu kodowemu musi

odpowiadać dokładnie jeden element kodowany

odpowiadać dokładnie jeden element kodowany

Def.1. Kodowaniem nazywamy przyporządkowanie

Def.1. Kodowaniem nazywamy przyporządkowanie

poszczególnym obiektom zbioru kodowanego

poszczególnym obiektom zbioru kodowanego

odpowiadających im elementów zwanych słowami

odpowiadających im elementów zwanych słowami

kodowymi, przy czym każdemu słowu kodowemu musi

kodowymi, przy czym każdemu słowu kodowemu musi

odpowiadać dokładnie jeden element kodowany

odpowiadać dokładnie jeden element kodowany

Zbiorem

Zbiorem

kodowanym może

kodowanym może

być zbiór

być zbiór

dowolnych

dowolnych

obiektów (cyfr,

obiektów (cyfr,

liter, symboli

liter, symboli

graficznych,

graficznych,

stanów

stanów

logicznych,

logicznych,

poleceń do

poleceń do

wykonania itp.)

wykonania itp.)

A

A

B

B

C

C

010

010

111

111

100

100

001

001

Proces kodowania może być

Proces kodowania może być

opisem słownym, wzorem

opisem słownym, wzorem

(zależnością matematyczną),

(zależnością matematyczną),

tabelą kodową itp.

tabelą kodową itp.

Def.2. Kodem liczbowym nazywamy taki kod, który

Def.2. Kodem liczbowym nazywamy taki kod, który

liczbom dowolnego systemu będzie

liczbom dowolnego systemu będzie

przyporządkowywał słowa kodowe w postaci

przyporządkowywał słowa kodowe w postaci

zerojedynkowej (binarnej)

zerojedynkowej (binarnej)

Def.2. Kodem liczbowym nazywamy taki kod, który

Def.2. Kodem liczbowym nazywamy taki kod, który

liczbom dowolnego systemu będzie

liczbom dowolnego systemu będzie

przyporządkowywał słowa kodowe w postaci

przyporządkowywał słowa kodowe w postaci

zerojedynkowej (binarnej)

zerojedynkowej (binarnej)

Naturalny Kod Binarny

Minimalna długość

k

słowa binarnego

reprezentującego liczbę dziesiętną

A

musi

spełniać warunek:

A<2

k

<2A+1

Oznacza to, że aby zakodować liczbę dziesiętną w

zakresie 0-15 wystarczy wykorzystać jedną

tetradę (długość słowa kodowego k=4) gdyż

15<2

4

<31

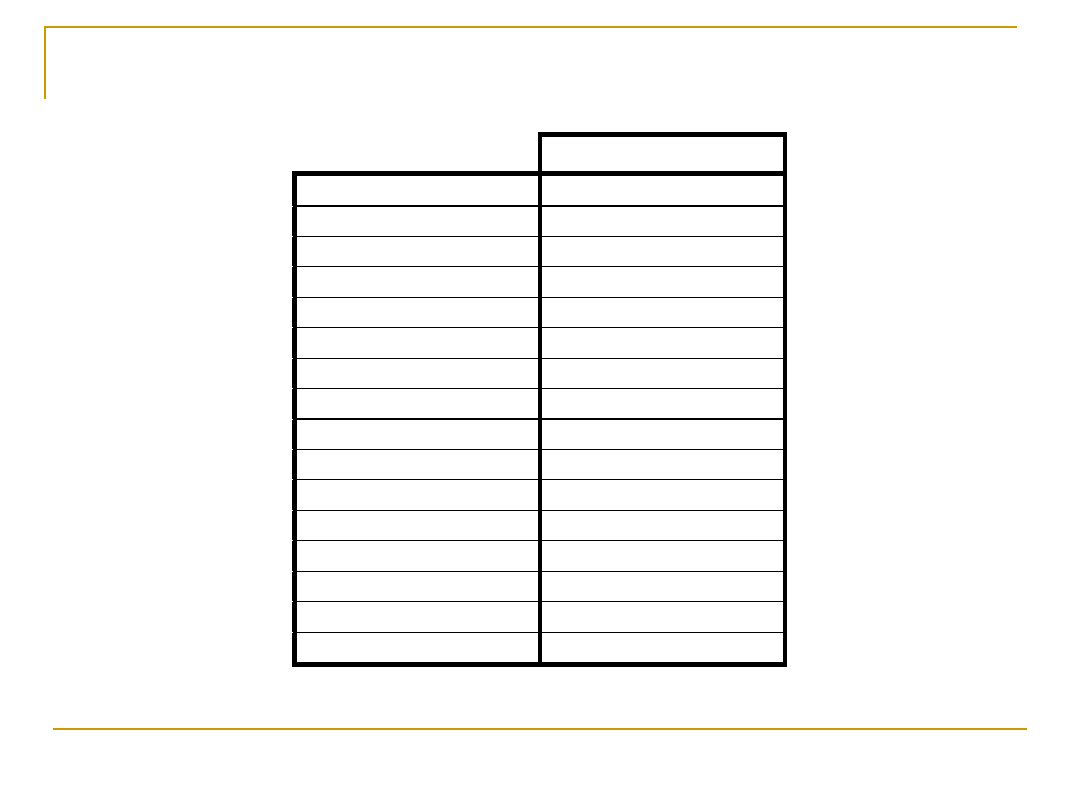
Def. Jeżeli dowolnej liczbie dziesiętnej

Def. Jeżeli dowolnej liczbie dziesiętnej

przyporządkujemy odpowiadająca jej liczbę

przyporządkujemy odpowiadająca jej liczbę

binarną, to otrzymamy naturalny kod binarny

binarną, to otrzymamy naturalny kod binarny

(NKB)

(NKB)

Def. Jeżeli dowolnej liczbie dziesiętnej

Def. Jeżeli dowolnej liczbie dziesiętnej

przyporządkujemy odpowiadająca jej liczbę

przyporządkujemy odpowiadająca jej liczbę

binarną, to otrzymamy naturalny kod binarny

binarną, to otrzymamy naturalny kod binarny

(NKB)

(NKB)

cd..

NKB

0

0000

1

0001

2

0010

3

0011

4

0100

5

0101

6

0110

7

0111

8

1000

9

1001

10

1010

11

1011

12

1100

13

1101

14

1110

15

1111

Kod prosty BCD

Gdy w systemie wygodnie jest operować liczbami

dziesiętnymi stosowany jest kod BCD. Liczba tetrad kodu

BCD jest bowiem równa liczbie pozycji dziesiętnych

reprezentowanej liczby. Np. dziesiętna liczba 6-pozycyjna

(000000-999999) jest kodowana na 24 bitach.

Konstrukcja:



każdej cyfrze dziesiętnej przyporządkowujemy

czterocyfrową liczbę dwójkową w kodzie NKB;



słowo kodowe w kodzie prostym BCD otrzymujemy

zapisując każdą cyfrę liczby dziesiętnej w postaci tetrady

binarnej

463

D

= 010001100011

BCD

67

D

= 01100111

BCD

Gdybyśmy zamiast kodu NKB użyli kodu np. Gray’a wówczas

otrzymalibyśmy kod BCD Gray’a.

Kod Gray'a

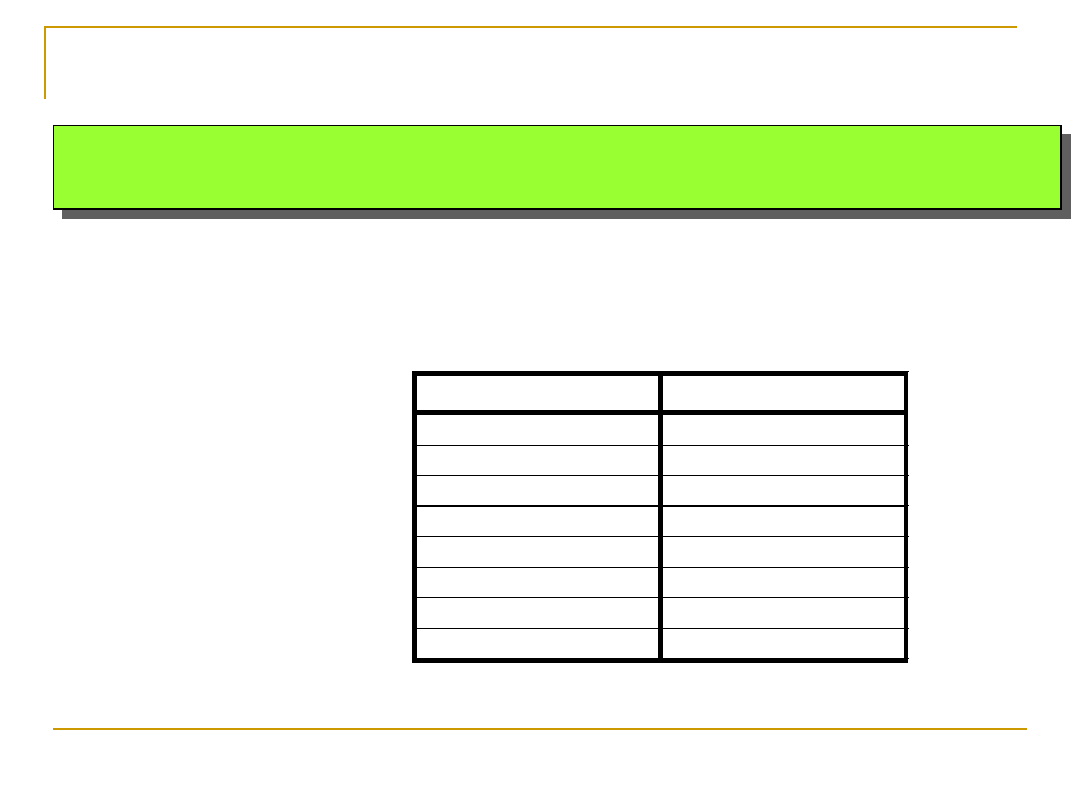
Kod Gray’a tworzy się z kodu naturalnego NKB

biorąc pod uwagę:

Def. Kod Gray’a to taki kod, którego kolejne słowa różnią

Def. Kod Gray’a to taki kod, którego kolejne słowa różnią

się tylko na jednej pozycji

się tylko na jednej pozycji

Def. Kod Gray’a to taki kod, którego kolejne słowa różnią

Def. Kod Gray’a to taki kod, którego kolejne słowa różnią

się tylko na jednej pozycji

się tylko na jednej pozycji

1

n

2

n

2

n

n

1

n

1

n

n

n

b

b

g

b

b

g

b

g





















NKB

Kod Gray’a

000

000

001

001

010

011

011

010

100

110

101

111

110

101

111

100

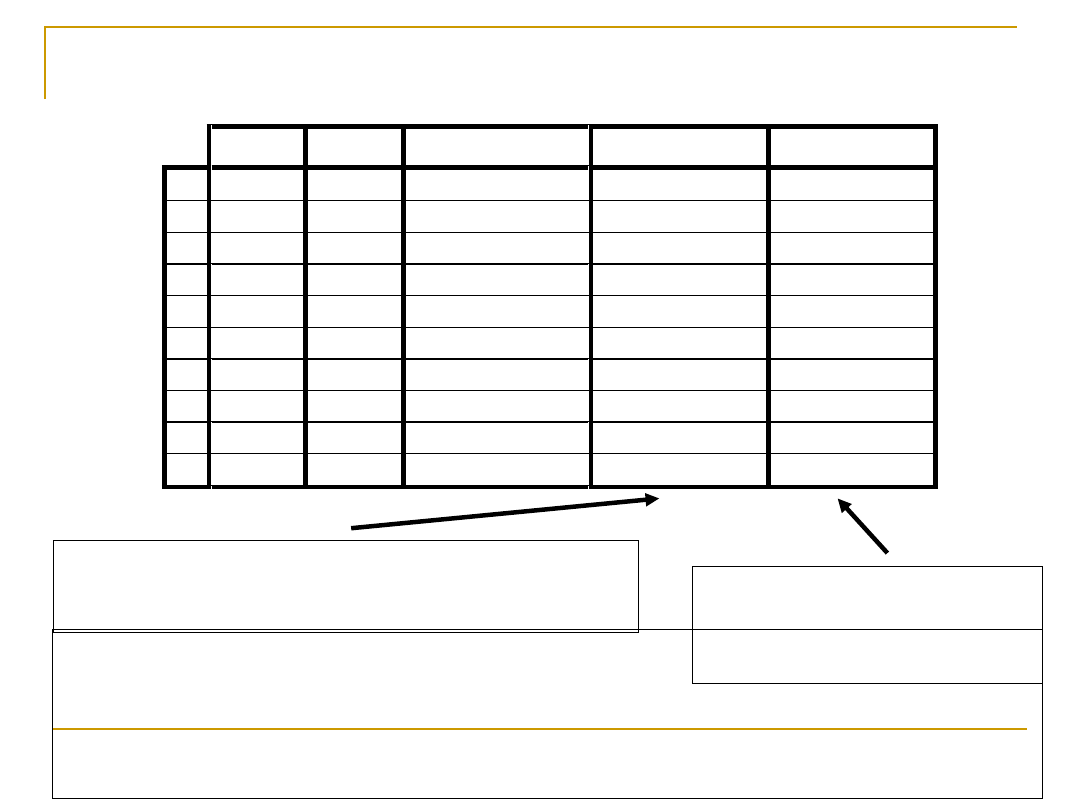
Inne kody binarne

NKB BCD Kod Gray’a

1 z 10

J ohnsona

0

0000

0000

0000

0000000001

00000

1

0001

0001

0001

0000000010

00001

2

0010

0010

0011

0000000100

00011

3

0011

0011

0010

0000001000

00111

4

0100

0100

0110

0000010000

01111

5

0101

0101

0111

0000100000

11111

6

0110

0110

0101

0001000000

11110

7

0111

0111

0100

0010000000

11100

8

1000

1000

1100

0100000000

11000

9

1001

1001

1101

1000000000

10000

Długość słowa kodu „1 z n” (w tabeli „1 z

Długość słowa kodu „1 z n” (w tabeli „1 z

10”) jest równa n, tj. liczności zbioru

10”) jest równa n, tj. liczności zbioru

kodowanego (liczbie kodowanych słów)

kodowanego (liczbie kodowanych słów)

Kod 5-bitowy

Kod 5-bitowy

stosowany do

stosowany do

kodowania cyfr

kodowania cyfr

dziesiętnych

dziesiętnych

Są to kody nadmiarowe (redundancyjne), w których liczba pozycji

Są to kody nadmiarowe (redundancyjne), w których liczba pozycji

binarnych jest większa niż wynika to z ogólnej zależności

binarnych jest większa niż wynika to z ogólnej zależności

Redundancję można wykorzystać do zwiększenia niezawodności

Redundancję można wykorzystać do zwiększenia niezawodności

operacji wykonywanych na liczbach

operacji wykonywanych na liczbach

1

2A

2

A

k







Kodowanie znaków

Początki:



Harald C. M. Morse (kropka - kreska - ....);



Anatol de Baudot (dalekopis);



w pierwszych maszynach cyfrowych - kod dalekopisowy 5-

bitowy, a potem 8-bitowy (EBCDIC);

W 1977 roku

ANSI

(American National Standards

Institute) zatwierdził

kod ASCII

(The American

Standard Code for Information Interchange).

Jest to

7-bitowy

kod (8 bit do kontroli parzystości), definiujący

128-elementowy

zestaw znaków (character set) o

wartościach kodowych od 0 do 127. Zestaw zawiera litery

łacińskie (duże i małe), cyfry i znaki interpunkcji oraz różne

znaki specjalne. Międzynarodowa Organizacja Standaryzacji

- ISO, nadała amerykańskiemu systemowi kodowania status

standardu międzynarodowego oznaczonego jako ISO 646.

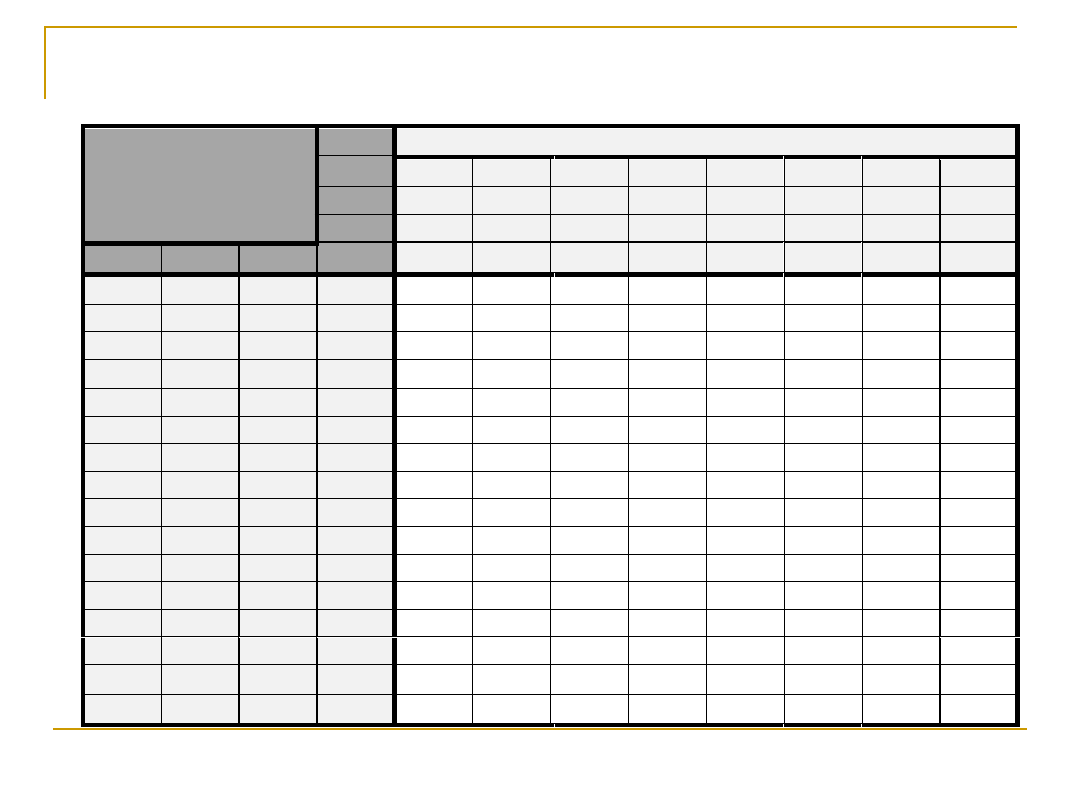
Kod ASCII

8

Bit kontroli parzystości

7

0

0

0

0

1

1

1

1

6

0

0

1

1

0

0

1

1

Numery bitów słowa

5

0

1

0

1

0

1

0

1

4

3

2

1

0

0

0

0

NUL

DEL

SP

0

@

P

‘

p

0

0

0

1

SOH DC1

!

1

A

Q

a

q

0

0

1

0

STX

DC2

„

2

B

R

b

r

0

0

1

1

ETX

DC3



3

C

S

c

s

0

1

0

0

EOT

DC4

$

4

D

T

d

t

0

1

0

1

ENQ NAK

%

5

E

U

e

u

0

1

1

0

ACK

SYN

&

6

F

V

f

v

0

1

1

1

BEL

ETB

`

7

G

W

g

w

1

0

0

0

BS

CAN

(

8

H

X

h

x

1

0

0

1

HT

EM

)

9

I

Y

i

y

1

0

1

0

LF

SUB

*

:

J

Z

j

z

1

0

1

1

VT

ESC

+

;

K

[

k

{

1

1

0

0

FF

FS

,

<

L

\

l

|

1

1

0

1

CR

GS

-

=

M

]

m

}

1

1

1

0

SO

RS

.

>

N



n

~

1

1

1

1

SI

US

/

?

O



o

DEL

Kodowanie znaków a problem
polskich liter

Kod ASCII rozszerzony wprowadza dodatkowe 128 znaków

wykorzystując mało używany bit parzystości:



IBM wprowadza



Code Page 474 dla USA



Code Page 852 dla Europy Wschodniej

1. W 1987 roku ISO tworzy standard ISO 8859 (rozszerzone ASCII):



ISO 8859-1 (Latin-1) - Europa zachodnia



ISO 8859-2 (Latin-2) - Europa wschodnia



...............................



ISO 8859-5 (cyrlica)



...............................



ISO 8859-7 (greka)



...............................

2. W 1990 roku Instytut Maszyn Matematycznych tworzy kod Mazovia

(rozpowszechniony w dobie kart graficznych Hercules)

3. Firma Microsoft tworzy własny zestaw znaków dla Europy

wschodniej Windows CP 1250

cd..

Litera Mazovia IBM Latin-2 Windows1250 ISO Latin-2

Ą

143

164

165

161

Ć

149

143

198

198

Ę

144

168

202

202

Ł

156

157

163

163

Ń

165

227

209

209

Ó

163

224

211

211

Ś

152

151

140

166

Ź

160

141

143

172

Ż

161

189

175

175

ą

134

165

185

177

ć

141

134

230

230

ę

145

169

234

234

ł

146

136

179

179

ń

164

228

241

241

ó

162

162

243

243

ś

158

152

156

182

ź

166

171

159

188

ż

167

190

191

191