1

Równowagi

fazowe

w układach

trójskładnikow

ych

(a)

Waldemar Ufnalski

Wprowadzenie do termodynamiki

chemicznej

Wykład 14a

C

B

A

x

B

x

A

1

f

az

a

ci

ek

ła

K

CA

K

AB

+



+



2

14.1. Reguła faz i

graficzna prezentacja

równowag fazowych

Wykład 14a

3

Układ trójskładnikowy dwufazowy (

+ )...

Liczba stopni swobody = k - f + 2 = 3 - 2 + 2 = 3

Bada się zależności:

1) Izobary (P = const):

f(T, x

A

x

B

)

P=const

= 0

T =

f(x

A

x

B

)

(P =

const )

2) Izotermy (T = const):

f(P, x

A

x

B

)

T=const

= 0

P =

f(x

A

x

B

)

(T =

const )

Są to równania opisujące powierzchnie w

przestrzeni 3 - wymiarowej

W narzuconych warunkach T,P maksymalna

liczba faz:

f

max

= 3.

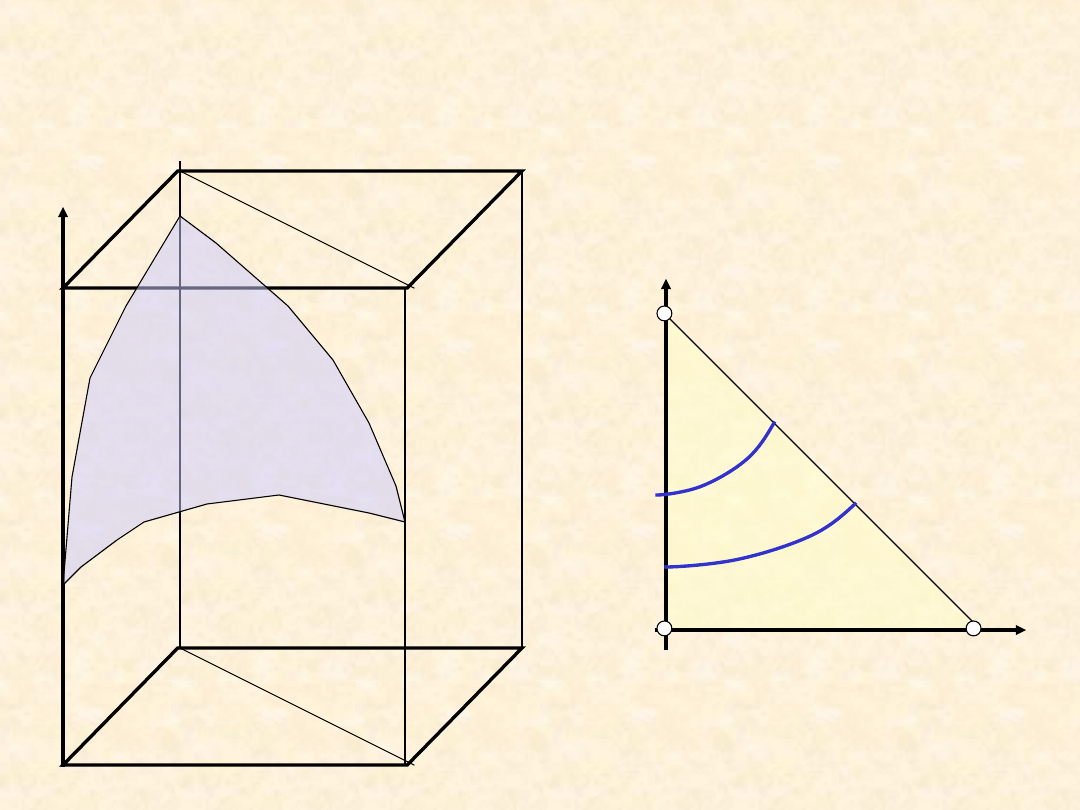
4

Układ trójskładnikowy dwufazowy (

+ )...

T



x

B



P =
const

x

A



Prostokątny układ współrzędnych...

T, P =
const

x

A



x

B



0

1

1

T

1

T

2

<

T

1

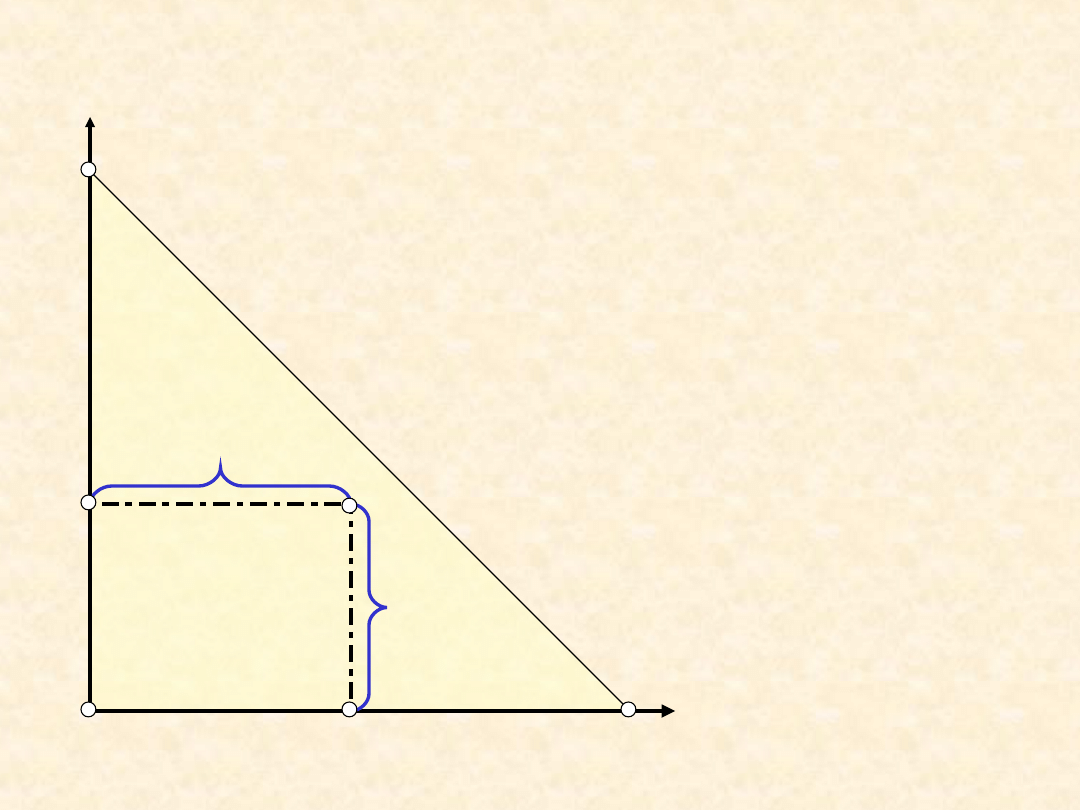
5

Układ
trójskładnikowy ...

Prostokątny układ współrzędnych...

x

A



x

B



0

1

1

C

B

A

T, P =
const

x

A

x

B

Punkt
reprezentuje fazę
trójskładnikową w
podanych
warunkach (T,P =
const)

x

A

+ x

B

 1

x

C

= 1 - x

A

- x

B

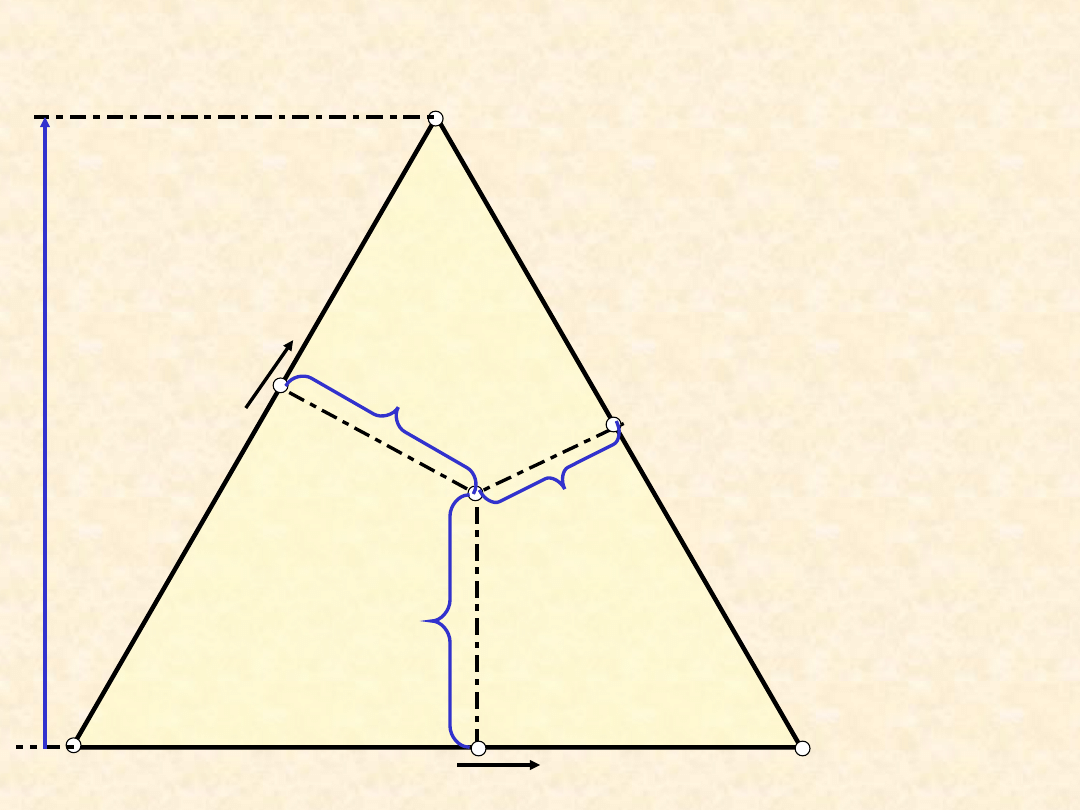
6

C

B

A

x

B

x

A

h

b

a

c

Trójkąt Gibbsa (I) ....

a + b + c = h

x

A

= a/h

x

B

= b/h

x

C

= c/h

Układ
trójskładnikowy ...

Punkt
reprezentuje fazę
trójskładnikową w
podanych
warunkach (T,P =
const)

7

a + b + c =

l

x

A

= a/l

x

B

= b/l

x

C

= c/l

C

B

A

x

B

x

A

l

b

a

c

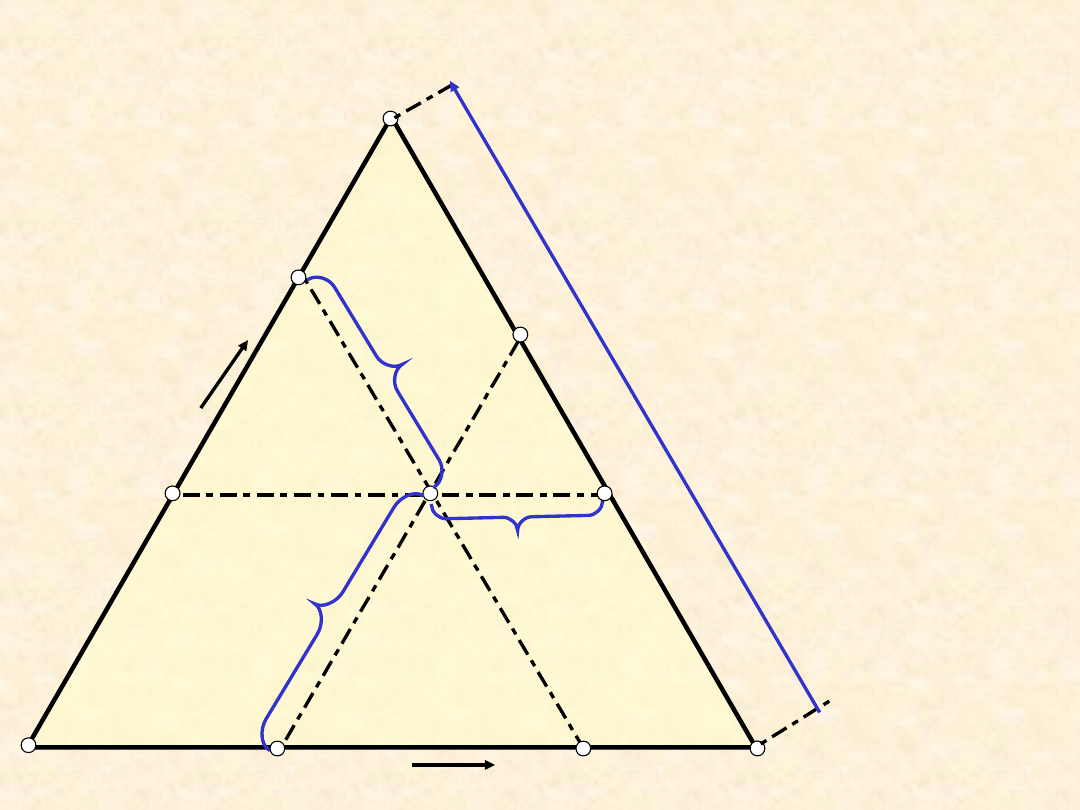
Trójkąt Gibbsa (II) ....

Układ
trójskładnikowy ...

Punkt
reprezentuje fazę
trójskładnikową w
podanych
warunkach (T,P =
const)

8

P =
const

T



C

B

A

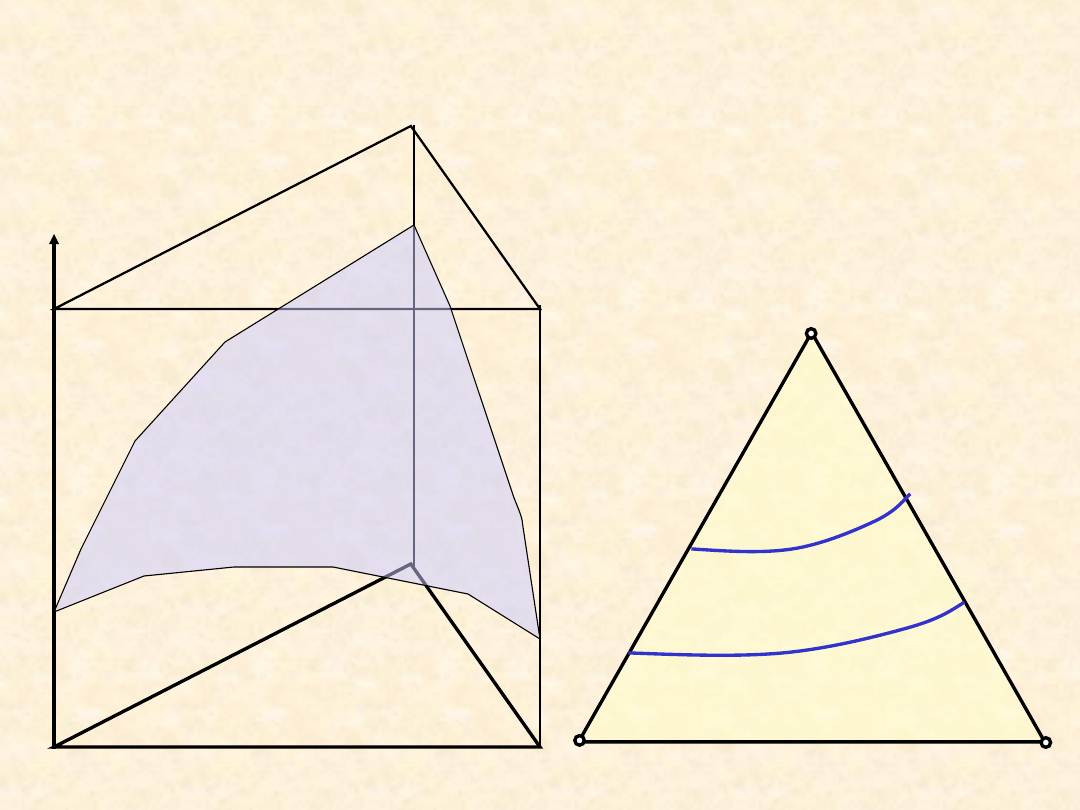
Układ trójskładnikowy dwufazowy (

+ )...

Trójkąt Gibbsa
(III) ....

C

B

A

T

1

T

2

<

T

1

T, P = const

9

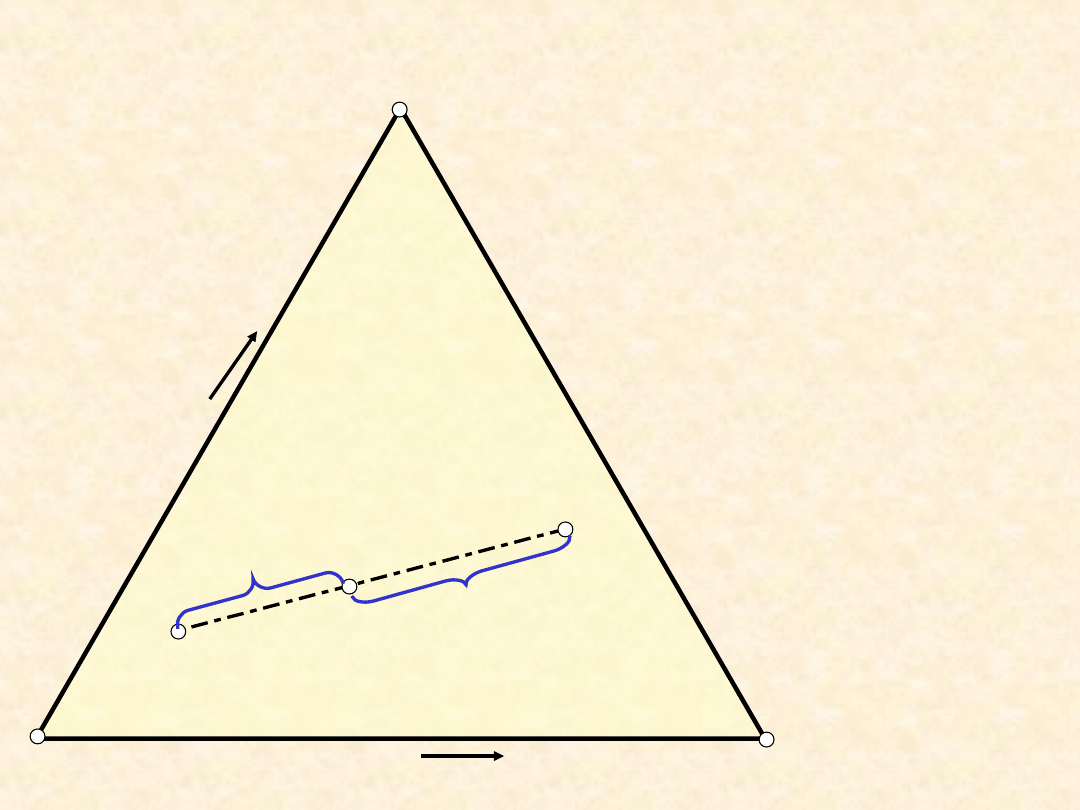
Układ trójskładnikowy - bilans
materiałowy...

C

B

A

x

B

x

A

a

b







Reguła dźwigni

Mieszanie dwóch

faz: + 

 

Rozpad układu

na dwie fazy

  + 

a·n



= b ·n



n



+ n





n



10

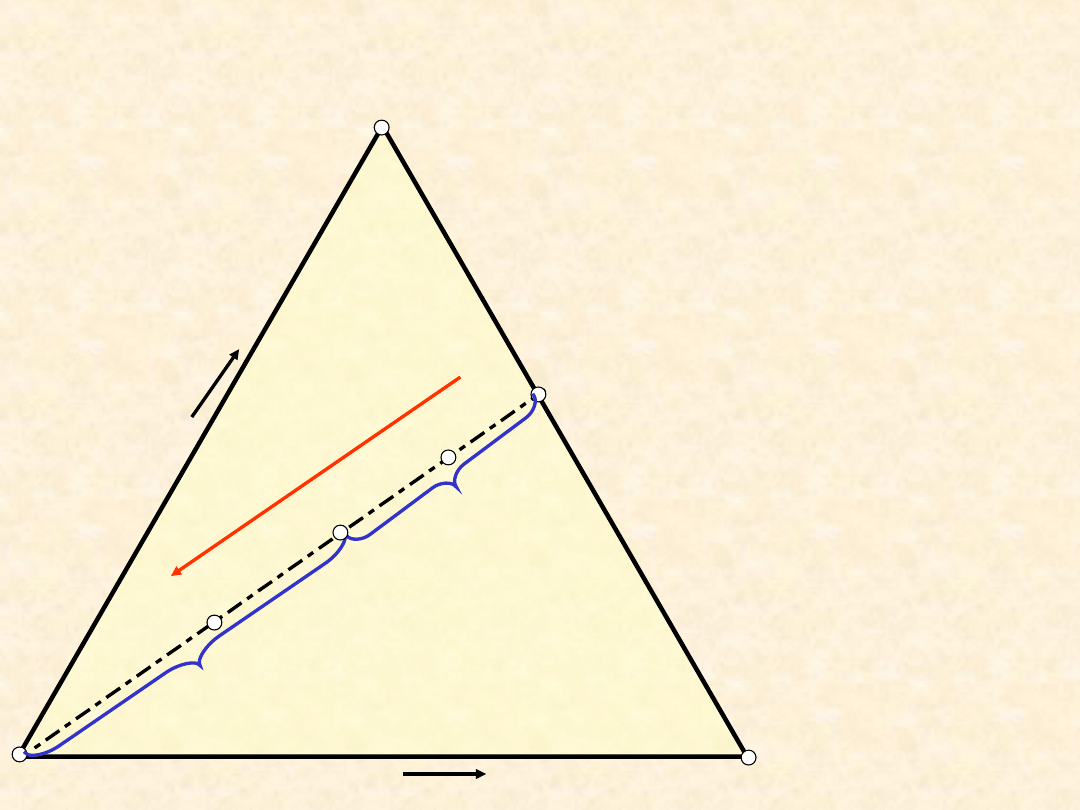
Układ trójskładnikowy - bilans
materiałowy...

Reguła dźwigni

Mieszanie

roztworu A + B z

czystym C:

R

AB

+ C    

a·n

AB

= b ·n

C

n



+

n

C



n



C

B

A

x

B

x

A

a

b







R

AB

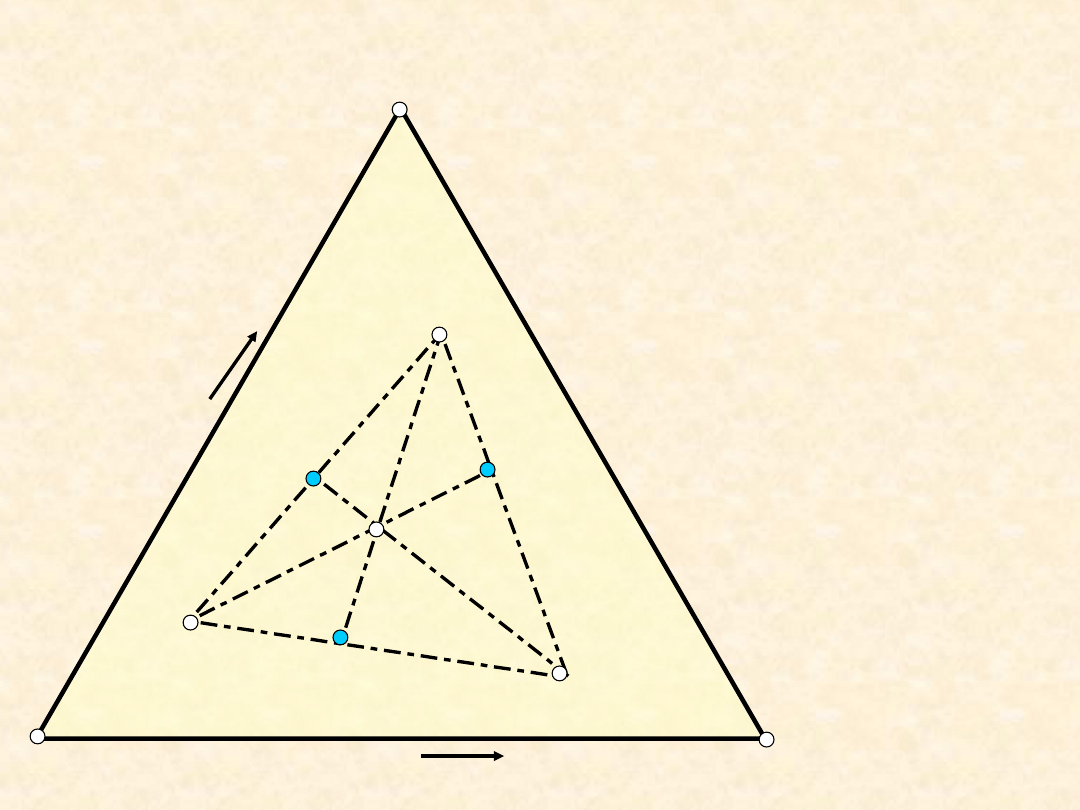
11

Układ trójskładnikowy - bilans
materiałowy...

C

B

A

x

B

x

A







Reguła dźwigni

Mieszanie trzech

faz: + 

+   

Rozpad układu

na trzy fazy

  +  + 



12

14.2. Równowaga ciecz -

ciecz

Wykład 14a

13

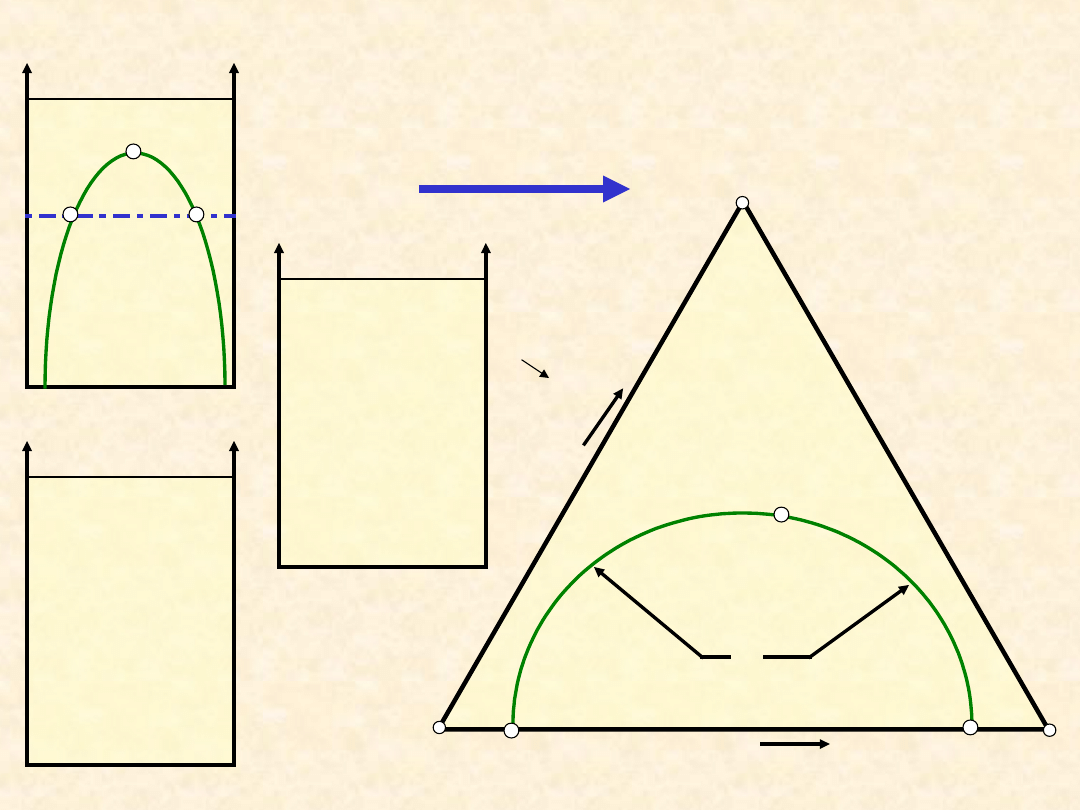
Równowaga ciecz - ciecz (typ I) ...

T

B

A

1 faza
ciekła

T

B

C

1 faza
ciekła

T

A

C

T

k

CA

+



T’

C

B

A

x

B

x

A

1 faza
ciekła

+ 

K

14

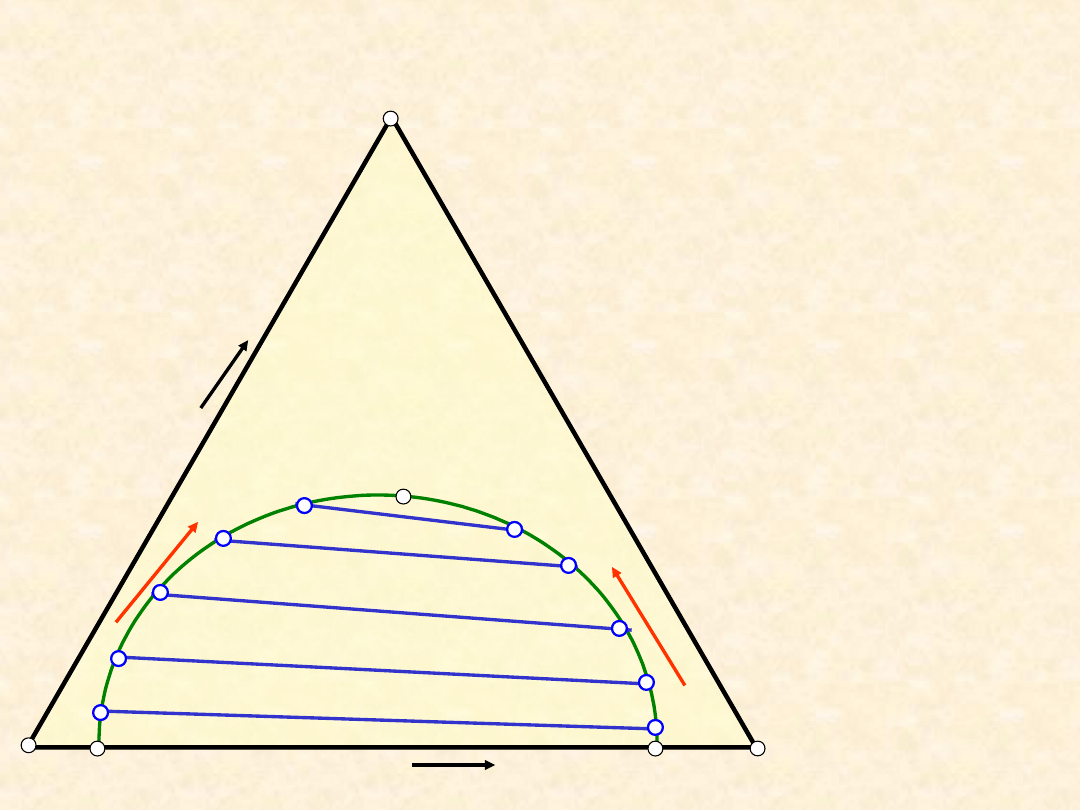
Równowaga ciecz - ciecz (typ I) ...

C

B

A

x

B

x

A

K





- Krzywa
binodalna -
roztwory
nasycone
-

Konody

(cięciwy
równowagi) -
łączą roztwory
nasycone
względem siebie

- Krytyczny

punkt
mieszalności (K)

15

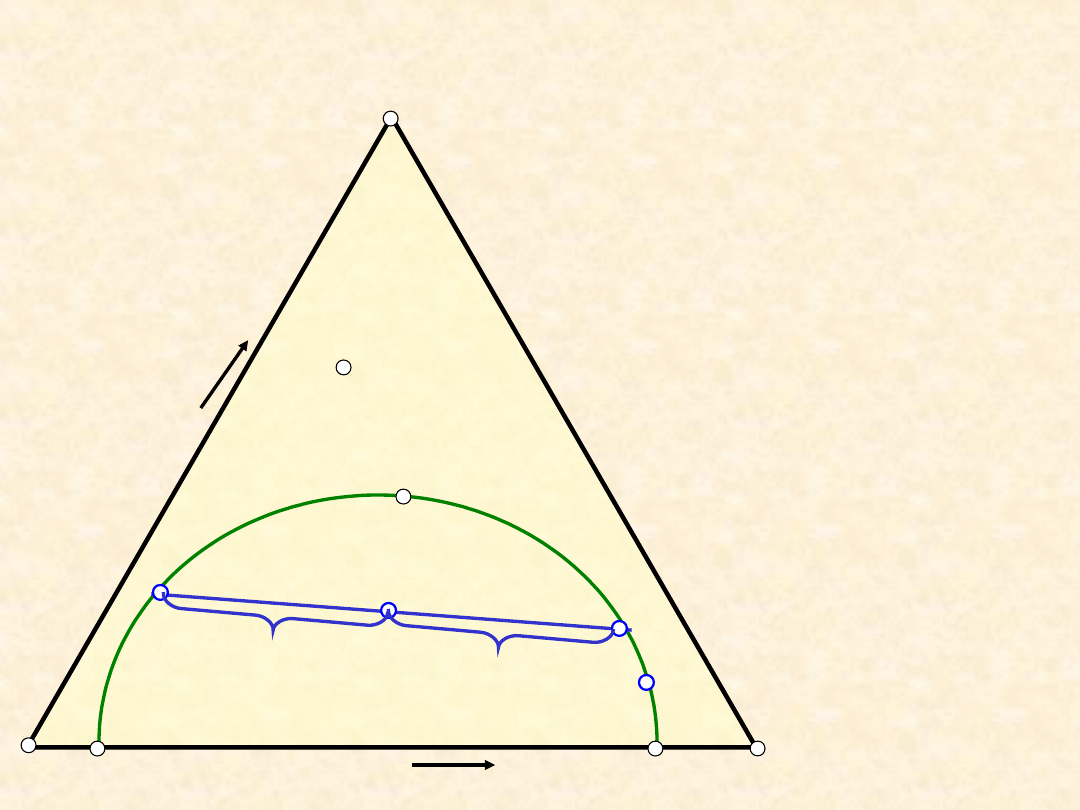
Reguła dźwigni

Rozpad układu

na dwie fazy

H  + 

a· n



= b ·n



n



+ n





n

H

Równowaga ciecz - ciecz (typ I) - bilans
materiałowy

C

B

A

x

B

x

A

K





M

H

b

a

16

Homogenizacja

mieszaniny

cieczy A + C

dodatkiem

wspólnego

„rozpuszczalnika

” B

Równowaga ciecz - ciecz (typ I) ...

C

B

A

x

B

x

A

K





1

2

3

4

17

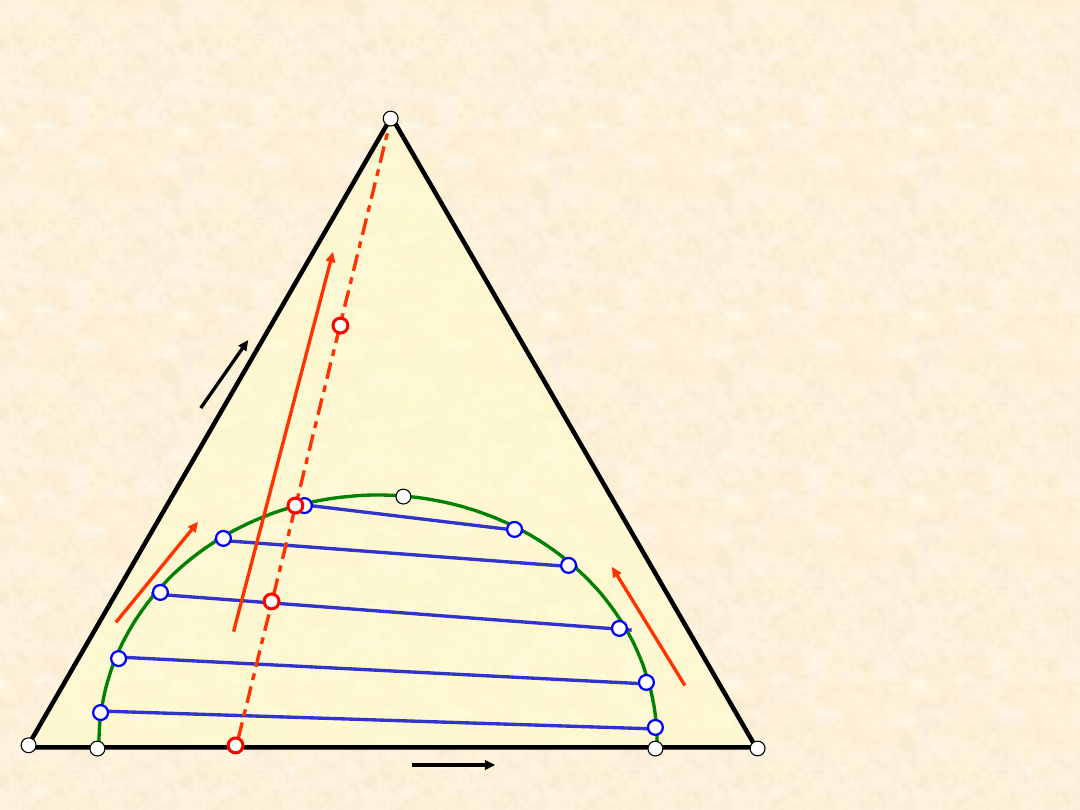
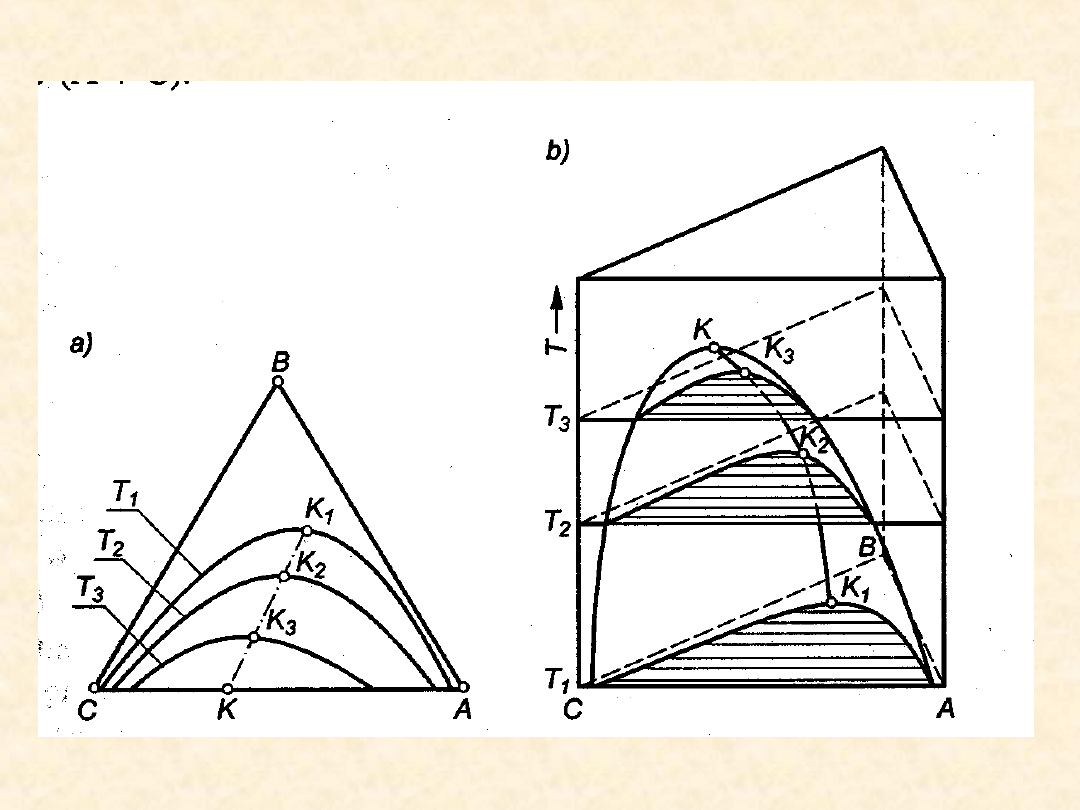
Równowaga ciecz - ciecz (typ I) - wpływ
temperatury (a)

18

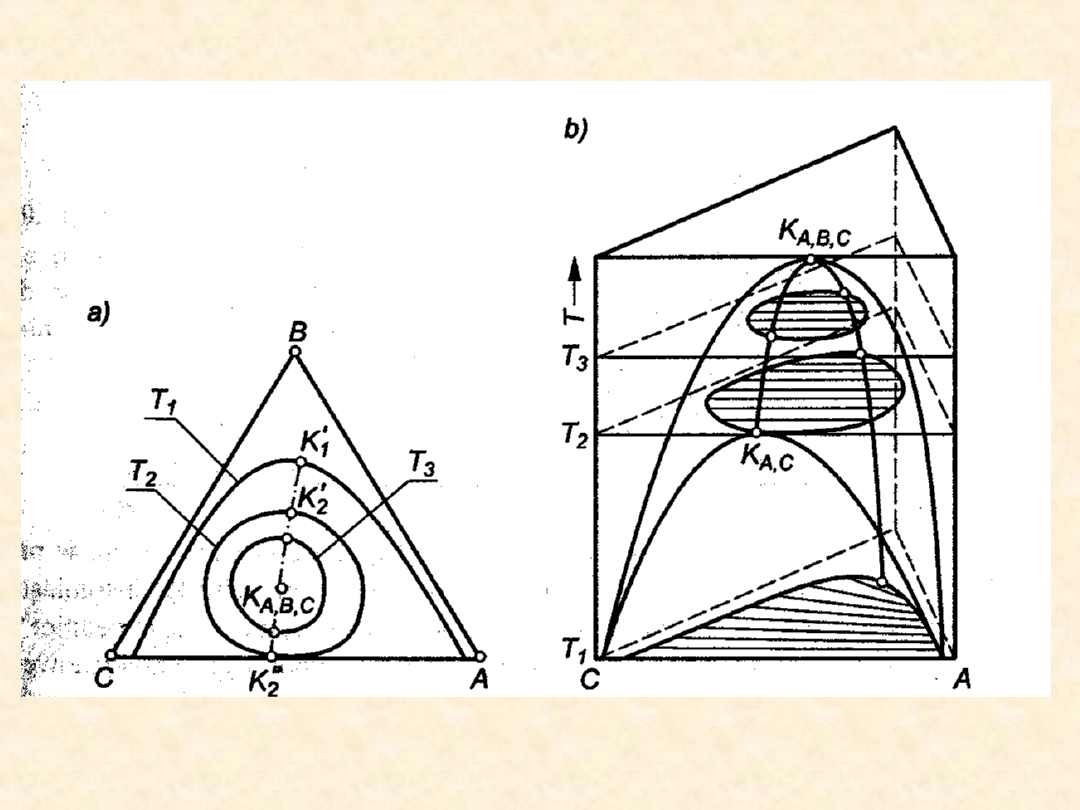
Równowaga ciecz - ciecz (typ I) - wpływ
temperatury (b)

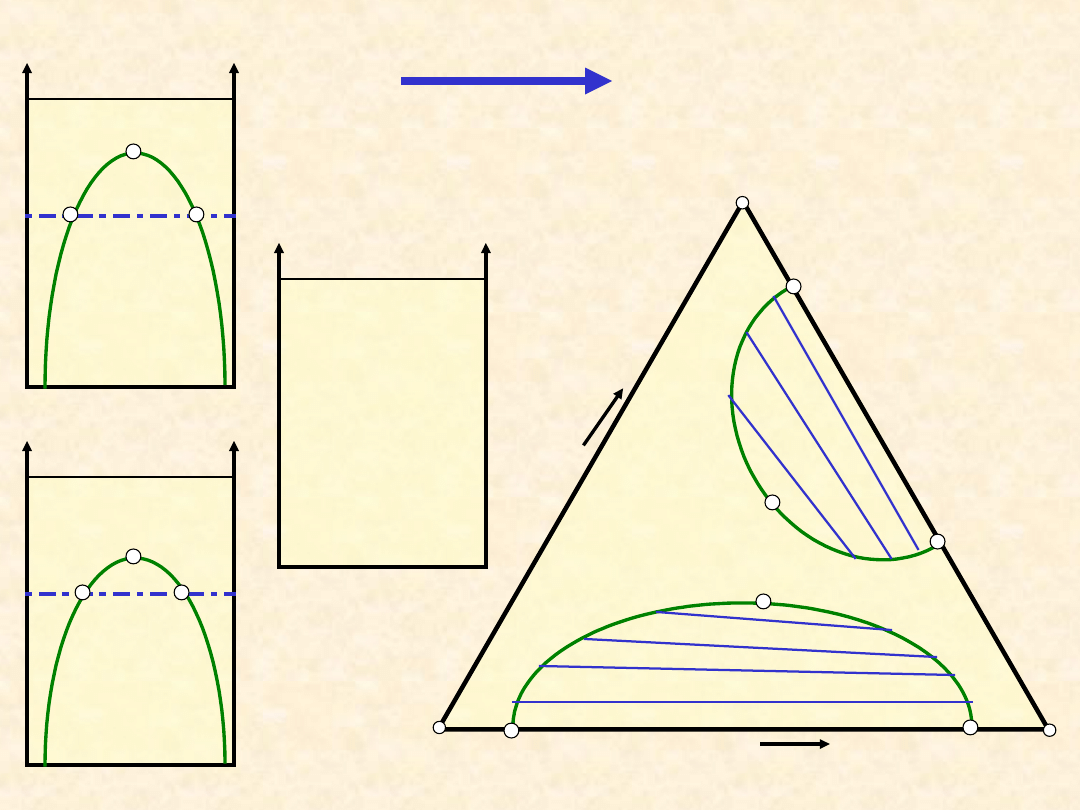
19

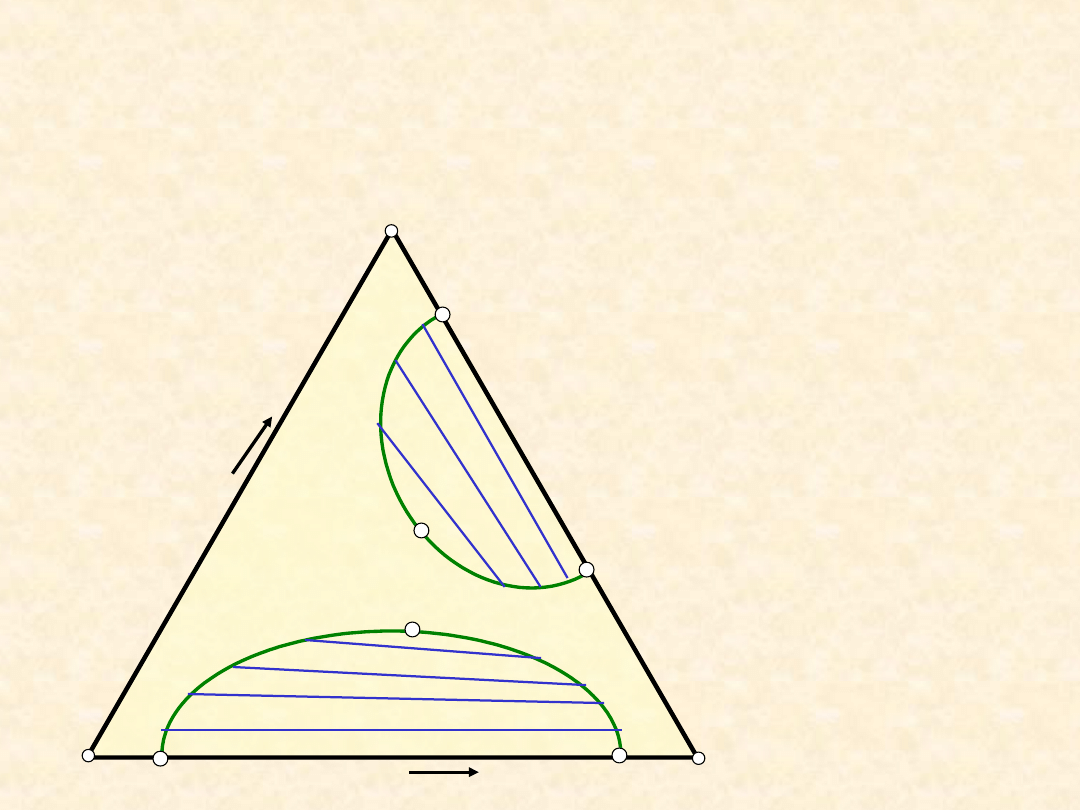
Równowaga ciecz - ciecz (typ IIa) ...

T

B

C

1 faza
ciekła

T

A

C

T

k

CA

+



T’

T

B

A

T

k

AB

+



T’

C

B

A

x

B

x

A

1

f

az

a

ci

ek

ła

K

CA

K

AB

+



+



20

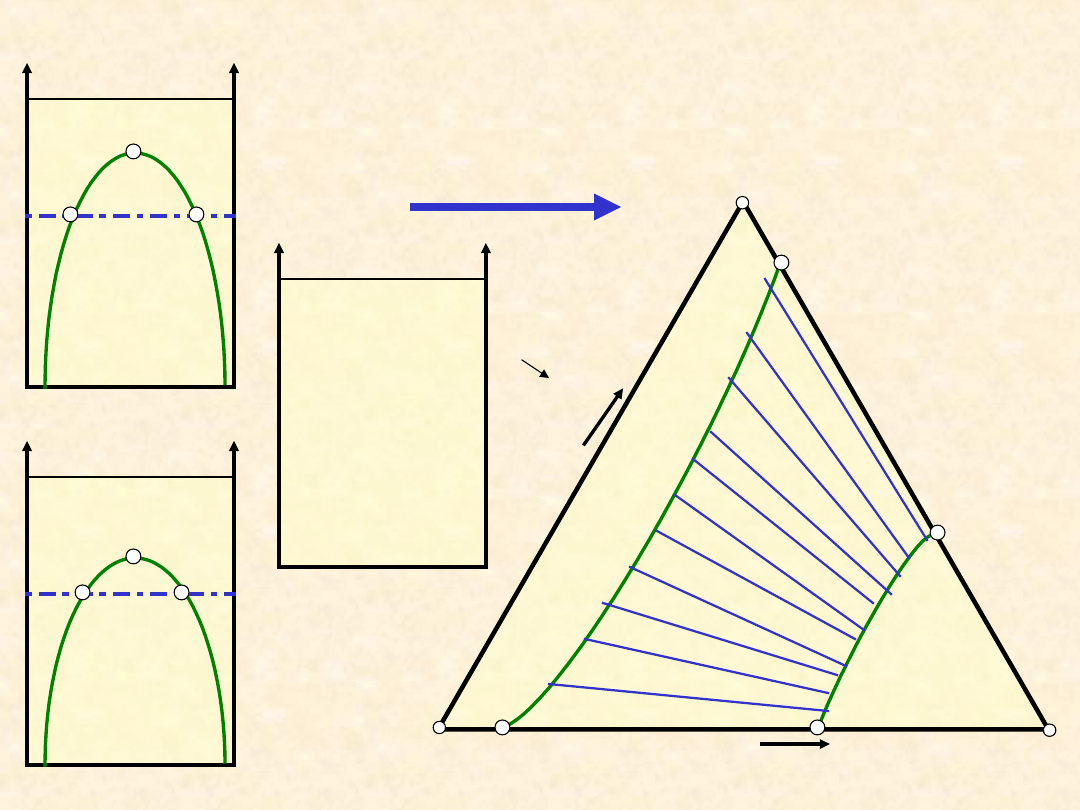
Równowaga ciecz - ciecz (typ IIb) ...

T

B

C

1 faza
ciekła

T

A

C

T

k

CA

+



T’

T

B

A

T

k

AB

+



T’

C

B

A

x

B

x

A

1

f

az

a

ci

ek

ła

+



1

fa

za

ci

ek

ł

a

21

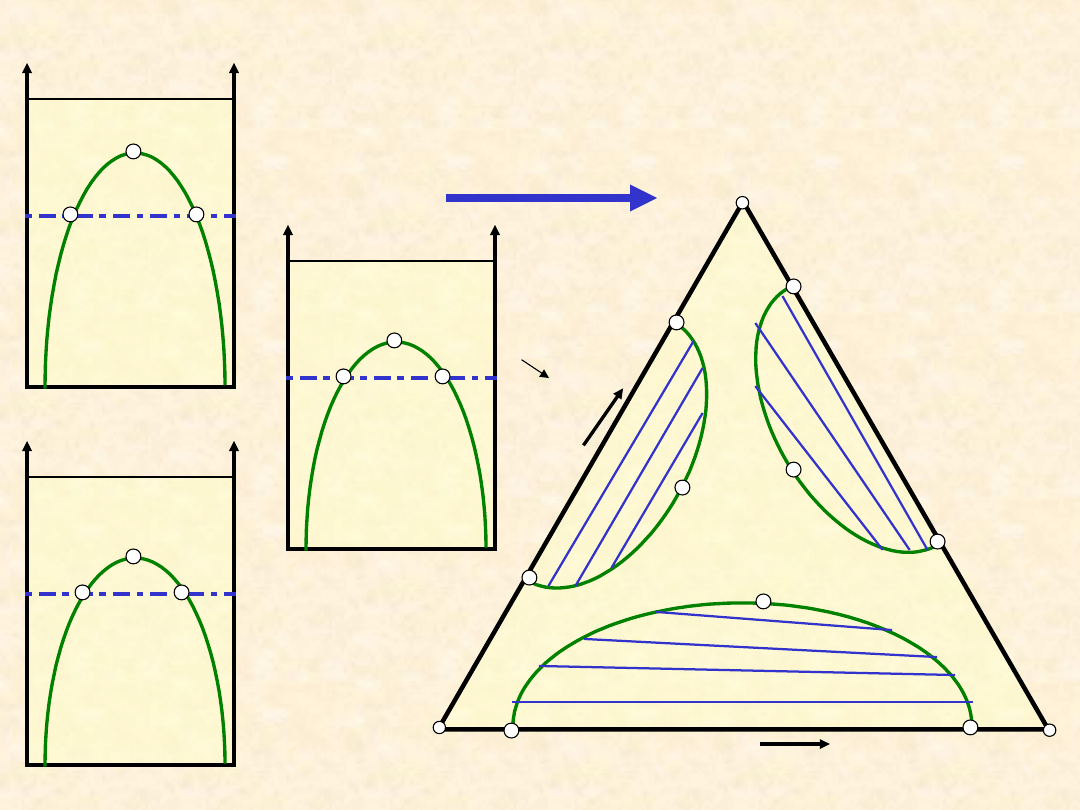
Równowaga ciecz - ciecz (typ IIIa) ...

T

A

C

T

k

CA

+



T’

T

B

A

T

k

AB

+



T’

T

B

C

T

k

CB

+



T’

C

B

A

x

B

x

A

K

CA

K

AB

+





+



K

CB



+



22

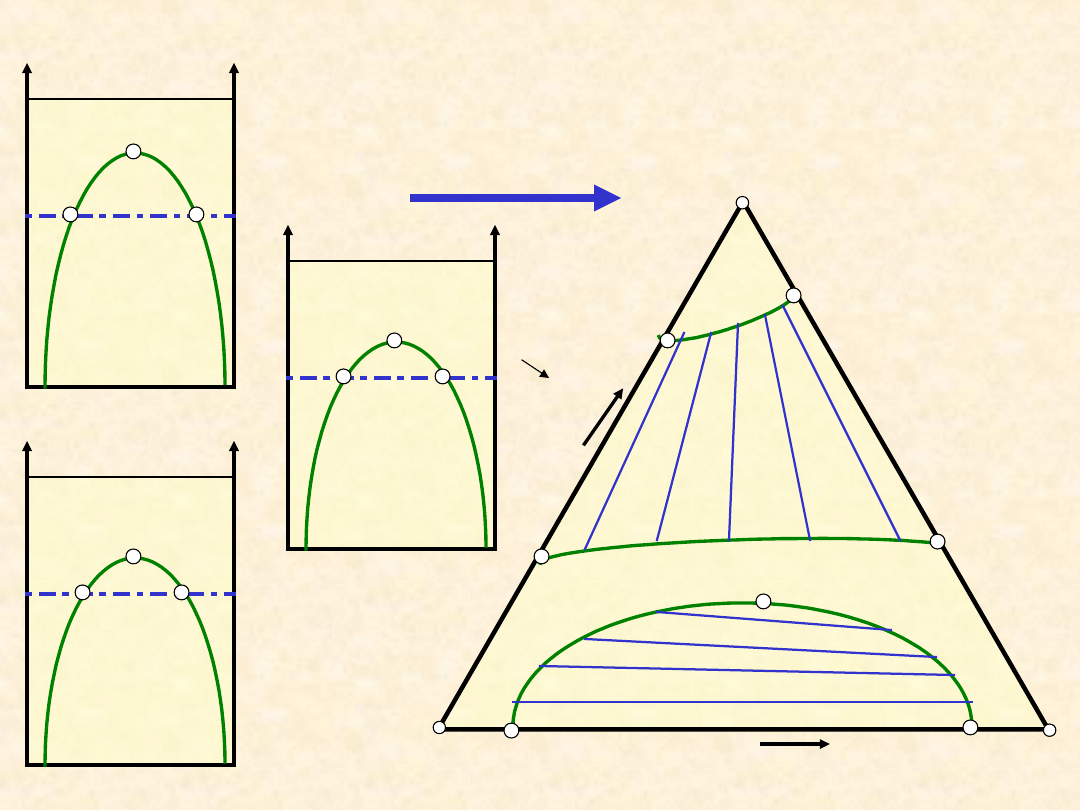
Równowaga ciecz - ciecz (typ IIIb) ...

T

A

C

T

k

CA

+



T’

T

B

A

T

k

AB

+



T’

T

B

C

T

k

CB

+



T’

C

B

A

x

B

x

A

K

CA

+



+



23

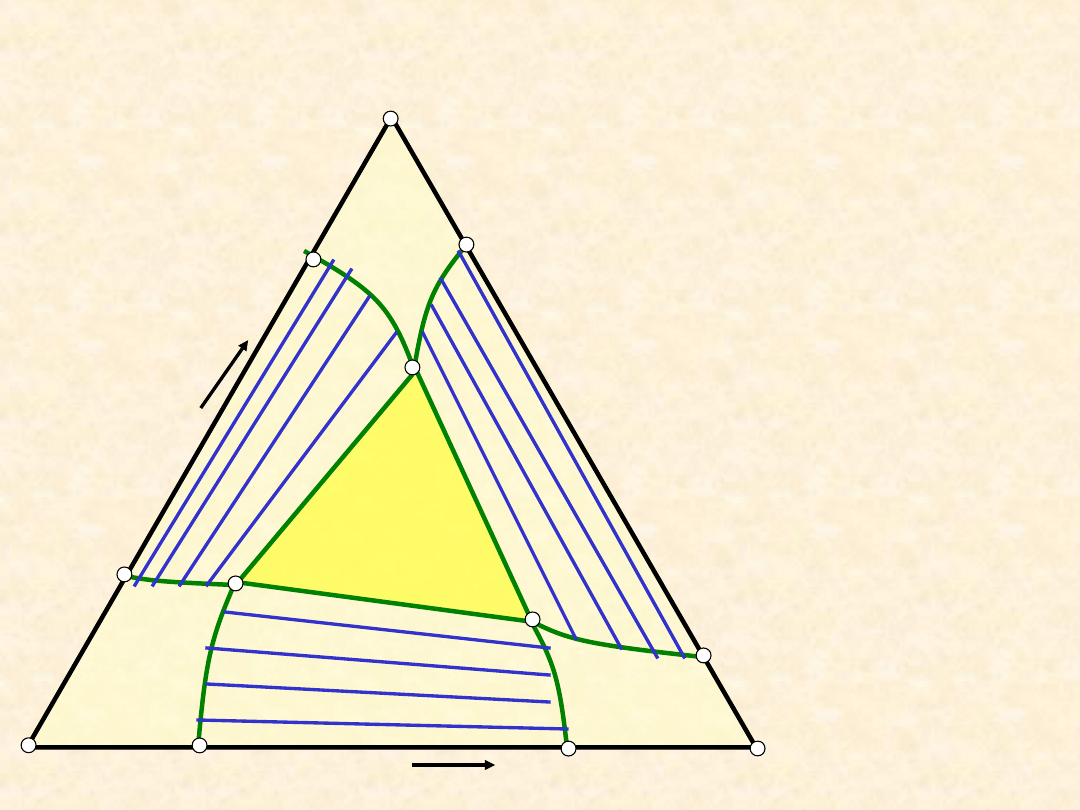
Równowaga ciecz - ciecz (typ IVa) ...

C

B

A

x

B

x

A







1/C

1/A

1/B

2/ +



2

/

+



2

/

+



3/ + 

+

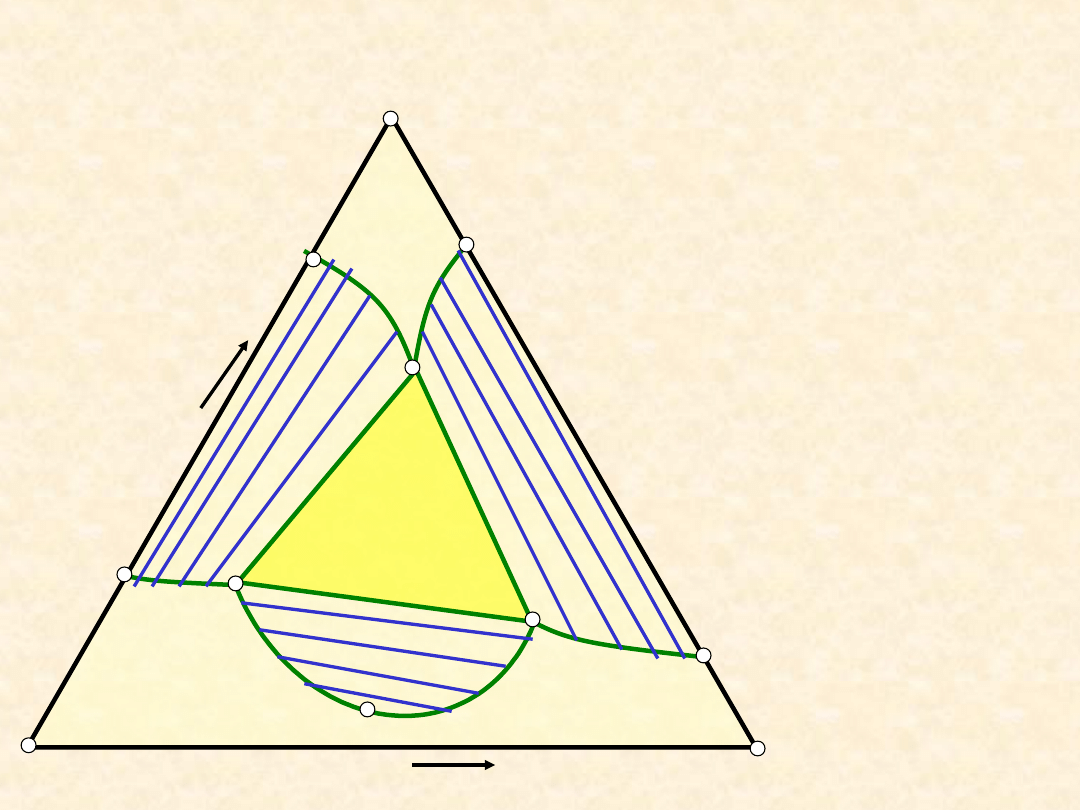
W polach
diagramu
podano:
- liczbę faz
- naturę faz lub
składnik
dominujący (w
przypadku
układu
jednofazowego)

24

Równowaga ciecz - ciecz (typ IVb) ...

C

B

A

x

B

x

A







1/B

2/ +



2

/

+



2

/

+



3/ + 

+

1

1

K





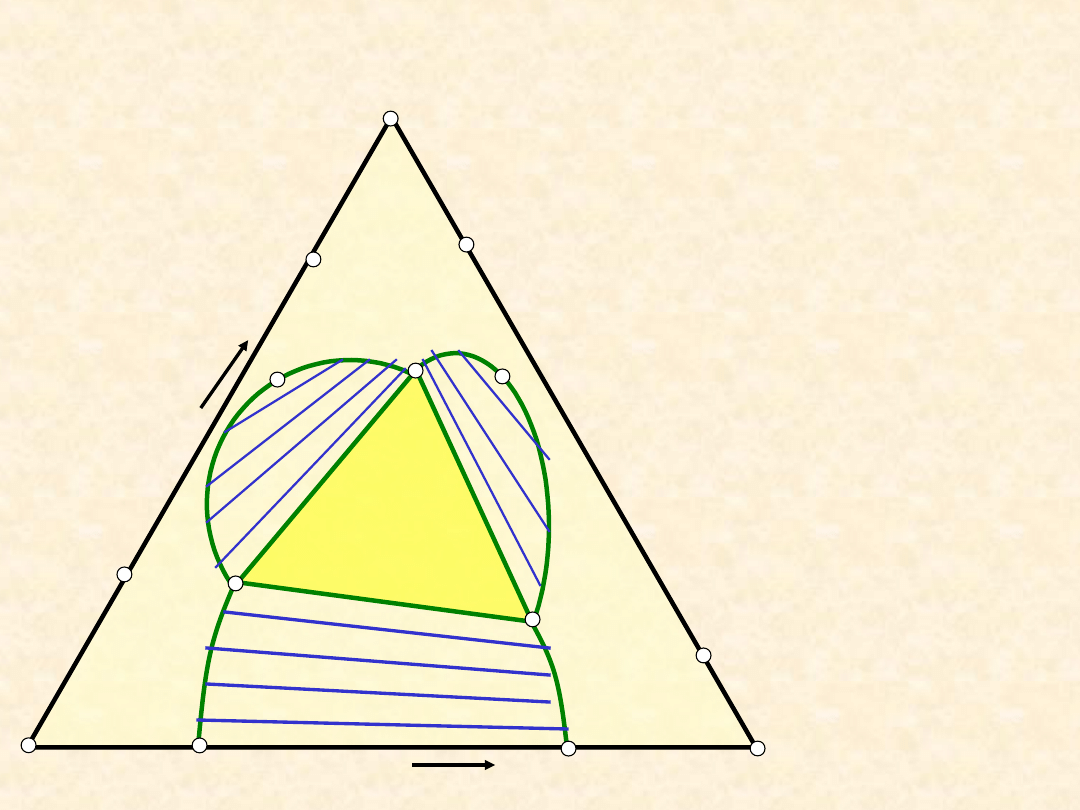
W polach
diagramu podano:
- liczbę faz
- naturę faz
- ewentualnie
składnik
dominujący (w
przypadku układu
jednofazowego

25

Równowaga ciecz - ciecz (typ IVc) ...

C

B

A

x

B

x

A







2/ +



3/ + 

+

2/



+



2

/

+



1

1

1

K



K



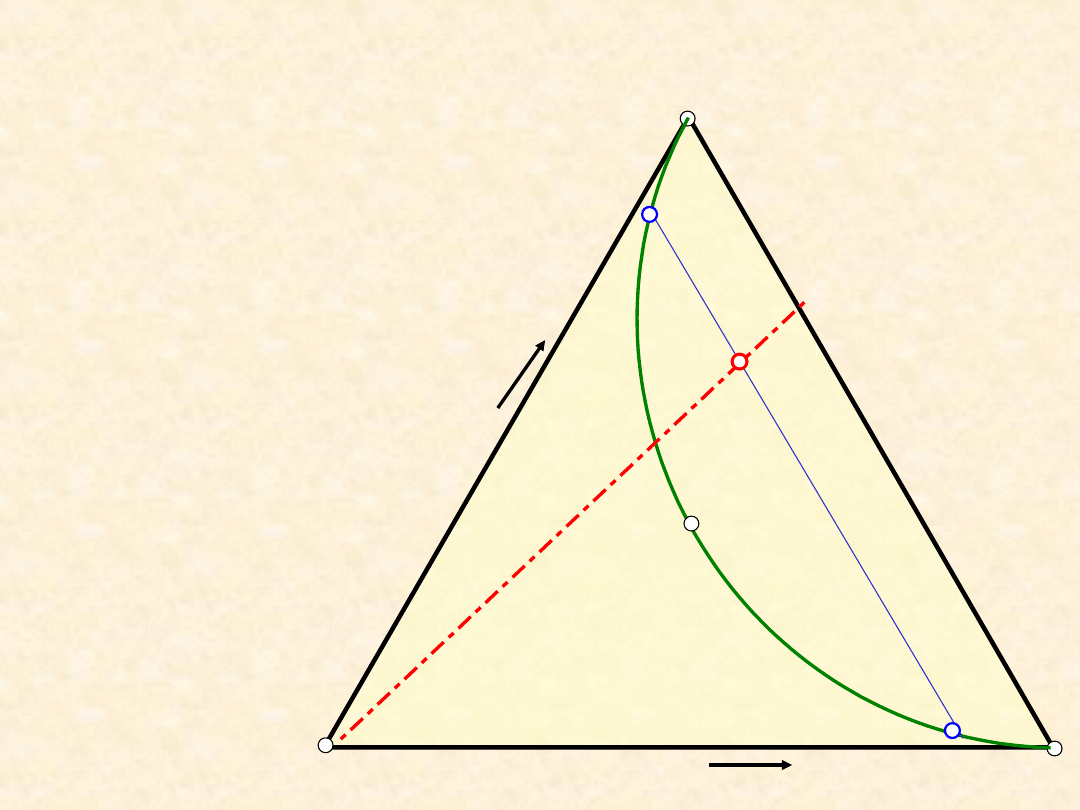
W polach
diagramu
podano:
- liczbę faz
- naturę faz

26

Równowaga ciecz - ciecz: prawo
podziału ...

C

B

A

x

B

x

A

K





Model:

- ciecze A i B są
praktycznie wzajemnie
niemieszalne
- ilość C jest niewielka
w stosunku do A i B
- roztwory  i  są

praktycznie
dwuskładnikowe

27

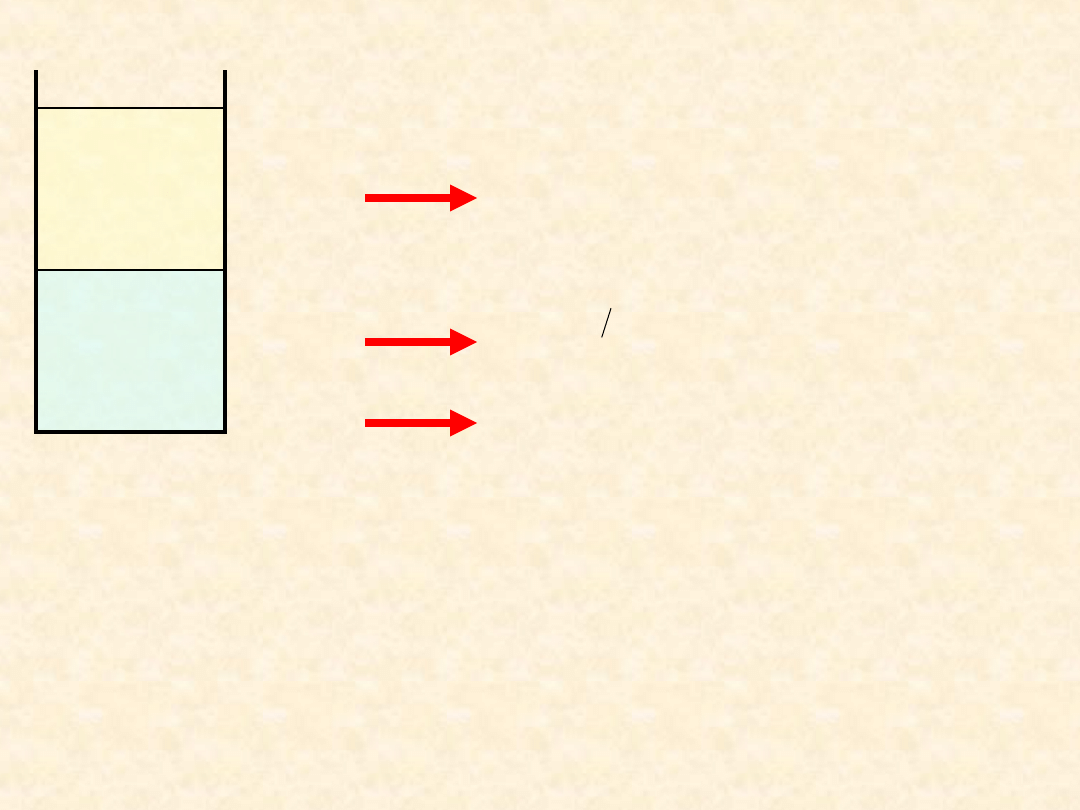
Równowaga ciecz - ciecz: prawo
podziału ...

Warunek równowagi dyfuzyjnej dotyczy
praktycznie wyłącznie składnika C
wchodzącego w skład obu faz:





















C

C

C

C

x

T

x

T

,

,



(1
)

 





 

















C

C

C

C

C

C

x

T

RTa

T

x

T

a

RT

T

,

,

ln

*

*







(2
)

















C

C

C

C

x

T

a

x

T

a

,

,



























C

C

C

C

C

C

x

T

x

x

T

x

,

,



 

 

 

T

K

T

T

x

x

C

C

C

C

C

























.

,

Współczynnik
podziału
(Nernsta):

28

Równowaga ciecz - ciecz: zasada
ekstrakcji

Jeżeli G

E

AC

>> 0 oraz G

E

BC

<< 0

(A

)

(B

)

x

C



x

C



1





,





C

1





,





C

 

1



T

K

C









C

C

x

x 

Przeważająca ilość składnika C gromadzi
się w rozpusz- czalniku B:
- wydzielanie reagenta z mieszaniny
poreakcyjnej
- usuwanie zanieczyszczeń
- zatężanie ilości śladowych (analiza
chemiczna)

29

14.3. Równowaga ciecz -

para

Wykład 14a

30

P

C

B

A

P

*

C

P

*

A

P

*

B

Równowaga ciecz - para: układ
doskonały...

T =
const.

P

A

C

g

c

P

B

A

g

c

P

B

C

g

c

31

Równowaga ciecz - para: układ
doskonały...

T =
const.

A

A

A

A

x

P

y

P

P

*





B

B

B

B

x

P

y

P

P

*













B

A

C

B

A

C

x

x

P

y

y

P

P













1

1

*

Prężności
cząstkowe
składnikó
w:

(3
b)

(3a
)
(3
c)







 



B

C

B

A

C

A

C

B

A

C

B

B

A

A

C

B

A

x

P

P

x

P

P

P

x

x

P

x

P

x

P

P

P

P

P

*

*

*

*

*

*

*

*



























1

(4)





B

A

B

A

B

C

A

A

C

B

C

B

A

y

y

P

P

y

P

P

y

P

P

P

P

P

P











1

*

*

*

*

*

*

*

*

*

(5)

Równanie powierzchni
parowania:

Równanie powierzchni
kondensacji:

32

Równowaga ciecz - para: układ
doskonały...

T =
const.

(6
b)

(6a
)

Równania cięciw równowagi:



 



B

C

B

A

C

A

C

A

A

A

x

P

P

x

P

P

P

x

P

y

*

*

*

*

*

*













 



B

C

B

A

C

A

C

B

B

B

x

P

P

x

P

P

P

x

P

y

*

*

*

*

*

*











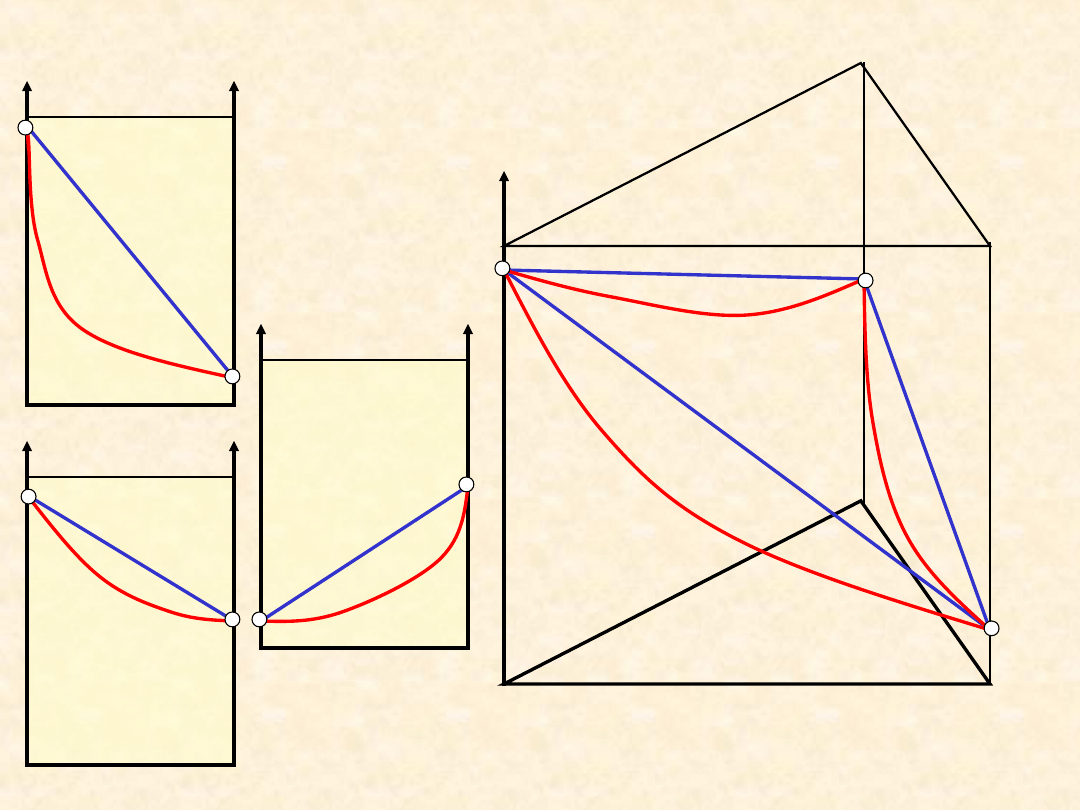
33

Równowaga ciecz - para: układ
doskonały...

T,P’ =
const.

C

B

A

x

B

x

A

c

g

c

+

g

P

B

C

g

c

P’

P

B

A

g

c

P’

P

A

C

g

c

P’

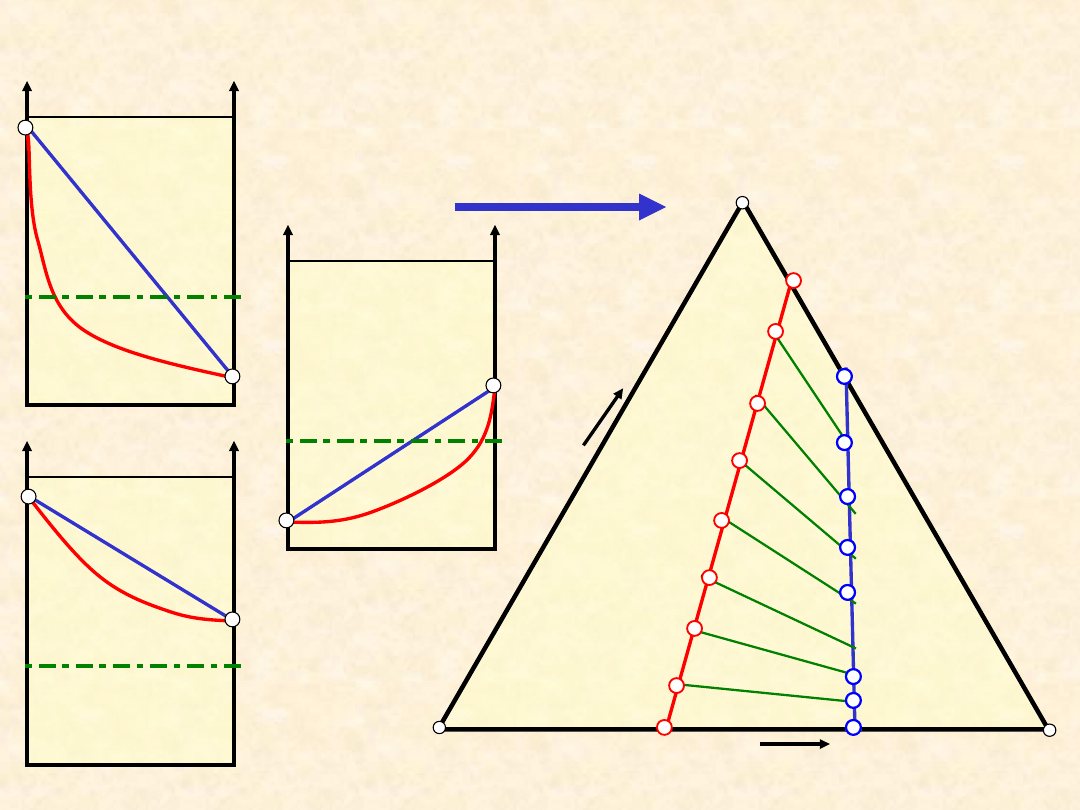
34

Równowaga ciecz - para: układ
doskonały...

T,P” =
const.

P

B

A

g

c

P
”

P

A

C

g

c

P
”

P

B

C

g

c

P
”

C

B

A

x

B

x

A

c

g

c

+

g

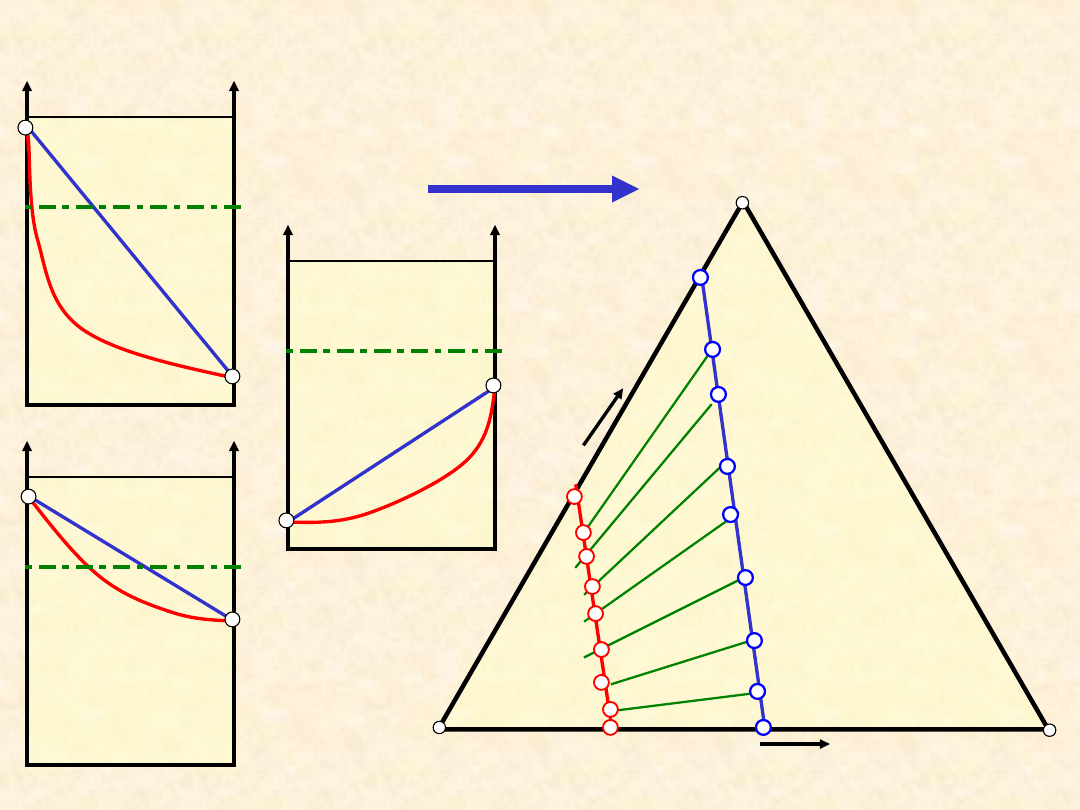
35

Równowaga ciecz - para: układ
doskonały...

P =
const.

T

A

C

g

c

T

B

C

g

c

T

B

A

g

c

T

C

B

A

T

*

C

T

*

A

T

*

B

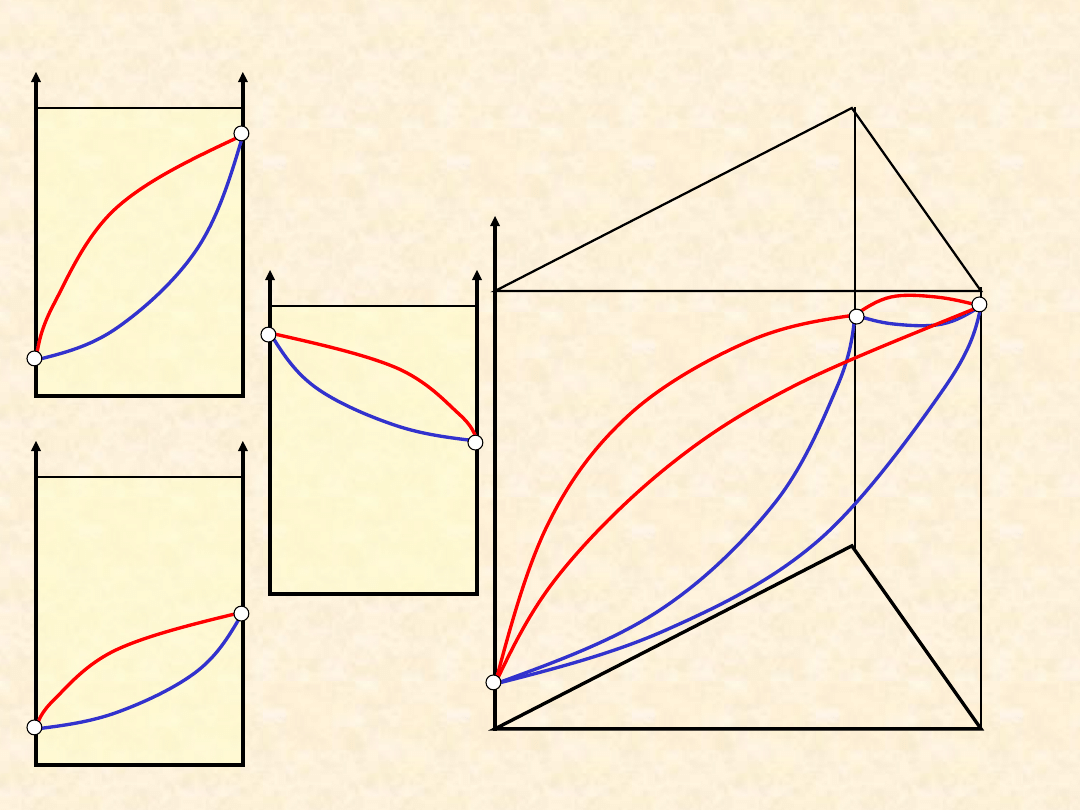
36

Równowaga ciecz - para: układ
doskonały...

P = const. - izobara van
Laara

(6
b)

(6a
)

(6
c)

(7
)

(8
)

Równanie powierzchni
wrzenia:





















T

T

T

R

S

x

y

A

A

par

A

A

*

*

ln





















T

T

T

R

S

x

y

B

B

par

B

B

*

*

ln





























T

T

T

R

S

x

x

y

y

x

y

C

C

par

B

A

B

A

C

C

*

*

ln

ln

1

1

 

 

 

C

B

A

B

B

A

A

x

x

x

x







exp

exp

exp











1

1

 





















T

T

T

R

S

T

C

B

A

C

B

A

par

C

B

A

*

/

/

*

/

/

/

/



37

Równowaga ciecz - para: układ
doskonały...

P = const. - izobara van
Laara

(9
)

Równanie powierzchni
kondensacji:



    

   

 

 

 

C

A

B

B

A

B

A

B

A

B

A

y

y

x

x















exp

exp

exp

exp

exp

exp

exp











1

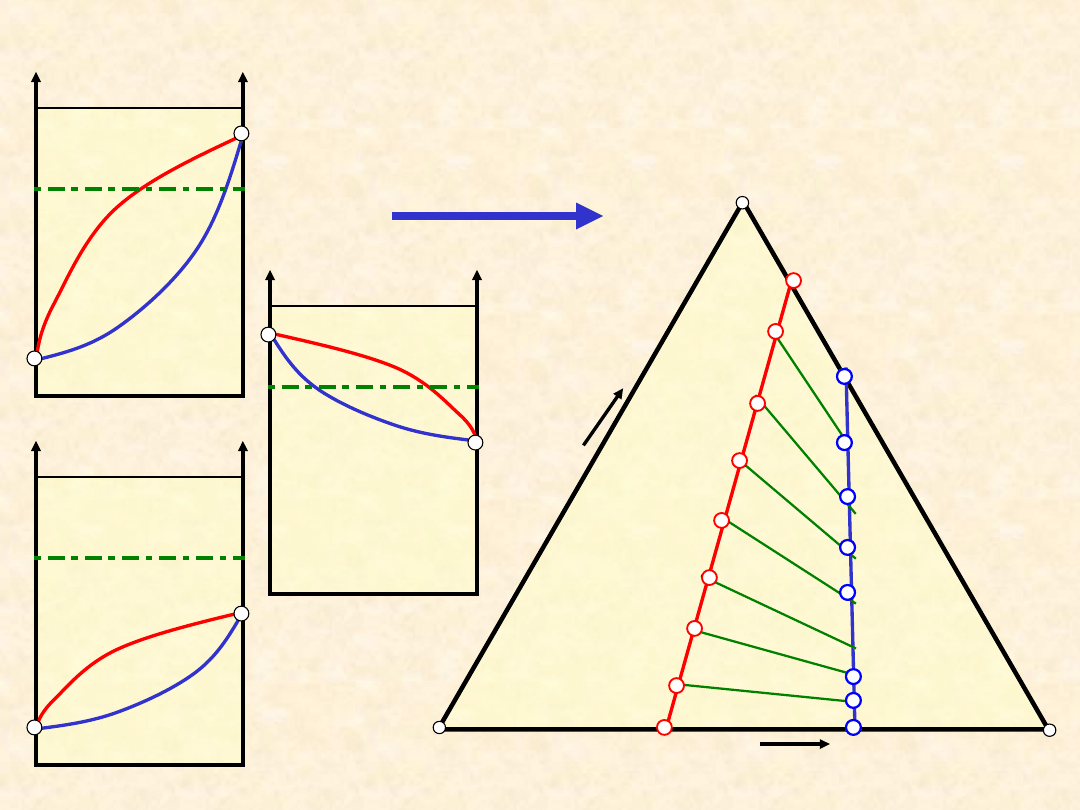
38

P,T’ =
const.

C

B

A

x

B

x

A

c

g

c

+

g

Równowaga ciecz - para: układ
doskonały...

T

B

A

g

c

T’

T

B

C

g

c

T’

T

A

C

g

c

T’

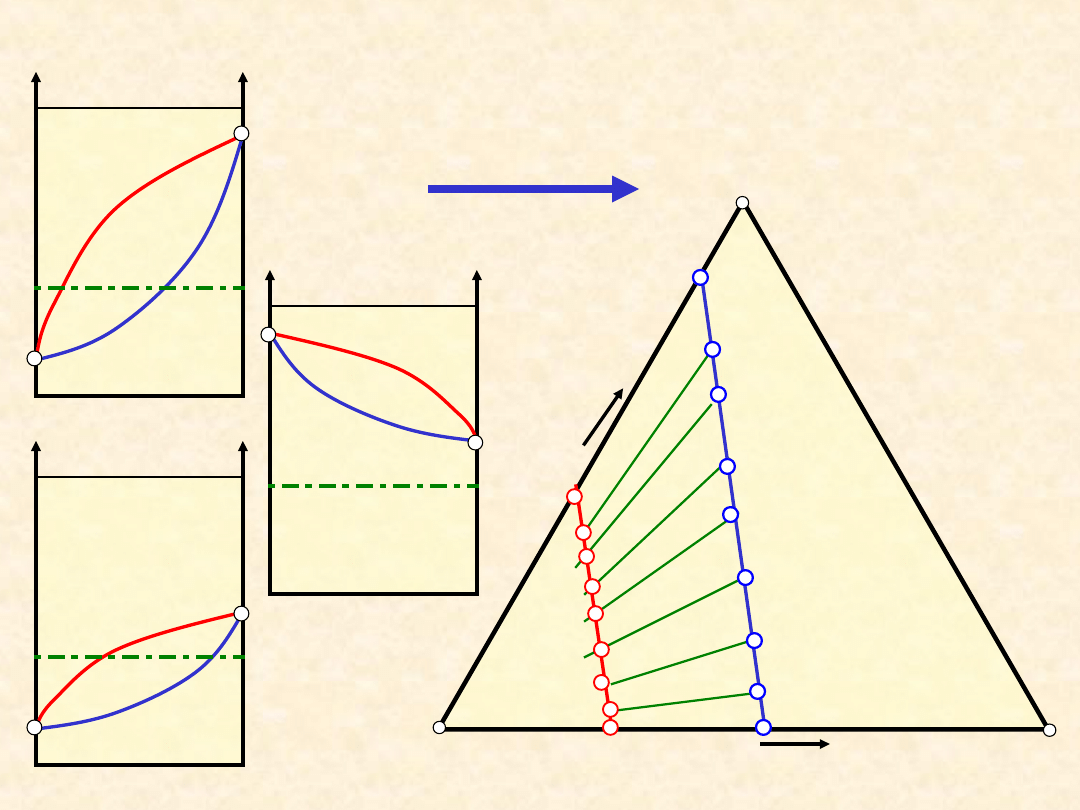
39

P,T” =
const.

Równowaga ciecz - para: układ
doskonały...

T

B

A

g

c

T”

T

B

C

g

c

T”

T

A

C

g

c

T”

C

B

A

x

B

x

A

c

g

c

+

g

40

Po to by być niepospolicie
uczonym trzeba zacząć od
pospolitego uczenia się.

Karol Dickens (1812 –

1870), powieściopisarz

angielski