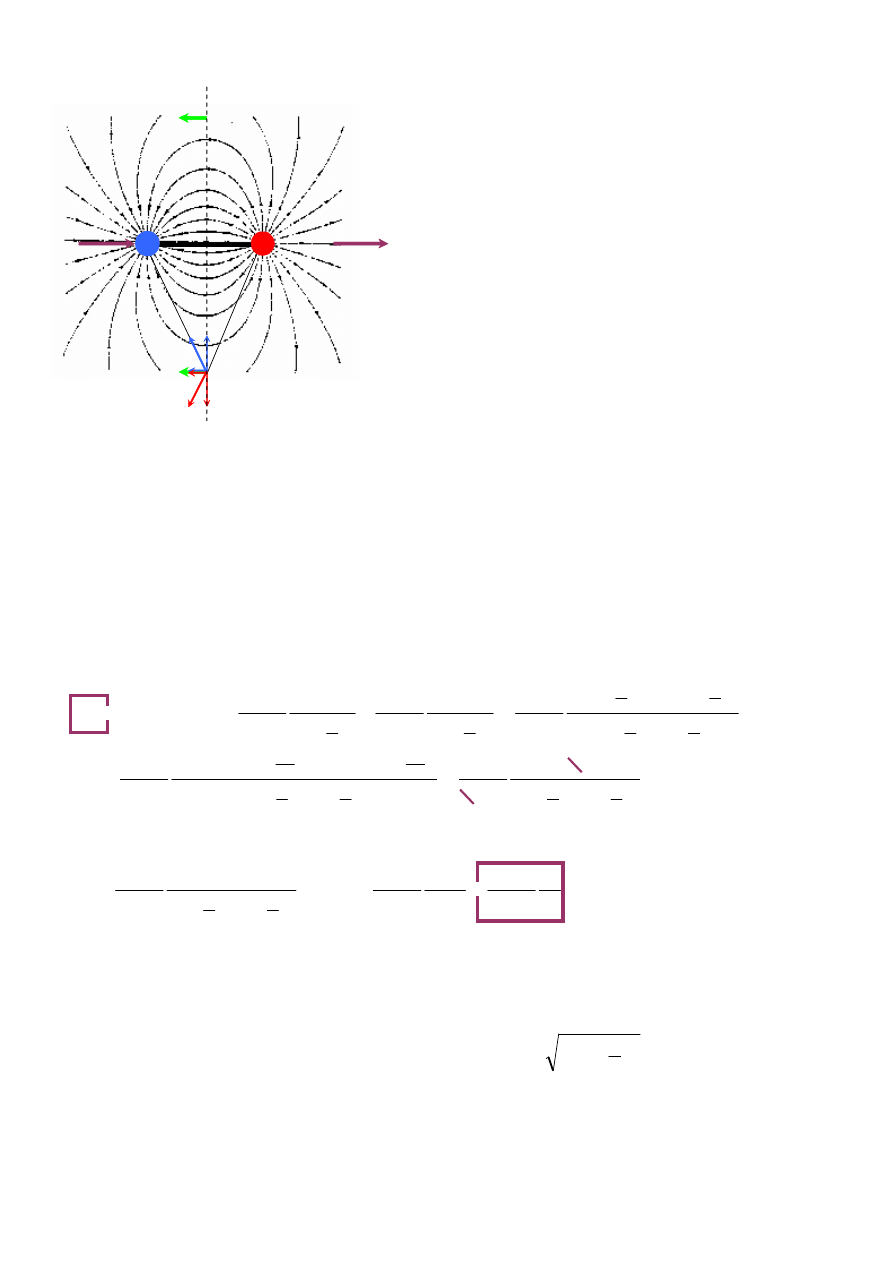
Natężenie pola elektrostatycznego wytworzonego przez dipol elektryczny

obliczamy sumę natężeń pola elektrycznego pochodzących od obu ładunków punktowych
(z prawa Coulomba):

E

(

−

)

+

E

(+)

w odległości r (

 d) od środka dipola

Kierunek równoległy do osi

np. po stronie lewej wektor wypadkowego natężenia pola elektrycznego zwrócony w prawo:
odległość od ładunku ujemnego: r

−

d/2

odległość od ładunku dodatniego: r + d/2
wartość:

( )

( )

( )

( )

( ) ( )

( ) ( )

(

) (

)

[

]

( ) ( )

( ) ( )

K

=

+

−

⋅

=

+

−

+

−

−

+

+

=

=

+

−

−

−

+

=

+

−

−

=

+

=

+

−

2

2

2

2

0

2

2

2

2

4

2

4

2

0

2

2

2

2

2

2

2

2

0

2

2

0

2

2

0

2

4

1

4

1

4

1

4

1

4

1

2

2

d

d

d

d

d

d

d

d

d

d

d

d

||

||

||

r

r

rd

q

r

r

rd

r

rd

r

q

r

r

r

q

r

q

r

q

r

q

E

E

E

ε

π

ε

π

ε

π

ε

π

ε

π

podstawiamy wyrażenie na dipolowy moment elektryczny: p = qd

( ) ( )

3

0

2

2

0

2

2

2

2

0

2

1

2

1

2

1

r

p

r

r

r

p

r

r

r

p

d

r

d

d

ε

π

ε

π

ε

π

=



 →



+

−

=

K

Kierunek prostopadły do osi

np. na dole

odległości od ładunku ujemnego i dodatniego jednakowe:

( )

2

2

2

d

r

+

składowe prostopadłe do osi dipola (

E

(

−

)

,

E

(+)

) kompensują się, równoległe do osi dipola

(

E

(

−

)

,

E

(+)

) dodają się

wektor wypadkowego natężenia pola elektrycznego zwrócony w lewo

2



,

,

„

„

−

+

E

| |

→

E

| |

→

E

⊥

→

d

E

⊥

→

wartość:

( )

( )

(

)

K

=

+

=

+

+

=

+

=

+

⊥

−

⊥

⊥

2

3

4

2

0

4

2

2

4

2

0

2

2

2

4

1

4

1

2

d

d

d

d

"

"

r

qd

r

r

q

E

E

E

ε

π

ε

π

podstawiamy wyrażenie na dipolowy moment elektryczny: p = qd

(

)

3

0

2

3

4

2

0

4

1

4

1

2

r

p

r

p

d

r

d

ε

π

ε

π



 →



+

=

K

E



= 2

E



