Regresja liniowa wielokrotna

0

1

2

( , )

( |

)

( )

x z

E Y X

a

a x a z

h

=

= =

= +

+

x

x

x

(

)

(

)

2

0

1

2

1

2

0

1

2

0

1

2

1

( , , )

( )

( , , )

n

i

i

i

n

i

i

i

i

S a a a

x

y

S a a a

a

a x a z y

h

=

=

=

-

=

+

+

-

�

�

Funkcja kryterialna:

Kryterium wyznaczenia

rozwiązania a

0

, a

1

, a

2

:

0 1 2

, ,

0 1 2

( , , )

min

a a a

S a a a

(

)

(

)

(

)

(

)

(

)

(

)

(

)

2

2

0

1

2

0

1

2

1

1

0

0

0

0

1

2

0

1

2

0

1

2

1

1

0

0

1

2

0

1

2

1

1

1

1

1

0

1

2

2

1

2

2

1 2

2

2

2

2

n

n

i

i

i

i

i

i

i

i

n

n

i

i

i

i

i

i

i

i

i

i

i

n

n

n

n

n

i

i

i

i

i

i

i

i

i

i

i

S

a

a x a z y

a

a x a z y

a

a

a

a

a x a z y

a

a x a z y

a

a x a z y

a

a

a x a z y

a

a

x

a

z

y

na

a

=

=

=

=

=

=

=

=

=

�

�

�

�

�

=

+

+

-

=

+

+

-

�

�

�

�

�

�

�

�

=

+

+

-

+

+

-

=

+

+

-

�

=

+

+

-

=

+

+

-

=

=

+

�

�

�

�

�

�

�

�

�

2

1

1

1

0

1

2

1

1

1

2

2

0

n

n

n

n

n

i

i

i

i

i

i

n

i

i

i

i

i

i

na

x

a

a

x a

z

y

z

y

=

=

=

=

=

=

+

-

=

+

+

=

�

�

�

�

� �

(

)

(

)

(

)

(

)

(

)

(

)

2

2

0

1

2

0

1

2

1

1

1

1

1

0

1

2

0

1

2

0

1

2

1

1

1

2

0

1

2

1

1

1

1

2

0

1

2

1

1

2

2

2

2

2

2

0

n

n

i

i

i

i

i

i

i

i

n

n

i

i

i

i

i

i

i

i

i

i

i

i

n

n

n

n

i

i

i i

n

n

i

i

i

i

i i

i

i

i

i

a

x

S

a

a x a z y

a

a x a z y

a

a

a

a

a x a z y

a

a x a z y

a

a x a z y x

a

a

x

a

x

a

z x

y

a

x

x

a

=

=

=

=

=

=

=

=

=

=

�

�

�

�

�

=

+

+

-

=

+

+

-

�

�

�

�

�

�

�

�

=

+

+

-

+

+

-

=

+

+

+

+

-

�

=

+

+

-

=

�

�

�

�

�

�

�

�

�

�

1

1

n

n

i i

i i

i

i

z x

y x

=

=

=

�

�

(

)

(

)

(

)

(

)

(

)

(

)

2

2

0

1

2

0

1

2

1

1

2

2

2

0

1

2

0

1

2

0

1

2

1

1

2

2

0

1

2

1

1

0

1

1

1

1

1

2

2

2

2

2

2

0

n

n

i

i

i

i

i

i

i

i

n

n

i

i

i

i

i

i

i

i

i

i

i

i

n

n

n

n

i

i i

i

n

n

i

i i

i

i

i i

i

i

i

i

S

a

a x a z y

a

a x a z y

a

a

a

a

a x a z y

a

a x a z y

a

a x a z y z

a

a

a

z

a

z x

a

z a

z x

z

y z

a

=

=

=

=

=

=

=

=

=

=

�

�

�

�

�

=

+

+

-

=

+

+

-

�

�

�

�

�

�

�

�

=

+

+

-

+

+

-

=

+

+

+

+

+

=

+

-

�

=

-

�

�

�

�

�

�

�

�

�

�

2

2

1

1

n

n

i

i i

i

i

z

y z

=

=

=

� �

0

1

2

1

1

1

2

0

1

2

1

1

1

1

2

0

1

2

1

1

1

1

n

n

n

i

i

i

i

i

i

n

n

n

n

i

i

i i

i i

i

i

i

i

n

n

n

n

i

i i

i

i i

i

i

i

i

na

a

x a

z

y

a

x a

x

a

z x

y x

a

z a

z x a

z

y z

=

=

=

=

=

=

=

=

=

=

=

+

+

=

+

+

=

+

+

=

�

� �

�

�

�

�

�

�

� �

1

1

1

0

2

1

1

1

1

1

2

2

1

1

1

1

n

n

n

i

i

i

i

i

i

n

n

n

n

i

i

i i

i i

i

i

i

i

n

n

n

n

i

i i

i

i i

i

i

i

i

n

x

z

y

a

x

x

z x

a

y x

a

z

z x

z

y z

=

=

=

=

=

=

=

=

=

=

=

�

�

�

�

�

�

�

�

�

�

�

�

� �

�

�

�

�

� �

�

=

�

�

�

�

� �

�

�

�

�

� �

� �

�

�

�

�

�

�

�

�

�

�

�

�

�

�

�

� �

�

�

� �

�

�

Met. Najmniejszych Kwadratów

dla pomiarów bezpośrednich i

pośrednich

Postulat:

Wynik kolejnego pomiaru y

j

można uważać za sumę

wielkości

x – nieznanej (poszukiwanej wielkości podlegającej
pomiarowi)

oraz



j

- błędu pomiarowego

czyli

y

j

= x + 

j

dla każdego j=1,...,n

Metoda

Najmniejszych

Kwadratów

postuluje

dobieranie tak wielkości 

j

, aby suma kwadratów

błędów 

j

była najmniejsza:

(

)

minimum

n

n

j

j

j

j

x y

=

=

e =

-

�

� �

2

2

1

1

Pomiary bezpośrednie

Przypadek równych błędów pomiarowych (pierwiastek z
wariancji 

2

)

Wykonujemy n pomiarów nieznanej wielkości x. Wyniki
pomiarów obarczone są błędem pomiarowym 

j

, o którym

zakładamy że ma rozkład normalny z wartością średnią równą
zeru:

y

j

= x + 

j

E(

j

)=0

(wart. oczekiwana) E(

j

2

)=

2

(wariancja)

(założenie to – o rozkładzie – jest często uzasadnione przez
centralne twierdzenie graniczne).

Najlepszym estymatorem dla x jest średnia
arytmetyczną:

którego wariancja wyraża się

a identyfikując błąd z odchyleniem standardowym
otrzymujemy

n

j

j

x y

y

n

=

= =

�

1

1

%

( )

/

x

n

s

=s

2

2

%

/

x

n

d = s

2

Przypadek różnych błędów pomiarowych (pierwiastków z
wariancji 

j

2

)

Wykonujemy n pomiarów nieznanej wielkości x. Wyniki
pomiarów obarczone są błędem pomiarowym 

j

, o którym

zakładamy że ma rozkład normalny z wartością średnią równą
zeru:

y

j

= x + 

j

E(

j

)=0

(wart. oczekiwana) E(

j

2

)=

j

2

=1/g

j

(wariancja)

Najlepszym estymatorem dla x jest (średnia ważona
pomiarów):

którego wariancja wyraża się

a estymatory błędów pomiarowych

mają rozkład normalny z wartością średnią równą zeru i
wariancją 

j

2

, a to oznacza że wielkości pochodzą ze

standardowego rozkładu Gaussa N(0,1), co powoduje że suma ich
kwadratów

ma rozkład 

2

o n-1 stopniach swobody. Własności te można

wykorzystać do weryfikacji słuszności założeń przy użyciu testu 

2

.

/

n

n

j

j

j

j

j

x

g y

g

=

=

=

�

�

1

1

%

( )

n

n

j

j

j

j

x

g

-

-

=

=

�

� �

�

s

=

=

�

� �

�

�

�

s

�

�

�

�

�

�

1

1

2

2

1

1

1

%

j

j

y

x

e = - %

/

j

j

e s

%

(

)

(

)

/

(

)/

(

)

n

n

n

j

j

j

j

j

j

j

j

j

y

x

y

x g

=

=

=

�=

e s

=

-

s

=

-

�

�

�

2

2

2

1

1

1

%

%

%

Przykład. Najlepsze wartości stałych fizycznych uzyskuje się przez
obliczanie średniej ważonej wszystkich pomiarów przeprowadzonych
przez

różne

ośrodki

naukowe-doświadczalne.

Dla

cząstek

elementarnych takie średnie są wyznaczane regularnie, bowiem
coraz bardziej doskonalone są metody pomiarowe. Np. średnia masa
neutralnego mezonu K uśredniono w oparciu o wyniki 4 doświadczeń
wykonanych różnymi technikami doświadczalnymi (tabela).

Wartość 

min

wynosi w tym przykładzie 7.2 (tabela) . Dla poziomu

istotności 5%, oraz stopni swobody n-1=4-1=3 wartość krytyczna


2

=7.95. Wniosek: uważamy ze uzyskany wynik ( masa mezonu K =

497.9 0.2 MeV ) stanowi najlepszą wartość z poziomem ufności

95%. Tak pozostało do czasu (upłynęło 20 lat) gdy przeprowadzono
nowe doświadczenia i uzyskano wynik 497.671 0.030 MeV .
UWAGA: jeśli test 

2

da rezultat negatywny (odrzucamy hipotezę o

dobrym dopasowaniu bowiem 

2

> 

2

kryt

) powodem tego może być

fakt, że co najmniej jeden z pomiarów jest obarczony błędem
systematycznym (nie o rozkładzie normalnym z wartością średnią 0)

.

Czasami niektóre pomiary odbiegają od innych. Usunięcie ich z
analizy pozwala na przyjęcie hipotezy zerowej, czyli test 

2

daje

wynik pozytywny.

j

Yj

j

1/(j)^2=Gj

Yj*Gj

Yj-x

Gj(Yj-x)^2

1

498.10

0.40

6.30

3038.0

0.20

0.3

2

497.44

0.33

10.00

4974.4

-0.46

2.1

3

498.90

0.50

4.00

1995.6

1.00

4.0

4

497.44

0.50

4.00

1989.8

-0.46

0.8



24.30

11997.8

7.2

estymata x = YjGj/Gj = 497.9 bład x = 1/(Gj)=0.20

Pomiary pośrednie

Często, interesujące nas w pracy doświadczalnej wielkości, nie
podlegają bezpośredniemu pomiarowi. Np. w kinetyce
chemicznej stała szybkości reakcji opisywana jest zwykle równaniem
Arrheniusa

gdzie: Q jest energią aktywacji procesu chemicznego i nie podlega
bezpośredniemu

pomiarowi

K(T) – stała szybkości reakcji jako funkcja wyłącznie

temperatury (bezwzględnej) procesu,

R – uniwersalna stała gazowa

Badania kinetyczne prowadzi się zwykle dla szeregu dobranych
warunków izotermicznych (przy różnych wartościach temperatury
bezwzględnej) i dla wyznaczonych stałych szybkości reakcji
poszukuje się stałych k

0

i Q w równaniu Arrheniusa. Dla ułatwienia

wyznaczenia

tych

stałych,

równanie

to

po

obustronnym

zlogarytmowaniu uzyskuje liniową postać

gdzie:

( )

exp

Q

K T

k

RT

�

�

=

-

�

�

�

0

Y A Bt

= +

ln( ( )) ;

ln

;

;

/

Y

K T

A

k

t

B

Q R

T

=

=

=

=-

0

1

Uogólniamy zagadnienie pomiarów pośrednich w następujący
sposób.

Załóżmy, że interesuje nas wyznaczenie zespołu r nieznanych (a
priori) wielkości (x

1

,...,x

r

), które nie podlegają bezpośredniemu

pomiarowi. Wiemy zaś (lub postulujemy), że istnieje liniowy (bądź
nieliniowy) związek między nimi a pewną mierzalną zmienną



. Na

początek, rozpatrywać będziemy związek liniowy:

Jeśli wektor wartości wsp. a

jr

zapisać w notacji wektora

kolumnowego

to powyższe relacje można zapisać jako:

a po zdefiniowaniu macierzy i wektorów:

powyższy układ równań można zapisać (dla n dokonanych
pomiarów):

...

lub

...

j

j

j

jr r

j

j

j

j

jr r

p

p x

p x

f

a

a x

a x

h =

+

+ +

=h +

+

+ +

=

0

1 1

0

1 1

0

,

,...,

T

j

j

j

jr

a a

a

�

�

=�

�

1

2

a

,...,

T

j

j

j

j

f

a

j

n

=h +

+

=

=

0

a x 0

1

[

]

[

]

[

]

,...,

;

,...,

;

,...,

...
...

...

T

T

T

r

n

n

r

r

n

r

r

rr

r

x

x

a

a

f

a

a

a

f

a

a

a

f

a

a

a

=

= h

h

=

� �

�

� � �

� �

�

� � �

� �

�

� � �

=

=

=

� �

�

� � �

� �

�

� � �

�

� � �

� �

1

1

0

01

0

1

11

12

1

1

2

21

22

2

2

1

2

xη

a

a

a

A

f

a

M

M

M O

M

M

= + +

0

fη a

Ax

Zakładamy, zgodnie z założeniami ogólnymi, że każdy pomiar
zmiennej



o wartości y

j

jest obarczony błędem 

j

o rozkładzie

normalnym ze średnią zero:

Zmienne y

j

są niezależne, stad związek między nimi jest wyrażony

zerowymi kowariancjami (cov(y

i

,y

j

)=0), a wtedy macierz kowariancji

zmierzonych wartości jest diagonalna, i także jej odwrotność zwana
macierzą wag pomiarów:

Wprowadzając wektor pomiarów i błędów:

Otrzymujemy układ równań

Poszukujemy rozwiązania tego układu przy warunku, że suma
kwadratów błędów 

j

ważonych przez czynniki g

j

jest minimalna

(jednocześnie to statystyka 

2

(n-r) dobroci dopasowania model do

danych):

( )

( )

;

;

/

j

j

j

j

j

j

j

y

E

E

g

=h +e

e =

e =s =

2

2

0

1

...
...

...

y

n

e

�

�

s

�

�

s

�

�

=

=

�

�

�

�

s

�

�

�

�

2

1

2
2

2

0

0

0

0

C

C

0

0

M M O

M

( )

( )

...
...

...

y

y

n

g

g

g

-

-

e

e

�

�

�

�

�

�

=

=

=

=

�

�

�

�

�

�

1

1

1

2

0

0

0

0

G

C

G

C

0

0

M M O

M

[

]

[

]

;

,...,

;

,...,

T

T

n

n

y

y

= +

=

= e

e

1

1

yη ε

y

ε

- + +

=

0

yε a

Ax 0

/

n

n

T

j

j

j j

y

j

j

g

=

=

�= e s =

e =

�

�

2

2

2

1

1

ε G ε

Stosując tzw. metodę mnożników Lagrangea można uzyskać
rozwiązanie tego zagadnienia ze względu na x, otrzymując wektor
estymat

z macierzą kowariancji wyznaczonych niewiadomych

Pierwiastki kwadratowe z elementów przekątni głównej można
utożsamiać z „ błędami pomiarowymi” estymat zmiennych x

i

, mimo

ze nie podlegały bezpośredniemu pomiarowi.

Wektor estymat błędów pomiarowych przyjmuje wartość

a wektor dopasowanych wartości pomiarów ( estymaty również)

z macierzą kowariancji

W ramach pracy własnej, proszę sobie udowodnić, że gdy r=1
( pomiary bezpośrednie o indywidualnej dokładności 

j

2

)

(

)

(

)

T

T

y

y

-

=-

+

1

0

x

A G A

A G y a

%

( )

(

)

T

y

-

-

=

=

1

1

x

x

C

G

A G A

%

%

(

)

(

) (

)

T

T

y

y

-

=

+ + =-

+

+ +

1

0

0

0

ε Ax y a

A A G A

A G y a

y a

%

%

(

)

(

)

T

T

y

y

-

= - =

+

-

1

0

0

η y ε A A G A

A G y a

a

%

%

( )

(

)

( )

T

T

T

y

-

-

-

=

=

=

1

1

1

η

η

x

C

G

A A G A

A

A G

A

%

%

%

/

;

/

/

/

n

n

n

n

n

T

y

j

j

j

j

j

j

j

j

j

j

j

j

x

y

g y

g

-

=

=

=

=

=

�

� �

�

=

s

=

s

s

=

�

� �

�

�

� �

�

�

�

�

�

�

1

2

2

2

1

1

1

1

1

A G A

1

1

%

Przykład. Dopasowanie linii prostej.

Niech zbiór wartości y

j

, pochodzący z pomiaru bezpośredniego,

odpowiada zbiorowi wartości t

j

(znanych dokładnie – tzw. zmienna

kontrolowana t). Jeżeli t

i

, co się zdarza nader często, jest również

obarczone błędami,, to dopasowanie prostej staje się problemem
nieliniowych, osobno omawianym.

Obliczenia macierzowe dają następujące wyniki:

;

,...,

;

macierzowo

j

j

j

j

y

x x t

j

n

x x

h = - e = +

=

-

+

=

=

1

2

1

2

0

1

η

t 0

a

0

j

t

y



1

0.0

1.4

0.5

2

1.0

1.5

0.2

3

2.0

3.7

1.0

4

3.0

4.1

0.5

(

)

.

.

.

.

T

T

T

y

y

y

t

t
t
t

-

-

-

-

�

� �

�

�

�

�

� �

�

�

�

-

-

-

-

-

-

-

-

-

�

�

�

�

�

�

�

� �

�

�

�

=

=

=

=

=

=

=

�

�

�

�

�

�

�

� �

�

�

�

-

-

-

-

-

-

-

-

�

�

�

�

�

�

�

� �

�

�

�

-

-

-

-

�

�

�

�

�

�

1

1

2

x

3

4

1

1 0

4 0 0 0

1

1

1

1

1

1

1

0 25 0 0

34 39

0094

0057

A

A

G

A G A

C

A G A

1

1

2

0

1

2

3

0 0 1 0

39 65

0057 0049

1

1

3

0 0 0 4

%

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

-

-

�

�

�

�

�

�

�

�

�

�

�

�

�

�

�

�

�

=

d =

=-

=

=

d =

�

�

�

�

�

�

�

�

-

�

�

�

�

�

�

�

�

-

�

�

�

�

�

η

0636

0094 0038

0019

0076

031

0636

0307

1702

0038 0031 0023

0016

017

x

xη

Ax

C

η

1066

0222

2768

0019 0023 0065

0107

026

3834

0076 0016 0107

0199

045

%

%

%

%

%

�

�

�

�

�

�

�

�

�

�

Minimum funkcji kryterialnej  = 4.507, dobroć dopasowania dla

l.st.sw.=4-2=2 testujemy względem 

2

kryt

(0.05,2)=5.99. Wniosek:

nie ma podstaw do podważenia dobrego dopasowania linii prostej
do danych empirycznych (poziom ufności dopasowania 95%,
poziom istotności 5%).

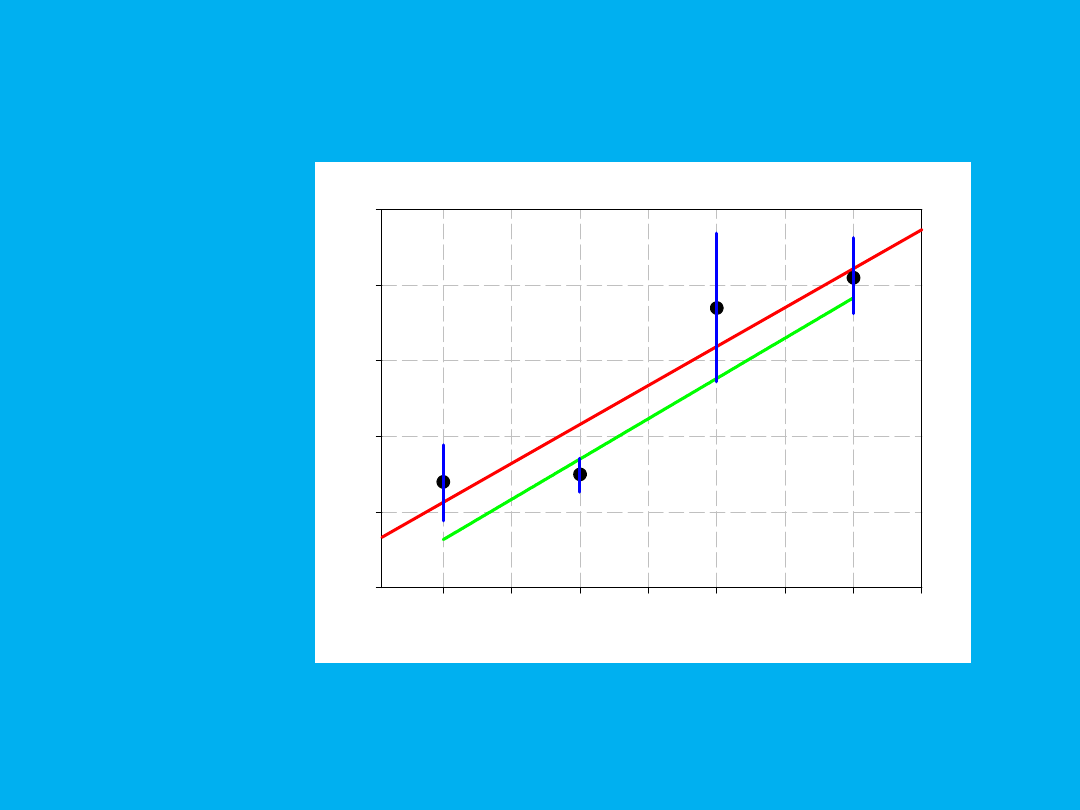
t

0.0

0.5

1.0

1.5

2.0

2.5

3.0

3.5

y

0

1

2

3

4

5

Linia czerwona - regresja z jednakowymi b�

�dami y=1.130+1.030*t

linia zielona - regresja z r�znymi b�

�dami y=0.636+1.066*t

Należy zwrócić uwagę, na fakt że błędy po dokonaniu dopasowania
(błędy a posteriori) są mniejsze niż błędy wyjściowe. Poniżej
porównanie 2 linii regresji, czerwona dla jednakowych błędów
wielkości mierzonych ( błędów a priori), zielona dla zróżnicowanych
błędów.

Wykonanie obliczeń przedstawione w pliku: Dopasowanie_liniowe.xls