GRANIASTOSŁUPY

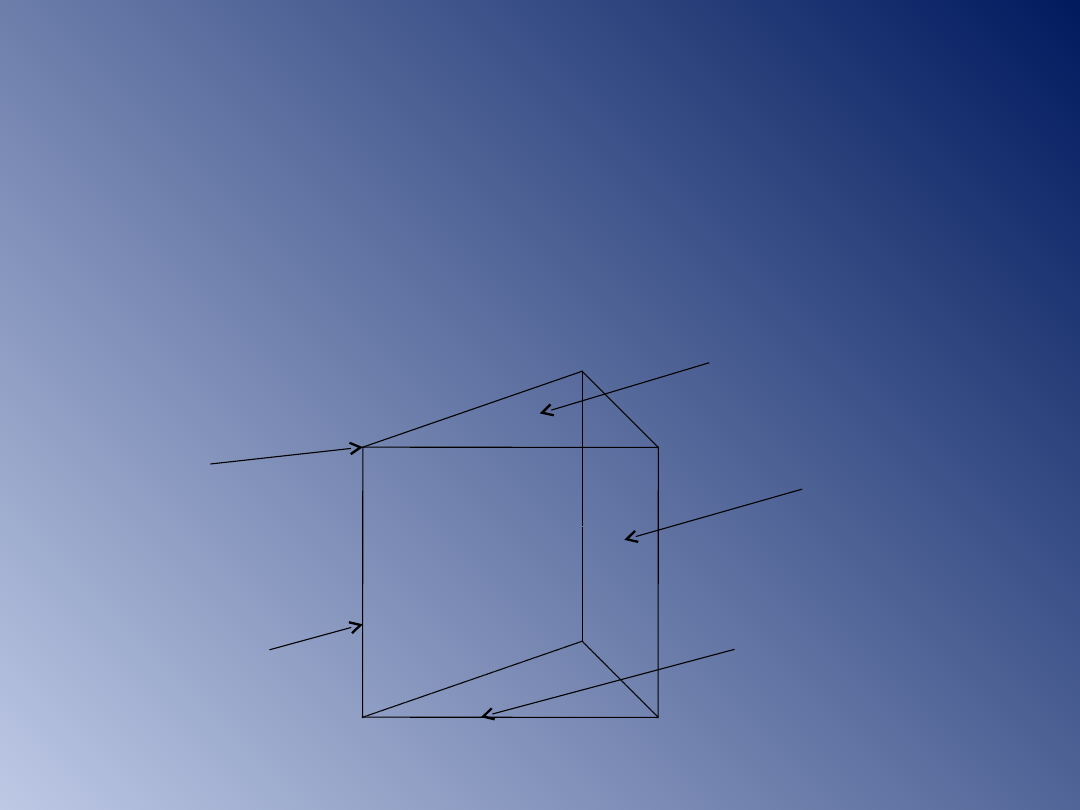
Graniastosłup

to figura przestrzenna, której

podstawami są dwa przystające wielokąty

zawarte

w płaszczyznach równoległych; krawędzie

boczne są do siebie równoległe.

krawędź boczna

krawędź
podstawy

wierzchołek

ściana boczna

podstawa

PODZIAŁ GRANIASTOSŁUPÓW:

I
 trójkątny – podstawą jest dowolny trójkąt
 czworokątny – podstawą jest czworokąt
 pięciokątny – podstawą jest pięciokąt
 sześciokątny – podstawą jest szęściokąt
 itd……

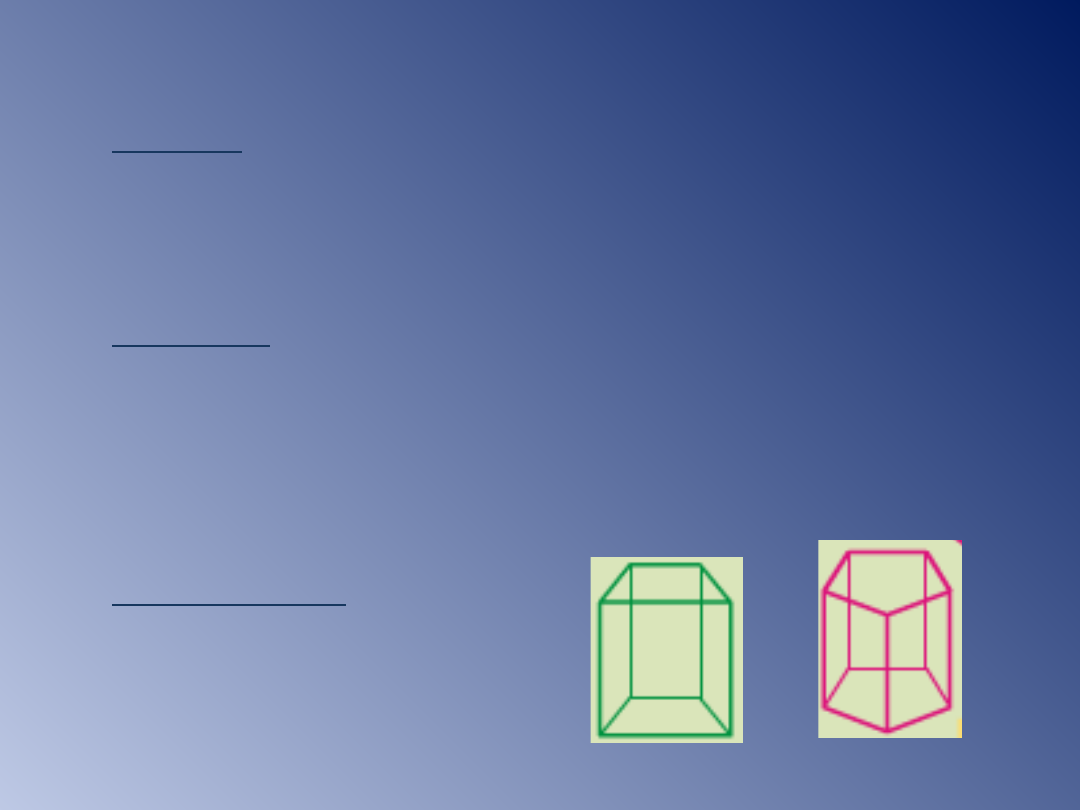
II
 prosty – graniastosłup, w którym

krawędzie

boczne są prostopadłe do podstawy;
 pochyły – graniastosłup, w którym

krawędzie

boczne nie są prostopadłe do

podstawy;
 prawidłowy – graniastosłup prosty

o podstawie wielokąta foremnego

Do rozwiązywania zadań potrzebne

będą wzory na pole powierzchni

(

P

)

i

objętość (

V

) dowolnego

graniastosłupa.

P=2·P

p

+P

b

V=P

p

·H

P

p

– pole podstawy

P

b

- pole powierzchni bocznej

H - wysokość graniastosłupa

Przykład 1.

Oblicz pole i objętość sześcianu o boku długości
8,5cm.

Zaczniemy od zapisania odpowiednich wzorów na
pole
i objętość figury przestrzennej, która ma sześć
ścian,
a każda ściana jest kwadratem.

P=6·a

2

P=6· (8,5)

2

=6·72,25=433,5 [cm

2

]

V=a

3

V=(8,5)

3

=614,125 [cm

3

]

Odp: Pole powierzchni sześcianu
wynosi 433,5 cm

2

,

a jego objętość 614,125 cm

3

.

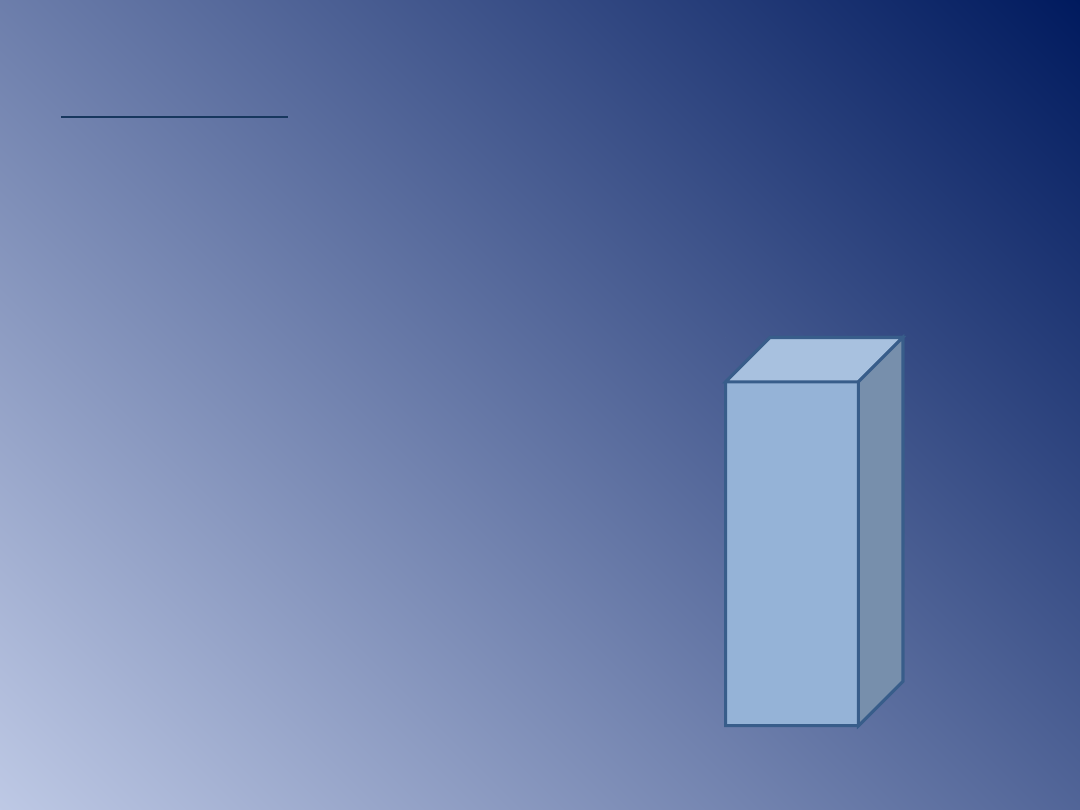
Przykład 2.

Oblicz pole powierzchni i objętość
graniastosłupa,
w którym wysokość ma długość 8cm,
podstawą jest kwadrat o boku długości 4cm.

Podstawą jest kwadrat, każda ściana
boczna jest prostokątem
o wymiarach: 4cm x 8cm

P

p

=a

2

P

p

=4

2

=16 [cm

2

]

a=4cm

h=8cm

P

b

=4·a·H

P

b

=4·4·8=128 [cm

2

]

P=2·P

p

+P

b

P=2·16+128=160 [cm

2

]

V=P

p

·H

V=16·8=128 [cm

3

]

Odp: Pole powierzchni graniastosłupa o
podstawie
kwadratowej wynosi 160 cm

2

, a jego

objętość
wynosi 128 cm

3

.

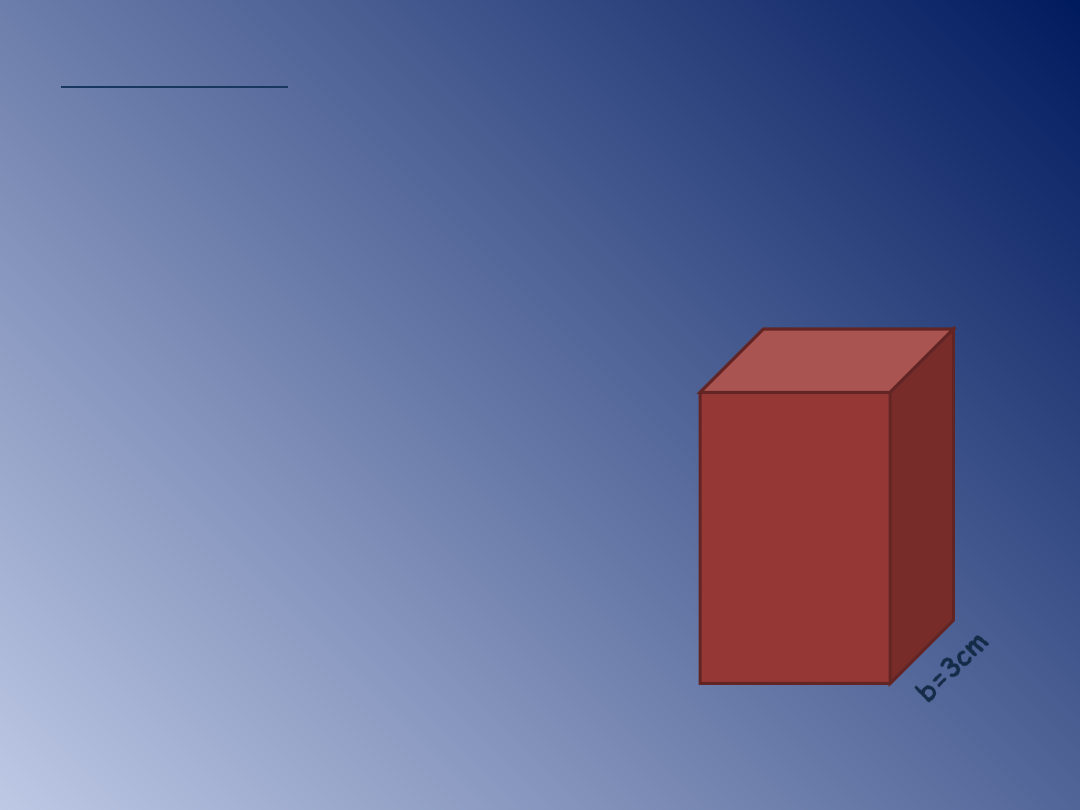
Przykład 3.

Oblicz pole i objętość prostopadłościanu
o wysokości 5cm; w którym podstawą jest
prostokąt
o wymiarach: 3cm i 2,5cm. Oblicz pole
przekroju płaszczyzną równoległą do
płaszczyzny podstawy.

P

p

=a·b

P

p

=2,5·3=7,5 [cm

2

]

P

b

=2·a·H+2·b·H

P

b

=2·2,5·5+2·3·5=55 [cm

2

]

P=2·P

p

+P

b

P=2·7,5+55=70 [cm

2

]

a=2,5cm

h=5cm

V=P

p

·H

V=7,5·5=37,5 [cm

3

]

Jeżeli poprowadzimy płaszczyznę równoległą do
płaszczyzny podstawy to w przekroju otrzymamy
prostokąt o wymiarach podstawy.

P

przekroju

=a·b

P

przekroju

=2,5·3=7,5 [cm

2

]

Odp: Pole powierzchni prostopadłościanu
wynosi 70cm

2

,

a jego objętość wynosi 37,5cm

3

.

Pole przekroju wynosi 7,5cm

2

.

Przykład 4.

Oblicz pole i objętość graniastosłupa o
podstawie trójkąta prostokątnego o
przyprostokątnych długości: 3cm i 4cm.
Wysokość graniastosłupa wynosi 11cm.

P

p

=½·a·b

P

p

=½·3·4=6 [cm

2

]

Podstawą graniastosłupa jest trójkąt
prostokątny. Korzystając z twierdzenia
Pitagorasa obliczmy długość
przeciwprostokątnej.

c

2

=a

2

+b

2

c

2

=3

2

+4

2

c

2

=9+16=25

c=5 lub c=-5 - odpada

b=4cm

a=3cm

c

P

b

=aH+bH+cH

P

b

=3·11+4·11+5·11=33+44+55

P

b

=132 [cm

2

]

P=2·P

p

+P

b

P=2·6+132=12+132=144 [cm

2

]

V=P

p

·H

V=6·11=66 [cm

3

]

Odp: Pole powierzchni graniastosłupa wynosi
144cm

2

,

jego objętość 66cm

3

.

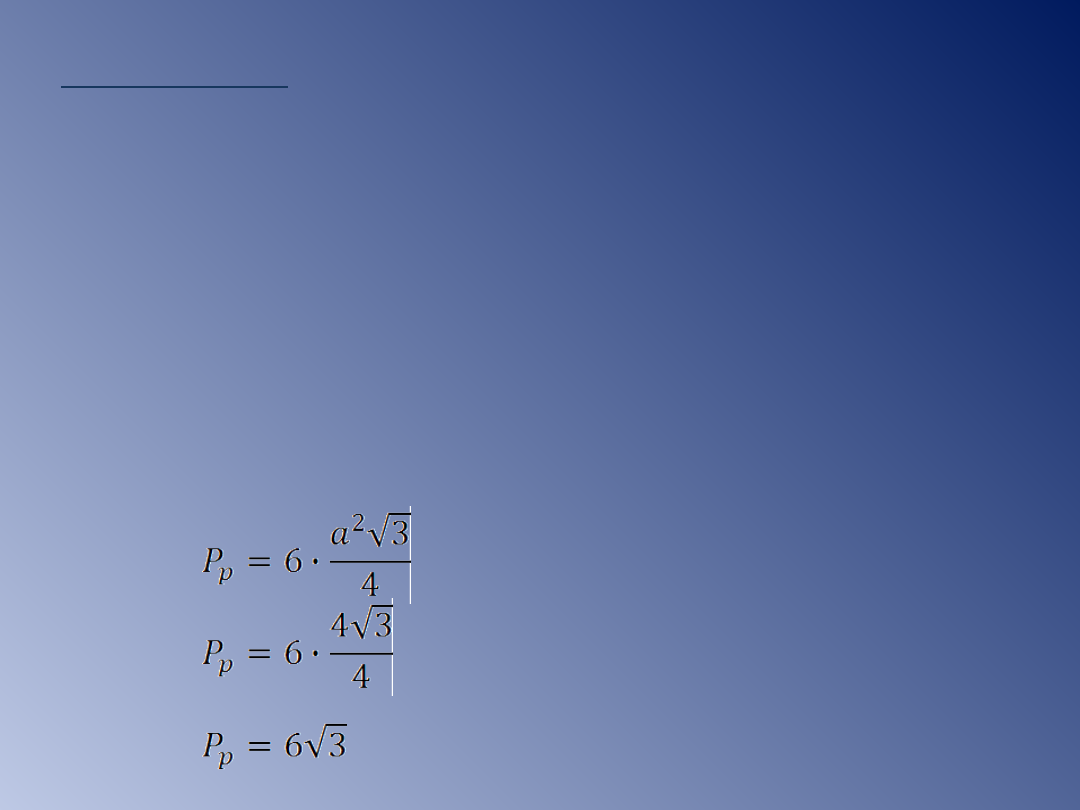
Przykład 5.

Oblicz pole i objętość graniastosłupa, w
którym podstawą jest sześciokąt foremny o
boku 2cm, wysokość graniastosłupa jest 3
razy większa od długości krawędzi
podstawy.

Sześciokąt foremny składa się z sześciu
trójkątów równobocznych.

P

p

= 6·P

Δrównobocznego

[cm

2

]

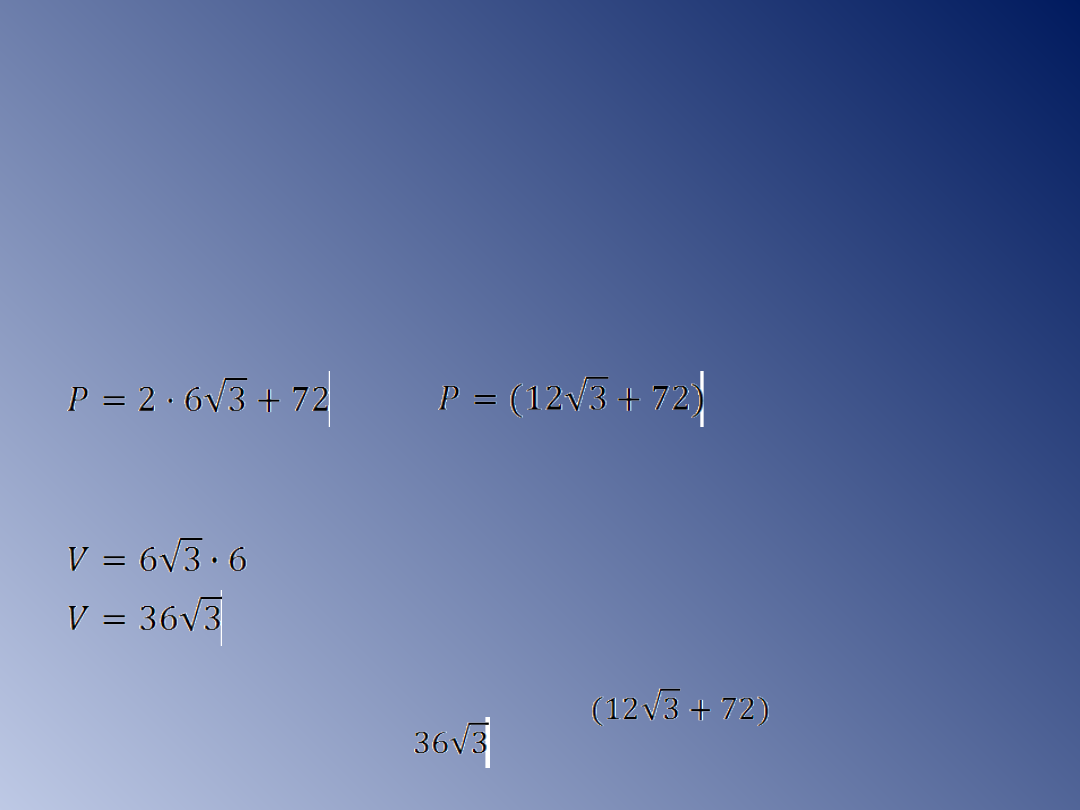
Wysokość graniastosłupa jest trzy razy większa
od długości krawędzi podstawy, czyli ma 6cm.

P

b

=6·a·H

P

b

=6·2·6=72 [cm

2

]

P=2·P

p

+P

b

[cm

2

]

V=P

p

·H

[cm

3

]

Odp: Pole graniastosłupa wynosi cm

2

,

a jego objętość cm

3

.

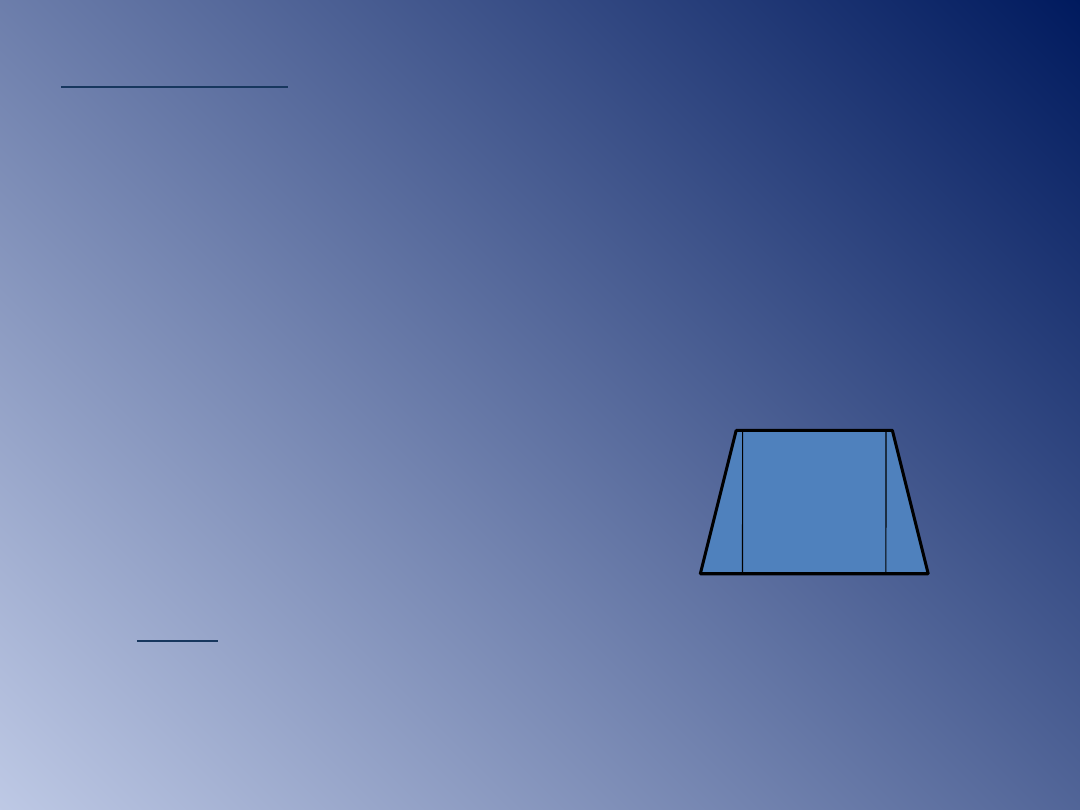
Przykład 6.

Oblicz pole i objętość graniastosłupa, w
którym podstawą jest trapez równoramienny
o wymiarach: 4cm, 5cm, 12cm, 5cm.
Wysokość graniastosłupa jest równa 10cm.

Zajmiemy się najpierw podstawą. Obliczymy
wysokość trapezu, a potem jego pole. (rys obok)

5

2

=4

2

+h

2

h

2

=5

2

-4

2

h

2

=25-16=9

h=3 lub h=-3 – odpada

4cm

5cm

5cm

12cm

h

P

p

=½·(a+b)·h

P

p

=½·(4+12)·3=24 [cm

2

]

H=10cm.

P

b

=2·5·10+12·10+4·10

P

b

=100+120+40

P

b

=260 [cm

2

]

P=2·P

p

+P

b

P=2·24+260
P=48+260
P=308 [cm

2

]

V=P

p

· H

V=24·10=240 [cm

3

]

Odp: Pole graniastosłupa wynosi 308cm

2

, jego objętość

240cm

3

.