Metody ilościowe w zarządzaniu bezpieczeństwem

Jednowymiarowa i 

wielowymiarowa

analiza danych

Dr inż. Wiesław Błażejczyk
156/25     tel. 813490
w.blazejczyk@aon.edu.pl

Metody ilościowe w zarządzaniu bezpieczeństwem

•Zbiorowość statystyczna (populacja):
zbiór dowolnych obiektów objętych 
badaniem statystycznym.
•Jednostka badania (jednostka 
statystyczna): element zbiorowości 
statystycznej (populacji).

PODSTAWOWE POJĘCIA

Rozróżnia się zbiorowość statystyczną
generalna –(obejmująca badaniem wszystkie elementy 
będące przedmiotem badania
próbną – jest to pewnie podzbiór zbiorowości generalnej 
odpowiednio (tzn. losowo) wybrany (Na ogół badania prowadzi 
się na zbiorowości próbnej i  i uogólnia wnioski na cała populację. 

Metody ilościowe w zarządzaniu bezpieczeństwem

Cecha statystyczna: właściwość jaką odznaczają się 
jednostki wchodzące w skład badanej populacji.

- cecha statystyczna jakościowa (niemierzalna): cecha 
określana słownie (np. płeć, zawód), w tym: cecha 
dychotomiczna
(podział dwudzielny);
- cecha statystyczna ilościowa (wzrost, czas pracy, 
dochód), w tym: cechy ciągłe (czas do uszkodzenia), 
cechy skokowe
(liczba uszkodzeń);
- cecha statystyczna quasi-ilościowa (porządkowa), np. 
stopnie w szkole.

Cechy mierzalne dzielimy na :

•skokowe ( dyskretne) (jeśli wszystkich wartości jest stosunkowo 
niewiele. np. liczba rodzeństwa, oceny studentów (przyjmują tylko 
niektóre wartości)

•ciągłe mogą przyjmować, każdą wartość z określonego 
przedziału, przy czym, ilość miejsc po przecinku uzależniona jest od 
dokładności prowadzonych pomiarów.

Metody ilościowe w zarządzaniu bezpieczeństwem

Prezentacja materiału statystycznego
Szereg statystyczny - zbiór wyników obserwacji jednostek 
według pewnej cechy uporządkowanych wg określonego 
kryterium. 
Szereg szczegółowy - uporządkowany ciąg wartości badanej 
cechy statystycznej, stosowany, gdy przedmiotem badania jest 
niewielka liczba jednostek, 
Szereg rozdzielczy: stanowi zbiorowość statystyczną, 
podzieloną na części (klasy) według określonej cechy jakościowej 
lub ilościowej z podaniem liczebności lub częstości każdej z 
wyodrębnionych klas. 
Szereg czasowy: wartości badanej cechy zmierzone w kolejnych 
momentach.
Szereg rozdzielczy skumulowany - uzyskuje się poprzez 
przyporządkowanie kolejnym wariantom cechy odpowiadających 
im liczebności (częstości) skumulowanych, informuje, dla ilu 
jednostek badanej zbiorowości cecha przyjmuje wartości nie 
większe od górnej granicy poszczególnego przedziału klasowego. 

Metody ilościowe w zarządzaniu bezpieczeństwem

Stosowanie szeregów statystycznych:
szereg rozdzielczy z przedziałami klasowymi - 

dla cech ciągłych

szeregi rozdzielcze bez przedziałów klasowych lub z przedziałami 
klasowymi - dla cech mierzalnych skokowych - zależnie od możliwości 
wartości (wariantów) cech: dla niewielkiej liczby wariantów - szereg 
rozdzielczy punktowy, dla dużej szereg rozdzielczy z przedziałami 
klasowymi. 

szereg rozdzielczy z cechą niemierzalną - 

szereg geograficzny 

(terytorialny) - przedstawia rozmieszczenie pewnych zjawisk w 
przestrzeni (np. zestawienie liczby gmin w Polsce).

szereg czasowy - 

(dynamiczny chronologiczny) powstaje w wyniku 

grupowania typologicznego i wariacyjnego, gdy podstawą 
grupowania jest zmiana badanego zjawiska w czasie

:

- szereg czasowy okresów - 

zawiera informację o rozmiarach 

zjawiska w krótszych lub dłuższych okresach

.

- szereg czasowy momentów - 

ujmuje wielkość zjawiska w danym 

momencie, najczęściej na początku lub końcu np. miesiąca

.

Metody ilościowe w zarządzaniu bezpieczeństwem

Metody ilościowe w zarządzaniu bezpieczeństwem

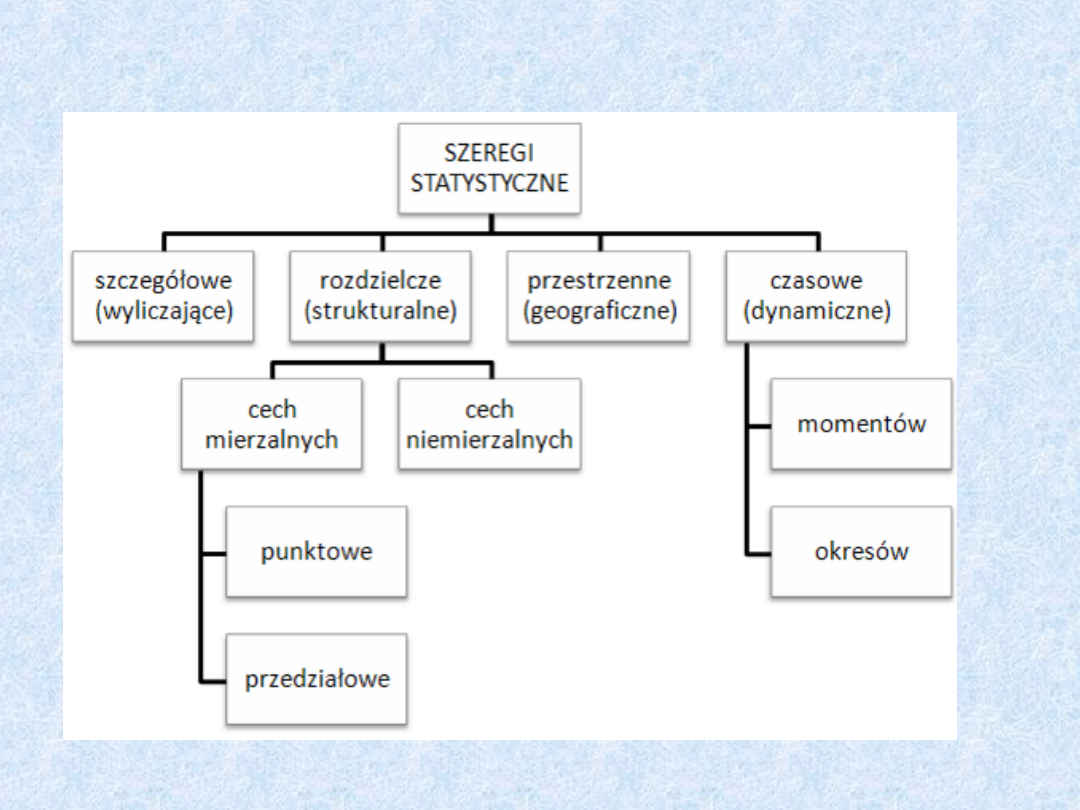
•SZEREGI STATYSTYCZNE

Szereg prosty:

Szereg rozdzielczy: punktowy

przedziałowy

i

x

i

 

i

x

i

n

i

 

i

x

id

-x

ig

n

i

1

x

1

 

1

x

1

n

1

 

1

x

1d

-x

1g

n

1

2

x

2

 

2

x

2

n

2

 

2

x

2d

-x

2g

n

2

..

.

...

 

...

...

...

 

...

 

...

n

x

n

 

k

x

k

n

k

 

k

x

kd

-x

kg

n

k

Metody ilościowe w zarządzaniu bezpieczeństwem

Miary opisowe w syntetyczny sposób 
charakteryzują struktury danych statystycznych:
•poziom cechy,
•zróżnicowanie wartości
•oraz kształt rozkładu.

Metody ilościowe w zarządzaniu bezpieczeństwem

Rodzaje miar:
•położenia (inne nazwy- miary tendencji centralnej, 
przeciętnego poziomu): średnia arytmetyczna, dominanta, 
kwantyle, kwartyle,
mediana
•rozproszenia (inne nazwy – miary zróżnicowania, 
zmienności, rozrzutu, dyspersji): rozstęp, wariancja, 
odchylenie standardowe,
typowy obszar zmienności, klasyczny współczynnik 
zmienności, odchylenie ćwiartkowe (kwartylowe)
•kształtu rozkładu: współczynnik skośności Pearsona, 
klasyczny współczynnik zmienności, pozycyjny 
współczynnik
asymetrii,

Metody ilościowe w zarządzaniu bezpieczeństwem

Średnie:
Średnia arytmetyczna:
a) średnia zwykła

b) średnia ważona

Miary położenia (przeciętne)

N

x

N

x

x

x

x

N

i

i

N



















1

2

1

N

n

x

N

n

x

n

x

n

x

x

k

i

i

i

k

k



















1

2

2

1

1

k

n

n

n

N













2

1

Metody ilościowe w zarządzaniu bezpieczeństwem

c) średnia z szeregu rozdzielczego 
przedziałowego

N

n

x

N

n

x

n

x

n

x

x

k

i

i

i

k

k



















1

2

2

1

1









k

n

n

n

N













2

1

W przypadku, gdy przedziały klasowe (pierwszy i ostatni) są otwarte, a 
ich liczebności są stosunkowo małe, można dokonać umownego ich 
zamknięcia ustalić wartości środków przedziałów. Nie można jednak tak 
postąpić w przypadku, gdy udział liczebności otwartych przedziałów w 
ogólnej sumie liczebności jest znaczny, czyli w tej sytuacji nie da się 
wyznaczyć średniej arytmetycznej. 

Metody ilościowe w zarządzaniu bezpieczeństwem

Średnia harmoniczna:
a) średnia harmoniczna zwykła

Zastosowanie średniej harmonicznej: w 
analizie indeksów statystycznych 
wyrażanych w jednostkach względnych, 
tzn. takich które możemy przedstawić jako 
stosunek (iloraz) dwu
innych wielkości. Na przykład:

Przykład: Dwa portfele inwestycyjne przyniosły zysk po 10000 
złotych każdy. W pierwszym portfelu zysk z każdej zainwestowanej 
złotówki wynosił 10 groszy, zaś w drugim 14 groszy. Jaka jest 
średnia stopa zysku z obu portfeli.
Stopa zysku z pierwszego portfela - 10%
Stopa zysku z drugiego portfela - 14%

Dlaczego 11,66 % a nie 12%?
Jaki zainwestowano kapitał? Jaka jest stopa zysku z całego 
kapitału?







N

i

i

x

N

H

1

1

netto

 

sprzeda

ż

netto

zysk 

sprzeda

żp

 

rentowno

śe



3

2

11

6

70

14

1

10

1

2









H

Metody ilościowe w zarządzaniu bezpieczeństwem

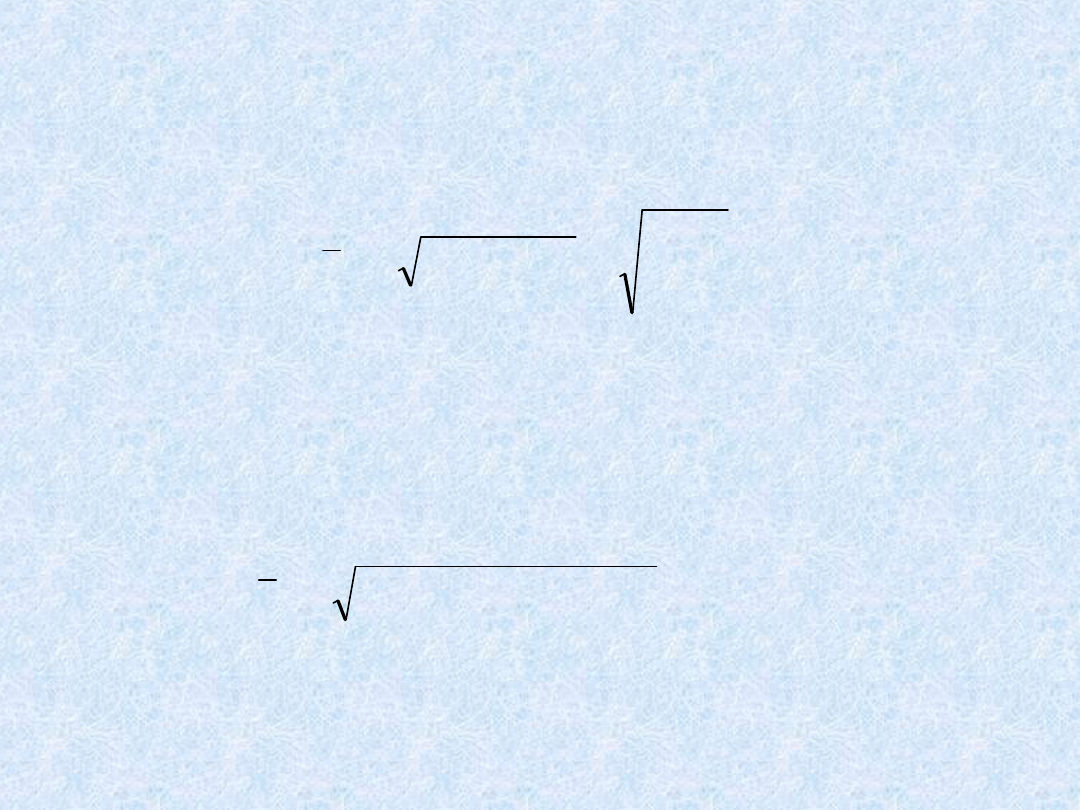
b) średnia harmoniczna ważona







k

i

i

i

x

n

N

H

1

Metody ilościowe w zarządzaniu bezpieczeństwem

Średnia geometryczna:.

Zastosowanie średniej geometrycznej: w analizie szeregów 
czasowych
Przykład: Miesięczne wskaźniki inflacji w trzech miesiącach 
pierwszego kwartału 1998 roku wynosiły odpowiednio: 3,2%, 1,7% 
oraz 0,6%. Jaka była średnia miesięczna inflacja w pierwszym 
kwartale?

N

N

i

i

N

N

g

x

x

x

x

x

x

















1

2

1

~

83

,

101

6

,

100

7

,

101

2

,

103

~

3











g

x

x

Metody ilościowe w zarządzaniu bezpieczeństwem

Wartość modalna (dominanta): wartość zmiennej, która 
w danym rozkładzie empirycznym występuje 
najczęściej.

Przeciętne pozycyjne

Liczba dzieci w 

małżeństwie

0

1

2

3

4

Liczba małżeństw

6

18 34 14

9

Wartość modalna ?

Metody ilościowe w zarządzaniu bezpieczeństwem

Kwantyle: wartości cechy, które dzielą badaną 
zbiorowość
na określone części.
Kwartyle (Q1, Q2 (Me), Q3): oddzielają ćwiartki.
Mediana (Me): dzieli badaną zbiorowość na połowę;
Dane dokładne:

2

1



N

x





1

2

1

2

2





N

N

x

x

Me
=

Gdy N jest nieparzyste

Gdy N jest parzyste

Mediana jest miarą pozycyjną, która rozdziela całą populację na dwie liczebnie 
równe części. Wynika z tego, że dla znalezienia mediany trzeba najpierw 
uporządkować zbiorowość niemalejąco według wartości badanej cechy. W 
szeregu przedziałowym przedziały skrajne mogą pozostać otwarte, gdyż nie mają 
one bezpośredniego wpływu na wartość mediany. W szeregach, dla których nie 
można się średnią arytmetyczną, do liczbowej charakterystyki przeciętnego 
poziomu zjawiska należy wykorzystywać medianę. 

Metody ilościowe w zarządzaniu bezpieczeństwem

Dane przedziałowe (grupowane)

N - liczba obserwacji
k - liczba (przedziałów) klas od pierwszej do tej, w której 
znajduje się mediana,
i

Me

 - rozpiętość (klasy) przedziału, w którym znajduje się 

mediana,
n

Me

 - liczność klasy, w której znajduje się mediana,

x

Me

 - dolna granica klasy, w której znajduje się mediana

Me

Me

k

i

i

N

Me

i

n

n

x

Me













1

1

2

Metody ilościowe w zarządzaniu bezpieczeństwem

Zestawienie miar opisu struktury dla szeregu rozdzielczego przedziałowego:

  

 

   

 

258,7

Me

248,0

Do

238,7

S

146,1

Q

111,2

V

S

56,5%

V

Q

44,8%

A

s

0,05

W

s

0,14

x

i

  

 

          

n

i

  

                    

   

  

 

                 

           

  

 

                   

                    

  

 

                         

                        

<0;100)

50

30

1500

-208,7

43553,

9

1306616,

3

<100;20

0)

150

38

5700

-108,7

11814,

7

448960,3

<200;30

0)

250

50

12500

-8,7

75,6

3780,7

<300;40

0)

350

31

10850

91,3

8336,5

258431,0

<400;50

0)

450

22

9900

191,3

36597,

4

805141,8

<500;60

0)

550

13

7150

291,3

84858,

2

1103156,

9

 

Suma

184

47600

 

 

3926087,

0

i

x

i

i

n

x 



x

x

i





2

)

(

x

x

i





i

i

n

x

x





2

)

(

Metody ilościowe w zarządzaniu bezpieczeństwem

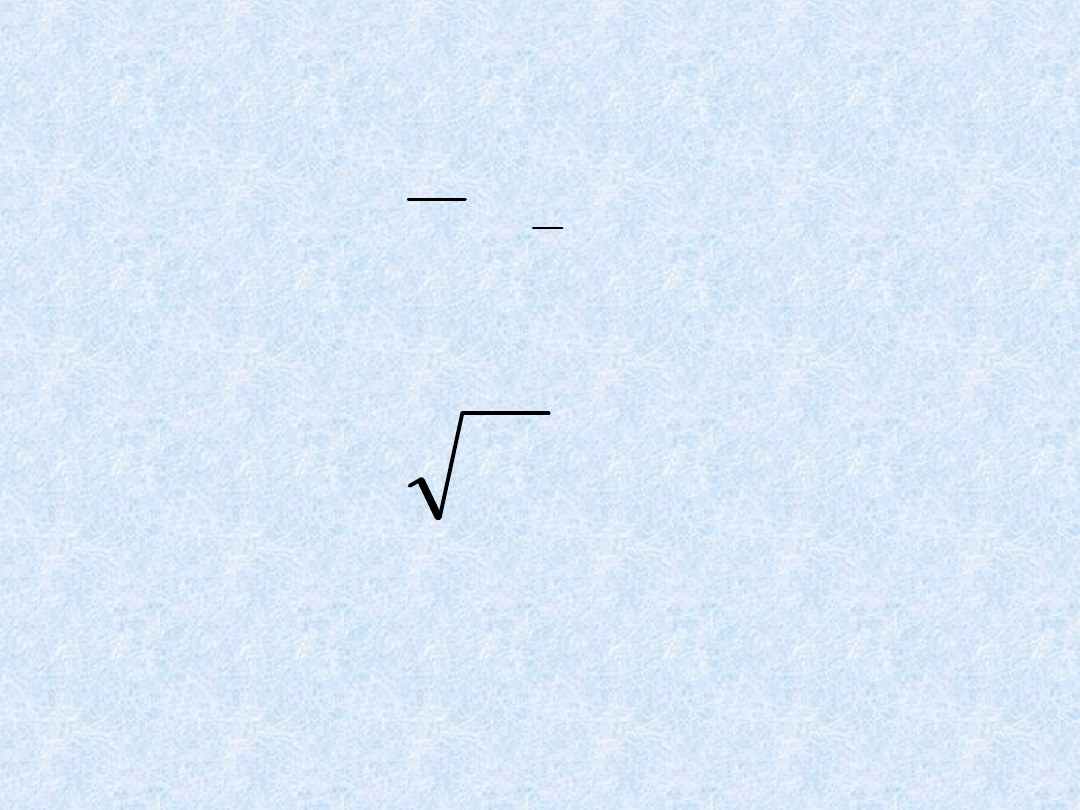
Miary zmienności

a) Wariancja
Dane dokładne:

Dane przedziałowe 
(grupowane):













N

i

i

N

x

x

s

1

2

1

2





i

m

i

i

N

n

x

x

s









1

2

1

2





i

m

i

i

N

n

x

x

s









1

2

1

2



Metody ilościowe w zarządzaniu bezpieczeństwem

Alternatywny sposób obliczania:

b) Odchylenie standardowe

2

2

2

x

x

s

i





2

s

s 

Metody ilościowe w zarządzaniu bezpieczeństwem

c) Odchylenie przeciętne

d) Odchylenie 
ćwiartkowe

Q < d < s









N

i

i

N

x

x

d

1

1

i

k

i

i

N

n

x

x

d









1

1

2

1

3

Q

Q

Q





Metody ilościowe w zarządzaniu bezpieczeństwem

Współczynnik zmienności

x

s

V

s



x

d

V

d



Me

Q

V

Q



Metody ilościowe w zarządzaniu bezpieczeństwem

Rozstęp
Całkowita zmienność w wartości cechy w próbie 
(wstępna ocena dyspersji, miara pozycyjna)

R= x

max

 – x

min

x

max

 – najwyższa wartość cechy

x

min

 – najniższa wartość cechy.

Metody ilościowe w zarządzaniu bezpieczeństwem

Typowy obszar zmienności wartości cechy w 
doświadczeniu

Przykład. Komunikat: Średnia temperatura lipca wynosi 17

0 

+- 2

0

Typowy obszar zmienności to przedział [15

0

, 19

0

]

s

x

x

s

x

typ









Metody ilościowe w zarządzaniu bezpieczeństwem

Miary asymetrii

Współczynnik asymetrii 
(skośności)

s

D

x

A

s





Q

Me

Q

Q

A

s

2

2

1

3







Metody ilościowe w zarządzaniu bezpieczeństwem

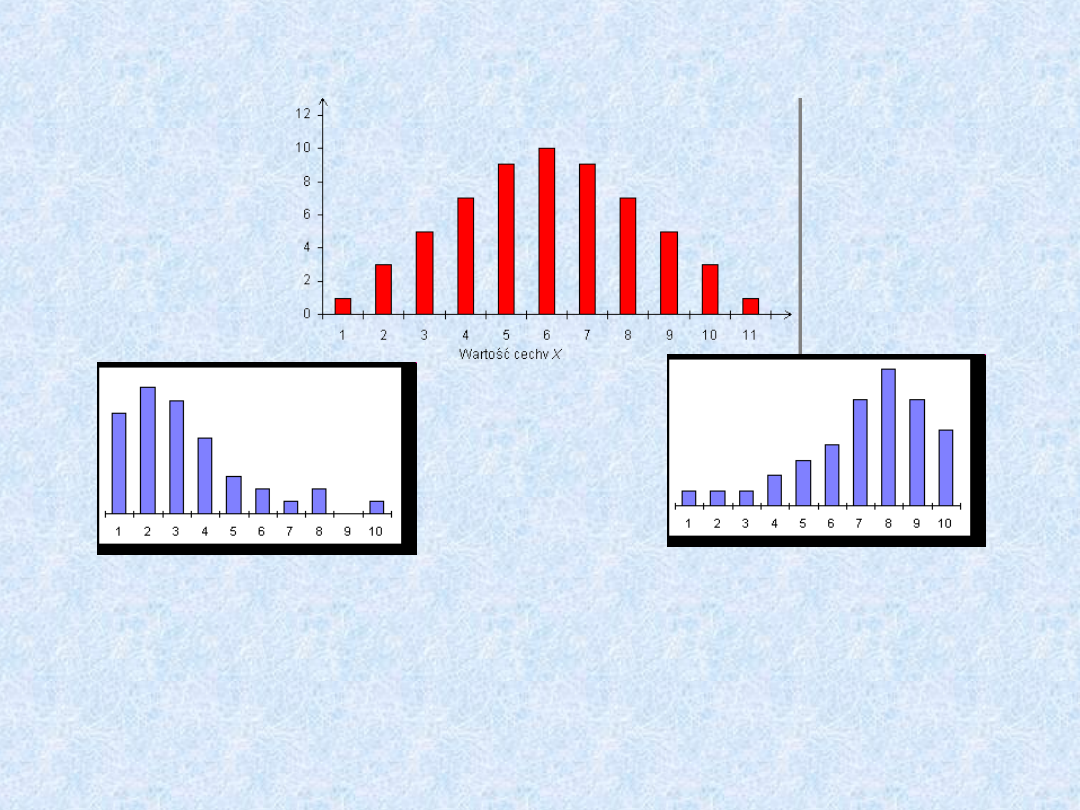
Wskaźnik asymetrii (zwany również miernikiem skośności) dla szeregu 
symetrycznego jest równy zero. W szeregach asymetrycznych miernik 
skośności może być większy lub mniejszy od zera, mówimy wówczas o 
asymetrii prawostronnej (dodatniej) lub asymetrii lewostronnej (ujemnej). 
W szeregu o skośności prawostronnej wartości skrajne położone są z prawej 
strony średniej. Powoduje to przesunięcie średniej arytmetycznej w 
kierunku prawym w stosunku do dominanty i mediany. W szeregu o 
skośności lewostronnej występuje sytuacja odwrotna. 

Metody ilościowe w zarządzaniu bezpieczeństwem

Metody analizy współzależności

Współczynnik korelacji liniowej Pearsona  - 
współczynnik określający poziom zależności liniowej 
między zmiennymi losowymi. 
Obserwujemy n par liczb (x

i

,y

i

), i=1,2...,n.

Wyznaczamy oszacowanie kowariancji zmiennych X i Y:

y

x

xy

y

y

x

x

x

y

Cov

y

x

Cov

i

n

i

i

n



















)

)(

(

)

,

(

)

,

(

1

1

i

n

i

i

n

y

x

xy







1

1

Metody ilościowe w zarządzaniu bezpieczeństwem

)

(

)

(

)

,

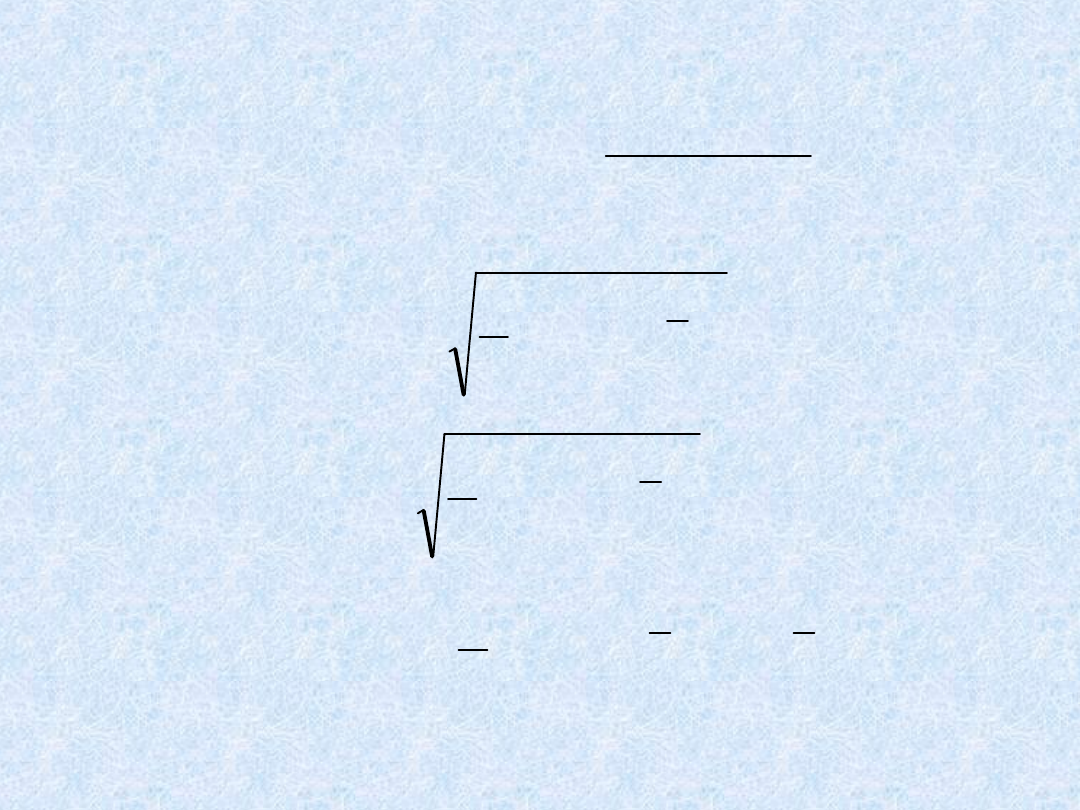
cov(

)

,

(

)

,

(

Y

S

X

S

Y

X

X

Y

r

Y

X

r















N

i

i

N

x

x

X

S

1

2

1

)

(

)

(









N

i

i

N

y

y

Y

S

1

2

1

)

(

)

(

)

)(

(

)

,

cov(

1

1

y

y

x

x

Y

X

i

N

i

i

N











Metody ilościowe w zarządzaniu bezpieczeństwem

Wyznaczamy empiryczne odchylenia standardowe
s(x) oraz s(y)

Interpretacja:
r = 0 - brak zależności liniowej;
r = 1 - dodatnia zależność liniowa;
r = -1 - ujemna zależność liniowa.

)

(

)

(

)

,

(

y

s

x

s

y

x

Cov

r

r

r

yx

xy









Metody ilościowe w zarządzaniu bezpieczeństwem

Analiza regresji

Badanie zależności dla przypadku gdy wartości jednej 
zmiennej zależą od wartości innej zmiennej (zmiennych).
W wielu przypadkach spotykanych w praktyce interesuje nas 
zależność obserwowanej zmiennej (zmiennej zależnej) Y od 
wartości jakie przyjmuje inna zmienna, zwana zmienną niezależną 
X. Zmienną zależną Y nazywamy czasami zmienną objaśnianą, a 
zmienną niezależną X nazywamy wówczas zmienną objaśniającą. 
Interesują nas zazwyczaj przypadki gdy zależność ta ma postać 
liniową

gdzie ε jest zmienną (zakłóceniem) o zerowej wartości średniej i stałej 
wariancji.













0

1

x

Y

Metody ilościowe w zarządzaniu bezpieczeństwem

Wartości parametrów modelu β

0

 oraz β 

1

 wyznaczamy na 

podstawie obserwacji par (X,Y).
Wykorzystujemy do tego celu tzw. metodę najmniejszej sumy
kwadratów błędów (nazywaną często potocznie metodą 
najmniejszych kwadratów).
Na podstawie obserwacji n par (X

i

,Y

i

), i=1,...,n poszukujemy 

takich wartości b0, b1 nieznanych parametrów modelu β 

0

 

oraz β 

1

, by zminimalizować wartość sumy:

Uzyskujemy w ten sposób taką prostą Y=b

1

X+b

0

, że zostanie

zminimalizowana suma kwadratów odległości pomiędzy 
zaobserwowanymi punktami (X

i

,Y

i

), a wyznaczoną prostą.

2

1

0

1

)

(

i

n

i

i

X

b

b

Y

S











Metody ilościowe w zarządzaniu bezpieczeństwem

Oszacowane równanie regresji zmiennej Y 
względem
zmiennej X przyjmuje teraz postać



























































































n

i

i

n

i

i

i

n

i

n

i

i

i

n

i

i

n

i

i

n

i

i

i

X

X

Y

Y

X

X

n

X

X

n

Y

X

Y

X

b

1

2

1

1

2

1

2

1

1

1

1

)

(

)

)(

(

/

/

X

b

Y

b

1

0





0

1

ˆ

b

X

b

Y







Metody ilościowe w zarządzaniu bezpieczeństwem

Przykład
W pewnej firmie analizowano wydajność n=20 pracowników. Celem 
badania było ustalenie zależności pomiędzy wartością zawartych 
przez danego pracownika w ciągu ostatniego roku transakcji a jego 
stażem pracy. Wyniki badania przedstawiają się następująco:

Lp. Staż(X) Obrót(Y) Lp. Staż(X) Obrót(Y)
1   1.250    172.000   11   3.000   215.000
2   1.000    158.000   12   3.500   222.000
3   1.000    184.000   13   4.000   219.000
4   2.000    175.000   14   4.750   225.000
5   2.500    185.000   15   4.000   228.000
6   2.000    201.000   16   4.500   240.000
7   2.000    197.000   17   4.000   210.000
8   2.750    209.000   18   5.000   226.000
9 3.000    200.000   19   5.500   238.000
10  3.250   189.000    20   5.000   243.000

Po podstawieniu do wzorów na b

0

 oraz b

1

 

uzyskujemy:
b

1

=15.6941 oraz b

0

=156.5789

Tak więc oszacowanie równania liniowej funkcji regresji Y względem X ma  
postać:
Y = 15.6941·X  + 156.5789
Równanie to możemy wykorzystać do predykcji (przewidywania) 
nieznanej
wartości obrotu Y dla znanej wartości stażu pracy X.

Metody ilościowe w zarządzaniu bezpieczeństwem

Analiza zależności w przypadku liczby 
zmiennych większej od dwu

Współczynniki korelacji cząstkowej i wielokrotnej 
(wielorakiej)
Przyjmijmy, że analizie poddane zostaje m zmiennych X

1

,X

2

...,X

m

 

opisujących dany obiekt. W szczególnym przypadku możemy wśród 
nich wyróżnić jedną zmienną zależną (objaśnianą) Y=X

1 

i m-1 

zmiennych niezależnych (objaśniających) X

2

,X

3

...,X

m

.

Załóżmy, że wzajemne zależności pomiędzy obserwowanymi 
zmiennymi opisane są macierzą R, której elementami są 
współczynniki korelacji pomiędzy poszczególnymi zmiennymi



















































1

1

1

3

2

1

2

23

21

1

13

12

m

m

m

m

m

r

r

r

r

r

r

r

r

r

R









Metody ilościowe w zarządzaniu bezpieczeństwem

W pewnych przypadkach może nas interesować związek 
pomiędzy dwiema zmiennymi (np. zmienną X

i 

oraz zmienną X

j

) 

z
wyłączeniem wpływu pozostałych zmiennych. Do opisu 
zależności tego typu wykorzystujemy współczynnik korelacji 
cząstkowej

gdzie R

ij

 jest dopełnieniem algebraicznym macierzy R.

Przypomnienie:
Dopełnienie algebraiczne R

ij

 wyznacza się wykreślając w macierzy 

R i-ty wiersz oraz j-tą kolumnę. Następnie oblicza się wyznacznik 
tak uzyskanej macierzy i mnoży się go przez współczynnik (-1)

i+j

.

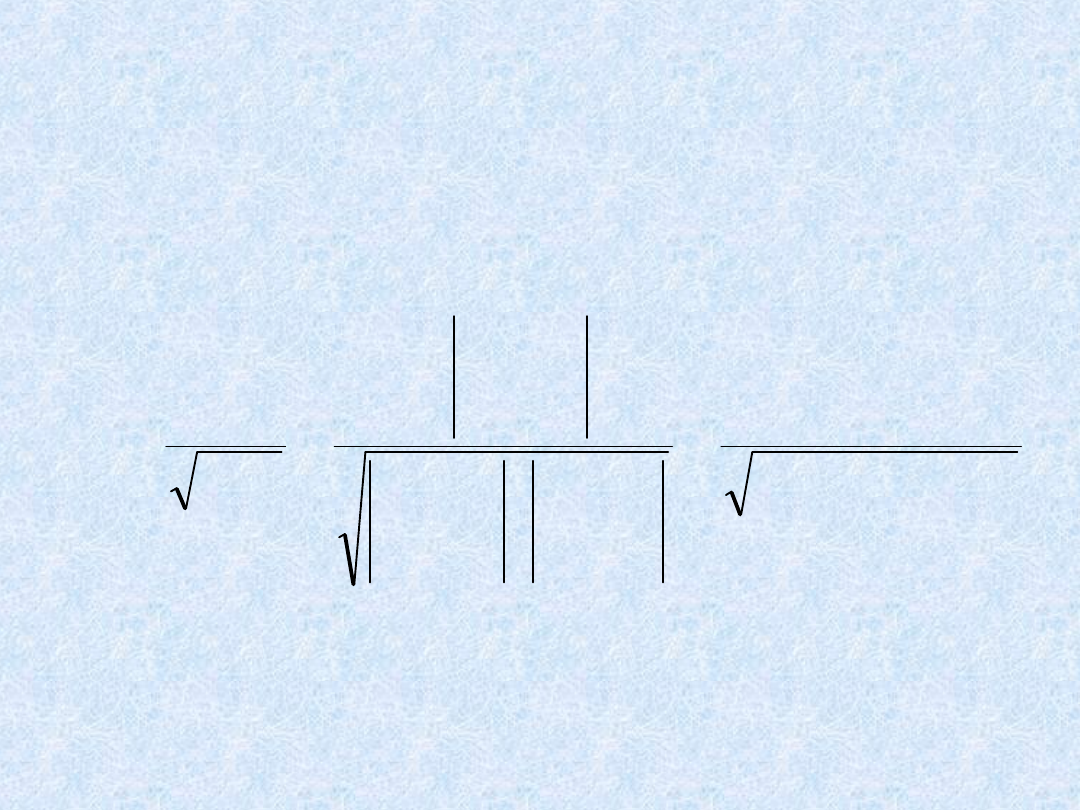
jj

ii

ij

kcz

ij

R

R

R

r





.

Metody ilościowe w zarządzaniu bezpieczeństwem

w przypadku trzech zmiennych X

1

,X

2

,X

3

, gdy interesuje nas 

związek pomiędzy zmiennymi X

1

oraz X

2

 przy wyłączeniu 

wpływu zmiennej X

3

 uzyskujemy:

)

1

)(

1

(

1

1

1

1

1

2

13

2

23

13

23

12

31

13

32

23

31

23

21

22

11

12

3

.

12

r

r

r

r

r

r

r

r

r

r

r

r

r

r

r

r

































Metody ilościowe w zarządzaniu bezpieczeństwem

Gdy interesuje nas związek pomiędzy jedną zmienną objaśnianą (np. 
X

1

) a pozostałymi zmiennymi objaśniającymi X

2

,X

3

...,X

m

 

wykorzystujemy współczynnik korelacji wielokrotnej 
(wielorakiej) wyznaczany ze wzoru:

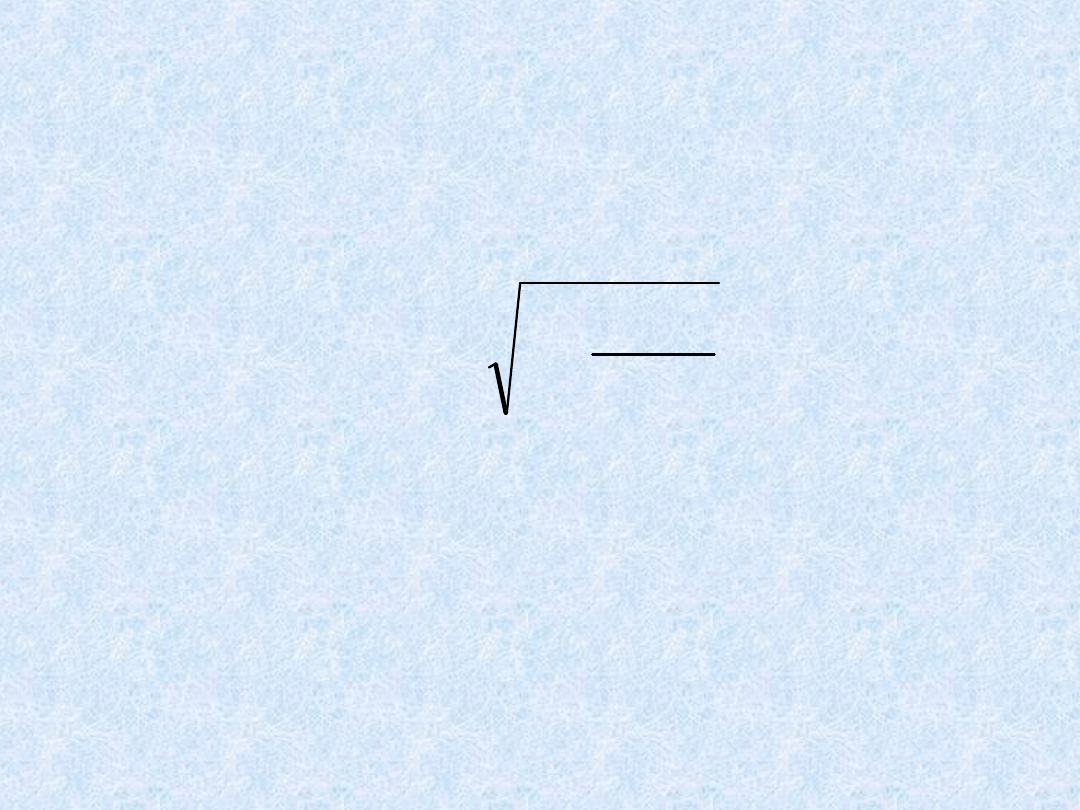
gdzie symbol det oznacza wyznacznik macierzy, macierz R jest 
macierzą współczynników korelacji pomiędzy wszystkimi zmiennymi 
(zmienną objaśnianą i zmiennymi objaśniającymi), zaś D jest macierzą 
współczynników korelacji pomiędzy zmiennymi objaśniającymi 
(powstaje przez skreślenie pierwszego wiersza i pierwszej kolumny 
macierzy R).

D

R

r

m

det

det

1

..

23

.

1



