Dane (ang. data, od łac. datum = to, co jest dane, l.mn data) - wszystko to co jest lub może być przetwarzane umysłowo lub komputerowo
(maszynowo) Dane przetwarzane przez komputer mają postać symboli - liczb, znaków, obrazów itp. Dane wchodzą w skład informacji (symbolom nadane jest znaczenie, np. wielkość fiz.) które z kolei składają się na wiedzę
Zbiór danych - zbiór pobranych z pewnego środowiska lub procesu Najprostszy przypadek zbioru danych - dysponujemy kolekcją m obiektów, przy czym dla każdego z nich dysponujemy n pomiarami. Reprezentacja - macierz o wymiarach m x n.
Analiza danych Poszukiwanie relacji w zbiorze danych Zbiór danych uzyskany wskutek przeprowadzonego eksperymentu - niewielka
liczba elementów lub prosta struktura zbioru - „klasyczne” metody analizy danych - analiza statystyczna. Zbiór danych uzyskany z przeprowadzonych obserwacji - bardzo duża liczba Zbiór danych uzyskany z przeprowadzonych obserwacji - bardzo duża liczba elementów, skomplikowana struktura zbioru - eksploracja danych (ang. data mining) - metody statystyczne są na ogół niewystarczające
Cele analizy danych:
1. Eksploracyjna analiza danych, wizualizacja danych - brak jakichkolwiek założeń, na temat tego czego szukamy - techniki interaktywne i wizualne (wykresy)Efektywne dla stosunkowo niewielkich, niskowymiarowych (2-4) zbiorów danych - np. techniki rzutowania
2. Modelowanie opisowe - model opisowy służy charakteryzacji wszystkich danych (a przez to procesu) - np. estymacja rozkładu rawdopodobieństwa danych, analiza skupień (dzielenie wielowymiarowej przestrzeni na grupy),
tworzenie modeli opisujących związki między rekordami
Segmentacja - np. stosowana powszechnie w badaniach marketingowych do
dzielenia osób na jednorodne grupy na podstawie rodzaju dokonywanych
zakupów i danych demograficznych,
Grupowanie danych - np. analiza długoterminowych zmian klimatycznych -
3. Modelowanie przewidujące (predykcyjne) - zbudowanie modelu na
podstawie którego można będzie przewidzieć (niekoniecznie w czasie) wartość
jednej zmiennej na podstawie znanych wartości innych zmiennych
4. Odkrywanie wzorców i reguł - zdobywanie wiedzy z danych poprzez poszukiwanie ukrytych wzorców
5. Wyszukiwanie według zawartości - wyszukiwanie na podstawie danego wzorca podobnych podzbiorów zbioru danych (który jest zazwyczaj bardzo duży) - np. wyszukiwanie treści w sieci Internet, wyszukiwanie obrazów podobnych do danego itp.
Wiele technik eksploracji danych (np. analiza skupień) używa miar opartych na
podobieństwie zbiorów danych.
Kryterium oceny podobieństwa - metryka:
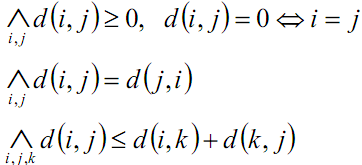
Metryka euklidesowa:
![]()
Metryka (ogólnie):
![]()
Metody wizualne - odkrywanie ukrytych struktur danych przez człowieka, idealne do przeszukiwania danych w celu znalezienia nieoczekiwanych
zależności
Wizualizacja danych
Statystyki opisowe:
Wartość średnia:
Niech x(1) … x(n) stanowią zbiór n wartości danych
![]()
Wartość średnia: jest szacowana na podstawie próbki Wartość średnia próbki
ma tę własność, że jest wartością „środkową" - minimalizuje
sumę kwadratów różnic między nią a wartościami danych.
Mediana:
Jest to wartość mającą równą liczbę punktów danych nad i pod sobą. Jeśli n jest liczbą parzystą, mediana jest zwykle definiowana jako wartość leżąca w połowie drogi między dwoma środkowymi wartościami).
Moda:
Najczęściej występująca wartość w danych
Uwaga: Czasem rozkłady mają więcej niż jedną modę (na przykład może być 10 obiektów, które na pewnej zmiennej przyjmują wartość 3 i kolejne 10, które przyjmują wartość 7, wszystkie zaś pozostałe wartości są przyjmowane mniej niż 10 razy) i stąd
są zwane wielomodalnymi. są zwane wielomodalnymi.
Pierwszy kwartyl (lub kwantyl), dolny kwartyl:
Wartość większa niż jedna czwarta punktów danych.
Trzeci kwartyl, górny kwartyl
Wartość większa niż trzy czwarte punktów danych.
Drugi kwartyl -> mediana
W podobny sposób definiowane są decyle i centyle
Wariancja:
![]()
![]()
Wariancja to średnia kwadratów różnic między wartością średnią a pojedynczymi wartościami danych. Jest to przykład miary rozrzutu lub
zmienności.
Odchylenie standardowe:
![]()
Rozstęp międzykwartylowy:
Różnica między trzecim a pierwszym kwartylem
Współczynnik skośności (Skośność):
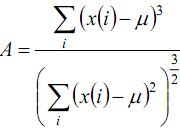
Miara asymetrii rozkładu.
Przyjmuje wartość 0, jeśli rozkład jest symetryczny,
wartości ujemne, jeśli rozkład jest lewostronny (wydłużone lewe wartości ujemne, jeśli rozkład jest lewostronny (wydłużone lewe
ramię rozkładu); dodatnie jeśli jest prawostronny
Kurtoza:
![]()
Miara spłaszczenia rozkładu.
Kurtoza przyjmuje wartość 0, jeśli spłaszczenie rozkładu jest jak dla rozkładu normalnego Kurtoza dodatnia - wartości cechy są bardziej skoncentrowane niż przy rozkładzie norm.
Kurtoza ujemna - wartości cechy są mniej skoncentrowane niż przy rozkładzie norm
Przedstawianie pojedynczych zmiennych
Histogram - pokazuje liczbę wartości danej zmiennej leżących w kolejnych
przedziałach
Przy małych zbiorach danych histogramy mogą być mylące: przypadkowe wahania wartości lub alternatywne wybory końców przedziałów mogą
doprowadzić do powstania bardzo różnych diagramów
Przy dużych zbiorach danych nawet ledwo uchwytne cechy histogramu mogą reprezentować rzeczywiste aspekty rozkładu
Histogram można wygładzić - estymacja jądrowa - wyrównanie histogramu wokół każdego z
punktów, wartość przypisana każdemu z punktów
![]()
przy czym K - funkcja jądrowa
h - szerokość f.j.
![]()
Zazwyczaj jest to funkcja jednomodalna z
wierzchołkiem w 0
Często jest to funkcja Gaussa
![]()
C - stała normująca
Wykres pudełkowy(box plot) - pojedyncza zmienna
Przedstawianie zaleznosci pomiędzy dwoma zmiennymi
Rozrzut(scatterplot) Bardzo duża liczba punktów.
Przesłanianie jednych punktów przez inne
Wykresy warstwicowe(box plot)
Wykres warstwicowy wymaga Wykres warstwicowy wymaga skonstruowania estymacji dwuwymiarowej gęstości -dwuwymiarowa funkcja jądrowa
Przedstawianie zależności więcej niż dwóch zmiennych Macierzowe wykresy rozrzutu
Dane wielowymiarowe są rzutowane na przestrzeń dwuwymiarową - definiowaną przez dwie z tych zmiennych Możliwe jest zatem badanie zależności pomiędzy parami zmiennych
Wykresy obrazkowe Wykresy obrazkowe
Wykresy gwiazdowe -promienie wychodzące w różnych kierunkach odpowiadają różnym
zmiennym - długości tych promieni odpowiadają ważności tych zmiennych
Wykresy kołowe Wykresy profili Twarze Chernoffa
Dane wielowymiarowe rzutowane są na przestrzeń dwuwymiarową
Analiza składowych głównych (Principal Component Analysis - PCA) Bardziej ogólny przypadek - rzutowanie wzdłuż dwóch różnych kierunków będących jakąkolwiek ważoną kombinację liniową zmiennych - np. 2x1 + 3x2 + x3
Można spowodować, przeszukiwanie różnych kierunków projekcji - duży nakład mocy
obliczeniowej. PCA - metoda opracowana w 1933 przez Hotellinga.
Cel - znalezienie takich kombinacji liniowej zmiennych (2 - w przypadku dwuwymiarowym), aby wariancja zrzutowanych danych na taką płaszczyznę była maksymalna - zmniejszenie wymiarowości danych X - macierz danych o wymiarach n x p (wiersze - przypadki; kolumny - zmienne)
Każdy i-ty wiersz macierzy traktowany jest jako transpozycja wektora kolumnowego xT
a - kolumnowy wektor rzutowania rozmiaru p x 1 (jeszcze nieznany) dający największą wariancję, gdy dane z macierzy X rzutowane są na a. Rzutowanie jakiegokolwiek wektora danych x jest kombinacją liniową
![]()
Rzutowanie wszystkich wektorów danych (czyli X) na a można zapisać jako Xa
Skalowanie wielowymiarowe (Multidimensional Scaling - MDS) PCA - rzutowanie wielowymiarowego zbioru danych na przestrzeń (często dwuwymiarową), w której dane mają maksymalny rozrzut. Może istnieć zakrzywanie
tak uzyskanej przestrzeni - wówczas PCA, może być nieefektywna. Inne kryterium niż maksymalizacja wariancji musi zostać wzięta pod uwagę -
odległość (lub niepodobieństwo). Można użyć innej miary odległości niż euklidesowa (nawet nie musi być to metryka). Można użyć innej miary odległości niż euklidesowa (nawet nie musi być to metryka).
Klasyczne skalowanie wielowymiarowe - minimalizacja wyrażenia
![]()
Odległość pomiędzy
elementami i oraz j w
przestrzeni p-wymiarowej Odległość pomiędzyelementami i oraz j w
przestrzeni 2-wymiarowej
Skalowaniu w dziedzinie czasu odpowiada odwrotne skalowanie w dziedzinie częstotliwości Jeżeli zmniejszymy skalę czasową („ściśniemy” sygnał) to będzie temu odpowiadać poszerzenie widma tego sygnału
Jeśli fmax jest maksymalną częstotliwością sygnału analogowego x(t), wówczas aby z
sygnału spróbkowanego odtworzyć sygnał oryginalny, częstotliwość próbkowania fp
musi musi być co najmniej dwa razy większa.
Próbkowanie sygnałów pasmowych
rekonstrukcja sygnału pasmowego z częstotliwością próbkowania mniejszą niż ω - inwersja częstotliwości
W praktyce nie jest możliwe zrealizowanie sumowania nieskończonej ilości składników, zatem
transformacie podlega tylko fragment sygnału
Transformowaniu ulega iloczyn sygnału i okna prostokątnego zatem w dziedzinie częstotliwości wyznaczany jest splot widma sygnału i okna prostokątnego
Transformata świergotowa (chirp transform)
Przeznaczona jest do obliczania widma Fouriera analizowanego sygnału w zadanym
zakresie częstotliwości z założoną rozdzielczością.
Transformata Wignera-Ville'a
R Reprezentacja czasowo-częstoliwościowa
R Idealnie odwzorowuje na płaszczyźnie czas-częstotliwość liniową zmianę częstotliwości
Reprezentacja VW posiada najlepszą koncentrację energii w przestrzeni czas- częstotliwość, ale występują pasożytnicze interferencje wzajemne o charakterze oscylacyjnym Konieczne jest redukcja interferencji - lokalne wygładzanie widma
• Rozdzielczość w dziedzinie czasu i częstotliwości jest ograniczona
• Im większa rozdzielczość w dziedzinie czasu (mniejsza szerokość okna w dziedzinie
czasu), tym mniejsza w dziedzinie częstotliwości (szersze okno w dziedzinie częstotliwości)
i na odwrót.
• Największa rozdzielczość w dziedzinie czasu i częstotliwości - najmniejsze pole kostki
Heisenberga- uzyskuje się dla okna Gaussa - transformata Gabora.
Transformata falkowa (wavelet transform)
![]()
Ciągła transformata falkowaAnalizowana funkcja powinna być całkowalna z kwadratem tzn:
![]()
Sygnał powinien charakteryzować się skończoną energią. Warunku tego nie spełnia np. zarówno sygnał stały, jaki i sinusoida zarówno sygnał stały, jaki i sinusoida
• Dla małych wartości skali s szerokość kostki Heisenbrga w dziedzinie czasu jest mała a
duża w dziedzinie częstotliwości
• Dla dużych wartości skali s szerokość kostki Heisenbrga w dziedzinie czasu jest duża a
mała w dziedzinie częstotliwości
• Jeżeli sygnał f(t) zostanie poddany przekształceniu falkowemu, to na płaszczyźnie
czasowo-częstotliwościowej zawarta jest informacja o zawartości wolno- i szybkozmiennych
składowych oraz ich lokalizacji w czasie z rozdzielczością zdeterminowaną przez kostkę
Heisenberga
Ortogonalność bazy falkowej zapewnia uniknięcie nadmiaru informacji o sygnale w jego
rozwinięciu falkowym - nie jest to bezwględnie wymagane wada rozwinięcia w szereg falkowy: brak tzw. niezmienności przesunięcia (shift invariance)
Dyskretna transformata falkowa
Ciągłe p.f. - ciągły sygnał, nieskończenie wiele falek
Rozwinięcie w szereg falkowy - sygnał dyskretny, nieskończenie wiele falek Realizacja praktyczna jest niemożliwa do osiągnięcia (w sensie przedstawionych zależności) Widmo falki - filtr pasmowoprzepustowy o szerokości zmieniającej się wraz ze zmianą skali Zwiększenie skali 2-krotne - 2 krotne zmniejszenie pasma falki i przesunięcie w stronę składowej stałej Wprowadzenie tzw. funkcji skalującej - filtr dolnoprzepustowy
Transformata Z jest przypadkiem ogólnym transformaty Fouriera ciągu x[n]
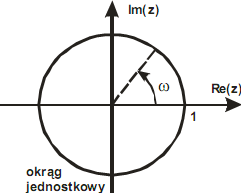
Obliczenie transformaty Z na okręgu jednostkowym →
transformata Fouriera
z=1 → ω=z
z=j → ω = π/2
z=-1 → ω =π
Zbiór takich z, że dla danego ciągu x[n] transformata Z jest zbieżna → obszar zbieżności Zbiór takich z, że dla danego ciągu x[n] transformata Z jest zbieżna → obszar zbieżności
![]()
warunek zbieżności transformaty Z
Transformata Z może być zbieżna dla ciągów, których transformata Fouriera nie jest zbieżna
np. skok jednostkowy x[n ]= u[n ] w ogólnym przypadku nie jest absolutnie sumowalny
ale gdy |r|>1 wówczas jest abs. Sumowalny
![]()
jest zbieżny dla |r|>1
![]()
![]()
Obszar zbieżności zależy tylko od z i zawiera wszystkie z dla których transformata Z istnieje
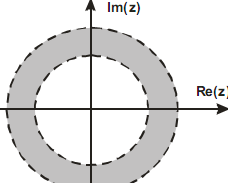
Obszarem zbieżności (OZ) jest pierścień
na płaszczyźnie zespolonej, którego
zewnętrzny promień może → ∞
Jeśli OZ zawiera okrąg jednostkowy,
wówczas istnieje transformata (dyskretna) Fouriera wielomian, miejsce zerowe - zera transformaty
Transformata Z zazwyczaj daje się wyrazić w postaci funkcji wymiernej:
![]()
Wielomiany w liczniku i mianowniku dają się rozłożyć na czynniki: W wielomianach występuje z-1
- kwestia przyjętej konwencji - zgodność z definicją
transformaty Z
![]()
γl l= 1...M pierwiastki licznika transformaty → zera transformaty
λl l= 1..N pierwiastki mianownika transformaty → bieguny transformaty
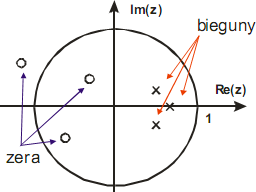
Właściwości obszaru zbieżności transformaty Z
1. OZ ma kształt dysku lub pierścienia ze środkiem w środku układu współrzędnych na płaszczyźnie zespolonej z
2. Transformata Fouriera ciągu x[n] jest bezwzględnie zbieżna wtedy i tylko wtedy,
jeśli OZ transformaty sygnału x[n] zawiera okrąg jednostkowy
3. OZ nie zawiera żadnych biegunów
4. Jeśli x[n] jest ciągiem skończonym wówczas OZ jest cała płaszczyzna zespolona oprócz punktu z=0 lub z=∞
5. Jeśli x[n] jest nieskończonym ciągiem prawostronnym, OZ jest obszar położony
na zewnątrz okręgu o promieniu równym modułowi największego bieguna Z{x[t]}
6. Jeśli x[n] jest nieskończonym ciągiem lewostronnym, OZ jest obszar położony
wewnątrz okręgu o promieniu równym modułowi najmniejszego bieguna Z{x[t]}
7. Jeśli x[n] jest nieskończonym ciągiem dwustronnym, OZ będzie pierścieniem ograniczony biegunami (nie zawiera oczywiście wewnątrz żadnych biegunów)
8. OZ jest obszarem spójnym


Odwrotne przekształcenie Z
Wyznaczenie ciągu x[n] na podstawie jego transformaty i informacji o obszarze zbieżności
Sposoby obliczania odwrotnej transformaty
• bezpośrednio ze wzoru
• metoda „długiego” dzielenia wielomianów
• metoda rozkładu na ułamki proste
• metoda residuów
Zysk obliczeniowy algorytmu radix-2
W każdym kroku algorytmu FFT wymagane jest przeprowadzenie N/2 mnożeń zespolonych
oraz N sumowań zespolonych Każdy dodatkowy współczynnik w potędze liczby 2 przy ilości N próbek wymaga przeprowadzenia osobnego kroku algorytmu FFT. Zatem zawsze mamy B =log2N kroków w algorytmie FFT. W całym algorytmie przeprowadzanych jest N/2*log2N mnożeń zespolonych oraz N*log2N sumowań zespolonych.
OBRAZ - Pojęcia podstawowe
Obraz - rozkład irradiancji (strumień promieniowania padający na jednostkę powierzchni [W/m2] na płaszczyźnie funkcja dwuwymiarowa:f(x,y) , przy czym:x, y - współrzędne przestrzenne (na płaszczyźnie) 0<f(x,y)<∞
Cyfrowe przetwarzanie obrazu - (digital image processing) przetwarzanie obrazu
cyfrowego za pomocą maszyny cyfrowej (komputera)
Wartości w wyniku kwantyzacji przybierają wartości całkowite L,zazwyczaj takie, że: L = 2k
[ 0,L-1] ---Zakres dynamiki obrazu
M*N*k Ilość bitów potrzebna do przechowania obrazu cyfrowego o
rozmiarach M x N
Kompresja pojęcia podstawowe
Kompresja danych - proces przekształcania pierwotnej reprezentacji (źródłowej) sekwencji danych w reprezentację o mniejszej liczbie bitów. Odwrotny proces rekonstrukcji oryginalnej reprezentacji danych na podstawie reprezentacji
skompresowanej nazywane jest dekompresją
Kompresja - pojęcia podstawowe skompresowanej nazywane jest dekompresją Kompresja - Wyznaczanie możliwie użytecznej w danym zastosowaniu reprezentacji przesyłanej lub gromadzonej informacji Kompresja bezstratna (odwracalna) - kodowanie - zrekonstruowany po
kompresji ciąg danych jest numerycznie identyczny z sekwencją źródłową z dokładnością do pojedynczego bitu Przykłady zastosowań: archiwizacja dokumentów tekstowych, historia
operacji finansowych na kontach bankowych, przechowywanie (niektórych) obrazów medycznych
Kompresja Kompresja -- pojęcia podstawowe pojęcia podstawowe Kompresja stratna (odwracalna) - nie jest możliwe odtworzenie danych źródłowych z dokładnością do pojedynczego bitu. Używane jest pojęcie tzw. wizualnej bezstratności. Eliminacji części informacji z obrazu może być niezauważalna, lub dopuszczalna dla obserwatora
Analiza obrazu pojęcia podstawowe
Analiza obrazu jest ściśle związana z konkretnym celem, który chcemy poprzez tą analizę osiągnąć.
Metod analizy jest stosunkowo Metod analizy jest stosunkowo mało, natomiast istnieje olbrzymia
ilość metod przetwarzania obrazów
Przetwarzanie obrazu - klasyfikacja metod
geometryczne(obrót,przesunięcie,odbicie,skalowanie
bezkontekstowe(punktowe)
kontekstowe(filtry medianowe,operacje splotu)
widmowe(z wykorzystaniem DFT,DWT,DCT,itp)
morfologiczne(dyletacje,erozje)
Operacje geometryczne:położenie piksela zmieniane jest zgodnie z zadaną relacją matematyczną.
Operacje arytmetyczne: nowa wartość intensywności piksela obliczana jest na podstawie jego poprzedniej wartości zgodnie z przyjętą relacją arytmetyczną
Segmentacja
Proces segmentacji obrazu jest czynnością spinającą poziom
wstępnego przetwarzania obrazu z programami analizy
poszczególnych obiektów.
Segmentacja jest techniką przetwarzania obrazu, umożliwiającą
wydzielenie obszarów obrazu spełniających pewne kryteria
jednorodności (kolor obszaru, poziom jasności, faktura, itp.) jednorodności (kolor obszaru, poziom jasności, faktura, itp.)
• segmentacja przez podział obszaru
• segmentacja przez rozrost obszaru
• segmentacja metodą wykrywania krawędzi
• segmentacja oparta na statystyce opisującej wnętrze regionów
Analiza obrazu, rozpoznawanie obrazu
Analiza obrazu, która może być przeprowadzona po segmentacji,przewiduje w pierwszej kolejności różne pomiary wykonywane na obiektach wydzielonych podczas procesu segmentacji.
Wynikiem analizy obrazu mogą być dane jakościwe I ilościowe, opisujące określone cechy obrazu
Przykład rozpoznawanie osób na podstawie twarzy
Algorytmy kompresji
Statyczne-jednakowe dla całej sekwencji danych o zbliżonym charakterze. Nie istnije koniecznośc dopisywania parametrów algorytmu w sekwencji wyjściowej
Póładaptacyjne- jednakowe dla całej sekwencji danych parametry alg kompresji wyznaczone na podstawie wstepnej analizy danych.Istnieje konieczność dopisywania parametrów algorytmu w nagłówku sekwencji wyjściowej
Adaptacyjne- zmienne,dostosowane dynamicznie do lokalnej statystyki danych źródłowych na podstawie analizy wejściwej sekwencji danych.Istnieje. Nie istnieje konieczność dopisywania parametrów algorytmu w sekwencji wyjściwej dla przyczynowej adaptacji wstecz. Konieczność dopisywania rzadziej zmienianych parametrów(adaptacja w przód)
KOMPRESJA BEZSTRATNA
![]()
Uzycie odpowiedni Przypisywanie ciągu skutecznych i predykcyjnych bitów(słów kodowych)
modeli statystycznych i poszczególnym danym
predykcyjnych, osczednego (poszczególnym
opisu lokalnych zaleznosci symbolom alfabetu
danych źródła informacji),calej
sekwencji danych wejściowych lub jej poszczególnym częścom
Faza modelowania: tworzona jest pośrednia reprezentacja cech, do
której dopasowuje się metodę binarnego kodowania sekwencji źródłowej. Możliwe jest to poprzez:
• przekształcenie danych z przestrzeni oryginalnej w inną z wykorzystaniem metrycznych zależności danych, określonego sposobu porządkowania danych lub zmiany wymiarowości oryginalnej dziedziny danych. oryginalnej dziedziny danych.
• utworzenie modelu deterministycznego, opisującego bezpośrednie (chwilowe, lokalne lub globalne) właściwości danych, np. ciagi jednakowych danych.
• utworzenie modelu probabilistycznego źródła informacji (przy założeniu stacjonarności i ergodyczności źródła) na podstawie określonego kontekstu wystąpienia danych.
Faza kodowania binarnego: polega na tworzeniu w sposób możliwie oszczędny wyjściowej sekwencji bitowej jednoznacznie reprezentującej lokalne dane
Możliwe rozwiązania stosowane w fazie modelowania:
1. Z uproszczonym modelem statystycznym w metodach:
# RLE (Run-Length Encoding - kodowanie długości serii) dla serii bitów (koder Z), bajtów (format PCX), bajtów (format PCX),
# Golomba (JPEG-LS),
# Huffmana (JPEG),
# kodowanie arytmetyczne w przypadku kodowania reszt predykcyjnych.
2. Z rozbudowanym dynamicznym modelem kontekstowym wyższych rzędów
3. Ze słownikiem (metody słownikowe) np. format GIF, PNG
4. Ze wstępną dekompozycją danych gdy tworzona jest reprezentacja pośrednia:
# metody predykcyjne i interpolacyjne,
# kodowanie map bitowych,
# skanowanie danych wg określonego porządku,
# całkowitoliczbowe kodowanie transformacyjne, (np. AVC)
# całkowitoliczbowe dekompozycje pasmowe i falkowe (np. JPEG2000)
Możliwe rozwiązania stosowane w fazie kodowania binarnego:
1. Przypisywanie słów kodowych pojedynczym symbolom alfabetu źródła - Metody
Huffmana, Shannona-Fano, Rice'a - kody o zmiennej długości słów
2. Przypisywanie słów kodowych (zazwyczaj o stałej długości) ciągom symboli wejściowych o zmiennej długości (RLE, kodowanie słownikowe). Modyfikacja tych metodo polega na użyciu adaptacyjnych koderów słownikowych o zmiennym rozmiarz
słownika (a więc i indeksów)
3. Utworzenie sekwencji kodowej w postaci jednego binarnego słowa kodowego wyznaczanegosukcesywnie dla całego ciągu wejściowego
Przegląd wybranych metod kodowania
Kod dwójkowy o stałej długości Poszczególne słowa kodu są dwójkową reprezentacją kolejnych liczb naturalnych
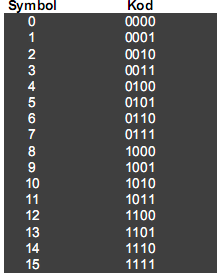
Zalety
- prosta budowa
-znany z góry współczynnik kompresji
Wady
- kompresja możliwa tylko wówczas gdy liczba kodowanych symboli jest mniejsz niż rozmiar alfabetu
Zastosowania
-niewielka liczba występujących symboli
-stosowany jako część składowa innych kodów
Kodowanie długości sekwencji (RLE - run length encoding) RLE-1, RLE-2
Kod strumieniowy, seria powtarzających się jednakowym symboli wejściowych
opisywana jest słowem kodowym określonej długości składającym się z reprezentacji
długości serii i symbolu
Przykład:
Niech będzie dany ciąg wejściowy:
![]()
25 znaków
W rozpatrywanym ciągu znak „a” powtarza się 3 razy, „b” powtarza się 7 razy, „c” - 4 razy, itd.
Informację o zapisie 3 znaków „a” można zapisać jako 3a, zapis 7 znaków „b” można zapisać jako 7b itd. Zatem ciąg wyjściowy będzie miał postać:
![]()
12 znakow
Może się zdarzyć, że w najgorszym przypadku (dane losowe) rozmiar sekwencji wyjściowej zwiększy się dwukrotnie RLE-2 pozwala nie zwiększać rozmiaru danych, w przypadku gdy w sekwencji wejściowej nie występuje ciąg jednakowych symboli
Wykorzystywany jest w tym celu specjalny symbol, który sygnalizuje pojawienie się pary (długość ciągu, symbol).Tylko ciągi o długości większej niż wartość progowa (zazwyczaj 2) zamieniane są na pary (długość ciągu, symbol). na pary (długość ciągu, symbol).
Przykład:
Niech będzie dany ciąg wejściowy:
![]()
Ciąg wyjściowy będzie miał postać:
![]()
Zastosowanie RLE:
Dokumenty, w których dominuje białe tło, np. fax
Formaty zapisu obrazu PCX, BMP, TGA
Jako filtr w dokumentach formatu PostScript i PDF
2D RLE - dwuwymiarowa wersja RLE
# Wersja dwuwymiarowa algorytmu uwzględnia wzajemne relacje # Wersja dwuwymiarowa algorytmu uwzględnia wzajemne relacje
między pikselami w płaszczyźnie obrazu.
# Inaczej zdefiniowane jest sąsiedztwo wystąpienia jednakowych symboli
# Obok bezpośredniego sąsiedztwa kolejno kodowanych pikseli (oprócz pierwszego piksela w serii jest to sąsiedztwo z lewej strony) uwzględnia się sąsiedztwo z góry i góra-skos
Przykład:
Niech będzie dany fragment obrazu z wyszczególnionymi wartościami pikseli: 2D RLE
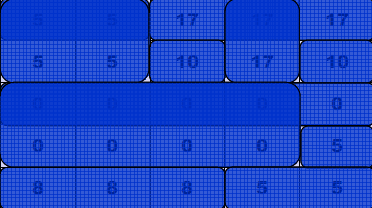
Wynik modelowania:
![]()
Wynik kodowania binarnego - PCX - w kodzie liczby powtórzeń dwa najstarsze bity
wskazują na rodzaj sąsiedztwa, pozostałe sześć oznaczają liczbę powtórzeń wartości
pikseli w danym sąsiedztwie
![]()
Kod Shannona-Fano
Jest to historycznie najstarsza metoda kodowania oparta na prawdopodobieństwie kumulatywnym.
1. Słowa kodowe przyporządkowywane są pojedynczym symbolom i mają różną liczbę bitów
2. Słowa symboli o większym prawdopodobieństwie wystąpienia na wejściu są krótsze - długość słów jest proporcjonalna do ilości Do konstrukcji kodu stosowana jest struktura drzewa binarnego
wejściu są krótsze - długość słów jest proporcjonalna do ilości informacji związanej z danym wydarzeniem
3. Kod jest przedrostkowy, czyli jednoznacznie dekodowalny
Do konstrukcji kodu stosowana jest struktura drzewa binarnego
Schemat budowy drzewa binarnego w kodzie Shannona-Fano:
1. Określane jest prawdopodobieństwo wystąpienia wszystkich symboli
alfabetu na podstawie częstości wystąpień w kodowanym ciągu danych
2. Symbole alfabetu są szeregowane w nierosnącym porządku wag.
Posortowany zbiór symboli traktowany jest jako grupa początkowa.
3. Otrzymana grupa dzielona jest na dwie części o możliwie równej sumie wag symboli z zachowaniem porządku listy (o częściej i występujących symbolach i o rzadziej występujących).
4. Symbolom z jednej podgrupy przyporządkowywane jest logiczne 0 (np. symbolom o większej wadze), a drugiej - logiczna 1.
5. Kroki 3 i 4 są powtarzane rekursywnie dla utworzonych podgrup o przynajmniej dwóch symbolach, czyli aż grupy będą jednoelementowe
6. Kolejnym symbolom z listy przypisywane są słowa kodowe, składające się z bitów kolejno przyporządkowanych grupom.
Przykład2
Kod Huffmana
Przedstawiona wersja kodu Huffmana jest statyczna -prawdopodobieństwa wystąpienia poszczególnych symboli w sekwencji wejściowej są stałe.
Póładaptacyjny (semiadaptacyjny) kod Huffmana
Statyczny kod Huffmana zakłada stacjonarność kodowanego źródła - w praktyce ten warunek nigdy nie jest spełniony Kodowanie Huffmana wymaga znajomości częstości występowania każdego symbolu nad alfabetem Drzewo Huffmana lub częstości występowania symboli musi być
dodane do danych wyjściowych (zazwyczaj w nagłówku
Adaptacyjny kod Huffmana
Stosowany, gdy charakterystyka danych jest zmienna Drzewo Huffmana jest modyfikowane po zakodowaniu każdego nowego znaku. Rozpoczęcie z drzewem pustym lub rozkładem
jednolitym Lepsza efektywność, ale wolniejsze działanie Zastosowanie kodowania Huffmana:
Kompresja JPEG - kodowanie skwantowanych współczynników DCT ; Wykorzystywane w algorytmie LZ77/LZSS (gzip, PKZip, ARJ, LHArc), MPEG.
Zalety
-prostota
-brak ograniczeń patentowych
-brak konieczności przesylania do dekodera informacji o modelu
-dobry współczynnik kompresji
Wady:
- powolne uaktualnianie drzewa Huffmana po zakodowaniu każdego symbolu (kodowanie danych o nieznanej statystyce),
-problemy implementacyjne - możliwe przepełnienie drzewa.
Przykład3
Przykład: jeśli dany jest alfabet o długości n = 6, wówczas:
![]()
![]()
Dwa pierwsze symbole alfabetu otrzymują dwubitowe słowa kodowe,
pozostałe zaś - trzybitowe
Można udowodnić, że jeśli rozkład prawdopodobieństwa symboli Można udowodnić, że jeśli rozkład prawdopodobieństwa symboli
danego źródła jest zrównoważony
(suma dwóch najmniejszych prawdopodobieństw jest większa od prawdopodobieństwa największego),
oraz uporządkowany zgodnie z nierosnącym prawdopodobieństwem kolejnych symboli alfabetu, wówczas kod dwójkowy prawie stałej długości jest optymalnym kodem symboli.
Kod Golomba
Stosowany w przypadkach, gdy nieznana jest statystyka źródła albo w przypadkach, kiedy jest ona na tyle znana, że proces kodowania
może zostać uproszczony Jest to kod symboli, szczególny przypadek kodów przedziałowych
(alfabet jest dzielony na przedziały). Wykorzystywany jest kod dwójkowy prawie stałej długości i kod
unarny Dla kodu o n-elementowym alfabecie pierwszym r symbolom przypisywane są słowa bitowe, bitowe. a pozostałym k+1
![]()
![]()
Można udowodnić, że jeśli rozkład prawdopodobieństwa symboli Można udowodnić, że jeśli rozkład prawdopodobieństwa symboli
danego źródła jest zrównoważony
(suma dwóch najmniejszych prawdopodobieństw jest większa od
prawdopodobieństwa największego),
oraz uporządkowany zgodnie z nierosnącym prawdopodobieństwem
kolejnych symboli alfabetu, wówczas kod dwójkowy prawie stałej długości jest optymalnym kodem symboli.Kod Golomba jest kodem sparametryzowanym, przy czym parametr m > 0 W kodzie Golomba z parametrem m, liczba całkowita n jest eprezentowana za pomocą dwóch liczb q i r, takich, że:
![]()
![]()
Czyli ilorazu i reszty z dzielenia n przez m
q może przyjmować wartości 0, 1, 2, … i jest reprezentowany za
pomocą kodu unarnego
r może przyjmować wartości 0, 1, 2, … m - 1.
Kodowania słownikowe
Metody słownikowe - polegają na utworzeniu listy najczęściej występujących wzorców i zakodowaniu ich wystąpienia w sekwencji wejściowej za pomocą indeksów na liście
Słownik - lista często występujących wzorców w sekwencji wejściowej, tworzona statycznie lub dynamicznie. Metody słownikowe - polegają na utworzeniu listy najczęściej występujących wzorców i zakodowaniu ich wystąpienia w sekwencji wejściowej za pomocą indeksów na liście Słownik statyczny - słownik jest zawsze taki sam - rozwiązanie Słownik statyczny - słownik jest zawsze taki sam - rozwiązanie optymalne jeżeli kodowana sekwencja wejściowa jest znana (albo gdy kolejne wyrazy w sekwencji wejściowej zależą od poprzednich).
Przykłady zastosowań
- lista osób - niektóre imiona (i nazwiska) powtarzają się.
- program w postaci kodu źródłowego - słowa kluczowe tworzą znany i stały zestaw.
Słownik dynamiczny - tworzony jest na bieżąco podczas kodowania
- dostosowuje się do charakteru danych
algorytmy kodowania wykorzystujące słownik dynamiczny
wykorzystują metody opracowane przez Jacoba Ziva i Abraham Lempela w:
R 1977 roku (LZ77)
R 1978 roku (LZ78)
Dekoder pozwala na odtworzenie sekwencji wejściowej na podstawie odkodowanej części danych (słownik nie musi być dołączany do sekwencji kodowej)
LZ77 - kodowanie:
1. Ustawienie struktury okna na początku czytanego strumienia danych wejściowych
2. Poszukiwanie najdłuższego łańcucha danych w buforze kodowania (zaczynającego się od danej znajdującej się na pierwszej pozycji w
buforze), który ma swój dokładny odpowiednik w słowniku
3. Tworzenie sekwencji kodowej tego łańcucha składającej się ze wskaźnika jego położenia w słowniku, długości oraz pierwszego symbolu w buforze występującego bezpośrednio po kodowanej
frazie
4. Przesunięcie okna wzdłuż sekwencji wejściowej o długość zakodowanej frazy
5. Powtarzanie pkt. 2, 3, 4 aż do zakodowania ostatniego symbolu ze zbioru danych wejściowych
LZ77 - przykład kodowania
Długość okna - 13 Rozmiar bufora kodowania - 6
![]()
Jeden znak został zakodowany - okno przesuwane jest o 1 pozycję. W buforze kodowania szukany jest, poczynając od końca symbol d. Ponieważ nie istnieje żadne dopasowanie, zwracana jest trójka liczb: (0,0,kod(d))
Założenia:
Długość okna - 13 Rozmiar bufora kodowania - 6 Założenia:
![]()
Przesuwając się od końca przez bufor słownikowy, trafiamy na dopasowanie dla a,
z przesunięciem 4,
z przesunięciem 7,
z przesunięciem 2 o długości 1, ale także
Długość dopasowania wynosi w tym przypadku 4
Ciąg abra kodowany jest za pomocą trójki liczb: (7,4,kod(r))
Długość okna - 13 Rozmiar bufora kodowania - 6 Założenia:
![]()
Zatem okno przesuwane jest o 5 pozycji
Przesuwając się od końca przez bufor słownikowy, trafiamy na dopasowanie z przesunięciem 3 o długości 3, Długość dopasowania może być jednak rozszerzona do 5, Dlatego wygenerowany ciąg ma postać: (3,5,kod(d))
LZ77 - odkodowanie
Warunki początkowe: odkodowany ciąg ma postać
![]()
Odebrane trójki: (0,0,kod(d)), (7,4,kod(r)), (3,5,kod(d))
1 trójka (0,0,kod(d)) wskazuje na brak dopasowania
2 trójka (7,4,kod(r)) wskazuje na przesunięcie wskaźnika kopiowania i ilość skopiowanych znaków
3 trójka (3,5,kod(d)) wskazuje na przesunięcie wskaźnika kopiowania i ilość skopiowanych znaków
Na końcu dopisany jest odkodowany znak r - kod(r)
Na końcu dopisany jest odkodowany znak d - kod(d)
LZ77 - możliwe usprawnienia, zastosowania
Zamiast 3 liczb można wysyłać tylko 2 - kopiowany ciąg (bez kodu ostatniej litery) lub 0 i kod nowej litery - (LZSS)Wykorzystanie adaptacyjnej wersji algorytmu Huffmana na sekwencji
kodowej LZ&&Zastosowanie: zip, gzip, png, ARJ, rar, PKZip, LHarc
LZ77 - wady
Jeśli kodowany ciąg jest periodyczny, ale długość okresu jest większa niż bufor słownikowy - długość sekwencji kodowej jest dłuższa niż sekwencji wejściowej
LZ78 - właściwości
Zamiast okna przesuwanego wzdłuż strumienia danych wejściowych, stosowany jest słownik budowany jako zupełnie osobna, nieprzesuwna struktura Słownik modyfikowany jest na bieżąco; kolejno odnajdywane w trakcie kodowania frazy ze słownika, odpowiadające sekwencjom
wejściowym, wchodzą w skład nowych fraz uzupełnione o symbol wchodzący w skład kodu łańcucha.Nowe frazy są umieszczane na kolejnych pozycjach w słowniku, który jest w ten sposób dynamicznie rozbudowywany. Rozmiar słownika może rosnąć w sposób nieograniczony !.
LZ78 - kodowanie
Przykład: zakodować następującą sekwencję wejściową za pomocą LZ78
![]()
Inicjalizacja: na pierwszej pozycji słownika wpisywana jest fraza NULL, oznaczająca nieobecność w słowniku szukanej frazy albo
pustą zawartość słownika pustą zawartość słownika
Słownik jest przeszukiwany w celu znalezienia najdłuższej frazy z kolejno czytanych symboli wejściowych Zapisywany jest indeks najdłuższej frazy oraz występującego bezpośrednio po niej symbolu, jako sekwencji kodowej
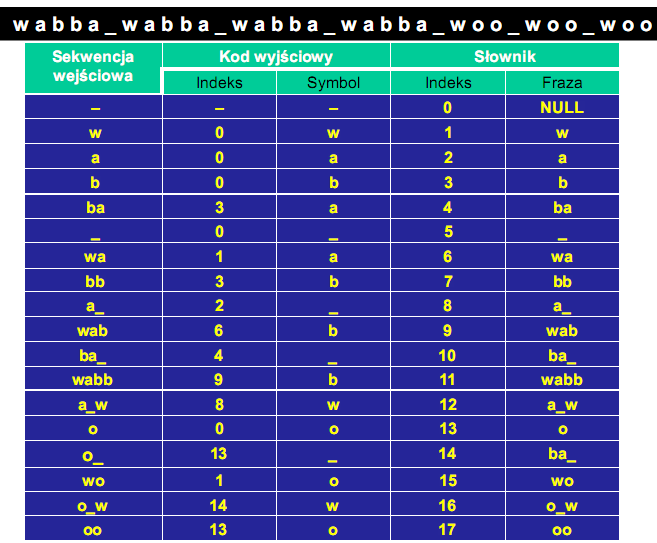
LZ78 - możliwe usprawnienia
Rezygnacja z drugiego elementu pary - koder wysyła tylko indeks kodowanego elementu słownika (Welch)Aby było to możliwe, potrzebny słownik początkowy, zawierający wszystkie używane litery
Konstrukcja słownika jak w klasycznym LZ78 Konstrukcja słownika jak w klasycznym LZ78
LZW - Lampel Ziv Welch
LZW - kodowanie
Przykład: zakodować następującą sekwencję wejściową za pomocą LZ78
![]()
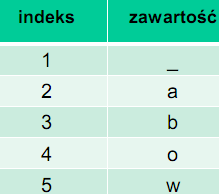
Dana jest początkowa wartość słownika
KOMPRESJA STRATNA
Źródło danych użytkownika
![]()
(zmienna losowa) praeksztalcenie operacja
zmiana danych danych skompreso odwrotna do
wejsciowych w -wanych np. wykorz kodowania
wersje -ystanie niedoskona
skompresowana -losci zmyslu sluchu,
wzroku
KOMPRESJA STRATNA -- KRYTERIA OCENY
Różnica pomiędzy danymi oryginalnymi - {x} a danymi uzyskanymi w wyniku
rekonstrukcji - {y}, (x-y)2 |x-y|
Błąd średniokwadratowy (średnia arytmetyczna z kwadratów błędów poszczególnych elementów ciągu) ang. mean squared error - σd2 σ2
![]()
Stosunek sygnału do szumu, ang. Signal to Noise Ratio, błąd średniokwadratowy odniesiony do poziomu amplitudy danych oryginalnych - SNR
![]()
![]()
KOMPRESJA STRATNA - KRYTERIA OCENY c.d.
Szczytowy stosunek sygnału do szumu, ang. Peak Signal to Noise Ratio, błąd średniokwadratowy odniesiony do maksymalnej amplitudy danych oryginalnych -PSNR
![]()
Średnia wartość błędu bezwzględnego
![]()
Maksymalna wartość błędu bezwzględnego
![]()
JPEG
Standard Digital Compression and Coding Continuous-Tone Still Images znany jako JPEG
(Joint Photographic Experts Group) od nazwy organizacji, która go opracowała(późne lata '80)
Dobrz spełnia swe zadania w przypadku obrazów fotograficznych o płynnych przejściach między barwami.Osiąga natomiast gorsze wyniki w przypadku kodowania prostych rysunków o ostrych konturach, takich jak na przykład kadry pochodzące z filmów rysunkowych.
Standard opisuje metody :
-stratna, której podstawą jest dyskretna tranformata kosinusowa(DTC)
-bezstratna (obecnie mało popularna ze względu na niską wydajnośc)
JPEG - charakterystyka formatu
1. Obsługa obrazów w odcieniach szarości (8 bitów na piksel) i RGB (24 bity na piksel).
2. Wykorzystanie dwóch niedoskonałości ludzkiego wzroku: R mniejszą rozdzielczość widzenia kolorów niż jasności,R małą wrażliwość na amplitudę szybkich zmian jasności.
3. Rozbudowane środki informowania o absolutnej przestrzeni barw obrazu (możliwość umieszczenia profilu koloru w pliku).
4. Obsługa wyświetlania progresywnego (zwiększanie rozdzielczości obrazka w miarę napływania nowych danych).
5. JPEG jest przystosowany do transmisji w sieci - może być dekodowany przy sekwencyjnym dostępie do danych.
JPEG - schemat kompresji
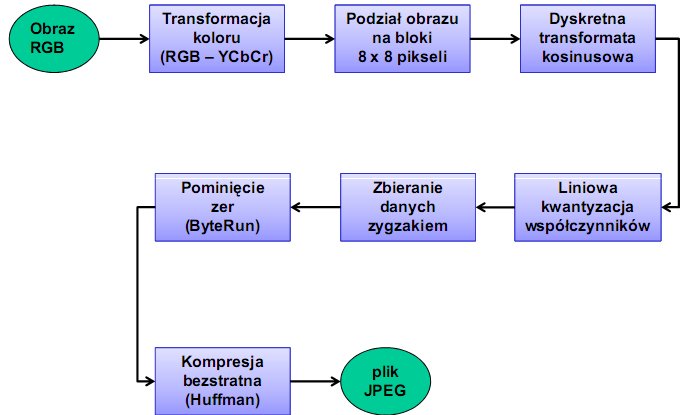
Transformacja koloru RGB do YCbCr i obniżenie rozdzielczości
Y (Luminancja) = 0,299SR + 0,587SG + 0,114SB
Cr (Składowa antyczerwona)
Cb (Składowa antyniebieska) = 128 + 0,5SR - 0,418688SG - 0,081312SB
= 128 - 0,168736SR - 0,331264SG + 0,5SB
Składowe chrominancyjne mogą zostać poddane próbkowaniu ze zmniejszoną
rozdzielczością.
W zależności od wymaganej jakości, składowe chrominancyjne mogą zostać:
1.Pozostawione bez zmian, tzw. format 4:4:4.
2.Rozdzielczość pozioma jest zmniejszana o połowę (format 4:2:2).
3.Rozdzielczość pozioma i pionowa jest zmniejszana o połowę (format 4:2:0).
Podzia obrazu na bloki
Każda ze składowych jest oddzielnie dzielona na bloki o rozmiarach 8 x 8 pikseli.Jeżeli składowe Cr i Cb były przeskalowane, bloki tych składowych obejmują obszar 16 x 8 lub 16 x 16 oryginalnego obrazka.Problem powstaje, jeżeli rozmiary obrazu nie są wielokrotnością 8.Najgorszym rozwiązaniem jest uzupełnienie zerami, Najgorszym rozwiązaniem jest uzupełnienie zerami, lepszym - kolorem ostatniego piksela.Najlepsze jest dodanie takich pikseli, aby odwrotna transformata cosinusowa
odtworzyła piksele należące do obrazka jak najbardziej zbliżone wartościami do oryginalnych.
W praktyce wykonuje się to najczęściej dla trzech pierwszych współczynników transformaty.
DCT - właściwości
Określona na zbiorze liczb rzeczywistych - założona jest parzystość transformowanego sygnału
Po lewej stronie badanego przedziału nie ma nieciągłości, więc amplitudy cosinusów o wyższych częstotliwościach są małe.
Transformata cosinusowa ma w sumie 8 wariantów wynikających znastępujących możliwości:
- po prawej może nastąpić odbicie tylko po osi Y, albo po obu osiach.
- symetria po lewej może być ustawiona na pierwszej próbce sygnału, albo w połowie między pierwszą próbką a jej lustrzanym odbiciem.
- symetria po prawej też może być ustawiona na próbce lub między próbkami.
JPEG : odbicie po prawej tylko w osi Y, symetria po obu stronach między próbkami.Podobnie jak algorytm FFT dla obliczania DFT istnieje wersja szybka dla DCT
Kwantyzacja współczynników DCT, zbieranie danych zygzakiem
Dwuwymiarowa DCT na kwadracie 8-bitowych pikseli o rozmiarach 8 x 8,Wynik: macierz 16-bitowych współczynników, o rozmiarach 8 x 8 Kwantyzacja liniowa: podzielenie przez pewną liczbę i odrzuceniu części ułamkowej.Współczynniki DCT zbierane są w
kolejności zygzakowatej.Największe współczynniki znajdują się na początku, na końcu z reguły występuje dużo zer - zastępowane są odpowiednim
znakiem („zera do końca”)Otrzymany strumień kompresowany jest z użyciem kodowania Huffmana -słownik dynamiczny lub predefiniowany
Geneza standardu - niedoskonałości JPEG
-Zniekształcenia obrazów z kompresją JPEG są nie do zaakceptowania przy niskich przepływnościach,
- Potrzeba standardu, który zapewniałby stratną i bezstratną kompresję w jednym strumieniu bitowym,
-JPEG nie obsługuje obrazów wielkoformatowych (powyżej 64x64K) - np. zdjęcia lotnicze, satelitarne
- JPEG posiada wiele sposobów implementacji (44), wiele z nich są specyficzne i zależą od sposobu zaimplementowania - problem z kompatybilnością dekoderów
- JPEG jest wrażliwy na błędy bitowe (np. powstałe przy transmisji)
-JPEG jest optymalizowany dla obrazów naturalnych - obrazy wygenerowane sztucznie (np.komputerowo) po skompresowane JPEG-em wyglądają nieszczególnie,
Geneza standardu - niedoskonałości JPEG
- JPEG jest wysoce nieefektywny przy kompresji obrazów binarnych (np. tekstu)
Powyższe przesłanki skłoniło grupę roboczą, która zajmowała się standardem
JPEG do opracowania nowego standardu kompresji obrazów
Co zatem powinien nowy standard zapewniać?
Efektywną kompresję obrazów nieruchomych z użyciem jednego zestawu
lgorytmów (enkoder-dekoder),
w odcieniach szarości, kolorowych…
o różnej zawartość(obrazy naturalne, naukowe, medyczne, itp.)
w różnych trybach pracy (klient-serwer, czasu rzeczywistego)
JPEG 2000
Ogólne właściwości:
- Jeden enkoder - wiele sposobów (możliwości) odkodowania
-Bardzo dobra jakość skompresowanych obrazów (nawet przy cr ok. 1:80)
-Wykorzystanie dwuwymiarowej dyskretnej transformaty falkowej (DWT) zamiast DCT
1996 - RICOH - zainicjowanie prac
Listopad 1997: 24 propozycji nowego standardu kompresji obrazów
Styczeń 2001 - IS 15444-1
JPEG 2000 - schemat kompresji - dekompresji
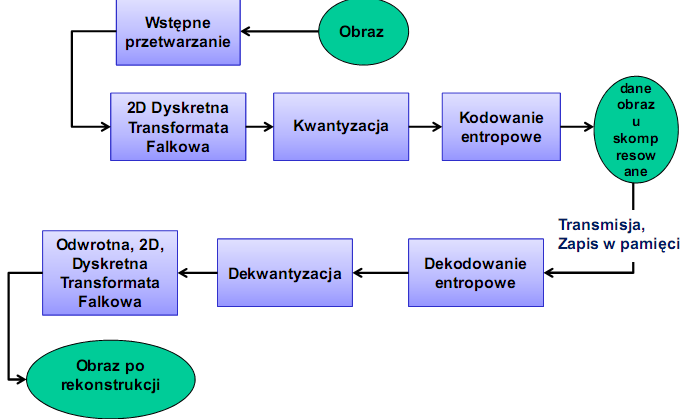
Preztwarzanie wstępne
1. Obraz źródłowy podlega rozłożeniu na 1-256(max) części składowe (obraz może nie zmieścić się w pamięci przydzielonej koderowi
2. Każda składowa rozkładana jest na prostokątne części (kafelki) (64x64, 128x128,…), które są podstawowymi elementami obrazu podlegające dalszemu przetwarzaniu - mogą być kompresowane niezależnie.Im mniejsze kafelki tym większe zniekształcenia (artefakty) obrazu
3. Zmiana zakresu zmian amplitudy z (0 - 255) na (-128 - 128) (dla 8 bitowego obrazu).
4. RGB YCrCb podobnie jak w JPEG , zmniejszenie korelacji pomiędzy pikselami - efektywniejsza kompresja Transformacja RGB w YCrCb może być odwracalna (typ integer, DTF -
całkowitoliczbowa) lub nieodwracalna (typ float, DTF - zmiennoprzecinkowa)
Tak uzyskany element podstawowy jest transformowany za pomocą dwuwymiarowej dyskretnej transformaty falkowej (2D DTF) - zespół filtrówcyfrowych o współczynnikach zmienno- lub stałopozycyjnych.
2D transformata falkowa:
Współczynniki transformaty odpowiadające poszczególnym pasmom częstotliwości (przestrzennej) zgrupowane w tzw. poziomach dekompozycji - w obrębie każdej przetwarzanej części obrazu
Predykcyjna transformata falkowa - algorytm obliczeniowo szybszy, mniej zmiennych pomocniczych - oszczędność pamięci pamięci.
1. Podział - próbki dzielone są na dwie grupy nazywane parzystymi i nieparzystymi
2. Obliczenie aproksymacji i detali:
3. Skalowanie aproksymacji i detali
Kwantyzacja
Współczynniki transformaty falkowej są kwantyzowane za pomocą kwantyzatora ze martwą strefą. Dla każdego podpasma b używany jest ten sam rozmiar kwantyzacji ∆b, wg zależności:
![]()
![]()
Całkowe przekształcanie Fouriera
Definicja
proste przechowanie odwrotne prezekształcenir
![]()
![]()
całka Fouriera jest miarą „zawartości” oscylacji o pulsacji ω w funkcji x(t)
Warunkiem istnienia transformaty Fouriera jest spełnienie przez x(t) warunków Dirichleta:
![]()
1.
2.
x(t) posiada skończone wartości maksimów i minimów w każdym skończonym przedziale
3.posiada skończoną liczbę punktów nieciągłości w każdym skończonym przedziale
Podstawowe własności przekształcenia Fouriera
Liniowość
![]()
D: Własność ta wynika bezpośrednio z liniowości operacji całkowania
Symetria
![]()
Skalowanie
![]()
Skalowaniu w dziedzinie czasu odpowiada odwrotne skalowanie w dziedzinie częstotliwośc
Jeżeli zmniejszymy skalę czasową („ściśniemy” sygnał) to będzie temu odpowiadać
poszerzenie widma tego sygnału
Przesunięcie w dziedzinie czasu
![]()
Przesunięcie sygnału w dziedzinie czasu odpowiada przesunięciu w fazie jego transformaty Fouriera. Moduły dowolnego (spełniającego warunki transf.) sygnału i sygnału przesuniętego są sobie równe.
Przesunięcie w dziedzinie częstotliwości (modulacja zespolona)
![]()
Modulacja rzeczywista
![]()
Iloczyn sygnałów
![]()
Splot sygnałów
![]()
Pochodna sygnału
![]()
Całka sygnału
![]()
Korelacja sygnału
![]()
Równość Parservala
![]()
Wyszukiwarka
Podobne podstrony:
SPSS paca domowa 1 odpowiedzi, Studia, Kognitywistyka UMK, I Semestr, Statystyczna analiza danych
Analiza danych wyjściowych
Metody analizy danych
sciaga kolo1 analiza fin, WTD, analiza matematyczna
ANALIZA MATEMATYCZNA - ściąga, Edukacja, Analiza matematyczna
07 Analiza danych
17 Rejestracja i analiza danych dotyczących z k
Analiza danych w Systemach Informacji Przestrzennej
Materiał na egzamin, Analiza danych (Program R)
Analiza danych1
Materiały zastane wtórna analiza danych
Analiza danych, ocena stanu zdrowia[1]
Analiza danych eksperymantalnych
Interaktywny system regułowej analizy danych marketingowych dotyczących satysfakcji klienta
Metody analizy danych
więcej podobnych podstron