Analiza danych

eksperymentalnych

Przyczyny niepewności wyników eksperymentu:

• błędy grube
• błędy systematyczne
• błędy przypadkowe

Wszystkie wyniki pomiarów, włączając te uzyskane

instrumentem

o bardzo dużej precyzji i przy wysokiej dbałości

eksperymentalnej,

nie są dokładne, lecz mają przybliżony charakter.

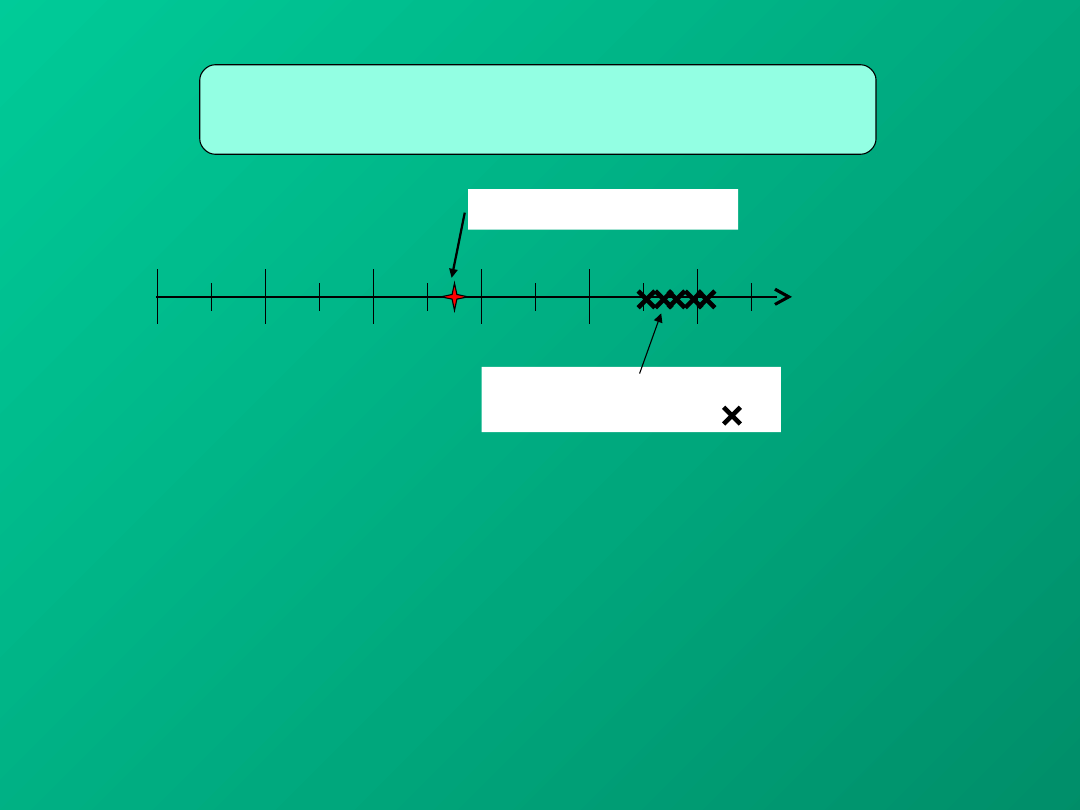
Błąd gruby

• wynika z niedbałości lub ewidentnej pomyłki

eksperymentatora, wyraźnej niesprawności sprzętu
albo

nieoczekiwanego

zaburzenia

układu

pomiarowego

• objawia się istnieniem jednego wyniku znacząco

odstającego od pozostałych, uzyskanych w danej
serii pomiarów

• wynik pomiaru obarczony błędem grubym jest

zazwyczaj łatwo zauważalny i należy go odrzucić.

23,3 ppm; 24,5 ppm; 27,9 ppm ; 33,5
ppm; 0,02 ppm

ppm = g/g

W wątpliwych sytuacjach trzeba stosować
czasami skomplikowane testy statystyczne !!!!

x

i

– wyniki pomiarów

(oznaczone
symbolem )

x

0

– wartość

prawdziwa

błąd gruby

BŁĘDY „GRUBE”
ODRZUCAMY

Błędy grube

Błąd systematyczny

• błąd

polegający

na

stałym

lub

zmiennym,

systematycznym

odchyleniu

wyniku

pomiaru

od

rzeczywistej

wartości wielkości mierzonej

• przesunięcie wyniku następuje zwykle

w tę sama stronę

• metody statystyczne nie mają tu zastosowania.

 niedoskonałość przyrządów pomiarowych

 błędne wyskalowanie, niewyzerowanie

 błąd paralaksy

 w analityce – złe wzorce

 nieuwzględnienie zmiany warunków pomiaru
do warunków skalowania (inne warunki pomiaru
próbki i wzorca)

Oddziaływania systematyczne:

x

i

– wyniki pomiarów

(oznaczone
symbolem )

x

0

– wartość

prawdziwa

Z błędem systematycznym mamy do
czynienia, gdy przy powtarzaniu pomiaru
występuje ta sama różnica między
wartościami zmierzonymi a wartością
rzeczywistą, natomiast rozrzut wyników
poszczególnych pomiarów jest mały. Błędy te
są powodowane

oddziaływaniami

systematycznymi

Błędy (niepewności) systematyczne

Błędy przypadkowe

powstaje na skutek działania

czynników

losowych

jest miarą rozrzutu

otrzymywanych

wyników
wokół wartości najbardziej prawdopodobnej.

błędu przypadkowego w zasadzie

nie da się

wyeliminować

a także nie da się go

oszacować
przed dokonaniem pomiaru

staramy się tak zaprojektować i
przeprowadzić pomiar,
aby wartość błędu przypadkowego była jak
najmniejsza

po zakończeniu pomiaru dokonujemy oceny
wielkości
błędu losowego przy użyciu narzędzi
statystycznych.

 niedokładność odczytu (niedokładna ocena części
działki miernika, niezbyt staranne wyznaczenie
optimum ostrości obrazu w pomiarach optycznych)

 fluktuacja warunków pomiaru (temperatura,
ciśnienie, wilgotność, napięcie w sieci elektrycznej)

 obecność źródeł zakłócających;

 nieokreśloność mierzonej wielkości;

 niedoskonałość zmysłów obserwatora;

Oddziaływania przypadkowe:

x

i

– wyniki pomiarów

(oznaczone
symbolem )

x

0

– wartość

prawdziwa

Błąd przypadkowy spowodowany jest losowym
odchyleniem wyniku pomiaru od wartości
rzeczywistej. Fluktuacje czasowe i przestrzenne
wielkości nie mierzonej. Charakter losowy.
Źródłem błędów przypadkowych są tzw.

oddziaływania przypadkowe:

Błędy (niepewności) przypadkowe

„

„

Dane należy

Dane należy

torturować tak długo,

torturować tak długo,

aż zaczną zeznawać”

aż zaczną zeznawać”

*

*

* - Napotkane w sieci internetowej

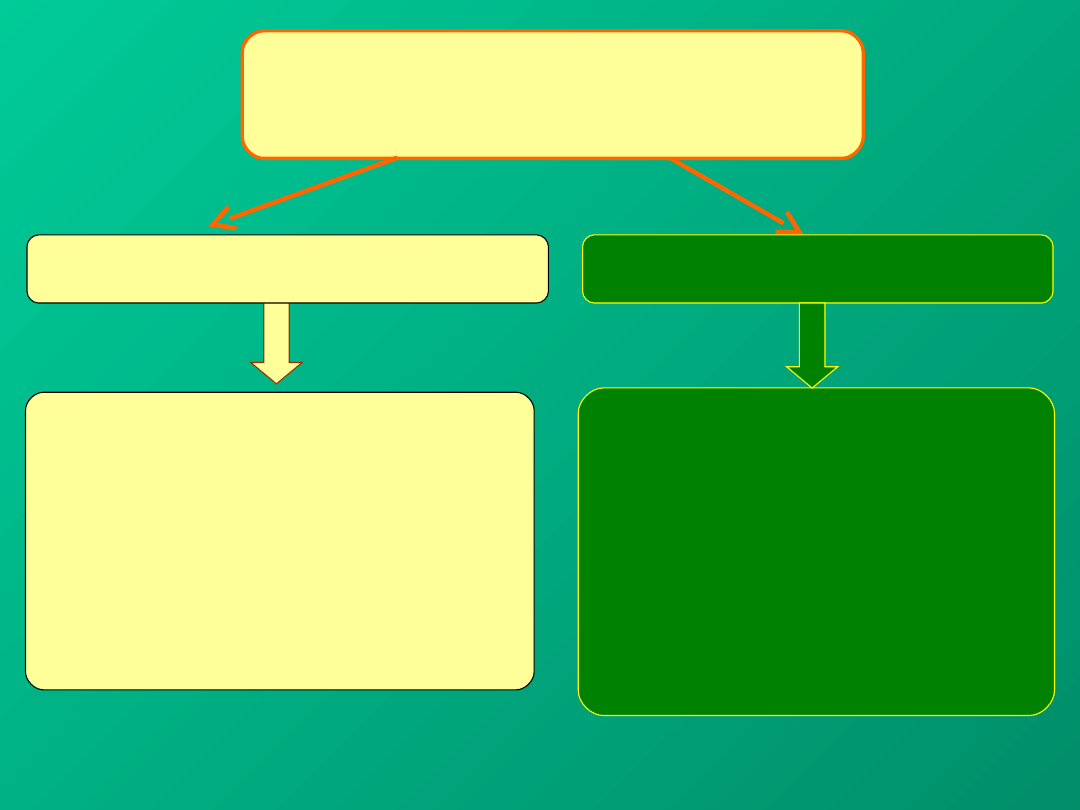
WIELKOŚCI MIERZONE

W pomiarach bezpośrednich

W pomiarach pośrednich

Pomiar kilku wielkości x

1

,x

2

,

…x

n

Obliczenie wielkości
pośredniej
zgodnie ze wzorem
funkcyjnym:

y=f(x

1

,x

2

,…x

n

)

Na przykład pomiar okresu
drgań
i długości wahadła
matematycznego. Obliczenie
wartości przyspieszenia
ziemskiego g.

Pomiar jednej
wielkości
(np. pomiar masy
ciała,
pomiar
temperatury, itd.

2

2

T

l

4

g

g

l

2

T











l, T – wielkości wejściowe, zmierzone w
pomiarach
bezpośrednich, mają swoje
niepewności

Czy wzór powyższy jest słuszny w każdych
warunkach?
Jak policzyć niepewność g?

Pomiar wielkości T nie wpływa na pomiar
wielkości l (wielkości nieskorelowane)

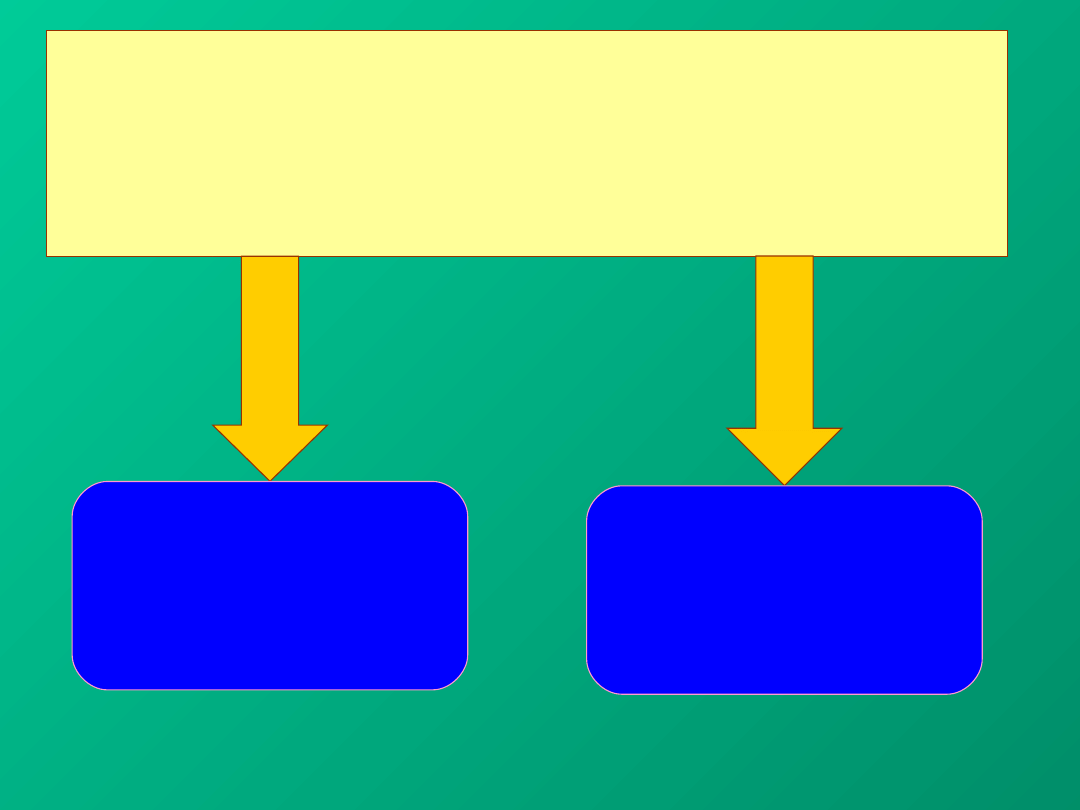
Zgodnie z Przewodnikiem niepewności

klasyfikujemy na dwie kategorie

w zależności od metody ich obliczania:

TYPU A

TYPU B

BŁĄD  NIEPEWNOŚĆ

Omyłka, uchyb, błąd

*)

,

niepewność

SYNONIMY?

* -

Asystent zwraca się do studentki:

A z jakim błędem wyznaczyła Pani
grubość próbki?

Studentka:

No, wie Pan! Ja nie robię błędów

Anegdota (podobno autentyczna). Przeczytane w pracy:

Marek W.Gutowski: Wykład wprowadzający do zajęć na I
Pracowni Fizycznej

METODA TYPU A
Błędy (niepewności)
przypadkowe

Metoda szacowania
niepewności, która
opiera się na obliczeniach
statystycznych
(statystyczna analiza serii
pomiarów –
n  4)

Najczęściej pomiar jednokrotny

METODA TYPU B
Błędy (niepewności)
systematyczne

Metoda szacowania niepewności,
która
Wykorzystuje inne metody niż
statystyczne:

 doświadczenie eksperymentatora

 porównanie z wcześniej
wykonywanymi
podobnymi pomiarami

 certyfikat producenta
wykorzystywanych
w pomiarach przyrządów

 analiza materiału wzorcowego
(odniesienia)

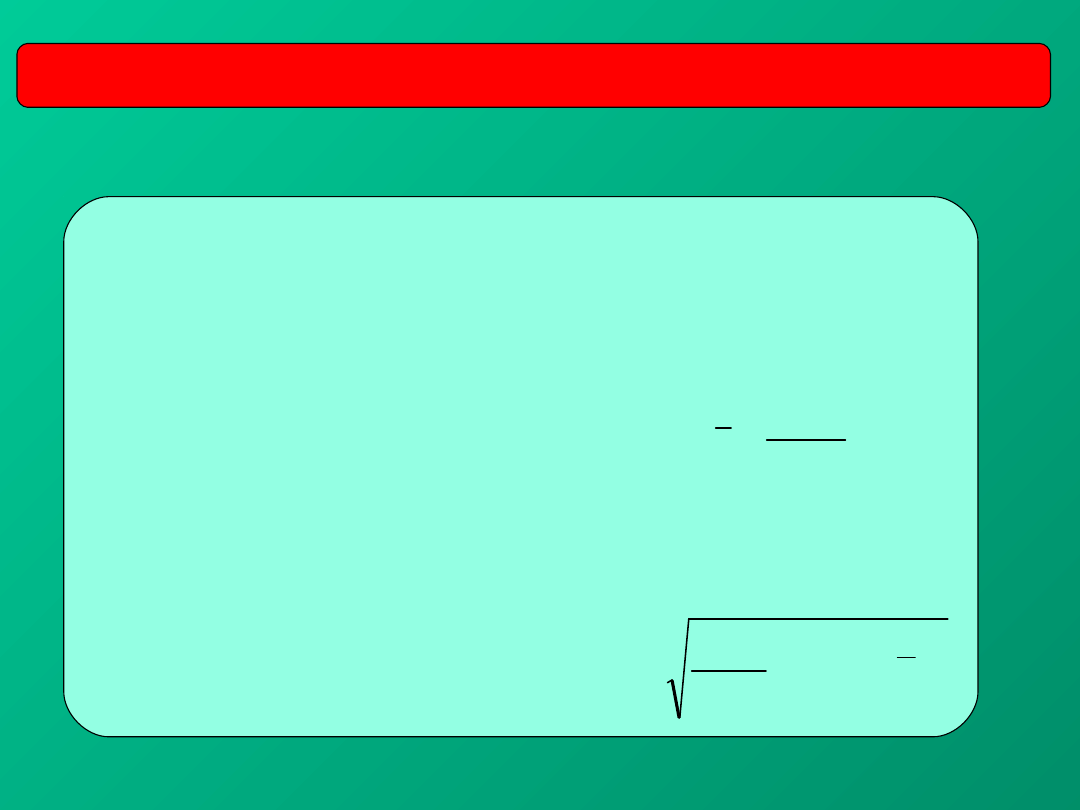
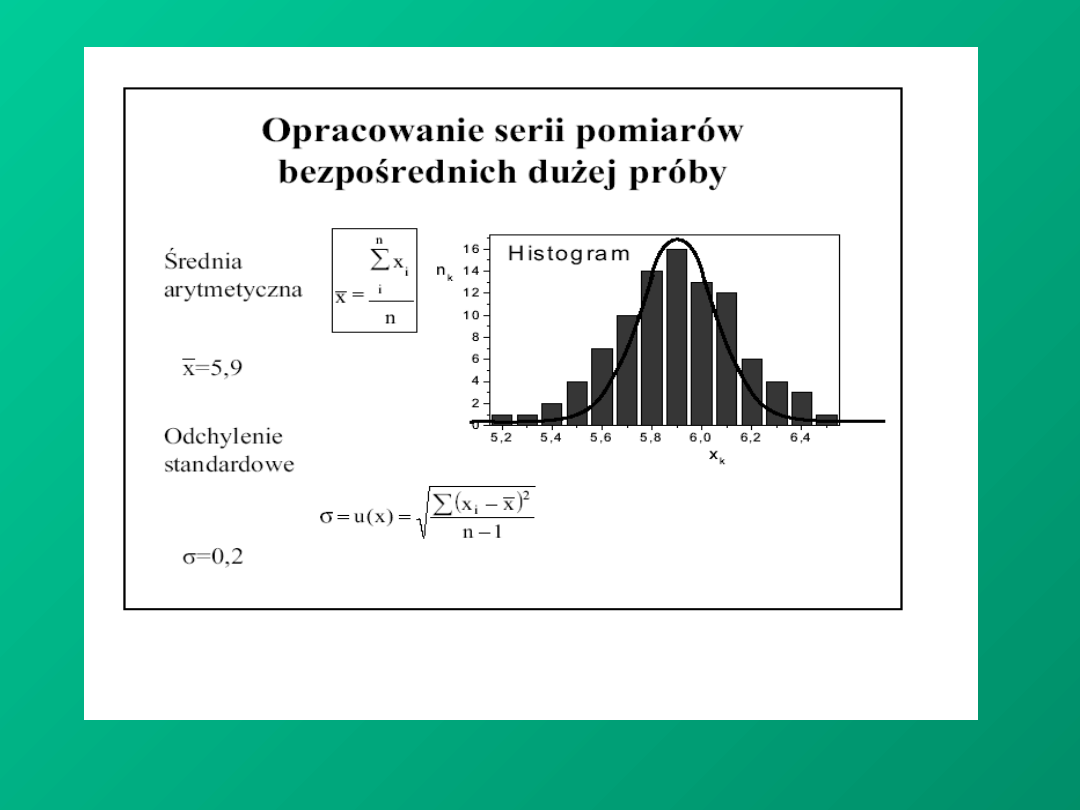
OCENA NIEPEWNOŚCI TYPU A W POMIARACH BEZPOŚREDNICH

n

x

x

n

1

i

i























n

1

i

2

i

x

x

x

1

n

1

S

)

x

(

u

1. Wykonujemy serię (skończoną)

pomiarów

2. Wielkością najbardziej

prawdopodobną
jest średnia arytmetyczna :

3.

Niepewność standardowa

pojedynczego pomiaru u(x)

(tzw. odchylenie standardowe
pojedynczego

pomiaru S

x

)

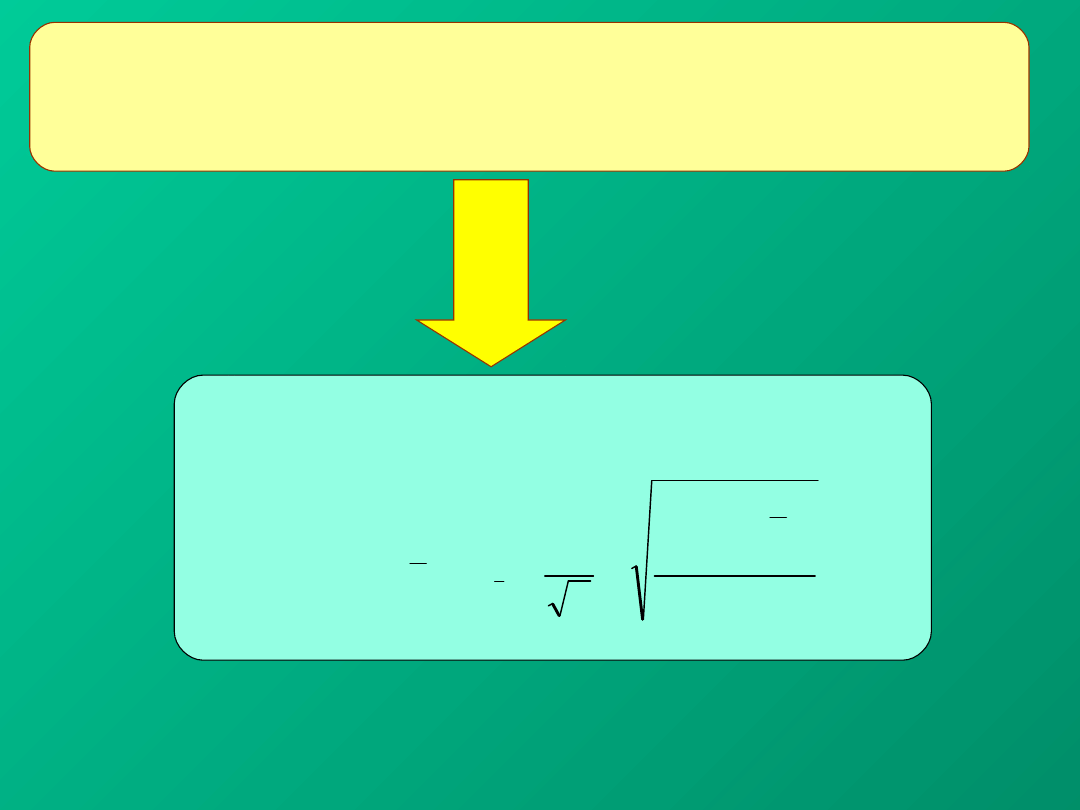
Eksperymentatora bardziej interesuje niepewność
wyniku czyli wartości średniej

Niepewność standardowa
średniej:

 









1

n

n

x

x

n

S

S

x

u

n

1

i

2

i

x

x















OCENA NIEPEWNOŚCI TYPU A W POMIARACH POŚREDNICH

)

x

,...

x

,

x

(

f

y

K

2

1



K

2

1

x

,...

x

,

x

)

x

(

u

),...

x

(

u

),

x

(

u

K

2

1

x

1

, x

2

,…,x

K

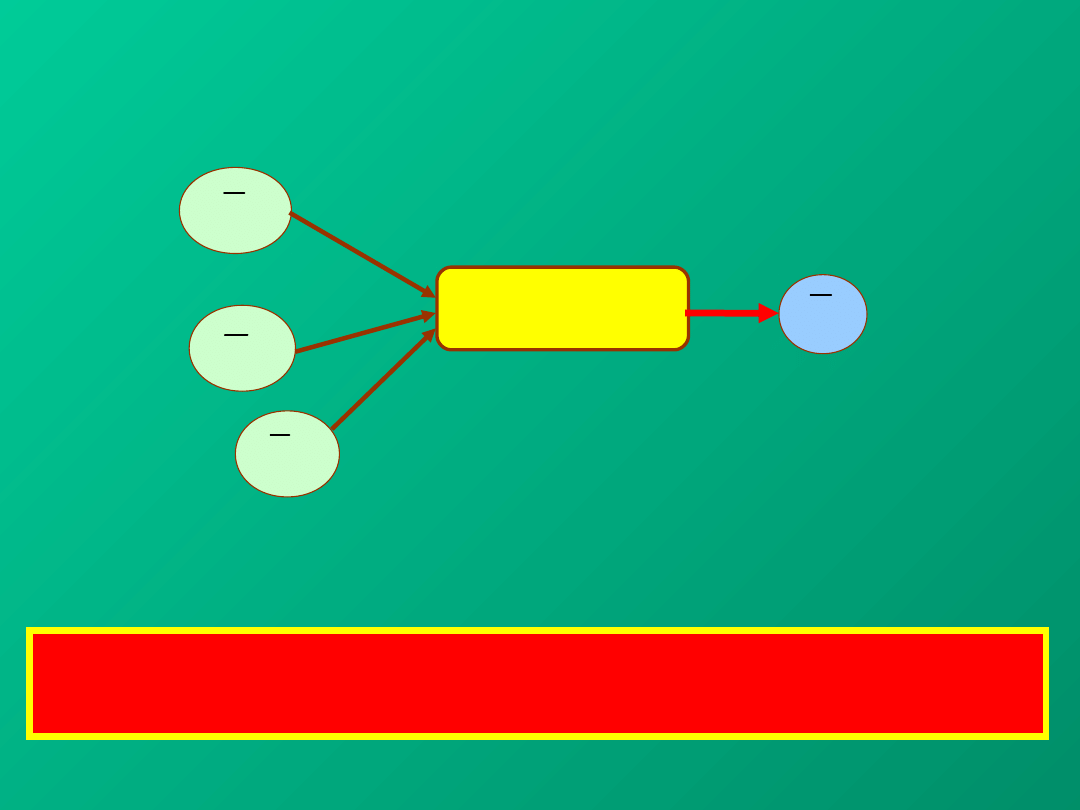
– wielkości wejściowe nieskorelowane,

każde określone w pomiarach
bezpośrednich. Znamy: oraz
niepewności standardowe średnich:

PYTANIE 1. Jak obliczyć wielkość y ?

PYTANIE 2. Jak obliczyć niepewność standardową
wielkości y ?

(*)





K

2

1

x

,...,

x

,

x

f

y 

1

x

2

x

K

x

y

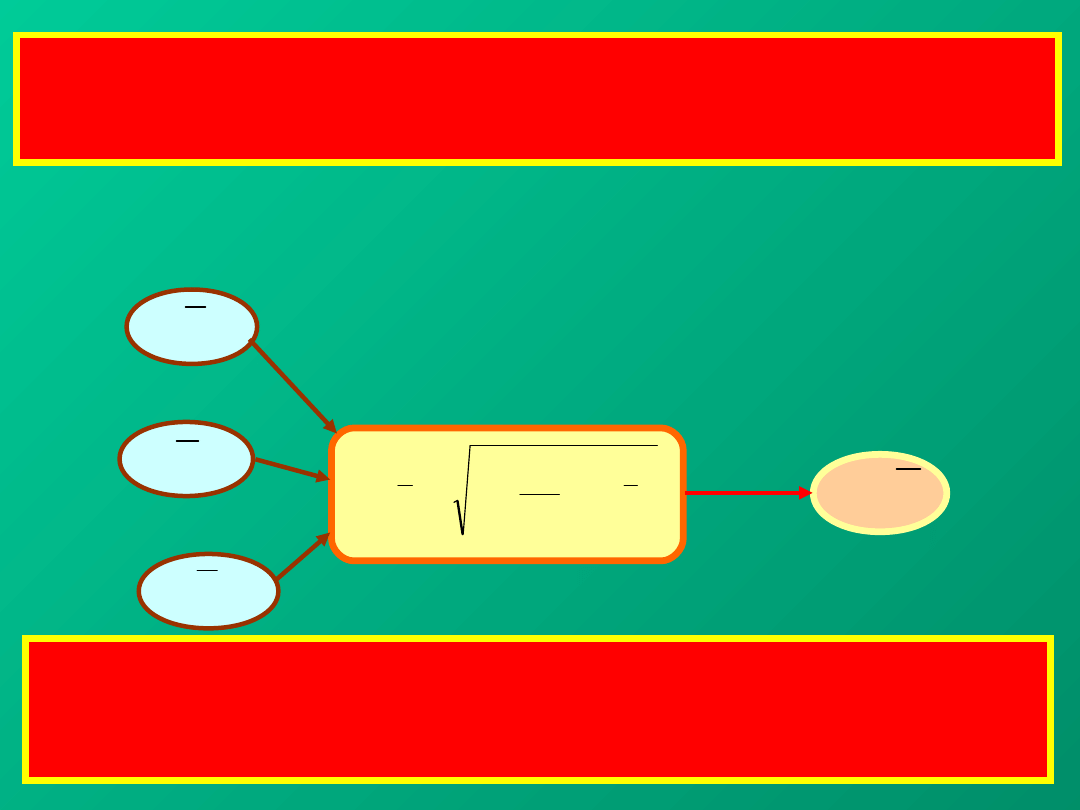
1.

Schemat przenoszenia wielkości wejściowych

2.

Niepewność y nazywa się złożoną niepewnością

standardową (ang. combined standard uncertainty)























K

1

i

i

2

2

i

c

)

x

(

u

x

f

)

y

(

u

)

x

(

u

1

)

x

(

u

2

)

x

(

u

K

)

y

(

u

c

Schemat przenoszenia niepewności

wielkości wejściowych

Metoda szacowania niepewności
wykorzystująca
inne metody niż statystyczne:

wcześniejsze doświadczenie
eksperymentatora
specyfikacja producenta odnośnie
używanego
w pomiarach przyrządu (klasa
przyrządu)
z kalibracji (wcześniej wykonanej)
badania na materiale odniesienia
(chemia
analityczna)

Najczęściej jeden lub dwa pomiary

METODA TYPU B

100

pomiaru

zakres

K

x

k







Parametry metrologiczne
aparatury:

Klasa przyrządu K

(dana przez

producenta)
Niepewność pomiaru wynikająca z
klasy
przyrządu kx:

Dla woltomierza klasy 0,2 na
zakresie 50 V
popełniamy „błąd” kx = 0,1 V

Rozdzielczość przyrządu :

Dla pomiarów długości:
1 mm dla linijki ; 0,1 mm dla
suwmiarki;
0,01 mm dla śruby
mikrometrycznej

Dla pomiarów temperatury:
0,1 °C dla termometru
lekarskiego;
10 °C dla termometru
„zaokiennego”

Dla mierników wychyłowych –
„odstęp”
pomiędzy kreskami (ew. połowa)

x

x

x

k

d

g











Rozdzielczość przyrządu:

Dla mierników analogowych - zmiana
ostatniej cyfry np. 5,23 V ( niepewność
0,01 V)

Niepewność wynikająca z rozdzielczości
aparatury 

d

Maksymalna (graniczna) niepewność
pomiaru szacowana metodą typu B
wynosi:

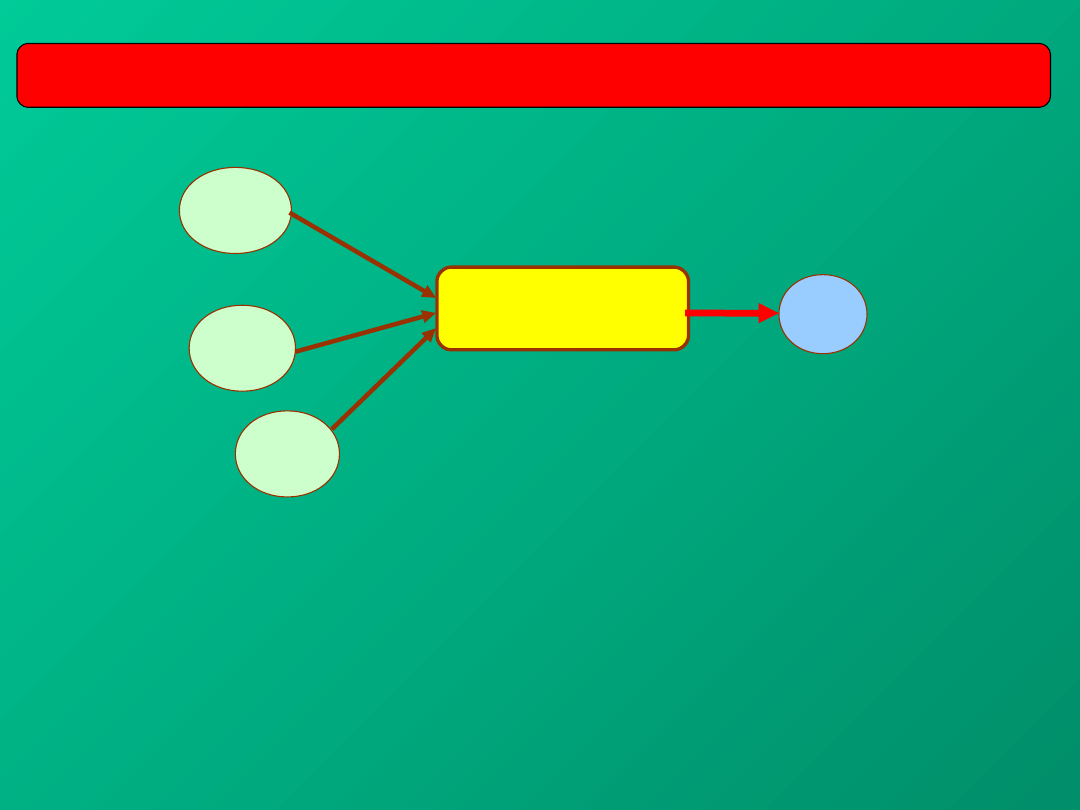
OCENA NIEPEWNOŚCI TYPU B W POMIARACH POŚREDNICH

x

1

y

x

2

x

K





K

2

1

x

,...,

x

,

x

f

y 

x

1,

x

2

, …,x

K

– wielkości pomiarów

jednokrotnych

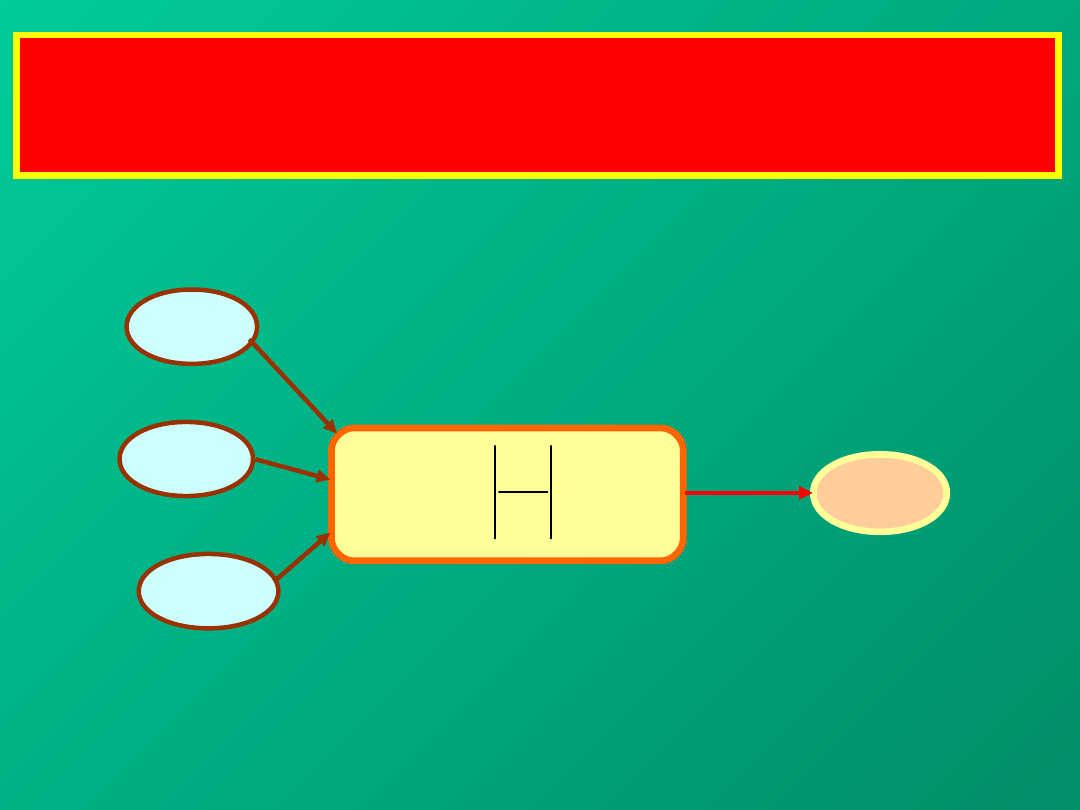
Maksymalna (graniczna) niepewność pomiaru 

g

(y)

może być oszacowana tzw. metodą różniczki zupełnej



g

x

1



g

x

2



g

x

K



g

(y)

i

g

K

1

i

i

g

x

x

f

y

















UWAGA: Metoda „różniczki zupełnej” prowadzi do
zawyżonych wyników niepewności (zwłaszcza dla K> 3)

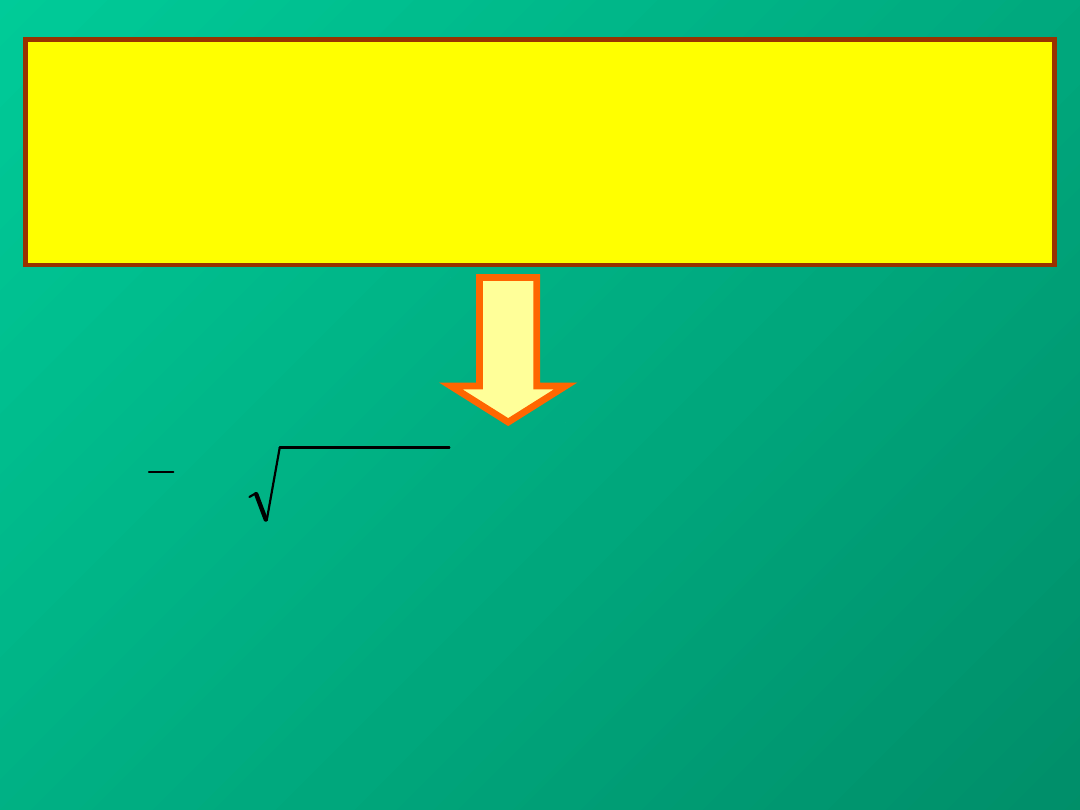
A w jaki sposób obliczyć niepewność wielkości, która
uzależniona jest od oddziaływań systematycznych i
przypadkowych ?

2

B

2

A

c

u

u

)

x

(

u





Standardowa
niepewność
całkowita

PAMIĘTAJ !!!

Do obliczania wielkości pośrednich i
niepewności używaj wielkości
niezaokrąglonych

Przedstawianie błędów

pomiarowych

i zaokrąglanie wyników

W ogólnym przypadku wynik pomiaru przedstawiamy
w postaci:

X

R

= X

M

± ΔX

gdzie:
X

R

- wartość rzeczywista wielkości mierzonej,

X

M

- wartość uzyskana w wyniku pomiaru,

ΔX - niepewność lub błąd pomiaru.
 
 Powyższy zapis oznacza, że:
- najlepszym przybliżeniem wartości mierzonej jest
według eksperymentatora liczba X

M

;

- z rozsądnym prawdopodobieństwem szukana
wartość znajduje się gdzieś pomiędzy X

m

- ΔX i X

m

+

ΔX.

Przedstawianie błędów

pomiarowych

i zaokrąglanie wyników II

Błąd pomiaru ΔX

jest wielkością oszacowaną

.

Nie ma więc sensu podawać wszystkich cyfr, które
otrzymujemy z obliczeń. Obliczone wartości X

m

i

ΔX podajemy zaokrąglone. Oznacza to, że
przybliżamy wartości otrzymane z obliczeń.
  

Cyframi znaczącymi

danej liczby różnej od zera

nazywamy wszystkie jej cyfry z wyjątkiem
występujących na początku zer.
Do cyfr znaczących zalicza się również zera końcowe,
jeśli są one wynikiem obliczeń, a nie zaokrągleń.
Oznacza to, że pierwsza liczba znacząca musi być
różna od zera, natomiast druga, trzecia i dalsze mogą
być zerami.

Przedstawianie błędów

pomiarowych

i zaokrąglanie wyników III

Przy zaokrąglaniu

wyniku pomiaru

stosowane są

powszechnie przyjęte zasady zaokrągleń : liczbę
kończącą się cyframi 0-4 zaokrąglamy w dół, a 5 - 9
w górę .
Oszacowane

błędy

zaokrąglamy zawsze w górę,

ponieważ w żadnym przypadku nie wolno pomniejszać
błędów. Zawsze lepiej podać zawyżoną wartość błędu
niż go niedoszacować .

Obliczenia wykonujemy zawsze z większą liczbą cyfr,
niż chcemy podać wynik. Zaokrągleń dokonujemy
dopiero po zakończeniu obliczeń.
Błędy pomiarów zaokrąglane są do pierwszej cyfry
znaczącej (wyjątek: 1, 2). Ostatnia cyfra znacząca w
każdym wyniku pomiaru powinna stać na tym samym
miejscu dziesiętnym, co błąd pomiaru.

DLACZEGO MUSIMY

DLACZEGO MUSIMY

ZAOKRĄGLAĆ BŁĘDY I WYNIKI

ZAOKRĄGLAĆ BŁĘDY I WYNIKI

KOŃCOWE

KOŃCOWE

:

:

PRZYKŁAD:

PRZYKŁAD:

Pewien

eksperymentator

Pewien

eksperymentator

wykonał

kilkaset

pomiarów

wykonał

kilkaset

pomiarów

grubości włosa i uzyskał wynik:

grubości włosa i uzyskał wynik:

100,543

100,543

6

6

787

787

2

2

341

341

1

1





5,800

5,800

2

2

341

341

7

7

894

894

4

4

3

3





m

m

rozmiar

rozmiar

atomu

atomu

rozmiar jądra

rozmiar jądra

rozmiar kwarka

rozmiar kwarka

Liczbę cyfr znaczących danego wyniku znajdujemy licząc z

lewa na prawo cyfry: od pierwszej cyfry niezerowej.

ZAPAMIĘTAJ POJĘCIE: CYFRA ZNACZĄCA!

PRZEPIS „KUCHENNY” ZAOKRĄGLANIA :

Do jednego miejsca znaczącego, gdy

na skutek zaokrąglenia błąd ten nie

zwiększy się nie więcej niż o 10%

0,12501 może być tylko 0,2 lub 0,13

Którą wybieramy?

Sprawdzamy:

(0,2 – 0,12501)/0,12501=0,5998 ( blisko 60%)

3. W zależności od wartości tej cyfry
postępujemy

według następujących zasad:



Jeśli jest to 0,1,2,3 lub 4 to zaokrąglamy w dół

tzn. gdyby wynik był 123,37489 to dostaniemy

123,37  0,13



Jeśli jest to 6,7,8 lub 9 to zaokrąglamy w

górę tzn. dla wyniku 123,37602 zostanie:

123,38 0,13

 Również zaokrąglamy w górę jeśli jest to 5, a

po niej następują jakiekolwiek cyfry różne od

zera
W sytuacji np. wyniku 123,3750000001
lub 123,3753210023
zaokrąglamy do

123,38  0,13

ZAPAMIĘTAJ !

ZAPAMIĘTAJ !

PRAWIDŁOWO ZAOKRĄGLONE:

PRAWIDŁOWO ZAOKRĄGLONE:

WARTOŚĆ WIELKOŚCI FIZYCZNEJ

WARTOŚĆ WIELKOŚCI FIZYCZNEJ

I JEJ NIEPEWNOŚĆ MAJĄ TAKĄ

I JEJ NIEPEWNOŚĆ MAJĄ TAKĄ

SAMĄ ILOŚĆ MIEJSC

SAMĄ ILOŚĆ MIEJSC

DZIESIĘTNYCH !

DZIESIĘTNYCH !

NIE !!!

R = 123, 35602   0,12501 

TAK !!!!

R = 123,36   0,13 

PRAWIDŁOWO: 36,35  0,04

0

C

2,5  0,4

kg

3,7110

-2

 0,02 10

-2

m

NIEPRAWIDŁOWO: 36,35 

0,04

2,51  0,4

kg

3,7110

-2



0,023 10

-2

m

12,34567 

0,22643 Bq

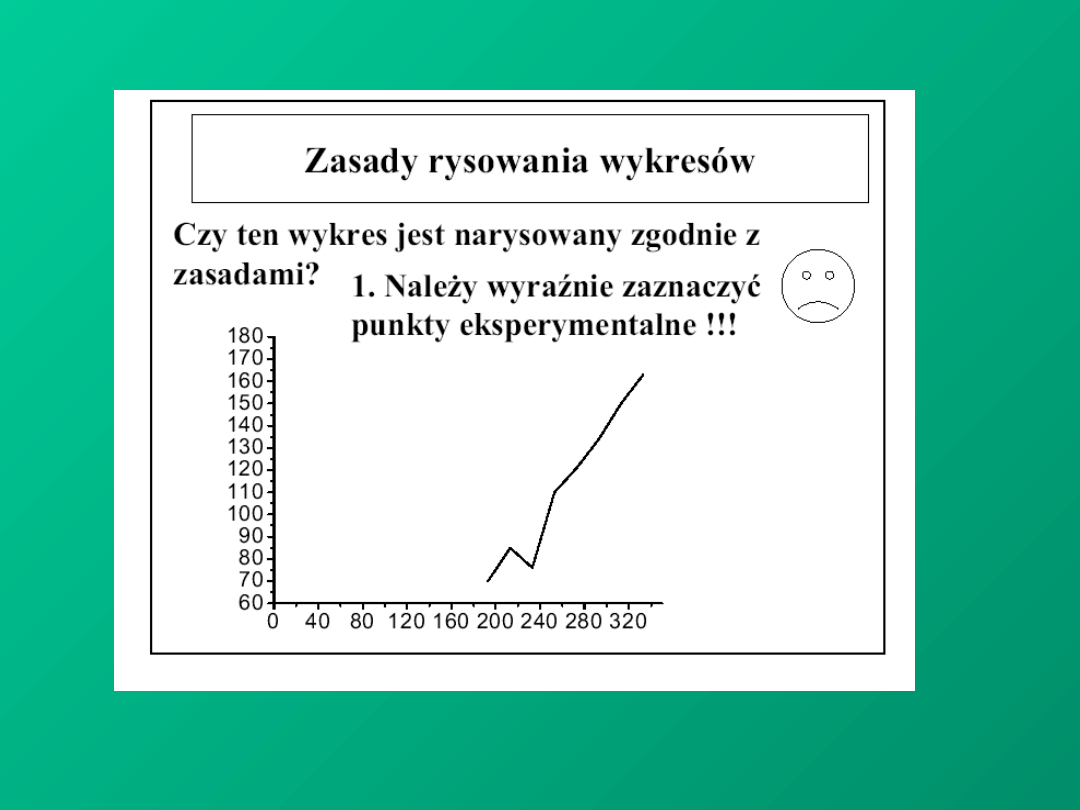
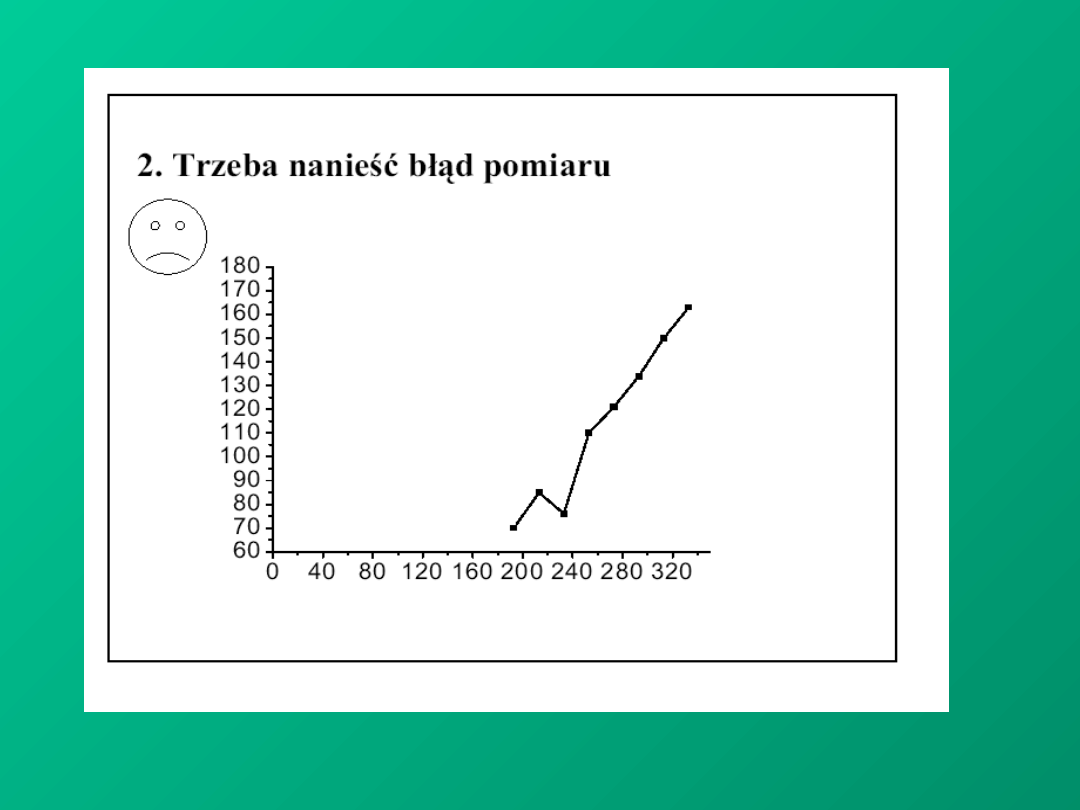
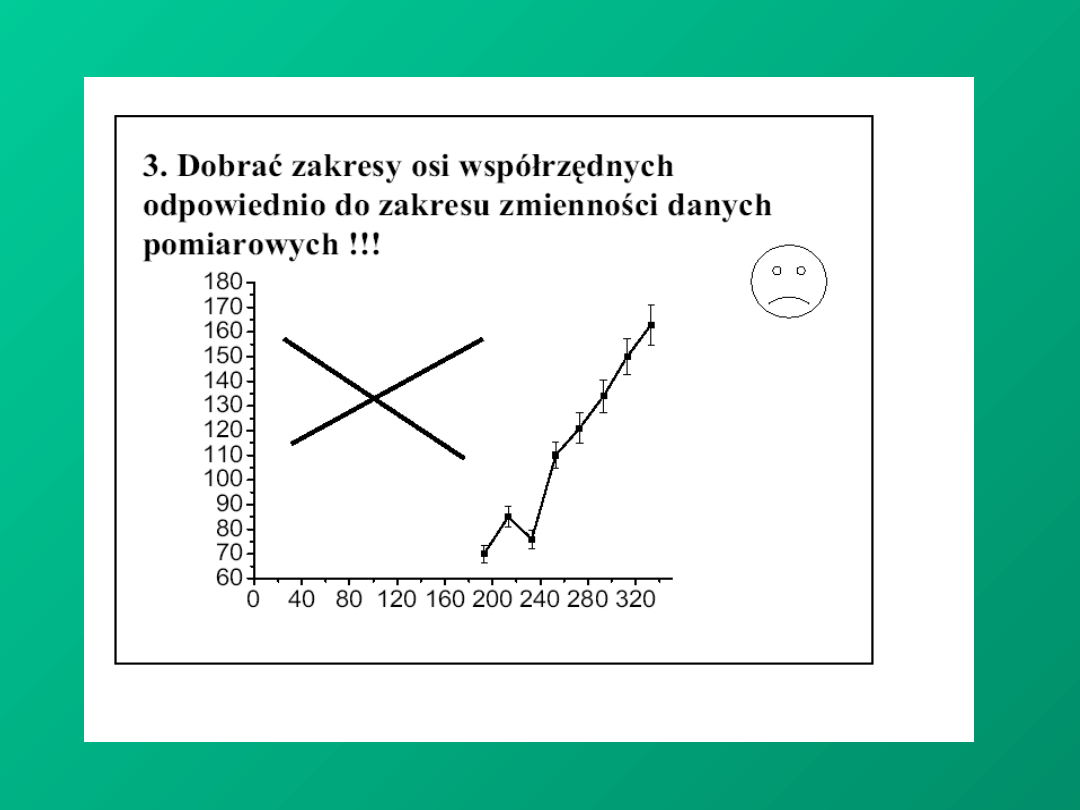
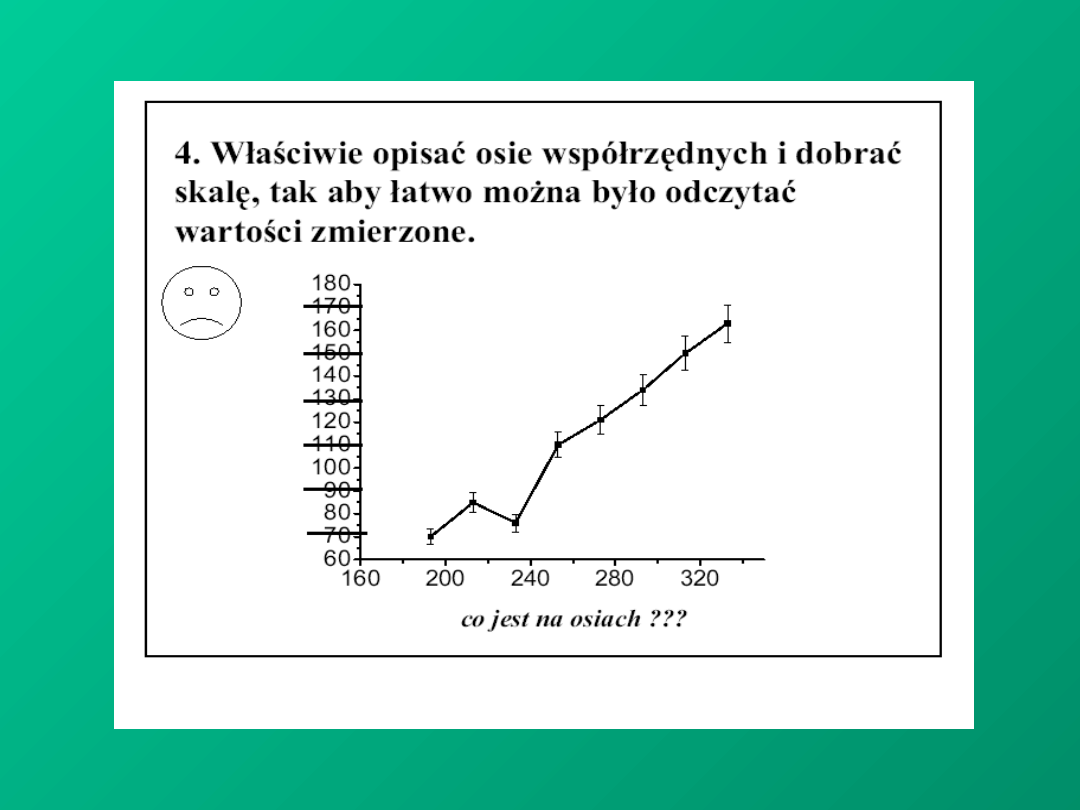
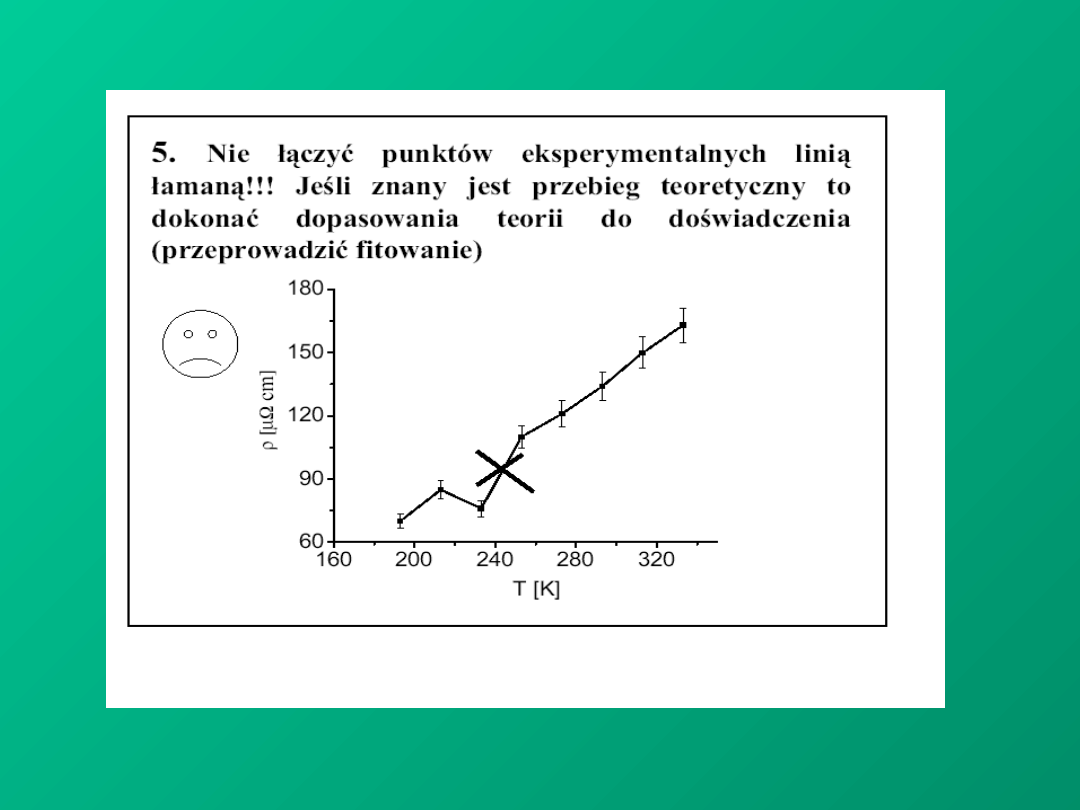
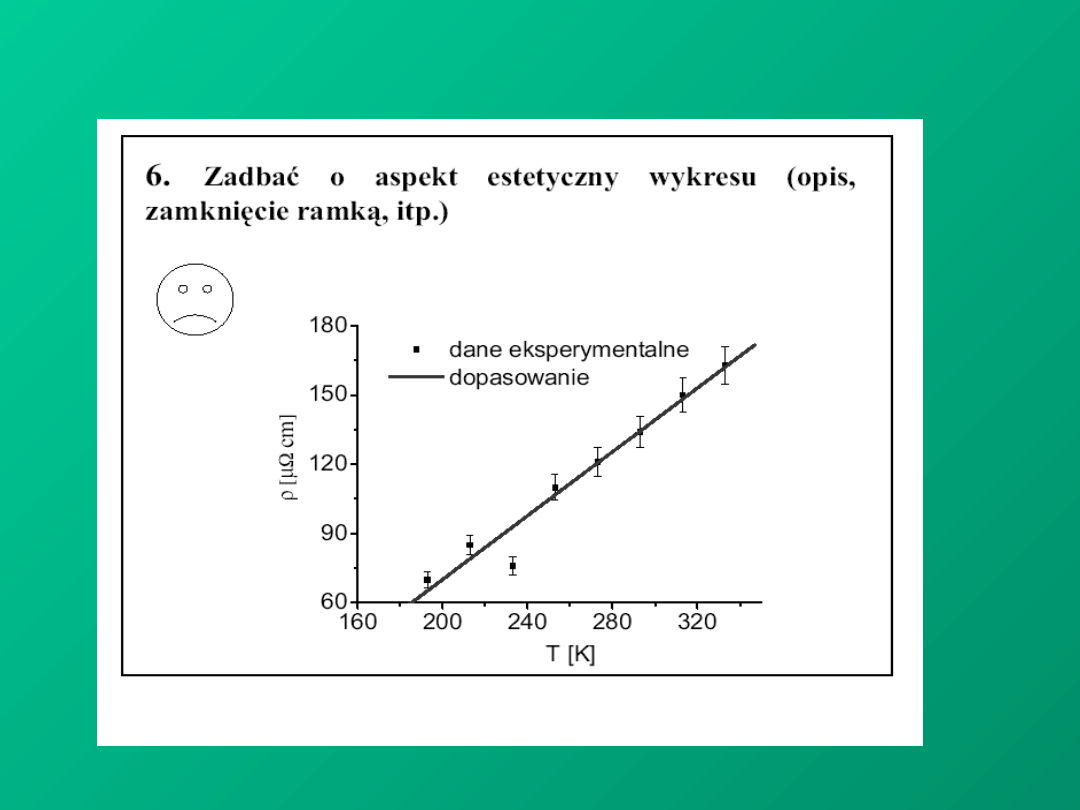
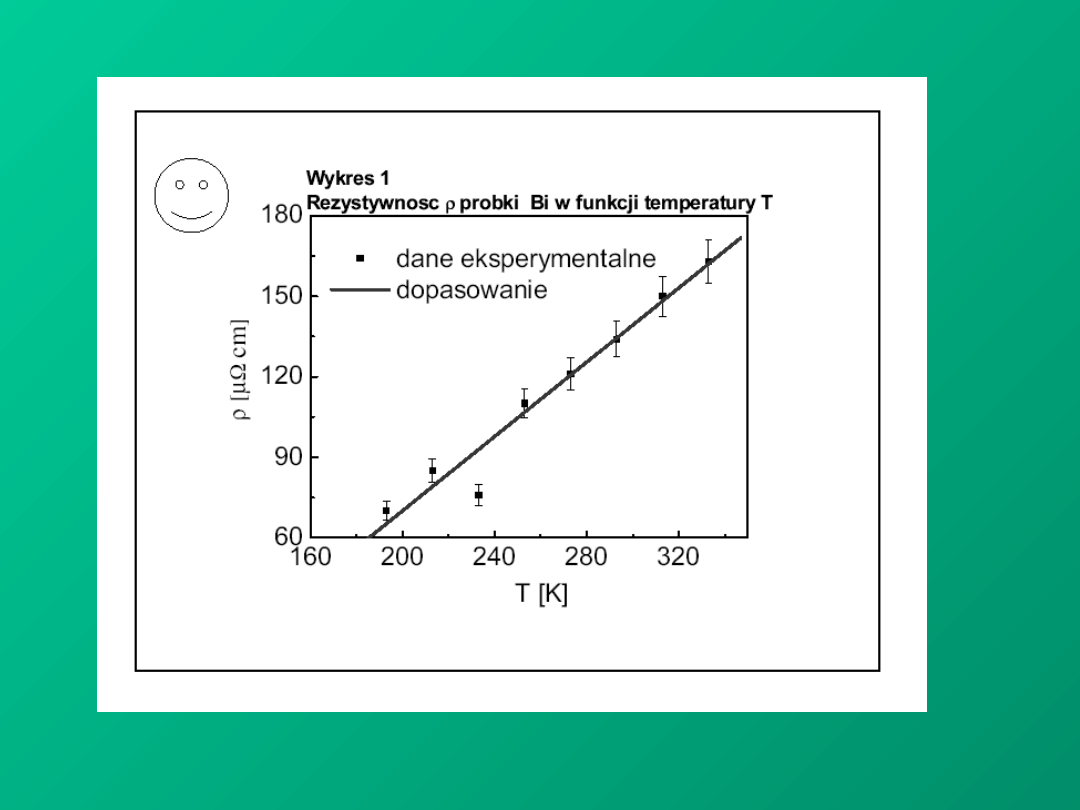
PRECYZJA

PRECYZJA

A DOKŁADNOŚĆ ?

A DOKŁADNOŚĆ ?

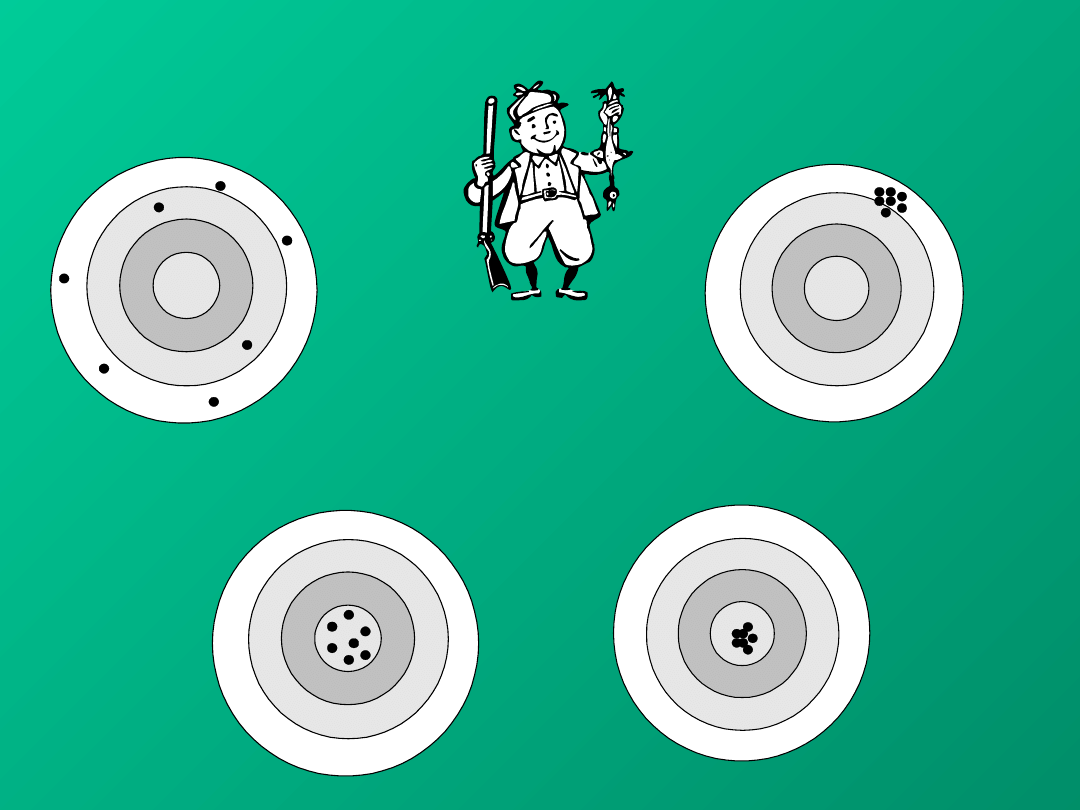
STRZELAMY DO TARCZY

Nieprecyzyjnie i niedokładnie

Precyzyjnie ale niedokładnie

Nieprecyzyjnie ale dokładnie

Precyzyjnie i dokładnie