3. Rozkłady wielowymiarowe.

3.1. Wstępne określenia.

Definicja 3.1.1. Wektor losowy
nazywamy dwuwymiarową zmienną losową, jeżeli jest określony jego rozkład, tzn. jeśli dla każdego prostokąta na płaszczyźnie
określone jest prawdopodobieństwo, że wektor losowy
zaznacza pewny punkt tego prostokąta.

Definicja 3.1.2. Dystrybuantą wektora losowego
nazywamy funkcję

.

Dla dwuwymiarowej zmiennej losowej
dyskretnej wystarczy podać prawdopodobieństwa

Definicja 3.1.3. W niektórych sytuacjach fizycznych jest pożyteczne określenie rozkłady zmiennych oddzielnie — rozkłady brzegowe

Definicja 3.1.4. Zmienne losowe
i
nazywamy niezależnymi jeśli

Definicja 3.1.5. Rozkład warunkowy zmiennej losowej
pod warunkiem, że
nazywamy wielkość

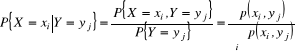
oraz

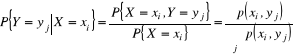
Dla dwuwymiarowej zmiennej losowej
ciągłej wystarczy podać prawdopodobieństwo w postaci

.

Gęstość brzegowa zmiennej losowej
określamy całką

oraz zmiennej losowej
wzorem

Gęstością warunkową nazywamy zmiennej losowej
pod warunkiem, że
nazywamy wielkość

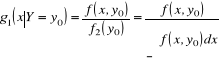
oraz zmiennej losowej
pod warunkiem, że

.

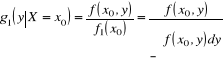
Zmienne losowe
i
niezależne jeśli

.

3.2. Funkcje zmiennych losowych.

Załóżmy, że pewną zależność funkcjonalną

.

Rozkład zmiennej losowej
określa się wzorem

w przypadku zmiennej skokowej oraz

Łatwo jest sprawdzić następujące wzory

,

więc gęstość zmiennej losowej
ma postać

,

Podobnie sprawdzamy, że

,

,

.

Jeśli zmienne losowe
i
niezależne, to

,

,

,

.

Wartość oczekiwania zmiennej losowej
określa się jako

w przypadku dyskretnym, lub

w przypadku ciągłym.

Mamy zawsze

,

a dla zmiennych losowych
i
niezależnych mamy też

.

Definicja 3.2.1. Ostatni wzór sugeruje, że różnica

,

zwana kowariancją, może być użyta jak miara zależności zmiennych losowych
i
.

Definicja 3.2.2. Wówczas współczynnik korelacji określamy wzorem

.

Współczynnik korelacji równia się zero
jeśli zmienne losowe
i
są niezależne. W tym przypadku

.

Z tego, że
nie wynika niezależność zmiennych losowych
i
, za wyjątkiem, gdy mają one rozkład normalny.

Ponadto mamy zawsze

i

wtedy i tylko wtedy, gdy
. Przy czym jeśli
, to
, oraz jeżeli
, to
.

Przykład 3.2.1. Rozpatrzymy
niezależnych powtórzeń pewnego doświadczenia, w wyniku którego mamy trzy możliwe zdarzenia
z prawdopodobieństwom
,
—
i
z prawdopodobieństwom
. Niech
i
oznaczają ilości zdarzeń
i
. Przy tym ilość realizacji zdarzenia
wynosić będzie
. Łączny rozkład
ma postać

,

gdzie
,
.

Rozkłady brzegowe maja postać dwumianową

,

.

Przykład 3.2.2. Zmienna losowa
ma dwuwymiarowy rozkład normalny z gęstością

.

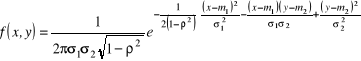
Drogą prostego całkowania przekonujemy się, że rozkłady brzegowe zmiennych losowych
i
są normalne o parametrach

.

Rozkład warunkowy zmiennej losowej
pod warunkiem, że
, ma postać

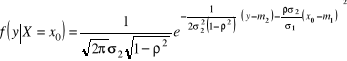
i jest rozkładem normalnym o parametrach

.

3.3. Centralne twierdzenie graniczne.

Jest to uogólnienie twierdzenia de Moivre'a - Laplace'a. Jeżeli zmienne losowe
są niezależne mają jednakowy rozkład o wartości przeciętnej
i odchyleniu standardowym
, to dla dowolnych
i
(
) zachodzi relacja

.

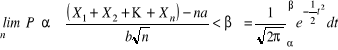
Przykład 3.3.1. Komputer dokonał milion operacji. W każdej operacji otrzymujemy wynik z nadmiarem
z prawdopodobieństwom
i niedomiarem
z prawdopodobieństwom
. Kolejny błędy są niezależne i sumują się. Jaki rozsądne granicy błędu możemy przypisać w wynikowi?

Nich
oznacza wielkość błędu w j-tej operacji. Mamy
, a zatem

,

,

więc
. Na mocy centralnego twierdzenia granicznego mamy

.

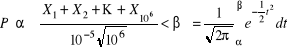
Jeśli
, a
, to prawa strona wynosi 0,99. Więc z prawdopodobieństwom 99% błąd sumy
zawarty jest w granicach
.

3.4. Elementy teorii informacji.

Pojęcia wstępne. Teorią informacji jest nauka, która bada podstawowe prawa związane z otrzymaniem, przekazaniem, obróbką i zachowaniem informacji.

Było by dobrze określić - co to jest informacja? Pojęcie podstawowe?

Do typowych zagadnień teorii informacji nalezą:

• określenie właściwych metod kodowania, które dają możliwość przekazania informacji za pomocą minimalnej liczby symboli;

• ocena możliwości linii transferu danych, kiedy wiadome są parametry źródła informacji, konkretnego kanału łączności oraz punktu dostarczania;

• określenie objętości pamięci urządzeń technicznych dla rozwiązywania konkretnych zagadnień;

• ocena parametrów wprowadzenia i wyprowadzenia informacji dla konkretnej realizacji technicznej;

• rozwiązywanie problemów małej czułości wszystkich węzłów związanych z otrzymaniem, przekazaniem, obróbką i zachowaniem informacji, co do zakłóceń różnego typu.

Rozwiązanie wymienionych zagadnień opiera się na dwóch podstawowych pojęciach - liczbie możliwych stanów układu fizycznego oraz ich prawdopodobieństwie.

Niech przez
odnotowany będzie pewny układ fizyczny oraz przez
jego różne stany fizyczne. Notację
wykorzystujemy dla tego, żeby zaznaczyć, że układ
przebywa w stanie
(
). Wówczas prawdopodobieństwo, że układ znajduje się w tym stanie notujemy jak
(
). Oczywistym jest, że spełniony jest warunek normowania, mianowicie
.

Popularnym sformułowaniem opisanej sytuacji układu fizycznego w różnych stanach
,
, jest w postaci tablicy standardowej

			...		...
			...		...

Definicja 3.4.1. Entropią układu fizycznego
nazywamy liczbę skalarna

.

Niestety, w teorii informacji, za zwykle przyjmuje się, że
, oraz mówi się, że entropia mierze się w dwójkowych jednostkach.

Właściwości entropii:

• 
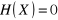
  , jeśli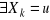
  (prawdopodobne), a wszystkie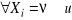
  (nieprawdopodobne) (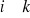
  ,
  );

• 
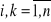
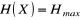
  , jeśli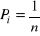
  ,
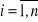
  (wszystkie stany jednakowe);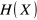

• 
  — rośnie przy zwiększeniu liczby stanów układu fizycznego;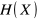

• 
  — wielkość addytywna.

Definicja 3.4.2. Wielkość fizyczna, w szczególności entropia, która będąc określoną dla układu
, gdzie przyjmuje wartość
, dla układu złożonego

jest sumą ich wartości

.

Zmiana podstawy logarytmu
oznacza mnożenie entropii przez stałą liczbę. Jeśli
, to za jednostkę pomiaru entropii przyjęto entropię układu fizycznego
,
, albo

ponieważ

.

Taka jednostka pomiaru w teorii informacji nazywa się „bit” (binary digit).

Entropia fizycznego układu ze stanami o równym prawdopodobieństwie
,
jest entropią układu
,
, tzn.

.

Entropia warunkowa. Rozważamy dwa układy fizyczne
i
. Oznaczymy przez
prawdopodobieństwo warunkowe tego, że układ
znajduje się w stanie
jeśli układ
jest w stanie
, tj.

.

Definicja 3.4.3. Entropię warunkową
układu
za warunku, że układ
znajduje się w stanie
określa wzór

,

gdzie

.

Definicja 3.4.4. Pełną entropią warunkową
układu
nazywamy

.

Definicja 3.4.5. Informacją cząstkową o tym, że układ
znajduje się w stanie
nazywamy wielkość

.

Definicja 3.4.6. Ilość informacji, która może być otrzymana o układzie fizycznym
przy obserwacji układu fizycznego
określamy wzorem

.

Z powyższych definicji wynika

.

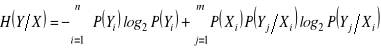
Zaznaczmy, że dla niezależnych układów fizycznych
i
mamy
. Wówczas
.

RACHUNEK PRAWDOPODOBIEŃSTWA