ANALIZA MATEMATYCZNA - WAŻNIEJSZE WZORY I DEFINICJE

Jeśli każdej liczbie
przyorządkujemy według pewnego przepisu liczbę
, to mówimy, że został określony ciąg o wyrazie ogólnym
. Liczbę przyporządkowaną 1 oznaczamy -
, 2 -
i tak dalej aż do
. Liczby te to wyrazy ciągu. Przykładowy wyraz ogólny ciągu:
. Przykładowo wyraz
. Ciąg
jest rosnący, gdy dla każdego n
. Monotonicznośc ciągu badamy więc obliczając
. Jeśli mamy sytuację
, to to będzie równe
. Kolejna rzecz to granice ciągów. Na poczatek należy oszacować, do czego dąży mianownik i licznik ułamka (bo z takimi zwykle mamy do czynienia). Zawsze
dąży do 0. Sytuacja
dąży do -1, bo ułamek dąży do 0. Z kolei w sytuacji
dąży
, bo ułamek dąży do 0 szybko, a trójka jest obojętna, bo mamy 2n dążące do nieskończoności.

W sytuacji trudniejszej, jak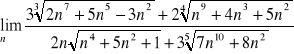
będziemy mieli
, a to będzie równe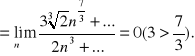
Widzimy, że tu nie ważne jest, co stoi przy n, ale ważna jest potęga. N wyciągnęliśmy wsprytnie z pierwiastka. Przy liczeniu należy pamiętać o regule, że
, oraz, że
dąży błyskawicznie do 0. Istnieje cos takiego, jak liczba e zwana stałą Eulera. Jest ona równa
. Jeśli mamy sytuację, że
, to to jest równe
. Z kolei jeśli
, to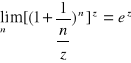
. Z kolei jeśli
, to wówczas
. Jeśli y przez n jest równe
, to wynik będzie e do 5/3 potęgi, bo liczy się to, co przy n. Jeśli mamy do czynienia z sytuacją przy liczeniu granic, że
, gdzie x i y to jakieś długie pierwiastki, to zwykle robimy tak:
. Przy obliczaniu granic z wykorzystaniem e jeśli mamy sytuację
, to w liczniku zmieniamy na 2n + 7 - 4, by był podobny do mianownika, a potem to będize równoważne
.
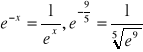
. Teraz szeregi liczbowe i zbieżność.

Szereg to wyrażenie
. Jeśli suma jest skończona, to szereg jest zbieżny, zaś jeśli nie, lub gdy nieistnieje, to rozbieżny. Przykład zbieżnego szeregu:
= 1. Do badania zbieżności służą dwa kryteria. Pierwsze to ilorazowe d'Lamberta, które przyjmuje postać:
, oraz pierwiastkowe Cauchiego, gdzie
. Jeśli wynik będzie mniejszy od 1, to szereg zbieżny, zaś gdy większy, to rozbieżny. Równy 1 nie roztrzyga zbieżności szeregu. Gdy przy badaniu w kryterium d'Lamberta mamy sytuację, że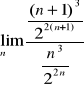
, to to jest równe
. Co do kryterium pierwiastkowego, to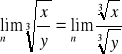
, oraz
dąży do 1, jak również
. Dodatkowo:
. Kolejna ciekawa sytuacja. Jeśli
, to to jest równe
.
.
dąży do 1. Jeśli mamy sumę od n równego 1 do nieskończoności, to cała granica dąży do nieskończoności. Możemy wyrzucić ułamek, jak i część całkowitą przed limes. Jeśli mamy na przykład
, to granica wyniesie 3/2, bo liczą się grube ryby, czyli iksy z największa potęgą i liczby przy nich stojące. Mając do czynienia z dytuacją, że x dąży do minus nieskończoności, najlepiej x zamienić na patametr, który dąży do nieskończoności i zmienić znak. Minus cosinus x razy cosinus x daje sinus x do kwadratu. Sinus z nieskończoności szacując daje 0. Sinus z x przez x daje szacunkowo 0 przez 0, a wynik: 1. 1 - cosinus do kwadratu równy jest sinusowi nieskończoności,
dąży do 2. Funkcję f(x) nazywamy ciągłą w punkcie
, gdy istnieje
, czyli gdy istnieją obie granice jednostronne
i
, które są sobie równe, oraz gdy
=
. Jeśli chcemy sprawdzić, czy jakąś funkcję da się rozszerzyć w sposób ciągły w danym punkcie, to do danej w ułamku funkcji należy podstawić w pierwszym przypadku x0 dodatnie, a w drugim ujemne i zobaczyc, czy są równe. Kolejna rzecz to pochodne. Oto najważniejsze wzory:

,
,
,
,
,
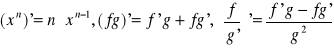
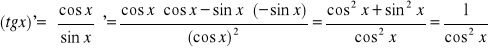
, (sinx)' = cos x,
, (cosx)' = - sinx,

Pochodne funkcji złożonych:

, gdzie t będzie parametrem.

Kolejny temat, to obliczanie granic funkcji korzystając z twierdzenia de Hospitala, które brzmi, że:

Stąd wniosek, że najpierw szacujemy, czy mamy 0/0 lub nieskończoność przez nieskończoność. Jeśli tak, to liczymy pochodną licznika i mianownika. Jeśli przy okazji tej reguły mamy do czynienia z granicą
, to wówczas zerem jest x do kwadratu, a nieskończonością logarytm z x. Wtedy należy podzielić to działanie na dwie części i w jednej podzielić x kwadrat przez odwrotnośc lnx, a w drugiej lnx podzielić przez odwrotność x do kwadratu. I każdą część liczymy osobno byleby nie było sytuacji oszacowanej 0 razy nieskończoność. Ostatnie zagadnienie jest związane ze zbadaniem monotoniczności i ekstremum funkcji. Załóżmy, że mamy jakąś funckję. Najpierw szacujemy jej dziedzinę, nastepnie wyznaczamy jej pochodną i sprawdzamy dla jakiej pochodnej funkcja jest równa zeru i dla jakiej jest większa od 0. Wyniki będą wyznaczały wszystkie dane.

---