
Teoria produkcji

Funkcja produkcji w okresie krótkim.
Prawo malejących przychodów
Produkcja
jest procesem łączenia zasobów w
celu wytworzenia towarów i usług. Sposób
łączenia ze sobą zasobów nazywa się
technologią.
Do prezentacji technologii w
sposób uproszczonego modelu służy
funkcja
produkcji
. Obrazuje ona matematyczną
zależność pomiędzy wielkością produkcji a
rozmiarem nakładów poszczególnych czynników
produkcji. Funkcja produkcji ma jednoznaczny
charakter przyczynowo skutkowy – przyczyną
procesu produkcji są określone nakłady czynników
produkcji ewentualnie ich zmiany, natomiast
efektem jest uzyskanie określonej wielkości
produkcji bądź też zmiana tej wielkości.

Funkcja produkcji w okresie krótkim.
Prawo malejących przychodów
Ogólna postać funkcji produkcji jest następująca:
Q = f (A,L,K,N)
gdzie:
A – współczynnik proporcjonalności:
L – nakłady pracy
K - nakłady kapitału
N – nakłady czynnika naturalnego

Funkcja produkcji w okresie krótkim.
Prawo malejących przychodów
Uproszczona analiza pozwala uwzględniać tylko jeden czynnik
produkcji, gdyż zakładamy, że pozostałe czynniki nie ulegają
zmianie, a więc nie mają one także wpływu na wielkość
produkcji.
Funkcję taką nazywamy jednoczynnikową funkcją
produkcji.
Przykładem funkcji jednoczynnikowej może być funkcja kapitału:
Q = f(k)
lub też funkcja siły roboczej
Q= f (L)
Krótki okres w ekonomii to taki, w którym nie występuje postęp
techniczny, czyli nie zmienia się technologia produkcji.
Zakładamy, że produkcja odbywa się przy pomocy tych samych
maszyn i urządzeń, na tym samym terenie i na tej samej
infrastrukturze technicznej.

Funkcja produkcji w okresie krótkim.
Prawo malejących przychodów
Do analizy przyjmiemy uproszczoną jednoczynnikową
funkcję
produkcji pracy. W krótkim okresie znacznie łatwiej jest
zmienić ilość zatrudnionych niż wielkość zasobów
kapitałowych.
Dodatkowe założenia to:
•
nie występuje czynnik naturalny
•
czynniki produkcji mogą być z sobą łączone w różnych
proporcjach,
•
produkt jest jednorodny (homogeniczny)
Proces produkcji przyczynia się do wytworzenia produktu
całkowitego (PC). Produkt przeciętny danego czynnika
produkcji otrzymujemy dzieląc wielkość produkcji
całkowitej
przez nakład czynnika zmiennego.

Funkcja produkcji w okresie krótkim.
Prawo malejących przychodów
W omawianym przypadku produkt przeciętny pracy otrzymujemy
jako iloraz produktu całkowitego i ilości zatrudnionych.
PPL = PC/L
gdzie:
• PPL oznacza wielkość produkcji przypadająca na jednego
pracownika, a L ilość zatrudnionych.
W analizie ekonomicznej kluczowe znaczenie mają wielkości
marginalne. Marginalny (krańcowy) produkt pracy informuje nas o
tym, o ile wzrośnie produkcja przy zatrudnieniu jednego
dodatkowego pracownika, czyli:
PMl = ΔPC/ΔL
Obie omawiane wielkości mają swoją interpretację geometryczną.
Produkt przeciętny jest miarą tangensa kąta linii łączącej
początek
układu współrzędnych z krzywą produktu całkowitego w danym
punkcie.
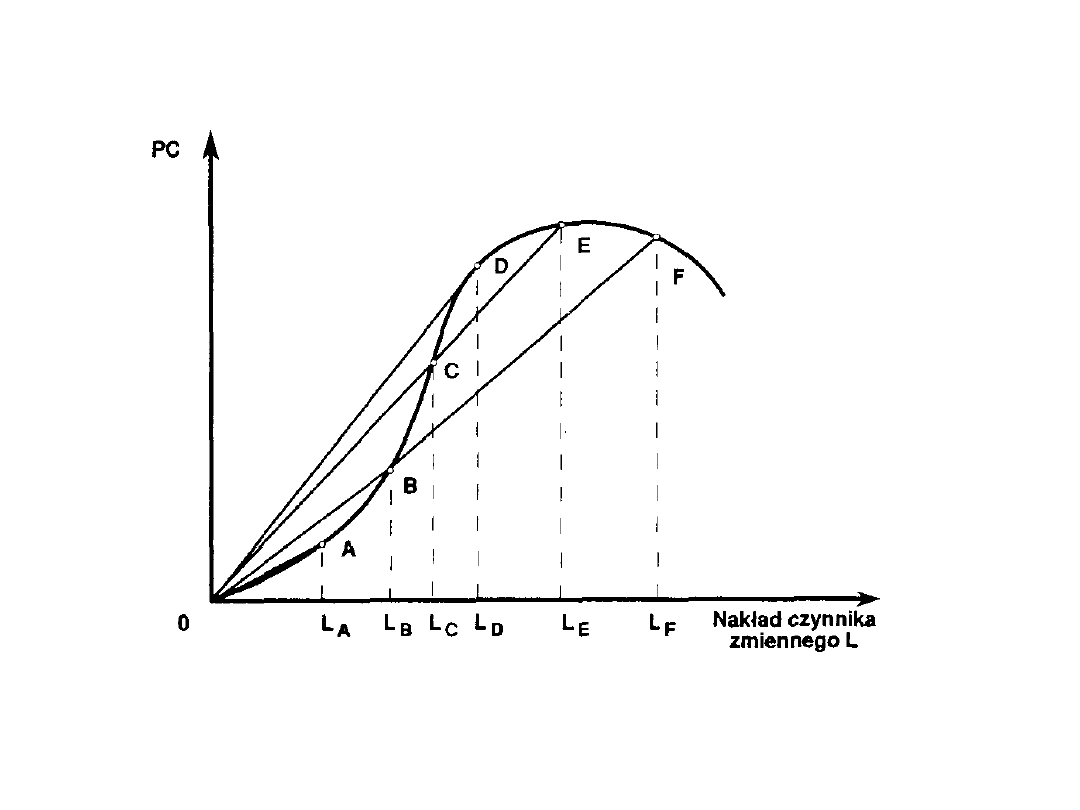
Geometryczne wyznaczanie zmian produktu
przeciętnego
Źródło: M.Rekowski, Mikroekonomia, Poznań, WSB, 1996, s.146.

Zwiększając nakład czynnika zmiennego od zera,
poprzez
LA do LF otrzymujemy kolejno punkty O, A, …F. Łącząc te
punkty z początkiem układu współrzędnych otrzymujemy
odpowiednie proste, będące miarą produktu przeciętnego
pracy.
Natomiast produkt marginalny pracy jest miarą tangensa
kąta stycznej do krzywej produktu całkowitego w danym
punkcie.
Na obu rysunkach można zauważyć zmienny przebieg
funkcji produktu całkowitego. Zwiększenie liczby
zatrudnionych powoduje, że początkowo wzrasta on więcej
niż proporcjonalnie, następnie pojawia się punkt przegięcia
funkcji i wzrost staje się mniej niż proporcjonalny, by
następnie zacząć maleć w wielkościach bezwzględnych.

Można to zilustrować następującym przykładem. Istnieje
pewien zasobów majątku produkcyjnego, np hala
wyposażona w zestaw maszyn. Początkowo każdy
zatrudniony będzie zwiększał produkcję więcej niż
proporcjonalnie ponieważ jest w stanie obsługiwać dwie
maszyny. Punkt przegięcia funkcji (C) oznacza sytuację, w
której liczba zatrudnionych jest na tyle wysoka, że każdy
nowozatrudniony jest przypisywany już tylko do jednej
maszyny. Natomiast w ekstremum każdemu robotnikowi
przypisana jest tylko jedna maszyna. Dalsze zwiększanie
zatrudnienia spowoduje, że część robotników nie będzie
miała stanowisk pracy. Nie mając zajęcia, będzie
absorbować uwagę pozostałych, obniżając ich efektywność
pracy.
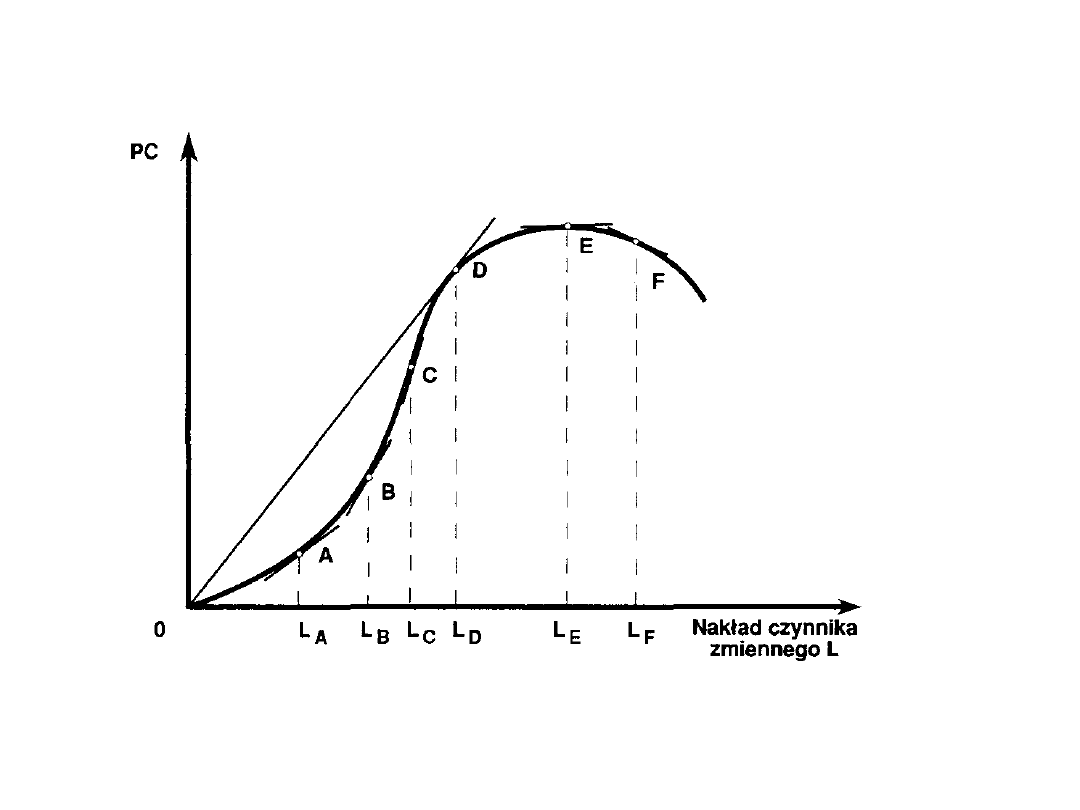
Geometryczne wyznaczanie zmian produktu
marginalnego
Źródło: M.Rekowski, Mikroekonomia, Poznań, WSB, 1996,
s.147.

Przykład ten jest ilustracją prawa malejących
przychodów.
Głosi ono, że przy zwiększaniu nakładów czynnika
zmiennego, ceteris paribus, osiąga się taki punkt, po
przekroczeniu którego, każda, dodatkowo zaangażowana
w proces produkcji jednostka czynnika zmiennego daje
coraz mniejsze przyrosty produkcji. Działanie tego prawa
widać wyraźnie na wykresie zmian produktu marginalnego.
W punkcie C produkt marginalny osiąga swoje maksimum
– nachylenie stycznej do krzywej produktu całkowitego
jest
największe. Od punktu C produkt marginalny zaczyna
maleć. W punkcie D zrównuje się z produktem
przeciętnym, który jednocześnie osiąga tutaj swoje
maksimum (styczna do krzywej produktu całkowitego
przechodzi przez początek układu współrzędnych)

W punkcie E produkt marginalny staje się zerowy, bowiem
styczna jest równoległa do osi odciętych.
Zależności pomiędzy produktem marginalnym a przeciętnym
ilustruje rys. 3. Punkt przegięcia funkcji jest tym razem punkt
A w
górnym wykresie. W tym punkcie produkt marginalny osiąga
swoje maksimum
. Natomiast produkt przeciętny nadal
wzrasta. W punkcie B zrównuje się malejącym produktem
marginalnym osiągając swoje maksimum. Poniżej punktu B
oba
produkty mają tendencję malejącą, z tym, że w produkcie
marginalnym jest ona silniejsza. Poniżej C produkt marginalny
staje się ujemny, produkt przeciętny dalej maleje.
W punkcie przegięcia funkcji druga pochodna jest równa
zero, co jest warunkiem koniecznym do osiągnięcia przez
pierwszą pochodna ekstremum. Produkt marginalny, przy
założeniu ciągłości wszystkich funkcji jest pierwszą
pochodną produktu całkowitego.
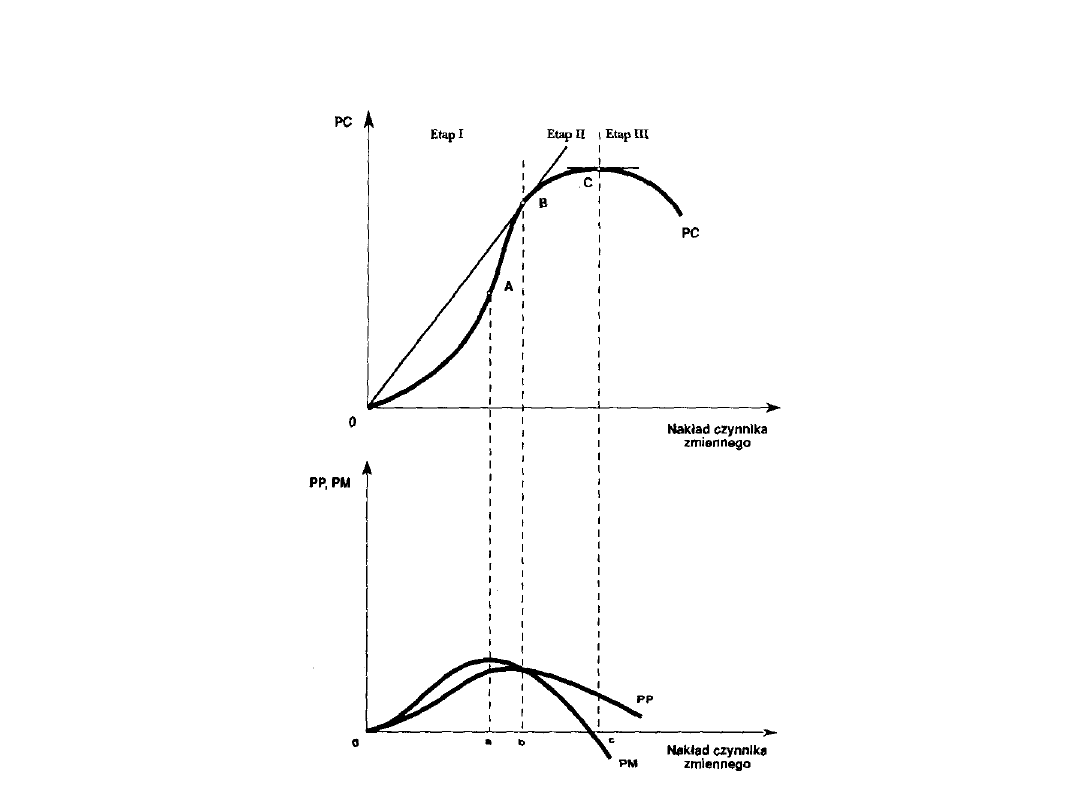
Krzywe produktu całkowitego, przeciętnego i
marginalnego
Źródło:
M.Rekowski,
Mikroekonomia,
Poznań, WSB,
1996, s.147.
Przykład Zbiory pszenicy w ciągu roku (w
tonach)
Nakłady pracy
(liczba
pracowników)
Np
Produkt
całkowity (w
tonach)
Pc
Produkt
przeciętny (w
tonach)
Pc/Np
Produkt
krańcowy (w
tonach)
ΔPc/ ΔNp
0
0
-
-
1
5
5
5
2
12
6
7
3
21
7
9
4
32
8
11
5
40
8
8
6
42
7
2
7
42
6
0
8
40
5
-2

Funkcja produkcji w długim okresie czasu.
Efekty skali produkcji.
Izokwanty produkcji i linia jednakowego
kosztu. Optimum produkcji

Specyfiką długiego okresu jest zmienność wszystkich
czynników produkcji. Oznacza to przykładowo zmianę
parku maszynowego, przebudowę hali produkcyjnej,
wymianę infrastruktury technicznej, czy też zatrudnienie
pracowników o wyższych kwalifikacjach. Przestaje działać
prawo malejącej produkcyjności krańcowej, gdyż odnosi się
ono tylko do takich sytuacji, w których przynajmniej jeden z
czynników jest stały. W długim okresie istotne stają się
efekty
skali, czyli zmiany wielkości produkcji pod wpływem
proporcjonalnych zmian wszystkich czynników produkcji.
Można tutaj wyróżnić:
1. Stałe efekty skali. W tym przypadku, gdy nakłady
wszystkich czynników produkcji wzrastają w tym samym
stopniu, produkt całkowity również rośnie w tym samym
stopniu. Na przykład, jeśli w gospodarstwie rolnym
zasoby pracy, kapitału i ziemi powiększą się dwukrotnie,
to plonowanie również zwiększy się dwukrotnie. Oznacza
to jednocześnie, że koszt przeciętny nie ulegnie zmianie.

2. Malejące efekty skali. Występują one wówczas,
gdy m-krotne powiększenie nakładów wszystkich
czynników produkcji spowoduje wzrost produktu
całkowitego mniej niż m razy, czyli m
k
razy przy
założeniu, że k<0. W tym przypadku dwukrotne
powiększenie zasobów w gospodarstwie rolnym
spowoduje mniej niż dwukrotny wzrost plonowania.
Malejące efekty skali oznaczają jednocześnie dla
gospodarstwa wzrost kosztów przeciętnych.
3. Rosnące efekty skali. Można o nich mówić
wówczas, gdy m-krotne powiększenie nakładów
wszystkich czynników produkcji spowoduje wzrost
produktu całkowitego m
k
razy, gdzie k>0. Oznacza
to, że dwukrotne powiększenie nakładów czynników
produkcji zwiększy plonowanie więcej niż
dwukrotnie, np. trzykrotnie
.
B.Klimczak, Mikroekonomia, Wrocław AE 2003, s.194 - 196.
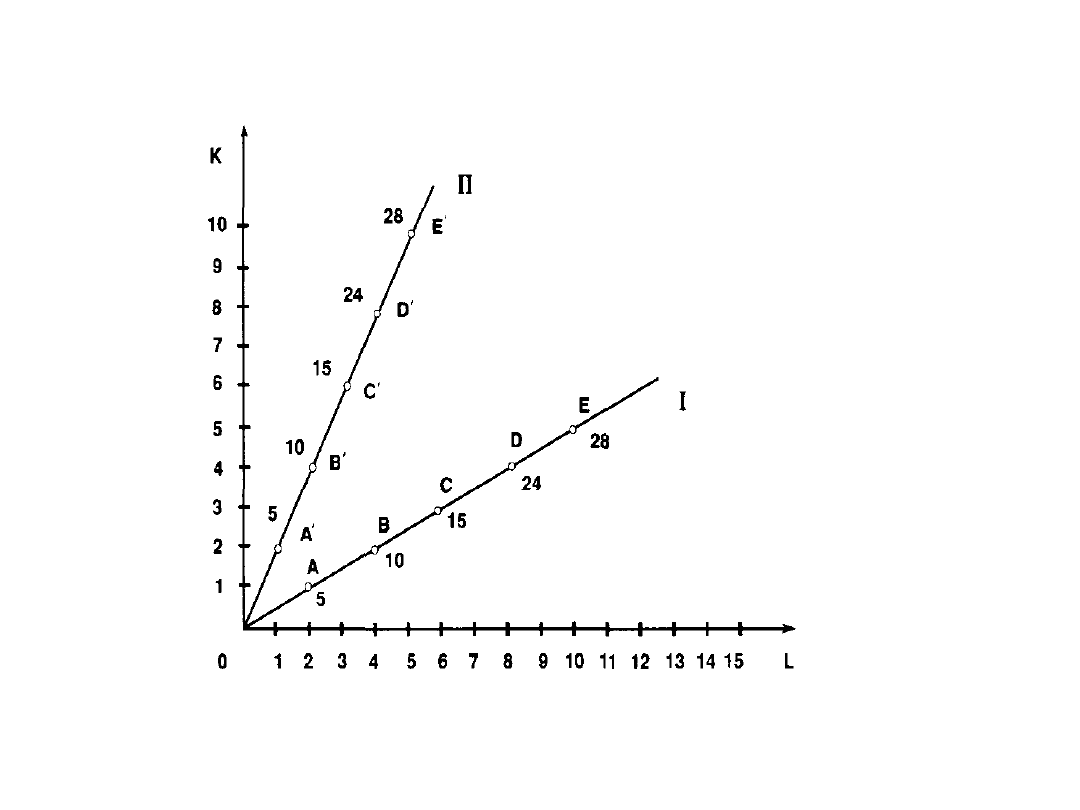
Rys. 4 Procesy produkcji I i II
Źródło: M.Rekowski, Mikroekonomia, Poznań WSB 1996,
s.150.

Istnieją dwie możliwości łączenia ze sobą
czynników produkcji:
w proporcjach stałych i
zmiennych
. Można to zaprezentować na
przykładzie funkcji dwuczynnikowej,
uwzględniającej pracę i kapitał z pominięciem
ziemi (czynnika naturalnego).
Rysunek 4 prezentuje dwa rodzaje technologii. W
obu stosunek pracy do kapitału jest stały. W
pierwszy procesie produkcji stosunek pracy do
kapitału wynosi ½ a w drugim 2. Zmiana
technologii pierwszej na drugą spowoduje
przesunięcie krzywej produkcji. Wielkość produktu
całkowitego nie ulegnie jednak, ceteris paribus,
dla tej samej wysokości nakładów zmianie.

Bardziej skomplikowana jest sytuacja w
przypadku produkcji o zmiennej proporcji
czynników.
Punktem wyjścia jest zdefiniowanie izokwanty
produkcji (krzywej jednakowego kosztu). Jest to
„geometryczne miejsce takich ilościowych
kombinacji czynników produkcji, które zapewniają
jednakowy poziom produkcji (produktu)
”.
A.Becla i in., Mikroekonomia, Wrocław, Wydawnictwo I-BiS,
2001, s.151.
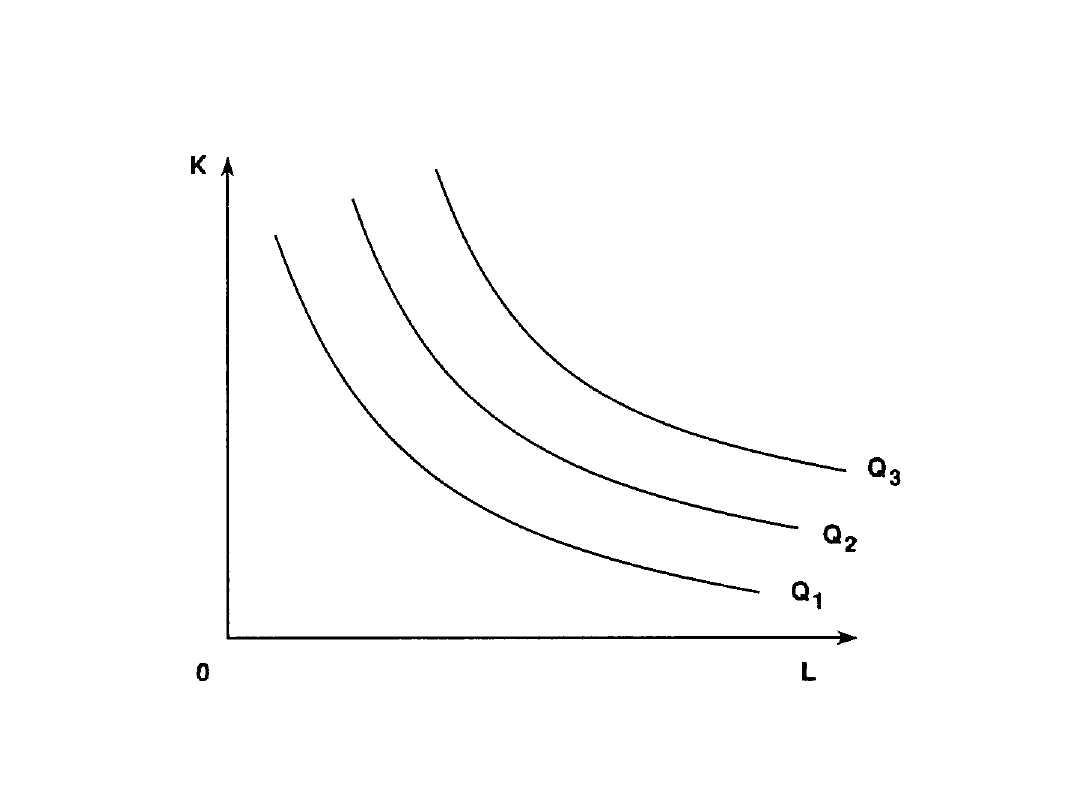
Rys. 5 Izokwanty produkcji
Źródło: M.Rekowski, Mikroekonomia, Poznań WSB 1996, s.153.
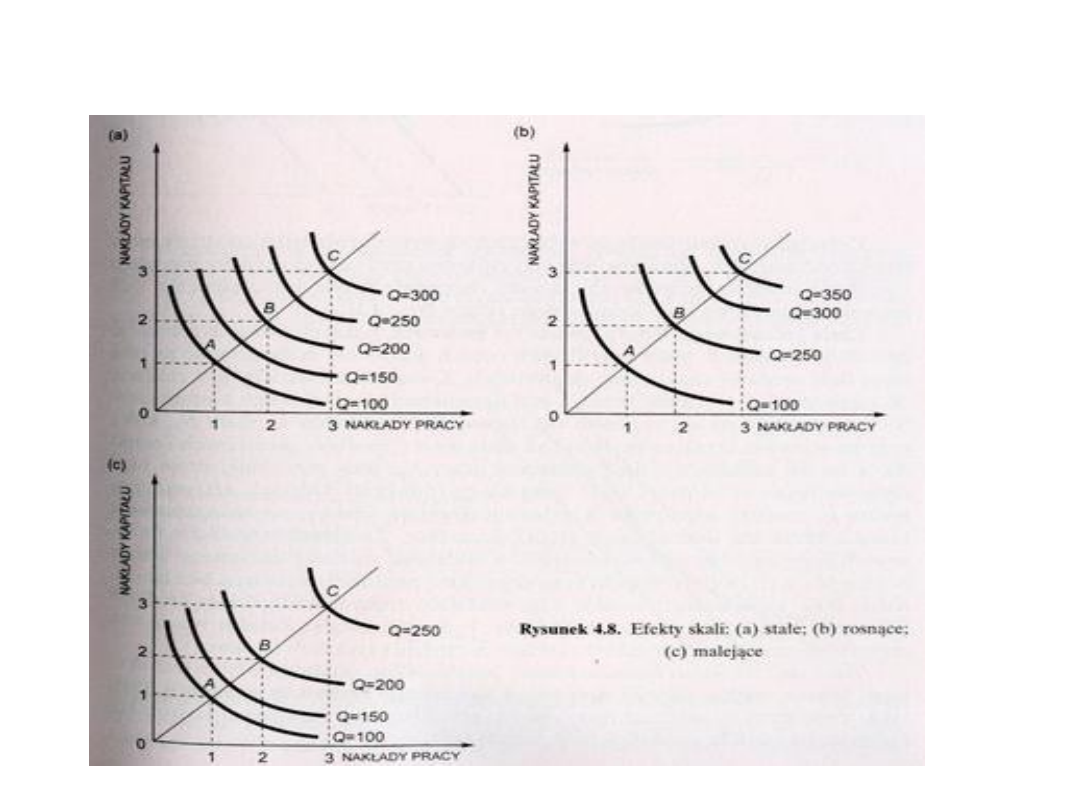
Izokwanty mogą być też wykorzystane do zilustrowana stałych,
rosnących i malejących efektów skali.

Przypadek pierwszy (a) odzwierciedla stale efekty
skali - produkcja rośnie proporcjonalnie do
wzrostu nakładów ze 100 do 150, a następnie
200, 250 i 300 jednostek (izokwanty są od siebie
jednakowo oddalone).
Przypadek drugi (b) pokazuje rosnące efekty skali
- produkcja rośnie więcej niż proporcjonalnie do
wzrostu nakładów: ze 100 aż do 350 jednostek
(odległości między izokwantami maleją).
Malejące efekty skali (c) przejawiają się w tym,
że produkcja rośnie mniej niż proporcjonalnie do
wzrostu nakładów: ze 100 do 150, 200 i 250
jednostek (odległości między izokwantami
rosną).

Każda kombinacja pracy i kapitału w ramach danej izokwanty
zapewnia jednakowy poziom produkcji.
Ponieważ izokwant, przy założeniu ciągłości funkcji
produkcji·,
jest nieskończenie wiele, tworzą one mapę izokwant.
Podobnie jak w przypadku krzywych obojętności, tak samo w
przypadku izokwant, przejście na wyższą krzywą oznacza
wyższy poziom produkcji.
Przesuwanie w ramach jednej izokwanty oznacza zmianę
proporcji praca – kapitał, a zatem i zmianę technologii.
Nachylenie izokwanty jest negatywne, czyli zmniejszenie
nakładów jednego czynnika produkcji powoduje zwiększenie
nakładów drugiego.
Matematycznie można to przedstawić w postaci:
ΔL * PML = - ΔK * PMK
gdzie:
PM i PMK to produkty krańcowe pracy i kapitału, a K i L, praca i kapitał

Stosunek w jakim można zastąpić jeden czynnik przez drugi
nosi nazwę krańcowej (marginalnej) technicznej stopy
substytucji. Po przekształceniu równania otrzymujemy:
KSTS = -ΔK/ΔL = PML/PMK
Analogiczne do krzywych obojętności, w przypadku
izokwant funkcjonuje prawo malejącej krańcowej stopy
technicznej substytucji. Zgodnie z nim w miarę zastępowania
czynna kapitału przez coraz to większa ilość czynnika pracy,
zmniejsza się ilość kapitału, którą można zastąpić dodatkową
jednostką pracy. Jest to zgodne z logiką. Jeżeli zmniejszamy
ilość maszyn a w to miejsce zatrudniamy ludzi, na przykład
na
budowie, wycofanie każdego kolejnego dźwigu, spowoduje
konieczność zatrudniania rosnącej ilości pracowników
Niezbędnych do wnoszenia materiałów budowlanych na
wysokości.

W praktyce całkowita substytucja nie jest możliwa. Nie da
się całkowicie zastąpić pracowników zajmujących się
wykończeniem wnętrz maszynami. Takie jest też założenie
funkcji produkcji. Wartość tej funkcji tylko od jednego
czynników, przy zerowym poziomie drugiego wynosi zero.
Aby określić optimum produkcji w warunkach zmiennych
proporcji czynników potrzebne jest także określenie
krzywej jednakowego kosztu (izokoszty). Producent działa
w warunkach własnego ograniczenia budżetowego,
a pracę oraz kapitał musi nabywać w warunkach
rynkowych.
Nakłady te są dla niego jednocześnie kosztami produkcji,
wpływającymi na efektywność firmy.

Wprowadzamy dwie nowe zmienne. Pierwsza to, w -
czyli
cena za jednostkę pracy oraz r - cena za usługę
jednostki
kapitału. Całkowite koszty zakupu czynników produkcji
oznaczamy jako TC.
Izokoszta przyjmuje wtedy postać
TC – wL + rK
Jest to linia prosta analogiczna do linii budżetowej.
Następnie na mapę izokwant nakładamy izokosztę.
Łączymy w ten sposób czynnik technologiczny z
czynnikiem kosztowym.
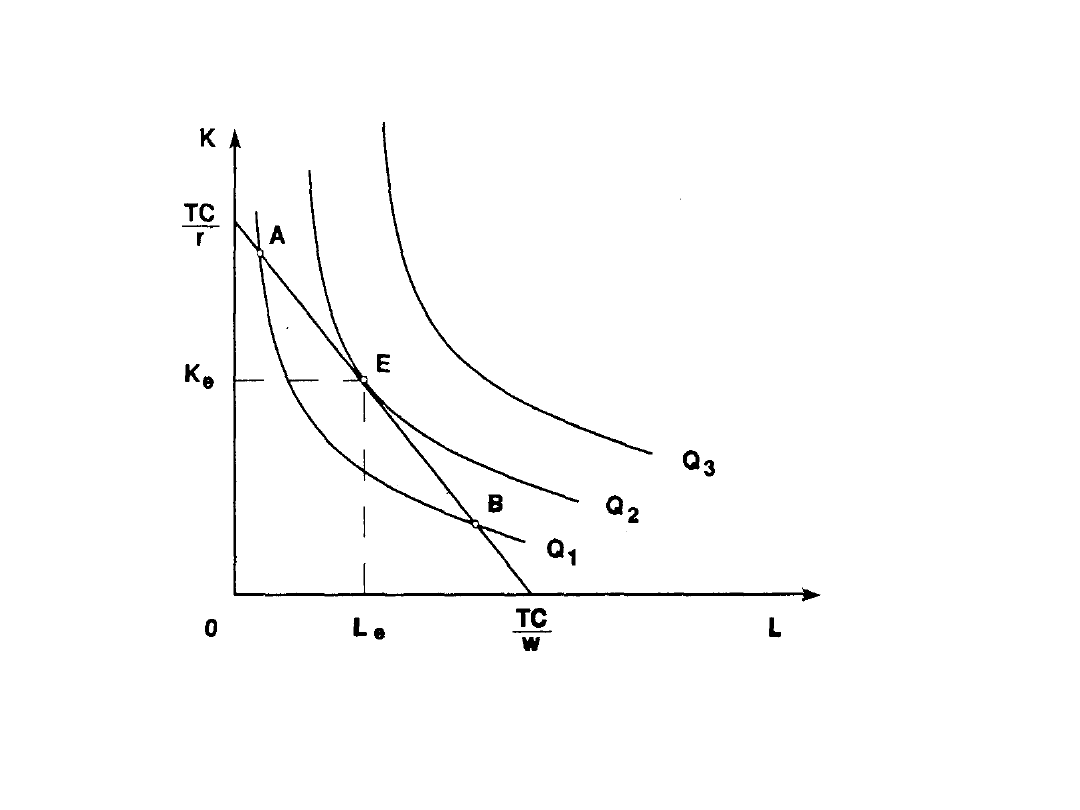
Optimum produkcji przedsiębiorstwa
Źródło: M.Rekowski, Mikroekonomia, Poznań WSB 1996, s.161.

Ponieważ izokwant jest nieskończenie wiele, zawsze znajdzie
się styczna z krzywa jednakowego kosztu. Będzie to najwyższa
izokwanta dostępna dla producenta przy jego ograniczeniu
kosztowym. Inaczej mówiąc, osiąga on maksymalną produkcję przy
danym ograniczeniu kosztowym.
W punkcie równowagi nachylenie stycznej do izokwanty produkcji
oraz izokoszty jest równe. Wypływa z tego zależność:
KSTS = PML/PMK = w/r
Przekształcając to równanie uzyskujemy rozwiązanie z punktu
widzenia zasady najmniejszego kosztu.
PML/w = PMK/r
W punkcie równowagi wyrównuje się stosunek krańcowego
produktu pracy do ceny pracy ze stosunkiem krańcowego produktu
kapitału do ceny kapitału.
Interpretować to można jako wyrównywanie się krańcowych
użyteczności pieniądza przeznaczonych na zakup pracy i kapitału.
Ostatnia złotówka wydana na zakup kapitału daje taki sam przyrost
produkcji jak ostatnia złotówka wydana na zakup jednostki pracy
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
Wyszukiwarka
Podobne podstrony:
teoria produkcji, Ekonomia
Notatki do prezentacji teoria produkcji i kosztow
Teoria produkcji 2
Teoria produkcji slajdy
5 teoria produkcji ujecie neoklasyczne
Ściągi mikro, Ściąga wykład 9, Teoria produkcji- zajmuje się rzeczową stroną procesów wytwórczych, a
Teoria produkcji
4 Teoria przedsiębiorstwa i teoria produkcji notatki, ekonomia
mikroekonomia4-Teoria produkcji, Administracja, I ROK, Mikroekonomia
4 teoria produkcji
Teoria produkcji[1], MIKRO
W6 Teoria produkcji
teoria produkcji
teoria produkcji, 2 semestr WSB, Mikroekonomia
więcej podobnych podstron